Автор – Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.

Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.

Ответ: 11
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №15. Графы. Поиск количества путей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
На уроке рассмотрен материал для подготовки к ОГЭ по информатике, рассмотрены примеры того, как решать 9 задание. Дан теоретический материал по теме «Анализирование информации, представленной в виде схем и поиск количества путей».
Содержание:
- ОГЭ по информатике 9 задания объяснение
- Поиск количества путей
- 9 задание как решать
- Актуальное
- Тренировочные
9-е задание: «Анализирование информации, представленной в виде схем».
Уровень сложности — повышенный,
Максимальный балл — 1,
Примерное время выполнения — 4 минуты.
* до 2020 г — это было задание № 11 ОГЭ
Поиск количества путей
- Если в город R из города A можно добраться только из городов X, Y и Z, то количество различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть:
- где NR — это количество путей из вершины A в вершину R
- Число путей не бесконечно, исключением является только схема, в которой есть циклы – замкнутые пути.
- Часто подобные задания целесообразней решать с конца (рассмотрим пример ниже).
NR = NX + NY + NZ
9 задание как решать
-
Подробный видеоразбор по ОГЭ 9 задания:
- Рассмотрено 3 задачи. Перемотайте видеоурок на решение нужной задачи.
Актуальное
Решение задания 9.3. Демонстрационный вариант огэ по информатике 2022 г.:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город В?

✍ Решение:
-
✎ 1 способ (дерево):
- Поскольку нас интересуют пути, проходящие через город В, то вычеркнет те дороги, которые минуют город В:
- Как видим, таких дорог получилось две — Б->Д и А->Г. Учтем это при дальнейших расчетах.
- Решим задание с конца. Т.е. так как траектория поиска путей — от А до K, то мы будем рассматривать сначала город K.
- В город K можно попасть из трех городов — Д, E и Ж; запишем это так:

K = Д + Е + Ж
Д = В (Б -> Д не учитываем) Е = Д + В Ж = В + Г
К = Д + Е + Ж Д = В Е = Д + В Ж = В + Г ----- Б = А = 1 A = 1 В = Б + А Д = B Ж = B + Г Г = В (А - Г не учитываем) Теперь возвращаемся, подставляя найденные значения: ↑ В = Б + А = 2 Г = В = 2 Д = В = 2 Ж = B + Г = 2 + 2 = 4 Е = Д + В = 2 + 2 = 4
К = Д + Е + Ж = 2 + 4 + 4 = 10
✎ 2 способ (дерево):
К Д - Е - К -------------- Е - К Д - К Б - В - Е - К Ж - К Г - Ж - К А ---------------- Д - К Е - К В - Е - К Ж - К Г - Ж - К ---------------- Г - Ж - К
К Д - Е - К -------------- Е - К Д - К Б - В - Е - К Ж - К Г - Ж - К А ---------------- Д - К Е - К В - Е - К Ж - К Г - Ж - К ---------------- Г - Ж - К
Ответ: 10
Решение задания 9.4:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город Ж?

✍ Решение:
-
✎ 1 способ (с конца):
- Поскольку нас интересуют пути, проходящие через город Ж, то вычеркнем те дороги, которые минуют город Ж:
- Решим задание с конца. Т.е. так как траектория поиска путей — от А до K, то мы будем рассматривать сначала город K.
- В город K можно попасть из трех городов — И, E и Ж; запишем это так:

K = И + Ж
И = Ж Ж = Д + В + Е
К = И + Ж И = Ж Ж = Д + В + Е ----- Д = Б + В Е = В + Г В = Б + А + Г А = 1 Г = А = 1 Б = А = 1 Теперь возвращаемся, подставляя найденные значения: ↑ В = Б + А + Г = 1 + 1 + 1 = 3 Д = Б + В = 1 + 3 = 4 Е = В + Г = 3 + 1 = 4 Ж = Д + В + Е = 4 + 3 + 4 = 11 И = Ж = 11 К = И + Ж = 22
Ответ: 22
Тренировочные
Решение задания 9.1:
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город H?

Типовые задания для тренировки
✍ Решение:
- Решим задание с конца. Т.е. так как траектория поиска путей от А до Н, то мы будем рассматривать сначала город Н.
- В город Н можно попасть из трех городов — C, D и G; запишем это так:
H = C + D + G
C = D + A D = A + E G = D + E + F
Далее, рассмотрим каждый город, дойдя до первого — города А. Для него существует только одни путь. Также, для городов, выходящих только из города А, тоже существует только 1 путь. Таким образом имеем:
H = C + D + G C = D + A D = A + E G = D + E + F ----- D = Е + A A = 1 E = A + B F = B B = 1 Теперь возвращаемся, подставляя найденные значения: ↑ F = B = 1 E = A + B = 1 + 1 = 2 D = Е + A = 2 + 1 = 3 G = D + E + F = 3 + 2 + 1 = 6 D = A + E = 1 + 2 = 3 C = D + A = 3 + 1 = 4 H = C + D + G = 4 + 3 + 6 = 13
Ответ: 13
Решение задания 9.2:
На карту нанесены 4 города (A, B, C и D).
Известно, что:
между городами A и C — три дороги,
между городами C и B — две дороги,
между городами A и B — две дороги,
между городами C и D — две дороги,
между городами B и D — четыре дороги.
По каждой из этих дорог можно ехать в обе стороны.
Сколькими различными способами можно проехать из A в D, посещая каждый город не более одного раза?
Типовые задания для тренировки
✍ Решение:
- Построим все возможные ветви для движения из города A. Будем выполнять произведение количества дорог для каждой ветви, так как движение возможно в обе стороны:
A * B * C * D = 2 * 2 * 2 = 8 (A и B - две дороги, C и B - две дороги, C и D - две дороги) A * B * D = 2 * 4 = 8 (A и B - две дороги, B и D - четыре дороги) A * C * D = 3 * 2 = 6 (A и C - три дороги, C и D - две дороги) A * C * B * D = 3 * 2 * 4 = 24 (A и C - три дороги, C и B - две дороги, B и D - четыре дороги)
8 + 8 + 6 + 24 = 46
Ответ: 46
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение: Количество путей в пункт К складывается из количества путей в пункты И и З.
Т.к. нам неизвестно количество путей в пункты И и З, нам надо спуститься на уровень ниже и расписать из чего состоят эти пути:
Дальше всё делаем поэтому же принципу, пока не дойдем до начала путей.
Теперь мы можем рассчитать значения
Теперь полученные данные для наглядности перенесем на схему
Ответ: 36
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Простейшие задачи на графы
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
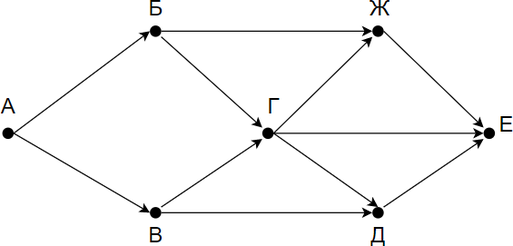
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем:
Г = Б + В
Д = Г + В
Ж = Б + Г
Е = Ж + Г + Д
Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
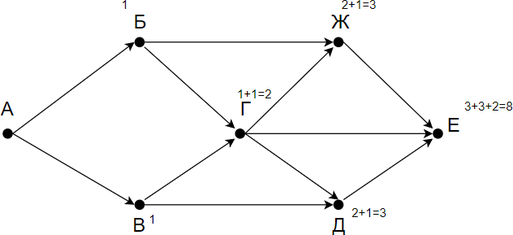
Ответ: 8
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
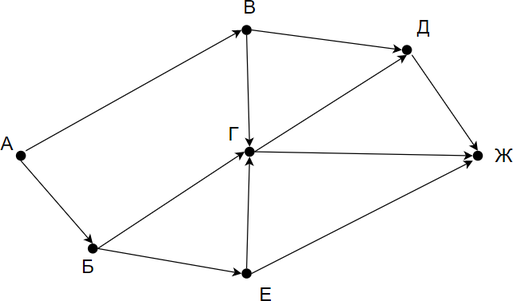
Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем:
Г = Б + В + Е
Д = В + Г
Ж = Д + Г + Е
Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
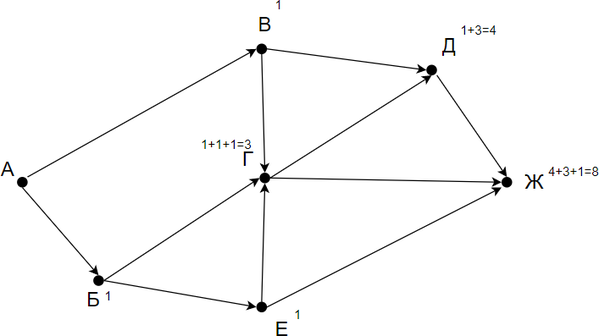
Ответ: 8
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
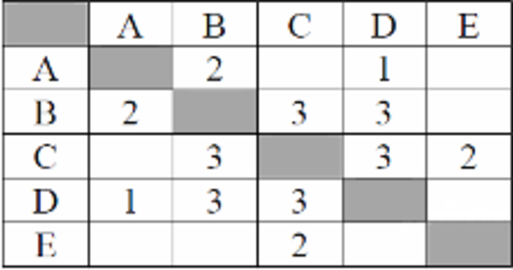
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Самый короткий путь: A—D—C—E. Длина маршрута 6 км.
Ответ: 6
Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
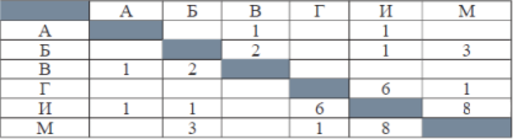
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.
Ответ: 1
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.
Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами. 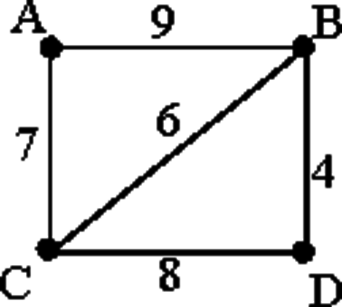
Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—D: длина маршрута 13 км.
A—C—D: длина маршрута 15 км.
A—B—C—D: длина маршрута 23 км.
A—C—B—D: длина маршрута 17 км.
Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.
Ответ: 13
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
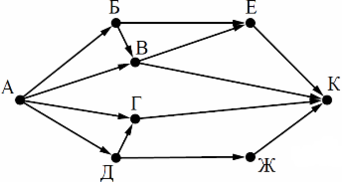
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NЖ = NД = 1;
NВ = NА + NБ = 1 + 1 = 2;
NГ = NА + NД = 1 + 1 = 2;
NД = NА = 1;
NБ = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8.
Ответ: 8
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
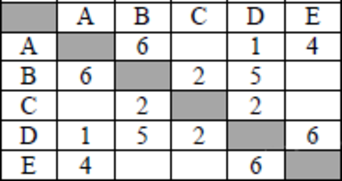
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Проанализируем некоторые возможные маршруты.
Маршрут B—D—E, длина 11 км.
Маршрут B—C—D—E, длина 10 км.
Маршрут B—С—D—A—E, длина 9 км.
Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км.
Ответ: 9

УСТАЛ? Просто отдохни
На чтение 23 мин Просмотров 27 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- ЕГЭ по информатике 2022 — Задание 13 (Лёгкое!)
- Как считать схему дорог по информатике
- 9 задание ОГЭ информатика
- ОГЭ по информатике 9 задания объяснение
- Поиск количества путей
- 9 задание как решать
- Задача №15. Графы. Поиск количества путей.
- Как считать схему дорог по информатике
ЕГЭ по информатике 2022 — Задание 13 (Лёгкое!)

Сегодня разберём одно из самых лёгких заданий из ЕГЭ по информатике — задание 13. Вы с похожим типом задач могли встретится на экзамене в 9 классе по информатике.
Приступим к практическим тренировкам решения 13 задания ЕГЭ по информатике 2022.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Решение:
Нужно подсчитать количество путей от начальной точки А до конечной точки К.
Будем использовать специальную технику для решения 13 задания из ЕГЭ по информатике 2022
Ставим 1 (единицу) возле начальной точки A. Далее, просматриваем ближайшие точки и анализируем, сколько входит стрелок в эти точки. В точку Б «перетекает» 1 из точки А. В точку Г тоже входит одна стрелка из точки А. Значит, тоже в эту точку «перетекает» 1 из А.
В точку В входят две стрелки. Значит, в точку В «втекает» сумма двух точек, из которых выходят эти стрелки! Получается 1 + 1 = 2.
И продолжаем в том же духе.

Число в конечной точке показывает правильный ответ!
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Ж?
Отличие этой задачи от предыдущей заключается в том, что пути, которые будем засчитывать, обязательно должны проходить через пункт Ж. Чтобы выполнить это условие, зачеркнём стрелку из пункта Е в пункт И. Так же зачеркнём стрелку из пункта З в пункт И. По этим стрелкам ходить нельзя, т.к. если мы по ним пойдём, не будет пройден пункт Ж.
Основная техника же решения будет такой же, как и в прошлой задаче.
Продолжаем отработку 13 задания ЕГЭ по информатике 2022
На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П

Сколько существует различных путей из пункта А в пункт П, не проходящих через пункт Е?
Такая же задача, как и предыдущие две, только здесь, при построении путей, мы не должны проходить через точку E.
Зачеркнём те дороги, которые поведут наши пути через пункт E.

Далее, применим старый метод, который использовали ранее.
Рассмотрим задачу, которая была на реальном экзамене по информатике в этом году.
Задача (ЕГЭ по информатике, 2020, Москва)
На рисунке — схема дорог, связывающих города А, Б, В, Г, Е, Ж, К, Л, М. По каждой дороге можно двигаться в одном направлении, указанном стрелкой. Какая наибольшая длина пути из А в М ?

Решение:
В этой задаче отличается вопрос от привычного нахождения количества путей. Здесь нужно найти наибольшую длину пути из начального пункта в конечный.
Возле начальной точки ставим число 0.

Смотрим сколько входит в узел стрелок. Выбираем стрелку, которая идёт из узла с наибольшим числом. При переходе по стрелочке добавляем 1.
Число, которое получится возле конечной точки и будет ответом. В этой задачке стрелок получилось 7, это и будет ответ.
Источник
Как считать схему дорог по информатике
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Начнем считать количество путей с конца маршрута – с города К. NK — количество различных путей из города А в город K, N — общее число путей.
В «K» можно приехать из Е, Ж, З или И, поэтому N = NК = NЕ + NЖ + N З + NИ (1)
Преобразуем первые вершины:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Начнем считать количество путей с конца маршрута – с города Ж. NX — количество различных путей из города А в город X, N — общее число путей.
В «Ж» можно приехать из Е, К, З или В, поэтому N = NЖ = NЕ + NК + N З + NВ (1)
N = NЖ = 3 + 8 + 3 + 5 + 1 + 2 + 1 + 1 = 24.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Начнем считать количество путей с конца маршрута – с города Ж. NX — количество различных путей из города А в город X, N — общее число путей.
В «Ж» можно приехать из Е, К, З, В или Б, поэтому N = NЖ = NЕ + NК + N З + NВ + NБ (1)
Преобразуем первые вершины с учетом значений вторых:
N = NЖ = 13 + 12 + 5 + 2 + 1 = 33
Источник
9 задание ОГЭ информатика
ОГЭ по информатике 9 задания объяснение
Поиск количества путей
- Если в город R из города A можно добраться только из городов X, Y и Z, то количество различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть:
9 задание как решать
- Подробный видеоразбор по ОГЭ 9 задания:
Решение задания 9.1:
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город H? 
- Решим задание с конца. Т.е. так как траектория поиска путей от А до Н, то мы будем рассматривать сначала город Н.
- В город Н можно попасть из трех городов — C, D и G; запишем это так:
- Теперь аналогично рассмотрим города C, D и G:
Далее, рассмотрим каждый город, дойдя до первого — города А. Для него существует только одни путь. Также, для городов, выходящих только из города А, тоже существует только 1 путь. Таким образом имеем:
Решение задания 9.2. Сборник Ушакова Д.М., 2018 г. ВАРИАНТ 2:
На карту нанесены 4 города (A, B, C и D).
Известно, что:
между городами A и C — три дороги,
между городами C и B — две дороги,
между городами A и B — две дороги,
между городами C и D — две дороги,
между городами B и D — четыре дороги.
По каждой из этих дорог можно ехать в обе стороны.
Сколькими различными способами можно проехать из A в D, посещая каждый город не более одного раза?
- Построим все возможные ветви для движения из города A. Будем выполнять произведение количества дорог для каждой ветви, так как движение возможно в обе стороны:
- Полученные результаты для каждого способа движения из города A в город D следует сложить:
Решение задания 9.3. Демонстрационный вариант огэ по информатике 2022 г.:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город В?

Поскольку нас интересуют пути, проходящие через город В, то вычеркнет те дороги, которые минуют город В:

Источник
Задача №15. Графы. Поиск количества путей.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.

Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.

Ответ: 11
Источник
Как считать схему дорог по информатике
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт В?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Е = Д = 1 (В не учитываем, поскольку путь не должен проходить через город В).
Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт Е?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
И = В + Г = 5 (Е не учитываем, поскольку путь не должен проходить через город Е).
Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город Е.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, проходящих через пункт И?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
К = И = 10. (Е не учитываем, поскольку путь должен проходить через И)
Примечание. Необходимо найти количество различных путей из города А в город Л, проходящих через город И.
Количество путей из пункта А в пункт Л, проходящих через пункт И, равно произведению количества путей из пункта А в пункт И В и количества путей из пункта И в пункт Л.
Найдем количество путей из пункта А в пункт И:
Из пункта И в пункт Л есть только один путь И — К — Л.
Тогда количество путей из пункта А в пункт Л, проходящих через пункт И, равно 10 · 1 = 10.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, проходящих через пункт Е?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
К = Е = 10. (И и В не учитываем, поскольку путь должен проходить через город Е).
Л = К + Е = 20. (Д и Ж не учитываем, поскольку путь должен проходить через город Е).
Примечание. Необходимо найти количество различных путей из города А в город Л, проходящих через город Е.
Количество путей из пункта А в пункт Л, проходящих через пункт Е, равно произведению количества путей из пункта А в пункт Е и количества путей из пункта Е в пункт Л.
Найдем количество путей из пункта А в пункт Е:
Найдем количество путей из пункта Е в пункт Л (при этом Е — исходный пункт):
Тогда количество путей из пункта А в пункт Л, проходящих через пункт Е, равно 10 · 2 = 20.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, не проходящих через пункт Е?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
И = Г = 3 (Е не учитываем, поскольку путь не должен проходить через город Е).
К = И = 3 (Е не учитываем, поскольку путь не должен проходить через город Е).
Л = Д + Ж + К = 3 + 3 + 3 = 9 (Е не учитываем, поскольку путь не должен проходить через город Е).
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Д?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Е = Д = 3 (В и Г не учитываем, поскольку путь должен проходить через город Д).
Примечание. Необходимо найти количество различных путей из города А в город К, проходящих через город Д.
Количество путей из города А в город К, проходящих через город Д, равно произведению количества путей из города А в город Д и количества путей из города Д в город К.
Найдем количество путей из города А в город Д:
Найдем количество путей из города Д в город К (при этом Д — исходный пункт):
Тогда количество путей из города А в город К, проходящих через город Д, равно 3 · 3 = 9.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Г?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Е = Г = 3 (В и Д не учитываем, поскольку путь должен проходить через город Г).
Примечание. Необходимо найти количество различных путей из города А в город К, проходящих через город Г.
Количество путей из города А в город К, проходящих через город Г, равно произведению количества путей из города А в город Г и количества путей из города Г в город К.
Найдем количество путей из города А в город Г:
Найдем количество путей из города Г в город К (при этом Г — исходный пункт):
Тогда количество путей из города А в город К, проходящих через город Г, равно 3 · 3 = 9.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город П, проходящих через город Е?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Ж = Е = 3. (В и Г не учитываем, поскольку в этих вершинах не проходим через Е).
Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город Е.
Заметим, что путь из города А в город П обязательно должен проходить через город Ж. По условию задачи путь должен также проходить через город Е. Тогда количество путей из города А в город П, проходящих через город Е, равно произведению количества путей из города А в город Е, количества путей из города Е в город Ж и количества путей из города Ж в город П.
Найдем количество путей из города А в город Е:
Из города Е в город Ж есть только один путь.
Найдем количество путей из города Ж в город П (при этом Ж — исходный пункт):
Тогда количество путей из города А в город П, проходящих через город Е, равно 3 · 1 · 7 = 21.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город П, проходящих через город В?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Ж = В = 3. (Е и Г не учитываем, поскольку в этих вершинах не проходим через В).
Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город В.
Заметим, что путь из города А в город П обязательно должен проходить через город Ж. По условию задачи путь должен также проходить через город В. Тогда количество путей из города А в город П, проходящих через город В, равно произведению количества путей из города А в город В, количества путей из города В в город Ж и количества путей из города Ж в город П.
Найдем количество путей из города А в город В:
Из города В в город Ж есть только один путь.
Найдем количество путей из города Ж в город П (при этом Ж — исходный пункт):
Тогда количество путей из города А в город П, проходящих через город В, равно 3 · 1 · 7 = 21.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город П, проходящих через город М?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Л = М = 17 (Ж и К не учитываем, поскольку путь должен проходить через М).
П = Л + М = 34 (К не учитываем, поскольку путь должен проходить через М).
Примечание. Необходимо найти количество различных путей из города А в город П, проходящих через город М.
Количество путей из города А в город П, проходящих через город М, равно произведению количества путей из города А в город М и количества путей из города М в город П.
Найдем количество путей из города А в город М:
Найдем количество путей из города М в город П (при этом М — исходный пункт):
Тогда количество путей из города А в город П, проходящих через город М, равно 17 · 2 = 34.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, не проходящих через пункт В?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Г = А = 1 (В не учитываем, поскольку путь не должен проходить через город В).
Д = Б = 1 (В не учитываем, поскольку путь не должен проходить через город В).
Е = Г + Д = 2 (В не учитываем, поскольку путь не должен проходить через город В).
Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, не проходящих через пункт В?
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х. При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
Г = А = 1 (В не учитываем, поскольку путь не должен проходить через город В).
Д = Б = 1 (В не учитываем, поскольку путь не должен проходить через город В).
Е = Г + Д = 2 (В не учитываем, поскольку путь не должен проходить через город В).
Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.
Источник
