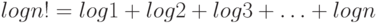Как найти количество различных чисел в массиве

Раз речь пошла о циклах, то я вам покажу, как надо писать циклы!:)

#include <iostream>

int main()
{
    int a[] = { 0, 1, 2, 3, 4, 5, 4, 3, 2, 1, 0 };
    const size_t N = sizeof(a) / sizeof(*a);

    size_t count = 0;
    for (size_t i = 0; i < N; i++)
    {
        size_t j = 0;
        while (j < i && a[j] != a[i]) ++j;

        count += j == i;
    }

    std::cout << count << std::endl;
}

Или более содержательная программа

#include <iostream>
#include <cstdlib>
#include <ctime>

int main()
{
    const size_t N = 20;
    int a[N];

    std::srand((unsigned int)std::time(nullptr));

    for ( int &x : a ) x = std::rand() % N;

    for (int x : a) std::cout << x << ' ';
    std::cout << std::endl;

    size_t count = 0;

    for (size_t i = 0; i < N; i++)
    {
        size_t j = 0;
        while (j < i && a[j] != a[i]) ++j;

        count += j == i;
    }

    std::cout << "There are " << count << " unique elements" << std::endl;
}

Вывод программы на консоль может выглядеть, к примеру, следующим образом

10 17 12 15 5 1 17 19 0 6 13 5 4 13 6 4 18 10 5 11
There are 13 unique elements

Вобщем я сделал программу, но она немного не правильно работает, если одинаковые числа идут подряд, то она их не выводит. Подскажите в чём дело? Вот полное условие: В массиве M(k) много совпадающих элементов. Найти количество различных элементов в нем. Здесь я сделал немного иначе: массив различных элементов выводится на экран, но смысл остался прежним. Задача сделать это с использованием циклов массивов и условий.

#include <locale>
#include <iostream>
#include <conio.h>
void main()
{
	setlocale(LC_ALL, "rus");
	using namespace std;
	int n, i, r=0, c=1;
	int *a = new int[99999];
	int	*b = new int[99999];
	int t, k=0;
	cout << "Введите размер массива" << endl;
	cin >> n;
	cout << "Введите размерность" << endl;
	cin >> t;
	cout << endl;
	srand((unsigned)time(NULL));
	cout << "Цикл" << endl;
	for (i = 0; i < n; i++)   // Создаём рандомный массив
	{
		a[i] = rand() % t;
		cout << a[i] << endl;
	}
	cout << endl;
	for (i = 0; i < n; i++)
	{
		for (int h=0; h < n+1; h++) {


			if (a[i] != a[h] && i!=h) {
				k++;
				if (k==i+1) {
					cout << a[i] << endl;
					break;
				}
			}
			if (a[i] == a[h] && i != h) {

				break;
			}
			

		}
		k = 0;
	}
	_getch();
}

Дан массив и целое число k, найти количество различных элементов в каждом подмассиве размера k.

Например,

Потренируйтесь в этой проблеме

Обратите внимание, что проблема конкретно нацелена подмассивы которые являются смежными (т. е. занимают последовательные позиции) и по своей сути поддерживают порядок элементов.

 
Наивным решением является рассмотрение каждого подмассива в заданном массиве и подсчет всех отдельных элементов в нем с помощью двух вложенных циклов, как показано ниже в C, Java и Python. Временная сложность этого подхода составляет O(n.k²), куда n размер ввода и k размер подмассива.

Мы знаем, что множество не хранит повторяющихся элементов. Мы можем воспользоваться этим фактом и вставить все элементы текущего подмассива в набор. Тогда размер набора будет равен количеству отдельных элементов. Это снижает временную сложность до O(n.k) но использует O(k) дополнительное пространство.

Алгоритм может быть реализован следующим образом на C++, Java и Python. Мы можем даже расширить решение для печати содержимого набора, как показано здесь.

Мы можем дополнительно уменьшить временную сложность до O(n) с помощью раздвижное окно техника. Идея состоит в том, чтобы сохранить частоту элементов в текущем окне на карте и отслеживать количество отдельных элементов в текущем окне (размером k). Код можно оптимизировать для получения количества элементов в любом окне, используя количество элементов в предыдущем окне, вставляя новый элемент в предыдущее окно справа и удаляя элемент слева.

Ниже приведена программа на C++, Java и Python, которая демонстрирует это:

4.3. Применения сортировки.

4.3.1.
Найти количество различных чисел среди элементов данного
массива. Число действий порядка . (Эта задача
уже была в
“Переменные, выражения, присваивания”
.)

Решение. Отсортировать числа, а затем посчитать
количество различных, просматривая элементы массива по
порядку.

4.3.2.
Дано n отрезков на прямой
( ). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками
(“максимальное число слоев”). Число действий – порядка .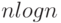

Решение. Упорядочим все левые и правые концы отрезков
вместе (при этом левый конец считается меньше правого
конца, расположенного в той же точке прямой). Далее
двигаемся слева направо, считая число слоев. Встреченный
левый конец увеличивает число слоев на 1, правый –
уменьшает. Отметим, что примыкающие друг к другу отрезки
обрабатываются правильно: сначала идет левый конец (правого
отрезка), а затем – правый (левого отрезка).

4.3.3.
Дано точек на плоскости. Указать -звенную
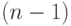
несамопересекающуюся незамкнутую ломаную, проходящую через
все эти точки. (Соседним отрезкам ломаной разрешается
лежать на одной прямой.) Число действий порядка .

Решение. Упорядочим точки по –координате, а при
равных –координатах – по –координате. В таком
порядке и можно проводить ломаную.

4.3.4.
Та же задача, если ломаная должна быть замкнутой.

Решение. Возьмем самую левую точку (то есть точку
с наименьшей -координатой) и проведем из нее лучи во
все остальные точки. Теперь упорядочим эти лучи снизу
вверх, а точки на одном луче упорядочим по расстоянию от
начала луча (это делается для всех лучей, кроме нижнего
и верхнего). Ломаная выходит из выбранной (самой левой)
точки по нижнему лучу, затем по всем остальным лучам
(в описанном порядке) и возвращается по верхнему лучу.

4.3.5.
Дано точек на плоскости. Построить их выпуклую
оболочку – минимальную выпуклую фигуру, их содержащую.
(Резиновое колечко, натянутое на вбитые в доску гвозди – их
выпуклая оболочка.) Число операций не более .

Указание.
Упорядочим точки – годится любой из порядков,
использованных в двух предыдущих задачах. Затем,
рассматривая точки по очереди, будем строить выпуклую
оболочку уже рассмотренных точек. (Для хранения выпуклой
оболочки полезно использовать дек, см.
“Типы данных”
.
Впрочем, при упорядочении точек по углам это излишне.)

4.4. Нижние оценки для числа сравнений при
сортировке

Пусть имеется различных по весу камней и весы, которые
позволяют за одно взвешивание определить, какой из двух
выбранных нами камней тяжелее. (В программистских терминах:
мы имеем доступ к функции тяжелее(i,j:1..n):boolean.)
Надо упорядочить камни по весу, сделав как можно меньше
взвешиваний (вызовов функции тяжелее ).

Разумеется, число взвешиваний зависит не только от
выбранного нами алгоритма, но и от того, как оказались
расположены камни. Сложностью алгоритма назовем число
взвешиваний при наихудшем расположении камней.

4.4.1.
Доказать, что сложность произвольного алгоритма сортировки камней не меньше ! (где ).

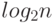
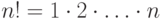
Решение. Пусть имеется алгоритм сложности не более .
Для каждого из ! возможных расположений камней
запротоколируем результаты взвешиваний (обращений к функции тяжелее ); их можно записать в виде последовательности
из не более чем нулей и единиц. Для единообразия
дополним последовательность нулями, чтобы ее длина стала
равной . Тем самым у нас имеется !
последовательностей из нулей и единиц. Все эти
последовательности разные – иначе наш алгоритм дал бы
одинаковые ответы для разных порядков (и один из ответов
был бы неправильным). Получаем, что 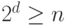! – что
и требовалось доказать.

Другой способ объяснить то же самое – рассмотреть дерево
вариантов, возникающее в ходе выполнения алгоритма,
и сослаться на то, что дерево высоты не может иметь
более листьев.

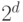
Несложно заметить, что 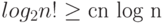при
подходящем , поскольку в сумме

вторая половина слагаемых не меньше каждое.

Тем самым любой алгоритм сортировки, использующий только
сравнения элементов массива и их перестановки, требует не
менее 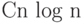действий, так что наши алгоритмы близки
к оптимальным. Однако алгоритм сортировки, использующий
другие операции, может действовать и быстрее. Вот один из
примеров.

4.4.2.
Имеется массив целых чисел , причем
все числа неотрицательны и не превосходят m.
Отсортировать этот массив; число действий порядка .

Решение. Для каждого числа от 0 до m подсчитываем,
сколько раз оно встречается в массиве. После этого исходный
массив можно стереть и заполнить заново в порядке
возрастания, используя сведения о кратности каждого числа.

Отметим, что этот алгоритм не переставляет числа в массиве,
как большинство других, а “записывает их туда заново”.

Есть также метод сортировки, в котором последовательно
проводится ряд “частичных сортировок” по отдельным
битам. Начнем с такой задачи.

4.4.3.
В массиве целых чисел переставить
элементы так, чтобы четные числа шли перед нечетными (не
меняя взаимный порядок в каждой из групп).

Решение. Сначала спишем (во вспомогательный массив) все
четные, а потом – все нечетные.

4.4.4.
Имеется массив из чисел от до , каждое из
которых мы будем рассматривать как -битовое слово из
нулей и единиц. Используя проверки ” -ый бит
равен ” и ” -ый бит
равен ” вместо
сравнений, отсортировать все числа за время
порядка .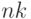

Решение. Отсортируем числа по последнему биту
(см. предыдущую задачу), затем по предпоследнему и так
далее. В результате они будут отсортированы. В самом деле,
индукцией по легко доказать, что после шагов
любые
два числа, отличающиеся только в последних битах, идут
в правильном порядке. (Вариант: после шагов -битовые концы чисел идут в правильном порядке.)

Аналогичный алгоритм может быть применен для -ичной
системы счисления вместо двоичной. При этом полезна такая
вспомогательная задача:

4.4.5.
Даны чисел и функция , принимающая (на них)
значения . Требуется переставить числа в таком
порядке, чтобы значения функции не убывали (сохраняя
порядок для чисел с равными значениями ). Число действий
порядка .

Указание.
Завести списков суммарной длины (как это сделать,
смотри в
“Типы данных”
о типах данных)
и помещать
в -ый список числа, для которых значение
функции
равно . Вариант: посчитать для всех , сколько
имеется
чисел с , после чего легко определить,
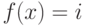
с какого
места нужно начинать размещать числа с .

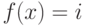
4.4.6.
Даны целых чисел в диапазоне от
до . Как
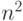
отсортировать их, сделав порядка действий?

Usually there is a compromise between speed, memory, and complexity for any algorithm. As others have said, the more information you know about your data, the faster you can make your algorithm. Say you had numbers between 1 and 100 (as an example), you would be able to really optimize the algorithm with this information.

I took the time to write up on example algorithm that is generic for any data set. This assumes that your set size is sufficiently small or that you have enough memory available. Basically the short version is to allocate an array with as many elements as the original two dimensional array. Then you loop over the original array and drop unique elements into boxes in the new array. Finally count the number of elements in the new array:

#include <stdio.h>      /* printf, scanf, puts, NULL */
#include <stdlib.h>     /* srand, rand */
#include <time.h>       /* time */
typedef int bool;
#define TRUE 1
#define FALSE 0

/* The actual algorithm function - finds the number of unique values */
int NumberUniqueValues(int **array, int width, int height)
{
  int i = 0, j = 0, k = 0, maxFilled = 0;
  bool wasFound = FALSE;
  int *newElements = malloc(sizeof(int) * width * height);

  for (i = 0; i < height; i++) {
    for (j = 0; j < width; j++) {
      wasFound = FALSE;
      for (k = 0; k < maxFilled; k++) {
        if (newElements[k] == array[i][j]) {
          wasFound = TRUE;
          break;
        }
      }

      if (!wasFound) newElements[maxFilled++] = array[i][j];
    }
  }

  /* Free space */
  free(newElements);
  return maxFilled;
}

int main ()
{
  /* variables */
  int i = 0, j = 0;
  int originalWidth = 10;
  int originalHeight = 10;

  /* initialize array */
  int **originalArray = (int **)malloc(originalHeight * sizeof(int*));
  for (i = 0; i < originalHeight; i++) {
    originalArray[i] = (int *)malloc(originalWidth * sizeof(int));
  }

  /* initialize random seed, then fill with random values */
  srand (time(NULL));
  for (i = 0; i < originalHeight; i++) {
    for (j = 0; j < originalWidth; j++) {
      originalArray[i][j] = rand() % 100;
    }
  }

  printf("Number unique values: %dn", NumberUniqueValues(originalArray, originalWidth, originalHeight));

  /* Free space */
  for (i = 0; i < originalHeight; i++) free(originalArray[i]);
  free(originalArray);

  return 0;
}

Again, this might not be the fastest algorithm for your case since I don’t know all the details but it will at least work. Best of luck!