Как найти количество ребер в многограннике

План урока:

Понятие многогранника

Теорема Эйлера

Призма

Типичные задачи на призмы

Понятие многогранника

Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.

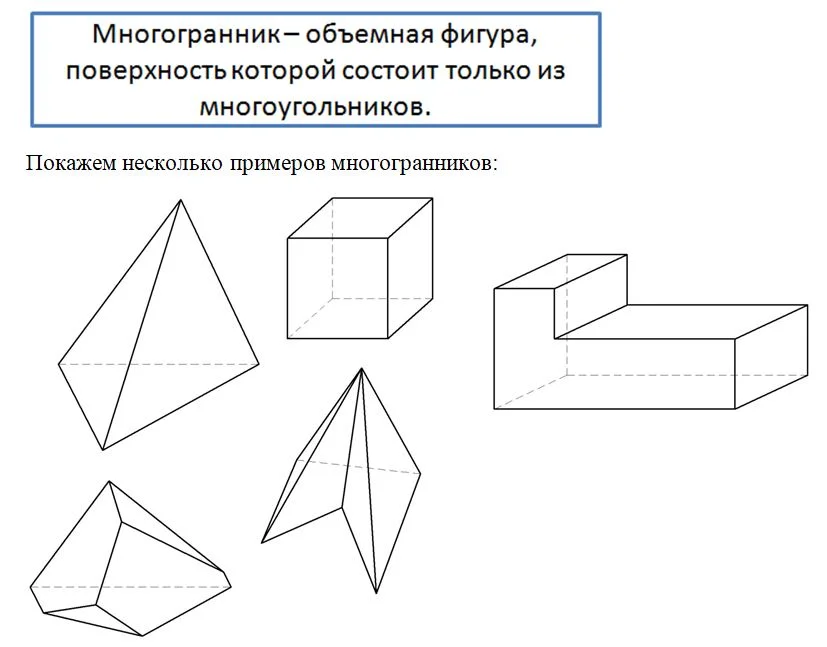
Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».

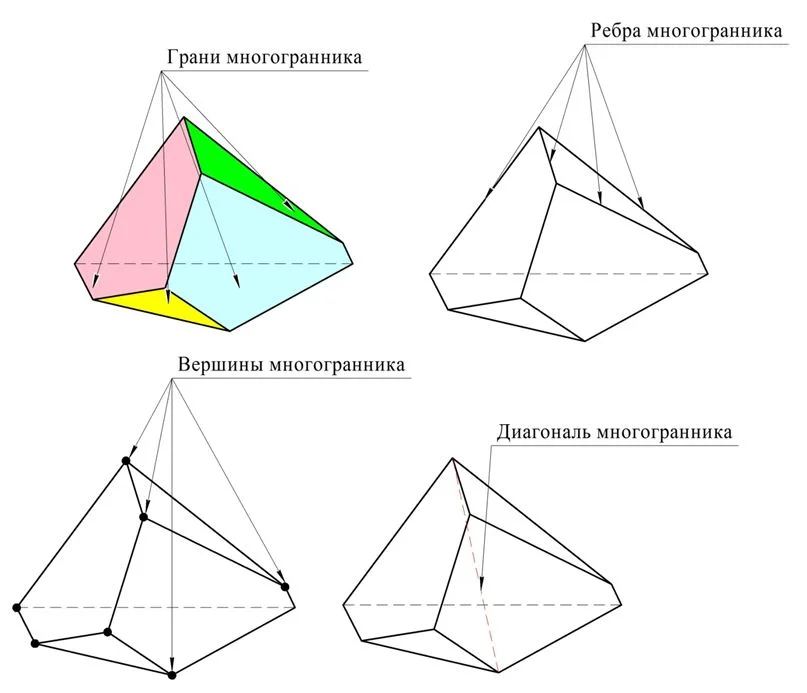
Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.

Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника. Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу.

Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:

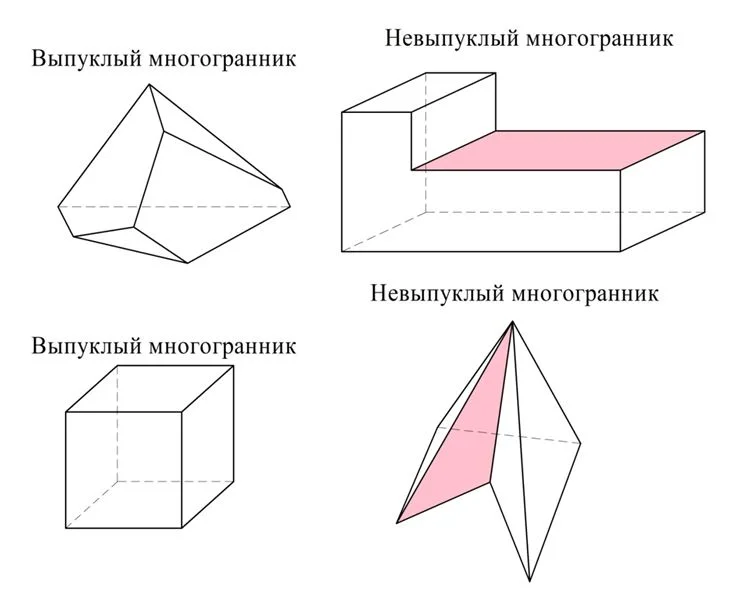
На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.

Теорема Эйлера

У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?

Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:

4 + 4 – 6 = 2

Если выполнить такие же действия для параллелепипеда, то снова получится двойка:

6 + 8 – 12 = 2

Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:

Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.

Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?

Решение. Запишем теорему Эйлера:

Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?

Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:

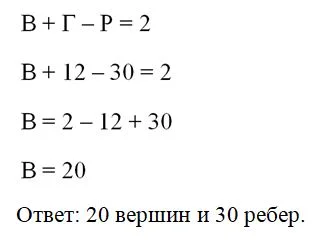
Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?

Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:

Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?

Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:

Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:

Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.

Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.

Призма

Пусть в некоторой плос-ти α есть n-угольник с вершинами А₁, А₂, А₃,…, А_n. Пусть в другой плос-ти β, которая параллельна α, есть равный ему многоуг-к В₁В₂В₃…В_n, причем отрезки А₁В₁, А₂В₂, А₃В₃…, А_nВ_n параллельны друг другу:

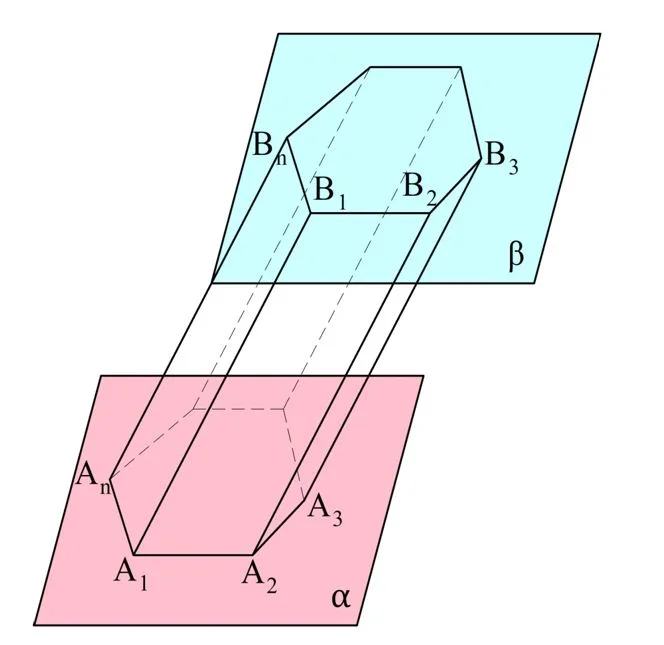
В результате мы получили геометрическую фигуру, которую именуют призмой. Многоуг-ки А₁А₂А₃…А_n и В₁В₂В₃…В_n именуются основаниями призмы, а все остальные грани – это боковые грани призмы. Можно доказать, что боковые грани – это параллелограммы. Действительно, в четырехуг-ке А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию. Также они равны по теореме 12 из этого урока. Это и значит, что А₁А₂В₂В₁ – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:

Ребра призмы, не принадлежащие основанию, именуются боковыми ребрами призмы. Ясно, что любые два соседних ребра параллельны, ведь они являются сторонами параллелограммами. Но тогда по свойству транзитивности параллельности получается, что вообще любые два боковых ребра параллельны. Если из какой-нибудь точки основания построен перпендикуляр к противоположному основанию, то он именуется высотой призмы:

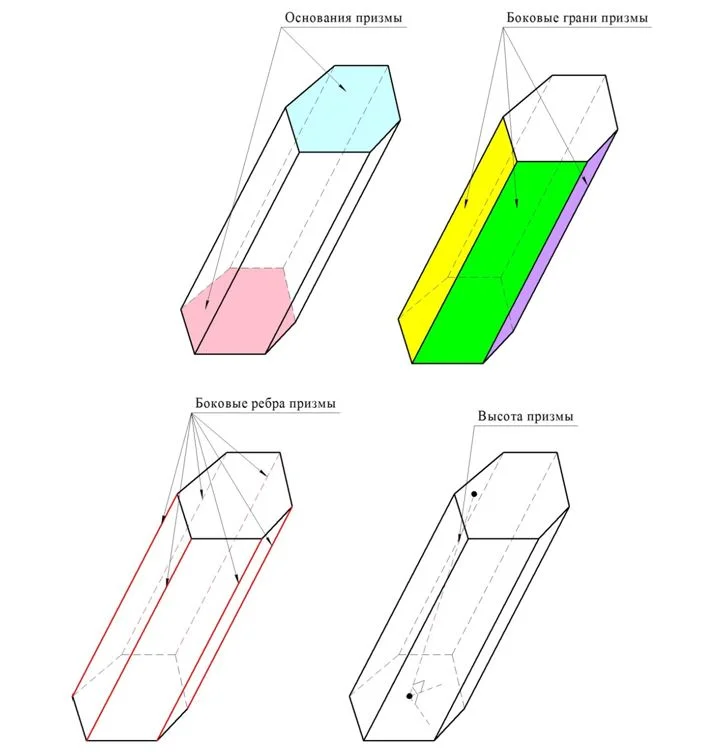
Естественно, что высота перпендикулярна обоим основаниям. Возможна ситуация, когда высота падает не на основание, а на какую-нибудь точку плос-ти основания, не находящуюся внутри него. Ясно, что все высоты призмы имеют одинаковую длину независимо от того, через какие точки они проведены, ведь высота по своей сути – это расстояние между плос-тями оснований.

Особый интерес вызывают призмы, где боковые ребра и основания перпендикулярны друг другу. Такие призмы именуются прямыми. Ясно, что у них боковые грани оказываются уже не просто параллелограммами, а уже прямоуг-ками. При этом любое боковое ребро одновременно является и высотой. Все остальные призмы именуют наклонными.

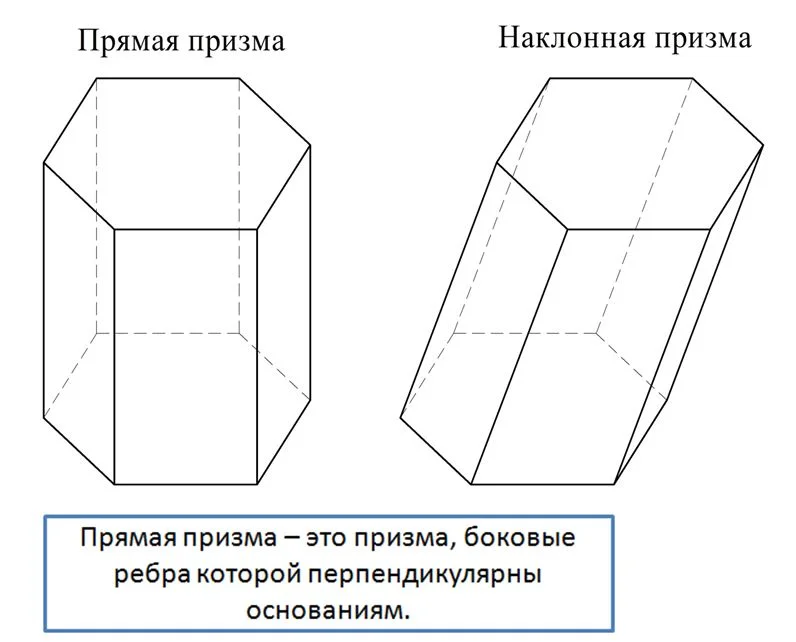
Если в основании призмы находится n-угольник, то призму называют n-угольной. В частности, в основании треугольной призмы лежит треуг-к, в основании десятиугольной призмы находится десятиугольник и т. д. Наконец, в особую группу выделяют прямые призмы, основаниями которых представляют собой правильные многоуг-ки. Их так и именуют – правильные призмы.

Если сложить площадь всех граней призмы, то получится сумма, которую именуют площадью полной поверхности призмы. Обычно ее обозначают как S_полн. Если же складываются только площади боковых граней, то в сумме получается площадь боковой поверхности призмы, обозначаемая как S_бок. Если площадь основания призмы обозначить как S_осн., то справедлива будет очевидная формула:

Действительно, пусть есть прямая призма с основаниями А₁А₂…А_n и B₁B₂…B_n:

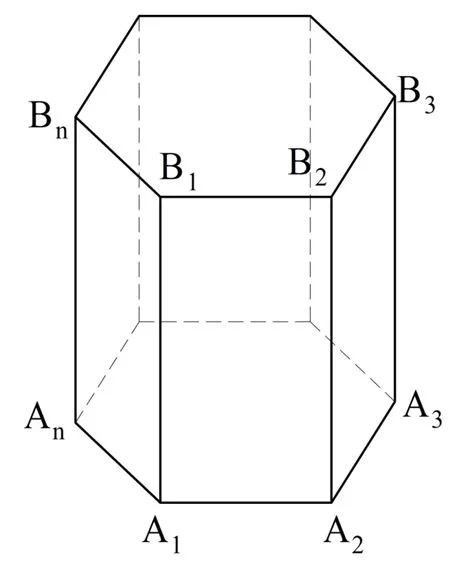
Так как ее боковые ребра перпендикулярны основаниям, то они должны быть перпендикулярны и тем ребрам, которые образуют основания. Это значит, каждая боковая грань – это прямоуг-к. При этом боковые ребра – это одновременно и высоты призмы. Тогда площадь боковых граней вычисляется так:

Отметим наконец, что параллелепипед можно считать частным случаем призмы, а прямоугольный параллелепипед – частным случаем прямой призмы.

Типичные задачи на призмы

Призмы нередко встречаются в заданиях ЕГЭ, поэтому важно уметь решать задачи, в которых используются эти фигуры.

Задание. Сколько диагоналей имеет n-угольная призма?

Решение. В любом многограннике диагональ соединяет точки, не лежащие на одной грани. Каждая вершина призмы принадлежит одному из оснований, причем в n-угольной призме каждому основанию принадлежат n вершин.

Возьмем произвольную вершину на одном из оснований и посчитаем, сколько диагоналей из нее можно провести. Если соединять ее отрезками с другими вершинами, принадлежащему тому же основанию, то получатся диагонали грани, но не диагонали призмы (зеленые линии на рисунке):

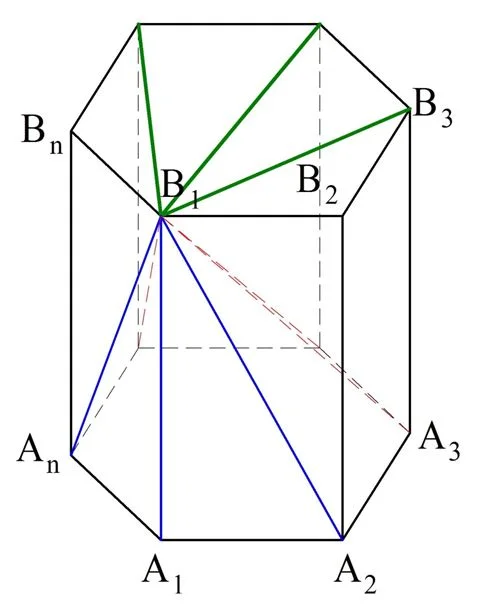
Значит, остается только провести прямые к тем вершинами, которые лежат в другом основании. Так как в другом основании находятся n вершин, то и отрезков будет ровно n. Однако три из них не будут диагоналями (показаны на рисунке синим цветом), так как будут либо являться одним из ребер призмы либо одной из диагоналей. Получается, что из вершины можно провести (n – 3) диагоналей. Так как в основании находятся n вершин, то всего можно построить n•(n– 3) диагоналей.

Ответ: n•(n – 3) диагоналей.

Задание. Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?

Решение. Выполним построение по условию задачи:

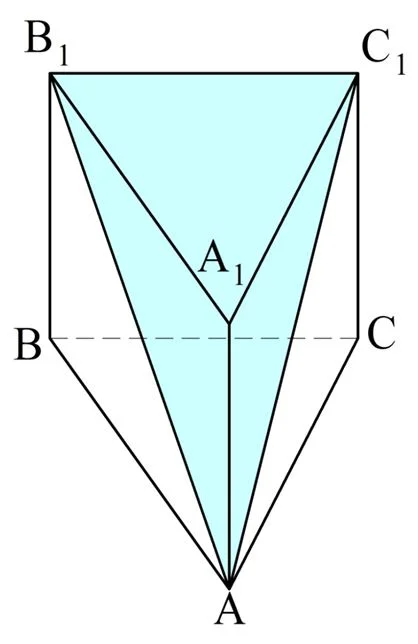
Здесь сечение проведено через ребро В₁С₁ и противолежащую ей вершину А. Призма правильная, поэтому ее основания ∆АВС и ∆А₁В₁С₁ – это равносторонние треуг-ки, и все их стороны равны 8 см. По определению правильная призма обязательно ещё и прямая. Тогда боковые грани – прямоуг-ки.

∆АВВ₁ – прямоугольный, с помощью теоремы Пифагора мы можем вычислить его гипотенузу АВ₁:

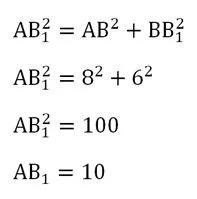
Аналогично можно вычислить, что и диагональ АС₁ также равна 10 см. Вообще в правильных призмах все грани – это равные друг другу прямоуг-ки, поэтому и диагонали у них одинаковы.

Длина ребра В₁С₁ составляет 8 см. Получается, нам надо вычислить площадь равнобедренного ∆АВ₁С₁ с основанием 8 см и боковыми сторонами 10 см. Это можно сделать множеством способов. Самый простой из них заключается в использовании формулы Герона. Для ее применения сначала вычислим полупериметр ∆АВ₁С₁:

Задание. В основании призмы находится равносторонний ∆АВС. Ребро АА₁ образует одинаковые углы с ребрами АС и АВ. Докажите, что ребра АА₁ и ВС перпендикулярны и что СС₁В₁В – прямоуг-к.

Решение. Выполняем построение:

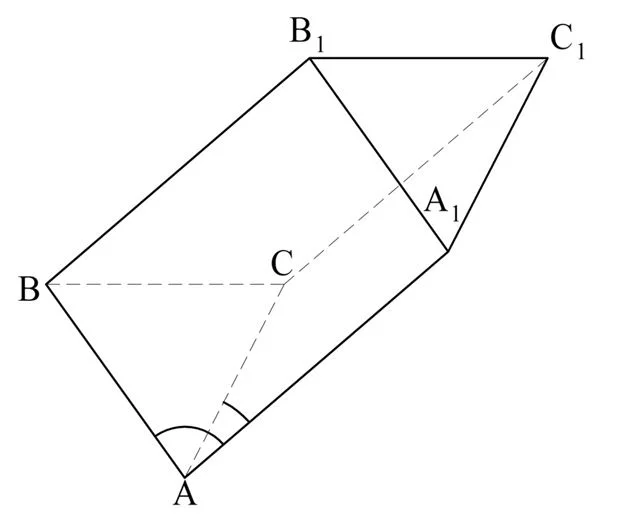
По условию ∠А₁АВ и ∠А₁АС одинаковы. Проведем диагонали А₁В и А₁С. В итоге мы получим ∆А₁АВ и А₁АС. У них есть АА₁ – общая сторона, стороны АВ и АС одинаковы (ведь ∆АВС – равносторонний), а углы между ними одинаковы. Значит, ∆А₁АВ и А₁АС равны, и тогда диагонали А₁В и А₁С одинаковы.

Получается, что точка А₁ равноудалена вершин В и С. Аналогично и точка А равноудалена от В и С, ведь АВ и АС одинаковы. Это значит, что и А₁, и А лежат на серединных перпендикулярах, проведенных к отрезку ВС:

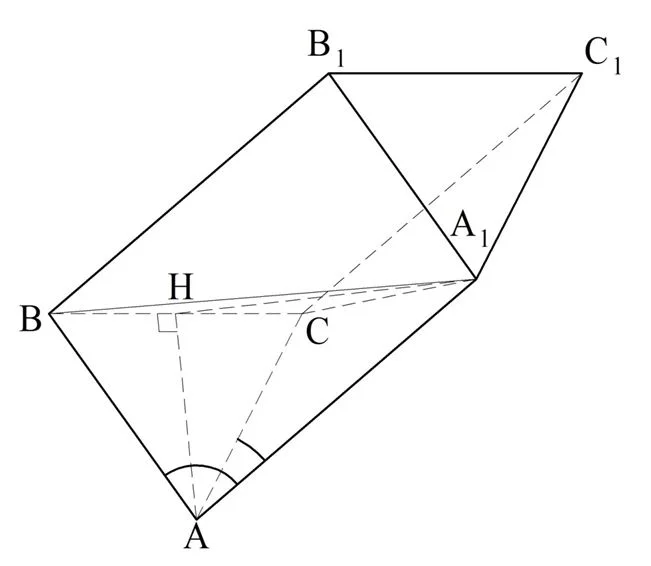
Обозначим середину ВС как Н, тогда НА₁ и НА – серединные перпендикулярны. То есть ВС⊥АН и ВС⊥А₁Н. Но это значит (по признаку перпендикулярности прямой и плос-ти), что ВС перпендикулярен всей плос-ти АНА₁. Из этого вытекает, что ВС⊥АА₁, ч. т. д.

Осталось показать, что грань СС₁В₁В – это прямоуг-к. Так как ВВ₁||АА₁, и ВС⊥АА₁, то и ВС⊥ВВ₁. Значит в параллелограмме СС₁В₁В (напомним, что в призме все боковые грани – параллелограммы) есть прямой угол. Это значит, что он является прямоуг-ком, ч. т. д.

Задание. Призма АВСА₁В₁С₁ – наклонная. Известно, что АС = АВ = 13 и ВС = 10. Боковые ребра призмы образуют с основанием АВС угол 45°. Проекция точки А₁ на плос-ть АВС совпадает с точкой пересечения медиан в ∆АВС. Какова площадь грани СС₁В₁В?

Решение. Снова выполняем построение:

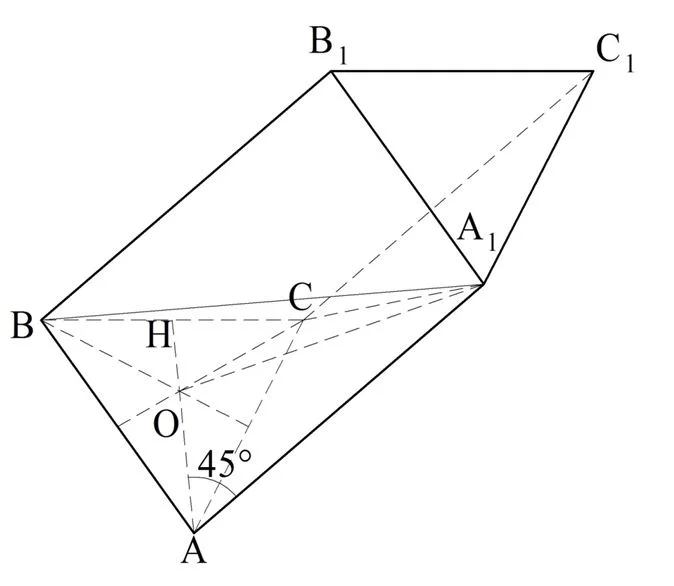
Здесь О – это проекция точки А₁ и одновременно точка пересечения медиан. H– середина отрезка ВС, то есть АН – как раз одна из медиан. Заметим, что так как ∆АВС равнобедренный, и ВС – это его основание, то АН одновременно является и высотой, то есть ∠ВНА = 90°. Раз Н – середина ВС, то ВН будет вдвое короче ВС:

Напомним, точка пересечения медиан делит их в отношении 2:1, поэтому мы можем найти ОА:

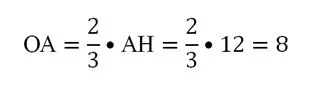
Понятно, что ОА – это проекция прямой ОА на плос-ть АВС. Тогда угол между ребром АА₁ и плос-тью АВС, по условию равный 45° – это ∠ОАА₁.

Из прямоугольного ∆АОА₁ с помощью тригонометрии мы найдем длину ребра АА₁:

Теперь покажем, что грань СС₁В₁В – прямоуг-к. Ясно, что ОА₁⊥ВН, ведь ОА₁ – перпендикуляр ко всей плос-ти АВС. Но также ВН⊥АН. Значит, ВН перпендикулярен плос-ти АОА₁, и, в частности, перпендикулярен ребру АА₁. Но тогда и ВВ₁⊥ВН, ведь ВВ₁||АА₁. Значит, грань СС₁В₁В – прямоуг-к, ведь в ней есть прямой угол. Для нахождения площади прямоуг-ка надо перемножить две его смежные стороны:

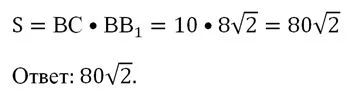
Задание. Ребро при основании правильной 6-угольной призмы имеет длину 23, а боковое ребро равно 50. Вычислите площадь поверхности призмы (и полную, и боковую).

Решение.

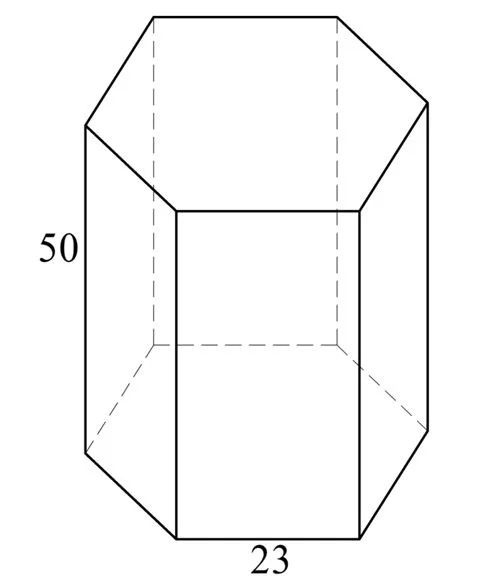
Сначала найдем площадь и периметр основания. Формулы для правильных многоуг-ков мы уже изучали:

Здесь а – сторона шестиугольника, R и r – радиусы описанной и вписанной окружности, n– число сторон шестиугольника. Во второй формуле мы использовали известный факт, что длина стороны правильного 6-угольника совпадает с радиусом описанной около него окружности.

Далее вычисляем площадь боковой поверхности:

Добавив к этому значению удвоенную площадь поверхности основания, найдем и полную площадь призмы:

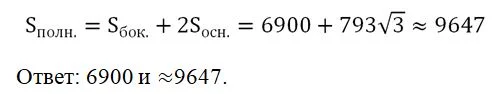
Задание. В правильной треугольной призме АВСА₁В₁С₁, у которой все ребра одинаковы и равны единице, вычислите угол между гранью АВС и сечением АСВ₁:

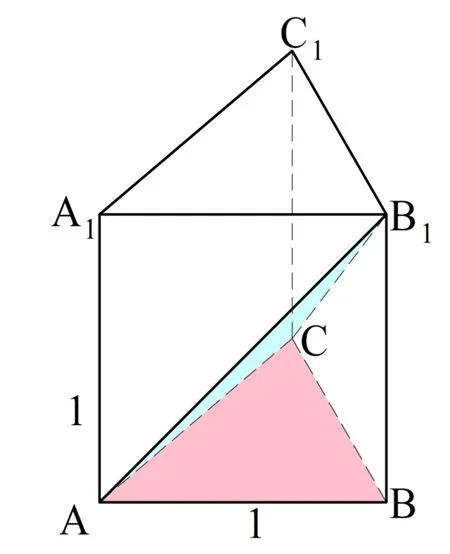
Решение. Вспомним, что для нахождения угла между плос-тями необходимо построить в этих плос-тях перпендикуляры к линии их пересечения, причем эти перпендикуляры должны падать на одну и ту же точку.

Пересекаются плос-ти АВС и АСВ₁ по грани АС. Заметим, что и ∆АВС, и ∆АСВ₁ – равнобедренные, причем у них общее основание АС. Действительно, АВ = ВС, так как в основании правильной призмы лежит равносторонний треуг-к, а АВ₁ = СВ₁, так как это диагонали равных граней АВВ₁А₁ и ВСС₁В₁.

Если мы отметим середину отрезка АС (например, точкой Н) и соединим ее с В и В₁, то мы получим две медианы НВ и НВ₁, которые одновременно будут и высотой. Это значит, что именно ∠ВНВ₁ и будет искомым углом между плос-тями:

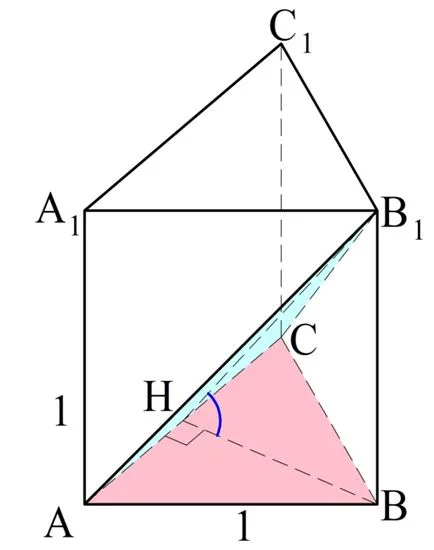
Осталось найти ∠ВНВ₁. Длину ВВ₁ мы уже знаем, она составляет 1.

АН вдвое короче АС:

Теперь заметим, что ∆НВВ₁ – прямоугольный, поэтому для него можно использовать тригонометрию:

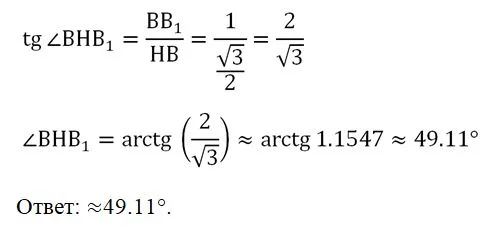
Задание. Найдите угол между прямыми А₁D и СD₁ в правильной призме, показанной на рисунке:

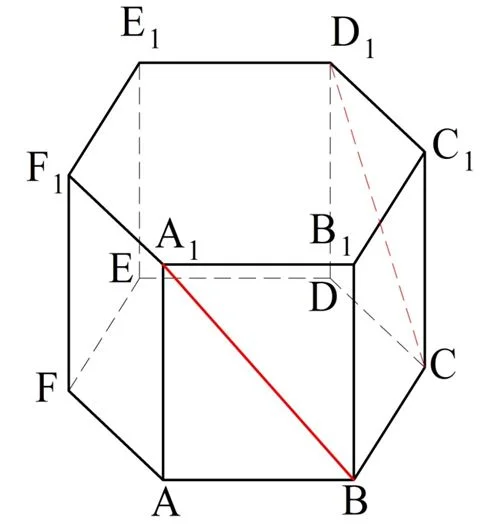
Все ребра этой призмы равны единице.

Решение. Сначала внимательно рассмотрим верхнее основание призмы. Так как оно представляет собой правильный многоуг-к, то вокруг него можно описать окружность. Обозначим центр этой окружности как О и проведем радиусы к вершинам:

Так как в правильном шестиуг-ке радиус описанной окружности равен стороне шестиугольника, то получается, что ∆А₁ОВ₁, ∆В₁ОС₁ и ∆С₁ОD₁ – равносторонние. Тогда ∠А₁ОВ₁, ∠B₁OC₁ и ∠С₁ОD₁ составляют по 60°. Тогда ∠А₁ОD₁ равен 180°, то есть точки А₁, О и D₁ находятся на одной прямой А₁D₁. Также заметим, что эта прямая параллельна ребру В₁С₁, ведь ∠D₁OC₁и ∠ОС₁B₁ являются накрест лежащими для этих прямых (при секущей ОС₁) и при том они одинаковы. Так как отрезки А₁О и D₁O как стороны равносторонних треуг-ков равны 1, то

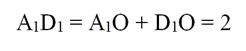
Теперь вернемся к призме:

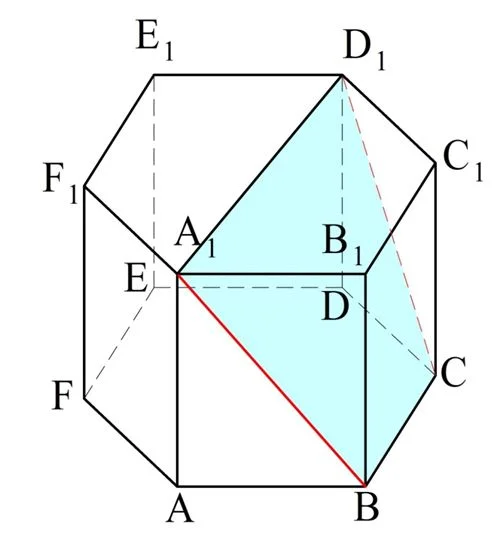
Так как А₁D₁||В₁С₁ и В₁С₁||ВС, то и А₁D₁||ВС. Это значит, что через А₁D₁ и ВС можно провести плос-ть, в которой будут лежать и интересующие нас прямые А₁В и СD₁. Для нахождения угла между ними надо рассмотреть четырехуг-к А₁D₁CB. Раз А₁D₁||ВС, то этот четырехуг-к является трапецией.

Далее найдем длину А₁В. Для этого используем ∆АВА₁:

Аналогично из ∆СDD₁ можно определить, что СD₁ имеет такую же длину. Это значит, что А₁D₁CB – равнобедренная трапеция.

Теперь рассмотрим отдельно эту трапецию, чтобы найти искомый угол:

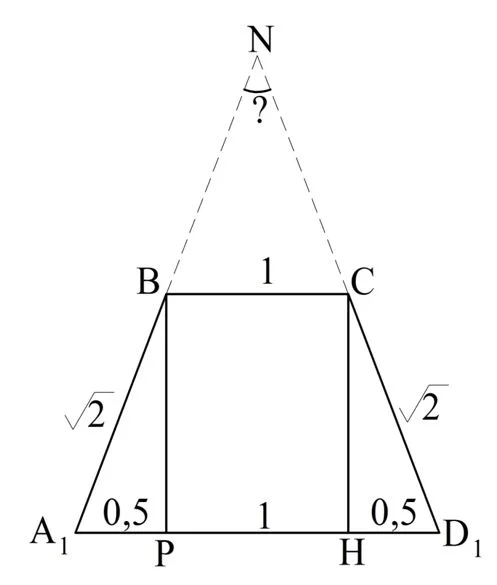
Опустим из вершин трапеции В и С перпендикуляры на А₁D₁. В итоге получим прямоуг-к ВСРН, где

Сегодня мы более детально изучили понятие многогранника и познакомились с новой геометрической фигурой – призмой. Призма довольно часто встречается в задаче С2 на ЕГЭ. Также мы узнали о теореме Эйлера, из которой вытекают некоторые важные факты. Один из них заключается в том, что не бывает выпуклых многогранников, у которых ни одна грань не является треуг-ком, четырехуг-ком или пятиуг-ком.

• Сделаем поясняющий рисунок:

• Тогда:

• Найдем общую сумму ребер:

Кому понравилась публикация, ставим пальцы вверх и подписываемся!) Всех благ!)

Правильный многогранник или плато́ново тело — это выпуклый многогранник, грани которого являются равными правильными многоугольниками, обладающий пространственной симметрией следующего типа: все многогранные углы при его вершинах правильные и равны друг другу^[1][2] (правильность углов означает, что у каждого многогранного угла равны все их линейные^[3] углы и все двугранные углы^[4]).

Альтернативные варианты определения изложены ниже.

Список правильных многогранников[править | править код]

В трёхмерном евклидовом пространстве существует всего пять правильных многогранников^[5] (упорядочены по числу граней):

Изображение	Правильный многогранник	Число вершин	Число рёбер	Число граней	Число сторон у грани	Число рёбер, примыкающих к вершине	Тип пространственной симметрии
	Тетраэдр	4	6	4	3	3	Td
	Гексаэдр	8	12	6	4	3	Oh
	Октаэдр	6	12	8	3	4	Oh
	Додекаэдр	20	30	12	5	3	Ih
	Икосаэдр	12	30	20	3	5	Ih

Название каждого многогранника происходит от греческого наименования количества его граней и слова «грань».

История[править | править код]

Правильные многогранники известны с древнейших времён.
Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона.
В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками.
Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору.
Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона.
В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела».
Платон писал о них в своём трактате Тимей (360 год до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Огню соответствовал тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр.
Данные сопоставления пояснялись следующими ассоциациями: жар огня ощущается чётко и остро, как пирамидки-тетраэдры;
мельчайшие компоненты воздуха октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры;
в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды.
По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца».

Аристотель добавил пятый элемент — эфир — и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал.
Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке.
Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра.
В 18-м предложении утверждается, что не существует других правильных многогранников.
Математик из Базельского университета Андреас Шпейзер отстаивал точку зрения, что построение пяти правильных многогранников является главной целью дедуктивной системы геометрии в том виде, как та была создана греками и канонизирована в «Началах» Евклида^[6].
Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.

В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками.
В книге «Тайна мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну).
Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб.
Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками.
Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).

Комбинаторные свойства[править | править код]

• Эйлером была выведена формула, связывающая число вершин (В), граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением:

  В + Г = Р + 2.

• Отношение количества вершин правильного многогранника к количеству рёбер одной его грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.

• Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:

  p — число рёбер в каждой грани;

  q — число рёбер, сходящихся в каждой вершине.

Символы Шлефли для правильных многогранников приведены в следующей таблице:

Многогранник	Вершины	Рёбра	Грани	Символ Шлефли
тетраэдр		4	6	4	{3, 3}
гексаэдр (куб)		8	12	6	{4, 3}
октаэдр		6	12	8	{3, 4}
додекаэдр		20	30	12	{5, 3}
икосаэдр		12	30	20	{3, 5}

• Другой комбинаторной характеристикой многогранника, которую можно выразить через числа p и q, является общее количество вершин (В), рёбер (Р) и граней (Г). Поскольку любое ребро соединяет две вершины и лежит между двумя гранями, выполняются соотношения:

  

Из этих соотношений и формулы Эйлера можно получить следующие выражения для В, Р и Г:

Геометрические свойства[править | править код]

Углы[править | править код]

С каждым правильным многогранником связаны определённые углы, характеризующие его свойства. Двугранный угол между смежными гранями правильного многогранника {p, q} задаётся формулой:

Иногда удобнее пользоваться выражением через тангенс:

где принимает значения 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.

Угловой дефект при вершине многогранника — это разность между 2π и суммой углов между рёбрами каждой грани при этой вершине.
Дефект при любой вершине правильного многогранника:

По теореме Декарта, он равен делённым на число вершин (то есть суммарный дефект при всех вершинах равен ).

Трёхмерным аналогом плоского угла является телесный угол. Телесный угол Ω при вершине правильного многогранника выражается через двугранный угол между смежными гранями этого многогранника по формуле:

Телесный угол, стягиваемый гранью правильного многогранника, с вершиной в центре этого многогранника, равен телесному углу полной сферы ( стерадиан), делённому на число граней. Он также равен угловому дефекту дуального к данному многогранника.

Различные углы правильных многогранников приведены в следующей таблице. Числовые значения телесных углов даны в стерадианах.
Константа  — золотое сечение.

Многогранник	Двугранный угол θ		Плоский угол между рёбрами при вершине	Угловой дефект (δ)	Телесный угол при вершине (Ω)	Телесный угол, стягиваемый гранью
тетраэдр	70.53°		60°
куб	90°	1	90°
октаэдр	109.47°	√2	60°, 90°
додекаэдр	116.57°		108°
икосаэдр	138.19°		60°, 108°

Радиусы, площади и объёмы[править | править код]

С каждым правильным многогранником связаны три концентрические сферы:

• Описанная сфера, проходящая через вершины многогранника;
• Срединная сфера, касающаяся каждого его ребра в середине;
• Вписанная сфера, касающаяся каждой его грани в её центре.

Радиусы описанной () и вписанной () сфер задаются формулами:

где θ — двугранный угол между смежными гранями многогранника. Радиус срединной сферы задаётся формулой:

где h — величина описанная выше, при определении двугранных углов (h = 4, 6, 6, 10 или 10). Отношения описанных радиусов к вписанным радиусам симметрично относительно p и q:

Площадь поверхности S правильного многогранника {p, q} вычисляется, как площадь правильного p-угольника, умноженная на число граней Г:

Объём правильного многогранника вычисляется, как умноженный на число граней объём правильной пирамиды, основанием которой служит правильный p-угольник, а высотой — радиус вписанной сферы r:

Приведённая таблица содержит список различных радиусов, площадей поверхностей и объёмов правильных многогранников. Значение длины ребра a в таблице приравнены к 2.

Многогранник (a = 2)	Радиус вписанной сферы (r)	Радиус срединной сферы (ρ)	Радиус описанной сферы (R)	Площадь поверхности (S)	Объём (V)
тетраэдр
куб
октаэдр
додекаэдр
икосаэдр

Константы φ и ξ задаются выражениями

Среди правильных многогранников как додекаэдр, так и икосаэдр представляют собой лучшее приближение к сфере. Икосаэдр имеет наибольшее число граней, наибольший двугранный угол и плотнее всего прижимается к своей вписанной сфере. С другой стороны, додекаэдр имеет наименьший угловой дефект, наибольший телесный угол при вершине и максимально заполняет свою описанную сферу.

Варианты определения[править | править код]

В геометрии «правильность» фигур понимают как в смысле равенства всех её однородных элементов, так и в смысле максимальной симметричности фигуры среди всех аналогичных. Так, правильный многоугольник имеет равные стороны и равные углы, правильный многогранный угол — равные грани (то есть плоские^[3] углы) и равные двугранные углы. С другой стороны, -угольник, который имеет максимально возможное число число осей симметрии (равное ) является правильным и в первом смысле^[7].

Определения через равенство элементов[править | править код]

В случае правильного выпуклого многогранника естественно потребовать равенства друг другу всех его рёбер, углов его граней (плоских углов) и двугранных углов между гранями^[7]. Равенство рёбер и углов граней равносильно тому, что все грани являются равными правильными многоугольниками. И большинство встречающихся в литературе определений содержат именно это условие в качестве своей первой части^[8].

Равенство плоских и двугранных равносильно тому, что правильными и равными являются многогранные углы при всех вершинах. Это условие составляет вторую часть определения, приведенного выше. Однако многие авторы заменяют это условие на одно из более слабых, которое также является достаточными для того, чтобы многогранник с равными правильными гранями был правильным:

• в каждой вершине многогранника сходится одинаковое число рёбер (учебник Л. С. Атанасяна^[9], учебник А. В. Погорелова^[⇨], справочник В. А. Гусева и А. Г. Мордковича^[10]);
• в каждой вершине многогранника сходится одинаковое число граней (учебник Смирновых^[11]);
• все двугранные углы многогранника равны между собой (учебник А. Д. Александрова^[7], «Элементарная геометрия» Ж. Адамара^[2]).

Выбор одного из первых двух вариантов в большинстве российских школьных учебников связан с тем, что изучение правильных многогранников в школе носит ознакомительный характер^[8].

В учебнике А. В. Погорелова^[12] более слабым заменено и первое условие: вместо равенства правильных многоугольников требуется лишь равное число сторон у них^[8].

Определение через симметрию[править | править код]

Правильные многогранники могут быть определены как самые симметричные из всех многогранников в следующем смысле. Пусть выбраны произвольная грань многогранника, произвольная сторона этой грани (ребро) и любой из концов этой стороны (вершина). Тогда если отметить на том же многограннике любой аналогичный набор из грани , ребра и вершины , то существует самосовмещающее движение многогранника, которое переводит в , в и в . Можно доказать, что это определение задаёт тот же самый класс правильных многогранников, то есть оно равносильно определениям, приведенным выше^[13].

В больших размерностях[править | править код]

В четырёхмерном пространстве существует шесть правильных многогранников (многоячейников):

Пятиячейник

Тессеракт

Шестнадцатиячейник

Двадцатичетырёхъячейник

Стодвадцатиячейник

Шестисотячейник

В пространствах более высоких размерностей ( существуют по три правильных многогранника (политопа):

• n-мерный правильный симплекс
• n-мерный гиперкуб
• n-мерный гипероктаэдр

См. также[править | править код]

• Двойственный многогранник
• Звёздчатый многогранник
• Многогранник Джонсона
• Полуправильный многогранник
• Правильные многомерные многогранники

Примечания[править | править код]

Ссылки[править | править код]

• Смирнов Е. Ю. Группы Кокстера и правильные многогранники // Летняя школа «Современная математика». — Дубна, 2008.
• Weisstein, Eric W. Platonic Solids (англ.) на сайте Wolfram MathWorld.
• Фанаты математики/геометрия. (англ.)
• Бумажные модели правильных многогранников. (англ.)
• Наука/геометрия/платоновы и архимедовы тела. (англ.)
• Платоновы, Архимедовы тела, призмы, тела Кеплера-Пуансо и усечённые тела Кеплера-Пуансо. (англ.)
• М. Веннинджер. Модели многогранников. — Москва: Мир, 1974. — 236 с.
• Гончар В. В. Модели многогранников. — Москва: Аким, 1997. — 64 с. — ISBN 5-85399-032-2.
• Гончар В. В., Гончар Д. Р. Модели многогранников. — Ростов-на-Дону: Феникс, 2010. — 143 с. — ISBN 978-5-222-17061-8.

Все рёбра правильного многогранника равны, а также равны все двугранные углы, содержащие две грани с общим ребром.

Возникают вопросы:

1. какие правильные многоугольники могут быть гранями правильного многогранника?

2. Сколько граней может иметь правильный многогранник?

2. В каждой вершине многогранника должно быть не меньше трёх углов.

Только правильные треугольники, четырёхугольники (квадраты) и пятиугольники могут быть гранями правильного многогранника.

Существуют ли правильные многогранники с такими гранями, и сколько граней они имеют? Очевидно, меньшее возможное число граней — четыре.

С помощью теоремы Эйлера мы можем получить ответ на вопрос:

какие правильные многогранники могут существовать?

1. Пусть количество рёбер правильного многогранника, выходящих из одной вершины, равно (m), а гранями являются правильные (n)-угольники.

2. Выразим входящие в формулу Эйлера величины (В) (вершины) и (Г) (грани) через:

(Р) (рёбра), (m), (n), где (n) и (m) — целые числа, и (m ≥ 3), (n =) (3), (4) или (5).

4. Так как каждое ребро многогранника содержится в двух гранях, то (Гn = 2Р).

5. Подставляя полученные выражения для (Г) и (В) в формулу Эйлера (Г + В – Р = 2), получаем

6. Поделив обе части равенства на (2Р), получим

7. Решим это уравнение при полученном в предыдущем доказательстве значении (n =) (3) и найдём допустимые значения (m).

По смыслу (Р > 0), значит, (3 ≤ m ≤5).

3. (m=3, n=5, P=30, Г=12) — додекаэдр;
4. (m=4, n=3, P=12, Г=8) — октаэдр;
5. (m=5, n=3, P=30, Г=20) — икосаэдр.

Доказано существование правильных многогранников:

тетраэдр с (4) гранями, (6) рёбрами и (4) вершинами:

куб с (6) гранями, (12) рёбрами и (8) вершинами:

октаэдр с (8) гранями, (12) рёбрами и (6) вершинами:

додекаэдр с (12) гранями, (30) рёбрами и (20) вершинами:

икосаэдр с (20) гранями, (30) рёбрами и (12) вершинами: