Как определить количество решений логического уравнения
Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.
Задача: Решить систему логических уравнений:
Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем инверсию к обеим частям первого уравнения:
Представим импликацию через базовые операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:
Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.
Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.
Решение 2: Составим таблицу истинности для системы:
Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.
Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.
Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных решений имеет система логических уравнений:
Приведенная система уравнений равносильна уравнению:
Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго – x 3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1=0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.
Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2=0 получаем, что x 3=0 или x 3=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.
Задача №23. Решение систем логических уравнений.
Решение систем логических уравнений методом замены переменных
Метод замены переменных применяется, если некоторые переменные входят в состав уравнений только в виде конкретного выражения, и никак иначе. Тогда это выражение можно обозначить новой переменной.
Сколько существует различных наборов значений логических переменных x1, х2, х3, х4, х5, х6, х7, х8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → х2) → (х3→ х4) = 1
(х3 → х4) → (х5 → х6) = 1
(х5 → х6) → (х7 → х8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, х6, х7, х8, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Сделаем замену переменных:
(x1 → х2) = y1; (х3 → х4) = y2; (х5 → х6) = y3; (х7 → х8) = y4.
Тогда можно записать систему в виде одного уравнения:
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1. Конъюнкция равна 1 (истинна), когда каждый операнд принимает значение 1. Т.е. каждая из импликаций должна быть истинна, а это выполняется при всех значениях, кроме (1 → 0). Т.е. в таблице значений переменных y1, y2, y3, y4 единица не должна стоять левее нуля:
Т.е. условия выполняются для 5 наборов y1-y4.
Т.к. y1 = x1 → x2, то значение y1 = 0 достигается на единственном наборе x1, x2: (1, 0), а значение y1 = 1 – на трех наборах x1, x2: (0,0) , (0,1), (1,1). Аналогично для y2, y3, y4.
Поскольку каждый набор (x1,x2) для переменной y1 сочетается с каждым набором (x3,x4) для переменной y2 и т.д., то количества наборов переменных x перемножаются:
Кол-во наборов на x1…x8
Сложим количество наборов: 1 + 3 + 9 + 27 + 81 = 121.
Сколько существует различных наборов значений логических переменных x1, x2, . x9, y1, y2, . y9, которые удовлетворяют всем перечисленным ниже условиям?
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, . x9, y1, y2, . y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Сделаем замену переменных:
(x1 ≡ y1) = z1, (x2 ≡ y2) = z2,…. ,(x9 ≡ y9) = z9
Систему можно записать в виде одного уравнения:
(¬ z1 ≡ z2) ∧ (¬ z2 ≡ z3) ∧ …..∧ (¬ z8 ≡ z9)
Эквивалентность истинна, только если оба операнда равны. Решениями этого уравнения будут два набора:
| z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Т.к. zi = (xi ≡ yi), то значению zi = 0 соответствуют два набора (xi,yi): (0,1) и (1,0), а значению zi = 1 – два набора (xi,yi): (0,0) и (1,1).
Тогда первому набору z1, z2,…, z9 соответствует 2 9 наборов (x1,y1), (x2,y2),…, (x9,y9).
Столько же соответствует второму набору z1, z2,…, z9. Тогда всего 2 9 +2 9 = 1024 наборов.
Решение систем логических уравнений методом визуального определения рекурсии.
Этот метод применяется, если система уравнений достаточно проста и порядок увеличения количества наборов при добавлении переменных очевиден.
Сколько различных решений имеет система уравнений
где x1, x2, … x10 — логические переменные?
В ответе не нужно перечислять все различные наборы значений x1, x2, … x10, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решим первое уравнение. Дизъюнкция равна 1, если хотя бы один из ее операндов равен 1. Т.е. решениями являются наборы:

Для x1=0 существуют два значения x2 ( 0 и 1), а для x1=1 только одно значение x2 (1), такие, что набор (x1,x2) является решением уравнения. Всего 3 набора.
Добавим переменную x3 и рассмотрим второе уравнение. Оно аналогично первому, значит для x2=0 существуют два значения x3 ( 0 и 1), а для x2=1 только одно значение x3 (1), такие, что набор (x2,x3) является решением уравнения. Всего 4 набора.

Несложно заметить, что при добавлении очередной переменной добавляется один набор. Т.е. рекурсивная формула количества наборов на (i+1) переменных:
Ni+1 = Ni + 1. Тогда для десяти переменных получим 11 наборов.
Решение систем логических уравнений различного типа
Сколько существует различных наборов значений логических переменных x1, . x4, y1. y4, z1. z4, которые удовлетворяют всем перечисленным ниже условиям?
В ответе не нужно перечислять все различные наборы значений переменных x1, . x4, y1, . y4, z1, . z4, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Заметим, что три уравнения системы одинаковы на различных независимых наборах переменных.
Рассмотрим первое уравнение. Конъюнкция истинна (равна 1) только тогда, когда все ее операнды истинны (равны 1). Импликация равна 1 на всех наборах, кроме (1,0). Значит, решением первого уравнения будут такие наборы x1, x2, x3, x4, в которых 1 не стоит левее 0 (5 наборов):
Методы решения систем логических уравнений
статья по информатике и икт (10 класс) по теме

Методы решения систем логических уравнений при подготовке к ЕГЭ (задание В15)
Скачать:
| Вложение | Размер |
|---|---|
| Методы решения систем логических уравнений | 296.5 КБ |
Предварительный просмотр:
Методы решения систем логических уравнений
Решить систему логических уравнений можно, например, с помощью таблицы истинности (если количество переменных не слишком велико) или с помощью дерева решений, предварительно упростив каждое уравнение.
1. Метод замены переменных.
Ввод новых переменных позволяет упростить систему уравнений, сократив количество неизвестных. Новые переменные должны быть независимыми друг от друга . После решения упрощенной системы надо снова вернуться к первоначальным переменным.
Рассмотрим применение этого метода на конкретном примере.
Пример. Сколько различных решений имеет система уравнений
((X1 ≡ X2) ∧ (X3 ≡ X4)) ∨ (¬(X1 ≡ X2) ∧ ¬(X3 ≡ X4)) = 0
((X3 ≡ X4) ∧ (X5 ≡ X6)) ∨ (¬(X3 ≡ X4) ∧ ¬(X5 ≡ X6)) = 0
((X5 ≡ X6) ∧ (X7 ≡ X8)) ∨ (¬(X5 ≡ X6) ∧ ¬(X7 ≡ X8)) = 0
((X7 ≡ X8) ∧ (X9 ≡ X10)) ∨ (¬(X7 ≡ X8) ∧ ¬(X9 ≡ X10)) = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Введем новые переменные: А=(X1 ≡ X2); В=(X3 ≡ X4); С=(X5 ≡ X6); D=(X7 ≡ X8); E=(X9 ≡ X10).
(Внимание! Каждая их переменных x1, x2, …, x10 должна входить только в одну из новых переменных А,В,С,D,Е, т.е. новые переменные независимы друг от друга).
Тогда система уравнений будет выглядеть так:
Построим дерево решений полученной системы:
Рассмотрим уравнение А=0, т.е. (X1 ≡ X2)=0. Оно имеет 2 корня:
Из этой же таблицы видно, что уравнение А=1 тоже имеет 2 корня. Расставим кол-во корней на дереве решений:
Чтобы найти количество решений одной ветви, надо перемножить количества решений на каждом ее уровне. Левая ветвь имеет 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2=32 решения; правая ветвь имеет тоже 32 решения. Т.е. вся система имеет 32+32=64 решения.
2. Метод рассуждений.
Сложность решения систем логических уравнений состоит в громоздкости полного дерева решений. Метод рассуждений позволяет не строить все дерево полностью, но понять при этом, сколько оно будет иметь ветвей. Рассмотрим этот метод на конкретных примерах.
Пример 1. Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1→x2) / (x2→x3) / (x3→x4) / (x4→x5 ) = 1
(y1→y2) / (y2→y3) / (y3→y4) / (y4→y5 ) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Первое и второе уравнения содержат независимые переменные, которые связаны третьим условием. Построим дерево решений первого и второго уравнений.
Чтобы представить дерево решений системы из первого и второго уравнений, надо каждую ветвь первого дерева продолжить деревом для переменных у . Построенное таким образом дерево будет содержать 36 ветвей. Некоторые из этих ветвей не удовлетворяют третьему уравнению системы. Отметим на первом дереве количество ветвей дерева «у» , которые удовлетворяют третьему уравнению:
Поясним: для выполнения третьего условия при х1=0 должно быть у1=1, т.е все ветви дерева «х» , где х1=0 можно продолжить только одной ветвью из дерева «у» . И только для одной ветви дерева «х» (правой) подходят все ветви дерева «у». Таким образом, полное дерево всей системы содержит 11 ветвей. Каждая ветвь представляет собой одно решение исходной системы уравнений. Значит, вся система имеет 11 решений.
Пример 2. Сколько различных решений имеет система уравнений
(X1 ≡ X2) ∨ (X1 ∧ X10) ∨ (¬X1 ∧ ¬ X10)= 1
(X2 ≡ X3) ∨ (X2 ∧ X10) ∨ (¬X2 ∧ ¬ X10)= 1.
(X9 ≡ X10) ∨ (X9 ∧ X10) ∨ (¬X9 ∧ ¬ X10)= 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение : Упростим систему. Построим таблицу истинности части первого уравнения:
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/informatika/zadanie-23/
http://nsportal.ru/shkola/informatika-i-ikt/library/2014/10/08/metody-resheniya-sistem-logicheskikh-uravneniy
[/spoiler]
Как найти количество решений логического уравнения?
Frrrrrrr
Ученик
(208),
на голосовании
3 года назад
Я понимаю, что можно просто перебрать все варианты решений и что их не такмного в этой задаче, но есть ли более простой и менее энергозатратный способ решения таких заданий?
Голосование за лучший ответ
Артём Морозов
Профи
(964)
3 года назад
Нужно построить таблицу истинности, построил её на скрине ниже. В условии должно получится 1, считаем количество 1 в последнем столбце – их 7. Ответ: 7 решений
FrrrrrrrУченик (208)
3 года назад
0→0=1, поэтому ответ не 7, а 10
Артём Морозов
Профи
(964)
Frrrrrrr, извиняюсь запутался в конце
Задачи на логические уравнения являются большой темой для изучения. На эту тему уходит 2 – 3 90-минутных занятия (больше только на последнюю программистскую задачу). Далее дается подборка разнообразных логических уравнений от простых к сложным. Для решения большинства уравнений будем использовать деревья решений и комбинаторику, поэтому тема логических уравнений находится на стыке трех разделов: «Логика», «Деревья и графы», «Комбинаторика».
Задача 4.5.1. Сколько различных решений имеет уравнение
(K ∧ L) ∨ (M ∧ N) = 1
где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Задача 4.5.2. Сколько различных решений имеет логическое уравнение
(J ∨ ⌐K ∨ L ∨ ⌐M) ∧ (N ∨ ⌐N) = 1
Задача 4.5.3. Сколько различных решений имеет логическое уравнение
⌐((J → K) → (L ∧ M ∧ N)) ∨ ⌐((L ∧ M ∧ N) → (⌐J ∨ K)) ∨ (M ∧ J) = 0
Примечание. Дерево является типичным способом решения уравнений. Если вы смотрите на уравнение и растерялись, не видите решений — это явный признак того, что надо строить дерево.
Задача 4.5.4. Сколько различных решений имеет система логических уравнений:
(x1 ≡ x2) ≡ (x3 ≡ x4) = 0
(x3 ≡ x4) ≡ (x5 ≡ x6) = 0
(x5 ≡ x6) ≡ (x7 ≡ x8) = 0
(x7 ≡ x8) ≡ (x9 ≡ x10) = 0
Примечание. Продемонстрируем, что количество решений в исходных переменных получается как произведение, а не сумма, начав строить дерево для исходных переменных:

Как видите, дерево быстро ветвится, и нужно переходить к новым обозначениям, чтобы ускорить расчеты.
Задача 4.5.5. Сколько различных решений имеет система логических уравнений:
(x1 ≡ x2) → (x2 ≡ x3) = 1
(x2 ≡ x3) → (x3 ≡ x4) = 1
…
(x5 ≡ x6) → (x7 ≡ x8) = 1
Ошибка. Если вы ввели новые обозначения, как в предыдущей задаче, то вы неправы. Переменные в этой задаче не образуют изолированные группы.
Примечание: поиск закономерности в дереве с выведением формулы обсчета – типичный прием при решении систем уравнений.
Задача 4.5.6. Сколько различных решений имеет система логических уравнений:
⌐(x1 ≡ x2) ∧ ⌐(x1 ≡ x3) ∧ (x2 ≡ x3) = 0
⌐(x3 ≡ x4) ∧ ⌐(x3 ≡ x5) ∧ (x4 ≡ x5) = 0
⌐(x5 ≡ x6) ∧ ⌐(x5 ≡ x7) ∧ (x6 ≡ x7) = 0
⌐(x7 ≡ x8) ∧ ⌐(x7 ≡ x9) ∧ (x8 ≡ x9) = 0
Задача 4.5.7. Сколько различных решений имеет система логических уравнений:
(x1 ∧ x2) ∨ (⌐x1 ∧ ⌐x2) ∨ (⌐x3 ∧ x4) ∨ (x3 ∧ ⌐x4) = 1
(x3 ∧ x4) ∨ (⌐x3 ∧ ⌐x4) ∨ (⌐x5 ∧ x6) ∨ (x5 ∧ ⌐x6) = 1
(x5 ∧ x6) ∨ (⌐x5 ∧ ⌐x6) ∨ (⌐x7 ∧ x8) ∨ (x7 ∧ ⌐x8) = 1
…
(x13 ∧ x14) ∨ (⌐x13 ∧ ⌐x14) ∨ (⌐x15 ∧ x16) ∨ (x15 ∧ ⌐x16) = 1
Задача 4.5.8. Сколько различных решений имеет система логических уравнений:
x1 ∨ x2 ∧ x3 = 1
x2 ∨ x3 ∧ x4 = 1
…
x7 ∨ x8 ∧ x9 = 1
x8 ∨ x9 ∧ x10 = 1
Ошибка. Первый подвох заключается в приоритете операций. Вы помните, что в отсутствии скобок логическое «и» выполняется раньше логического «или», то есть сперва делаем второе действие, а потом – первое.
Задача 4.5.9. Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, y1, y2, y3, y4, z1, z2, z3, z4, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(¬x1 ∧ y1 ∧ z1) ∨ (x1 ∧ ¬y1 ∧ z1) ∨ (x1 ∧ y1 ∧ ¬z1) = 1
(¬x2 ∧ y2 ∧ z2) ∨ (x2 ∧ ¬y2 ∧ z2) ∨ (x2 ∧ y2 ∧ ¬z2) = 1
(¬x3 ∧ y3 ∧ z3) ∨ (x3 ∧ ¬y3 ∧ z3) ∨ (x3 ∧ y3 ∧ ¬z3) = 1
(¬x4 ∧ y4 ∧ z4) ∨ (x4 ∧ ¬y4 ∧ z4) ∨ (x4 ∧ y4 ∧ ¬z4) = 1
Примечание. Обратите внимание, что если система уравнений красива, то и дерево красиво, а при его обсчете появляются закономерности.
Задача 4.5.10. Сколько существует решений у системы логических уравнений?
(x1 ∧ ((x1 ∧ x2) → x3) ∧ (¬x1 ∨ y1) = 1
(x2 ∨ x3) ∧ ((x2 ∧ x3) → x4) ∧ (¬x2 ∨ y2) = 1
…
(x6 ∨ x7) ∧ ((x6 ∧ x7) → x8) ∧ (¬x6 ∨ y6) = 1
(x7 ∨ x8) ∧ (¬x7 ∨ y7) = 1
(¬x8 ∨ y8) = 1
Задача 4.5.11. Сколько существует решений системы логических уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(⌐y1 ∨ y2) ∧ (⌐y2 ∨ y3) ∧ (⌐y3 ∨ y4) = 1
(x1 → y1) ∧ (x2 → y2) ∧ (x3 → y3) ∧ (x4 → y4) = 1
Задача 4.5.11А. Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (y1 → y2) ∧ (y1 → x1) = 1
(x2 → x3) ∧ (y2 → y3) ∧ (y2 → x2) = 1
…
(x8 → x9) ∧ (y8 → y9) ∧ (y8 → x8) = 1
(y9 → x9) = 1
Задача 4.5.12. Сколько существует решений системы логических уравнений?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) ∧ (x5→ x6) = 1
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5) ∧ (y5 → y6) = 1
(z1 → z2) ∧ (z2→ z3) ∧ (z3 → z4) ∧ (z4 → z5) ∧ (z5 → z6) = 1
x6 ∧ y6 ∧ z6 = 0
Задача 4.5.13. Сколько существует решений у системы логических уравнений?
((x1 ≡ y1) → (x2 ≡ y2)) ∧ (x1 → x2) ∧ (y1 → y2) = 1
((x2 ≡ y2) → (x3 ≡ y3)) ∧ (x2 → x3) ∧ (y2 → y3) = 1
…
((x8 ≡ y8) → (x9 ≡ y9)) ∧ (x8 → x9) ∧ (y8 → y9) = 1
Задача 4.5.14. Сколько существует различных наборов значений логических переменных x1, x2, … x3, y1, y2, … y5, которые удовлетворяют всем перечисленным ниже условиям?
(¬ (x1 ≡ x2) ∨ ¬ (y1 ≡ y2)) = 1
(¬ (x2 ≡ x3) ∨ ¬ (y2 ≡ y3)) = 1
(¬ (x3 ≡ x4) ∨ ¬ (y3 ≡ y4)) = 1
(¬ (x4 ≡ x5) ∨ ¬ (y4 ≡ y5)) = 1
x5 ∨ y5 = 1
Задача 4.5.15. Сколько существует различных наборов значений логических переменных x1, x2,…, x8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 ∨ x2) → (x3 ∧ x4) = 1
(x3 ∨ x4) → (x5 ∧ x6) = 1
(x5 ∨ x6) → (x7 ∧ x8) = 1
Задача 4.5.16. Сколько существует различных наборов значений логических переменных x1, x2,…, x7, y1, y2, …, y7, которые удовлетворяют всем перечисленным ниже условиям?
((x1 ∨ y1) → (x2 ∨ y2)) ∧ (x1 → y1) = 1
((x2 ∨ y2) → (x3 ∨ y3)) ∧ (x2 → y2) = 1
…
((x6 ∨ y6) → (x7 ∨ y7)) ∧ (x6 → y6) = 1
Задача 4.5.17. Сколько существует решений у системы логических уравнений?
¬((¬x1 ∧ x2 ∧ ¬x3) ∨ (¬x1 ∧ x2 ∧ x3) ∨ (x1 ∧ ¬x2 ∧ ¬x3)) = 1,
¬((¬x2 ∧ x3 ∧ ¬x4) ∨ (¬x2 ∧ x3 ∧ x4) ∨ (x2 ∧ ¬x3 ∧ ¬x4)) = 1,
…
¬((¬x8 ∧ x9 ∧ ¬x10) ∨ (¬x8 ∧ x9 ∧ x10) ∨ (x8 ∧ ¬x9 ∧ ¬x10)) = 1.
Следующая задача встречалась на ресурсах, посвященных подготовке к ЕГЭ. Маловероятно, что подобная задача встретится на реальном ЕГЭ, так как она очень сложна. Но стоит её решить, чтобы закрепить ряд приемов. После её решения вы будете способны решить любую систему логических уравнений.
Задача 4.5.18. Сколько существует решений у системы логических уравнений?
(x1 ∨ x2) ∧ ((x1 ∧ x2) → y1) = 1
(x2 ∨ x3) ∧ ((x2 ∧ x3) → y2) = 1
…
(x6 ∨ x7) ∧ ((x6 ∧ x7) → y6) = 1
(x7 ∨ x8) ∧ (x7 ∨ y7) = 1
(x8 ∨ y8) = 1
Линейное изложение материала о логических уравнениях, где задачи приводятся от простых к сложным, может привести к тому, что ученик запутается в приемах решения («за деревьями не увидит леса»). Поэтому я рекомендую просмотреть «Приложение С», в котором приводится обзор приемов и логические уравнения сравниваются между собой. Кроме того, некоторые интересные и усложненные логические уравнения приводятся еще в двух параграфах последних глав книги – «Комбинаторика при решении логических уравнений» и «Прогрессии и рекурсии в логических уравнениях». Когда вы дойдете до них, вы увидите, какие навыки остались в вашей долгосрочной памяти от изучения данного параграфа.
(Старый формат ЕГЭ) 23. Логические уравнения с множеством переменных
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Системы логических уравнений
Сколько существует различных наборов значений (x_1, x_2, … x_{10}), которые удовлетворяют всем перечисленным ниже условиям?
((x_1 wedge x_2) rightarrow (x_3 wedge x_4)=1)
((x_3 wedge x_4) rightarrow (x_5 wedge x_6)=1)
((x_5 wedge x_6) rightarrow (x_7 wedge x_8)=1)
((x_7 wedge x_8) rightarrow (x_9 wedge x_{10})=1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_{10}), при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Внешняя операция в отдельно взятом уравнении — это импликация, в результате которой должна быть истина. Импликация будет истинна, если:
(0 rightarrow 1)
(0 rightarrow 0)
(1 rightarrow 1)
Если скобка ((x_1 wedge x_2)=1) ((x_1=1 , x_2=1)), то для скобки ((x_3 wedge x_4)) возможен только вариант ((x_3=1, x_4=1)), при любых других конъюнкция будет равна 0.
Если ((x_1 wedge x_2)=0) (это возможно в следующих случаях (x_1=0, x_2=1; x_1=1, x_2=0; x_1=0, x_2=0)), то для скобки ((x_3 wedge x_4)) возможны любые значения, импликация этих скобок будет истинна. Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_{i},x_{i+1}, i in [1; 9]).
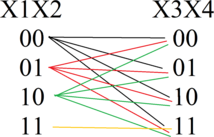
Теперь найдем общее количество решений, подставляя в отображении соответствующие x, учитывая предыдущие значения:
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 3 & 9 & 27 & 81\
hline
01 & 1 & 3 & 9 & 27 & 81\
hline
10 & 1 & 3 & 9 & 27 & 81\
hline
11 & 1 & 4 & 13 & 40 & 121\
hline
end{array})
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\
hline
01 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27 \
hline
10 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\
hline
11 & 1 & 1+1+1+1 & 3+3+3+4 & 9+9+9+13 & 27+27+27+40\
hline
end{array})
В итоге получаем: (81+81+81+121=364).
Ответ: 364
Сколько существует различных наборов значений (x_1, x_2, …x_{10}), которые удовлетворяют всем перечисленным ниже условиям?
((x_1 wedge x_2) rightarrow (x_3 vee x_4)=1)
((x_3 wedge x_4) rightarrow (x_5 vee x_6)=1)
((x_5 wedge x_6) rightarrow (x_7 vee x_8)=1)
((x_7 wedge x_8) rightarrow (x_9 vee x_{10})=1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_{10}), при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Внешняя операция в отдельно взятом уравнении — это импликация, в результате которой должна быть истина. Импликация истинна, если:
(0 rightarrow 1)
(0 rightarrow 0)
(1 rightarrow 1)
Если скобка ((x_1 wedge x_2)=1) (это верно в таких случаях (x_1=1 , x_2=1)), то для скобки ((x_3 wedge x_4)) возможны только варианты ((x_3=0 , x_4=1; x_3=1 , x_4=0; x_3=0 , x_4=0)), при ((x_3=0 , x_4=0)) ((x_3 vee x_4)=0) импликация становится равна 0.
Если ((x_1 wedge x_2)=0) (это верно в таких случаях (x_1=0 , x_2=1; x_1=1 , x_2=0; x_1=0 , x_2=0)), то для скобки ((x_3 wedge x_4)) возможны любые значения, импликация этих скобок будет истинна. Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_{i},x_{i+1}, i in [1; 9]).
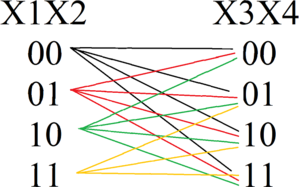
Теперь найдем общее количество решений, подставляя в отображении соответствующие x, учитывая предыдущие значения:
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 3 & 11 & 41 & 153\
hline
01 & 1 & 4 & 15 & 56 & 209\
hline
10 & 1 & 4 & 15 & 56 & 209\
hline
11& 1 & 4 & 15 & 56 & 209\
hline
end{array})
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 1+1+1+1 & 3+4+4 & 15+15+11 & 41+56+56\
hline
01 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
10 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
11 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
end{array})
В итоге получаем: (153+209+209+209=780).
Ответ: 780
Сколько существует различных наборов значений логических переменных (x_1, x_2, … x_6, y_1, y_2, … y_6,) которые удовлетворяют всем перечисленным ниже условиям?
((x_1 rightarrow (x_2 wedge y_1)) wedge (y_1 rightarrow y_2) = 1)
((x_2 rightarrow (x_3 wedge y_2)) wedge (y_2 rightarrow y_3) = 1)
…
((x_5 rightarrow (x_6 wedge y_5)) wedge (y_5 rightarrow y_6) = 1)
(x_6 rightarrow y_6 = 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_6, y_1, y_2, … y_6,) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2017, Демонстрационная версия)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,y_{i},iin [1;6].)
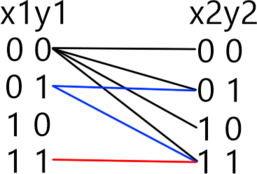
Также надо учитывать последнее уравнение, для которого не подходит только набор 1 0. Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,y,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|c|} hline
&x_1y_1&x_2y_2&x_3y_3&x_4y_4&x_5y_5&x_6y_6\
hline
00&1&1&1&1&1&1\
hline
01&1&2&3&4&5&6\
hline
10&1&1&1&1&1&0\
hline
11&1&3&6&10&15&21\
hline
end{array}]
Суммируем и получаем ответ: (1+6+0+21=28.)
Ответ: 28
Сколько существует различных наборов значений логических переменных (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10},) которые удовлетворяют всем перечисленным ниже условиям:
(((x_1rightarrow x_2)rightarrow(x_3rightarrow x_4)) wedge ((x_3rightarrow x_4)rightarrow(x_5rightarrow x_6))= 1)
(((x_5rightarrow x_6)rightarrow(x_7rightarrow x_8)) wedge ((x_7rightarrow x_8)rightarrow(x_9rightarrow x_{10}))= 1)
(x_1wedge x_3wedge x_5wedge x_7wedge x_9= 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10},) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2017, СтатГрад, 30 сентября 2016)
Чтобы выполнилось последнее уравнение, все (x) с нечётными номерами должны быть равны 1.
Перепишем нашу систему, заменяя такие (x) на 1 и разделяя каждую конъюнкцию на два уравнения:
((x_1rightarrow x_2)rightarrow(x_3rightarrow x_4)= 1)
((x_3rightarrow x_4)rightarrow(x_5rightarrow x_6)= 1)
((x_5rightarrow x_6)rightarrow(x_7rightarrow x_8)= 1)
((x_7rightarrow x_8)rightarrow(x_9rightarrow x_{10})= 1)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на два, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,x_{i+1},iin {2, 4, 6, 8, 10}.)
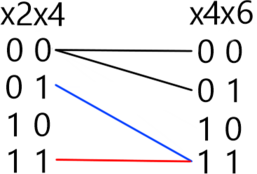
Также можно заметить, что для таких пар при наборе 1 0 уравнения истинны не будут, так как внешняя импликация будет равна 0 . Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|} hline
&x_2x_4&x_4x_6&x_6x_8&x_8x_{10}\
hline
00&1&1&1&1\
hline
01&1&1&1&1\
hline
11&1&2&3&4\
hline
end{array}]
Суммируем и получаем ответ: (1+1+4=6.)
Ответ: 6
Сколько существует различных наборов значений логических переменных (x_1, x_2,…, x_{10},) которые удовлетворяют всем перечисленным ниже условиям?
(neg (x_1 equiv x_2) equiv (x_3 equiv x_4) = 1)
(neg (x_3 equiv x_4) equiv (x_5 equiv x_6) = 1)
(neg (x_5 equiv x_6) equiv (x_7 equiv x_8) = 1)
(neg (x_7 equiv x_8) equiv (x_9 equiv x_{10}) = 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2,…, x_{10},) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2019, Основная волна)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на два, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,x_{i+1},iin {1, 3, 5, 7, 9}.)
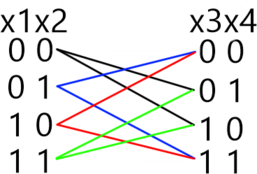
Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|} hline
&x_1x_2&x_3x_4&x_5x_6&x_7x_8&x_9x_{10}\
hline
00&1&2&4&8&16\
hline
01&1&2&4&8&16\
hline
10&1&2&4&8&16\
hline
11&1&2&4&8&16\
hline
end{array}]
Суммируем и получаем ответ: (16+16+16+16=64.)
Ответ: 64
Сколько существует различных наборов значений логических переменных (x_1, x_2, …, x_8, y_1, y_2, …, y_8,) которые удовлетворяют всем перечисленным ниже условиям?
((x_1wedge y_1)equiv (neg x_2vee neg y_2 ))
((x_2wedge y_2)equiv (neg x_3vee neg y_3 ))
…
((x_7wedge y_7)equiv (neg x_8vee neg y_8 ))
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, …, x_8, y_1, y_2, …, y_8,) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2019, Досрочная волна)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,y_{i},iin [1;8].)
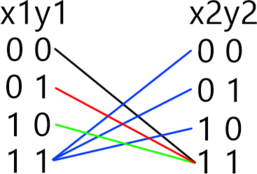
Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|c|c|c|} hline
&x_1y_1&x_2y_2&x_3y_3&x_4y_4&x_5y_5&x_6y_6&x_7y_7&x_8y_8\
hline
00&1&1&3&3&9&9&27&27\
hline
01&1&1&3&3&9&9&27&27\
hline
10&1&1&3&3&9&9&27&27\
hline
11&1&3&3&9&9&27&27&81\
hline
end{array}]
Суммируем и получаем ответ: (27+27+27+81=162.)
Ответ: 162

УСТАЛ? Просто отдохни
- Пособие
- – Системы логических уравнений
Системы логических уравнений
Задача на подсчет количества решений системы логических уравнений является одним из самых сложных заданий ЕГЭ. Методы решения таких задач лучше изучать на примерах.
Задача: Сколько различных решений имеет система логических уравнений:
( begin{cases}x_1 ∨ x_2 = 1\ x_2 ∨ x_3 = 1\ … \ x_9 ∨ x_{10} = 1 end{cases} )
Решение: В общем случаем, при небольшом количестве переменных в одном уравнении лучше решать следующим методом, который называется методом отображения:
- Составляем таблицы наборов данных для каждого уравнения
- Выявляем связи между таблицами
- Подсчитываем количество наборов в каждой строке каждой таблицы
- Суммируем количество наборов в таблице, соответсвующей последнему уравнению
Составим таблицу для первого уравнения ( x_1 + x_2 = 1 ). Если подходить к составлению таблицы формально, то надо составить таблицу истинности для выражения в уравнении и вычеркнуть из нее все строки, которые не удовлетворяют уравнению:
| ( x_1 ) | ( x_2 ) | ( x_1 + x_2 ) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Первая строка, выделенная красным цветом, не удовлетворяет уравнению, потому что значение выражения ( x_1 + x_2 ) ложно, а по уравнению значение должно быть истинным. Поэтому вычеркиваем ее и составляем таблицу наборов данных первого уравнения:
| № | ( x_1 ) | ( x_2 ) | N |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 |
В эту таблицу добавили столбец с номером строки и столбец с количеством наборов. В таблице для первого уравнения для всех строк это количество равно 1.
Для второго уравнения таблица будет такой же, потому что уравнение подобно первому только с другими переменными. Разместим эти таблицы рядом и выявим связи между строками (отобразим):
| Таблица 1 | Таблица 2 | ||||||
| № | ( x_1 ) | ( x_2 ) | N | ( x_2 ) | ( x_3 ) | N | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 2 | 1 | 0 | 1 | 1 | 0 | 2 | |
| 3 | 1 | 1 | 1 | 1 | 1 | 2 |
В таблицах есть общая переменная ( x_2 ), по ней и будем строить связи. Для первой строки таблицы 2 значение ( x_2 ) ложно, что соответствует строке 2 таблицы 1. Проводим красную линию, а в столбец N таблицы 2 ставим значение количества набора данных таблицы 1 из строки 2.
Для второй строки таблицы 2 для переменной ( x_2 ) соответствуют значения строк 1 и 3 таблицы 1. Проводим зеленую линии, а в столбец N таблицы 2 ставим значение суммы количеств наборов данных таблицы 1 из строк 1 и 3.
Для третьей строки таблицы 2 для переменной ( x_2 ) также соответствуют значения строк 1 и 3 таблицы 1. Проводим синие линии, а в столбец N таблицы 2 ставим значение суммы количеств наборов данных таблицы 1 из строк 1 и 3.
Так как все уравнения подобны, то таблицы наборов и связи между ними будут такие же, поэтому все можно свести к одной таблице только со столбцами, соответствующими количеству наборов данных:
| ( x_1x_2 ) | ( x_2x_3 ) | ( x_3x_4 ) | ( x_4x_5 ) | ( x_5x_6 ) | ( x_6x_7 ) | ( x_7x_8 ) | ( x_8x_9 ) | ( x_9x_{10} ) |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Столбец 1 содержит значения 1. Для каждого следующего столбца заполняем строки по выработанному алгоритму:
Для каждого следующего столбца для строки 1 берем значение из строки 2 предыдущего столбца. Для строк 2 и 3 – сумму значений из строк 1 и 3.
Суммируем последний столбец, соответствующий последнему уравнению: 34 + 55 + 55 = 144. Ответ: система имеет 144 решения – наборов данных.
Задача: Сколько различных решений имеет система логических уравнений:
( begin{cases}x_1 ∨ x_2 ∧ x_3= 1\ x_2 ∨ x_3 ∧ x_4 = 1\ … \ x_8 ∨ x_9 ∧ x_{10} = 1 end{cases} )
Решение: Составим таблицу наборов данных для первого уравнения ( x_1 + x_2 ⋅ x_3 = 1 ) . Можно это сделать формально как в предыдущем примере, но лучше попробуем заполнить методом рассуждений. Для ( x_1 = 0, x_2 = 0 ) нет решения уравнения, потому что каким бы не было значение переменной ( x_3), результат будет ложным. Для ( x_1 = 0, x_2 = 1 ) переменная ( x_3) должна быть истинна, чтобы результат удовлетворял бы уравнению, поэтому заполняем первую строку :
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
Для ( x_1 = 1, x_2 = 0 ) переменная ( x_3) может быть как истинной, так и ложной, поэтому добавляем две строки 1,0,0 и 1,0,1:
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
Для ( x_1 = 1, x_2 = 1 ) переменная ( x_3) также может быть как истинной, так и ложной, поэтому добавляем еще две строки 1,1,0 и 1,1,1:
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Для второго уравнения получим таблицу с такими же наборами данных, так как уравнения подобны. Добавим в таблицы столбцы для номера строк, количества наборов и расположим рядом для выявления связей:
| Таблица 1 | Таблица 2 | ||||||||
| № | ( x_1 ) | ( x_2 ) | ( x_3 ) | N | ( x_2 ) | ( x_3 ) | ( x_4 ) | N | |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
| 3 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | |
| 4 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 | |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 |
Таблицы связаны переменными ( x_2) и ( x_3), поэтому для набора значений ( x_2) и ( x_3) строки таблицы 2 ищем такие же наборы этих переменных в таблице 1. Вычисляем связи:
( N_{2-1} = N_{1-3})
( N_{2-2} = N_{1-4})
( N_{2-3} = N_{1-4})
( N_{2-4} = N_{1-1} + N_{1-5})
( N_{2-5} = N_{1-1} + N_{1-5})
В индексе для ( N) первая цифра – номер таблицы, вторая – номер строки.
Все уравнения подобны, поэтому и наборы данных и связи будут одинаковы. Строим таблицу системы только со столбцами количества набора данных:
| № | ( x_1x_2x_3 ) | ( x_2x_3x_4 ) | ( x_3x_4x_5 ) | ( x_4x_5x_6 ) | ( x_5x_6x_7 ) | ( x_6x_7x_8 ) | ( x_7x_8x_9 ) | ( x_8x_9x_{10} ) |
| 1 | 1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 |
| 2 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 3 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 4 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 |
| 5 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 |
Суммируем последний столбец: 9 + 13 + 13 + 19 + 19 = 73. Ответ: 73 решения.
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x5, y1, y2, …, y5, которые удовлетворяют всем перечисленным ниже условиям?
( (x_1 ∨ y_1) ≡ ¬(x_2 ∨ y_2) = 1 )
( (x_2 ∨ y_2) ≡ ¬(x_3 ∨ y_3) = 1 )
….
( (x_8 ∨ y_8) ≡ ¬(x_9 ∨ y_9) = 1 )
Решение: Преобразуем первое уравнение ( (x_1 + y_1) ≡ overline{(x_2 + y_2)} = 1 ).
( (x_1 + y_1) ≡ (overline{x_2} ⋅ overline{y_2}) = 1 ).
Заполним таблицу наборов данных этого уравнения методом рассуждений:
Для набора ( x_1 = 0, y_1 = 0 ) первое выражение в скобках будет ложно, поэтому и второе выражение в скобках также должно быть ложно, чтобы условие тождественного равенства этих выражений выполнилось. Второе выражение будет ложно при трех наборах данных: (( x_2 = 0, y_2 = 1 ) ), (( x_2 = 1, y_2 = 0 ) ), (( x_2 = 1, y_2 = 1 ) ). Добавим в таблицу полученные три набора:
| ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
Для набора (x_1 = 0, y_1 = 1 ) первое выражение в скобках будет истинно, поэтому и второе выражение должно быть истинно, что может быть только при ( x_2 = 0, y_2 = 0 ) . Для наборов ((x_1 = 1, y_1 = 0 ) ) и (( x_1 = 1, y_1 = 1 ) ) также будет выполняться условие тождественности только при наборе ( x_2 = 0, y_2 = 0 ). Добавим в таблицу еще три строки:
| ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
Для второго уравнения таблица наборов данных будет с такими же данными, так как уравнения подобны. Расположим таблицы для первого и второго уравнений рядом, добавил столбцы номера строки, количества наборов и выявим связи:
| Таблица 1 | Таблица 2 | ||||||||||
| № | ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) | N | ( x_2 ) | ( y_2 ) | ( x_3 ) | ( y_3 ) | N | |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 3 | |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 3 | |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 5 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 6 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
В таблицах общими являются столбцы ( x_2) и ( y_2), поэтому для строки таблицы 2 ищем в таблице 1 строки с таким же набором ( x_2) и ( y_2). По полученным связям составляем выражения для подсчета количества наборов:
( N_{2-1} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-2} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-3} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-4} = N_{1-1} )
( N_{2-5} = N_{1-2} )
( N_{2-6} = N_{1-3} )
В индексах (N) первое число номер таблицы, а второе – номер строки. Строим таблицу всех уравнений:
| № | ( x_1y_1x_2y_2 ) | ( x_2y_2x_3y_3 ) | ( x_3y_3x_4y_4 ) | ( x_4y_4x_5y_5 ) | ( x_5y_5x_6y_6 ) | ( x_6y_6x_7y_7 ) | ( x_7y_7x_8y_8 ) | ( x_8y_8x_9y_9 ) |
| 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 2 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 3 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 4 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
| 5 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
| 5 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
Суммируем последний столбец: 81 + 81 + 81 + 27 + 27 + 27 = 324. Ответ: 324 набора значений.
Решим эту же задачу другим способом, при котором выявляем связи между парами переменных. Строим таблицу отображения следующим образом:
В столбце соответствующему паре переменных ( x_1y_1 ) записываем в строках все возможные наборы этих переменных. Во втором столбце – все возможные наборы данных для пары переменных ( x_2y_2 ). Устанавливаем связи тем же способом, каким мы заполняли таблицу уравнения в первом варианте решения задачи.
| ( x_1y_1 ) | ( x_2y_2 ) | Подсчет |
| 00 | 00 | 01 + 10 + 11 |
| 01 | 01 | 00 |
| 10 | 10 | 00 |
| 11 | 11 | 00 |
Рассматриваем первое уравнение: ( (x_1 + y_1) ≡ (overline{x_2} ⋅ overline{y_2}) = 1 )
Для набора ( x_1 = 0, y_1 = 0 ) первое выражение в скобках будет ложно, поэтому и второе выражение в скобках также должно быть ложно, чтобы условие тождественного равенства этих выражений выполнилось. Второе выражение будет ложно при трех наборах данных: (( x_2 = 0, y_2 = 1 ) ), (( x_2 = 1, y_2 = 0 ) ), (( x_2 = 1, y_2 = 1 ) ). Проводим линии от строки с набором 00 первого столбца к соответствующим строкам наборов второго столбца.
Для набора (x_1 = 0, y_1 = 1 ) первое выражение в скобках будет истинно, поэтому и второе выражение должно быть истинно, что может быть только при ( x_2 = 0, y_2 = 0 ) . Проводим линию от строки 01 первого столбца к строке 00 второго столбца. Для наборов ((x_1 = 1, y_1 = 0 ) ) и (( x_1 = 1, y_1 = 1 ) ) также будет выполняться условие тождественности только при наборе ( x_2 = 0, y_2 = 0 ). Проводим линии соответствующим образом.
В последнем столбце записываем формулу подсчета, в которой показано из каких наборов состоит количество наборов для пары переменных ( x_2y_2 ).
Строим таблицу со столбцами, соответствующим парам переменных всех уравнений. В этих столбцах будем подсчитывать количество наборов для пар:
| ( x_1y_1 ) | ( x_2y_2 ) | ( x_3y_3 ) | ( x_4y_4 ) | ( x_5y_5 ) | ( x_6y_6 ) | ( x_7y_7 ) | ( x_8y_8 ) | ( x_9y_9 ) | |
| 00 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 | 81 |
| 01 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 10 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 11 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
Заполняем таблицу по полученным формулам. В первом столбце ставим единицы. Во втором столбце в строку 00 записываем сумму значений строк 01, 10, 11 первого столбца. В строку 01 второго столбца – значение строки 00 первого столбца. В строки 10,11 второго столбца также записываем значение строки 00 первого столбца. В третьем столбце для подсчета используем значения строк предыдущего – второго столбца. Аналогичным образом заполняем и остальные столбцы.
Суммируем последний столбец: 81 + 81 + 81 + 81 = 324. Получили тот же ответ.
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x5, y1, y2, …, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) = 1
(y1 → y2) ∧ (y2 →y3) ∧ (y3 → y4) ∧ (y4 → y5) = 1
(¬y1 ∨ x1) ∧ (¬y2 ∨ x2) ∧ (¬y3 ∨ x3) ∧ (¬y4 ∨ x4) ∧ (¬y5 ∨ x5) = 1
Решение: Составим таблицу наборов данных для первого уравнения. Как видно все члены конъюнкции должны быть истинны,чтобы результат был бы истинным, а истинны они могут быть при любом наборе в выражениях в скобках за исключением набора 1 0, то есть для соседних переменных запрещена эта комбинация. Исходя из этого таблица будет выглядеть так:
| x1 | x2 | x3 | x4 | x5 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для второго уравнения таблица будет содержать такие же наборы данных. Расположим таблицы рядом. Так как в третьем уравнении переменных 10, то возможных наборов для таблицы – 1024. Метод отображения применить проблематично. Поэтому попробуем рассуждать. Если значения из первой строки таблицы первого уравнения подставить в третье уравнение, то можно заметить, что только один набор из второй таблицы позволит выражению третьего уравнения быть истинным, когда все переменные y1..y5 ложны. Записываем для первой строки количество наборов 1:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Если значения из второй строки таблицы первого уравнения подставить в третье уравнение, то необходимо, чтобы ложны были бы y1…y4, а значение y5 может быть как ложно, так и истинно. Таких наборов 2 – первая и вторая строка таблицы 2. Записываем для второй строки количество наборов 2:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Аналогично рассуждая заметим, что для каждой следующей строки количество наборов из второй таблицы удовлетворяющих уравнению 3 увеличивается на 1. Наконец, для набора из последней строки первой таблицы все наборы из второй таблицы будут удовлетворять уравнению 3:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 3 | |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 4 | |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 6 |
Просуммируем записанные значения количеств наборов для строк: 1 + 2 + 3 + 4 + 5 + 6 = 20. Ответ: 20
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x6, y1, y2, …, y6, z1, z2, …, z6, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) = 1
(y1 → y2) ∧ (y2 →y3) ∧ (y3 → y4) ∧ (y4 → y5) = 1
(z1 → z2) ∧ (z2 → z3) ∧ (z3 → z4) ∧ (z4 → z5) = 1
x5 ∧ y5 ∧ z5 = 0
Решение: Первые три уравнения этой задачи подобны уравнениям предыдущей задачи, поэтому просто скопируем таблицу наборов данных x1…x5:
| x1 | x2 | x3 | x4 | x5 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для второго и третьего уравнений таблицы будут с такими же наборами данных, мы их не будем повторять. Составим таблицу наборов данных для уравнения 4. Конъюнкция будет ложна, когда ложна хотя бы одна переменная:
| x5 | y5 | z5 | |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
В первой строке таблицы значение x5 ложно. Смотрим в таблице для первого уравнения сколько наборов со значением x5 равным 0 – только одно. Аналогично для значения y5 = 0 находится один набор в таблице второго уравнения, а для z5 = 0 – один набор из таблицы третьего уравнения. Перемножаем найденные количества наборов и получаем количество наборов для первой строки (1 ⋅ 1 ⋅ 1 = 1). Для второй строки количество наборов для x5 и y5 уже известно, а для z5 = 1 из таблицы третьего уравнения находим 5 наборов, перемножаем и получаем 5 наборов для второй строки (1 ⋅ 1 ⋅ 5 = 5). Аналогично заполняем количество для остальных строк:
| x5 | y5 | z5 | |
| 0 | 0 | 0 | 1 ⋅ 1 ⋅ 1 = 1 |
| 0 | 0 | 1 | 1 ⋅ 1 ⋅ 5 = 5 |
| 0 | 1 | 0 | 1 ⋅ 5 ⋅ 1 = 5 |
| 0 | 1 | 1 | 1 ⋅ 5 ⋅ 5 = 25 |
| 1 | 0 | 0 | 5 ⋅ 1 ⋅ 1 = 5 |
| 1 | 0 | 1 | 5 ⋅ 1 ⋅ 5 = 25 |
| 1 | 1 | 0 | 5 ⋅ 5 ⋅ 1 = 25 |
Складываем полученные значения: 1 + 5 + 5 + 25 + 5 + 25 + 25 = 91. Ответ: 91.
