Алгори́тм Евкли́да — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел (или общей меры двух отрезков). Алгоритм назван в честь греческого математика Евклида (III век до н. э.), который впервые описал его в VII[1] и X[2] книгах «Начал». Это один из старейших численных алгоритмов, используемых в наше время[3].
В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары. Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как евклидово кольцо. Позже алгоритм Евклида был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.
Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA[4], широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений[5], при построении непрерывных дробей[6], в методе Штурма[7]. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких как теорема Лагранжа о сумме четырёх квадратов[8] и основная теорема арифметики[9].
История[править | править код]
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля (IV век до н. э.)[3]. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел[1] и в X книге для нахождения наибольшей общей меры двух однородных величин[2]. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.
Историками математики было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника)[10]. Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Описание[править | править код]
Алгоритм Евклида для целых чисел[править | править код]
Пусть 

определена тем, что каждое 
Тогда НОД(a, b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности[11].
Существование таких r1, r2, …, rn, то есть возможность деления с остатком m на n для любого целого m и целого n ≠ 0, доказывается индукцией по m.
Корректность этого алгоритма вытекает из следующих двух утверждений[12]:
I. Пусть a = b⋅q + r, тогда НОД (a, b) = НОД (b, r).
Доказательство
- Пусть k — любой общий делитель чисел a и b, не обязательно наибольший, тогда a = t1⋅k и b = t2⋅k, где t1 и t2 — целые числа из определения.
- Тогда k является также общим делителем чисел b и r, так как b делится на k по определению, а
(выражение в скобках есть целое число, следовательно, k делит r без остатка).
- Обратное также верно и доказывается аналогично пункту 2: любой делитель b и r так же является делителем a и b.
- Следовательно, все общие делители пар чисел (a, b) и (b, r) совпадают. Другими словами, нет общего делителя у чисел (a, b), который не был бы также делителем (b, r), и наоборот.
- В частности, наибольший общий делитель остаётся тем же самым, так как в предположении, что НОД (a, b) > НОД (b, r) или НОД (a, b) < НОД (b, r) получаются противоречия, следовательно, НОД (a, b) = НОД (b, r). Что и требовалось доказать.
II. НОД(r, 0) = r для любого ненулевого r (так как 0 делится на любое целое число).
Геометрический алгоритм Евклида[править | править код]
Пусть даны два отрезка длины a и b. Вычтем из большего отрезка меньший и заменим больший отрезок полученной разностью. Повторяем эту операцию, вычитая из большего отрезка меньший, пока отрезки не станут равны. Если это произойдёт, то исходные отрезки соизмеримы, и последний полученный отрезок есть их наибольшая общая мера. Если общей меры нет, то процесс бесконечен. В таком виде алгоритм описан Евклидом[2] и реализуется с помощью циркуля и линейки.
Пример[править | править код]
Для иллюстрации алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала от 1071 отнимем кратное значение 462, пока не получим разность меньше, чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147:
- 1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим разность меньше, чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21:
- 462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим разность меньше, чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка:
- 147 = 7 × 21 + 0.
Таким образом последовательность a > b > r1 > r2 > r3 > … > rn в данном конкретном случае будет выглядеть так:
- 1071 > 462 > 147 > 21.
Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462) = 21.
В табличной форме шаги были следующие:
| Шаг k | Равенство | Частное и остаток |
|---|---|---|
| 0 | 1071 = q0 462 + r0 | q0 = 2 и r0 = 147 |
| 1 | 462 = q1 147 + r1 | q1 = 3 и r1 = 21 |
| 2 | 147 = q2 21 + r2 | q2 = 7 и r2 = 0; алгоритм заканчивается |
Если требуется найти НОД для более чем двух чисел, алгоритм аналогичен, на каждом шаге все числа, кроме
наименьшего, заменяются остатками по модулю наименьшего. Нулевые остатки, если получатся, вычёркиваются. Алгоритм завершается, когда остаётся одно ненулевое число, это и есть НОД.
Применения[править | править код]
Расширенный алгоритм Евклида и соотношение Безу[править | править код]
Формулы для 
- НОД
Здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу[13]. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.
Цепные дроби[править | править код]
Алгоритм Евклида достаточно тесно связан с цепными дробями[6]. Отношение a/b допускает представление в виде цепной дроби:
-
.
При этом цепная дробь без последнего члена равна отношению коэффициентов Безу t/s, взятому со знаком минус:
-
.
Последовательность равенств, задающая алгоритм Евклида, может быть переписана в форме:
Последнее слагаемое в правой части равенства всегда равно обратному значению левой части следующего уравнения. Поэтому первые два уравнения могут быть объединены в форме:
Третье равенство может быть использовано, чтобы заменить знаменатель выражения r1/r0, получим:
Последнее отношение остатков rk/rk−1 всегда может быть заменено с использованием следующего равенства в последовательности, и так до последнего уравнения. Результатом является цепная дробь:
В приведённом выше примере НОД(1071, 462) был посчитан и были найдены частные qk, равные 2, 3 и 7 соответственно. Поэтому 1071/462 может быть записана как:
Линейные диофантовы уравнения[править | править код]
Диофантово уравнение — это уравнение с целочисленными коэффициентами и с одним или несколькими переменными, причём ставится задача поиска лишь его целых корней. Такое уравнение может иметь бесконечно много решений, конечное число решений или не иметь их вовсе. Простейшее диофантово уравнение — линейное с двумя неизвестными:

где a, b, c — целые числа. С помощью алгоритма Евклида может быть найдено полное решение уравнения такого типа[5]. Сначала с помощью этого алгоритма можно определить d = НОД(a, b). Затем, используя расширенный алгоритм Евклида, определяются такие k и l, что:

То есть x = k и y = l — это частное решение уравнения при c = d. Получается, что если c = q⋅d, то x = q⋅k, y = q⋅l — частное решение исходного уравнения, так как:

Обратно, если существует хотя бы одно решение уравнения, то c кратно d. Это следует из того, что d делит и a, и b (а значит, и всю левую часть), поэтому должно делить и c (правую часть). Таким образом, линейное диофантово уравнение имеет хотя бы одно решение тогда и только тогда, когда c кратно НОД(a, b).
Вариации и обобщения[править | править код]
Евклидово кольцо[править | править код]
Кольца, в которых применим алгоритм Евклида, называются евклидовыми кольцами[14]. К ним относятся, в частности, кольца целых чисел и кольца многочленов.
Обобщённый алгоритм Евклида для многочленов[править | править код]
Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k[x] от одной переменной над произвольным полем k, поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел получается последовательность полиномиальных остатков (PRS)[15].
Пример для кольца Z[x]
Пусть cont(f) по определению — НОД коэффициентов многочлена 
![{displaystyle Z[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf91b78e978789ccc3b0f842ac2671630764ab94)
![{displaystyle Z[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf91b78e978789ccc3b0f842ac2671630764ab94)






Таким образом, задача поиска НОД двух произвольных многочленов сводится к задаче поиска НОД примитивных полиномов.
Пусть есть два примитивных многочлена p1(x) и p2(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p1(x)) = m и deg(p2(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами.
Под псевдоделением будем понимать, что самому делению предшествует умножение полинома 


где 

Итак, ![p_{1}(x),p_{2}(x)in Z[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e297db2632ebbea8d15bc4d9ff331c2ccfc3e8ed)

1. Вычисление НОД содержаний:


2. Вычисление примитивных частей:


3. Построение последовательности полиномиальных остатков:







4. Возврат результата:
Если 


Ускоренные версии алгоритма[править | править код]
- Одним из методов ускорения целочисленного алгоритма Евклида является использование симметричного остатка[16]:
-
- где
- Одна из версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. Применение стратегии «разделяй и властвуй» позволяет уменьшить асимптотическую сложность алгоритма[16].
Вычислительная сложность алгоритма[править | править код]
Число шагов в алгоритме Евклида для НОД(x,y). Более светлые точки (красные и жёлтые) указывают на относительно меньшее количество шагов, тогда как более тёмные точки (фиолетовые и синие) на большее количество шагов. Самая большая тёмная область следует за прямой y = Φx, где Φ — золотое сечение.
Вычислительная сложность алгоритма Евклида изучена полностью.[17] Эта сложность может быть описана произведением количества шагов деления, требуемых алгоритмом, на вычислительную сложность одного шага. Первый известный анализ алгоритма Евклида был предложен Рейнаудом в 1811.[18] Он показал, что число шагов алгоритма для пары чисел (u, v) ограничено v. Позже он улучшил оценку до v/2 + 2. Эмиль Леже в 1837 году изучил наихудший случай, когда для вычисления НОД подаются последовательные числа Фибоначчи.[19] Затем, в 1841 году, Пьер Джосеф Финк показал,[20] что количество шагов алгоритма не превышает 2 log2 v + 1. Следовательно, алгоритм работает за полиномиальное время от размера меньшего из пары чисел (u, v).[19] Анализ Финка был уточнён Габриэлем Ламе в 1844 году.[21] Он показал, что количество шагов, необходимых для завершения алгоритма, не более чем в пять раз превышает h — количество цифр в десятичном представлении меньшего из пары чисел (u, v).[22][23]
Когда НОД вычисляется для чисел, которые вписываются в одно машинное слово, каждый шаг алгоритма занимает постоянное время. В данном случае анализ Ламе предполагает, что вычислительная сложность оценивается как O(h). Однако в модели расчёта, подходящей для вычислений с числами больше одного машинного слова, оценка сложности вычисления одного остатка может быть O(h2).[24] В этом случае общее время для всех этапов алгоритма можно проанализировать с помощью телескопического ряда, показав, что это также O(h2). Для ускорения алгоритма Евклида могут быть использованы современные алгоритмические методы, основанные на методе Шёнхаге — Штрассена для быстрого целочисленного умножения. Это приводит к квазиполиномиальному времени.[25]
Количество шагов[править | править код]
Число шагов для вычисления НОД двух натуральных чисел a и b обозначим как T(a, b). Если g — это наибольший общий делитель a и b, тогда a = mg и b = ng для двух взаимно простых чисел m и n. Тогда T(a, b) = T(m, n), что можно заметить, если разделить уравнения, полученные при вычислении НОД для пары (a, b), на g.[26] Используя тот же принцип, число шагов алгоритма остаётся неизменным, если a и b умножаются на общий множитель w, что эквивалентно равенству T(a, b) = T(wa, wb). Следовательно, количество шагов T может сильно различаться между соседними парами чисел, такими как (a, b) и (a, b+1), так как данная величина зависит от НОД.
Рекурсивный характер алгоритма Евклида даёт следующее уравнение T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1, где T(x, 0) = 0 по предположению.[17]
Наихудший случай[править | править код]
Если для алгоритма Евклида требуются N шагов для пары натуральных чисел a > b > 0, наименьшие значения a и b, для которых это выполняется — числа Фибоначчи FN+2 и FN+1 соответственно.[27] Тогда, если алгоритм Евклида требует N шагов для пары чисел (a,b), где a > b, выполняются следующие неравенства a ≥ FN+2 и b ≥ FN+1. Доказать это можно по математической индукции. Если N = 1, тогда a делится на b без остатка. Наименьшие натуральные числа, для которых это верно, равны b = 1 и a = 2, соответственно F2 и F3. Предположим теперь, что результат выполняется для всех значений N до M − 1. Первый шаг алгоритма Евклида с M шагами a = q0b + r0, и алгоритм Евклида для пары чисел (b,r0), где b > r0, требует M − 1 шагов. По предположению индукции имеем b ≥ FM+1 и r0 ≥ FM. Следовательно, a = q0b + r0 ≥ b + r0 ≥ FM+1 + FM = FM+2, что является искомым неравенством. Это доказательство, опубликованное Габриэлем Ламе в 1844 году, представляет собой начало теории сложности вычислений,[28] а также первое практическое применение чисел Фибоначчи.[27]
Теорема Ламе[править | править код]
Число делений с остатком в процессе применения алгоритма Евклида не превосходит упятеренного количества цифр меньшего числа 
Среднее[править | править код]
Существуют различные способы вычисления среднего количества шагов алгоритма. Первый способ вычисления — среднее время T(a), необходимое для вычисления НОД заданного числа a и меньшего натурального числа b, выбранного с равной вероятностью из целых чисел от 0 до a − 1.[17]
Однако, поскольку T(a, b) сильно колеблется в зависимости от НОД двух чисел, усреднённая функция T(a) также является «шумной».[30] Для того, чтобы уменьшить этот шум, второе среднее τ(a) берётся по всем числам, взаимно простым с a.
где φ(a) функция Эйлера. Это среднее плавно растёт с ростом a.[31]
Константа (константа Портера[32]) в этой формуле 
Третье среднее значение Y(n) определяется как среднее число шагов, требуемых, когда a и b выбираются случайным образом (с равномерным распределением) от 1 до n.
Вычислительная сложность шага[править | править код]
На каждом шаге алгоритма Евклида вычисляется коэффициент qk и остаток rk для заданной пары целых чисел rk−2 и rk−1. Эти величины связаны следующим соотношением:
- rk−2 = qk rk−1 + rk
Вычислительная сложность каждого шага связана главным образом с нахождением qk, так как остаток rk можно быстро вычислить, используя rk−2, rk−1, и qk
- rk = rk−2 − qk rk−1
Вычислительная сложность операции деления чисел размером h бит оценивается как O(h(ℓ+1)), где ℓ размер частного.[24]
Для сравнения, исходный алгоритм Евклида, с использованием вычитания, может быть намного медленнее. В большинстве случаев коэффициент qk является малым числом. Вероятность данного частного q примерно равна ln|u/(u − 1)|, где u = (q + 1)2.[33] Для иллюстрации вероятность частного 1, 2, 3 или 4 составляет примерно 41,5 %, 17,0 %, 9,3 % и 5,9 % соответственно. Так как операция вычитания быстрее, чем деление, особенно для чисел больше одного машинного слова,[34] алгоритм Евклида с использованием вычитания может быть более конкурентоспособным в сравнении с алгоритмом, использующим деление.[35] Это используется в бинарном алгоритме вычисления НОД.[36]
Оценка сложности алгоритма вычисляется как произведение количества шагов на время выполнения одного шага. Она показывает, что алгоритм Евклида растёт квадратично O(h2), где h — среднее число цифр в двух начальных числах a и b в десятичной записи. Пусть h0, h1, …, hN−1 представляют число цифр в последовательных остатках r0, r1, …, rN−1. Так как число шагов N растёт линейно с h, время работы ограничено следующим выражением:
Примечания[править | править код]
- ↑ 1 2 Мордухай-Болтовской, 1949, с. 11—13.
- ↑ 1 2 3 Мордухай-Болтовской, 1949, с. 103—105.
- ↑ 1 2 Кнут, 2001, с. 378.
- ↑ Menezes, 1996, с. 286.
- ↑ 1 2 Курант, 2001, с. 74—76.
- ↑ 1 2 Виноградов, 1952, с. 14—18.
- ↑ Энгелер, 1987, с. 24—31.
- ↑ Тихомиров, 2003, с. 11—14.
- ↑ Калужин, 1969, с. 6—14.
- ↑ Цейтен, 1932, с. 112—114.
- ↑ Виноградов, 1952, с. 9—10.
- ↑ Курант, 2001, с. 67—70.
- ↑ Хассе, 1953, с. 29—30.
- ↑ Курош, 1973, с. 91—92.
- ↑ Панкратьев, 2007, с. 54—58.
- ↑ 1 2 Gathen, 2013, с. 313—326.
- ↑ 1 2 3 Knuth, 1997, с. 344.
- ↑ Shallit, 1994, с. 414.
- ↑ 1 2 Shallit, 1994, с. 401—419.
- ↑ Shallit, 1994, с. 413.
- ↑ Lame, 1844, с. 867—870.
- ↑ Grossman, 1924, с. 443.
- ↑ Абрамов С. А. Математические построения и программирование. — М., Наука, 1978. — Тираж 100 000 экз. — c. 170
- ↑ 1 2 Knuth, 1997, с. 257—261.
- ↑ Moeller, 2005, с. 1.
- ↑ Ore, 1948, с. 45.
- ↑ 1 2 Knuth, 1997, с. 343.
- ↑ LeVeque, 1996, с. 3.
- ↑ Абрамов С. А. Математические построения и программирование. — М., Наука, 1978. — Тираж 100 000 экз. — c. 170
- ↑ Knuth, 1997, с. 353.
- ↑ Tonkov, 1974, с. 47—57.
- ↑ Weisstein, Eric W. Porter’s Constant (англ.) на сайте Wolfram MathWorld.
- ↑ Knuth, 1997, с. 352.
- ↑ Wagon, 1999, с. 335—336.
- ↑ Cohen, 1993, с. 14.
- ↑ Cohen, 1993, с. 14—15, 17-18.
Литература[править | править код]
- Абрамов С. А. Самый знаменитый алгоритм // Квант / под ред. И. К. Кикоин, Ю. А. Осипьян, В. В. Козлов, А. Л. Семёнов, А. А. Гайфуллин — МИАН, 1985. — вып. 11. — С. 44—46. — ISSN 0130-2221
- Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — 180 с. — ISBN 978-5-811-40535-0.
- Калужин Л. А. Основная теорема арифметики. — Популярные лекции по математике. — М.: Наука, 1969. — 33 с.
- Кнут Д. Э. Искусство программирования. — Вильямс, 2001. — Т. 2. — 829 с. — ISBN 5-8459-0081-6.
- Курант Р., Роббинс Г. Дополнение к главе I, § 4. // Что такое математика? — 3-e изд., испр. и доп. — М., 2001. — 568 с. — ISBN 5-900916-45-6.
- Курош А. Г. Лекции по общей алгебре / под ред. О. Н. Головин — 2-е изд. — М.: Наука, 1973. — 400 с. — ISBN 978-5-8114-0617-3
- Начала Евклида / пер.с греч. и комм. Д. Д. Мордухая-Болтовского под ред. Выгодского М. Я. и Веселовского И. Н.. — ГИТТЛ, 1949. — Т. 2. — 511 с.
- Панкратьев Е. В. Элементы компьютерной алгебры. — ИНТУИТ, 2007. — 217 с. — ISBN 978-5-955-60099-4.
- Тихомиров В. М. Великие математики прошлого и их великие теоремы. — 2-е изд., испр. — МЦНМО, 2003. — 16 с. — ISBN 5-94057-110-7.
- Хассе Г. Лекции по теории чисел. — Изд. иностранной литературы, 1953. — 527 с.
- Цейтен Г. Г. История математики в Древности и в Средние века. — ГТТИ, 1932. — 232 с.
- Энгелер Э. Метаматематика элементарной математики. — М.: Мир, 1987. — 128 с.
- Cohen H. A Course in Computational Algebraic Number Theory. — Springer-Verlag, 1993. — ISBN 0-387-55640-0.
- von zur Gathen J., Gerhard J. Modern Computer Algebra. — Cambridge University Press, 2013. — 808 с. — ISBN 978-1-107-03903-2.
- Grossman H. On the Number of Divisions in Finding a G.C.D. (англ.) // The American Mathematical Monthly. — 1924. — Vol. 31, iss. 9. — P. 443. — doi:10.2307/2298146. — JSTOR 2298146.
- Knuth D. E. The Art of Computer Programming. — 3. — Addison–Wesley, 1997. — Т. 2: Seminumerical Algorithms. — ISBN 0-201-89684-2.
- Lamé G. Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers (фр.). — Comptes Rendus Acad. Sci., 1844. — No 19.
- LeVeque W. J. Fundamentals of Number Theory (англ.). — Dover, 1996. — ISBN 0-486-68906-9.
- Menezes A., van Oorschot P., Vanstone S. Handbook of Applied Cryptography. — CRC-Press, 1996. — 816 с. — (Discrete Mathematics and Its Applications). — ISBN 0-8493-8523-7.
- Moeller Niels. Mathematics of Computation (англ.). — 2005.
- Ore O. Number Theory and Its History (англ.). — McGraw–Hill, 1948.
- Shallit J. Origins of the analysis of the Euclidean algorithm (англ.) // Historia Math.. — 1994. — Vol. 21. — doi:10.1006/hmat.1994.1031.
- Tonkov T. On the average length of finite continued fractions (англ.) // Acta Arithmetica. — 1974. — Vol. 26.
- Wagon S. Mathematica in Action (англ.). — Springer-Verlag, 1999. — ISBN 0-387-98252-3.
Ссылки[править | править код]
- Реализация алгоритма Евклида на языке Pascal
- Алгоритм Евклида на e-maxx.ru
- Реализация расширенного алгоритма Евклида на языке C
Пусть требуется
найти количество шагов (или операций
деления) алгоритма Евклида, применённого
к a > b > 0.
Вновь используем обозначения, введённые
в 1.2, и рассмотрим поведение последовательности
остатков в предположении, что алгоритм
завершился за n
шагов (значение n
заранее неизвестно):
c0 > c1 > c2 > c3 > … >cn 1 > cn > cn + 1 = 0.
Оказывается, остатки убывают не менее
чем вдвое за каждую пару шагов.
Лемма
1.1. При
i = 1, 2, …, n 2
выполняется
неравенство
ci > 2ci + 2.
Доказательство:
ci = qi +1 ci +1 + ci + 2 ci +1 + ci + 2 > 2ci + 2.
Лемма
1.2. Пусть
k
такое
натуральное число, что применение
алгоритма Евклида к c0
и c1
не заканчивается
после 2k
шагов
(делений), т. е.
c2k + 1 1.
Тогда
c1 > 2k.
Доказательство:
по лемме 1.1 имеем
c1 > 2c3 > 4c5 > … > 2kc2 k + 1 2k.
Теорема
1.1. Число
делений, требуемых алгоритмом Евклида
при применении к
c0, c1 ,
не превосходит
2 log2 c1
.
Доказательство.
Пусть k
такое натуральное число, что c1 2k.
Тогда по лемме 1.2 число шагов алгоритма
Евклида не превосходит 2k
(от противного: если превосходит, то
c1 > 2k).
Если k
такое, что 2k 1 < c1 2k,
то k = log2 c1
и можно взять именно это k
для оценки
числа шагов. Тогда 2k = 2 log2 c1.
Отметим, что слова
«не превосходит»
в формулировке теоремы выражают оценку
худшего
случая. При этом худший случай согласно
теореме определяется только значением
c1,
поскольку после первого шага алгоритма
далее роль играет не c0,
а остаток c2
от деления c0
на c1,
который лежит в диапазоне 0…c1 1.
При работе с целыми
числами стандартной длины в языке Турбо
Паскаль MaxInt = 32767 = 215 1.
Поэтому c1 215 1
и число шагов алгоритма Евклида не
превосходит 2 log2 c1 = 215 = 30.
Наше рассмотрение
основывалось на локальном свойстве
последовательности остатков. Оказывается,
можно применить другой метод анализа,
основанный на исследовании поведения
последовательности остатков «в целом»,
который может дать лучшую оценку.
1.6. Числа Фибоначчи и анализ алгоритма Евклида
Сначала приведём
неформальные соображения. Медленное
убывание последовательности остатков
естественно ожидать в том случае, когда
частное от деления на каждом шаге равно
1 (возможно, кроме последнего), а остаток
принимает наибольшее из возможных
значений. Рассмотрим остатки в порядке,
обратном порядку вычислений. Наименьшим
остатком на предпоследнем шаге будет
1, т. е. cn = 1
и cn 2 = 1 cn 1 + 1.
Наименьшим остатком на предыдущем шаге
будет 2, т. е. cn 1 = 2
и тогда cn 2 = 12 + 1 = 3.
Следовательно, ранее должно было бы
быть cn 3 = 13 + 2,
т. е. cn 3 = 5.
Аналогично ещё
раньше cn 4 = 15 + 3 = 8
и т.д. В этой последовательности легко
угадывается последовательность
Фибоначчи. Далее формально рассмотрим
связь последовательности остатков,
порождаемых алгоритмом Евклида, и чисел
Фибоначчи.
Лемма
1.3. Пусть
применение алгоритма Евклида к c0, c1
требует n
шагов, тогда
c1 Fn + 1, c2 Fn, c3 Fn 1, …, cn 1 F3, cn F2.
Доказательство.
Запишем последовательность этих
неравенств в виде
cn i Fi + 2, i = 0, 1, …, n 1.
Доказательство
проведём по индукции:
(а) при i = 0
имеем cn F2 = 1,
поскольку cn = gcd(c0, c1) 1;
при i = 1
cn 1 F3 = 2,
поскольку из cn 1 = 1
следовало бы cn = 0;
(б) пусть наше
предположение верно при i = 0, 1, …, k ,
в том числе при i = k 1
имеем cn k + 1 Fk + 1, а
при i = k
cn k Fk + 2;
докажем, что при i = k + 1
справедливо cn k 1 Fk + 3.
Действительно,
cn k 1 = qn k cn k + cn k + 1 cn k + cn k + 1 Fk + 2 + Fk + 1 = Fk + 3.
Теорема
1.2. Пусть
k такое
натуральное число, что c1 < Fk + 2,
тогда
применение алгоритма Евклида к числам
c0, c1 завершится
не более чем за k
шагов. При этом ровно k
шагов потребуется при c1 = Fk + 1,
c0 = Fk + 2.
Доказательство
(от противного).
Если алгоритм Евклида завершается за
число шагов s > k,
то по лемме
1.3 имеем
c1 Fs + 1
и при s = k + 1
это даёт c1 Fk + 2,
что противоречит условию теоремы 1.2.
При этом очевидно,
что если c1 = Fk + 1
и c0 = Fk + 2,
то потребуется в точности k
шагов (на
последнем шаге ck = F2 = 1).
Это фактически
теорема Ламе.
Габриель Ламе (G. Lamé)
французский математик и инженер
(17951870),
в 182032
гг. жил и работал в России. Теорема Ламе
(1845 г.)
исторически первое применение чисел
Фибоначчи к анализу алгоритмов.
Следствие
теоремы 1.2.
Если a 0,
b 0
и b < N,
то число шагов в алгоритме Евклида,
применённом к числам a
и b,
не превосходит
log(5
N) 2.
Доказательство.
Пусть Fk + 1 b < Fk + 2,
тогда число шагов не превосходит k
(по теореме). Из неравенства Fk + 1 b
и (1.3) следует
Поскольку то
Логарифмируя
последнее неравенство, получимk < log(5 (b + 1)) 1
или k log(5 (b + 1)) 2.
Учитывая, что b + 1 N,
получаем требуемое неравенство.
Для того чтобы
сопоставить этот результат с теоремой
1.1, перейдём от log
к log2:
log(5 N) = 1.44 log2 N + 1.672.
Таким образом,
число шагов алгоритма Евклида не
превосходит
1.44 log2 N 0.32.
Пусть N = 215 = 32768,
тогда по теореме 1.2 число шагов не более
22 (по теореме 1.1
не более 30, см. 1.4).
This article is about an algorithm for the greatest common divisor. For the mathematics of space, see Euclidean geometry. For other uses of “Euclidean”, see Euclidean (disambiguation).
Euclid’s method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common “unit” length. The length DC being shorter, it is used to “measure” BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus’s example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).
In mathematics, the Euclidean algorithm,[note 1] or Euclid’s algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout’s identity.
The version of the Euclidean algorithm described above (and by Euclid) can take many subtraction steps to find the GCD when one of the given numbers is much bigger than the other. A more efficient version of the algorithm shortcuts these steps, instead replacing the larger of the two numbers by its remainder when divided by the smaller of the two (with this version, the algorithm stops when reaching a zero remainder). With this improvement, the algorithm never requires more steps than five times the number of digits (base 10) of the smaller integer. This was proven by Gabriel Lamé in 1844 (Lamé’s Theorem),[1][2] and marks the beginning of computational complexity theory. Additional methods for improving the algorithm’s efficiency were developed in the 20th century.
The Euclidean algorithm has many theoretical and practical applications. It is used for reducing fractions to their simplest form and for performing division in modular arithmetic. Computations using this algorithm form part of the cryptographic protocols that are used to secure internet communications, and in methods for breaking these cryptosystems by factoring large composite numbers. The Euclidean algorithm may be used to solve Diophantine equations, such as finding numbers that satisfy multiple congruences according to the Chinese remainder theorem, to construct continued fractions, and to find accurate rational approximations to real numbers. Finally, it can be used as a basic tool for proving theorems in number theory such as Lagrange’s four-square theorem and the uniqueness of prime factorizations.
The original algorithm was described only for natural numbers and geometric lengths (real numbers), but the algorithm was generalized in the 19th century to other types of numbers, such as Gaussian integers and polynomials of one variable. This led to modern abstract algebraic notions such as Euclidean domains.
Background: greatest common divisor[edit]
The Euclidean algorithm calculates the greatest common divisor (GCD) of two natural numbers a and b. The greatest common divisor g is the largest natural number that divides both a and b without leaving a remainder. Synonyms for GCD include greatest common factor (GCF), highest common factor (HCF), highest common divisor (HCD), and greatest common measure (GCM). The greatest common divisor is often written as gcd(a, b) or, more simply, as (a, b),[3] although the latter notation is ambiguous, also used for concepts such as an ideal in the ring of integers, which is closely related to GCD.
If gcd(a, b) = 1, then a and b are said to be coprime (or relatively prime).[4] This property does not imply that a or b are themselves prime numbers.[5] For example, 6 and 35 factor as 6 = 2 × 3 and 35 = 5 × 7, so they are not prime, but their prime factors are different, so 6 and 35 are coprime, with no common factors other than 1.
A 24×60 rectangle is covered with ten 12×12 square tiles, where 12 is the GCD of 24 and 60. More generally, an a×b rectangle can be covered with square tiles of side-length c only if c is a common divisor of a and b.
Let g = gcd(a, b). Since a and b are both multiples of g, they can be written a = mg and b = ng, and there is no larger number G > g for which this is true. The natural numbers m and n must be coprime, since any common factor could be factored out of m and n to make g greater. Thus, any other number c that divides both a and b must also divide g. The greatest common divisor g of a and b is the unique (positive) common divisor of a and b that is divisible by any other common divisor c.[6]
The greatest common divisor can be visualized as follows.[7] Consider a rectangular area a by b, and any common divisor c that divides both a and b exactly. The sides of the rectangle can be divided into segments of length c, which divides the rectangle into a grid of squares of side length c. The GCD g is the largest value of c for which this is possible. For illustration, a 24×60 rectangular area can be divided into a grid of: 1×1 squares, 2×2 squares, 3×3 squares, 4×4 squares, 6×6 squares or 12×12 squares. Therefore, 12 is the GCD of 24 and 60. A 24×60 rectangular area can be divided into a grid of 12×12 squares, with two squares along one edge (24/12 = 2) and five squares along the other (60/12 = 5).
The greatest common divisor of two numbers a and b is the product of the prime factors shared by the two numbers, where each prime factor can be repeated as many times as divides both a and b.[8] For example, since 1386 can be factored into 2 × 3 × 3 × 7 × 11, and 3213 can be factored into 3 × 3 × 3 × 7 × 17, the GCD of 1386 and 3213 equals 63 = 3 × 3 × 7, the product of their shared prime factors (with 3 repeated since 3 × 3 divides both). If two numbers have no common prime factors, their GCD is 1 (obtained here as an instance of the empty product), in other words they are coprime. A key advantage of the Euclidean algorithm is that it can find the GCD efficiently without having to compute the prime factors.[9][10] Factorization of large integers is believed to be a computationally very difficult problem, and the security of many widely used cryptographic protocols is based upon its infeasibility.[11]
Another definition of the GCD is helpful in advanced mathematics, particularly ring theory.[12] The greatest common divisor g of two nonzero numbers a and b is also their smallest positive integral linear combination, that is, the smallest positive number of the form ua + vb where u and v are integers. The set of all integral linear combinations of a and b is actually the same as the set of all multiples of g (mg, where m is an integer). In modern mathematical language, the ideal generated by a and b is the ideal generated by g alone (an ideal generated by a single element is called a principal ideal, and all ideals of the integers are principal ideals). Some properties of the GCD are in fact easier to see with this description, for instance the fact that any common divisor of a and b also divides the GCD (it divides both terms of ua + vb). The equivalence of this GCD definition with the other definitions is described below.
The GCD of three or more numbers equals the product of the prime factors common to all the numbers,[13] but it can also be calculated by repeatedly taking the GCDs of pairs of numbers.[14] For example,
- gcd(a, b, c) = gcd(a, gcd(b, c)) = gcd(gcd(a, b), c) = gcd(gcd(a, c), b).
Thus, Euclid’s algorithm, which computes the GCD of two integers, suffices to calculate the GCD of arbitrarily many integers.
Description[edit]
Procedure[edit]
The Euclidean algorithm proceeds in a series of steps, with the output of each step used as the input for the next. Track the steps using an integer counter k, so the initial step corresponds to k = 0, the next step to k = 1, and so on.
Each step begins with two nonnegative remainders rk−2 and rk−1, with rk−2 > rk−1. The kth step performs division-with-remainder to find the quotient qk and remainder rk so that:
That is, multiples of the smaller number rk−1 are subtracted from the larger number rk−2 until the remainder rk is smaller than rk−1. Then the algorithm proceeds to the (k+1)th step starting with rk−1 and rk.
In the initial step k = 0, the remainders are set to r−2 = a and r−1 = b, the numbers for which the GCD is sought. In the next step k = 1, the remainders are r−1 = b and the remainder r0 of the initial step, and so on. The algorithm proceeds in a sequence of equations
The algorithm need not be modified if a < b: in that case, the initial quotient is q0 = 0, the first remainder is r0 = a, and henceforth rk−2 > rk−1 for all k ≥ 1.
Since the remainders are non-negative integers that decrease with every step, the sequence 
Proof of validity[edit]
The validity of the Euclidean algorithm can be proven by a two-step argument.[16] In the first step, the final nonzero remainder rN−1 is shown to divide both a and b. Since it is a common divisor, it must be less than or equal to the greatest common divisor g. In the second step, it is shown that any common divisor of a and b, including g, must divide rN−1; therefore, g must be less than or equal to rN−1. These two opposite inequalities imply rN−1 = g.
To demonstrate that rN−1 divides both a and b (the first step), rN−1 divides its predecessor rN−2
- rN−2 = qN rN−1
since the final remainder rN is zero. rN−1 also divides its next predecessor rN−3
- rN−3 = qN−1 rN−2 + rN−1
because it divides both terms on the right-hand side of the equation. Iterating the same argument, rN−1 divides all the preceding remainders, including a and b. None of the preceding remainders rN−2, rN−3, etc. divide a and b, since they leave a remainder. Since rN−1 is a common divisor of a and b, rN−1 ≤ g.
In the second step, any natural number c that divides both a and b (in other words, any common divisor of a and b) divides the remainders rk. By definition, a and b can be written as multiples of c : a = mc and b = nc, where m and n are natural numbers. Therefore, c divides the initial remainder r0, since r0 = a − q0b = mc − q0nc = (m − q0n)c. An analogous argument shows that c also divides the subsequent remainders r1, r2, etc. Therefore, the greatest common divisor g must divide rN−1, which implies that g ≤ rN−1. Since the first part of the argument showed the reverse (rN−1 ≤ g), it follows that g = rN−1. Thus, g is the greatest common divisor of all the succeeding pairs:[17][18]
- g = gcd(a, b) = gcd(b, r0) = gcd(r0, r1) = … = gcd(rN−2, rN−1) = rN−1.
Worked example[edit]
Subtraction-based animation of the Euclidean algorithm. The initial rectangle has dimensions a = 1071 and b = 462. Squares of size 462×462 are placed within it leaving a 462×147 rectangle. This rectangle is tiled with 147×147 squares until a 21×147 rectangle is left, which in turn is tiled with 21×21 squares, leaving no uncovered area. The smallest square size, 21, is the GCD of 1071 and 462.
For illustration, the Euclidean algorithm can be used to find the greatest common divisor of a = 1071 and b = 462. To begin, multiples of 462 are subtracted from 1071 until the remainder is less than 462. Two such multiples can be subtracted (q0 = 2), leaving a remainder of 147:
- 1071 = 2 × 462 + 147.
Then multiples of 147 are subtracted from 462 until the remainder is less than 147. Three multiples can be subtracted (q1 = 3), leaving a remainder of 21:
- 462 = 3 × 147 + 21.
Then multiples of 21 are subtracted from 147 until the remainder is less than 21. Seven multiples can be subtracted (q2 = 7), leaving no remainder:
- 147 = 7 × 21 + 0.
Since the last remainder is zero, the algorithm ends with 21 as the greatest common divisor of 1071 and 462. This agrees with the gcd(1071, 462) found by prime factorization above. In tabular form, the steps are:
| Step k | Equation | Quotient and remainder |
|---|---|---|
| 0 | 1071 = q0 462 + r0 | q0 = 2 and r0 = 147 |
| 1 | 462 = q1 147 + r1 | q1 = 3 and r1 = 21 |
| 2 | 147 = q2 21 + r2 | q2 = 7 and r2 = 0; algorithm ends |
Visualization[edit]
The Euclidean algorithm can be visualized in terms of the tiling analogy given above for the greatest common divisor.[19] Assume that we wish to cover an a×b rectangle with square tiles exactly, where a is the larger of the two numbers. We first attempt to tile the rectangle using b×b square tiles; however, this leaves an r0×b residual rectangle untiled, where r0 < b. We then attempt to tile the residual rectangle with r0×r0 square tiles. This leaves a second residual rectangle r1×r0, which we attempt to tile using r1×r1 square tiles, and so on. The sequence ends when there is no residual rectangle, i.e., when the square tiles cover the previous residual rectangle exactly. The length of the sides of the smallest square tile is the GCD of the dimensions of the original rectangle. For example, the smallest square tile in the adjacent figure is 21×21 (shown in red), and 21 is the GCD of 1071 and 462, the dimensions of the original rectangle (shown in green).
Euclidean division[edit]
At every step k, the Euclidean algorithm computes a quotient qk and remainder rk from two numbers rk−1 and rk−2
- rk−2 = qk rk−1 + rk
where the rk is non-negative and is strictly less than the absolute value of rk−1. The theorem which underlies the definition of the Euclidean division ensures that such a quotient and remainder always exist and are unique.[20]
In Euclid’s original version of the algorithm, the quotient and remainder are found by repeated subtraction; that is, rk−1 is subtracted from rk−2 repeatedly until the remainder rk is smaller than rk−1. After that rk and rk−1 are exchanged and the process is iterated. Euclidean division reduces all the steps between two exchanges into a single step, which is thus more efficient. Moreover, the quotients are not needed, thus one may replace Euclidean division by the modulo operation, which gives only the remainder. Thus the iteration of the Euclidean algorithm becomes simply
- rk = rk−2 mod rk−1.
Implementations[edit]
Implementations of the algorithm may be expressed in pseudocode. For example, the division-based version may be programmed as[21]
function gcd(a, b)
while b ≠ 0
t := b
b := a mod b
a := t
return a
At the beginning of the kth iteration, the variable b holds the latest remainder rk−1, whereas the variable a holds its predecessor, rk−2. The step b := a mod b is equivalent to the above recursion formula rk ≡ rk−2 mod rk−1. The temporary variable t holds the value of rk−1 while the next remainder rk is being calculated. At the end of the loop iteration, the variable b holds the remainder rk, whereas the variable a holds its predecessor, rk−1.
(If negative inputs are allowed, or if the mod function may return negative values, the last line must be changed into return max(a, −a).)
In the subtraction-based version, which was Euclid’s original version, the remainder calculation (b := a mod b) is replaced by repeated subtraction.[22] Contrary to the division-based version, which works with arbitrary integers as input, the subtraction-based version supposes that the input consists of positive integers and stops when a = b:
function gcd(a, b)
while a ≠ b
if a > b
a := a − b
else
b := b − a
return a
The variables a and b alternate holding the previous remainders rk−1 and rk−2. Assume that a is larger than b at the beginning of an iteration; then a equals rk−2, since rk−2 > rk−1. During the loop iteration, a is reduced by multiples of the previous remainder b until a is smaller than b. Then a is the next remainder rk. Then b is reduced by multiples of a until it is again smaller than a, giving the next remainder rk+1, and so on.
The recursive version[23] is based on the equality of the GCDs of successive remainders and the stopping condition gcd(rN−1, 0) = rN−1.
function gcd(a, b)
if b = 0
return a
else
return gcd(b, a mod b)
(As above, if negative inputs are allowed, or if the mod function may return negative values, the instruction “return a” must be changed into “return max(a, −a)”.)
For illustration, the gcd(1071, 462) is calculated from the equivalent gcd(462, 1071 mod 462) = gcd(462, 147). The latter GCD is calculated from the gcd(147, 462 mod 147) = gcd(147, 21), which in turn is calculated from the gcd(21, 147 mod 21) = gcd(21, 0) = 21.
Method of least absolute remainders[edit]
In another version of Euclid’s algorithm, the quotient at each step is increased by one if the resulting negative remainder is smaller in magnitude than the typical positive remainder.[24][25] Previously, the equation
- rk−2 = qk rk−1 + rk
assumed that |rk−1| > rk > 0. However, an alternative negative remainder ek can be computed:
- rk−2 = (qk + 1) rk−1 + ek
if rk−1 > 0 or
- rk−2 = (qk − 1) rk−1 + ek
if rk−1 < 0.
If rk is replaced by ek. when |ek| < |rk|, then one gets a variant of Euclidean algorithm such that
- |rk| ≤ |rk−1| / 2
at each step.
Leopold Kronecker has shown that this version requires the fewest steps of any version of Euclid’s algorithm.[24][25] More generally, it has been proven that, for every input numbers a and b, the number of steps is minimal if and only if qk is chosen in order that 

Historical development[edit]
The Euclidean algorithm was probably invented before Euclid, depicted here holding a compass in a painting of about 1474.
The Euclidean algorithm is one of the oldest algorithms in common use.[27] It appears in Euclid’s Elements (c. 300 BC), specifically in Book 7 (Propositions 1–2) and Book 10 (Propositions 2–3). In Book 7, the algorithm is formulated for integers, whereas in Book 10, it is formulated for lengths of line segments. (In modern usage, one would say it was formulated there for real numbers. But lengths, areas, and volumes, represented as real numbers in modern usage, are not measured in the same units and there is no natural unit of length, area, or volume; the concept of real numbers was unknown at that time.) The latter algorithm is geometrical. The GCD of two lengths a and b corresponds to the greatest length g that measures a and b evenly; in other words, the lengths a and b are both integer multiples of the length g.
The algorithm was probably not discovered by Euclid, who compiled results from earlier mathematicians in his Elements.[28][29] The mathematician and historian B. L. van der Waerden suggests that Book VII derives from a textbook on number theory written by mathematicians in the school of Pythagoras.[30] The algorithm was probably known by Eudoxus of Cnidus (about 375 BC).[27][31] The algorithm may even pre-date Eudoxus,[32][33] judging from the use of the technical term ἀνθυφαίρεσις (anthyphairesis, reciprocal subtraction) in works by Euclid and Aristotle.[34]
Centuries later, Euclid’s algorithm was discovered independently both in India and in China,[35] primarily to solve Diophantine equations that arose in astronomy and making accurate calendars. In the late 5th century, the Indian mathematician and astronomer Aryabhata described the algorithm as the “pulverizer”,[36] perhaps because of its effectiveness in solving Diophantine equations.[37] Although a special case of the Chinese remainder theorem had already been described in the Chinese book Sunzi Suanjing,[38] the general solution was published by Qin Jiushao in his 1247 book Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections).[39] The Euclidean algorithm was first described numerically and popularized in Europe in the second edition of Bachet’s Problèmes plaisants et délectables (Pleasant and enjoyable problems, 1624).[36] In Europe, it was likewise used to solve Diophantine equations and in developing continued fractions. The extended Euclidean algorithm was published by the English mathematician Nicholas Saunderson,[40] who attributed it to Roger Cotes as a method for computing continued fractions efficiently.[41]
In the 19th century, the Euclidean algorithm led to the development of new number systems, such as Gaussian integers and Eisenstein integers. In 1815, Carl Gauss used the Euclidean algorithm to demonstrate unique factorization of Gaussian integers, although his work was first published in 1832.[42] Gauss mentioned the algorithm in his Disquisitiones Arithmeticae (published 1801), but only as a method for continued fractions.[35] Peter Gustav Lejeune Dirichlet seems to have been the first to describe the Euclidean algorithm as the basis for much of number theory.[43] Lejeune Dirichlet noted that many results of number theory, such as unique factorization, would hold true for any other system of numbers to which the Euclidean algorithm could be applied.[44] Lejeune Dirichlet’s lectures on number theory were edited and extended by Richard Dedekind, who used Euclid’s algorithm to study algebraic integers, a new general type of number. For example, Dedekind was the first to prove Fermat’s two-square theorem using the unique factorization of Gaussian integers.[45] Dedekind also defined the concept of a Euclidean domain, a number system in which a generalized version of the Euclidean algorithm can be defined (as described below). In the closing decades of the 19th century, the Euclidean algorithm gradually became eclipsed by Dedekind’s more general theory of ideals.[46]
|
“[The Euclidean algorithm] is the granddaddy of all algorithms, because it is the oldest nontrivial algorithm that has survived to the present day.” |
| Donald Knuth, The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd edition (1981), p. 318. |
Other applications of Euclid’s algorithm were developed in the 19th century. In 1829, Charles Sturm showed that the algorithm was useful in the Sturm chain method for counting the real roots of polynomials in any given interval.[47]
The Euclidean algorithm was the first integer relation algorithm, which is a method for finding integer relations between commensurate real numbers. Several novel integer relation algorithms have been developed, such as the algorithm of Helaman Ferguson and R.W. Forcade (1979)[48] and the LLL algorithm.[49][50]
In 1969, Cole and Davie developed a two-player game based on the Euclidean algorithm, called The Game of Euclid,[51] which has an optimal strategy.[52] The players begin with two piles of a and b stones. The players take turns removing m multiples of the smaller pile from the larger. Thus, if the two piles consist of x and y stones, where x is larger than y, the next player can reduce the larger pile from x stones to x − my stones, as long as the latter is a nonnegative integer. The winner is the first player to reduce one pile to zero stones.[53][54]
Mathematical applications[edit]
Bézout’s identity[edit]
Bézout’s identity states that the greatest common divisor g of two integers a and b can be represented as a linear sum of the original two numbers a and b.[55] In other words, it is always possible to find integers s and t such that g = sa + tb.[56][57]
The integers s and t can be calculated from the quotients q0, q1, etc. by reversing the order of equations in Euclid’s algorithm.[58] Beginning with the next-to-last equation, g can be expressed in terms of the quotient qN−1 and the two preceding remainders, rN−2 and rN−3:
- g = rN−1 = rN−3 − qN−1 rN−2 .
Those two remainders can be likewise expressed in terms of their quotients and preceding remainders,
- rN−2 = rN−4 − qN−2 rN−3 and
- rN−3 = rN−5 − qN−3 rN−4 .
Substituting these formulae for rN−2 and rN−3 into the first equation yields g as a linear sum of the remainders rN−4 and rN−5. The process of substituting remainders by formulae involving their predecessors can be continued until the original numbers a and b are reached:
- r2 = r0 − q2 r1
- r1 = b − q1 r0
- r0 = a − q0 b.
After all the remainders r0, r1, etc. have been substituted, the final equation expresses g as a linear sum of a and b, so that g = sa + tb.
The Euclidean algorithm, and thus Bezout’s identity, can be generalized to the context of Euclidean domains.
Principal ideals and related problems[edit]
Bézout’s identity provides yet another definition of the greatest common divisor g of two numbers a and b.[12] Consider the set of all numbers ua + vb, where u and v are any two integers. Since a and b are both divisible by g, every number in the set is divisible by g. In other words, every number of the set is an integer multiple of g. This is true for every common divisor of a and b. However, unlike other common divisors, the greatest common divisor is a member of the set; by Bézout’s identity, choosing u = s and v = t gives g. A smaller common divisor cannot be a member of the set, since every member of the set must be divisible by g. Conversely, any multiple m of g can be obtained by choosing u = ms and v = mt, where s and t are the integers of Bézout’s identity. This may be seen by multiplying Bézout’s identity by m,
- mg = msa + mtb.
Therefore, the set of all numbers ua + vb is equivalent to the set of multiples m of g. In other words, the set of all possible sums of integer multiples of two numbers (a and b) is equivalent to the set of multiples of gcd(a, b). The GCD is said to be the generator of the ideal of a and b. This GCD definition led to the modern abstract algebraic concepts of a principal ideal (an ideal generated by a single element) and a principal ideal domain (a domain in which every ideal is a principal ideal).
Certain problems can be solved using this result.[59] For example, consider two measuring cups of volume a and b. By adding/subtracting u multiples of the first cup and v multiples of the second cup, any volume ua + vb can be measured out. These volumes are all multiples of g = gcd(a, b).
Extended Euclidean algorithm[edit]
The integers s and t of Bézout’s identity can be computed efficiently using the extended Euclidean algorithm. This extension adds two recursive equations to Euclid’s algorithm[60]
- sk = sk−2 − qksk−1
- tk = tk−2 − qktk−1
with the starting values
- s−2 = 1, t−2 = 0
- s−1 = 0, t−1 = 1.
Using this recursion, Bézout’s integers s and t are given by s = sN and t = tN, where N+1 is the step on which the algorithm terminates with rN+1 = 0.
The validity of this approach can be shown by induction. Assume that the recursion formula is correct up to step k − 1 of the algorithm; in other words, assume that
- rj = sj a + tj b
for all j less than k. The kth step of the algorithm gives the equation
- rk = rk−2 − qkrk−1.
Since the recursion formula has been assumed to be correct for rk−2 and rk−1, they may be expressed in terms of the corresponding s and t variables
- rk = (sk−2 a + tk−2 b) − qk(sk−1 a + tk−1 b).
Rearranging this equation yields the recursion formula for step k, as required
- rk = sk a + tk b = (sk−2 − qksk−1) a + (tk−2 − qktk−1) b.
Matrix method[edit]
The integers s and t can also be found using an equivalent matrix method.[61] The sequence of equations of Euclid’s algorithm
can be written as a product of 2×2 quotient matrices multiplying a two-dimensional remainder vector
Let M represent the product of all the quotient matrices
This simplifies the Euclidean algorithm to the form
To express g as a linear sum of a and b, both sides of this equation can be multiplied by the inverse of the matrix M.[61][62] The determinant of M equals (−1)N+1, since it equals the product of the determinants of the quotient matrices, each of which is negative one. Since the determinant of M is never zero, the vector of the final remainders can be solved using the inverse of M
Since the top equation gives
- g = (−1)N+1 ( m22 a − m12 b),
the two integers of Bézout’s identity are s = (−1)N+1m22 and t = (−1)Nm12. The matrix method is as efficient as the equivalent recursion, with two multiplications and two additions per step of the Euclidean algorithm.
Euclid’s lemma and unique factorization[edit]
Bézout’s identity is essential to many applications of Euclid’s algorithm, such as demonstrating the unique factorization of numbers into prime factors.[63] To illustrate this, suppose that a number L can be written as a product of two factors u and v, that is, L = uv. If another number w also divides L but is coprime with u, then w must divide v, by the following argument: If the greatest common divisor of u and w is 1, then integers s and t can be found such that
- 1 = su + tw .
by Bézout’s identity. Multiplying both sides by v gives the relation
- v = suv + twv = sL + twv .
Since w divides both terms on the right-hand side, it must also divide the left-hand side, v. This result is known as Euclid’s lemma.[64] Specifically, if a prime number divides L, then it must divide at least one factor of L. Conversely, if a number w is coprime to each of a series of numbers a1, a2, …, an, then w is also coprime to their product, a1 × a2 × … × an.[64]
Euclid’s lemma suffices to prove that every number has a unique factorization into prime numbers.[65] To see this, assume the contrary, that there are two independent factorizations of L into m and n prime factors, respectively
- L = p1p2…pm = q1q2…qn .
Since each prime p divides L by assumption, it must also divide one of the q factors; since each q is prime as well, it must be that p = q. Iteratively dividing by the p factors shows that each p has an equal counterpart q; the two prime factorizations are identical except for their order. The unique factorization of numbers into primes has many applications in mathematical proofs, as shown below.
Linear Diophantine equations[edit]
Diophantine equations are equations in which the solutions are restricted to integers; they are named after the 3rd-century Alexandrian mathematician Diophantus.[66] A typical linear Diophantine equation seeks integers x and y such that[67]
- ax + by = c
where a, b and c are given integers. This can be written as an equation for x in modular arithmetic:
- ax ≡ c mod b.
Let g be the greatest common divisor of a and b. Both terms in ax + by are divisible by g; therefore, c must also be divisible by g, or the equation has no solutions. By dividing both sides by c/g, the equation can be reduced to Bezout’s identity
- sa + tb = g
where s and t can be found by the extended Euclidean algorithm.[68] This provides one solution to the Diophantine equation, x1 = s (c/g) and y1 = t (c/g).
In general, a linear Diophantine equation has no solutions, or an infinite number of solutions.[69] To find the latter, consider two solutions, (x1, y1) and (x2, y2), where
- ax1 + by1 = c = ax2 + by2
or equivalently
- a(x1 − x2) = b(y2 − y1).
Therefore, the smallest difference between two x solutions is b/g, whereas the smallest difference between two y solutions is a/g. Thus, the solutions may be expressed as
- x = x1 − bu/g
- y = y1 + au/g.
By allowing u to vary over all possible integers, an infinite family of solutions can be generated from a single solution (x1, y1). If the solutions are required to be positive integers (x > 0, y > 0), only a finite number of solutions may be possible. This restriction on the acceptable solutions allows some systems of Diophantine equations with more unknowns than equations to have a finite number of solutions;[70] this is impossible for a system of linear equations when the solutions can be any real number (see Underdetermined system).
Multiplicative inverses and the RSA algorithm[edit]
A finite field is a set of numbers with four generalized operations. The operations are called addition, subtraction, multiplication and division and have their usual properties, such as commutativity, associativity and distributivity. An example of a finite field is the set of 13 numbers {0, 1, 2, …, 12} using modular arithmetic. In this field, the results of any mathematical operation (addition, subtraction, multiplication, or division) is reduced modulo 13; that is, multiples of 13 are added or subtracted until the result is brought within the range 0–12. For example, the result of 5 × 7 = 35 mod 13 = 9. Such finite fields can be defined for any prime p; using more sophisticated definitions, they can also be defined for any power m of a prime p m. Finite fields are often called Galois fields, and are abbreviated as GF(p) or GF(p m).
In such a field with m numbers, every nonzero element a has a unique modular multiplicative inverse, a−1 such that aa−1 = a−1a ≡ 1 mod m. This inverse can be found by solving the congruence equation ax ≡ 1 mod m,[71] or the equivalent linear Diophantine equation[72]
- ax + my = 1.
This equation can be solved by the Euclidean algorithm, as described above. Finding multiplicative inverses is an essential step in the RSA algorithm, which is widely used in electronic commerce; specifically, the equation determines the integer used to decrypt the message.[73] Although the RSA algorithm uses rings rather than fields, the Euclidean algorithm can still be used to find a multiplicative inverse where one exists. The Euclidean algorithm also has other applications in error-correcting codes; for example, it can be used as an alternative to the Berlekamp–Massey algorithm for decoding BCH and Reed–Solomon codes, which are based on Galois fields.[74]
Chinese remainder theorem[edit]
Euclid’s algorithm can also be used to solve multiple linear Diophantine equations.[75] Such equations arise in the Chinese remainder theorem, which describes a novel method to represent an integer x. Instead of representing an integer by its digits, it may be represented by its remainders xi modulo a set of N coprime numbers mi:[76]
The goal is to determine x from its N remainders xi. The solution is to combine the multiple equations into a single linear Diophantine equation with a much larger modulus M that is the product of all the individual moduli mi, and define Mi as
Thus, each Mi is the product of all the moduli except mi. The solution depends on finding N new numbers hi such that
With these numbers hi, any integer x can be reconstructed from its remainders xi by the equation
Since these numbers hi are the multiplicative inverses of the Mi, they may be found using Euclid’s algorithm as described in the previous subsection.
Stern–Brocot tree[edit]
The Euclidean algorithm can be used to arrange the set of all positive rational numbers into an infinite binary search tree, called the Stern–Brocot tree.
The number 1 (expressed as a fraction 1/1) is placed at the root of the tree, and the location of any other number a/b can be found by computing gcd(a,b) using the original form of the Euclidean algorithm, in which each step replaces the larger of the two given numbers by its difference with the smaller number (not its remainder), stopping when two equal numbers are reached. A step of the Euclidean algorithm that replaces the first of the two numbers corresponds to a step in the tree from a node to its right child, and a step that replaces the second of the two numbers corresponds to a step in the tree from a node to its left child. The sequence of steps constructed in this way does not depend on whether a/b is given in lowest terms, and forms a path from the root to a node containing the number a/b.[77] This fact can be used to prove that each positive rational number appears exactly once in this tree.
For example, 3/4 can be found by starting at the root, going to the left once, then to the right twice:
The Stern–Brocot tree, and the Stern–Brocot sequences of order i for i = 1, 2, 3, 4
The Euclidean algorithm has almost the same relationship to another binary tree on the rational numbers called the Calkin–Wilf tree. The difference is that the path is reversed: instead of producing a path from the root of the tree to a target, it produces a path from the target to the root.
Continued fractions[edit]
The Euclidean algorithm has a close relationship with continued fractions.[78] The sequence of equations can be written in the form
The last term on the right-hand side always equals the inverse of the left-hand side of the next equation. Thus, the first two equations may be combined to form
The third equation may be used to substitute the denominator term r1/r0, yielding
The final ratio of remainders rk/rk−1 can always be replaced using the next equation in the series, up to the final equation. The result is a continued fraction
In the worked example above, the gcd(1071, 462) was calculated, and the quotients qk were 2, 3 and 7, respectively. Therefore, the fraction 1071/462 may be written
as can be confirmed by calculation.
Factorization algorithms[edit]
Calculating a greatest common divisor is an essential step in several integer factorization algorithms,[79] such as Pollard’s rho algorithm,[80] Shor’s algorithm,[81] Dixon’s factorization method[82] and the Lenstra elliptic curve factorization.[83] The Euclidean algorithm may be used to find this GCD efficiently. Continued fraction factorization uses continued fractions, which are determined using Euclid’s algorithm.[84]
Algorithmic efficiency[edit]
Number of steps in the Euclidean algorithm for gcd(x,y). Lighter (red and yellow) points indicate relatively few steps, whereas darker (violet and blue) points indicate more steps. The largest dark area follows the line y = Φx, where Φ is the golden ratio.
The computational efficiency of Euclid’s algorithm has been studied thoroughly.[85] This efficiency can be described by the number of division steps the algorithm requires, multiplied by the computational expense of each step. The first known analysis of Euclid’s algorithm is due to A. A. L. Reynaud in 1811,[86] who showed that the number of division steps on input (u, v) is bounded by v; later he improved this to v/2 + 2. Later, in 1841, P. J. E. Finck showed[87] that the number of division steps is at most 2 log2 v + 1, and hence Euclid’s algorithm runs in time polynomial in the size of the input.[88] Émile Léger, in 1837, studied the worst case, which is when the inputs are consecutive Fibonacci numbers.[88] Finck’s analysis was refined by Gabriel Lamé in 1844,[89] who showed that the number of steps required for completion is never more than five times the number h of base-10 digits of the smaller number b.[90][91]
In the uniform cost model (suitable for analyzing the complexity of gcd calculation on numbers that fit into a single machine word), each step of the algorithm takes constant time, and Lamé’s analysis implies that the total running time is also O(h). However, in a model of computation suitable for computation with larger numbers, the computational expense of a single remainder computation in the algorithm can be as large as O(h2).[92] In this case the total time for all of the steps of the algorithm can be analyzed using a telescoping series, showing that it is also O(h2). Modern algorithmic techniques based on the Schönhage–Strassen algorithm for fast integer multiplication can be used to speed this up, leading to quasilinear algorithms for the GCD.[93][94]
Number of steps[edit]
The number of steps to calculate the GCD of two natural numbers, a and b, may be denoted by T(a, b).[95] If g is the GCD of a and b, then a = mg and b = ng for two coprime numbers m and n. Then
- T(a, b) = T(m, n)
as may be seen by dividing all the steps in the Euclidean algorithm by g.[96] By the same argument, the number of steps remains the same if a and b are multiplied by a common factor w: T(a, b) = T(wa, wb). Therefore, the number of steps T may vary dramatically between neighboring pairs of numbers, such as T(a, b) and T(a, b + 1), depending on the size of the two GCDs.
The recursive nature of the Euclidean algorithm gives another equation
- T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1
where T(x, 0) = 0 by assumption.[95]
Worst-case[edit]
If the Euclidean algorithm requires N steps for a pair of natural numbers a > b > 0, the smallest values of a and b for which this is true are the Fibonacci numbers FN+2 and FN+1, respectively.[97] More precisely, if the Euclidean algorithm requires N steps for the pair a > b, then one has a ≥ FN+2 and b ≥ FN+1. This can be shown by induction.[98] If N = 1, b divides a with no remainder; the smallest natural numbers for which this is true is b = 1 and a = 2, which are F2 and F3, respectively. Now assume that the result holds for all values of N up to M − 1. The first step of the M-step algorithm is a = q0b + r0, and the Euclidean algorithm requires M − 1 steps for the pair b > r0. By induction hypothesis, one has b ≥ FM+1 and r0 ≥ FM. Therefore, a = q0b + r0 ≥ b + r0 ≥ FM+1 + FM = FM+2,
which is the desired inequality.
This proof, published by Gabriel Lamé in 1844, represents the beginning of computational complexity theory,[99] and also the first practical application of the Fibonacci numbers.[97]
This result suffices to show that the number of steps in Euclid’s algorithm can never be more than five times the number of its digits (base 10).[100] For if the algorithm requires N steps, then b is greater than or equal to FN+1 which in turn is greater than or equal to φN−1, where φ is the golden ratio. Since b ≥ φN−1, then N − 1 ≤ logφb. Since log10φ > 1/5, (N − 1)/5 < log10φ logφb = log10b. Thus, N ≤ 5 log10b. Thus, the Euclidean algorithm always needs less than O(h) divisions, where h is the number of digits in the smaller number b.
Average[edit]
The average number of steps taken by the Euclidean algorithm has been defined in three different ways. The first definition is the average time T(a) required to calculate the GCD of a given number a and a smaller natural number b chosen with equal probability from the integers 0 to a − 1[95]
However, since T(a, b) fluctuates dramatically with the GCD of the two numbers, the averaged function T(a) is likewise “noisy”.[101]
To reduce this noise, a second average τ(a) is taken over all numbers coprime with a
There are φ(a) coprime integers less than a, where φ is Euler’s totient function. This tau average grows smoothly with a[102][103]
with the residual error being of order a−(1/6) + ε, where ε is infinitesimal. The constant C in this formula is called Porter’s constant[104] and equals
where γ is the Euler–Mascheroni constant and ζ’ is the derivative of the Riemann zeta function.[105][106] The leading coefficient (12/π2) ln 2 was determined by two independent methods.[107][108]
Since the first average can be calculated from the tau average by summing over the divisors d of a[109]
it can be approximated by the formula[110]
where Λ(d) is the Mangoldt function.[111]
A third average Y(n) is defined as the mean number of steps required when both a and b are chosen randomly (with uniform distribution) from 1 to n[110]
Substituting the approximate formula for T(a) into this equation yields an estimate for Y(n)[112]
Computational expense per step[edit]
In each step k of the Euclidean algorithm, the quotient qk and remainder rk are computed for a given pair of integers rk−2 and rk−1
- rk−2 = qk rk−1 + rk.
The computational expense per step is associated chiefly with finding qk, since the remainder rk can be calculated quickly from rk−2, rk−1, and qk
- rk = rk−2 − qk rk−1.
The computational expense of dividing h-bit numbers scales as O(h(ℓ+1)), where ℓ is the length of the quotient.[92]
For comparison, Euclid’s original subtraction-based algorithm can be much slower. A single integer division is equivalent to the quotient q number of subtractions. If the ratio of a and b is very large, the quotient is large and many subtractions will be required. On the other hand, it has been shown that the quotients are very likely to be small integers. The probability of a given quotient q is approximately ln |u/(u − 1)| where u = (q + 1)2.[113] For illustration, the probability of a quotient of 1, 2, 3, or 4 is roughly 41.5%, 17.0%, 9.3%, and 5.9%, respectively. Since the operation of subtraction is faster than division, particularly for large numbers,[114] the subtraction-based Euclid’s algorithm is competitive with the division-based version.[115] This is exploited in the binary version of Euclid’s algorithm.[116]
Combining the estimated number of steps with the estimated computational expense per step shows that the Euclid’s algorithm grows quadratically (h2) with the average number of digits h in the initial two numbers a and b. Let h0, h1, …, hN−1 represent the number of digits in the successive remainders r0, r1, …, rN−1. Since the number of steps N grows linearly with h, the running time is bounded by
Alternative methods[edit]
Euclid’s algorithm is widely used in practice, especially for small numbers, due to its simplicity.[117] For comparison, the efficiency of alternatives to Euclid’s algorithm may be determined.
One inefficient approach to finding the GCD of two natural numbers a and b is to calculate all their common divisors; the GCD is then the largest common divisor. The common divisors can be found by dividing both numbers by successive integers from 2 to the smaller number b. The number of steps of this approach grows linearly with b, or exponentially in the number of digits. Another inefficient approach is to find the prime factors of one or both numbers. As noted above, the GCD equals the product of the prime factors shared by the two numbers a and b.[8] Present methods for prime factorization are also inefficient; many modern cryptography systems even rely on that inefficiency.[11]
The binary GCD algorithm is an efficient alternative that substitutes division with faster operations by exploiting the binary representation used by computers.[118][119] However, this alternative also scales like O(h²). It is generally faster than the Euclidean algorithm on real computers, even though it scales in the same way.[93] Additional efficiency can be gleaned by examining only the leading digits of the two numbers a and b.[120][121] The binary algorithm can be extended to other bases (k-ary algorithms),[122] with up to fivefold increases in speed.[123] Lehmer’s GCD algorithm uses the same general principle as the binary algorithm to speed up GCD computations in arbitrary bases.
A recursive approach for very large integers (with more than 25,000 digits) leads to quasilinear integer GCD algorithms,[124] such as those of Schönhage,[125][126] and Stehlé and Zimmermann.[127] These algorithms exploit the 2×2 matrix form of the Euclidean algorithm given above. These quasilinear methods generally scale as O(h (log h)2 (log log h)).[93][94]
Generalizations[edit]
Although the Euclidean algorithm is used to find the greatest common divisor of two natural numbers (positive integers), it may be generalized to the real numbers, and to other mathematical objects, such as polynomials,[128] quadratic integers[129] and Hurwitz quaternions.[130] In the latter cases, the Euclidean algorithm is used to demonstrate the crucial property of unique factorization, i.e., that such numbers can be factored uniquely into irreducible elements, the counterparts of prime numbers. Unique factorization is essential to many proofs of number theory.
Rational and real numbers[edit]
Euclid’s algorithm can be applied to real numbers, as described by Euclid in Book 10 of his Elements. The goal of the algorithm is to identify a real number g such that two given real numbers, a and b, are integer multiples of it: a = mg and b = ng, where m and n are integers.[28] This identification is equivalent to finding an integer relation among the real numbers a and b; that is, it determines integers s and t such that sa + tb = 0. If such an equation is possible, a and b are called commensurable lengths, otherwise they are incommensurable lengths.[131][132]
The real-number Euclidean algorithm differs from its integer counterpart in two respects. First, the remainders rk are real numbers, although the quotients qk are integers as before. Second, the algorithm is not guaranteed to end in a finite number N of steps. If it does, the fraction a/b is a rational number, i.e., the ratio of two integers
and can be written as a finite continued fraction [q0; q1, q2, …, qN]. If the algorithm does not stop, the fraction a/b is an irrational number and can be described by an infinite continued fraction [q0; q1, q2, …].[133] Examples of infinite continued fractions are the golden ratio φ = [1; 1, 1, …] and the square root of two, √2 = [1; 2, 2, …].[134] The algorithm is unlikely to stop, since almost all ratios a/b of two real numbers are irrational.[135]
An infinite continued fraction may be truncated at a step k [q0; q1, q2, …, qk] to yield an approximation to a/b that improves as k is increased. The approximation is described by convergents mk/nk; the numerator and denominators are coprime and obey the recurrence relation
where m−1 = n−2 = 1 and m−2 = n−1 = 0 are the initial values of the recursion. The convergent mk/nk is the best rational number approximation to a/b with denominator nk:[136]
Polynomials[edit]
Polynomials in a single variable x can be added, multiplied and factored into irreducible polynomials, which are the analogs of the prime numbers for integers. The greatest common divisor polynomial g(x) of two polynomials a(x) and b(x) is defined as the product of their shared irreducible polynomials, which can be identified using the Euclidean algorithm.[128] The basic procedure is similar to that for integers. At each step k, a quotient polynomial qk(x) and a remainder polynomial rk(x) are identified to satisfy the recursive equation
where r−2(x) = a(x) and r−1(x) = b(x). Each quotient polynomial is chosen such that each remainder is either zero or has a degree that is smaller than the degree of its predecessor: deg[rk(x)] < deg[rk−1(x)]. Since the degree is a nonnegative integer, and since it decreases with every step, the Euclidean algorithm concludes in a finite number of steps. The last nonzero remainder is the greatest common divisor of the original two polynomials, a(x) and b(x).[137]
For example, consider the following two quartic polynomials, which each factor into two quadratic polynomials
Dividing a(x) by b(x) yields a remainder r0(x) = x3 + (2/3)x2 + (5/3)x − (2/3). In the next step, b(x) is divided by r0(x) yielding a remainder r1(x) = x2 + x + 2. Finally, dividing r0(x) by r1(x) yields a zero remainder, indicating that r1(x) is the greatest common divisor polynomial of a(x) and b(x), consistent with their factorization.
Many of the applications described above for integers carry over to polynomials.[138] The Euclidean algorithm can be used to solve linear Diophantine equations and Chinese remainder problems for polynomials; continued fractions of polynomials can also be defined.
The polynomial Euclidean algorithm has other applications, such as Sturm chains, a method for counting the zeros of a polynomial that lie inside a given real interval.[139] This in turn has applications in several areas, such as the Routh–Hurwitz stability criterion in control theory.[140]
Finally, the coefficients of the polynomials need not be drawn from integers, real numbers or even the complex numbers. For example, the coefficients may be drawn from a general field, such as the finite fields GF(p) described above. The corresponding conclusions about the Euclidean algorithm and its applications hold even for such polynomials.[128]
Gaussian integers[edit]
Distribution of Gaussian primes u + vi in the complex plane, with norms u2 + v2 less than 500
The Gaussian integers are complex numbers of the form α = u + vi, where u and v are ordinary integers[note 2] and i is the square root of negative one.[141] By defining an analog of the Euclidean algorithm, Gaussian integers can be shown to be uniquely factorizable, by the argument above.[42] This unique factorization is helpful in many applications, such as deriving all Pythagorean triples or proving Fermat’s theorem on sums of two squares.[141] In general, the Euclidean algorithm is convenient in such applications, but not essential; for example, the theorems can often be proven by other arguments.
The Euclidean algorithm developed for two Gaussian integers α and β is nearly the same as that for ordinary integers,[142] but differs in two respects. As before, we set r−2 = α and r−1 = β, and the task at each step k is to identify a quotient qk and a remainder rk such that
where every remainder is strictly smaller than its predecessor: |rk| < |rk−1|. The first difference is that the quotients and remainders are themselves Gaussian integers, and thus are complex numbers. The quotients qk are generally found by rounding the real and complex parts of the exact ratio (such as the complex number α/β) to the nearest integers.[142] The second difference lies in the necessity of defining how one complex remainder can be “smaller” than another. To do this, a norm function f(u + vi) = u2 + v2 is defined, which converts every Gaussian integer u + vi into an ordinary integer. After each step k of the Euclidean algorithm, the norm of the remainder f(rk) is smaller than the norm of the preceding remainder, f(rk−1). Since the norm is a nonnegative integer and decreases with every step, the Euclidean algorithm for Gaussian integers ends in a finite number of steps.[143] The final nonzero remainder is gcd(α, β), the Gaussian integer of largest norm that divides both α and β; it is unique up to multiplication by a unit, ±1 or ±i.[144]
Many of the other applications of the Euclidean algorithm carry over to Gaussian integers. For example, it can be used to solve linear Diophantine equations and Chinese remainder problems for Gaussian integers;[145] continued fractions of Gaussian integers can also be defined.[142]
Euclidean domains[edit]
A set of elements under two binary operations, denoted as addition and multiplication, is called a Euclidean domain if it forms a commutative ring R and, roughly speaking, if a generalized Euclidean algorithm can be performed on them.[146][147] The two operations of such a ring need not be the addition and multiplication of ordinary arithmetic; rather, they can be more general, such as the operations of a mathematical group or monoid. Nevertheless, these general operations should respect many of the laws governing ordinary arithmetic, such as commutativity, associativity and distributivity.
The generalized Euclidean algorithm requires a Euclidean function, i.e., a mapping f from R into the set of nonnegative integers such that, for any two nonzero elements a and b in R, there exist q and r in R such that a = qb + r and f(r) < f(b).[148] Examples of such mappings are the absolute value for integers, the degree for univariate polynomials, and the norm for Gaussian integers above.[149][150] The basic principle is that each step of the algorithm reduces f inexorably; hence, if f can be reduced only a finite number of times, the algorithm must stop in a finite number of steps. This principle relies on the well-ordering property of the non-negative integers, which asserts that every non-empty set of non-negative integers has a smallest member.[151]
The fundamental theorem of arithmetic applies to any Euclidean domain: Any number from a Euclidean domain can be factored uniquely into irreducible elements. Any Euclidean domain is a unique factorization domain (UFD), although the converse is not true.[151] The Euclidean domains and the UFD’s are subclasses of the GCD domains, domains in which a greatest common divisor of two numbers always exists.[152] In other words, a greatest common divisor may exist (for all pairs of elements in a domain), although it may not be possible to find it using a Euclidean algorithm. A Euclidean domain is always a principal ideal domain (PID), an integral domain in which every ideal is a principal ideal.[153] Again, the converse is not true: not every PID is a Euclidean domain.
The unique factorization of Euclidean domains is useful in many applications. For example, the unique factorization of the Gaussian integers is convenient in deriving formulae for all Pythagorean triples and in proving Fermat’s theorem on sums of two squares.[141] Unique factorization was also a key element in an attempted proof of Fermat’s Last Theorem published in 1847 by Gabriel Lamé, the same mathematician who analyzed the efficiency of Euclid’s algorithm, based on a suggestion of Joseph Liouville.[154] Lamé’s approach required the unique factorization of numbers of the form x + ωy, where x and y are integers, and ω = e2iπ/n is an nth root of 1, that is, ωn = 1. Although this approach succeeds for some values of n (such as n = 3, the Eisenstein integers), in general such numbers do not factor uniquely. This failure of unique factorization in some cyclotomic fields led Ernst Kummer to the concept of ideal numbers and, later, Richard Dedekind to ideals.[155]
Unique factorization of quadratic integers[edit]
Distribution of Eisenstein primes u + vω in the complex plane, with norms less than 500. The number ω is a cube root of 1.
The quadratic integer rings are helpful to illustrate Euclidean domains. Quadratic integers are generalizations of the Gaussian integers in which the imaginary unit i is replaced by a number ω. Thus, they have the form u + vω, where u and v are integers and ω has one of two forms, depending on a parameter D. If D does not equal a multiple of four plus one, then
If, however, D does equal a multiple of four plus one, then
If the function f corresponds to a norm function, such as that used to order the Gaussian integers above, then the domain is known as norm-Euclidean. The norm-Euclidean rings of quadratic integers are exactly those where D is one of the values −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, or 73.[156][157] The cases D = −1 and D = −3 yield the Gaussian integers and Eisenstein integers, respectively.
If f is allowed to be any Euclidean function, then the list of possible values of D for which the domain is Euclidean is not yet known.[158] The first example of a Euclidean domain that was not norm-Euclidean (with D = 69) was published in 1994.[158] In 1973, Weinberger proved that a quadratic integer ring with D > 0 is Euclidean if, and only if, it is a principal ideal domain, provided that the generalized Riemann hypothesis holds.[129]
Noncommutative rings[edit]
The Euclidean algorithm may be applied to some noncommutative rings such as the set of Hurwitz quaternions.[clarification needed][130] Let α and β represent two elements from such a ring. They have a common right divisor δ if α = ξδ and β = ηδ for some choice of ξ and η in the ring. Similarly, they have a common left divisor if α = dξ and β = dη for some choice of ξ and η in the ring. Since multiplication is not commutative, there are two versions of the Euclidean algorithm, one for right divisors and one for left divisors.[130] Choosing the right divisors, the first step in finding the gcd(α, β) by the Euclidean algorithm can be written
where ψ0 represents the quotient and ρ0 the remainder.[clarification needed] This equation shows that any common right divisor of α and β is likewise a common divisor of the remainder ρ0. The analogous equation for the left divisors would be
With either choice, the process is repeated as above until the greatest common right or left divisor is identified. As in the Euclidean domain, the “size” of the remainder ρ0 (formally, its norm) must be strictly smaller than β, and there must be only a finite number of possible sizes for ρ0, so that the algorithm is guaranteed to terminate.[159]
Most of the results for the GCD carry over to noncommutative numbers.[clarification needed] For example, Bézout’s identity states that the right gcd(α, β) can be expressed as a linear combination of α and β.[160] In other words, there are numbers σ and τ such that
The analogous identity for the left GCD is nearly the same:
Bézout’s identity can be used to solve Diophantine equations. For instance, one of the standard proofs of Lagrange’s four-square theorem, that every positive integer can be represented as a sum of four squares, is based on quaternion GCDs in this way.[159]
See also[edit]
- Euclidean rhythm, a method for using the Euclidean algorithm to generate musical rhythms
Notes[edit]
- ^ Some widely used textbooks, such as I. N. Herstein’s Topics in Algebra and Serge Lang’s Algebra, use the term “Euclidean algorithm” to refer to Euclidean division
- ^ The phrase “ordinary integer” is commonly used for distinguishing usual integers from Gaussian integers, and more generally from algebraic integers.
References[edit]
- ^ Lamé, Gabriel (1844). “Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers”. Comptes rendus des séances du l’Académie des Sciences (in French). 19: 867–870.
- ^ Shallit, Jeffrey (1994-11-01). “Origins of the analysis of the Euclidean algorithm”. Historia Mathematica. 21 (4): 401–419. doi:10.1006/hmat.1994.1031. ISSN 0315-0860.
- ^ Stark 1978, p. 16
- ^ Stark 1978, p. 21
- ^ LeVeque 1996, p. 32
- ^ LeVeque 1996, p. 31
- ^ Grossman, J. W. (1990). Discrete Mathematics. New York: Macmillan. p. 213. ISBN 0-02-348331-8.
- ^ a b Schroeder 2005, pp. 21–22
- ^ Schroeder 2005, p. 19
- ^ Ogilvy, C. S.; Anderson, J. T. (1966). Excursions in number theory. New York: Oxford University Press. pp. 27–29.
- ^ a b Schroeder 2005, pp. 216–219
- ^ a b LeVeque 1996, p. 33
- ^ Stark 1978, p. 25
- ^ Ore 1948, pp. 47–48
- ^ Stark 1978, p. 18
- ^ Stark 1978, pp. 16–20
- ^ Knuth 1997, p. 320
- ^ Lovász, L.; Pelikán, J.; Vesztergombi, K. (2003). Discrete Mathematics: Elementary and Beyond. New York: Springer-Verlag. pp. 100–101. ISBN 0-387-95584-4.
- ^ Kimberling, C. (1983). “A Visual Euclidean Algorithm”. Mathematics Teacher. 76: 108–109.
- ^ Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra. John Wiley & Sons, Inc. pp. 270–271. ISBN 978-0-471-43334-7.
- ^ Knuth 1997, pp. 319–320
- ^ Knuth 1997, pp. 318–319
- ^ Stillwell 1997, p. 14
- ^ a b Ore 1948, p. 43
- ^ a b Stewart, B. M. (1964). Theory of Numbers (2nd ed.). New York: Macmillan. pp. 43–44. LCCN 64010964.
- ^ Lazard, D. (1977). “Le meilleur algorithme d’Euclide pour K[X] et Z“. Comptes rendus de l’Académie des Sciences (in French). 284: 1–4.
- ^ a b Knuth 1997, p. 318
- ^ a b Weil, A. (1983). Number Theory. Boston: Birkhäuser. pp. 4–6. ISBN 0-8176-3141-0.
- ^ Jones, A. (1994). “Greek mathematics to AD 300”. Companion encyclopedia of the history and philosophy of the mathematical sciences. New York: Routledge. pp. 46–48. ISBN 0-415-09238-8.
- ^ van der Waerden, B. L. (1954). Science Awakening. translated by Arnold Dresden. Groningen: P. Noordhoff Ltd. pp. 114–115.
- ^ von Fritz, K. (1945). “The Discovery of Incommensurability by Hippasus of Metapontum”. Annals of Mathematics. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
- ^ Heath, T. L. (1949). Mathematics in Aristotle. Oxford Press. pp. 80–83.
- ^ Fowler, D. H. (1987). The Mathematics of Plato’s Academy: A New Reconstruction. Oxford: Oxford University Press. pp. 31–66. ISBN 0-19-853912-6.
- ^ Becker, O. (1933). “Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid”. Quellen und Studien zur Geschichte der Mathematik B. 2: 311–333.
- ^ a b Stillwell 1997, p. 31
- ^ a b Tattersall 2005, p. 70
- ^ Rosen 2000, pp. 86–87
- ^ Ore 1948, pp. 247–248
- ^ Tattersall 2005, pp. 72, 184–185
- ^ Saunderson, Nicholas (1740). The Elements of Algebra in Ten Books. University of Cambridge Press. Retrieved 1 November 2016.
- ^ Tattersall 2005, pp. 72–76
- ^ a b Gauss, C. F. (1832). “Theoria residuorum biquadraticorum”. Comm. Soc. Reg. Sci. Gött. Rec. 4. Reprinted in Gauss, C. F. (2011). “Theoria residuorum biquadraticorum commentatio prima”. Werke. Vol. 2. Cambridge Univ. Press. pp. 65–92. doi:10.1017/CBO9781139058230.004. ISBN 9781139058230. and Gauss, C. F. (2011). “Theoria residuorum biquadraticorum commentatio secunda”. Werke. Vol. 2. Cambridge Univ. Press. pp. 93–148. doi:10.1017/CBO9781139058230.005. ISBN 9781139058230.
- ^ Stillwell 1997, pp. 31–32
- ^ Lejeune Dirichlet 1894, pp. 29–31
- ^ Richard Dedekind in Lejeune Dirichlet 1894, Supplement XI
- ^ Stillwell 2003, pp. 41–42
- ^ Sturm, C. (1829). “Mémoire sur la résolution des équations numériques”. Bull. Des sciences de Férussac (in French). 11: 419–422.
- ^ Ferguson, H. R. P.; Forcade, R. W. (1979). “Generalization of the Euclidean algorithm for real numbers to all dimensions higher than two”. Bulletin of the American Mathematical Society. New Series. 1 (6): 912–914. doi:10.1090/S0273-0979-1979-14691-3. MR 0546316.
- ^ Peterson, I. (12 August 2002). “Jazzing Up Euclid’s Algorithm”. ScienceNews.
- ^ Cipra, Barry Arthur (16 May 2000). “The Best of the 20th Century: Editors Name Top 10 Algorithms” (PDF). SIAM News. Society for Industrial and Applied Mathematics. 33 (4). Archived from the original (PDF) on 22 September 2016. Retrieved 19 July 2016.
- ^ Cole, A. J.; Davie, A. J. T. (1969). “A game based on the Euclidean algorithm and a winning strategy for it”. Math. Gaz. 53 (386): 354–357. doi:10.2307/3612461. JSTOR 3612461. S2CID 125164797.
- ^ Spitznagel, E. L. (1973). “Properties of a game based on Euclid’s algorithm”. Math. Mag. 46 (2): 87–92. doi:10.2307/2689037. JSTOR 2689037.
- ^ Rosen 2000, p. 95
- ^ Roberts, J. (1977). Elementary Number Theory: A Problem Oriented Approach. Cambridge, MA: MIT Press. pp. 1–8. ISBN 0-262-68028-9.
- ^ Jones, G. A.; Jones, J. M. (1998). “Bezout’s Identity”. Elementary Number Theory. New York: Springer-Verlag. pp. 7–11.
- ^ Rosen 2000, p. 81
- ^ Cohn 1962, p. 104
- ^ Rosen 2000, p. 91
- ^ Schroeder 2005, p. 23
- ^ Rosen 2000, pp. 90–93
- ^ a b Koshy, T. (2002). Elementary Number Theory with Applications. Burlington, MA: Harcourt/Academic Press. pp. 167–169. ISBN 0-12-421171-2.
- ^ Bach, E.; Shallit, J. (1996). Algorithmic number theory. Cambridge, MA: MIT Press. pp. 70–73. ISBN 0-262-02405-5.
- ^ Stark 1978, pp. 26–36
- ^ a b Ore 1948, p. 44
- ^ Stark 1978, pp. 281–292
- ^ Rosen 2000, pp. 119–125
- ^ Schroeder 2005, pp. 106–107
- ^ Schroeder 2005, pp. 108–109
- ^ Rosen 2000, pp. 120–121
- ^ Stark 1978, p. 47
- ^ Schroeder 2005, pp. 107–109
- ^ Stillwell 1997, pp. 186–187
- ^ Schroeder 2005, p. 134
- ^ Moon, T. K. (2005). Error Correction Coding: Mathematical Methods and Algorithms. John Wiley and Sons. p. 266. ISBN 0-471-64800-0.
- ^ Rosen 2000, pp. 143–170
- ^ Schroeder 2005, pp. 194–195
- ^ Graham, R.; Knuth, D. E.; Patashnik, O. (1989). Concrete mathematics. Addison-Wesley. p. 123.
- ^ Vinogradov, I. M. (1954). Elements of Number Theory. New York: Dover. pp. 3–13.
- ^ Crandall & Pomerance 2001, pp. 225–349
- ^ Knuth 1997, pp. 369–371
- ^ Shor, P. W. (1997). “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer”. SIAM Journal on Scientific and Statistical Computing. 26 (5): 1484–1509. arXiv:quant-ph/9508027. Bibcode:1995quant.ph..8027S. doi:10.1137/s0097539795293172. S2CID 2337707.
- ^ Dixon, J. D. (1981). “Asymptotically fast factorization of integers”. Math. Comput. 36 (153): 255–260. doi:10.2307/2007743. JSTOR 2007743.
- ^ Lenstra, H. W. Jr. (1987). “Factoring integers with elliptic curves”. Annals of Mathematics. 126 (3): 649–673. doi:10.2307/1971363. hdl:1887/2140. JSTOR 1971363.
- ^ Knuth 1997, pp. 380–384
- ^ Knuth 1997, pp. 339–364
- ^ Reynaud, A.-A.-L. (1811). Traité d’arithmétique à l’usage des élèves qui se destinent à l’École Polytechnique (6th ed.). Paris: Courcier. Note 60, p. 34. As cited by Shallit (1994).
- ^ Finck, P.-J.-E. (1841). Traité élémentaire d’arithmétique à l’usage des candidats aux écoles spéciales (in French). Derivaux.
- ^ a b Shallit 1994.
- ^ Lamé, G. (1844). “Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers”. Comptes Rendus Acad. Sci. (in French). 19: 867–870.
- ^ Grossman, H. (1924). “On the Number of Divisions in Finding a G.C.D”. The American Mathematical Monthly. 31 (9): 443. doi:10.2307/2298146. JSTOR 2298146.
- ^ Honsberger, R. (1976). Mathematical Gems II. The Mathematical Association of America. pp. 54–57. ISBN 0-88385-302-7.
- ^ a b Knuth 1997, pp. 257–261
- ^ a b c Crandall & Pomerance 2001, pp. 77–79, 81–85, 425–431
- ^ a b Möller, N. (2008). “On Schönhage’s algorithm and subquadratic integer gcd computation” (PDF). Mathematics of Computation. 77 (261): 589–607. Bibcode:2008MaCom..77..589M. doi:10.1090/S0025-5718-07-02017-0.
- ^ a b c Knuth 1997, p. 344
- ^ Ore 1948, p. 45
- ^ a b Knuth 1997, p. 343
- ^ Mollin 2008, p. 21
- ^ LeVeque 1996, p. 35
- ^ Mollin 2008, pp. 21–22
- ^ Knuth 1997, p. 353
- ^ Knuth 1997, p. 357
- ^ Tonkov, T. (1974). “On the average length of finite continued fractions”. Acta Arithmetica. 26: 47–57. doi:10.4064/aa-26-1-47-57.
- ^ Knuth, Donald E. (1976). “Evaluation of Porter’s constant”. Computers & Mathematics with Applications. 2 (2): 137–139. doi:10.1016/0898-1221(76)90025-0.
- ^ Porter, J. W. (1975). “On a Theorem of Heilbronn”. Mathematika. 22: 20–28. doi:10.1112/S0025579300004459.
- ^ Knuth, D. E. (1976). “Evaluation of Porter’s Constant”. Computers and Mathematics with Applications. 2 (2): 137–139. doi:10.1016/0898-1221(76)90025-0.
- ^ Dixon, J. D. (1970). “The Number of Steps in the Euclidean Algorithm”. J. Number Theory. 2 (4): 414–422. Bibcode:1970JNT…..2..414D. doi:10.1016/0022-314X(70)90044-2.
- ^ Heilbronn, H. A. (1969). “On the Average Length of a Class of Finite Continued Fractions”. In Paul Turán (ed.). Number Theory and Analysis. New York: Plenum. pp. 87–96. LCCN 76016027.
- ^ Knuth 1997, p. 354
- ^ a b Norton, G. H. (1990). “On the Asymptotic Analysis of the Euclidean Algorithm”. Journal of Symbolic Computation. 10: 53–58. doi:10.1016/S0747-7171(08)80036-3.
- ^ Knuth 1997, p. 355
- ^ Knuth 1997, p. 356
- ^ Knuth 1997, p. 352
- ^ Wagon, S. (1999). Mathematica in Action. New York: Springer-Verlag. pp. 335–336. ISBN 0-387-98252-3.
- ^ Cohen 1993, p. 14
- ^ Cohen 1993, pp. 14–15, 17–18
- ^ Sorenson, Jonathan P. (2004). “An analysis of the generalized binary GCD algorithm”. High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams. Fields Institute Communications. Vol. 41. Providence, RI: American Mathematical Society. pp. 327–340. ISBN 9780821887592. MR 2076257.
The algorithms that are used the most in practice today [for computing greatest common divisors] are probably the binary algorithm and Euclid’s algorithm for smaller numbers, and either Lehmer’s algorithm or Lebealean’s version of the k-ary GCD algorithm for larger numbers.
- ^ Knuth 1997, pp. 321–323
- ^ Stein, J. (1967). “Computational problems associated with Racah algebra”. Journal of Computational Physics. 1 (3): 397–405. Bibcode:1967JCoPh…1..397S. doi:10.1016/0021-9991(67)90047-2.
- ^ Knuth 1997, p. 328
- ^ Lehmer, D. H. (1938). “Euclid’s Algorithm for Large Numbers”. The American Mathematical Monthly. 45 (4): 227–233. doi:10.2307/2302607. JSTOR 2302607.
- ^ Sorenson, J. (1994). “Two fast GCD algorithms”. J. Algorithms. 16: 110–144. doi:10.1006/jagm.1994.1006.
- ^ Weber, K. (1995). “The accelerated GCD algorithm”. ACM Trans. Math. Softw. 21: 111–122. doi:10.1145/200979.201042. S2CID 14934919.
- ^ Aho, A.; Hopcroft, J.; Ullman, J. (1974). The Design and Analysis of Computer Algorithms. New York: Addison–Wesley. pp. 300–310. ISBN 0-201-00029-6.
- ^ Schönhage, A. (1971). “Schnelle Berechnung von Kettenbruchentwicklungen”. Acta Informatica (in German). 1 (2): 139–144. doi:10.1007/BF00289520. S2CID 34561609.
- ^ Cesari, G. (1998). “Parallel implementation of Schönhage’s integer GCD algorithm”. In G. Buhler (ed.). Algorithmic Number Theory: Proc. ANTS-III, Portland, OR. Lecture Notes in Computer Science. Vol. 1423. New York: Springer-Verlag. pp. 64–76.
- ^ Stehlé, D.; Zimmermann, P. (2005). “Gal’s accurate tables method revisited”. Proceedings of the 17th IEEE Symposium on Computer Arithmetic (ARITH-17). Los Alamitos, CA: IEEE Computer Society Press.
- ^ a b c Lang, S. (1984). Algebra (2nd ed.). Menlo Park, CA: Addison–Wesley. pp. 190–194. ISBN 0-201-05487-6.
- ^ a b Weinberger, P. (1973). “On Euclidean rings of algebraic integers”. Proc. Sympos. Pure Math. Proceedings of Symposia in Pure Mathematics. 24: 321–332. doi:10.1090/pspum/024/0337902. ISBN 9780821814246.
- ^ a b c Stillwell 2003, pp. 151–152
- ^ Boyer, C. B.; Merzbach, U. C. (1991). A History of Mathematics (2nd ed.). New York: Wiley. pp. 116–117. ISBN 0-471-54397-7.
- ^ Cajori, F (1894). A History of Mathematics. New York: Macmillan. p. 70. ISBN 0-486-43874-0.
- ^ Joux, Antoine (2009). Algorithmic Cryptanalysis. CRC Press. p. 33. ISBN 9781420070033.
- ^ Fuks, D. B.; Tabachnikov, Serge (2007). Mathematical Omnibus: Thirty Lectures on Classic Mathematics. American Mathematical Society. p. 13. ISBN 9780821843161.
- ^ Darling, David (2004). “Khintchine’s constant”. The Universal Book of Mathematics: From Abracadabra to Zeno’s Paradoxes. John Wiley & Sons. p. 175. ISBN 9780471667001.
- ^ Williams, Colin P. (2010). Explorations in Quantum Computing. Springer. pp. 277–278. ISBN 9781846288876.
- ^ Cox, Little & O’Shea 1997, pp. 37–46
- ^ Schroeder 2005, pp. 254–259
- ^ Grattan-Guinness, Ivor (1990). Convolutions in French Mathematics, 1800-1840: From the Calculus and Mechanics to Mathematical Analysis and Mathematical Physics. Volume II: The Turns. Science Networks: Historical Studies. Vol. 3. Basel, Boston, Berlin: Birkhäuser. p. 1148. ISBN 9783764322380.
Our subject here is the ‘Sturm sequence’ of functions defined from a function and its derivative by means of Euclid’s algorithm, in order to calculate the number of real roots of a polynomial within a given interval
- ^ Hairer, Ernst; Nørsett, Syvert P.; Wanner, Gerhard (1993). “The Routh–Hurwitz Criterion”. Solving Ordinary Differential Equations I: Nonstiff Problems. Springer Series in Computational Mathematics. Vol. 8 (2nd ed.). Springer. pp. 81ff. ISBN 9783540566700.
- ^ a b c Stillwell 2003, pp. 101–116
- ^ a b c Hensley, Doug (2006). Continued Fractions. World Scientific. p. 26. ISBN 9789812564771.
- ^ Dedekind, Richard (1996). Theory of Algebraic Integers. Cambridge Mathematical Library. Cambridge University Press. pp. 22–24. ISBN 9780521565189.
- ^ Johnston, Bernard L.; Richman, Fred (1997). Numbers and Symmetry: An Introduction to Algebra. CRC Press. p. 44. ISBN 9780849303012.
- ^ Adams, William W.; Goldstein, Larry Joel (1976). Introduction to Number Theory. Prentice-Hall. Exercise 24, p. 205. ISBN 9780134912820.
State and prove an analogue of the Chinese remainder theorem for the Gaussian integers.
- ^ Stark 1978, p. 290
- ^ Cohn 1962, pp. 104–105
- ^ Lauritzen, Niels (2003). Concrete Abstract Algebra: From Numbers to Gröbner Bases. Cambridge University Press. p. 130. ISBN 9780521534109.
- ^ Lauritzen (2003), p. 132
- ^ Lauritzen (2003), p. 161
- ^ a b Sharpe, David (1987). Rings and Factorization. Cambridge University Press. p. 55. ISBN 9780521337182.
- ^ Sharpe (1987), p. 52
- ^ Lauritzen (2003), p. 131
- ^ Lamé, G. (1847). “Mémoire sur la résolution, en nombres complexes, de l’équation An + Bn + Cn = 0″. J. Math. Pures Appl. (in French). 12: 172–184.
- ^ Edwards, H. (2000). Fermat’s last theorem: a genetic introduction to algebraic number theory. Springer. p. 76.
- ^ Cohn 1962, pp. 104–110
- ^ LeVeque, W. J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. pp. II:57, 81. ISBN 978-0-486-42539-9. Zbl 1009.11001.
- ^ a b Clark, D. A. (1994). “A quadratic field which is Euclidean but not norm-Euclidean”. Manuscripta Mathematica. 83: 327–330. doi:10.1007/BF02567617. S2CID 895185. Zbl 0817.11047.
- ^ a b Davidoff, Giuliana; Sarnak, Peter; Valette, Alain (2003). “2.6 The Arithmetic of Integer Quaternions”. Elementary Number Theory, Group Theory and Ramanujan Graphs. London Mathematical Society Student Texts. Vol. 55. Cambridge University Press. pp. 59–70. ISBN 9780521531436.
- ^ Ribenboim, Paulo (2001). Classical Theory of Algebraic Numbers. Universitext. Springer-Verlag. p. 104. ISBN 9780387950709.
Bibliography[edit]
- Cohen, H. (1993). A Course in Computational Algebraic Number Theory. New York: Springer-Verlag. ISBN 0-387-55640-0.
- Cohn, H. (1962). Advanced Number Theory. New York: Dover. ISBN 0-486-64023-X.
- Cox, D.; Little, J.; O’Shea, D. (1997). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra (2nd ed.). Springer-Verlag. ISBN 0-387-94680-2.
- Crandall, R.; Pomerance, C. (2001). Prime Numbers: A Computational Perspective (1st ed.). New York: Springer-Verlag. ISBN 0-387-94777-9.
- Lejeune Dirichlet, P. G. (1894). Dedekind, Richard (ed.). Vorlesungen über Zahlentheorie (Lectures on Number Theory) (in German). Braunschweig: Vieweg. LCCN 03005859. OCLC 490186017.. See also Vorlesungen über Zahlentheorie
- Knuth, D. E. (1997). The Art of Computer Programming, Volume 2: Seminumerical Algorithms (3rd ed.). Addison–Wesley. ISBN 0-201-89684-2.
- LeVeque, W. J. (1996) [1977]. Fundamentals of Number Theory. New York: Dover. ISBN 0-486-68906-9.
- Mollin, R. A. (2008). Fundamental Number Theory with Applications (2nd ed.). Boca Raton: Chapman & Hall/CRC. ISBN 978-1-4200-6659-3.
- Ore, O. (1948). Number Theory and Its History. New York: McGraw–Hill.
- Rosen, K. H. (2000). Elementary Number Theory and its Applications (4th ed.). Reading, MA: Addison–Wesley. ISBN 0-201-87073-8.
- Schroeder, M. (2005). Number Theory in Science and Communication (4th ed.). Springer-Verlag. ISBN 0-387-15800-6.
- Stark, H. (1978). An Introduction to Number Theory. MIT Press. ISBN 0-262-69060-8.
- Stillwell, J. (1997). Numbers and Geometry. New York: Springer-Verlag. ISBN 0-387-98289-2.
- Stillwell, J. (2003). Elements of Number Theory. New York: Springer-Verlag. ISBN 0-387-95587-9.
- Tattersall, J. J. (2005). Elementary Number Theory in Nine Chapters. Cambridge: Cambridge University Press. ISBN 978-0-521-85014-8.
External links[edit]
- Demonstrations of Euclid’s algorithm
- Weisstein, Eric W. “Euclidean Algorithm”. MathWorld.
- Euclid’s Algorithm at cut-the-knot
- Euclid’s algorithm at PlanetMath.
- The Euclidean Algorithm at MathPages
- Euclid’s Game at cut-the-knot
- Music and Euclid’s algorithm
Эта статья посвящена алгоритму определения наибольшего общего делителя. По математике пространства см. Евклидова геометрия. Чтобы узнать о других значениях слова «евклидово», см. Евклидово (значения).
Метод Евклида для нахождения наибольшего общего делителя (НОД) двух начальных длин BA и DC, которые определены как кратные общей «единичной» длины. Поскольку длина DC короче, она используется для «измерения» BA, но только один раз, потому что остаток EA меньше DC. EA теперь измеряет (в два раза) более короткую длину DC, а остаток FC короче, чем EA. Затем FC измеряет (трижды) длину EA. Поскольку остатка нет, процесс завершается тем, что FC является GCD. Справа Никомах Пример с числами 49 и 21, результатом которых является их НОД 7 (получено из Heath 1908: 300).
В математика, то Евклидов алгоритм,[примечание 1] или же Алгоритм Евклида, является эффективным методом вычисления наибольший общий делитель (НОД) двух целых чисел (чисел), наибольшее число, которое делит их оба без остаток. Назван в честь древнегреческого математик Евклид, который впервые описал это в его Элементы (ок. 300 г. до н. э.). Это пример алгоритм, пошаговая процедура для выполнения вычислений в соответствии с четко определенными правилами, и это один из старейших широко используемых алгоритмов. Его можно использовать для уменьшения фракции к их самая простая форма, и является частью многих других теоретико-числовых и криптографических вычислений.
Алгоритм Евклида основан на том принципе, что наибольший общий делитель двух чисел не меняется, если большее число заменяется его разностью с меньшим числом. Например, 21 – это НОД 252 и 105 (как 252 = 21 × 12 и 105 = 21 × 5), и то же число 21 также является НОД 105 и 252 – 105 = 147. Поскольку эта замена уменьшает большее из двух чисел, повторение этого процесса дает последовательно меньшие пары чисел, пока два числа не станут равными. Когда это происходит, они являются НОД исходных двух чисел. К поменять шаги или используя расширенный алгоритм Евклида, НОД можно выразить как линейная комбинация двух исходных чисел, то есть суммы двух чисел, каждое из которых умножено на целое число (Например, 21 = 5 × 105 + (−2) × 252). Тот факт, что НОД всегда можно выразить таким образом, известен как Личность Безу.
Версия алгоритма Евклида, описанная выше (и Евклидом), может предпринять много шагов вычитания, чтобы найти НОД, когда одно из заданных чисел намного больше другого. Более эффективная версия алгоритма сокращает эти шаги, вместо этого заменяя большее из двух чисел его остатком при делении на меньшее из двух (в этой версии алгоритм останавливается при достижении нулевого остатка). Благодаря этому усовершенствованию алгоритм никогда не требует больше шагов, чем пятикратное количество цифр (основание 10) меньшего целого числа. Это было доказано Габриэль Ламе в 1844 году и знаменует собой начало теория сложности вычислений. Дополнительные методы повышения эффективности алгоритма были разработаны в ХХ веке.
Алгоритм Евклида имеет множество теоретических и практических приложений. Используется для уменьшения фракции к их самая простая форма и для выполнения разделение в модульная арифметика. Вычисления с использованием этого алгоритма являются частью криптографические протоколы которые используются для защиты Интернет коммуникации и методы взлома этих криптосистем путем факторинг больших составных чисел. Алгоритм Евклида можно использовать для решения Диофантовы уравнения, например, поиск чисел, удовлетворяющих множественным сравнениям в соответствии с Китайская теорема об остатках, строить непрерывные дроби, и найти точные рациональные приближения к действительным числам. Наконец, его можно использовать в качестве основного инструмента для доказательства теорем в теория чисел Такие как Теорема Лагранжа о четырех квадратах и единственность простых факторизаций. Первоначальный алгоритм был описан только для натуральных чисел и геометрической длины (действительных чисел), но алгоритм был обобщен в 19 веке для других типов чисел, таких как Гауссовские целые числа и многочлены одной переменной. Это привело к современному абстрактная алгебраическая такие понятия, как Евклидовы области.
Фон: наибольший общий делитель
Алгоритм Евклида вычисляет наибольший общий делитель (НОД) двух натуральные числа а и б. Наибольший общий делитель грамм это наибольшее натуральное число, которое делит оба а и б не оставляя остатка. Синонимы к GCD включают наибольший общий делитель (GCF), наивысший общий фактор (HCF), старший общий делитель (HCD), а наибольшая общая мера (GCM). Наибольший общий делитель часто записывается как gcd (а, б) или, проще, как (а, б),[1] хотя последнее обозначение неоднозначно, оно также используется для таких понятий, как идеальный в кольцо целых чисел, который тесно связан с GCD.
Если gcd (а, б) = 1, то а и б как говорят совмещать (или относительно простые).[2] Это свойство не означает, что а или же б сами простые числа.[3] Например, ни 6, ни 35 не являются простыми числами, так как они оба имеют два простых множителя: 6 = 2 × 3 и 35 = 5 × 7. Тем не менее, 6 и 35 взаимно просты. Никакое натуральное число, кроме 1, не делит 6 и 35, так как у них нет общих простых делителей.
Прямоугольник 24 на 60 покрыт десятью квадратными плитками 12 на 12, где 12 – это НОД 24 и 60. В общем, а-к-б прямоугольник можно покрыть квадратными плитками со стороной c только если c является общим делителем а и б.
Позволять грамм = gcd (а, б). С а и б оба кратны грамм, их можно написать а = мг и б = нг, и нет большего числа грамм > грамм для чего это правда. Натуральные числа м и п должны быть взаимно простыми, поскольку любой общий фактор может быть исключен из м и п сделать грамм больше. Таким образом, любое другое число c что разделяет оба а и б должен также разделить грамм. Наибольший общий делитель грамм из а и б является единственным (положительным) общим делителем числа а и б который делится на любой другой общий делитель c.[4]
НОД можно визуализировать следующим образом.[5] Рассмотрим прямоугольную область а к б, и любой общий делитель c что разделяет оба а и б точно. Стороны прямоугольника можно разделить на отрезки длины c, который делит прямоугольник на сетку квадратов со стороной c. Наибольший общий делитель грамм это наибольшее значение c для которых это возможно. Для иллюстрации прямоугольную область 24 на 60 можно разделить на сетку из: квадратов 1 на 1, квадратов 2 на 2, квадратов 3 на 3, квадратов 4 на 4, 6 на -6 квадратов или 12 на 12 квадратов. Следовательно, 12 – это наибольший общий делитель 24 и 60. Прямоугольную область 24 на 60 можно разделить на сетку из квадратов 12 на 12, с двумя квадратами вдоль одного края (24/12 = 2) и пятью квадраты по другой (60/12 = 5).
НОД двух чисел а и б представляет собой произведение простых множителей, общих для двух чисел, где один и тот же простой множитель может использоваться несколько раз, но только до тех пор, пока произведение этих множителей делит оба а и б.[6] Например, поскольку 1386 можно разложить на 2 × 3 × 3 × 7 × 11, а 3213 можно разложить на 3 × 3 × 3 × 7 × 17, наибольший общий делитель 1386 и 3213 равен 63 = 3 × 3 × 7, произведение их общих простых факторов. Если два числа не имеют общих простых делителей, их наибольший общий делитель равен 1 (получен здесь как пример пустой продукт ), другими словами, они взаимно просты. Ключевым преимуществом алгоритма Евклида является то, что он может эффективно находить НОД без вычисления простых множителей.[7][8] Факторизация больших целых чисел считается вычислительно очень сложной задачей, а безопасность многих широко используемых криптографические протоколы основано на его невозможности.[9]
Другое определение НОД полезно в продвинутой математике, особенно в теория колец.[10] Наибольший общий делитель грамм двух ненулевых чисел а и б также является их наименьшей положительной целочисленной линейной комбинацией, то есть наименьшим положительным числом вида ua + vb куда ты и v целые числа. Множество всех целых линейных комбинаций а и б фактически совпадает с набором всех кратных грамм (мг, куда м является целым числом). На современном математическом языке идеальный создано а и б идеал, порожденныйграмм один (идеал, порожденный одним элементом, называется главный идеал, а все идеалы целых чисел являются главными идеалами). Некоторые свойства НОД на самом деле легче увидеть с помощью этого описания, например тот факт, что любой общий делитель а и б также делит НОД (он делит оба члена ua + vb). Эквивалентность этого определения GCD другим определениям описывается ниже.
НОД трех или более чисел равен произведению простых множителей, общих для всех чисел,[11] но его также можно вычислить, многократно взяв НОД пар чисел.[12] Например,
- gcd (а, б, c) = gcd (а, gcd (б, c)) = gcd (gcd (а, б), c) = gcd (gcd (а, c), б).
Таким образом, алгоритма Евклида, который вычисляет НОД двух целых чисел, достаточно для вычисления НОД произвольного числа целых чисел.
Описание
Процедура
Алгоритм Евклида состоит из ряда шагов, так что выходные данные каждого шага используются в качестве входных данных для следующего. Позволять k быть целым числом, которое считает шаги алгоритма, начиная с нуля. Таким образом, начальный шаг соответствует k = 0, следующий шаг соответствует k = 1 и так далее.
Каждый шаг начинается с двух неотрицательных остатков рk−1 и рk−2. Поскольку алгоритм гарантирует, что остатки неуклонно уменьшаются с каждым шагом, рk−1 меньше, чем его предшественник рk−2. Цель k-й шаг – найти частное qk и остаток рk которые удовлетворяют уравнению
и что 0 ≤ рk < рk−1. Другими словами, кратные меньшему числу рk−1 вычитаются из большего числа рk−2 до остатка рk меньше чем рk−1.
На начальном этапе (k = 0) остатки р−2 и р−1 равный а и б, числа, для которых ищется НОД. На следующем шаге (k = 1) остатки равны б а остальное р0 начального шага и т. д. Таким образом, алгоритм можно записать в виде последовательности уравнений
Если а меньше чем б, первый шаг алгоритма меняет местами числа. Например, если а < б, начальное частное q0 равен нулю, а остаток р0 является а. Таким образом, рk меньше, чем его предшественник рk−1 для всех k ≥ 0.
Поскольку остатки уменьшаются с каждым шагом, но никогда не могут быть отрицательными, остаток рN должен в конечном итоге равняться нулю, после чего алгоритм останавливается.[13] Последний ненулевой остаток рN−1 является наибольшим общим делителем а и б. Номер N не может быть бесконечным, потому что есть только конечное число неотрицательных целых чисел между начальным остатком р0 и ноль.
Доказательство действительности
Справедливость алгоритма Евклида может быть доказана двухэтапным аргументом.[14] На первом шаге последний ненулевой остаток рN−1 показано деление обоих а и б. Поскольку это общий делитель, он должен быть меньше или равен наибольшему общему делителю. грамм. На втором шаге показано, что любой общий делитель числа а и б, включая грамм, должен разделить рN−1; следовательно, грамм должно быть меньше или равно рN−1. Эти два вывода несовместимы, если рN−1 = грамм.
Чтобы продемонстрировать, что рN−1 разделяет оба а и б (первый шаг), рN−1 делит своего предшественника рN−2
- рN−2 = qN рN−1
так как последний остаток рN равно нулю. рN−1 также делит своего следующего предшественника рN−3
- рN−3 = qN−1 рN−2 + рN−1
потому что он делит оба члена в правой части уравнения. Повторяя тот же аргумент, рN−1 делит все предыдущие остатки, включая а и б. Ни один из предыдущих остатков рN−2, рN−3и т. д. разделить а и б, поскольку они оставляют остаток. С рN−1 является общим делителем а и б, рN−1 ≤ грамм.
На втором этапе любое натуральное число c что разделяет оба а и б (другими словами, любой общий делитель а и б) делит остатки рk. По определению, а и б можно записать как кратное c : а = MC и б = NC, куда м и п натуральные числа. Следовательно, c делит начальный остаток р0, поскольку р0 = а − q0б = MC − q0NC = (м − q0п)c. Аналогичный аргумент показывает, что c также делит последующие остатки р1, р2и т. д. Следовательно, наибольший общий делитель грамм должен разделить рN−1, откуда следует, что грамм ≤ рN−1. Поскольку первая часть аргумента показала обратное (рN−1 ≤ грамм), следует, что грамм = рN−1. Таким образом, грамм является наибольшим общим делителем всех последующих пар:[15][16]
- грамм = gcd (а, б) = gcd (б, р0) = gcd (р0, р1) =… = НОД (рN−2, рN−1) = рN−1.
Пример работы
Анимация алгоритма Евклида на основе вычитания. Исходный прямоугольник имеет размеры а = 1071 и б = 462. Квадраты размером 462 × 462 помещаются в него, оставляя прямоугольник 462 × 147. Этот прямоугольник выложен плиткой из 147 × 147 квадратов, пока не останется прямоугольник 21 × 147, который, в свою очередь, выложен плиткой 21 × 21 квадратом, не оставляя непокрытой области. Наименьший квадрат размером 21 – это НОД 1071 и 462.
Для иллюстрации можно использовать алгоритм Евклида, чтобы найти наибольший общий делитель а = 1071 и б = 462. Для начала, кратные 462 вычитаются из 1071, пока остаток не станет меньше 462. Два таких кратных можно вычесть (q0 = 2), оставляя остаток от 147:
- 1071 = 2 × 462 + 147.
Затем из 462 вычитаются числа, кратные 147, пока остаток не станет меньше 147. Можно вычесть три кратных (q1 = 3), оставив остаток от 21:
- 462 = 3 × 147 + 21.
Затем из 147 вычитаются числа, кратные 21, пока остаток не станет меньше 21. Можно вычесть семь кратных (q2 = 7), не оставляя остатка:
- 147 = 7 × 21 + 0.
Поскольку последний остаток равен нулю, алгоритм заканчивается 21 как наибольший общий делитель 1071 и 462. Это согласуется с НОД (1071, 462), найденным путем разложения на простые множители. над. В табличной форме шаги следующие:
| Шаг k | Уравнение | Частное и остаток |
|---|---|---|
| 0 | 1071 = q0 462 + р0 | q0 = 2 и р0 = 147 |
| 1 | 462 = q1 147 + р1 | q1 = 3 и р1 = 21 |
| 2 | 147 = q2 21 + р2 | q2 = 7 и р2 = 0; алгоритм заканчивается |
Визуализация
Алгоритм Евклида можно представить себе в терминах мозаичной аналогии, приведенной выше для наибольшего общего делителя.[17] Предположим, что мы хотим покрыть а-к-б прямоугольник с квадратными плитками ровно, где а является большим из двух чисел. Сначала мы пытаемся выложить прямоугольник, используя б-к-б квадратная плитка; однако это оставляет р0-к-б остаточный прямоугольник без элементов, где р0 < б. Затем мы пытаемся замостить остаточный прямоугольник с помощью р0-к-р0 квадратная плитка. Остается второй остаточный прямоугольник р1-к-р0, который мы пытаемся выложить плиткой, используя р1-к-р1 квадратная плитка и т. д. Последовательность завершается, когда нет остаточного прямоугольника, то есть когда квадратные плитки точно покрывают предыдущий остаточный прямоугольник. Длина сторон самой маленькой квадратной плитки – это НОД размеров исходного прямоугольника. Например, самая маленькая квадратная плитка на соседнем рисунке имеет размер 21 на 21 (показано красным), а 21 – это НОД 1071 и 462, размеры исходного прямоугольника (показаны зеленым).
Евклидово деление
На каждом шагу k, алгоритм Евклида вычисляет частное qk и остальное рk из двух номеров рk−1 и рk−2
- рk−2 = qk рk−1 + рk
где рk неотрицательно и строго меньше, чем абсолютная величина из рk−1. Теорема, лежащая в основе определения Евклидово деление гарантирует, что такое частное и остаток всегда существуют и уникальны.[18]
В исходной версии алгоритма Евклида частное и остаток находятся путем повторного вычитания; то есть, рk−1 вычитается из рk−2 повторно до остатка рk меньше чем рk−1. После того рk и рk−1 обмениваются, и процесс повторяется. Евклидово деление сокращает все шаги между двумя обменами до одного шага, что, таким образом, более эффективно. Более того, частные не нужны, поэтому можно заменить евклидово деление на операция по модулю, что дает только остаток. Таким образом, итерация алгоритма Евклида становится просто
- рk = рk−2 мод рk−1.
Реализации
Реализации алгоритма могут быть выражены в псевдокод. Например, версия на основе разделения может быть запрограммированный в качестве[19]
функция gcd (a, b) пока b ≠ 0 t: = b b: = a мод б а: = т возвращаться а
В начале kй итерации переменная б держит последний остаток рk−1, а переменная а держит своего предшественника, рk−2. Шаг б := а мод б эквивалентно приведенной выше формуле рекурсии рk ≡ рk−2 мод рk−1. В временная переменная т имеет ценность рk−1 а следующий остаток рk рассчитывается. В конце итерации цикла переменная б держит остаток рk, а переменная а держит своего предшественника, рk−1.
В версии на основе вычитания, которая была исходной версией Евклида, вычисление остатка (б: = а мод б) заменяется повторным вычитанием.[20] В отличие от версии на основе деления, которая работает с произвольными целыми числами в качестве ввода, версия на основе вычитания предполагает, что ввод состоит из положительных целых чисел и останавливается, когда а = б:
функция gcd (a, b) пока а ≠ б если а> б а: = а - б еще б: = б - а возвращаться а
Переменные а и б поочередно удерживая предыдущие остатки рk−1 и рk−2. Предположить, что а больше чем б в начале итерации; тогда а равно рk−2, поскольку рk−2 > рk−1. Во время итерации цикла а уменьшается кратно предыдущему остатку б до того как а меньше чем б. потом а следующий остаток рk. потом б уменьшается кратно а пока он снова не станет меньше, чем а, давая следующий остаток рk+1, и так далее.
Рекурсивная версия[21] основан на равенстве НОД последовательных остатков и условия остановки НОД (рN−1, 0) = рN−1.
функция gcd (a, b) если б = 0 возвращаться а еще возвращаться gcd (b, a мод б)
Например, НОД (1071, 462) вычисляется из эквивалентного НОД (462, 1071 mod 462) = НОД (462, 147). Последний НОД вычисляется из НОД (147, 462 mod 147) = НОД (147, 21), который, в свою очередь, вычисляется из НОД (21, 147 mod 21) = НОД (21, 0) = 21.
Метод наименьших абсолютных остатков
В другой версии алгоритма Евклида частное на каждом шаге увеличивается на единицу, если результирующий отрицательный остаток меньше по величине, чем типичный положительный остаток.[22][23] Ранее уравнение
- рk−2 = qk рk−1 + рk
предположил, что |рk−1| > рk > 0. Однако альтернативный отрицательный остаток еk можно вычислить:
- рk−2 = (qk + 1) рk−1 + еk
если рk−1 > 0 или же
- рk−2 = (qk − 1) рk−1 + еk
если рk−1 < 0.
Если рk заменяется на еk. когда |еk| < |рk|, то получается такой вариант алгоритма Евклида, что
- |рk| ≤ |рk−1| / 2
на каждом шагу.
Леопольд Кронекер показал, что эта версия требует наименьшего количества шагов по сравнению с любой версией алгоритма Евклида.[22][23] В более общем плане было доказано, что для каждого входного числа а и б, количество шагов минимально тогда и только тогда, когда qk выбирается для того, чтобы 

Историческое развитие
Вероятно, алгоритм Евклида был изобретен раньше Евклид, изображенный здесь, держащий компас на картине около 1474 г.
Алгоритм Евклида – один из самых старых широко используемых алгоритмов.[25] Он появляется в Евклида Элементы (ок. 300 г. до н.э.), особенно в Книге 7 (Предложения 1–2) и Книге 10 (Предложения 2–3). В Книге 7 алгоритм сформулирован для целых чисел, тогда как в Книге 10 он сформулирован для длин отрезков прямой. (В современном использовании можно сказать, что он был сформулирован для действительные числа. Но длины, площади и объемы, представленные в современном обиходе действительными числами, не измеряются в одних и тех же единицах, и нет естественных единиц длины, площади или объема; понятие действительных чисел в то время было неизвестно.) Последний алгоритм является геометрическим. НОД двух длин а и б соответствует наибольшей длине грамм это меры а и б равномерно; другими словами, длина а и б оба целые числа кратные длины грамм.
Вероятно, алгоритм не был обнаружен Евклид, который обобщил результаты более ранних математиков в своей Элементы.[26][27] Математик и историк Б. Л. ван дер Варден предполагает, что Книга VII происходит из учебника по теория чисел написано математиками в школе Пифагор.[28] Алгоритм, вероятно, был известен Евдокс Книдский (около 375 г. до н.э.).[25][29] Алгоритм может даже предшествовать Евдоксу,[30][31] судя по использованию технического термина ἀνθυφαίρεσις (ангиферез, взаимное вычитание) в работах Евклида и Аристотеля.[32]
Спустя столетия алгоритм Евклида был независимо открыт как в Индии, так и в Китае.[33] в первую очередь решить Диофантовы уравнения возникшие в астрономии и создании точных календарей. В конце V века индийский математик и астроном Арьябхата описал алгоритм как «измельчитель»,[34] возможно, из-за его эффективности при решении диофантовых уравнений.[35] Хотя частный случай Китайская теорема об остатках уже было описано в китайской книге Сунзи Суаньцзин,[36] общее решение было опубликовано Цинь Цзюшао в его книге 1247 г. Шушу Цзючжан (數 書 九章 Математический трактат в девяти разделах ).[37] Впервые был описан алгоритм Евклида. численно и популяризован в Европе во втором издании Баше Problèmes plaisants et délectables (Приятные и приятные проблемы, 1624).[34] В Европе он также использовался для решения диофантовых уравнений и при разработке непрерывные дроби. В расширенный алгоритм Евклида был опубликован английским математиком Николас Сондерсон,[38] кто приписал это Роджер Котс как метод эффективного вычисления непрерывных дробей.[39]
В 19 веке алгоритм Евклида привел к развитию новых систем счисления, таких как Гауссовские целые числа и Целые числа Эйзенштейна. В 1815 г. Карл Гаусс использовали алгоритм Евклида, чтобы продемонстрировать уникальную факторизацию Гауссовские целые числа, хотя его работа была впервые опубликована в 1832 году.[40] Гаусс упомянул алгоритм в своем Disquisitiones Arithmeticae (опубликовано в 1801 г.), но только как метод для непрерывные дроби.[33] Питер Густав Лежен Дирихле кажется, был первым, кто описал алгоритм Евклида как основу большей части теории чисел.[41] Лежен Дирихле отметил, что многие результаты теории чисел, такие как уникальная факторизация, будут верны для любой другой системы чисел, к которой можно применить алгоритм Евклида.[42] Лекции Лежена Дирихле по теории чисел редактировал и дополнял Ричард Дедекинд, который использовал алгоритм Евклида для изучения алгебраические целые числа, новый общий тип номера. Например, Дедекинд первым доказал Теорема Ферма о двух квадратах используя уникальную факторизацию гауссовских целых чисел.[43] Дедекинд также определил понятие Евклидова область, система счисления, в которой может быть определена обобщенная версия алгоритма Евклида (как описано ниже ). В последние десятилетия XIX века алгоритм Евклида постепенно уступил место более общей теории Дедекинда. идеалы.[44]
|
«[Алгоритм Евклида] – дедушка всех алгоритмов, потому что это самый старый нетривиальный алгоритм, сохранившийся до наших дней». |
| Дональд Кнут, Искусство программирования, Vol. 2: получисловые алгоритмы, 2-е издание (1981), стр. 318. |
Другие приложения алгоритма Евклида были разработаны в 19 веке. В 1829 г. Чарльз Штурм показал, что алгоритм был полезен в Штурмовая цепь метод подсчета действительных корней многочленов в любом заданном интервале.[45]
Алгоритм Евклида был первым алгоритм целочисленного отношения, который представляет собой метод нахождения целочисленных отношений между соизмеримыми действительными числами. Несколько романов алгоритмы целочисленных отношений были разработаны, например, алгоритм Геламан Фергюсон и Р.В. Форкэйд (1979)[46] и LLL алгоритм.[47][48]
В 1969 году Коул и Дэви разработали игру для двух игроков, основанную на алгоритме Евклида, под названием Игра Евклида,[49] который имеет оптимальную стратегию.[50] Игроки начинают с двумя стопками а и б камни. Игроки по очереди снимают м кратно меньшей стопке большей. Таким образом, если две стопки состоят из Икс и у камни, где Икс больше чем у, следующий игрок может уменьшить большую стопку из Икс камни в Икс − мой камни, если последнее является целым неотрицательным числом. Побеждает тот игрок, который первым уменьшит одну стопку камней до нуля.[51][52]
Математические приложения
Личность Безу
Личность Безу утверждает, что наибольший общий делитель грамм двух целых чисел а и б можно представить как линейную сумму двух исходных чисел а и б.[53] Другими словами, всегда можно найти целые числа s и т такой, что грамм = са + tb.[54][55]
Целые числа s и т можно рассчитать из частных q0, q1и т.д., изменив порядок уравнений в алгоритме Евклида.[56] Начиная с предпоследнего уравнения, грамм можно выразить через частное qN−1 и два предыдущих остатка, рN−2 и рN−3:
- грамм = рN−1 = рN−3 − qN−1 рN−2 .
Эти два остатка могут быть аналогичным образом выражены через их частные и предшествующие остатки,
- рN−2 = рN−4 − qN−2 рN−3 и
- рN−3 = рN−5 − qN−3 рN−4 .
Подставляя эти формулы для рN−2 и рN−3 в первое уравнение дает грамм как линейную сумму остатков рN−4 и рN−5. Процесс замены остатков формулами с участием их предшественников может быть продолжен до тех пор, пока исходные числа а и б достигаются:
- р2 = р0 − q2 р1
- р1 = б − q1 р0
- р0 = а − q0 б.
После всего остального р0, р1и т. д., окончательное уравнение выражает грамм как линейную сумму а и б: грамм = са + tb. Личность Безу, и, следовательно, предыдущий алгоритм, оба могут быть обобщены в контексте Евклидовы области.
Основные идеалы и связанные с ними проблемы
Тождество Безу дает еще одно определение наибольшего общего делителя грамм двух чисел а и б.[10] Рассмотрим набор всех чисел ua + vb, куда ты и v – любые два целых числа. С а и б оба делятся на грамм, каждое число в наборе делится на грамм. Другими словами, каждое число в наборе является целым числом, кратным грамм. Это верно для любого общего делителя а и б. Однако, в отличие от других общих делителей, наибольший общий делитель является членом множества; личности Безу, выбрав ты = s и v = т дает грамм. Меньший общий делитель не может быть членом множества, так как каждый член множества должен делиться на грамм. И наоборот, любое кратное м из грамм можно получить, выбрав ты = РС и v = мт, куда s и т являются целыми числами личности Безу. Это можно увидеть, умножив личность Безу на м,
- мг = мса + mtb.
Следовательно, набор всех чисел ua + vb эквивалентен множеству кратных м из грамм. Другими словами, множество всех возможных сумм целых кратных двух чисел (а и б) эквивалентен множеству кратных gcd (а, б). Говорят, что НОД является генератором идеальный из а и б. Это определение НОД привело к современному абстрактная алгебраическая концепции главный идеал (идеал, порожденный одним элементом) и главная идеальная область (а домен в котором каждый идеал является главным идеалом).
С помощью этого результата можно решить некоторые проблемы.[57] Например, рассмотрим две мерные чашки объема. а и б. Добавляя / вычитая ты кратные первой чашки и v кратные второй чашки, любой объем ua + vb можно измерить. Все эти объемы кратны грамм = gcd (а, б).
Расширенный алгоритм Евклида
Целые числа s и т тождества Безу можно эффективно вычислить с помощью расширенный алгоритм Евклида. Это расширение добавляет к алгоритму Евклида два рекурсивных уравнения[58]
- sk = sk−2 − qksk−1
- тk = тk−2 − qkтk−1
с начальными значениями
- s−2 = 1, т−2 = 0
- s−1 = 0, т−1 = 1.
Используя эту рекурсию, целые числа Безу s и т даны s = sN и т = тN, куда N + 1 шаг, на котором алгоритм завершается с рN + 1 = 0.
Справедливость этого подхода можно показать по индукции. Предположим, что формула рекурсии верна до шага k – 1 алгоритм; другими словами, предположим, что
- рj = sj а + тj б
для всех j меньше, чем k. В k-й шаг алгоритма дает уравнение
- рk = рk−2 − qkрk−1.
Поскольку формула рекурсии считается правильной для рk−2 и рk−1, они могут быть выражены через соответствующие s и т переменные
- рk = (sk−2 а + тk−2 б) − qk(sk−1 а + тk−1 б).
Преобразование этого уравнения приводит к формуле рекурсии для шага k, как требуется
- рk = sk а + тk б = (sk−2 − qksk−1) а + (тk−2 − qkтk−1) б.
Матричный метод
Целые числа s и т также можно найти с помощью эквивалента матрица метод.[59] Последовательность уравнений алгоритма Евклида
может быть записано как произведение матриц частных 2 на 2, умноженных на двумерный вектор остатка
Позволять M представляют собой произведение всех матриц частных
Это упрощает алгоритм Евклида до вида
Выражать грамм как линейная сумма а и б, обе части этого уравнения можно умножить на обратный матрицы M.[59][60] В детерминант из M равно (−1)N+1, так как он равен произведению определителей факторных матриц, каждая из которых отрицательна. Поскольку определитель M никогда не равен нулю, вектор конечных остатков может быть решен с помощью обратного к M
Поскольку верхнее уравнение дает
- грамм = (−1)N+1 ( м22 а − м12 б),
два целых числа личности Безу равны s = (−1)N+1м22 и т = (−1)Nм12. Матричный метод столь же эффективен, как и эквивалентная рекурсия, с двумя умножениями и двумя сложениями на шаг алгоритма Евклида.
Лемма Евклида и единственная факторизация
Личность Безу важна для многих приложений алгоритма Евклида, таких как демонстрация уникальная факторизация чисел в простые множители.[61] Чтобы проиллюстрировать это, предположим, что число L можно записать как произведение двух факторов ты и v, то есть, L = УФ. Если другой номер ш также разделяет L но совпадает с ты, тогда ш должен разделить v, по следующему аргументу: если наибольший общий делитель ты и ш равно 1, то целые числа s и т можно найти так, что
- 1 = вс + tw .
по личности Безу. Умножая обе стороны на v дает отношение
- v = внедорожник + twv = sL + twv .
С ш делит оба члена в правой части, он также должен делить левую часть, v. Этот результат известен как Лемма евклида.[62] В частности, если простое число делит L, то он должен делить хотя бы один множитель L. И наоборот, если число ш взаимно проста с каждым из ряда чисел а1, а2, …, ап, тогда ш также взаимно прост с их продуктом, а1 × а2 × … × ап.[62]
Леммы Евклида достаточно, чтобы доказать, что каждое число имеет уникальное разложение на простые числа.[63] Чтобы убедиться в этом, предположим противное, что существуют две независимые факторизации L в м и п простые множители соответственно
- L = п1п2…пм = q1q2…qп .
Поскольку каждое простое число п разделяет L по предположению, он также должен делить один из q факторы; поскольку каждый q тоже простое, это должно быть так п = q. Итеративное деление на п факторов показывает, что каждый п имеет равный аналог q; две простые факторизации идентичны, за исключением их порядка. Уникальное разложение чисел на простые числа имеет множество применений в математических доказательствах, как показано ниже.
Линейные диофантовы уравнения
Диофантовы уравнения – уравнения, решения в которых ограничены целыми числами; они названы в честь александрийского математика 3-го века Диофант.[64] Типичный линейный Диофантово уравнение ищет целые числа Икс и у такой, что[65]
- топор + к = c
куда а, б и c даны целые числа. Это можно записать в виде уравнения для Икс в модульная арифметика:
- топор ≡ c мод б.
Позволять грамм быть наибольшим общим делителем а и б. Оба термина в топор + к делятся на грамм; следовательно, c также должно делиться на грамм, либо уравнение не имеет решений. Разделив обе стороны на c/грамм, уравнение сводится к тождеству Безу
- са + tb = грамм
куда s и т можно найти по расширенный алгоритм Евклида.[66] Это дает одно решение диофантова уравнения, Икс1 = s (c/грамм) и у1 = т (c/грамм).
В общем случае линейное диофантово уравнение не имеет решений или имеет бесконечное число решений.[67] Чтобы найти последнее, рассмотрим два решения: (Икс1, у1) и (Икс2, у2), куда
- топор1 + к1 = c = топор2 + к2
или эквивалентно
- а(Икс1 − Икс2) = б(у2 − у1).
Поэтому наименьшая разница между двумя Икс решения б/грамм, тогда как наименьшая разница между двумя у решения а/грамм. Таким образом, решения могут быть выражены как
- Икс = Икс1 − бу/грамм
- у = у1 + au/грамм.
Позволяя ты чтобы варьироваться по всем возможным целым числам, бесконечное семейство решений может быть сгенерировано из одного решения (Икс1, у1). Если решения должны быть положительный целые числа (Икс > 0, у > 0), возможно лишь конечное число решений. Это ограничение на приемлемые решения позволяет некоторым системам диофантовых уравнений с большим количеством неизвестных, чем у уравнений, иметь конечное число решений;[68] это невозможно для система линейных уравнений когда решения могут быть любыми настоящий номер (видеть Недоопределенная система ).
Мультипликативные инверсии и алгоритм RSA
А конечное поле представляет собой набор чисел с четырьмя обобщенными операциями. Эти операции называются сложением, вычитанием, умножением и делением и имеют свои обычные свойства, такие как коммутативность, ассоциативность и распределенность. Примером конечного поля является набор из 13 чисел {0, 1, 2, …, 12} с использованием модульная арифметика. В этом поле сокращаются результаты любой математической операции (сложение, вычитание, умножение или деление). по модулю 13; то есть числа, кратные 13, добавляются или вычитаются, пока результат не будет находиться в диапазоне 0–12. Например, результат 5 × 7 = 35 mod 13 = 9. Такие конечные поля могут быть определены для любого простого числа. п; используя более сложные определения, они также могут быть определены для любой мощности м премьер п м. Конечные поля часто называют Галуа поля, и сокращенно GF (п) или GF (п м).
В таком поле с м числа, каждый ненулевой элемент а имеет уникальный модульный мультипликативный обратный, а−1 такой, что аа−1 = а−1а ≡ 1 модм. Это обратное можно найти, решив уравнение сравнения топор ≡ 1 модм,[69] или эквивалентное линейное диофантово уравнение[70]
- топор + мой = 1.
Это уравнение можно решить с помощью алгоритма Евклида, как описано над. Нахождение мультипликативных инверсий – важный шаг в Алгоритм RSA, который широко используется в электронная коммерция; в частности, уравнение определяет целое число, используемое для дешифрования сообщения.[71] Хотя алгоритм RSA использует кольца вместо полей, алгоритм Евклида все еще может использоваться для нахождения мультипликативного обратного, если он существует. У алгоритма Евклида есть и другие приложения в коды с исправлением ошибок; например, его можно использовать как альтернативу Алгоритм Берлекампа-Месси для расшифровки BCH и Коды Рида – Соломона, основанные на полях Галуа.[72]
Китайская теорема об остатках
Алгоритм Евклида также можно использовать для решения нескольких линейных диофантовых уравнений.[73] Такие уравнения возникают в Китайская теорема об остатках, который описывает новый метод представления целого числа Икс. Вместо представления целого числа цифрами оно может быть представлено остатками Икся по модулю набора N взаимно простые числа мя:[74]
Цель – определить Икс из его N остатки Икся. Решение состоит в том, чтобы объединить несколько уравнений в одно линейное диофантово уравнение с гораздо большим модулем M это продукт всех индивидуальных модулей мя, и определим Mя в качестве
Таким образом, каждый Mя является произведением всех модулей Кроме мя. Решение зависит от поиска N новые номера чася такой, что
С этими числами чася, любое целое число Икс может быть восстановлен по его остаткам Икся по уравнению
Поскольку эти числа чася являются мультипликативными обратными Mя, их можно найти с помощью алгоритма Евклида, как описано в предыдущем подразделе.
Стерн – Броко
Алгоритм Евклида можно использовать для упорядочивания множества всех положительных рациональное число в бесконечность двоичное дерево поиска, называется Стерн – Броко Число 1 (выраженное дробью 1/1) помещается в корень дерева, а расположение любого другого числа а/б можно найти, вычислив gcd (а,б) с использованием исходной формы алгоритма Евклида, в котором каждый шаг заменяет большее из двух заданных чисел его разницей на меньшее число (не его остаток), останавливаясь при достижении двух равных чисел. Шаг алгоритма Евклида, который заменяет первое из двух чисел, соответствует шагу в дереве от узла до его правого дочернего элемента, а шаг, который заменяет второе из двух чисел, соответствует шагу в дереве от узла. слева от него. Построенная таким образом последовательность шагов не зависит от того, а/б дается в наименьших терминах и образует путь от корня до узла, содержащего число а/б.[75] Этот факт можно использовать, чтобы доказать, что каждое положительное рациональное число встречается в этом дереве ровно один раз.
Например, 3/4 можно найти, начав с корня, перейдя один раз влево, а затем дважды вправо:
Дерево Штерна – Броко и последовательности Штерна – Броко порядка я за я = 1, 2, 3, 4
Алгоритм Евклида имеет почти такое же отношение к другому двоичному дереву рациональных чисел, называемому Дерево Калкина – Уилфа. Разница в том, что путь является обратным: вместо создания пути от корня дерева к цели, он создает путь от цели к корню.
Непрерывные дроби
Алгоритм Евклида тесно связан с непрерывные дроби.[76] Последовательность уравнений можно записать в виде
Последний член в правой части всегда равен обратной левой части следующего уравнения. Таким образом, первые два уравнения могут быть объединены в
Третье уравнение можно использовать для замены члена знаменателя р1/р0, уступая
Окончательное соотношение остатков рk/рk−1 всегда можно заменить, используя следующее уравнение в серии, вплоть до последнего уравнения. Результат – непрерывная дробь
В отработанном примере над, был вычислен НОД (1071, 462), а частные qk были 2, 3 и 7 соответственно. Следовательно, дробь 1071/462 может быть записана
что подтверждается расчетом.
Алгоритмы факторизации
Вычисление наибольшего общего делителя – важный шаг в нескольких целочисленная факторизация алгоритмы,[77] Такие как Алгоритм ро Полларда,[78] Алгоритм Шора,[79] Метод факторизации Диксона[80] и Факторизация эллиптической кривой Ленстры.[81] Для эффективного нахождения этого НОД можно использовать алгоритм Евклида. Факторизация непрерывной дроби использует непрерывные дроби, которые определяются с помощью алгоритма Евклида.[82]
Алгоритмическая эффективность
Количество шагов в алгоритме Евклида для gcd (Икс,у). Светлые (красные и желтые) точки указывают на относительно небольшое количество шагов, тогда как более темные (фиолетовые и синие) точки указывают на большее количество шагов. Самая большая темная область следует за линией у = Φx, куда Φ это Золотое сечение.
Вычислительная эффективность алгоритма Евклида тщательно изучена.[83] Эту эффективность можно описать числом шагов деления, которое требует алгоритм, умноженным на вычислительные затраты на каждый шаг. Первый известный анализ алгоритма Евклида принадлежит А.А.Л. Рейно в 1811 г.[84] кто показал, что количество шагов деления на входе (ты, v) ограничен v; позже он улучшил это до v/ 2 + 2. Позже, в 1841 г., П. Дж. Э. Финк показал[85] что количество шагов деления не превышает 2 log2 v + 1, и, следовательно, алгоритм Евклида работает во времени, полиномиальном от размера входных данных.[86] Эмиль Леже в 1837 г. изучал худший случай, когда входы последовательные Числа Фибоначчи.[86] Анализ Финка был уточнен Габриэль Ламе в 1844 г.,[87] кто показал, что количество шагов, необходимых для выполнения, никогда не превышает пятикратное количество час десятичных цифр меньшего числаб.[88][89]
в модель единой стоимости (подходит для анализа сложности вычисления НОД для чисел, которые укладываются в одно машинное слово), каждый шаг алгоритма занимает постоянное время, и анализ Ламе подразумевает, что общее время работы также О(час). Однако в модели вычислений, подходящей для вычислений с большими числами, вычислительные затраты на вычисление одного остатка в алгоритме могут достигать О(час2).[90] В этом случае общее время для всех шагов алгоритма можно проанализировать с помощью телескопическая серия, показывая, что это также О(час2). Современные алгоритмические техники, основанные на Алгоритм Шёнхаге – Штрассена для быстрого целочисленного умножения может использоваться, чтобы ускорить это, что приводит к квазилинейные алгоритмы для НОД.[91][92]
Кол-во ступеней
Количество шагов для вычисления НОД двух натуральных чисел, а и б, может быть обозначено Т(а, б).[93] Если грамм это НОД а и б, тогда а = мг и б = нг для двух взаимно простых чисел м и п. потом
- Т(а, б) = Т(м, п)
как можно увидеть, разделив все шаги в алгоритме Евклида на грамм.[94] По тому же аргументу количество шагов остается прежним, если а и б умножаются на общий коэффициент ш: Т(а, б) = Т(ва, wb). Следовательно, количество ступеней Т может сильно различаться между соседними парами чисел, например T (а, б) и т(а, б + 1), в зависимости от размера двух НОД.
Рекурсивный характер алгоритма Евклида дает еще одно уравнение
- Т(а, б) = 1 + Т(б, р0) = 2 + Т(р0, р1) = … = N + Т(рN−2, рN−1) = N + 1
куда Т(Икс, 0) = 0 по предположению.[93]
Худший случай
Если алгоритм Евклида требует N шаги для пары натуральных чисел а > б > 0 наименьшие значения а и б для которых это верно, являются Числа Фибоначчи FN+2 и FN+1, соответственно.[95] Точнее, если алгоритм Евклида требует N шаги для пары а > б, то есть а ≥ FN+2 и б ≥ FN+1. Это можно показать индукция.[96] Если N = 1, б разделяет а без остатка; наименьшие натуральные числа, для которых это верно, б = 1 и а = 2, которые F2 и F3, соответственно. Теперь предположим, что результат верен для всех значений N вплоть до M – 1. Первый шаг M-шаговый алгоритм а = q0б + р0, а алгоритм Евклида требует M – 1 ступенька для пары б > р0. По предположению индукции имеем б ≥ FM+1 и р0 ≥ FM. Следовательно, а = q0б + р0 ≥ б + р0 ≥ FM+1 + FM = FM+2, которое является искомым неравенством. Это доказательство, опубликованное Габриэль Ламе в 1844 г., представляет собой начало теория сложности вычислений,[97] а также первое практическое применение чисел Фибоначчи.[95]
Этого результата достаточно, чтобы показать, что количество шагов в алгоритме Евклида никогда не может превышать количество его цифр более чем в пять раз (основание 10).[98] Если алгоритм требует N шаги, то б Больше или равно FN+1 что, в свою очередь, больше или равно φN−1, куда φ это Золотое сечение. С б ≥ φN−1, тогда N – 1 ≤ журналφб. Поскольку журнал10φ > 1/5, (N – 1) / 5 <журнал10φ бревноφб = журнал10б. Таким образом, N ≤ 5 журнал10б. Таким образом, алгоритм Евклида всегда требует меньше, чем О(час) подразделения, где час это количество цифр в меньшем числе б.
Средний
Среднее количество шагов, выполняемых алгоритмом Евклида, было определено тремя различными способами. Первое определение – это среднее время Т(а), необходимого для расчета НОД заданного числа а и меньшее натуральное число б выбираются с равной вероятностью из целых чисел от 0 до а − 1[93]
Однако, поскольку Т(а, б) сильно колеблется в зависимости от НОД двух чисел, усредненная функция Т(а) также “шумно”.[99]
Чтобы уменьшить этот шум, второй средний τ(а) берется по всем числам, взаимно простым с а
Есть φ(а) взаимно простые целые числа меньше а, куда φ является Функция Эйлера. Это среднее значение тау плавно растет с а[100][101]
с остаточной ошибкой порядка а−(1/6) + ε, куда ε является бесконечно малый. Постоянная C (Константа Портера[102]) в этой формуле равно
куда γ это Константа Эйлера – Маскерони а ζ ‘- производная из Дзета-функция Римана.[103][104] Старший коэффициент (12 / π2) ln 2 определяли двумя независимыми методами.[105][106]
Поскольку первое среднее значение может быть вычислено из среднего тау путем суммирования по делителям d иза[107]
его можно аппроксимировать формулой[108]
где Λ (d) это Функция Мангольдта.[109]
Третье среднее Y(п) определяется как среднее количество шагов, необходимых, когда оба а и б выбираются случайным образом (с равномерным распределением) от 1 до п[108]
Подставляя приближенную формулу для Т(а) в это уравнение дает оценку для Y(п)[110]
Вычислительные затраты на шаг
На каждом шагу k алгоритма Евклида, фактор qk и остальное рk вычисляются для данной пары целых чисел рk−2 и рk−1
- рk−2 = qk рk−1 + рk.
Вычислительные затраты на шаг связаны в основном с поиском qk, так как остаток рk можно быстро рассчитать из рk−2, рk−1, и qk
- рk = рk−2 − qk рk−1.
Вычислительные затраты на деление час-битовые числа масштабируются как О(час(ℓ+1)), где ℓ – длина частного.[90]
Для сравнения: оригинальный алгоритм Евклида, основанный на вычитании, может быть намного медленнее. Одно целочисленное деление эквивалентно частному q количество вычитаний. Если соотношение а и б очень велико, частное велико, и потребуется много вычитаний. С другой стороны, было показано, что частные с большой вероятностью будут небольшими целыми числами. Вероятность данного частного q примерно ln |ты/(ты – 1) | куда ты = (q + 1)2.[111] Для иллюстрации вероятность частного 1, 2, 3 или 4 составляет примерно 41,5%, 17,0%, 9,3% и 5,9% соответственно. Так как операция вычитания быстрее деления, особенно для больших чисел,[112] алгоритм Евклида, основанный на вычитании, конкурирует с версией, основанной на делении.[113] Это эксплуатируется в двоичная версия алгоритма Евклида.[114]
Комбинирование расчетного количества шагов с расчетными вычислительными затратами на шаг показывает, что алгоритм Евклида растет квадратично (час2) со средним количеством цифр час в первых двух числах а и б. Позволять час0, час1, …, часN−1 представляют количество цифр в последовательных остатках р0, р1, …, рN−1. Поскольку количество ступеней N растет линейно с час, время работы ограничено
Альтернативные методы
Алгоритм Евклида широко используется на практике, особенно для малых чисел, из-за своей простоты.[115] Для сравнения можно определить эффективность альтернатив алгоритму Евклида.
Один неэффективный подход к нахождению НОД двух натуральных чисел а и б вычислить все их общие делители; НОД тогда является наибольшим общим делителем. Общие делители можно найти, разделив оба числа на последовательные целые числа от 2 до меньшего числа. б. Количество шагов этого подхода линейно растет с увеличением б, или экспоненциально по количеству цифр. Другой неэффективный подход – найти простые множители одного или обоих чисел. Как указано над, НОД равняется произведению простых множителей двух чисел а и б.[6] Настоящие методы для простые множители также неэффективны; многие современные системы криптографии даже полагаются на эту неэффективность.[9]
В двоичный алгоритм GCD – эффективная альтернатива, которая заменяет деление более быстрыми операциями за счет использования двоичный представление, используемое компьютерами.[116][117] Однако эта альтернатива также масштабируется как О(час²). Как правило, он быстрее, чем алгоритм Евклида на реальных компьютерах, хотя масштабируется таким же образом.[91] Дополнительную эффективность можно получить, изучив только первые цифры двух чисел. а и б.[118][119] Бинарный алгоритм может быть расширен на другие базы (k-арные алгоритмы),[120] с пятикратным увеличением скорости.[121] Алгоритм Лемера GCD использует тот же общий принцип, что и двоичный алгоритм, для ускорения вычислений GCD с произвольной базой.
Рекурсивный подход для очень больших целых чисел (более 25000 цифр) приводит к квазилинейный целочисленные алгоритмы НОД,[122] такие как у Шёнхаге,[123][124] и Stehlé и Zimmermann.[125] Эти алгоритмы используют матричную форму 2 × 2 алгоритма Евклида, заданного над. Эти квазилинейные методы обычно масштабируются как О(час (бревно час)2 (журнал журнал час)).[91][92]
Обобщения
Хотя алгоритм Евклида используется для нахождения наибольшего общего делителя двух натуральных чисел (положительных целых чисел), он может быть обобщен на действительные числа и другие математические объекты, такие как многочлены,[126] квадратичные целые числа[127] и Кватернионы Гурвица.[128] В последних случаях алгоритм Евклида используется для демонстрации ключевого свойства уникальной факторизации, то есть того, что такие числа могут быть однозначно разложены на множители. неприводимые элементы, аналоги простых чисел. Уникальная факторизация необходима для многих доказательств теории чисел.
Рациональные и действительные числа
Алгоритм Евклида можно применить к действительные числа, как описано Евклидом в книге 10 его Элементы. Цель алгоритма – определить реальное число грамм такие, что два заданных действительных числа, а и б, являются целыми кратными ему: а = мг и б = нг, куда м и п находятся целые числа.[26] Это отождествление эквивалентно нахождению целочисленное отношение среди реальных чисел а и б; то есть определяет целые числа s и т такой, что са + tb = 0. Евклид использует этот алгоритм для решения вопроса о несоизмеримые длины.[129][130]
Алгоритм Евклида с действительными числами отличается от своего целочисленного аналога в двух отношениях. Во-первых, остатки рk являются действительными числами, хотя частные qk как и раньше, являются целыми числами. Во-вторых, не гарантируется, что алгоритм закончит конечное число N шагов. Если это так, дробь а/б – рациональное число, то есть отношение двух целых чисел
и может быть записана в виде конечной цепной дроби [q0; q1, q2, …, qN]. Если алгоритм не останавливается, дробь а/б является иррациональный номер и описывается бесконечной цепной дробью [q0; q1, q2, …].[131] Примеры бесконечных цепных дробей: Золотое сечение φ = [1; 1, 1, …] и квадратный корень из двух, √2 = [1; 2, 2, …].[132] Алгоритм вряд ли остановится, так как почти все соотношения а/б двух действительных чисел иррациональны.[133]
Бесконечная цепная дробь может быть усечена на шаге k [q0; q1, q2, …, qk] чтобы приблизиться к а/б это улучшается как k увеличена. Приближение описывается формулой сходящиеся мk/пk; числитель и знаменатели взаимно просты и подчиняются отношение повторения
куда м−1 = п−2 = 1 и м−2 = п−1 = 0 – начальные значения рекурсии. Сходящийся мk/пk лучший Рациональное число приближение к а/б со знаменателем пk:[134]
Полиномы
Многочлены от одной переменной Икс можно складывать, умножать и разложить на неприводимые многочлены, которые являются аналогами простых чисел для целых чисел. Многочлен наибольшего общего делителя грамм(Икс) двух многочленов а(Икс) и б(Икс) определяется как произведение их общих неприводимых многочленов, которые можно идентифицировать с помощью алгоритма Евклида.[126] Основная процедура аналогична работе с целыми числами. На каждом шагу k, фактор-полином qk(Икс) и полином остатка рk(Икс) идентифицируются так, чтобы удовлетворять рекурсивному уравнению
куда р−2(Икс) = а(Икс) и р−1(Икс) = б(Икс). Каждый фактор-полином выбирается таким образом, чтобы каждый остаток был либо равен нулю, либо имел степень меньше, чем степень его предшественника: град [рk(Икс)] рk−1(Икс)]. Поскольку степень является неотрицательным целым числом и уменьшается с каждым шагом, алгоритм Евклида завершается за конечное число шагов. Последний ненулевой остаток – это наибольший общий делитель двух исходных многочленов, а(Икс) и б(Икс).[135]
Например, рассмотрим следующие два многочлена четвертой степени, каждый из которых делится на два квадратичных многочлена
Разделение а(Икс) к б(Икс) дает остаток р0(Икс) = Икс3 + (2/3)Икс2 + (5/3)Икс − (2/3). На следующем этапе б(Икс) делится на р0(Икс) дающий остаток р1(Икс) = Икс2 + Икс + 2. Наконец, разделив р0(Икс) к р1(Икс) дает нулевой остаток, указывая, что р1(Икс) является полиномом наибольшего общего делителя а(Икс) и б(Икс), в соответствии с их факторизацией.
Многие из приложений, описанных выше для целых чисел, переносятся на полиномы.[136] Алгоритм Евклида можно использовать для решения линейных диофантовых уравнений и китайских задач остатка для многочленов; также могут быть определены непрерывные дроби многочленов.
У полиномиального алгоритма Евклида есть и другие приложения, например Цепи Штурма, метод подсчета нули полинома что лежат внутри данного реальный интервал.[137] Это, в свою очередь, имеет приложения в нескольких областях, таких как Критерий устойчивости Рауса – Гурвица. в теория управления.[138]
Наконец, коэффициенты многочленов не обязательно должны быть взяты из целых, действительных или даже комплексных чисел. Например, коэффициенты могут быть взяты из общего поля, такого как конечные поля GF (п) описано выше. Соответствующие выводы об алгоритме Евклида и его приложениях справедливы даже для таких многочленов.[126]
Гауссовские целые числа
Распределение гауссовских простых чисел ты + vi в комплексной плоскости, с нормами ты2 + v2 менее 500
Целые гауссовы числа сложные числа формы α = ты + vi, куда ты и v обычные целые числа[заметка 2] и я это квадратный корень из отрицательного.[139] Определяя аналог алгоритма Евклида, можно показать, что гауссовские целые числа однозначно факторизуемы с помощью аргумента над.[40] Эта уникальная факторизация полезна во многих приложениях, например при выводе всех Пифагорейские тройки или доказывая Теорема Ферма о суммах двух квадратов.[139] В целом алгоритм Евклида удобен в таких приложениях, но не является существенным; например, теоремы часто можно доказать другими аргументами.
Алгоритм Евклида, разработанный для двух целых гауссовских чисел α и β почти такая же, как и для обычных целых чисел,[140] но отличается в двух отношениях. Как и раньше, задача на каждом шаге k заключается в определении частного qk и остаток рk такой, что
куда рk−2 = α, куда рk−1 = β, и где каждый остаток строго меньше, чем его предшественник: |рk| < |рk−1|. Первое отличие состоит в том, что частные и остатки сами являются целыми гауссовскими числами и, следовательно, являются сложные числа. Факторы qk обычно находятся путем округления действительной и комплексной частей точного отношения (например, комплексного числа α/β) до ближайших целых чисел.[140] Второе отличие состоит в необходимости определения того, как один комплексный остаток может быть «меньше» другого. Для этого функция нормы ж(ты + vi) = ты2 + v2 определено, которое преобразует каждое целое гауссовское число ты + vi в обычное целое число. После каждого шага k алгоритма Евклида норма остатка ж(рk) меньше нормы предыдущего остатка, ж(рk−1). Поскольку норма является неотрицательным целым числом и уменьшается с каждым шагом, алгоритм Евклида для целых гауссовских чисел завершается за конечное число шагов.[141] Последний ненулевой остаток равен gcd (α, β), гауссовское целое число наибольшей нормы, которое делит оба α и β; он уникален с точностью до умножения на единицу, ±1 или же ±я.[142]
Многие другие приложения алгоритма Евклида переносятся на гауссовские целые числа. Например, его можно использовать для решения линейных диофантовых уравнений и китайских задач остатка для гауссовских целых чисел;[143] также могут быть определены цепные дроби гауссовских целых чисел.[140]
Евклидовы области
Набор элементов на двоих бинарные операции, обозначаемые как сложение и умножение, называется Евклидова область если он образует коммутативное кольцо р и, грубо говоря, если на них можно выполнить обобщенный алгоритм Евклида.[144][145] Две операции такого кольца не обязательно должны быть сложением и умножением в обычной арифметике; скорее, они могут быть более общими, например, операции математическая группа или же моноид. Тем не менее, эти общие операции должны соответствовать многим законам, регулирующим обычную арифметику, например: коммутативность, ассоциативность и распределенность.
Обобщенный алгоритм Евклида требует Евклидова функция, т.е. отображение ж из р в множество неотрицательных целых чисел, таких что для любых двух ненулевых элементов а и б в р, существуют q и р в р такой, что а = qb + р и ж(р) < ж(б).[146] Примерами таких отображений являются абсолютное значение для целых чисел, степень для одномерные многочлены, а норма для целых гауссовских чисел над.[147][148] Основной принцип заключается в том, что каждый шаг алгоритма уменьшает ж неумолимо; следовательно, если ж может быть сокращен только конечное количество раз, алгоритм должен остановиться за конечное количество шагов. Этот принцип основан на хороший порядок свойство неотрицательных целых чисел, которое утверждает, что каждый непустой набор неотрицательных целых чисел имеет наименьший член.[149]
В основная теорема арифметики применяется к любому евклидовому домену: любое число из евклидовой области может быть однозначно разложено на неприводимые элементы. Любая евклидова область – это уникальная область факторизации (UFD), хотя обратное неверно.[149] Евклидовы области и UFD являются подклассами GCD домены, области, в которых всегда существует наибольший общий делитель двух чисел.[150] Другими словами, может существовать наибольший общий делитель (для всех пар элементов в области), хотя его невозможно найти с помощью алгоритма Евклида. Евклидова область всегда главная идеальная область (PID), область целостности в котором каждый идеальный это главный идеал.[151] И снова обратное неверно: не каждый PID является евклидовой областью.
Уникальная факторизация евклидовых областей полезна во многих приложениях. Например, уникальная факторизация гауссовских целых чисел удобна при выводе формул для всех Пифагорейские тройки и в доказательстве Теорема Ферма о суммах двух квадратов.[139] Уникальная факторизация также была ключевым элементом в попытке доказательства Последняя теорема Ферма опубликовано в 1847 году Габриэлем Ламе, тем же математиком, который проанализировал эффективность алгоритма Евклида, основываясь на предположении Джозеф Лиувиль.[152] Подход Ламе потребовал уникальной факторизации чисел вида Икс + ωy, куда Икс и у целые числа, и ω = е2я/п является пкорень -й степени из 1, то есть ωп = 1. Хотя этот подход успешен для некоторых значений п (Такие как п = 3, то Целые числа Эйзенштейна ), в целом такие числа нет фактор однозначно. Эта неудача уникальной факторизации в некоторых циклотомические поля вел Эрнст Куммер к концепции идеальные числа и позже, Ричард Дедекинд к идеалы.[153]
Уникальная факторизация квадратичных целых чисел
Распределение простых чисел Эйзенштейна ты + vω в комплексной плоскости, с нормами менее 500. Количество ω это кубический корень из 1.
В квадратичное целое число кольца полезны для иллюстрации евклидовых областей. Квадратичные целые числа являются обобщениями гауссовских целых чисел, в которых мнимая единица я заменяется числом ω. Таким образом, они имеют вид ты + vω, куда ты и v целые числа и ω имеет одну из двух форм, в зависимости от параметра D. Если D не равно четырем плюс один, тогда
Если, однако, D равно кратному четырем плюс одному, тогда
Если функция ж соответствует норма функция, такая как та, которая используется для упорядочивания целых чисел Гаусса над, то домен известен как норм-евклидова. Норм-евклидовы кольца целых квадратичных чисел – это в точности те кольца, в которых D является одним из значений −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, или 73.[154][155] Случаи D = −1 и D = −3 дать Гауссовские целые числа и Целые числа Эйзенштейна, соответственно.
Если ж может быть любой евклидовой функцией, то список возможных значений D для которой область евклидова, пока не известно.[156] Первый пример евклидовой области, которая не была евклидовой по норме (с D = 69) был опубликован в 1994 году.[156] В 1973 году Вайнбергер доказал, что квадратичное целочисленное кольцо с D > 0 евклидово тогда и только тогда, когда оно главная идеальная область при условии, что обобщенная гипотеза Римана держит.[127]
Некоммутативные кольца
Алгоритм Евклида может быть применен к некоторым некоммутативным кольцам, таким как набор Кватернионы Гурвица.[требуется разъяснение ][128] Позволять α и β представляют собой два элемента из такого кольца. У них общий правый делитель δ если α = ξδ и β = ηδ для некоторого выбора ξ и η в ринге. Точно так же у них есть общий левый делитель, если α = dξ и β = dη для некоторого выбора ξ и η в ринге. Поскольку умножение не коммутативно, существует две версии алгоритма Евклида: одна для правых делителей, другая для левых делителей.[128] Выбор правильных делителей – первый шаг в поиске gcd (α, β) алгоритмом Евклида можно записать
куда ψ0 представляет собой частное и ρ0 остаток.[требуется разъяснение ] Это уравнение показывает, что любой общий правый делитель числа α и β также является общим делителем остатка ρ0. Аналогичное уравнение для левых делителей будет
При любом выборе процесс повторяется, как указано выше, до тех пор, пока не будет определен наибольший общий правый или левый делитель. Как и в евклидовой области, «размер» остатка ρ0 должен быть строго меньше чем β, и должно быть только конечное число возможных размеров для ρ0, так что алгоритм гарантированно завершится.[требуется разъяснение ][157]
Большинство результатов для НОД переносятся на некоммутативные числа.[требуется разъяснение ] Например, Личность Безу заявляет, что право gcd (α, β) можно выразить как линейную комбинацию α и β.[158] Другими словами, есть числа σ и τ такой, что
Аналогичная идентичность для левого НОД почти такая же:
Тождество Безу можно использовать для решения диофантовых уравнений. Например, одно из стандартных доказательств Теорема Лагранжа о четырех квадратах, что каждое положительное целое число может быть представлено в виде суммы четырех квадратов, основано на кватернионных НОД таким образом.[157]
Смотрите также
- Евклидов ритм, метод использования алгоритма Евклида для генерации музыкальных ритмов.
Примечания
- ^ Некоторые широко используемые учебники, такие как И. Н. Герштейн с Темы по алгебре и Серж Ланг с Алгебра, используйте термин «алгоритм Евклида» для обозначения Евклидово деление
- ^ Фраза «обычное целое число» обычно используется для отличия обычных целых чисел от гауссовых целых чисел и, в более общем смысле, от алгебраические целые числа.
Рекомендации
- ^ Старк 1978, п. 16
- ^ Старк 1978, п. 21 год
- ^ Левек 1996, п. 32
- ^ Левек 1996, п. 31 год
- ^ Гроссман, Дж. У. (1990). Дискретная математика. Нью-Йорк: Макмиллан. п. 213. ISBN 0-02-348331-8.
- ^ а б Шредер 2005, стр. 21–22
- ^ Шредер 2005, п. 19
- ^ Огилви, К.С.; Андерсон, Дж. Т. (1966). Экскурсии по теории чисел. Нью-Йорк: Oxford University Press. С. 27–29.
- ^ а б Шредер 2005, стр. 216–219
- ^ а б Левек 1996, п. 33
- ^ Старк 1978, п. 25
- ^ Руда 1948 г., стр. 47–48
- ^ Старк 1978, п. 18
- ^ Старк 1978, стр. 16–20
- ^ Кнут 1997, п. 320
- ^ Ловас, Л.; Pelikán, J .; Вестергомби, К. (2003). Дискретная математика: элементарная и не только. Нью-Йорк: Springer-Verlag. С. 100–101. ISBN 0-387-95584-4.
- ^ Кимберлинг, К. (1983). «Визуальный евклидов алгоритм». Учитель математики. 76: 108–109.
- ^ Даммит, Дэвид С .; Фут, Ричард М. (2004). Абстрактная алгебра. John Wiley & Sons, Inc., стр. 270–271. ISBN 978-0-471-43334-7.
- ^ Кнут 1997, стр. 319–320
- ^ Кнут 1997, стр. 318–319
- ^ Стиллвелл 1997, п. 14
- ^ а б Руда 1948 г., п. 43
- ^ а б Стюарт, Б. М. (1964). Теория чисел (2-е изд.). Нью-Йорк: Макмиллан. С. 43–44. LCCN 64010964.
- ^ Лазард, Д. (1977). “Лучший алгоритм Евклида для K[Икс] et Z“. Comptes rendus de l’Académie des Sciences (На французском). 284: 1–4.
- ^ а б Кнут 1997, п. 318
- ^ а б Вайль, А. (1983). Теория чисел. Бостон: Биркхойзер. С. 4–6. ISBN 0-8176-3141-0.
- ^ Джонс, А. (1994). «Греческая математика до 300 г. н.э.». Сопутствующая энциклопедия истории и философии математических наук. Нью-Йорк: Рутледж. С. 46–48. ISBN 0-415-09238-8.
- ^ ван дер Варден, Б. Л. (1954). Пробуждение науки. перевод Арнольда Дрездена. Гронинген: P. Noordhoff Ltd., стр.114–115.
- ^ фон Фриц, К. (1945). «Открытие несоизмеримости Гиппасом из Метапонта». Анналы математики. 46 (2): 242–264. Дои:10.2307/1969021. JSTOR 1969021.
- ^ Хит, Т. (1949). Математика у Аристотеля. Oxford Press. стр.80–83.
- ^ Фаулер, Д. (1987). Математика Платоновской академии: новая реконструкция. Оксфорд: Издательство Оксфордского университета. С. 31–66. ISBN 0-19-853912-6.
- ^ Беккер, О. (1933). “Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid”. Quellen und Studien zur Geschichte der Mathematik B. 2: 311–333.
- ^ а б Стиллвелл 1997, п. 31 год
- ^ а б Таттерсолл 2005, п. 70
- ^ Розен 2000, стр. 86–87
- ^ Руда 1948 г., стр. 247–248
- ^ Таттерсолл 2005, стр. 72, 184–185
- ^ Сондерсон, Николай (1740). Элементы алгебры в десяти книгах. Кембриджский университет Press. Получено 1 ноября 2016.
- ^ Таттерсолл 2005, стр. 72–76
- ^ а б Гаусс, К.Ф. (1832 г.). «Theoria резидуум биквадратичный». Comm. Soc. Рег. Sci. Gött. Rec. 4. Перепечатано в Гаусс, К. Ф. (2011). «Theoria резидуум biquadraticorum commentatio prima». Werke. 2. Cambridge Univ. Нажмите. С. 65–92. Дои:10.1017 / CBO9781139058230.004. и Гаусс, К. Ф. (2011). “Theoria резидуум biquadraticorum commentatio secunda”. Werke. 2. Cambridge Univ. Нажмите. С. 93–148. Дои:10.1017 / CBO9781139058230.005.
- ^ Стиллвелл 1997, стр. 31–32
- ^ Лежен Дирихле 1894, стр. 29–31
- ^ Ричард Дедекинд в Лежен Дирихле 1894, Дополнение XI
- ^ Stillwell 2003, стр. 41–42
- ^ Штурм, К. (1829 г.). “Mémoire sur la résolution des équations numériques”. Бык. des Sciences de Férussac (На французском). 11: 419–422.
- ^ Вайсштейн, Эрик В. «Целочисленное отношение». MathWorld.
- ^ Петерсон И. (12 августа 2002 г.). “Разбудить алгоритм Евклида”. НаукаНовости.
- ^ Сипра, Барри Артур (16 мая 2000 г.). «Лучшее из 20 века: редакция назвала 10 лучших алгоритмов» (PDF). Новости SIAM. Общество промышленной и прикладной математики. 33 (4). Архивировано из оригинал (PDF) 22 сентября 2016 г.. Получено 19 июля 2016.
- ^ Коул, А. Дж .; Дэви, А. Дж. Т. (1969). «Игра, основанная на алгоритме Евклида и выигрышная стратегия для него». Математика. Газ. 53 (386): 354–357. Дои:10.2307/3612461. JSTOR 3612461.
- ^ Шпицнагель, Э. Л. (1973). «Свойства игры, основанной на алгоритме Евклида». Математика. Mag. 46 (2): 87–92. Дои:10.2307/2689037. JSTOR 2689037.
- ^ Розен 2000, п. 95
- ^ Робертс, Дж. (1977). Элементарная теория чисел: проблемно-ориентированный подход. Кембридж, Массачусетс: MIT Press. стр.1–8. ISBN 0-262-68028-9.
- ^ Jones, G.A .; Джонс, Дж. М. (1998). «Личность Безу». Элементарная теория чисел. Нью-Йорк: Springer-Verlag. С. 7–11.
- ^ Розен 2000, п. 81 год
- ^ Кон 1962, п. 104
- ^ Розен 2000, п. 91
- ^ Шредер 2005, п. 23
- ^ Розен 2000, стр. 90–93
- ^ а б Коши Т. (2002). Элементарная теория чисел с приложениями. Берлингтон, Массачусетс: Harcourt / Academic Press. С. 167–169. ISBN 0-12-421171-2.
- ^ Бах, Э.; Шаллит, Дж. (1996). Алгоритмическая теория чисел. Кембридж, Массачусетс: MIT Press. С. 70–73. ISBN 0-262-02405-5.
- ^ Старк 1978, стр. 26–36
- ^ а б Руда 1948 г., п. 44
- ^ Старк 1978, стр. 281–292
- ^ Розен 2000, стр. 119–125
- ^ Шредер 2005, стр. 106–107
- ^ Шредер 2005, стр. 108–109
- ^ Розен 2000, стр. 120–121
- ^ Старк 1978, п. 47
- ^ Шредер 2005, стр. 107–109
- ^ Стиллвелл 1997, стр. 186–187
- ^ Шредер 2005, п. 134
- ^ Луна, Т. К. (2005). Кодирование с исправлением ошибок: математические методы и алгоритмы. Джон Уайли и сыновья. п. 266. ISBN 0-471-64800-0.
- ^ Розен 2000, стр. 143–170
- ^ Шредер 2005, стр. 194–195
- ^ Грэм, Р.; Кнут, Д. Э.; Паташник, О. (1989). Конкретная математика. Эддисон-Уэсли. п. 123.
- ^ Виноградов, И.М. (1954). Элементы теории чисел. Нью-Йорк: Дувр. стр.3–13.
- ^ Crandall & Pomerance 2001, стр. 225–349
- ^ Кнут 1997, стр. 369–371
- ^ Шор, П.В. (1997). “Полиномиальные алгоритмы простой факторизации и дискретных логарифмов на квантовом компьютере”. Журнал SIAM по научным и статистическим вычислениям. 26: 1484–1509. arXiv:Quant-ph / 9508027. Bibcode:1995квант.ч..8027S. Дои:10.1137 / s0097539795293172.
- ^ Диксон, Дж. Д. (1981). «Асимптотически быстрая факторизация целых чисел». Математика. Вычислить. 36 (153): 255–260. Дои:10.2307/2007743. JSTOR 2007743.
- ^ Ленстра, Х. В., мл. (1987). «Факторинг целых чисел с эллиптическими кривыми». Анналы математики. 126 (3): 649–673. Дои:10.2307/1971363. JSTOR 1971363.
- ^ Кнут 1997, стр. 380–384
- ^ Кнут 1997, стр. 339–364
- ^ Рейно, А.-А.-Л. (1811 г.). Traité d’arithmétique à l’usage des élèves qui se destinent à l’École Polytechnique (6-е изд.). Париж: Курсье. Примечание 60, стр. 34. Как цитирует Шаллит (1994).
- ^ Finck, P.-J.-E. (1841 г.). Traité élémentaire d’arithmétique à l’usage des Candidats aux écoles spéciales (На французском). Derivaux.
- ^ а б Шаллит, Дж. (1994). «Истоки анализа алгоритма Евклида». Historia Math. 21: 401–419. Дои:10.1006 / hmat.1994.1031.CS1 maint: ref = harv (связь)
- ^ Ламе, Г. (1844 г.). “Note sur la limit du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers”. Comptes Rendus Acad. Sci. (На французском). 19: 867–870.
- ^ Гроссман, Х. (1924). «О количестве отделов при нахождении ОГТ». Американский математический ежемесячник. 31 (9): 443. Дои:10.2307/2298146. JSTOR 2298146.
- ^ Хонсбергер, Р. (1976). Математические жемчужины II. В Математическая ассоциация Америки. С. 54–57. ISBN 0-88385-302-7.
- ^ а б Кнут 1997, стр. 257–261
- ^ а б c Crandall & Pomerance 2001, стр. 77–79, 81–85, 425–431
- ^ а б Мёллер, Н. (2008). «Об алгоритме Шёнхаге и вычислении субквадратичного целочисленного НОД» (PDF). Математика вычислений. 77 (261): 589–607. Bibcode:2008MaCom..77..589M. Дои:10.1090 / S0025-5718-07-02017-0.
- ^ а б c Кнут 1997, п. 344
- ^ Руда 1948 г., п. 45
- ^ а б Кнут 1997, п. 343
- ^ Моллин 2008, п. 21 год
- ^ Левек 1996, п. 35 год
- ^ Моллин 2008, стр. 21–22
- ^ Кнут 1997, п. 353
- ^ Кнут 1997, п. 357
- ^ Тонков, Т. (1974). «О средней длине конечных цепных дробей». Acta Arithmetica. 26: 47–57.
- ^ Вайсштейн, Эрик В. “Константа Портера”. MathWorld.
- ^ Портер, Дж. У. (1975). «Об одной теореме Хейльбронна». Математика. 22: 20–28. Дои:10.1112 / S0025579300004459.
- ^ Кнут, Д. Э. (1976). «Оценка константы Портера». Компьютеры и математика с приложениями. 2 (2): 137–139. Дои:10.1016/0898-1221(76)90025-0.
- ^ Диксон, Дж. Д. (1970). «Число шагов в алгоритме Евклида». J. Теория чисел. 2 (4): 414–422. Bibcode:1970JNT ….. 2..414D. Дои:10.1016 / 0022-314X (70) 90044-2.
- ^ Хайльбронн, Х.А. (1969). «О средней длине класса конечных непрерывных дробей». У Пола Турана (ред.). Теория чисел и анализ. Нью-Йорк: Пленум. С. 87–96. LCCN 76016027.
- ^ Кнут 1997, п. 354
- ^ а б Нортон, Г. Х. (1990). «Об асимптотическом анализе алгоритма Евклида». Журнал символических вычислений. 10: 53–58. Дои:10.1016 / S0747-7171 (08) 80036-3.
- ^ Кнут 1997, п. 355
- ^ Кнут 1997, п. 356
- ^ Кнут 1997, п. 352
- ^ Вагон, С. (1999). Mathematica в действии. Нью-Йорк: Springer-Verlag. С. 335–336. ISBN 0-387-98252-3.
- ^ Коэн 1993, п. 14
- ^ Коэн 1993, стр. 14–15, 17–18
- ^ Соренсон, Джонатан П. (2004). «Анализ обобщенного бинарного алгоритма НОД». Высокие числа и проступки: лекции в честь 60-летия Хью Коуи Уильямса. Коммуникации Института Филдса. 41. Провиденс, Род-Айленд: Американское математическое общество. С. 327–340. ISBN 9780821887592. МИСТЕР 2076257.
Алгоритмы, которые сегодня чаще всего используются на практике [для вычисления наибольших общих делителей], вероятно, представляют собой двоичный алгоритм и алгоритм Евклида для меньших чисел, а также либо алгоритм Лемера, либо версию Лебелиана. k-арный алгоритм НОД для больших чисел.
- ^ Кнут 1997, стр. 321–323
- ^ Стейн, Дж. (1967). «Вычислительные проблемы, связанные с алгеброй Рака». Журнал вычислительной физики. 1 (3): 397–405. Bibcode:1967JCoPh … 1..397S. Дои:10.1016/0021-9991(67)90047-2.
- ^ Кнут 1997, п. 328
- ^ Лемер, Д. Х. (1938). «Алгоритм Евклида для больших чисел». Американский математический ежемесячник. 45 (4): 227–233. Дои:10.2307/2302607. JSTOR 2302607.
- ^ Соренсон, Дж. (1994). «Два быстрых алгоритма НОД». J. Алгоритмы. 16: 110–144. Дои:10.1006 / jagm.1994.1006.
- ^ Вебер, К. (1995). «Ускоренный алгоритм НОД». ACM Trans. Математика. Softw. 21: 111–122. Дои:10.1145/200979.201042.
- ^ Ахо, А.; Хопкрофт, Дж.; Ульман, Дж. (1974). Разработка и анализ компьютерных алгоритмов. Нью-Йорк: Аддисон – Уэсли. стр.300–310. ISBN 0-201-00029-6.
- ^ Шёнхаге, А. (1971). “Schnelle Berechnung von Kettenbruchentwicklungen”. Acta Informatica (на немецком). 1 (2): 139–144. Дои:10.1007 / BF00289520.
- ^ Чезари, Г. (1998). «Параллельная реализация целочисленного алгоритма НОД Шенхаге». В Г. Бюлер (ред.). Алгоритмическая теория чисел: Учеб. ANTS-III, Портленд, Орегон. Конспект лекций по информатике. 1423. Нью-Йорк: Springer-Verlag. С. 64–76.
- ^ Stehlé, D .; Циммерманн, П. (2005). “Точные таблицы Гала пересмотр метода “. Труды 17-й симпозиум IEEE по компьютерной арифметике (АРИФ-17 ). Лос-Аламитос, Калифорния: Пресса IEEE Computer Society.
- ^ а б c Ланг, С. (1984). Алгебра (2-е изд.). Менло-Парк, Калифорния: Аддисон – Уэсли. С. 190–194. ISBN 0-201-05487-6.
- ^ а б Вайнбергер П. «О евклидовых кольцах целых алгебраических чисел». Proc. Симпозиумы. Чистая математика. 24: 321–332.
- ^ а б c Stillwell 2003, стр. 151–152
- ^ Boyer, C.B .; Мерцбах, У. (1991). История математики (2-е изд.). Нью-Йорк: Вили. стр.116–117. ISBN 0-471-54397-7.
- ^ Кахори, Ф (1894). История математики. Нью-Йорк: Макмиллан. п.70. ISBN 0-486-43874-0.
- ^ Жу, Антуан (2009). Алгоритмический криптоанализ. CRC Press. п. 33. ISBN 9781420070033.
- ^ Fuks, D. B .; Табачников Серж (2007). Математический омнибус: тридцать лекций по классической математике. Американское математическое общество. п. 13. ISBN 9780821843161.
- ^ Дорогой, Дэвид (2004). «Постоянная Хинчина». Универсальная книга математики: от абракадабры до парадоксов Зенона. Джон Вили и сыновья. п. 175. ISBN 9780471667001.
- ^ Уильямс, Колин П. (2010). Исследования в области квантовых вычислений. Springer. С. 277–278. ISBN 9781846288876.
- ^ Кокс, Литтл и О’Ши 1997, стр. 37–46
- ^ Шредер 2005, стр. 254–259
- ^ Граттан-Гиннесс, Айвор (1990). Свертки во французской математике, 1800-1840: от исчисления и механики до математического анализа и математической физики. Том II: Повороты. Научные сети: исторические исследования. 3. Базель, Бостон, Берлин: Birkhäuser. п. 1148. ISBN 9783764322380.
Нашим предметом здесь является «последовательность Штурма» функций, определенных из функции и ее производной с помощью алгоритма Евклида, чтобы вычислить количество действительных корней многочлена в заданном интервале.
- ^ Хайрер, Эрнст; Nørsett, Syvert P .; Ваннер, Герхард (1993). «Критерий Рауса – Гурвица». Решение обыкновенных дифференциальных уравнений I: нежесткие задачи. Серия Спрингера в вычислительной математике. 8 (2-е изд.). Springer. стр. 81 и далее. ISBN 9783540566700.
- ^ а б c Stillwell 2003, стр. 101–116
- ^ а б c Хенсли, Дуг (2006). Непрерывные дроби. World Scientific. п. 26. ISBN 9789812564771.
- ^ Дедекинд, Ричард (1996). Теория алгебраических целых чисел. Кембриджская математическая библиотека. Издательство Кембриджского университета. С. 22–24. ISBN 9780521565189.
- ^ Johnston, Bernard L .; Ричман, Фред (1997). Числа и симметрия: введение в алгебру. CRC Press. п. 44. ISBN 9780849303012.
- ^ Адамс, Уильям У .; Гольдштейн, Ларри Джоэл (1976). Введение в теорию чисел. Прентис-Холл. Упражнение 24, с. 205. ISBN 9780134912820.
Сформулируйте и докажите аналог китайской теоремы об остатках для целых гауссовских чисел.
- ^ Старк 1978, п. 290
- ^ Кон 1962, стр. 104–105
- ^ Лауритцен, Нильс (2003). Конкретная абстрактная алгебра: от чисел к базису Грёбнера. Издательство Кембриджского университета. п. 130. ISBN 9780521534109.CS1 maint: ref = harv (связь)
- ^ Лауритцен (2003), п. 132
- ^ Лауритцен (2003), п. 161
- ^ а б Шарп, Дэвид (1987). Кольца и факторизация. Издательство Кембриджского университета. п.55. ISBN 9780521337182.CS1 maint: ref = harv (связь)
- ^ Шарп (1987), п. 52
- ^ Лауритцен (2003), п. 131
- ^ Ламе, Г. (1847). “Mémoire sur la résolution, en nombres complex, de l’équation A”п + Bп + Cп = 0″. J. Math. Pures Appl. (На французском). 12: 172–184.
- ^ Эдвардс, Х. (2000). Последняя теорема Ферма: генетическое введение в алгебраическую теорию чисел. Springer. п. 76.
- ^ Кон 1962, стр. 104–110
- ^ Левек, В. Дж. (2002) [1956]. Темы теории чисел, тома I и II. Нью-Йорк: Dover Publications. С. II: 57, 81. ISBN 978-0-486-42539-9. Zbl 1009.11001.
- ^ а б Кларк, Д. А. (1994). «Квадратичное поле, которое является евклидовым, но не евклидово по норме». Manuscripta Mathematica. 83: 327–330. Дои:10.1007 / BF02567617. Zbl 0817.11047.
- ^ а б Давыдов, Джулиана; Сарнак, Питер; Валетт, Ален (2003). «2.6 Арифметика целочисленных кватернионов». Элементарная теория чисел, теория групп и графы Рамануджана. Тексты студентов Лондонского математического общества. 55. Издательство Кембриджского университета. С. 59–70. ISBN 9780521531436.
- ^ Рибенбойм, Пауло (2001). Классическая теория алгебраических чисел. Universitext. Springer-Verlag. п. 104. ISBN 9780387950709.
Библиография
- Коэн, Х. (1993). Курс вычислительной алгебраической теории чисел. Нью-Йорк: Springer-Verlag. ISBN 0-387-55640-0.CS1 maint: ref = harv (связь)
- Кон, Х. (1962). Расширенная теория чисел. Нью-Йорк: Дувр. ISBN 0-486-64023-X.CS1 maint: ref = harv (связь)
- Кокс, Д.; Little, J .; О’Ши, Д. (1997). Идеалы, многообразия и алгоритмы: введение в вычислительную алгебраическую геометрию и коммутативную алгебру (2-е изд.). Springer-Verlag. ISBN 0-387-94680-2.CS1 maint: ref = harv (связь)
- Крэндалл, Р.; Померанс, К. (2001). Простые числа: вычислительная перспектива (1-е изд.). Нью-Йорк: Springer-Verlag. ISBN 0-387-94777-9.CS1 maint: ref = harv (связь)
- Лежен Дирихле, П. (1894). Дедекинд, Ричард (ред.). Vorlesungen über Zahlentheorie (Лекции по теории чисел) (на немецком). Брауншвейг: Vieweg. LCCN 03005859. OCLC 490186017.CS1 maint: ref = harv (связь). Смотрите также Vorlesungen über Zahlentheorie
- Кнут, Д. Э. (1997). Искусство программирования, Том 2: Получисленные алгоритмы (3-е изд.). Аддисон-Уэсли. ISBN 0-201-89684-2.CS1 maint: ref = harv (связь)
- Левек, В. Дж. (1996) [1977]. Основы теории чисел. Нью-Йорк: Дувр. ISBN 0-486-68906-9.CS1 maint: ref = harv (связь)
- Моллин, Р. А. (2008). Фундаментальная теория чисел с приложениями (2-е изд.). Бока-Ратон: Чепмен и Холл / CRC. ISBN 978-1-4200-6659-3.CS1 maint: ref = harv (связь)
- Руда, О. (1948). Теория чисел и ее история. Нью-Йорк: Макгроу – Хилл.CS1 maint: ref = harv (связь)
- Розен, К. Х. (2000). Элементарная теория чисел и ее приложения (4-е изд.). Ридинг, Массачусетс: Аддисон – Уэсли. ISBN 0-201-87073-8.CS1 maint: ref = harv (связь)
- Шредер, М. (2005). Теория чисел в науке и коммуникации (4-е изд.). Springer-Verlag. ISBN 0-387-15800-6.CS1 maint: ref = harv (связь)
- Старк, Х. (1978). Введение в теорию чисел. MIT Press. ISBN 0-262-69060-8.CS1 maint: ref = harv (связь)
- Стиллвелл, Дж. (1997). Числа и геометрия. Нью-Йорк: Springer-Verlag. ISBN 0-387-98289-2.CS1 maint: ref = harv (связь)
- Стиллвелл, Дж. (2003). Элементы теории чисел. Нью-Йорк: Springer-Verlag. ISBN 0-387-95587-9.CS1 maint: ref = harv (связь)
- Таттерсолл, Дж. Дж. (2005). Элементарная теория чисел в девяти главах. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-85014-8.CS1 maint: ref = harv (связь)
внешняя ссылка
- Демонстрации алгоритма Евклида
- Вайсштейн, Эрик В. «Евклидов алгоритм». MathWorld.
- Алгоритм Евклида в завязать узел
- Алгоритм Евклида в PlanetMath.org.
- Евклидов алгоритм на MathPages
- Игра Евклида в завязать узел
- Музыка и алгоритм Евклида
�������
��������, ��� ����� ����� � ��������� ������� ����� ���� ����� ������ �������.
���������
�������, ��������, � ���� �������� ����� ��������� Fn � Fn+1.
�������
Fn+1 = 1·Fn + Fn–1, �� ���� Fn–1 – ������� �� ������� Fn+1 �� Fn. ������� �������� ������� ��� ���������� (Fn+1, Fn) �������� n – 1 ��� (���������: F3 = 2F2).
��������� � ���������� �������������
| ����� | |
| ����� | �������� �.�., ������� �.�. |
| ��� ������� | 2002 |
| �������� | ������� � ������ ����� |
| ������������ | ����� |
| ������� | 1 |
| ����� | |
| ����� | 3 |
| �������� | �������� ������� � �������� ������� ���������� |
| ���� | ������� � ���������� |
| �������� | |
| ����� | 2 |
| �������� | �������� ������� |
| ���� | �������� ������� |
| ������ | |
| ����� | 03.065 |













![{frac {a}{b}}=[q_{0};q_{1},q_{2},cdots ,q_{n}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68001ba446fce18360827496bedbc1b26166244a)
![[q_{0};q_{1},q_{2},cdots ,q_{n-1}]=-{frac {t}{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6eacd1be720cddaf961dc11b2b4071013a362a1)



![{frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {1}{ddots +{cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},ldots ,q_{N}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae99fb7b3e5da350f429e339994c542c14bac614)
![{displaystyle {frac {1071}{462}}=2+{cfrac {1}{3+{cfrac {1}{7}}}}=[2;3;7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/519b5ba7183633ba364882ca312a0572e4b80d30)

























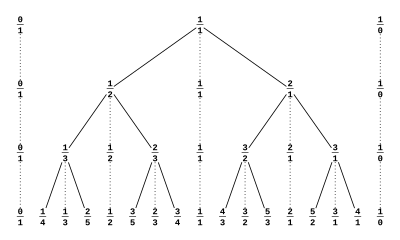




![{displaystyle {frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {1}{ddots +{cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},ldots ,q_{N}],.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd6202ce1dc46510c7894abba456c3b899c58bf)
![{displaystyle {frac {1071}{462}}=2+{cfrac {1}{3+{cfrac {1}{7}}}}=[2;3,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bb1b741861a853bc9f7bcbcd91315b07ffdac0)





















