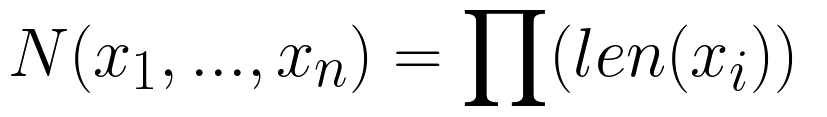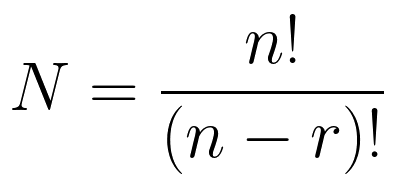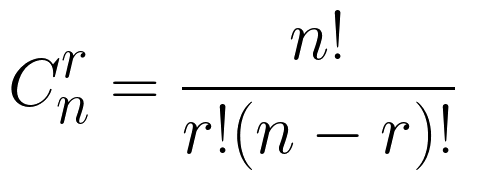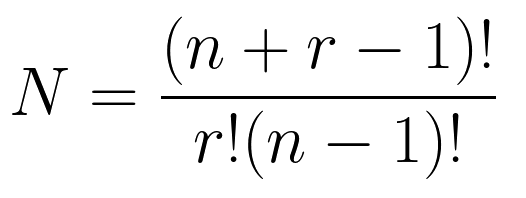Как найти количество сочетаний в питоне

Время на прочтение
4 мин

Количество просмотров 90K

Стандартная библиотека python, начиная с версии 2.2, предоставляет множество средств для генерирования комбинаторных объектов, но в интернете мне не удалось найти ни одной статьи, которая подробно рассказывала бы о работе с ними. Поэтому я решил исправить это упущение.

Начну с того, что расскажу о комбинаторике и ее основных формулах. Если же вы уже знакомы с этим разделом математики — можете пропустить эти абзацы.

Допустим, у нас есть строка, состоящая из n разных букв и мы хотим вычислить все способы переставить эти буквы местами так, чтобы получить новую строку. На первую позицию в строке мы можем выбрать одну из n букв, имеющихся у нас, на вторую позицию одну из n-1-ой буквы и так далее. В итоге получаем произведение n (n-1)… *1 = n! количество перестановок из n элементов без повторений.

Теперь представим, что количество букв в строке ограничено. У нас есть n доступных букв и мы хотим вычислить количество способов составить из них строку длины k, где k < n, каждую букву мы можем использовать лишь единожды. Тогда на первую позицию в строке мы можем поставить одну из n букв, на вторую позицию одну из n-1 буквы и на k-ую позицию одну из n-k+1 буквы. Общее количество строк будет равно n (n — 1) (n — 2) … (n — k + 2) (n — k + 1) = n!/(n-k)! количество размещений из n по k. Если же уникальность букв не требуется, то мы получим формулу n…nn = n^k количество размещений из n по k с повторениями.

До этого мы перебирали последовательности с учетом порядка элементов, а что если порядок для нас не имеет значения. Например, у нас есть есть n разных конфет и мы хотим выбрать k из них, чтобы подарить другу, при чем k < n. Сколько существует способов выбрать k конфет из n без учета порядка? Ответ прост, в начале найдем размещение из n по k без повторений, но тогда одинаковые наборы конфет, имеющие разный порядок их следования будут повторяться. Сколько существует способов переставить k конфет? Правильно, перестановка из k элементов без повторений. Итоговый ответ: размещения из n по k делим на перестановки из k без повторений. Формула: количество сочетаний из n по k.

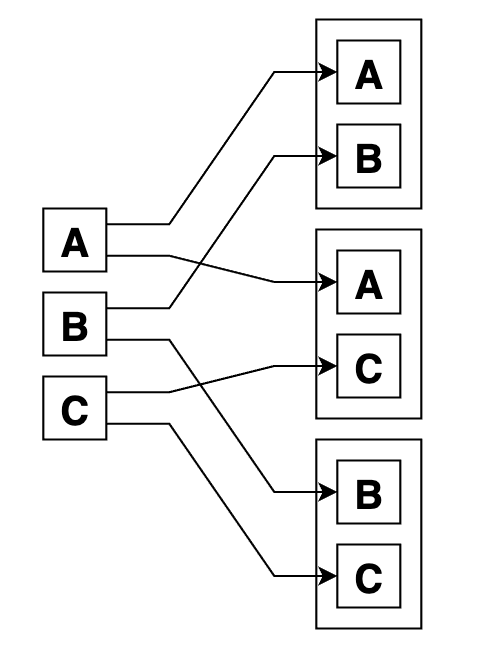
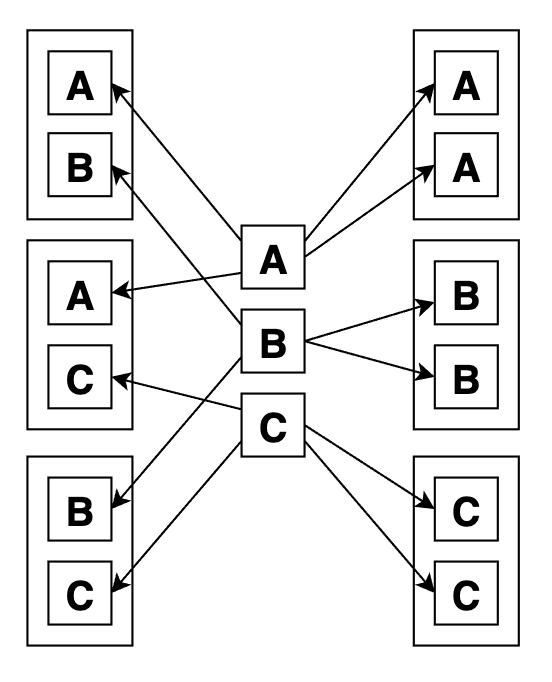
Рассмотрим случай посложнее, у нас есть n коробок каждая из которых содержит множество конфет одного вкуса, но в разных коробках вкусы разные. Сколько существует способов составить подарок другу из k конфет, при чем один и тот же вкус может встречаться любое количество раз? Так как порядок для нас значения не имеет, давайте разложим подарочные сладости следующим образом: в начале будут лежать последовательно конфеты первого вкуса, затем второго и так далее, а между конфетами разных вкусов положим спички, если конфеты какого-то вкуса отсутствуют в нашем подарке — спички, которые должны были окаймлять этот вкус слева и справа будут стоять рядом. Того у нас получится последовательность, состоящая из k конфет и n-1 спички, ибо вкусов всего n, а спички разделяют их. Теперь заметим, что по расположению спичек, мы можем восстановить исходное множество. Тогда ответом будет количество способов разместить n-1 спичку в n+k-1 ячейку без учета порядка, что равно количеству сочетаний из n+k-1 по n-1, формула: количество сочетаний из n по k с повторениями.

Теперь рассмотрим несколько задач на комбинаторику, чтобы закрепить материал.

Задача 1

Есть 20 человек, сколько существует способов разбить их на пары
Решение: возьмем первого человека, сколько существует способов выбрать ему пару: , возьмем второго человека, сколько существует способов выбрать ему пару: . Ответ: 19!!! = 654729075

Задача 2

Есть 10 мужчин и 10 девушек, сколько существует способов разбить их на компании, состоящие из одинакового количества и мужчин и девушек, пустая компания не считается
Решение:
Cпособ 1: количество способов собрать компанию из одного мужчины и одной девушки равно произведению количества способов выбрать одну девушку и количества способов выбрать одного мужчину. Количество способов выбрать одну девушку из 10 равно сочетанию из 10 по 1 без повторений, с мужчинами аналогично, поэтому возведем в квадрат. Далее аналогично вычислим сочетания из 10 по 2, из 10 по 3 и так далее до сочетания из 10 по 10. Итоговая формула: .
Способ 2: рассмотрим множество мужчин, входящих в компанию и множество девушек, не входящих в нее. По этому множеству можно однозначно восстановить компанию, а количество людей в нем всегда равно 10, так как , k — количество мужчин в компании, — количество девушек, не вошедших в нее. Количество таких множеств равно количеству сочетаний из 20 по 10, в конечном ответе мы также вычтем единицу, чтобы не учитывать пустую компанию, когда в нашем множестве 10 девушек. Итоговая формула: .

Итак, мы разобрались с теорией, теперь научимся генерировать комбинаторные объекты с помощью стандартной библиотеки python.
Работать мы будем с библиотекой itertools

from itertools import *

С помощью функции permutations можно сгенерировать все перестановки для итерируемого объекта.

Пример 1

for i in permutations('abc'):
    print(i, end=' ') # abc acb bac bca cab cba
print()
for i in permutations('abb'):
    print(i, end=' ') # abb abb bab bba bab bba 

Исходя из второго вызова заметим, что одинаковые элементы, стоящие на разных позициях, считаются разными.

Пример 2

for i in permutations('abc', 2):
    print(i, end=' ') # ab ac ba bc ca cb 

Размещение отличается от перестановки ограничением на количество доступных ячеек

Пример 3

for i in product('abc', repeat=2):
    print(i, end=' ') # aa ab ac ba bb bc ca cb cc

C помощью размещений с повторениями можно легко перебрать все строки фиксированной длины, состоящие из заданных символов

Пример 4

for i in combinations('abcd', 2):
    print(i, end=' ') # ab ac ad bc bd cd 

С помощью сочетаний без повторений можно перебрать все наборы не повторяющихся букв из заданной строки, массива или другого итерируемого объекта без учета порядка

Пример 5

for i in combinations_with_replacement('abcd', 2):
    print(i, end=' ') # aa ab ac ad bb bc bd cc cd dd  

Результат аналогичен вызову combinations, но в результат также добавлены множества с одинаковыми элементами.

Материалы:
Н.В. Горбачев “Сборник олимпиадных задач по математике”
Документация по python на русском

In this tutorial, you’ll learn how to use Python to get all combinations of a list. In particular, you’ll learn how to how to use the itertool.combinations method to generate a list of all combinations of values in a list.

The Quick Answer: Use itertools.combinations to Get All Combinations of a List

What Does it Mean to Get All Combinations of a List?

In your Python journey, you may encounter the need to get all combinations of the items in a list. But what does this mean?

Let’s say you have a list that looks like this: ['a', 'b', 'c'].

When you create a list of all possible combinations, you’ll end up with a list that looks like this: [(), ('a',), ('b',), ('c',), ('a', 'b'), ('a', 'c'), ('b', 'c'), ('a', 'b', 'c')]. Here we get a list of tuples that contain all possible combinations without replacement.

Now that you know what it means to get a list of all possible combinations of a list in Python, let’s see how you can get this done in Python!

Python comes built-in with a helpful library called itertools, that provides helpful functions to work with iteratable objects. One of the many functions it comes with it the combinations() function. This, as the name implies, provides ways to generate combinations of lists.

Let’s take a look at how the combinations() function works:

itertools.combinations(iterable, r)

• iterable refers to the iterable for which you want to find combinations,
• r refers to the length of the combinations you want to produce

Now that you know how the combinations() function works, let’s see how we can generate all possible combinations of a Python list’s items:

from itertools import combinations

sample_list = ['a', 'b', 'c']
list_combinations = list()

for n in range(len(sample_list) + 1):
    list_combinations += list(combinations(sample_list, n))

print(list_combinations)

# Returns: [(), ('a',), ('b',), ('c',), ('a', 'b'), ('a', 'c'), ('b', 'c'), ('a', 'b', 'c')]

Let’s break down what we’ve done here:

1. We import the combinations function from itertools
2. We create a sample list and an empty list to store our data in
3. We then create a for-loop to loop over all possible combinations of lengths. To make this dynamic, we use the range() function, since we may not know how long our list is at any given time.
4. We then create a list out of the combinations object that’s returned from passing in our sample list and our n parameter

We can see that our list includes a blank combination as well. If we wanted to omit this, we could change our for-loop to be from range(1, len(sample_list)+1), in order to have a minimum number of elements in our combination.

In the next section, you’ll learn how to get all combinations of only unique values in a list.

Want to learn more about Python for-loops? Check out my in-depth tutorial here to learn all you need to know!

How to Get All Combinations of Unique Values of a List in Python

In this section, you’ll learn how to get all combinations of only unique values of a list in Python. Since Python lists can contain duplicate values, we’ll need to figure out how to do this.

Say we have a list that looks like this: ['a', 'b', 'c', 'c']. Instead of including duplicate combinations of c in our final list, we’ll first need to remove duplicates from our list.

Let’s see how we can do this in Python:

from itertools import combinations

sample_list = ['a', 'b', 'c', 'c']
list_combinations = list()

sample_set = set(sample_list)
for n in range(len(sample_set) + 1):
    list_combinations += list(combinations(sample_set, n))

print(list_combinations)

This follows the same logic as the example above. The only difference is that we have first created a set out of our list. Sets are a unique data structure in Python that require each item to be unique. Therefore, it’s a helpful way to de-duplicate our list.

We then iterate over the length of the set and the set itself, to create all possible combinations.

How to Get All Combinations with Replacement of a List in Python

In this final section, you’ll learn how to get all combinations of a list in Python with replacements. Meaning, that a single element has the potential for being picked again.

Let’s see how this can be done in Python, using itertools and the combinations_with_replacement function. The function does exactly what it is described as: it gets the combinates with replacements.

from itertools import combinations_with_replacement

sample_list = ['a', 'b', 'c']
list_combinations = list()

for n in range(len(sample_list) + 1):
    list_combinations += list(combinations_with_replacement(sample_list, n))

print(list_combinations)

# Returns: [(), ('a',), ('b',), ('c',), ('a', 'a'), ('a', 'b'), ('a', 'c'), ('b', 'b'), ('b', 'c'), ('c', 'c'), ('a', 'a', 'a'), ('a', 'a', 'b'), ('a', 'a', 'c'), ('a', 'b', 'b'), ('a', 'b', 'c'), ('a', 'c', 'c'), ('b', 'b', 'b'), ('b', 'b', 'c'), ('b', 'c', 'c'), ('c', 'c', 'c')]

We can see here that each item has the potential for being included once, twice, or three times in a list of three items.

Conclusion

In this post, you learned how to get all combinations of a list in Python. You learned how to do this with the itertools.combinations function and the `itertools.combinations_with_replacement_ function. The functions allow you to pass in a list and get the combinations without and with replacements, respectively.

To learn more about the itertools.combinations function, check out the official documentation here.

Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Короче, это все о сочетаниях, перестановках, числе способов и тому подобному.

Почему важна комбинаторика? Нет, не только лишь для решения олимпиадных задач, но также комбинаторика – один из столпов теории вероятностей, которая в свою очередь служит фундаментом для машинного обучения – одно из мощнейших трендов в ПО начале 21-го века!

В встроенном в Python модуле itertools существует ряд комбинаторных функций. Это:

• product() – прямое (Декартово) произведение одного или нескольких итераторов.
• permutations() – перестановки и размещения элементов множества.
• combinations() – уникальные комбинации из элементов множества.
• combinations_with_replacement() – комбинации с замещением (повторами, возвратами).

О каждой из них расскажу подробно. Для начала импортируем все нужные функции из модуля:

from itertools import *

Прямое произведение

Прямое, или декартово произведение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств. Проще говоря мы берем из первого множества один элемент, а потом из второго выбираем элемент и составляем их в кортеж. Так вот все способы выбрать так элементы – составят декартово произведение. Пример:

>>> A = [1, 2, 3]
>>> B = "123"
>>> print(*product(A, B))
(1, 'a') (1, 'b') (1, 'c') (2, 'a') (2, 'b') (2, 'c') (3, 'a') (3, 'b') (3, 'c')

Примечания. Во-первых, заметьте, что элементы следуют в строгом лексографическом порядке: сначала берется нулевой элемент из первой последовательности и сочетается с каждым по очереди из второй последовательности. Во-вторых, аргументами функции могут быть любые итерируемые объекты конечной длины. Я взял для примера список и строку, причем строка автоматически разбивается на символы.

В коде произведение множеств эквивалентно вложенным циклам:

>>> print(*[(a, b) for a in A for b in B])
(1, '1') (1, '2') (1, '3') (2, '1') (2, '2') (2, '3') (3, '1') (3, '2') (3, '3')

Результат такой же, но рекомендую использовать именно библиотечную функцию, так как ее реализация, наверняка, будет лучше.

Вы можете передать в функцию больше последовательностей:

>>> print(*product([1, 2, 3]))
(1,) (2,) (3,)

>>> print(*product([1, 2, 3], [10, 20, 30]))
(1, 10) (1, 20) (1, 30) (2, 10) (2, 20) (2, 30) (3, 10) (3, 20) (3, 30)

>>> print(*product([1, 2, 3], [10, 20, 30], [100, 200, 300]))
(1, 10, 100) (1, 10, 200) (1, 10, 300) (1, 20, 100) (1, 20, 200) (1, 20, 300) (1, 30, 100) (1, 30, 200) (1, 30, 300) (2, 10, 100) (2, 10, 200) (2, 10, 300) (2, 20, 100) (2, 20, 200) (2, 20, 300) (2, 30, 100) (2, 30, 200) (2, 30, 300) (3, 10, 100) (3, 10, 200) (3, 10, 300) (3, 20, 100) (3, 20, 200) (3, 20, 300) (3, 30, 100) (3, 30, 200) (3, 30, 300)

Каждый выходной элемент будет кортежем (даже в случае, если в нем только один элемент!). Также обратите внимание на то, что функция product (как и все остальные из сегодняшнего набора) возвращает не список, а особый ленивый объект. Чтобы получить все элементы, нужно преобразовать его в список функцией list:

>>> product([1, 2, 3], 'abc')
<itertools.product object at 0x101aef8c0>

>>> list(product([1, 2, 3], 'abc'))
[(1, 'a'), (1, 'b'), (1, 'c'), (2, 'a'), (2, 'b'), (2, 'c'), (3, 'a'), (3, 'b'), (3, 'c')]

Количество элементов на выходе будет произведением длин всех последовательностей на входе:

В функцию product можно передать именованный параметр repeat, который указывает сколько раз повторять цепочку вложенных циклов (по умолчанию один раз). Если repeat >= 2, то это называют декартовой степенью. То есть множество умножается на себя несколько раз. Так при repeat=2 эквивалентным кодом будет:

>>> [(a, b, a1, b1) for a in A for b in B for a1 in A for b1 in B] == list(product(A, B, repeat=2))
True

В таком случае количество элементов в результате будет вычисляться по схожей формуле с учетом того, что каждый множитель будет в степени repeat:

Перестановки

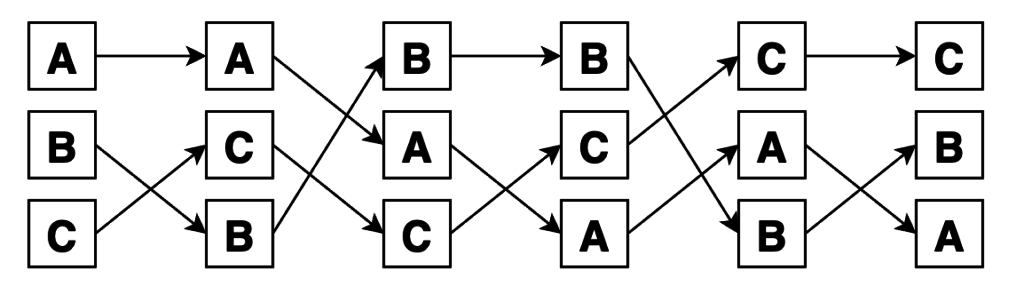
Функция permutations возвращает последовательные перестановки элементов входного множества. Первый элемент – будет исходным множеством. Второй – результат перестановки какой-то пары элементов и так далее, пока не будут перебраны все уникальные комбинации. Уникальность здесь рассматривается по позициям элементов в исходной последовательности, а не по и их значению, то есть элементы между собой алгоритмом не сравниваются. Важны только их индексы.

Число объектов остается неизменными, меняется только их порядок.

>>> print(*permutations("ABC"))
('A', 'B', 'C') ('A', 'C', 'B') ('B', 'A', 'C') ('B', 'C', 'A') ('C', 'A', 'B') ('C', 'B', 'A')

Второй параметр r отвечает за количество элементов в перестановках. По умолчанию будут выданы полные перестановки (длиной, равной длине n исходной последовательности), никакие элементы исходного множества не будут выброшены, а просто переставлены местами. Если задать 0 <= r <= n, в каждой выборке будет содержаться по r элементов. Иными словами из n входных элементов будем выбирать r объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по r.

Например размещения для двух элементов из коллекции из трех элементов:

>>> print(*permutations("ABC", 2))
('A', 'B') ('A', 'C') ('B', 'A') ('B', 'C') ('C', 'A') ('C', 'B')

# 2 из 4
>>> print(*permutations([1, 2, 3, 4], 2))
(1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)

Количество вариантов получится по формуле (n – длина исходной последовательности):

При r > n будет пустое множество, потому что невозможно из более короткой последовательности выбрать более длинную. Максимальное число вариантов – для полной перестановки равняется n! (факториал).

Размещения выглядят так. Сначала выбрали по 2 элемента из 3, а потом переставили их внутри групп всеми способами. Итого 6 вариантов:

Сочетания

combinations – функция, коротая выбирает все сочетания из входной последовательности. Пусть в ней имеется n различных объектов. Будем выбирать из них r объектов всевозможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по r, а их число равно:

Разница сочетаний и перестановок в том, что для сочетаний нам не важен порядок, а для перестановок он важен. Пример:

>>> print(*permutations([1, 2, 3], 2))
(1, 2) (1, 3) (2, 1) (2, 3) (3, 1) (3, 2)

>>> print(*combinations([1, 2, 3], 2))
(1, 2) (1, 3) (2, 3)

(1, 2) и (2, 1) – разные перестановки, но с точки зрения сочетаний – это одно и тоже, поэтому в combinations входит только один вариант из двух.

Второй параметр r – обязателен для этой функции. 0 <= r <= n. При r > n будет пустое множество.

Вот графический пример сочетаний из 3 по 2. Как видно, их вдвое меньше, чем размещений из 3 по 2, так как варианты с перестановками внутри групп не учтены по определению:

Сочетания с повторами

Функция combinations_with_replacement описывает, сколькими способами можно составить комбинацию по r элементов из элементов n типов (элементы в комбинации могут повторяться, но порядок их не важен). Обратите внимание на слово «тип«, в простых сочетаниях элементы не повторялись внутри одной выборки, они были как бы конкретными экземплярами.

На языке мешка с шарами, сочетания с повторами значит, что мы достаем шары из мешка, а потом кладем их обратно, записывая их цвета (цвет это и есть в данном случае аналог типа). Вполне может быть так, что мы достали красный шар два раза подряд, ведь после первого раза мы сунули его обратно в мешок. Пример:

>>> print(*combinations_with_replacement(['red', 'white', 'black'], 2))
('red', 'red') ('red', 'white') ('red', 'black') ('white', 'white') ('white', 'black') ('black', 'black')

Поэтому, имея возможность брать один и тот же элемент несколько раз, можно выбрать из последовательности в три элемента 4, и 5, и сколь угодно много (больше, чем было исходных типов). Например, по 4 из 2:

>>> print(*combinations_with_replacement(['red', 'black'], 4))
('red', 'red', 'red', 'red') ('red', 'red', 'red', 'black') ('red', 'red', 'black', 'black') ('red', 'black', 'black', 'black') ('black', 'black', 'black', 'black')

Вот графически сочетания с повторами по 2 из 3:

Формула числа элементов на выходе такова:

Бонус – брутфорс пароля

Как бонус предлагаю вам применение функции product() для брутфорса паролей. Сперва мы задаем набор символов, которые могут встречаться в пароле, наш алфавит, например такой:

import string
# все буквы и цифры
alphabet = string.digits + string.ascii_letters
# 0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ

А потом перебираем все возможные сочетания с длинами от минимальной до максимальной. Не забываем их склеить в строку:

def brute_force(alphabet, min_len, max_len):
    # функция - склеиватель последователностей символов в строку
    joiner = ''.join

    for cur_len in range(min_len, max_len + 1):
        yield from map(joiner, product(alphabet, repeat=cur_len))

Пример применения:

# сокращенный алфавит для иллюстрации работы
alphabet = '123AB'
print(*brute_force(alphabet, 1, 3), sep=', ')

# вывод: 1, 2, 3, A, B, 11, 12, 13, 1A, 1B, 21, 22, 23, 2A, 2B, 31, 32, 33, 3A, 3B, A1, A2, A3, AA, AB, B1, B2,
 B3, BA, BB, 111, 112, 113, 11A, 11B, 121, 122, 123, 12A, 12B, 131, 132, 133, 13A, 13B, 1A1, 1A2, 1A3, 1AA, 
1AB, 1B1, 1B2, 1B3, 1BA, 1BB, 211, 212, 213, 21A, 21B, 221, 222, 223, 22A, 22B, 231, 232, 233, 23A, 23B, 
2A1, 2A2, 2A3, 2AA, 2AB, 2B1, 2B2, 2B3, 2BA, 2BB, 311, 312, 313, 31A, 31B, 321, 322, 323, 32A, 32B,
 331, 332, 333, 33A, 33B, 3A1, 3A2, 3A3, 3AA, 3AB, 3B1, 3B2, 3B3, 3BA, 3BB, A11, A12, A13, A1A, A1B,
 A21, A22, A23, A2A, A2B, A31, A32, A33, A3A, A3B, AA1, AA2, AA3, AAA, AAB, AB1, AB2, AB3, ABA, 
ABB, B11, B12, B13, B1A, B1B, B21, B22, B23, B2A, B2B, B31, B32, B33, B3A, B3B, BA1, BA2, BA3, BAA, 
BAB, BB1, BB2, BB3, BBA, BBB

Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈 

9 927