Как найти количество спектральных линий

Как найти количество спектральных линий

Количество спектральных линий Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Квантовое число: 8 –> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

28 –> Конверсия не требуется




21 Водородный спектр Калькуляторы

Количество спектральных линий формула

Количество спектральных линий = (Квантовое число*(Квантовое число-1))/2

ns = (nquantum*(nquantum-1))/2

Что такое модель Бора?

Модель Бора или модель Резерфорда-Бора, представленная Нильсом Бором и Эрнестом Резерфордом в 1913 году, представляет собой систему, состоящую из небольшого плотного ядра, окруженного вращающимися электронами.

Источник

$begingroup$

Recently, I found that when electrons in an atomic sample de-excite from a higher energy level ($n_2$) to a lower energy level ($n_1$), the number of spectral lines observed in the spectrum is

$$frac{(n_2 – n_1)(n_2 – n_1 + 1)}{2}$$

Can anyone please tell me how to derive this?

Rodrigo de Azevedo's user avatar

asked Jul 4, 2021 at 2:44

K M F Ruhan's user avatar

$endgroup$

$begingroup$

When you move from level $n_1$ to level $n_2$, the total number of energy levels are $n_2-n_1+1$ (including $n_1$ and $n_2$).

Now, you want to find the total number of possible spectral lines in the atomic sample.

Note that if you chose any two energy levels (say $n_i$ and $n_j$), you will get a unique spectral line corresponding to those energy levels.

So, the total number of spectral lines possible are $$binom{n_2-n_1+1}{2}=dfrac{(n_2-n_1+1)(n_2-n_1)}{2}$$

answered Jul 4, 2021 at 3:12

V.G's user avatar

V.GV.G

1,2314 silver badges20 bronze badges

$endgroup$

3

Источник

Количество – спектральная линия

Cтраница 1

Количество спектральных линий, относящихся к одному атому, достаточно велико. В настоящее время наши представления о строении любой химической частицы ( будь то атом, ион или молекула) настолько детальны, что сведения о практически всех ее спектральных линиях имеются в справочных изданиях. Для атомов и их ионов наибольшей популярностью пользуются диаграммы уровней энергий с указанием на них длин волн спектральных линий и сил осцилляторов соответствующих переходов. На рис. 1.2 приведен пример Гротриановской диаграммы для атома натрия.
 [1]

Таким образом, было обнаружено, что поистине необозримое количество спектральных линий описывается сравнительно простыми зависимостями, отличительной особенностью которых является наличие целочисленных параметров.
 [2]

Построить схему возможных переходов между 2D – и 2Р – состояниями в слабом магнитном поле и определить количество спектральных линий, которые при этом наблюдаются.
 [3]

Интервал между спектральными линиями равен 1 / Т, поэтому при увеличении периода Тя ( уменьшении частоты) следования импульсов и сохранении их длительности / и увеличивается количество спектральных линий. Отсюда следует, что при переходе от периодической последовательности импульсов к одиночному импульсу ( Тиоо) частотный спектр преобразуется из линейчатого в сплошной, так как интервал между спектральными составляющими уменьшается до нуля ( FH 0) и содержит колебания всех частот от 0 до оо.
 [5]

Интервал между спектральными линиями равен 1 / ТИ) поэтому при увеличении периода Гц ( уменьшении частоты) следования импульсов и сохранении их длительности / я увеличивается количество спектральных линий. Отсюда следует, что при переходе от периодической последовательности импульсов к одиночному импульсу ( Ти оо) частотный спектр преобразуется из линейчатого в сплошной, так как интервал между спектральными составляющими уменьшается до нуля ( f, 0) и содержит колебания всех частот от 0 до оо. При переходе линейчатого спектра к сплошному форма огибающей остается неизменной, потому что она зависит не от периода повторения импульсов, а только от их формы.
 [7]

Числовые значения этих функций называют спектральными термами. Таким образом, необозримое количество спектральных линий описывается сравнительно простыми зависимостями (14.1), (14.3), отличительной особенностью которых является наличие целочисленных параметров.
 [8]

Такое слабое поле влияет на состояние спиновой системы лишь в случае, если его частота о2 настроена точно на какую-либо линию спектра. Воздействие слабого поля является чисто локальным, и в результате никогда не наблюдается уменьшения количества спектральных линий. IV-48) получим, что ухЯафф у – Д – Уровни энергии ядра А расщепляются согласно уравнению IV-46 на величину V2Yx 2 и – а 2л / АХ, а спектральные линии – на величину Yx a. Так как ядерный спин может влиять на уровни энергии другого спина лишь при спин-спиновой связи между ними и квантование спина ядра X по направлению эффективного поля непосредствено влияет только на уровни энергии этого спина, то в спектре ядра А расщепляются лишь те линии, которые имеют общие уровни энергии со спином X. По мере повышения интенсивности возмущающего поля оно будет воздействовать и на другую линию дублета ядра X; при этом внутренние из четырех линий ядра А будут увеличиваться и сближаться, а внешние – уменьшаться и удаляться.
 [9]

Раскаленные атомарные газы и пары при низких давлениях дают линейчатый спектр, состоящий из отдельных цветных линий, разделенных темными промежутками. Каждое вещество в газообразном состоянии имеет свой линейчатый спектр с определенными цветом, положением и количеством спектральных линий.
 [10]

Наличие тонкой структуры указывает на более – сложное строение электронных уровней, чем то, ск которому приводит изложенная выше элементарная разработка теории Бора. Согласно последней, электроны движутся по рутовым орбитам, однозначно характеризуемым единственным главным квантовым числом п, и количество спектральных линий не должно превышать числа парных комбинаций этих чисел, отвечающих обеим орбитам, между которыми происходит переход электрона. Однако число линий в тонкой структуре значительно больше.
 [11]

Опытными данными установлено, что, в зависимости от характера аниона соли, окраска пламени получается различной. Так, например, при внесении на платиновой спирали в пламя бунзеновской горелки насыщенных растворов солей натрия, лития, калия, рубидия пли цезия количество спектральных линий не изменяется, а изменяется лишь их интенсивность.
 [12]

При термодинамическом равновесии форма линий поглощения совпадает с формой линий испускания. Благодаря тому, что спектральные линии не строго монохроматичны, а занимают некоторую полосу частот, дискретно – дискретные переходы могут оказывать значительное влияние на величину среднего по Росселанду пробега фотонов, так как количество спектральных линий для элементов с большим Z может быть огромным.
 [13]

Страницы:  

   1

Источник

Спектр с линиями поглощения, отмеченными стрелками, в графическом представлении

Спектра́льная ли́ния — узкий участок энергетического спектра (например, спектра электромагнитного излучения), где интенсивность излучения усилена либо ослаблена по сравнению с соседними областями спектра. В первом случае линия называется эмиссионной линией, во втором — линией поглощения. Положение линии в электромагнитном спектре обычно задаётся длиной волны, частотой или энергией фотона. Кроме электромагнитного спектра, спектральные линии могут возникать в спектрах энергии частиц (например, в альфа-спектре при альфа-распаде радиоактивных ядер), в спектрах звуковых колебаний и вообще любых волновых процессов. Ниже, если нет специальных оговорок, имеются в виду электромагнитные спектры.

Чаще всего спектральные линии возникают при переходах между дискретными уровнями энергии в квантовых системах: молекулах, атомах и ионах, а также атомных ядрах. У каждого химического элемента атомы и ионы имеют собственную структуру энергетических уровней, и набор спектральных линий у них уникален, что позволяет по спектральным линиям определять присутствие и количественное содержание тех или иных химических элементов в исследуемом объекте.

Спектральные линии имеют малую ширину, но они не монохромны. Распределение интенсивности излучения в линии называется профилем или контуром спектральной линии, вид которого зависит от множества факторов, называемых механизмами уширения. Среди них — естественная ширина спектральной линии, доплеровское уширение и другие эффекты.

Спектральные линии наблюдаются во всех диапазонах электромагнитного излучения: от гамма-лучей до радиоволн, причём линии в разных диапазонах обусловлены различными процессами: например, линии атомных ядер попадают в гамма- и рентгеновский диапазоны, а различные линии молекул — в основном в инфракрасный и радиоволновой диапазоны. Профили и характеристики спектральных линий содержат различную информацию об условиях среды, где они возникли.

Описание[править | править код]

Спектральные линии представляют собой узкие участки спектра электромагнитного излучения, на которых интенсивность излучения усилена либо ослаблена по сравнению с соседними областями спектра. В первом случае линии называются эмиссионными линиями, во втором — линиями поглощения. Положение линии в спектре обычно задаётся либо длиной волны {displaystyle lambda ,} либо частотой {displaystyle nu =c/lambda ,} где c — скорость света, или же энергией фотона {displaystyle E=hnu ,} где h — постоянная Планка[1][2][3].

Название термина «спектральная линия» объясняется внешним видом спектра при наблюдении его с помощью спектрографа с призмой или дифракционной решёткой: узкие максимумы или минимумы в спектре выглядят как яркие или тёмные линии на фоне полосы непрерывной яркости[1][4].

Механизм возникновения[править | править код]

В большинстве случаев спектральные линии возникают из-за переходов между дискретными уровнями энергии в квантовых системах: молекулах, атомах и ионах, а также атомных ядрах. Также спектральные линии могут порождаться, например, циклотронным излучением и процессами в плазме[2][3][5]. Излучение в линиях кристаллами рассматривается как излучение экситонов — квазичастиц, представляющих собой связанное состояние электрона и дырки[6].

В атомах и других квантовых системах переходы с более высокого энергетического уровня i на более низкий j могут происходить самопроизвольно, в таком случае при переходе излучается фотон с энергией, равной разности энергии уровней, а такие переходы называются спонтанными. Если фотон с такой же энергией попадает в такой же атом на энергетическом уровне j, то фотон поглощается, а атом переходит на энергетический уровень i. Если же такой фотон попадает в атом на уровне i, то происходит вынужденное излучение ещё одного фотона с той же длиной волны и направлением движения, а атом переходит на уровень {displaystyle j.} При постоянно идущих переходах в одну сторону излучаются либо поглощаются фотоны одной и той же энергии, поэтому на фоне непрерывного спектра наблюдается светлая или тёмная линия[7][8].

Таким образом, длины волн спектральных линий характеризуют структуру энергетических уровней квантовой системы. В частности, каждый химический элемент и ион имеет собственную структуру энергетических уровней, а значит, уникальный набор спектральных линий[1][4]. Линии в наблюдаемом спектре могут быть отождествлены с линиями известных химических элементов, следовательно, по спектральным линиям можно определять присутствие тех или иных химических элементов в исследуемом объекте[9]. Количественное определение химического состава источника спектра по линиям является предметом спектрального анализа[10].

Кроме длины волны, линии характеризуются эйнштейновскими коэффициентами перехода. Можно рассмотреть спонтанные переходы с уровня i на {displaystyle j:} количество таких переходов, а значит, число испущенных фотонов в этой линии единичным объёмом (берётся 1 см3) пропорционально количеству n_{i} атомов в этом объёме, находящихся на уровне i. Эйнштейновский коэффициент спонтанного перехода A_{{ij}} является таким коэффициентом пропорциональности: количество фотонов, излучаемых в линии n_{i} атомами за промежуток времени dt равняется {displaystyle A_{ij}n_{i}dt.} Число обратных переходов с уровня j на уровень i в этом объёме, вызванных поглощением фотона, пропорционально не только количеству n_{j} атомов на уровне j, но и плотности излучения соответствующей частоты в линии: {displaystyle rho _{ji}.} Количество поглощённых фотонов выражается эйнштейновским коэффициентом поглощения {displaystyle B_{ji}} и за промежуток времени dt равно {displaystyle B_{ji}n_{j}rho _{ji}dt}. Аналогично и для вынужденных переходов с уровня i на {displaystyle j:} число излученных таким образом фотонов равняется {displaystyle B_{ij}n_{i}rho _{ji}dt}[2][11].

Среди спектральных линий выделяют запрещённые линии. Запрещённые линии соответствуют переходам, которые запрещены правилами отбора, поэтому эйнштейновские коэффициенты для них очень малы и вероятность перехода в единицу времени у них существенно меньше, чем у остальных переходов, называемых разрешёнными. Энергетические уровни, с которых возможны только запрещённые переходы, называются метастабильными: обычно время нахождения атома на метастабильном уровне составляет от 10−5 секунд до нескольких суток, а на обычном ― порядка 10−8 секунд. Это приводит к тому, что в обычных условиях такие линии не наблюдаются, поскольку за время нахождения атома на метастабильном уровне он многократно сталкивается с другими атомами и передаёт им свою энергию возбуждения. Однако при низкой плотности вещества столкновения атомов происходят достаточно редко, поэтому накапливается большое количество атомов в метастабильных состояниях, спонтанные переходы из них становятся частыми и запрещённые эмиссионные линии становятся такими же интенсивными, как и разрешённые[12][13].

Профиль спектральной линии[править | править код]

Линии в спектре имеют малую ширину, но не монохромны: распределение интенсивности излучения в линии называется профилем или контуром спектральной линии, вид которого зависит от множества факторов (см. ниже[⇨])[1][14]. Интенсивность излучения в спектре описывается функцией распределения энергии по длинам волн или частотам. Для отделения излучения или поглощения в линии от излучения в непрерывном спектре проводится экстраполяция соседних с линией областей спектра на область, где наблюдается линия, как если бы она отсутствовала. Можно обозначить интенсивность излучения наблюдаемого спектра на частоте nu как {displaystyle I_{nu },} а экстраполированного — как {displaystyle I_{nu }^{0}.} Для эмиссионных линий разность этих величин {displaystyle F_{nu }} называется интенсивностью излучения в линии на частоте {displaystyle nu ,} для линий поглощения — глубиной линии. Другой параметр — остаточная интенсивность — выражается как {displaystyle r_{nu }=I_{nu }/I_{nu }^{0}}[3][15][16]. Если в линии поглощения интенсивность спектра доходит до нуля, то линия называется насыщенной[17].

Полуширина, или же ширина линии — это разность между длинами волн или частотами, на которых интенсивность излучения или глубина линии составляет половину от максимальной. Этот параметр обозначается как {displaystyle FWHM} (от англ. Full Width at Half Maximum). Область линии, находящаяся внутри полуширины, называется центральной частью, а области, находящиеся по сторонам ― крыльями[3][14][16].

Для описания интенсивности линий поглощения используется понятие эквивалентной ширины {displaystyle W:} это размер области в длинах волн ({displaystyle W_{lambda }}) или в частотах ({displaystyle W_{nu }}), в котором непрерывный спектр излучает суммарно столько же энергии, сколько поглощается во всей линии. Формально она определяется через остаточную интенсивность как {textstyle W_{nu }=int _{nu _{1}}^{nu _{2}}(1-r_{nu })dnu } или {textstyle W_{lambda }=int _{lambda _{1}}^{lambda _{2}}(1-r_{lambda })dlambda } — аналогичные рассуждения можно провести для спектра по длинам волн, а не частотам. Теоретически, интегрирование должно производиться от {displaystyle 0} до {displaystyle infty ,} но на практике интегрируют на конечном интервале, включающем в себя основные части линии — как правило, ширина интервала составляет не более нескольких десятков нанометров[18][19]. Иными словами, это ширина прямоугольника с высотой, равной интенсивности непрерывного спектра, площадь которого равна площади над спектральной линией[3][16][20].

Поскольку количество фотонов, поглощаемых или излучаемых в линии, зависит только от количества атомов в соответствующем состоянии и плотности излучения (см. выше[⇨]), то, при прочих равных, чем больше ширина линии, тем меньше её глубина или интенсивность[21].

Механизмы уширения[править | править код]

Существует множество факторов, которые приводят к увеличению ширины линии и из-за которых спектральные линии не являются монохроматическими ― они называются механизмами уширения[1][3][14].

Естественная ширина[править | править код]

Естественная ширина спектральной линии, также называемая минимальной, обусловлена квантовыми эффектами[22]. В рамках классической механики такое явление объясняется радиационным затуханием, поэтому естественная ширина также называется радиационной[23]. Если среднее время жизни состояния, из которого переходит атом, равно T, то в силу принципа неопределённости энергия этого состояния определена с точностью до {displaystyle Delta E=hbar /T=h/(2pi T),} где hbar  — приведённая постоянная Планка, h — постоянная Планка. Тогда неопределённость частоты излучения, соответствующей этой энергии, составляет {displaystyle Delta nu =Delta E/h.} Поскольку энергия фотона в линии зависит от энергии и начального, и конечного состояния, то полуширина линии gamma выражается следующим образом[24]:

{displaystyle gamma ={frac {Delta E_{i}+Delta E_{j}}{hbar }}={frac {1}{T_{i}}}+{frac {1}{T_{j}}},}

где индексы обозначают уровни i и j[24]. Естественная ширина обязательно присутствует у всех линий, но, как правило, она очень мала по сравнению с остальными эффектами при их наличии[25]. Типичное значение естественной ширины линии составляет 10−3 Å[23], а особо малые естественные ширины имеют запрещённые линии[26].

Доплеровское уширение[править | править код]

Вклад в уширение линий может вносить эффект Доплера — в таком случае уширение называется доплеровским. Если источник излучения имеет ненулевую лучевую скорость относительно наблюдателя, то длина волны излучения, которое принимает наблюдатель, изменяется относительно той, которую излучает источник: в частности, наблюдается смещение линий в спектре. Если разные части источника движутся с разной лучевой скоростью, например, при его вращении, то смещение линий от различных частей источника оказывается разным, в спектре источника складываются линии с разным смещением и линии оказываются уширенными. Также, кроме движения отдельных частей источника, вклад в доплеровское уширение может вносить тепловое движение частиц, излучающих в линии[16][27].

Доплеровское смещение для небольших лучевых скоростей выражается формулой {textstyle {frac {Delta nu }{nu }}={frac {v_{r}}{c}},} где Delta nu  — смещение линии по частоте, nu  — частота линии, v_{r} — лучевая скорость, c — скорость света. При максвелловском распределении атомов по скоростям средняя скорость атома {displaystyle {bar {v}}} при температуре T и массе атома m составляет {textstyle {bar {v}}={sqrt {2kT/m}},} где k — постоянная Больцмана. Средняя скорость соответствует смещению от центра линии, на котором интенсивность линии в e раз меньше, чем в центре, а этот параметр достаточно близок к половине полуширины[27][28]. При температурах порядка нескольких тысяч кельвинов ширина линий в оптическом диапазоне принимает значения 10−2—10−1 Å[3][29].

Эффекты давления[править | править код]

Механизмы уширения линий, которые обусловлены влиянием посторонних частиц, называются эффектами давления, так как при увеличении давления увеличивается и влияние этих частиц. Например, к эффектам давления относятся столкновения возбуждённых атомов с другими частицами, в результате которых атомы теряют свою энергию возбуждения. В результате среднее время жизни атома в возбуждённом состоянии уменьшается, и, в соответствии с принципом неопределённости, увеличивается размытость уровня по сравнению с естественной (см. выше[⇨])[3][30]. Однако столкновения могут и делать линии более узкими: в случае, если эффекты давления ещё не слишком сильны, но длина свободного пробега атома оказывается меньше, чем длина волны излучаемого фотона, то за время излучения скорость атома может меняться, что уменьшает величину доплеровского уширения. Это явление известно как эффект Дикке[31].

Не меньшее влияние оказывает и прохождение частиц мимо излучающих атомов. При сближении частицы с атомом силовое поле вблизи последнего меняется, что приводит к смещению энергетических уровней в атоме. Из-за движения частиц смещение уровней постоянно меняется и различается между атомами в определённый момент времени, поэтому линии также оказываются уширенными. Наиболее сильно влияет эффект Штарка: прохождение заряженных частиц, таких как ионы и свободные электроны, вызывает переменное смещение энергетических уровней в атоме[32].

Эффект Зеемана и эффект Штарка[править | править код]

При воздействии магнитного поля энергетические уровни атомов расщепляются на несколько подуровней с близкими значениями энергии. С разных подуровней одного уровня возможны переходы на разные подуровни другого уровня, причём энергии таких переходов отличаются, и, следовательно, спектральная линия расщепляется на три или больше спектральных линии, каждая из которых соответствует определённому переходу между подуровнями. Это явление известно как эффект Зеемана. При эффекте Зеемана профили расщеплённых частей линии зачастую сливаются между собой, что вызывает наблюдаемое уширение линии, а не расщепление[3][33][34].

Эффект Штарка, возникающий в постоянном электрическом поле, также приводит к расщеплению энергетических уровней, и, как следствие — к расщеплению спектральных линий, как и эффект Зеемана[35].

Инструментальный профиль[править | править код]

Кроме механизмов уширения (см. выше[⇨]), на профиль линии влияет аппаратная функция приборов и их спектральное разрешение. Оптические инструменты имеют конечное разрешение, в частности, из-за дифракции, поэтому даже достаточно узкая линия всё равно будет иметь некоторую ширину и профиль, называемый инструментальным — зачастую инструментальный профиль и определяет наблюдаемую ширину линии[2][3][36].

Наблюдение и анализ[править | править код]

Спектральные линии встречаются во всех областях электромагнитного спектра: например, в гамма-диапазон попадает линия, образующаяся при аннигиляции электрона и позитрона, а также различные линии атомных ядер. К рентгеновскому диапазону относятся линии атомных ядер либо ионов с высокой степенью ионизации, в ультрафиолетовом и оптическом диапазоне наблюдаются линии различных ионов и атомов. В инфракрасном диапазоне преобладают линии вращательных и колебательных переходов молекул и присутствуют линии атомных переходов между высокими уровнями энергии. В диапазон радиоволн попадают линии молекул и линии переходов между высокими уровнями энергии атомов, а также линии переходов между уровнями сверхтонкого расщепления, например, радиолиния нейтрального водорода[3][5].

Эмиссионные линии можно наблюдать, например, в спектре нагретого разреженного газа. Если же пропустить излучение источника с непрерывным спектром через тот же самый газ в охлаждённом состоянии, то на фоне непрерывного спектра будут наблюдаться линии поглощения на тех же длинах волн[37].

Параметры спектральных линий и их профили содержат большое количество информации об условиях в среде, где они возникли, поскольку разные механизмы уширения приводят к образованию различных профилей[1][3][38]. Кроме того, интенсивность линии зависит от концентрации атомов или ионов, излучающих или поглощающей в этой линии. Например, для линий поглощения зависимость эквивалентной ширины линии от концентрации вещества называется кривой роста — следовательно, по интенсивности линии можно определять концентрацию того или иного вещества[39][40].

Кроме того, на длины волн спектральных линий может влиять красное смещение: доплеровское, гравитационное или космологическое, причём красное смещение для всех линий одинаково. Например, если известно, что красное смещение вызвано эффектом Доплера и известна его величина, можно определить лучевую скорость источника излучения[4][41][42].

История изучения[править | править код]

Задолго до открытия спектральных линий, в 1666 году Исаак Ньютон впервые наблюдал спектр Солнца, а в 1802 году Уильям Волластон создал щелевой спектроскоп. В 1814 году Йозеф Фраунгофер обнаружил в спектре Солнца спектральные линии поглощения, которые впоследствии стали называться фраунгоферовыми[43][44].

В 1842 году Кристиан Доплер предложил метод определения лучевых скоростей звёзд по смещению линий в их спектрах. В 1868 году Уильям Хаггинс впервые применил этот метод на практике[44].

В 1860 году Густав Кирхгоф и Роберт Бунзен определили, что каждая спектральная линия порождается определённым химическим элементом. В 1861 году Кирхгоф смог определить химический состав Солнца по линиям в его спектре, а в 1869 году Норман Локьер открыл неизвестный ранее элемент в спектре Солнца, названный гелием — на Земле этот элемент был обнаружен только в 1895 году[43][44].

В 1885 году Иоганн Бальмер эмпирически вывел формулу для длин волн некоторых спектральных линий водорода. В 1888 году Йоханнес Ридберг обобщил эту формулу для переходов между любыми двумя уровнями в атоме водорода — формулу Ридберга. В 1896 году Питер Зееман обнаружил расщепление спектральных линий в магнитном поле — эффект, позже названный в его честь[45][46].

Эти и другие открытые явления нуждались в теоретическом объяснении. После появления квантовой механики, в 1913 году Нильс Бор выдвинул свою квантовую теорию строения атома, которая объясняла формулу Ридберга, а в 1924 году Вольфганг Паули сформулировал принцип запрета, позволивший объяснить эффект Зеемана. В 1927 году Вернер Гейзенберг сформулировал принцип неопределённости, который обуславливает естественную ширину линии[45][47].

Дальнейшему изучению спектральных линий способствовало изобретение более совершенных оптических приборов. Кроме того, в 1958 году был изобретён лазер, который создаёт излучение в очень узких линиях, что позволяет эффективно использовать приборы с высоким спектральным разрешением[45][48].

Примечания[править | править код]

  1. ↑ 1 2 3 4 5 6 СПЕКТРА́ЛЬНАЯ ЛИ́НИЯ : [арх. 27 февраля 2021] / Анциферов П. С. // Социальное партнёрство — Телевидение. — М. : Большая российская энциклопедия, 2016. — С. 53. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 31). — ISBN 978-5-85270-368-2.
  2. ↑ 1 2 3 4 Юков Е. А. Спектральная линия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
  3. ↑ 1 2 3 4 5 6 7 8 9 10 11 12 Черепащук А. М. Спектральные линии. Астронет. Дата обращения: 2 августа 2021. Архивировано 2 августа 2021 года.
  4. ↑ 1 2 3 Spectral Line. Astronomy. Swinburne University of Technology. Дата обращения: 2 августа 2021. Архивировано 25 июля 2021 года.
  5. ↑ 1 2 Darling D. Spectral lines. Internet Encyclopedia of Science. Дата обращения: 3 августа 2021. Архивировано 3 августа 2021 года.
  6. ↑ Силин А. П. Экситон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
  7. ↑ Кононович, Мороз, 2004, с. 182—183.
  8. ↑ Karttunen et al., 2007, p. 95.
  9. ↑ Кононович, Мороз, 2004, с. 185.
  10. ↑ СПЕКТРА́ЛЬНЫЙ АНА́ЛИЗ : [арх. 25 февраля 2021] / Анциферов П. С. // Социальное партнёрство — Телевидение. — М. : Большая российская энциклопедия, 2016. — С. 55-56. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 31). — ISBN 978-5-85270-368-2.
  11. ↑ Соболев, 1985, с. 83—84.
  12. ↑ Черепащук А. М. Запрещённые спектральные линии. Астронет. Дата обращения: 3 августа 2021. Архивировано 3 августа 2021 года.
  13. ↑ Соболев, 1985, с. 293—296.
  14. ↑ 1 2 3 КО́НТУР СПЕКТРА́ЛЬНОЙ ЛИ́НИИ : [арх. 7 марта 2021] // Конго — Крещение. — М. : Большая российская энциклопедия, 2010. — С. 158. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 15). — ISBN 978-5-85270-346-0.
  15. ↑ Кононович, Мороз, 2004, с. 191—192.
  16. ↑ 1 2 3 4 Karttunen et al., 2007, pp. 99—100.
  17. ↑ Spectral Line Profile. Astronomy. Swinburne University of Technology. Дата обращения: 4 августа 2021. Архивировано 2 августа 2021 года.
  18. ↑ Соболев, 1985, с. 131.
  19. ↑ Tatum J. Stellar Atmospheres. 9.1: Introduction, Radiance, and Equivalent Width (англ.). Physics LibreTexts (25 января 2017). Дата обращения: 1 сентября 2021. Архивировано 1 сентября 2021 года.
  20. ↑ Equivalent Width. Astronomy. Swinburne University of Technology. Дата обращения: 2 августа 2021. Архивировано 26 февраля 2021 года.
  21. ↑ Соболев, 1985, с. 87—88.
  22. ↑ УШИРЕ́НИЕ СПЕКТРА́ЛЬНЫХ ЛИ́НИЙ : [арх. 1 марта 2021] / Анциферов П. С. // Уланд — Хватцев. — М. : Большая российская энциклопедия, 2017. — С. 158. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 33). — ISBN 978-5-85270-370-5.
  23. ↑ 1 2 Соболев, 1985, с. 88.
  24. ↑ 1 2 Karttunen et al., 2007, p. 99.
  25. ↑ Line broadening (англ.). Encyclopedia Britannica. Дата обращения: 4 августа 2021. Архивировано 4 августа 2021 года.
  26. ↑ Юков Е. А. Естественная ширина спектральной линии // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
  27. ↑ 1 2 Кононович, Мороз, 2004, с. 188—192.
  28. ↑ Tatum J. Stellar Atmospheres. 10.2: Thermal Broadening (англ.). Physics LibreTexts (25 января 2017). Дата обращения: 11 августа 2021. Архивировано 10 августа 2021 года.
  29. ↑ Соболев, 1985, с. 88—90.
  30. ↑ Соболев, 1985, с. 91—94.
  31. ↑ Corey G. C., McCourt F. R. Dicke narrowing and collisional broadening of spectral lines in dilute molecular gases (англ.) // The Journal of Chemical Physics. — Washington: AIP Publishing, 1984. — 1 September (vol. 81, iss. 5). — P. 2318–2329. — ISSN 0021-9606. — doi:10.1063/1.447930. Архивировано 16 августа 2021 года.
  32. ↑ Соболев, 1985, с. 91—98.
  33. ↑ Karttunen et al., 2007, pp. 100—101.
  34. ↑ Вайнштейн Л. А., Томозов Л. Н. Зеемана эффект. Астронет. Дата обращения: 5 августа 2021. Архивировано 2 августа 2021 года.
  35. ↑ Stark effect (англ.). Encyclopedia Britannica. Дата обращения: 7 августа 2021. Архивировано 25 марта 2018 года.
  36. ↑ Дмитриевский О. Д. Аппаратная функция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
  37. ↑ Karttunen et al., 2007, p. 96.
  38. ↑ Юков Е. А. Контур спектральной линии // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
  39. ↑ Соболев, 1985, с. 133—139.
  40. ↑ Черепащук А. М. Кривая роста. Астронет. Дата обращения: 4 августа 2021. Архивировано 2 августа 2021 года.
  41. ↑ Кононович, Мороз, 2004, с. 188—190.
  42. ↑ Karttunen et al., 2007, p. 413.
  43. ↑ 1 2 Karttunen et al., 2007, p. 207.
  44. ↑ 1 2 3 История астрономии. Институт истории естествознания и техники им. С.И. Вавилова. Дата обращения: 5 августа 2021. Архивировано 29 июня 2020 года.
  45. ↑ 1 2 3 A Timeline of Atomic Spectroscopy. Spectroscopy Online. Дата обращения: 5 августа 2021. Архивировано 23 января 2021 года.
  46. ↑ Karttunen et al., 2007, pp. 98—99.
  47. ↑ Spectroscopy and Quantium Mechanics. MIT Spectroscopy Lab. MIT Press. Дата обращения: 5 августа 2021. Архивировано 24 февраля 2020 года.
  48. ↑ The Era of Modern Spectroscopy. MIT Spectroscopy Lab. Дата обращения: 6 августа 2021. Архивировано 6 августа 2019 года.

Литература[править | править код]

  • Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
  • Соболев В. В. Курс теоретической астрофизики. — 3-е, переработанное. — М.: Наука, 1985. — 504 с.
  • Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 5th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2007. — 510 p. — ISBN 978-3-540-34143-7.
Источник

Самым простым из всех атомов является атом водорода, и он выступил в свое время в качестве своеобразного тест-объекта для теории Бора. К моменту появления теории атом водорода был тщательно исследован в ходе экспериментов: имелось знание о том, что он содержит единственный электрон. Ядром атома является протон.

Определение 1

Протон – это частица с положительным зарядом, модуль которого равен модулю заряда электрона, а масса больше массы электрона в 1836 раз.

Серия Бальмера и формула Ридберга

Начало XIX века ознаменовалось открытием линейчатого спектра.

Определение 2

Линейчатый спектр – это дискретные спектральные линии в видимой области излучения атома водорода.

В последующем закономерности, в соответствии с которыми ведут себя длины волн (или частоты) линейчатого спектра, подробно в количественном отношении исследовал И. Бальмер (в 1885 г.)

Определение 3

Серия Бальмера – совокупность спектральных линий атома водорода в видимой части спектра.

Позднее подобные серии спектральных линий обнаружились в ультрафиолетовой и инфракрасной частях спектра. В 1890 г. И. Ридберг составил запись эмпирической формулы для частот спектральных линий (формула Ридберга): 

νnm=R1m2-1n2.

Для серии Бальмера m = 2, n = 3, 4, 5, …. Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, … .

Определение 4

Неизменяемая R в формуле для частот спектральных линий носит название постоянной Ридберга и равна: R=3,29·1015 Гц.

До того, как Бор сформулировал постулаты, вопросы, каким же образом возникают линейчатые спектры и каков смысл целых чисел, входящих в формулы спектральных линий водорода (и некоторых других атомов), оставались без ответа.

Правило квантования

Постулаты Бора задали направление для развития новой науки – квантовой физики атома. Однако в них не было «рецепта», как определить параметры стационарных состояний (орбит) и соответствующих им значений энергии En.

Бором было сформулировано правило квантования, которое приводило к соотносимым с опытом значениям энергий стационарных состояний атома водорода. Ученый выдвинул гипотезу, что момент импульса электрона, совершающего вращение вокруг ядра, может принимать лишь дискретные значения, кратные постоянной Планка.

Определение 5

Для круговых орбит правило квантования Бора имеет запись:

meνrn=nh2π (n=1, 2, 3,…).

В данном выражении me является массой электрона, υ – его скоростью, rn обозначает радиус стационарной круговой орбиты.

Правило квантования Бора дает возможность путем вычисления определить радиусы стационарных орбит электрона в атоме водорода и отыскать значения энергий. Скорость электрона, который совершает вращение по круговой орбите некоторого радиуса r в кулоновском поле ядра, записывается в виде соотношения (в соответствии с 2 законом Ньютона):

ν2=e24πε0mer.

Самой близкой к ядру орбите соответствует значение n=1.

Определение 6

Боровский радиус – это радиус первой орбиты, расположенной ближе всех к ядру электрона атома водорода, определяемый как:

r1=α0=ε0h2πmee2=5,29·10-11 м.

Радиусы последующих орбит получают возрастание пропорционально n2.

Полная механическая энергия E системы из атомного ядра и электрона, вращающегося по стационарной круговой орбите радиусом rn, имеет запись:

En=Ek+Ep=meν22-e24πε0rn.

Заметим, что Ep<0, поскольку имеет место действие сил притяжения между электроном и ядром. Подставим в это выражение записи для υ2 и rn и получаем:

En=-mee48e02h2·1n2.

Определение 7

В квантовой физике атома целое число n=1, 2, 3, … носит название главного квантового числа.

В соответствии со вторым постулатом Бора: когда электрон переходит с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em<En, атом испускает квант света с частотой νnm, равной ΔEnmh:

νnm=∆Enmh=mee48ε02h31m2-1n2.

Это выражение полностью идентично с эмпирической формулой Ридберга для спектральных серий атома водорода, если за постоянную R взять:

R=mee48ε02h3.

Подставим в это выражение числовые значения всех переменных, получим

R=3,29·1015 Гц.

Полученное значение отлично коррелируется с эмпирическим значением R.

На рисунке 6.3.1 проиллюстрировано образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

Правило квантования

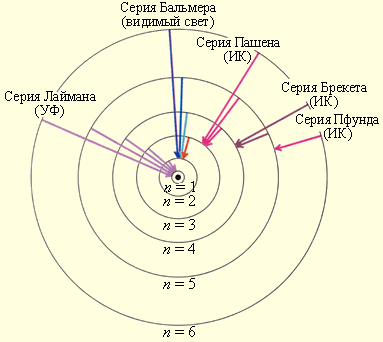
Рисунок 6.3.1. Стационарные орбиты атома водорода и образование спектральных серий.

Рисунок 6.3.2 демонстрирует диаграмму энергетических уровней атома водорода с указанием переходов для различных спектральных серий.

Правило квантования

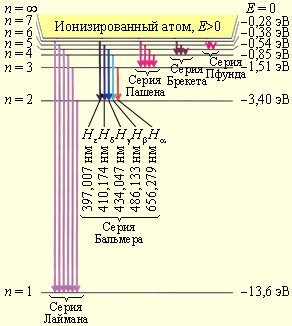
Рисунок 6.3.2. Диаграмма энергетических уровней атома водорода с указанием переходов для различных спектральных серий. Также имеется указание длин волн для первых пяти линий серии Бальмера.

Тот факт, что теория Бора для атома водорода и результаты эксперимента оказались так отлично согласованы между собой, стал весомым аргументом в пользу верности этой теории. Но при этом попытка использовать теорию применительно к более сложным атомам закончилась провалом. Бору не удалось дать физическую интерпретацию правилу квантования – это позже, спустя десятилетие, сделал де Бройль, опираясь на представления о волновых свойствах частиц. Его предположение заключалось в том, что каждая орбита в атоме водорода соответствует волне, получающей распространение по окружности около ядра атома. Стационарная орбита имеет место тогда, когда волна постоянно повторяет себя после каждого оборота вокруг ядра. Иначе говоря, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Такое явление подобно стационарной картине стоячих волн в струне с закрепленными концами.

Правило квантования

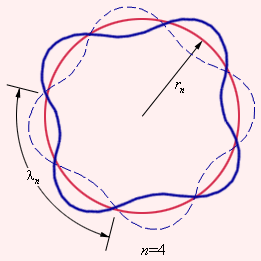
Рисунок 6.3.3. Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n=4.

Согласно дебройлевским идеям, в стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться целое число длин волн λ:

nλn=2πrn

Если подставить сюда формулу длины волны де Бройля λ=hp, где p=meυ – импульс электрона, то:

nhneν=2πrn или meνrn=nh2π.

Итак, правило квантования Бора находится во взаимосвязи с волновыми свойствами электронов.

Вообще можно сказать, что Бор достиг поразительных успехов в попытках объяснить спектральные закономерности. Появилось утверждение, что атомы являются квантовыми системами, а энергетические уровни стационарных состояний атомов дискретны. Практически одномоментно с возникновением боровской теории экспериментально было доказано, что существуют стационарные состояния атома и квантование энергии. Дискретность энергетических состояний атома опытным путем продемонстрировали в 1913 г. Д. Франк и Г. Герц, исследуя столкновение электронов с атомами ртути. Выяснилось, что при энергии электронов менее 4,9 эВ их столкновение с атомами ртути протекает согласно закону абсолютно упругого удара. А, когда энергия электронов равна 4,9 эВ, столкновение с атомами ртути будет иметь черты неупругого удара. Таким образом, выходит, что, столкнувшись с неподвижными атомами ртути, электроны лишаются всей своей кинетической энергии, что, в свою очередь, означает факт поглощения атомами ртути энергии электрона и перевода электронов из основного состояния в первое возбужденное состояние:

E2-E1=4,9 эВ.

В соответствии с концепцией Бора, когда будет происходить обратный самопроизвольный переход атома, ртуть будет испускать кванты с частотой

ν=E2-E1h=1,2·1015 Гц.

Линия спектра с подобной частотой в самом деле нашлась в ультрафиолетовой части спектра излучения атомов ртути.

Утверждения о дискретных состояниях находились в противоречии с классической физикой, в связи с чем также возник закономерный вопрос: не опровергает ли квантовая теория законы классической физической теории.

Квантовая физика отнюдь не стремилась отменить фундаментальные основы, такие как законы сохранения энергии, импульса, электрического разряда и подобное. По сформулированному Бором принципу соответствия квантовая физика вмещает в себя классические представления, и при некоторых условиях можно заметить планомерный переход от квантовых представлений к классическим. Энергетический спектр атома водорода как раз дает нам такой пример (рис. 6.3.2): при больших квантовых числах n≫1 дискретные уровни постепенно становятся ближе, что задает плавный переход в область непрерывного спектра, вытекающего из классической физики.

Постулаты Бора со своей «половинчатостью», «полуклассикой» стали важной ступенью развития квантовых основ, введение которых в физику потребовало серьезной перестройки механики и электродинамики, произошедшей в 20-е – 30-е годы XX века.

Квантовые числа

Видение Бора о том, что существуют определенные орбиты для движения электронов в атоме, оказалось очень условным. В действительности, траектория движения электрона в атоме почти не имеет общего с движением планет или спутников. Физический смысл есть лишь в возможности обнаружить электрон в том или ином месте, и эта вероятность описывается квадратом модуля волновой функции |Ψ|2. Волновая функция Ψ служит решением базового уравнения квантовой механики – уравнения Шредингера. Выяснилось, что состояние электрона в атоме описывается целым набором квантовых чисел.

Определение 8

Основное квантовое число n – квантовое число, задающее квантование энергии атома.

Орбитальное квантовое число l – число, применяемое для квантования момента импульса.

Магнитное квантовое число m – число, применяемое для квантования проекции момента импульса.

Квантовое число m введено в связи с тем, что проекция момента импульса на любое выделенное в пространстве направление (к примеру, направление вектора B→ магнитного поля) также принимает дискретный ряд значений.

Все виды квантовых чисел (n, l, m) находятся во взаимосвязи с правилами квантования. К примеру, орбитальное квантовое число l может принимать значения целого числа от 0 до (n – 1). Магнитное квантовое число m может принимать любые значения целого числа в интервале ±l. Тогда каждому значению главного квантового числа n, описывающему состояние энергии атома, соответствует целый ряд комбинаций квантовых чисел l и m. Одновременно с этим, с каждой такой комбинацией соотносится определенное распределение вероятности |Ψ|2 обнаружения электрона в разных точках пространства («электронное облако»).

Определение 9

s-состояния (1s, 2s, …, ns, …) – это состояния, при которых орбитальное квантовое число l равно нулю.

Описываются s-состояния сферически симметричными распределениями вероятности.

Когда l>0 сферическая симметрия электронного облака нарушается.

Определение 10

p-состояния – это состояния при l=1.

d-состояния – это состояния при l=2 и т.д.

Рис. 6.3.4 иллюстрирует кривые распределения вероятности ρ (r)=4πr2|Ψ|2 обнаружения электрона в атоме водорода на разных расстояниях от ядра в состояниях 1s и 2s.

Квантовые числа

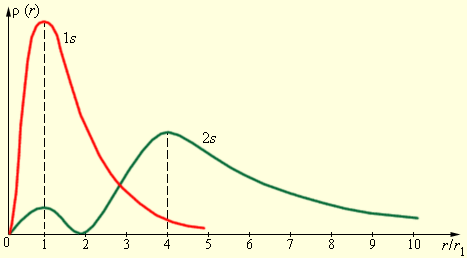
Рисунок 6.3.4. Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r1=5,29·10–11 м – радиус первой орбиты Бора.

На рисунке 6.3.4 наглядно продемонстрировано, что электрон в состоянии 1s (основное состояние атома водорода) имеет возможность быть обнаруженным на различных расстояниях от ядра. С самой высокой вероятностью электрон обнаружится на расстоянии, равном радиусу r1 первой боровской орбиты. Вероятность нахождения электрона в состоянии 2s достигает максимума на расстоянии r=4r1 от ядра. И в том, и в том случае атом водорода возможно представить, как сферически симметричное электронное облако, в центре которого расположено ядро.

Квантовые числа

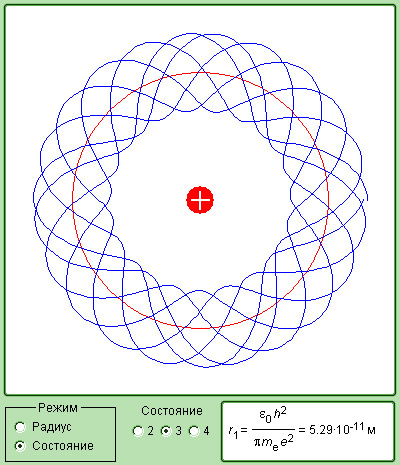
Рисунок 6.3.5. Модель квантования электронных орбит.

Квантовые числа

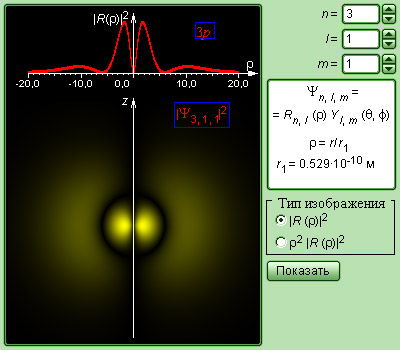
Рисунок 6.3.6. Модель атома водорода.

Квантовые числа

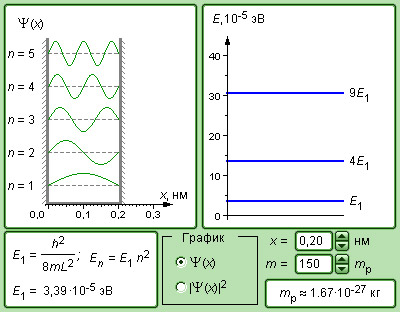
Рисунок 6.3.7. Модель частицы в потенциальной яме.

Источник

Добавить комментарий