Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.
Разница между формулами S и σ (“n” и “n–1”)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с “n–1”),
- полностью все данные – используется формула σ (с “n”).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 – μ = 15 – 20 = -5
x2 – μ = 26 – 20 = 6
x3 – μ = 15 – 20 = -5
x4 – μ = 24 – 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 – μ)² = (-5)² = 25
(x2 – μ)² = 6² = 36
(x3 – μ)² = (-5)² = 25
(x4 – μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi – μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле “=СТАНДОТКЛОНА(“
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
-
1
Look at your data set. This is a crucial step in any type of statistical calculation, even if it is a simple figure like the mean or median.[2]
- Know how many numbers are in your sample.
- Do the numbers vary across a large range? Or are the differences between the numbers small, such as just a few decimal places?
- Know what type of data you are looking at. What do your numbers in your sample represent? this could be something like test scores, heart rate readings, height, weight etc.
- For example, a set of test scores is 10, 8, 10, 8, 8, and 4.
-
2
Gather all of your data. You will need every number in your sample to calculate the mean.[3]
- The mean is the average of all your data points.
- This is calculated by adding all of the numbers in your sample, then dividing this figure by the how many numbers there are in your sample (n).
- In the sample of test scores (10, 8, 10, 8, 8, 4) there are 6 numbers in the sample. Therefore n = 6.
Advertisement
-
3
Add the numbers in your sample together. This is the first part of calculating a mathematical average or mean.[4]
- For example, use the data set of quiz scores: 10, 8, 10, 8, 8, and 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. This is the sum of all the numbers in the data set or sample.
- Add the numbers a second time to check your answer.
-
4
Divide the sum by how many numbers there are in your sample (n). This will provide the average or mean of the data.[5]
- In the sample of test scores (10, 8, 10, 8, 8, and 4) there are six numbers, so n = 6.
- The sum of the test scores in the example was 48. So you would divide 48 by n to figure out the mean.
- 48 / 6 = 8
- The mean test score in the sample is 8.
Advertisement
-
1
Find the variance. The variance is a figure that represents how far the data in your sample is clustered around the mean.[6]
- This figure will give you an idea of how far your data is spread out.
- Samples with low variance have data that is clustered closely about the mean.
- Samples with high variance have data that is clustered far from the mean.
- Variance is often used to compare the distribution of two data sets.
-
2
Subtract the mean from each of your numbers in your sample. This will give you a figure of how much each data point differs from the mean.[7]
- For example, in our sample of test scores (10, 8, 10, 8, 8, and 4) the mean or mathematical average was 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 8 = 2, 8 – 8 = 0, 8 – 8 = 0, and 4 – 8 = -4.
- Do this procedure again to check each answer. It is very important you have each of these figures correct as you will need them for the next step.
-
3
Square all of the numbers from each of the subtractions you just did. You will need each of these figures to find out the variance in your sample.[8]
- Remember, in our sample we subtracted the mean (8) from each of the numbers in the sample (10, 8, 10, 8, 8, and 4) and came up with the following: 2, 0, 2, 0, 0 and -4.
- To do the next calculation in figuring out variance you would perform the following: 22, 02, 22, 02, 02, and (-4)2 = 4, 0, 4, 0, 0, and 16.
- Check your answers before proceeding to the next step.
-
4
Add the squared numbers together. This figure is called the sum of squares.[9]
- In our example of test scores, the squares were as follows: 4, 0, 4, 0, 0, and 16.
- Remember, in the example of test scores we started by subtracting the mean from each of the scores and squaring these figures: (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- The sum of squares is 24.
-
5
Divide the sum of squares by (n-1). Remember, n is how many numbers are in your sample. Doing this step will provide the variance. The reason to use n-1 is to have sample variance and population variance unbiased. [10]
- In our sample of test scores (10, 8, 10, 8, 8, and 4) there are 6 numbers. Therefore, n = 6.
- n-1 = 5.
- Remember the sum of squares for this sample was 24.
- 24 / 5 = 4.8
- The variance in this sample is thus 4.8.
Advertisement
-
1
Find your variance figure. You will need this to find the standard deviation for your sample.[11]
- Remember, variance is how spread out your data is from the mean or mathematical average.
- Standard deviation is a similar figure, which represents how spread out your data is in your sample.
- In our example sample of test scores, the variance was 4.8.
-
2
Take the square root of the variance. This figure is the standard deviation.[12]
- Usually, at least 68% of all the samples will fall inside one standard deviation from the mean.
- Remember in our sample of test scores, the variance was 4.8.
- √4.8 = 2.19. The standard deviation in our sample of test scores is therefore 2.19.
- 5 out of 6 (83%) of our sample of test scores (10, 8, 10, 8, 8, and 4) is within one standard deviation (2.19) from the mean (8).
-
3
Go through finding the mean, variance and standard deviation again. This will allow you to check your answer.[13]
- It is important that you write down all steps to your problem when you are doing calculations by hand or with a calculator.
- If you come up with a different figure the second time around, check your work.
- If you cannot find where you made a mistake, start over a third time to compare your work.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
What is the standard deviation of 10 samples with a mean of 29.05?
Depends on the 10 samples of data. If all ten numbers were 29.05 then the standard deviation would be zero. Standard deviation is a measure of how much the data deviates from the mean.
-
Question
How do I calculate the standard deviation of 5 samples with the mean of 26?
You take the average of 26 and 5, divide by b squared and multiply by deviation equation constant.
-
Question
How do I find the standard deviation of 10 samples with a mean of 29.05?
Take each sample and subract the mean. Next, square each result, getting rid of the negative. Add the 10 results and divide the sun by 10 – 1 or 9. That is the standard deviation.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate standard deviation, start by calculating the mean, or average, of your data set. Then, subtract the mean from all of the numbers in your data set, and square each of the differences. Next, add all the squared numbers together, and divide the sum by n minus 1, where n equals how many numbers are in your data set. Finally, take the square root of that number to find the standard deviation. To learn how to find standard deviation with the help of example problems, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,558,048 times.
Reader Success Stories
-
“This article was the best statistics instructor I have ever been taught by. I have learned more from this little…” more
Did this article help you?
стандартное отклонение калькулятор
Среднеквадратическое отклонение (СО) - это показатель рассеяния значений во множестве данных относительно их математического ожидания. Обозначается также как СО. Символом среднеквадратического отклонения является σ(сигма). Можно также сказать, что это показатель изменчивости или дисперсии в этом множестве данных. Находите математическое ожидание, дисперсию, среднеквадратическое отклонение данных чисел с помощью этих бесплатных арифметических онлайн-калькуляторов среднеквадратического отклонения.
Среднеквадратическое отклонение калькулятор
Для Рассчитать среднее значение, дисперсия, стандартное отклонение :
Введите все цифры, разделенные запятыми ‘,’.
E.g: 13,23,12,44,55
дисперсия(стандартное отклонение)
население стандартное отклонение
дисперсия(население стандартное отклонение)
Среднеквадратическое отклонение (СО) - это показатель рассеяния значений во множестве данных относительно их математического ожидания. Обозначается также как СО. Символом среднеквадратического отклонения является σ(сигма). Можно также сказать, что это показатель изменчивости или дисперсии в этом множестве данных. Находите математическое ожидание, дисперсию, среднеквадратическое отклонение данных чисел с помощью этих бесплатных арифметических онлайн-калькуляторов среднеквадратического отклонения.
формула :
означать :
Средняя = сумма значений X / N (количество значений)
дисперсия :
дисперсия = s2
Среднеквадратическое отклонение :
население Среднеквадратическое отклонение :
пример:
Рассмотрим множество X цифр 5,10,15,20,25
шаг 1 :
Средняя = сумма значений X / N (количество значений)
= (5+10+15+20+25) / 5
= 75 / 5
= 15
шаг 2 :
Чтобы найти дисперсию,
Вычесть среднее из каждого из значений,
5-15 = -10
10-15 = -5
15-15 = 0
20-15 = 5
25-15 = 10
Теперь квадрат все ответы вы получили от вычитания.
(-10)2 = 100
(-5)2 = 25
(0)2 = 0
(5)2 = 25
(10)2 = 100
Добавить все квадраты чисел,
100 + 25 + 0 + 25 + 100 = 250
Разделите сумму квадратов (n-1)
250 / (5-1) = 250 / 4 = 62.5
Отсюда Разница = 62.5
шаг 3 :
Чтобы найти стандартное отклонение, найти квадратный корень из дисперсии,
√62.5 = 7.905
Следовательно Стандартное отклонение является 7.905
Чтобы найти минимальное и максимальное стандартное отклонение,
Минимальная CO = среднее – CO
= 15 – 7.905
= 7.094
Максимальная CO = среднее + CO
=15 + 7.905
= 22.906
шаг 4 :
Чтобы найти стандартный население отклонение,
Разделите сумму квадратов найденных на шаге 2 по n
250 / 5 = 50
Найти квадратный корень 50, √50 = 7.07
Этот инструмент поможет вам динамически вычислять статистические проблемы. Расчет среднее значение, дисперсия, стандартное отклонение легче.
Определение 2.13
Стандартным отклонением выборки x1, x2, …, xn называется число S, которое вычисляется по формуле:
.
Таким образом, выборочное стандартное отклонение
равно квадратному корню из выборочной дисперсии, следовательно, справедливы
формулы:
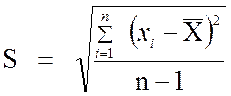либо 
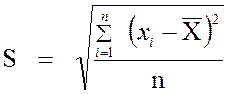
Пример 2.21 В течение пяти
дней студент Ковалев записывал стоимость обедов в студенческой столовой: 3,2;
4,8; 5,6; 4,5; 5,4. Найдем выборочную дисперсию и стандартное отклонение.
Сначала определим среднее:
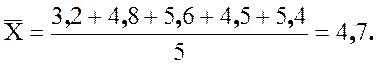
Вычислим дисперсию:
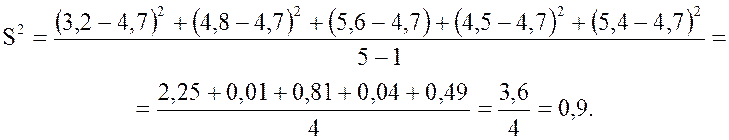
Найдем стандартное отклонение:
Округлим полученное значение: S =
0,95 условных рублей.
■
Определение 2.14 Выборочной
дисперсией вариационного ряда x1, x2, …, xn с
соответствующими частотами 
называется число 
, определяемое формулой:
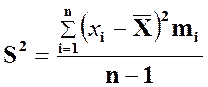или 
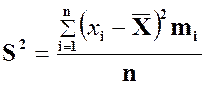
соответственно, при малом и большом значении n,где 
.
Пример
2.22 Для социологического
исследования были собраны данные о количественном составе 20 семей, приведенные
в следующей таблице.
Таблица 2.16 – Количественный
состав семей
|
Количество членов семьи |
1 2 3 |
|
|
2 3 8 |
Найдем среднее, дисперсию и стандартное отклонение:
n = 2 + 3 + 8 + 5 + 1 + 1 = 20;
.
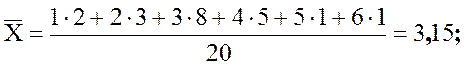
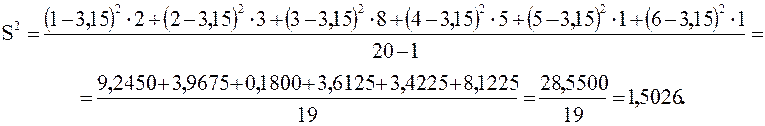
Округлим S2 = 1,50 и S = 1,23. Итак, 
– это среднее число членов семьи, S = 1,23 – это стандартное
отклонение от среднего.
■
Определение 2.15 Выборочной
дисперсией статистического ряда, состоящего из k
интервалов с соответствующими интервальными средними 
и
интервальными частотами , называется число 
, равное:
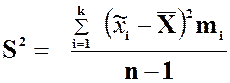или 
,
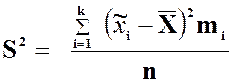соответственно, при малом и большом значении n,
где 
.
Пример
2.23 Результаты экзамена по высшей
математике пятидесяти студентов представлены следующим статистическим рядом.
Используется десятибалльная система оценок. Найдем среднее и стандартное
отклонение.
Таблица 2.17 – Итоги экзамена по высшей математике
|
Оценка |
0–2 |
2–4 |
4–6 |
6–8 |
8–1 |
|
|
3 |
9 |
16 |
14 |
8 |
Итак, 
Найдем интервальные средние:
Вычислим среднее:
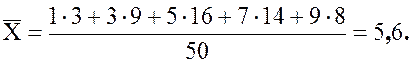
Найдем
дисперсию данной выборки:
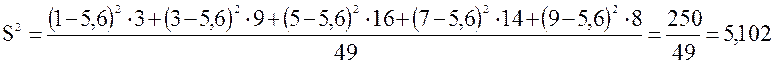Определим значение
стандартного отклонения:
.
Итак, средняя оценка студентов I
курса составляет 5,6 баллов. Стандартное отклонение 
баллов
показывает, что оценки большинства студентов отличаются от среднего не более,
чем на 2,26 баллов.
■
Таким образом, для вычисления
выборочной дисперсии необходимо найти значение среднего 
, вычислить
сумму квадратов отклонений выборочный значений от среднего и разделить ее на n –
1, где n – число всех наблюдений. Извлечение квадратного корня
при нахождении стандартного отклонения возвращает к первоначальному масштабу
единицы измерения.
Обработка и анализ статических
данных требует кропотливой и нелегкой вычислительной работы. Для организации
вычислений в математической статистике часто используются специальные таблицы.
Пример 2.24 Найдем среднее и стандартное
отклонение для статистического ряда из примера 1.4 о высоте городских зданий.
Все необходимые вычисления будем записывать в таблицу 2.18.
Из таблицы 2.18
берем необходимые промежуточные результаты:
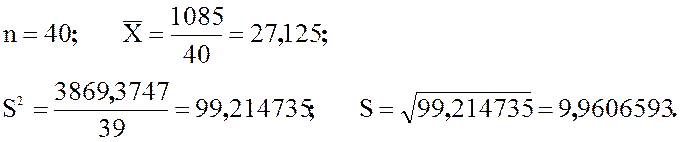
Итак, среднее высоты зданий равно 27,12
метров, а стандартное отклонение 
равно 9,96 метров.
Таблица 2.18 – Вычисление среднего и
стандартного отклонения высоты зданий
|
Высота |
Интервальное среднее |
Частота
|
|
|
|
|
|
5–10 10–15 15–20 20–25 25–30 30–35 35–40 40–45 35–50 |
7,5 12,5 17,5 22,5 27,5 32,5 37,5 42,5 47,5 |
2 3 5 6 8 7 5 3 1 |
15 37,5 87,5 135 220 227,5 187,5 127,5 47,5 |
-19,625 -14,625 -9,625 -4,625 0,375 5,375 10,375 15,375 20,375 |
385,14062 213,89062 92,64065 21,390625 0,140625 28,890625 107,64062 236,39062 415,14062 |
770,28124 641,67186 463,20312 128,34375 1,12500 202,23437 538,20310 709,17186 415,14062 |
|
Сумма |
40 |
1085 |
3869,3447 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Загрузить PDF
Загрузить PDF
Z-оценка (Z-тест) рассматривает определенную выборку данного набора данных и позволяет определить количество стандартных отклонений от среднего значения.[1]
Чтобы найти Z-оценку выборки, нужно вычислить среднее значение, дисперсию и стандартное отклонение выборки. Чтобы вычислить Z-оценку, необходимо вычесть среднее значение из чисел выборки, а затем полученный результат разделить на стандартное отклонение. Хотя вычислений довольно много, они не очень сложные.
-
1
Обратите внимание на набор данных. Чтобы вычислить среднее значение выборки, нужно знать значения некоторых величин.[2]
- Выясните, сколько чисел содержится в выборке. Например, рассмотрим пример пальмовой рощи, а выборка будет состоять из пяти чисел.
- Выясните, какую величину характеризуют эти числа. В нашем примере каждое число описывает высоту одной пальмы.
- Обратите внимание на разброс чисел (дисперсию). То есть выясните, различаются ли числа в большом диапазоне или они довольно близки.
- Выясните, сколько чисел содержится в выборке. Например, рассмотрим пример пальмовой рощи, а выборка будет состоять из пяти чисел.
-
2
Соберите данные. Чтобы выполнить вычисления, понадобятся все числа выборки.[3]
- Среднее значение – это среднее арифметическое всех чисел выборки.
- Чтобы вычислить среднее значение, сложите все числа выборки, а затем полученный результат разделите на количество чисел.
- Допустим, что n – это количество чисел выборки. В нашем примере n = 5, потому что выборка состоит из пяти чисел.
-
3
Сложите все числа выборки. Это первый шаг в процессе вычисления среднего значения.[4]
- Допустим, что в нашем примере выборка включает следующие числа: 7; 8; 8; 7,5; 9.
- 7 + 8 + 8 + 7,5 + 9 = 39,5. Это сумма всех чисел выборки.
- Проверьте ответ, чтобы убедиться, что суммирование выполнено верно.
-
4
Разделите найденную сумму на количество чисел выборки (n). Так вы вычислите среднее значение.[5]
- В нашем примере выборка включает пять чисел, которые характеризуют высоту деревьев: 7; 8; 8; 7,5; 9. Таким образом, n = 5.
- В нашем примере сумма всех чисел выборки равна 39,5. Разделите это число на 5, чтобы вычислить среднее значение.
- 39,5/5 = 7,9.
- Средняя высота пальмы равна 7,9 м. Как правило, среднее значение выборки обозначается как μ, поэтому μ = 7,9.
Реклама
-
1
Найдите дисперсию. Дисперсия – это величина, которая характеризует меру разброса чисел выборки относительно среднего значения.[6]
- С помощью дисперсии можно выяснить, как сильно разбросаны числа выборки.
- Выборка с низкой дисперсией включает числа, которые разбросаны близко относительно среднего значения.
- Выборка с высокой дисперсией включает числа, которые разбросаны далеко относительно среднего значения.
- Зачастую с помощью дисперсии сравнивают разброс чисел двух разных наборов данных или выборок.
-
2
Вычтите среднее значение из каждого числа выборки. Так вы определите, насколько каждое число выборки отличается от среднего значения.[7]
- В нашем примере с высотами пальм (7, 8, 8, 7,5, 9 м) среднее значение равно 7,9.
- 7 – 7,9 = -0,9, 8 – 7,9 = 0,1, 8 – 7,9 = 0,1, 7,5 – 7,9 = -0,4, 9 – 7,9 = 1,1.
- Выполните эти вычисления еще раз, чтобы убедиться, что они верны. На этом этапе важно не ошибиться в вычислениях.
-
3
Каждый полученный результат возведите в квадрат. Это необходимо для того, чтобы вычислить дисперсию выборки.[8]
- Напомним, что в нашем примере среднее значение (7,9) было вычтено из каждого числа выборки (7, 8, 8, 7,5, 9) и были получены следующие результаты: -0,9, 0,1, 0,1, -0,4, 1,1.
- Возведите в квадрат эти числа: (-0,9)^2 = 0,81, (0,1)^2 = 0,01, (0,1)^2 = 0,01, (-0,4)^2 = 0,16, (1,1)^2 = 1,21.
- Найденные квадраты: 0,81, 0,01, 0,01, 0,16, 1,21.
- Проверьте вычисления, прежде чем перейти к следующему шагу.
-
4
Сложите найденные квадраты. То есть вычислите сумму квадратов.[9]
- В нашем примере с высотами пальм были получены следующие квадраты: 0,81, 0,01, 0,01, 0,16, 1,21.
- 0,01 + 0,81 + 0,01 + 0,16 + 1,21 = 2,2
- В нашем примере сумма квадратов равна 2,2.
- Сложите квадраты еще раз, чтобы проверить, что вычисления верны.
-
5
Разделите сумму квадратов на (n-1). Напомним, что n – это количество чисел выборки. Так вы вычислите дисперсию.[10]
- В нашем примере с высотами пальм (7, 8, 8, 7,5, 9 м) сумма квадратов равна 2,2.
- Выборка включает 5 чисел, поэтому n = 5.
- n – 1 = 4
- Напомним, что сумма квадратов равна 2,2. Чтобы найти дисперсию, вычислите: 2,2/4.
- 2,2/4 = 0,55
- Дисперсия нашей выборки с высотами пальм равна 0,55.
Реклама
-
1
Определите дисперсию выборки. Она необходима для вычисления стандартного отклонения выборки.[11]
- Дисперсия характеризует меру разброса чисел выборки относительно среднего значения.
- Стандартное отклонение – это величина, которая определяет разброс чисел выборки.
- В нашем примере с высотами пальм дисперсия равна 0,55.
-
2
Извлеките квадратный корень из дисперсии. Так вы найдете стандартное отклонение.[12]
- В нашей выборке с высотами пальм дисперсия равна 0,55.
- √0,55 = 0,741619848709566. На данном этапе вы получите десятичную дробь с большим количеством знаков после запятой. В большинстве случаев значение стандартного отклонения можно округлить до сотых или тысячных. В нашем примере округлим полученный результат до сотых: 0,74.
- Таким образом, стандартное отклонение нашей выборки приблизительно равно 0,74.
-
3
Еще раз проверьте правильность вычислений среднего значения, дисперсии и стандартного отклонения. Так вы убедитесь, что получили точное значение стандартного отклонения.
- Запишите действия, которые вы выполнили, чтобы вычислить упомянутые величины.
- Так вы сможете найти шаг, на котором допустили ошибку (если она есть).
- Если в процессе проверки вы получили другие значения среднего значения, дисперсии и стандартного отклонения, повторите вычисления.
Реклама
-
1
Z-оценка вычисляется по следующей формуле: z = X – μ / σ. По этой формуле можно найти Z-оценку для любого числа выборки.[13]
- Напомним, что Z-оценка позволяет определить количество стандартных отклонений от среднего значения для рассматриваемого числа выборки.
- В приведенной формуле X – это определенное число выборки. Например, чтобы выяснить, на сколько стандартных отклонений число 7,5 удалено от среднего значения, в формулу вместо Х подставьте 7,5.
- В формуле μ – это среднее значение. В нашей выборке с высотами пальм среднее значение равно 7,9.
- В формуле σ – это стандартное отклонение. В нашей выборке с высотами пальм стандартное отклонение равно 0,74.
-
2
Вычтите среднее значение из рассматриваемого числа выборки. Это первый этап процесса вычисления Z-оценки.[14]
- Например, выясним, на сколько стандартных отклонений число 7,5 (нашей выборки с высотами пальм) удалено от среднего значения.
- Сначала вычтите: 7,5 – 7,9.
- 7,5 – 7,9 = -0,4.
- Дважды проверьте, что вы правильно вычислили среднее значение и разность.
-
3
Полученный результат (разность) разделите на стандартное отклонение. Так вы найдете Z-оценку.[15]
- В нашей выборке с высотами пальм вычислим Z-оценку числа 7,5.
- Вычтя среднее значение из 7,5, вы получили -0,4.
- Напомним, что стандартное отклонение нашей выборки с высотами пальм равно 0,74.
- -0,4 / 0,74 = -0,54
- Таким образом, в данном случае Z-оценка равна -0,54.
- Такая Z-оценка означает, что число 7,5 удалено на -0,54 стандартных отклонений от среднего значения выборки с высотами пальм.
- Z-оценка может быть как положительной, так и отрицательной.
- Отрицательная Z-оценка указывает на то, что выбранное число выборки меньше среднего значения, а положительная Z-оценка – на то, что число больше среднего значения.
Реклама
Об этой статье
Эту страницу просматривали 53 050 раз.
