Syntax
Description
example
sz = size(A)
returns a row vector whose elements are the lengths of the corresponding dimensions
of A. For example, if A is a 3-by-4 matrix,
then size(A) returns the vector [3 4].
If A is a table or timetable, then size(A)
returns a two-element row vector consisting of the number of rows and the number of
table variables.
example
szdim = size(A,dim)
returns the length of dimension dim when dim
is a positive integer scalar. You can also specify dim as a
vector of positive integers to query multiple dimension lengths at a time. For
example, size(A,[2 3]) returns the lengths of the second and
third dimensions of A in the 1-by-2 row vector
szdim.
example
szdim = size(A,dim1,dim2,…,dimN)
returns the lengths of dimensions dim1,dim2,…,dimN in the row
vector szdim.
example
[sz1,...,szN] = size(___)
returns the lengths of the queried dimensions of A
separately.
Examples
collapse all
Size of 4-D Array
Create a random 4-D array and return its size.
A = rand(2,3,4,5); sz = size(A)
Query the length of the second dimension of A.
Query the length of the last dimension of A.
szdimlast = size(A,ndims(A))
You can query multiple dimension lengths at a time by specifying a vector dimension argument. For example, find the lengths of the first and third dimensions of A.
Find the lengths of the second through fourth dimensions of A.
Alternatively, you can list the queried dimensions as separate input arguments.
Size of Table
Create a table with 5 rows and 4 variables.
LastName = {'Smith';'Johnson';'Williams';'Jones';'Brown'};
Age = [38;43;38;40;49];
Height = [71;69;64;67;64];
Weight = [176;163;131;133;119];
BloodPressure = [124 93; 109 77; 125 83; 117 75; 122 80];
A = table(Age,Height,Weight,BloodPressure,'RowNames',LastName)
A=5×4 table
Age Height Weight BloodPressure
___ ______ ______ _____________
Smith 38 71 176 124 93
Johnson 43 69 163 109 77
Williams 38 64 131 125 83
Jones 40 67 133 117 75
Brown 49 64 119 122 80
Find the size of the table. Although the BloodPressure variable contains two columns, size only counts the number of variables.
Dimension Lengths as Separate Arguments
Create a random matrix and return the number of rows and columns separately.
A = rand(4,3); [numRows,numCols] = size(A)
Input Arguments
collapse all
A — Input array
scalar | vector | matrix | multidimensional array
Input array, specified as a scalar, a vector, a matrix, or a
multidimensional array.
Data Types:
single | double |
int8 | int16 |
int32 | int64 |
uint8 | uint16 |
uint32 | uint64 |
logical | char |
string | struct |
function_handle | cell |
categorical | datetime |
duration | calendarDuration |
table | timetable
Complex Number Support: Yes
dim — Queried dimensions
positive integer scalar | vector of positive integer scalars | empty array
Queried dimensions, specified as a positive integer scalar, a vector of
positive integer scalars, or an empty array of size 0-by-0, 0-by-1, or
1-by-0. If an element of dim is larger than
ndims(A), then size returns
1 in the corresponding element of the output. If
dim is an empty array, then size
returns a 1-by-0 empty array.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
dim1,dim2,…,dimN — List of queried dimensions
positive integer scalars
List of queried dimensions, specified as positive integer scalars
separated by commas. If an element of the list is larger than
ndims(A), then size returns
1 in the corresponding element of the output.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output Arguments
collapse all
sz — Array size
row vector of nonnegative integers
Array size, returned as a row vector of nonnegative integers.
-
Each element of
szrepresents the length of
the corresponding dimension ofA. If any
element ofszis equal to
0, thenAis an empty
array. -
If
Ais a scalar, then
szis the row vector[1.
1] -
If
Ais a table or timetable, then
szis a two-element row vector containing
the number of rows and the number of variables. Multiple columns
within a single variable are not counted. -
If
Ais a character vector of type
char, thensize
returns the row vector[1 M]where
Mis the number of characters. However,
ifAis a string scalar,
sizereturns[1 1]
because it is a single element of a string array. For example,
compare the output ofsizefor a character
vector and
string:To
find the number of characters in a string, use thestrlength
function.
Data Types: double
szdim — Dimension lengths
nonnegative integer scalar | vector of nonnegative integer scalars | 1-by-0 empty array
Dimension lengths, returned as a nonnegative integer scalar when
dim is a positive integer scalar, a row vector of
nonnegative integer scalars when dim is a vector of
positive integers, or a 1-by-0 empty array when dim is an
empty array. If an element of the specified dimension argument is larger
than ndims(A), then size returns
1 in the corresponding element of
szdim.
Data Types: double
sz1,...,szN — Dimension lengths listed separately
nonnegative integer scalars
Dimension lengths listed separately, returned as nonnegative integer
scalars separated by commas.
-
When
dimis not specified and fewer than
ndims(A)output arguments are listed,
then all remaining dimension lengths are collapsed into the last
argument in the list. For example, ifAis a
3-D array with size[3 4 5], then
[sz1,sz2] = size(A)returnssz1and
= 3sz2 = 20. -
When
dimis specified, the number of output
arguments must equal the number of queried dimensions. -
If you specify more than
ndims(A)output
arguments, then the extra trailing arguments are returned as
1.
Data Types: double
Tips
-
To determine if an array is empty, a scalar, or a matrix, use the functions
isempty,isscalar, andismatrix. You can also
determine the orientation of a vector with theisrowandiscolumnfunctions.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For
more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
HDL Code Generation
Generate Verilog and VHDL code for FPGA and ASIC designs using HDL Coder™.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2019b: Specify dimensions as vector of positive integers or separate input arguments
You can specify dim as a vector of positive integers to query
multiple dimension lengths at a time. Alternatively, you can list the queried
dimensions as separate input arguments dim1,dim2,…,dimN. For an
example, see Size of 4-D Array.
размер
Синтаксис
sz = size(A)
szdim = size(A,dim)
[m,n] =
size(A)
[sz1,...,szN] = size(A)
Описание
пример
sz = size(A)A. Например, если A является матрицей 3 на 4, то size(A) возвращает векторный [3 4]. Длиной sz является ndims(A).
Если A является таблицей или расписанием, то size(A) возвращает двухэлементный вектор – строку, состоящий из количества строк и количества табличных переменных.
пример
szdim = size(A,dim)dim.
пример
[ возвращает количество строк и столбцов, когда m,n] =
size(A)A является матрицей.
пример
[ возвращает длину каждой размерности sz1,...,szN] = size(A)A отдельно.
Примеры
свернуть все
Размер матрицы
Создайте случайную матрицу и вычислите количество строк и столбцов.
A = rand(4,3); [m,n] = size(A)
Размер трехмерного массива
Создайте случайный трехмерный массив и найдите его размер.
A = rand(2,3,4); sz = size(A)
Найдите только длину второго измерения A.
Присвойте длину каждой размерности к отдельной переменной.
Размер таблицы
Составьте таблицу с 5 строками и 4 переменными.
LastName = {'Smith';'Johnson';'Williams';'Jones';'Brown'};
Age = [38;43;38;40;49];
Height = [71;69;64;67;64];
Weight = [176;163;131;133;119];
BloodPressure = [124 93; 109 77; 125 83; 117 75; 122 80];
A = table(Age,Height,Weight,BloodPressure,'RowNames',LastName)
A=5×4 table
Age Height Weight BloodPressure
___ ______ ______ _____________
Smith 38 71 176 124 93
Johnson 43 69 163 109 77
Williams 38 64 131 125 83
Jones 40 67 133 117 75
Brown 49 64 119 122 80
Найдите размер таблицы. Несмотря на то, что переменная BloodPressure содержит два столбца, size только считает количество переменных.
Несколько Выходных аргументов
Создайте трехмерный массив и присвойте длину каждой размерности к отдельной переменной. Каждый выходной аргумент соответствует одной размерности A.
A = ones(3,4,5); [sz1,sz2,sz3] = size(A)
Задайте только два выходных аргумента при вычислении размера A. Поскольку третий выходной аргумент не задан, длины вторых и третьих размерностей A сворачиваются в sz2.
Задайте больше чем три выходных переменные при вычислении размера A. Четвертые и пятые выходные аргументы установлены в 1.
[sz1,sz2,sz3,sz4,sz5] = size(A)
Входные параметры
свернуть все
A Входной массив
скаляр | вектор | матрица | многомерный массив
Входной массив, заданный как скаляр, вектор, матрица или многомерный массив.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | string | struct | function_handle | cell | categorical | datetime | duration | calendarDuration | table | timetable
Поддержка комплексного числа: Да
dim Запрошенная размерность
положительный целочисленный скаляр
Запрошенная размерность, заданная как положительный целочисленный скаляр. size возвращает длину размерности dim A.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Выходные аргументы
свернуть все
sz — Размер массивов
вектор – строка из неотрицательных целых чисел
Размер массивов, возвращенный как вектор – строка из неотрицательных целых чисел. Каждый элемент вектора представляет длину соответствующей размерности A. Если A является скаляром, то sz является вектором – строкой [1 1]. Если A является таблицей или расписанием, то sz является двухэлементным вектором – строкой, содержащим количество строк и количество переменных. Несколько столбцов в одной переменной не считаются.
Если A является вектором символов типа char, то size возвращает вектор – строку [1 N], где N является количеством символов. Однако, если A является скаляром строки, size возвращает [1 1], потому что это – один элемент массива строк. Например, сравните вывод size для вектора символов и строки:
Чтобы найти количество символов в строке, используйте функцию strlength.
Типы данных: double
szdim Длина заданного измерения
неотрицательный целочисленный скаляр
Длина заданного измерения, возвращенного как неотрицательный целочисленный скаляр.
Типы данных: double
m Количество строк
неотрицательный целочисленный скаляр
Количество строк, возвращенных как неотрицательный целочисленный скаляр, когда A является матрицей.
Типы данных: double
n Количество столбцов
неотрицательный целочисленный скаляр
Количество столбцов, возвращенных как неотрицательный целочисленный скаляр, когда A является матрицей.
Типы данных: double
sz1,...,szN — Длины размерности
неотрицательные целочисленные скаляры
Длины размерности, возвращенные как неотрицательные целочисленные скаляры. Когда конкретное количество выходных аргументов равно ndims(A), затем каждый аргумент является длиной соответствующей размерности A. Если больше, чем выходные аргументы ndims(A) заданы, то дополнительные выходные аргументы установлены в 1. Например, для матричного A с размером [4 5], [sz1,sz2,sz3] = size(A) возвращает sz1 = 4, sz2 = 5 и sz3 = 1.
Если меньше, чем выходные аргументы ndims(A) заданы, то все длины остального измерения сворачиваются в последний аргумент в списке. Например, если A является трехмерным массивом с размером [3 4 5], то [sz1,sz2] = size(A) возвращает sz1 = 3 и sz2 = 20.
Типы данных: double
Советы
-
Чтобы определить, пуст ли массив, скаляр или матрица, использует функции
isempty,isscalarиismatrix. Можно также определить ориентацию вектора с функциямиiscolumnиisrow.
Расширенные возможности
“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Выполнения на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Выполнения с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
size
Array dimensions
Syntax
-
d = size(X) [m,n] = size(X) m = size(X
,dim) [d1,d2,d3,...,dn] = size(X)
Description
d = size(X) returns the sizes of each dimension of array
X in a vector d with ndims(X) elements.
[m,n] = size(X) returns the size of matrix
X in separate variables m and n.
m = size(X,dim) returns the size of the dimension of
X specified by scalar dim.
[d1,d2,d3,...,dn] = size(X) returns the sizes of the first
n dimensions of array X in separate variables.
If the number of output arguments n does not equal ndims(X), then for:
n > ndims(X) |
size returns ones in the “extra” variables, i.e., outputs ndims(X)+1 through n. |
n < ndims(X) |
dn contains the product of the sizes of the remaining dimensions of X, i.e., dimensions n+1 through ndims(X). |
Note
For a Java array, size returns the length of the Java array as the number of rows. The number of columns is always 1. For a Java array of arrays, the result describes only the top level array.
Examples
Example 1. The size of the second dimension of rand(2,3,4) is 3.
-
m = size(rand(2,3,4),2) m = 3
Here the size is output as a single vector.
-
d = size(rand(2,3,4)) d = 2 3 4
Here the size of each dimension is assigned to a separate variable.
-
[m,n,p] = size(rand(2,3,4)) m = 2 n = 3 p = 4
Example 2. If X = ones(3,4,5), then
-
[d1,d2,d3] = size(X) d1 = d2 = d3 = 3 4 5
But when the number of output variables is less than ndims(X):
-
[d1,d2] = size(X) d1 = d2 = 3 20
The “extra” dimensions are collapsed into a single product.
If n > ndims(X), the “extra” variables all represent singleton dimensions:
-
[d1,d2,d3,d4,d5,d6] = size(X) d1 = d2 = d3 = 3 4 5 d4 = d5 = d6 = 1 1 1
See Also
exist, length, whos
 |
sinh | size (serial) |  |

Introduction to Size Function in MATLAB
MATLAB provides us with plenty of functionalities, useful in various computational problems. In this article, we will study a powerful MATLAB function called ‘MATLAB size’. Before we understand how to calculate size of an array in MATLAB, let us first understand what exactly SIZE function does. Size function in MATLAB will return a row vector, whose elements will be the size of the respective dimensions of the array passed in the input.
Syntax of Size function in MATLAB:
A = size(Y)
[a,b] = size(Y)
A = size(Y,dim)
[dim1,dim2,dim3,...,dimN] = size(Y)
Description of Size Function in MATLAB
- A = size(Y), this function will return the size of each dimension of the array passed as input.
- [a, b] = size(Y), this function will return the size of input matrix in 2 separate variables ‘a’ and ‘b’
- A = size(Y,dim), this function will return the size of Y’s dimension, specified by the input scalar dim.
- [dim1,dim2,dim3,…,dimN] = size(Y), this function will return the size of ‘n’ dimensions of input array X in separate variables.
In case the number of arguments ‘n’ in output are not equal to ndims(Y), then if:
| n > ndims(Y) | The function will return those present in the extra variable |
| n < ndims(Y) | ‘dn’ will contain the product of sizes of remaining dimensions of Y |
Now let us understand the computation of size in MATLAB with various examples:
Examples to Implement Size Function in MATLAB
Below are the examples Size Function in MATLAB:
Example #1
Let us first define our input array as: rand(2, 4, 5)
As we can see in our input, the size of the third dimension in rand(2,4, 5) is 5.Let us try to find the same with the help of ‘size’ function.
- To find out the size of third dimension, this is how our input will look like in MATLAB:
a = size(rand(2, 4, 5), 3)
Code:
a = size(rand(2, 4, 5), 3)
a
Output:
![]()
- As we can see in the output, we have got the size of 3rd dimension, i.e, 5.
For the same input array, we can also get the size as one vector. Let us understand how we can achieve it:
a = size(rand(2, 4, 5))
This is how our input and output will look like in MATLAB console:
Code:
a = size(rand(2, 4, 5))
a
Output:
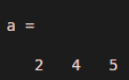
- As we can see in the output, we have got the size of all dimensions in single vector.
To assign sizes of dimensions to separate variables, we can use below code:
[a,b, c] = size(rand(2, 4, 5))
a = 2
b =4
c =5
This is how our input and output will look like in MATLAB console:
Code:
[a,b, c] = size(rand(2, 4, 5));
a,b,c
Output:
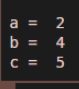
As we can observe in the output, we have got size for all dimensions in separate variables.
Example #2
Let us first define a different input array.
A = ones(4, 3, 2)
Here, we are creating 2 arrays of size 4 x 3, with all ‘unity’ elements.
To get size of the dimension, below is our code:
[a, b, c] = size(A)
This is how our input and output will look like in MATLAB console:
Code:
A = ones(4, 3, 2)
[a, b, c] = size(A)
Output:
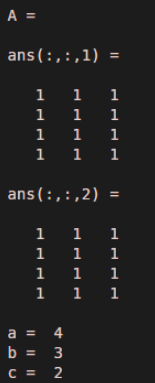
Example #3
Next, let us take the example when our output variables are less than ndims (Y). Here also, we will use the same array as in the above example
[a, b] = size(Y)
As we can see, the input has 3 size dimensions, but our output variables are only 2. In such cases, the last variable will be the product of all remaining dimensions.So, in our case, the product of last two dimensions is collapsed to last variable.
This is how our input and output will look like in MATLAB console:
Code:
Y = ones (4,3,2)
[a,b] = size(Y)
Output:
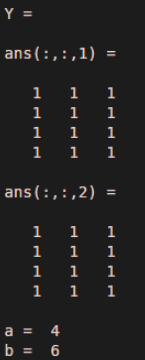
As we can observe in the output, the last variable contains product of 3 and 2, which are size of last 2 dimensions.
Conclusion
So,in this article we learnt, size function can be used to calculate size of any array in MATLAB. Also, we can pass the number of arguments as per our requirement. MATLAB provides us with the product of size in case we pass less arguments than required.
Recommended Articles
This is a guide to Size Function in MATLAB. Here we discuss the Introduction to size function in MATLAB along with its examples as well as code implementation. You can also go through our suggested articles to learn more –
- Introduction to MATLAB Functions
- Top 10 Advantages of Matlab
- Overview of Mean Function in Matlab
- How to Use Matlab? | Operators Used
Выше были рассмотрены операции с
простыми переменными. Однако с их помощью сложно описывать сложные данные, такие
как случайный сигнал, поступающий на вход фильтра или хранить кадр изображения
и т.п. Поэтому в языках высокого уровня предусмотрена возможность хранить
значения в виде массивов. В MatLab эту роль выполняют векторы и
матрицы.
Ниже показан пример задания вектора с
именем a, и содержащий
значения 1, 2, 3, 4:
a = [1 2 3 4]; %
вектор-строка
Для
доступа к тому или иному элементу вектора используется следующая конструкция
языка:
disp( a(1) ); % отображение
значения 1-го элемента вектора
disp( a(2) ); % отображение
значения 2-го элемента вектора
disp( a(3) ); % отображение
значения 3-го элемента вектора
disp( a(4) ); % отображение
значения 4-го элемента вектора
т.е.
нужно указать имя вектора и в круглых скобках написать номер индекса элемента,
с которым предполагается работать. Например, для изменения значения 2-го
элемента массива на 10 достаточно записать
a(2) = 10; % изменение
значения 2-го элемента на 10
Часто возникает необходимость
определения общего числа элементов в векторе, т.е. определения его размера. Это
можно сделать, воспользовавшись функцией length() следующим
образом:
N = length(a); % (N=4) число элементов массива
а
Если требуется задать вектор-столбец, то
это можно сделать так
a = [1; 2; 3; 4]; % вектор-столбец
или
так
b = [1 2 3 4]’; %
вектор-столбец
при
этом доступ к элементам векторов осуществляется также как и для векторов-строк.
Следует отметить, что векторы можно
составлять не только из отдельных чисел или переменных, но и из векторов.
Например, следующий фрагмент программы показывает, как можно создавать один
вектор на основе другого:
a = [1 2 3 4]; %
начальный вектор a
= [1 2 3 4]
b = [a 5 6]; % второй
вектор b = [1 2 3 4 5 6]
Здесь
вектор b состоит из шести
элементов и создан на основе вектора а. Используя этот прием, можно
осуществлять увеличение размера векторов в процессе работы программы:
a = [a 5]; % увеличение
вектора а на один элемент
Недостатком описанного способа задания
(инициализации) векторов является сложность определения векторов больших
размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную
задачу, в MatLab существуют
функции инициализации векторов нулями, единицами или случайными значениями:
a1 = zeros(1, 100); %
вектор-строка, 100 элементов с
% нулевыми
значениями
a2 = zeros(100, 1); % вектор-столбец,
100 элементов с
% нулевыми
значениями
a3 = ones(1, 1000); %
вектор-строка, 1000 элементов с
%
единичными значениями
a4 = ones(1000, 1); % вектор-столбец,
1000 элементов с
%
единичными значениями
a5 = rand(1000, 1); % вектор-столбец,
1000 элементов со
%
случайными значениями
Матрицы в MatLab задаются
аналогично векторам с той лишь разницей, что указываются обе размерности.
Приведем пример инициализации единичной матрицы размером 3х3:
E = [1 0 0; 0 1 0; 0 01]; %
единичная матрица 3х3
или
E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3
Аналогичным
образом можно задавать любые другие матрицы, а также использовать приведенные
выше функции zeros(), ones() и rand(), например:
A1 = zeros(10,10); % нулевая
матрица 10х10 элементов
или
A2 = zeros(10); % нулевая
матрица 10х10 элементов
A3 = ones(5); % матрица
5х5, состоящая из единиц
A4 = rand(100); %
матрица 100х100, из случайных чисел
Для доступа к элементам матрицы
применяется такой же синтаксис как и для векторов, но с указанием строки и
столбца где находится требуемый элемент:
A = [1 2 3;4 5 6;7 8 9]; %
матрица 3х3
disp( A(2,1) ); % вывод на
экран элемента, стоящего во
% второй строке первого столбца,
т.е. 4
disp( A(1,2) ); % вывод на
экран элемента, стоящего в
% первой строке второго столбца,
т.е. 2
Также
возможны операции выделения указанной части матрицы, например:
B1 = A(:,1); % B1 = [1; 4; 7] – выделение
первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение
первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых
двух
% строк
и 2-го и 3-го столбцов матрицы А.
Размерность любой матрицы или вектора в MatLab можно
определить с помощью функции size(), которая возвращает число строк и
столбцов переменной, указанной в качестве аргумента:
a = 5; % переменная
а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица
2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3
Оглавление
- Введение
- Глава 1. Структура программы. Основные математические операции и типы данных
- 1.1. Структура программы пакета MatLab
- 1.2. Простые переменные и основные типы данных в MatLab
- 1.3. Арифметические операции с простыми переменными
- 1.4. Основные математические функции MatLab
- 1.5. Векторы и матрицы в MatLab
- 1.6. Операции над матрицами и векторами
- 1.7. Структуры в MatLab
- 1.8. Ячейки в MatLab
- Глава 2. Условные операторы и циклы в MatLab
- 2.1. Условный оператор if
- 2.2. Условный оператор switch
- 2.3. Оператор цикла while
- 2.4. Оператор цикла for
- Глава 3. Работа с графиками в MatLab
- 3.1. Функция plot
- 3.2. Оформление графиков
- 3.3. Отображение трехмерных графиков
- 3.4. Отображение растровых изображений
- Глава 4. Программирование функций в MatLab
- 4.1. Порядок определения и вызова функций
- 4.2. Область видимости переменных
- Глава 5. Работа с файлами в MatLab
- 5.1. Функции save и load
- 5.2. Функции fwrite и fread
- 5.3. Функции fscanf и fprintf
- 5.4. Функции imread и imwrite
