Как найти количество сторон многоугольника через радиус

Посетитель сайта попросил буквально следующее: «Сделайте пожалуйста такой калькулятор, который зная радиус вписанной и описанной окружностей найдет длину стороны многоугольника».

То есть, задача формулируется так: некоторый правильный многоугольник вписан в окружность с известным радиусом и вокруг него описана окружность с другим известным радиусом. Требуется найти параметры этого правильного многоугольника: число сторон и длину одной стороны.

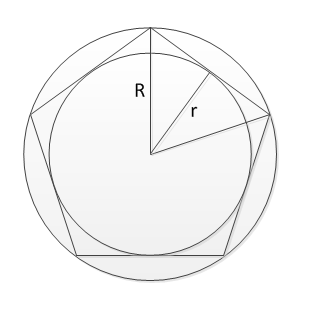
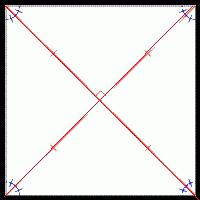
Чтобы было понятнее, графически эта ситуация изображена на картинке слева.

Посмотрев внимательно на треугольник, образованный перпендикуляром из центра окружности к стороне многоугольника (радиус вписанной окружности r), отрезком, соединяющим центр окружности и ближайшую к перпендикуляру вершину многоугольника (радиус описанной окружности R), и собственно, половиной стороны многоугольника, нетрудно заметить, что радиусы связаны между собой соотношением

где угол альфа, опирающийся на вершины многоугольника, связан следующим соотношением с числом сторон многоугольника n:

Таким образом, известные радиусы описанной и вписанной окружности дают нам однозначное соответствие с числом сторон правильного многоугольника.

Длина стороны определяется тривиально.

Теперь по поводу калькулятора — поскольку в расчете есть иррациональное число, получить по этой формуле целое число сторон невозможно. Но, с другой стороны, мы-то знаем, что число сторон — это целое число. Поэтому калькулятор сначала вычисляет число сторон как есть, потом округляет до ближайшего целого, и, исходя из этого целого числа, делает расчет длины стороны и обратный расчет одного из радиусов (из чистого любопытства).

Треугольник, квадрат, шестиугольник – эти фигуры известны практически всем. Но вот о том, что такое правильный многоугольник, знает далеко не каждый. А ведь это все те же геометрические фигуры. Правильным многоугольником называют тот, что имеет равные между собой углы и стороны. Таких фигур очень много, но все они имеют одинаковые свойства, и к ним применимы одни и те же формулы.

Свойства правильных многоугольников

Любой правильный многоугольник, будь то квадрат или октагон, может быть вписан в окружность. Это основное свойство часто используется при построении фигуры. Кроме того, окружность можно и вписать в многоугольник. При этом количество точек соприкосновения будет равняться количеству его сторон. Немаловажно, что окружность, вписанная в правильный многоугольник, будет иметь с ним общий центр. Эти геометрические фигуры подчинены одним теоремам. Любая сторона правильного n-угольника связана с радиусом описанной около него окружности R. Поэтому ее можно вычислить, используя следующую формулу: а = 2R ∙ sin180°. Через радиус окружности можно найти не только стороны, но и периметр многоугольника.

Как найти число сторон правильного многоугольника

Любой правильный n-угольник состоит из некоторого числа равных друг другу отрезков, которые, соединяясь, образуют замкнутую линию. При этом все углы образовавшейся фигуры имеют одинаковое значение. Многоугольники делятся на простые и сложные. К первой группе относятся треугольник и квадрат. Сложные многоугольники имеют большее число сторон. К ним также относят звездчатые фигуры. У сложных правильных многоугольников стороны находят путем вписывания их в окружность. Приведем доказательство. Начертите правильный многоугольник с произвольным числом сторон n. Опишите вокруг него окружность. Задайте радиус R. Теперь представьте, что дан некоторый n-угольник. Если точки его углов лежат на окружности и равны друг другу, то стороны можно найти по формуле: a = 2R ∙ sinα : 2.

Нахождение числа сторон вписанного правильного треугольника

Равносторонний треугольник – это правильный многоугольник. Формулы к нему применяются те же, что и к квадрату, и n-угольнику. Треугольник будет считаться правильным, если у него одинаковые по длине стороны. При этом углы равны 60⁰. Построим треугольник с заданной длиной сторон а. Зная его медиану и высоту, можно найти значение его сторон. Для этого будем использовать способ нахождения через формулу а = х : cosα, где х – медиана или высота. Так как все стороны треугольника равны, то получаем а = в = с. Тогда верным будет следующее утверждение а = в = с = х : cosα. Аналогично можно найти значение сторон в равнобедренном треугольнике, но х будет заданная высота. При этом проецироваться она должна строго на основание фигуры. Итак, зная высоту х, найдем сторону а равнобедренного треугольника по формуле а = в = х : cosα. После нахождения значения а можно вычислить длину основания с. Применим теорему Пифагора. Будем искать значение половины основания c : 2=√(х : cosα)^2 – (х^2) = √x^2 (1 – cos^2α) : cos^2α = x ∙ tgα. Тогда c = 2xtgα. Вот таким несложным способом можно найти число сторон любого вписанного многоугольника.

Вычисление сторон квадрата, вписанного в окружность

Как и любой другой вписанный правильный многоугольник, квадрат имеет равные стороны и углы. К нему применяются те же формулы, что и к треугольнику. Вычислить стороны квадрата можно через значение диагонали. Рассмотрим этот способ более детально. Известно, что диагональ делит угол пополам. Изначально его значение было 90 градусов. Таким образом, после деления образуются два прямоугольных треугольника. Их углы при основании будут равны 45 градусов. Соответственно каждая сторона квадрата будет равна, то есть: а = в = с = д = е ∙ cosα = е√2 : 2, где е – это диагональ квадрата, или основание образовавшегося после деления прямоугольного треугольника. Это не единственный способ нахождения сторон квадрата. Впишем эту фигуру в окружность. Зная радиус этой окружности R, найдем сторону квадрата. Будем вычислять ее следующим образом a4 = R√2. Радиусы правильных многоугольников вычисляют по формуле R = а : 2tg (360^{o :} 2n), где а – длина стороны.

Как вычислить периметр n-угольника

Периметром n-угольника называют сумму всех его сторон. Вычислить его несложно. Для этого необходимо знать значения всех сторон. Для некоторых видов многоугольников существуют специальные формулы. Они позволяют найти периметр намного быстрее. Известно, что любой правильный многоугольник имеет равные стороны. Поэтому для того, чтобы вычислить его периметр, достаточно знать хотя бы одну из них. Формула будет зависеть от количества сторон фигуры. В общем, она выглядит так: Р = an, где а – значение стороны, а n – количество углов. Например, чтобы найти периметр правильного восьмиугольника со стороной 3 см, необходимо умножить ее на 8, то есть Р = 3 ∙ 8 = 24 см. Для шестиугольника со стороной 5 см вычисляем так: Р = 5 ∙ 6 = 30 см. И так для каждого многоугольника.

Нахождение периметра параллелограмма, квадрата и ромба

В зависимости от того, сколько сторон имеет правильный многоугольник, вычисляется его периметр. Это намного облегчает поставленную задачу. Ведь в отличие от прочих фигур, в этом случае не нужно искать все его стороны, достаточно одной. По этому же принципу находим периметр у четырехугольников, то есть у квадрата и ромба. Несмотря на то что это разные фигуры, формула для них одна Р = 4а, где а – сторона. Приведем пример. Если сторона ромба или квадрата равна 6 см, то находим периметр следующим образом: Р = 4 ∙ 6 = 24 см. У параллелограмма равны только противоположные стороны. Поэтому его периметр находят, используя другой способ. Итак, нам необходимо знать длину а и ширину в фигуры. Затем применяем формулу Р = (а + в) ∙ 2. Параллелограмм, у которого равны все стороны и углы между ними, называется ромб.

Нахождение периметра равностороннего и прямоугольного треугольника

Периметр правильного равностороннего треугольника можно найти по формуле Р = 3а, где а – длина стороны. Если она неизвестна, ее можно найти через медиану. В прямоугольном треугольнике равное значение имеют только две стороны. Основание можно найти через теорему Пифагора. После того как станут известны значения всех трех сторон, вычисляем периметр. Его можно найти, применяя формулу Р = а + в + с, где а и в – равные стороны, а с – основание. Напомним, что в равнобедренном треугольнике а = в = а, значит, а + в = 2а, тогда Р = 2а + с. Например, сторона равнобедренного треугольника равна 4 см, найдем его основание и периметр. Вычисляем значение гипотенузы по теореме Пифагора с = √а² + в² = √16+16 = √32 = 5,65 см. Вычислим теперь периметр Р = 2 ∙ 4 + 5,65 = 13,65 см.

Как найти углы правильного многоугольника

Правильный многоугольник встречается в нашей жизни каждый день, например, обычный квадрат, треугольник, восьмиугольник. Казалось бы, нет ничего проще, чем построить эту фигуру самостоятельно. Но это просто только на первый взгляд. Для того чтобы построить любой n-угольник, необходимо знать значение его углов. Но как же их найти? Еще ученые древности пытались построить правильные многоугольники. Они догадались вписать их в окружности. А потом на ней отмечали необходимые точки, соединяли их прямыми линиями. Для простых фигур проблема построения была решена. Формулы и теоремы были получены. Например, Эвклид в своем знаменитом труде «Начало» занимался решением задач для 3-, 4-, 5-, 6- и 15-угольников. Он нашел способы их построения и нахождения углов. Рассмотрим, как это сделать для 15-угольника. Сначала необходимо рассчитать сумму его внутренних углов. Необходимо использовать формулу S = 180⁰(n-2). Итак, нам дан 15-угольник, значит, число n равно 15. Подставляем известные нам данные в формулу и получаем S = 180⁰(15 – 2) = 180⁰ х 13 = 2340⁰. Мы нашли сумму всех внутренних углов 15-угольника. Теперь необходимо получить значение каждого из них. Всего углов 15. Делаем вычисление 2340⁰ : 15 = 156⁰. Значит, каждый внутренний угол равен 156⁰, теперь при помощи линейки и циркуля можно построить правильный 15-угольник. Но как быть с более сложными n-угольниками? Много веков ученые бились над решением этой проблемы. Оно было найдено только лишь в 18-м веке Карлом Фридрихом Гауссом. Он смог построить 65537-угольник. С этих пор проблема официально считается полностью решенной.

Расчет углов n-угольников в радианах

Конечно, есть несколько способов нахождения углов многоугольников. Чаще всего их вычисляют в градусах. Но можно выразить их и в радианах. Как это сделать? Необходимо действовать следующим образом. Сначала выясняем число сторон правильного многоугольника, затем вычитаем из него 2. Значит, мы получаем значение: n – 2. Умножьте найденную разность на число п («пи» = 3,14). Теперь остается только разделить полученное произведение на число углов в n-угольнике. Рассмотрим данные вычисления на примере все того же пятнадцатиугольника. Итак, число n равно 15. Применим формулу S = п(n – 2) : n = 3,14(15 – 2) : 15 = 3,14 ∙ 13 : 15 = 2,72. Это, конечно же, не единственный способ рассчитать угол в радианах. Можно просто разделить размер угла в градусах на число 57,3. Ведь именно столько градусов эквивалентно одному радиану.

Расчет значения углов в градах

Помимо градусов и радиан, значение углов правильного многоугольника можно попробовать найти в градах. Делается это следующим образом. Из общего количества углов вычитаем 2, делим полученную разность на число сторон правильного многоугольника. Найденный результат умножаем на 200. К слову сказать, такая единица измерения углов, как грады, практически не используется.

Расчет внешних углов n-угольников

У любого правильного многоугольника, кроме внутреннего, можно вычислить еще и внешний угол. Его значение находят так же, как и для остальных фигур. Итак, чтобы найти внешний угол правильного многоугольника, необходимо знать значение внутреннего. Далее, нам известно, что сумма этих двух углов всегда равна 180 градусам. Поэтому вычисления делаем следующим образом: 180⁰ минус значение внутреннего угла. Находим разность. Она и будет равняться значению смежного с ним угла. Например, внутренний угол квадрата равен 90 градусов, значит, внешний будет составлять 180⁰ – 90⁰ = 90⁰. Как мы видим, найти его несложно. Внешний угол может принимать значение от +180⁰ до, соответственно, -180⁰.