В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
-
Расчет длины стороны
- Через радиус вписанной окружности
- Через радиус описанной окружности
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Через радиус вписанной окружности
Формула расчета
Через радиус описанной окружности
Формула расчета
Посетитель сайта попросил буквально следующее: «Сделайте пожалуйста такой калькулятор, который зная радиус вписанной и описанной окружностей найдет длину стороны многоугольника».
То есть, задача формулируется так: некоторый правильный многоугольник вписан в окружность с известным радиусом и вокруг него описана окружность с другим известным радиусом. Требуется найти параметры этого правильного многоугольника: число сторон и длину одной стороны.
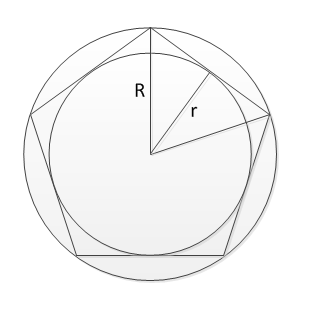
Чтобы было понятнее, графически эта ситуация изображена на картинке слева.
Посмотрев внимательно на треугольник, образованный перпендикуляром из центра окружности к стороне многоугольника (радиус вписанной окружности r), отрезком, соединяющим центр окружности и ближайшую к перпендикуляру вершину многоугольника (радиус описанной окружности R), и собственно, половиной стороны многоугольника, нетрудно заметить, что радиусы связаны между собой соотношением
где угол альфа, опирающийся на вершины многоугольника, связан следующим соотношением с числом сторон многоугольника n:
Таким образом, известные радиусы описанной и вписанной окружности дают нам однозначное соответствие с числом сторон правильного многоугольника.
Длина стороны определяется тривиально.
Теперь по поводу калькулятора — поскольку в расчете есть иррациональное число, получить по этой формуле целое число сторон невозможно. Но, с другой стороны, мы-то знаем, что число сторон — это целое число. Поэтому калькулятор сначала вычисляет число сторон как есть, потом округляет до ближайшего целого, и, исходя из этого целого числа, делает расчет длины стороны и обратный расчет одного из радиусов (из чистого любопытства).
Определение параметров правильного многоугольника по радиусам вписанной и описанной окружности
Радиус описанной окружности
Радиус вписанной окружности
Точность вычисления
Знаков после запятой: 3
Радиус вписанной окружности (для округленного числа сторон)
Длина стороны (для округленного числа сторон)
|
bezdelnik 8 лет назад
r – радиус вписанной в N-угольник окружности В любой правильный многоугольник можно вписать окружность. От длины стороны будет зависеть радиус вписанной окружности. Или наоборот – длина стороны зависит радиус вписанной окружности. Посмотрите на формулу, которая связывает эти величины Чтобы посчитать количество сторон, надо найти из этой формулы N. Получите ответ.
в избранное
ссылка
отблагодарить Rafail Вокруг окружности ЛЮБОГО радиуса можно описать ЛЮБОЙ правильный N-угольник.
bezdelnik spin, в приведенной Вами формуле два неизвестных a и n, поэтому по ней нельзя найти n.
spin а – длина стороны, n – число сторон многоугольника. Если задан многоугольник с известным количеством сторон, радиус вписанной окружности, то получается одно неизвестное.
Rafail О чём спорите, господа? разве Вы не прочитали мой комментарий, или не поняли смысл сказанного? Вокруг ЛЮБОЙ окружности можно описать ЛЮБОЙ многоугольник, поэтому вопрос вообще бессмысленен. При ЛЮБОМ радиусе r число сторон N может быть ЛЮБЫМ.
spin Никто не спорит. Понятно, что по тем данным, которые есть в вопросе однозначно посчитать количество сторон не получится.
все комментарии (еще 5) Знаете ответ? |
Как найти правильный многоугольник, зная радиус вписанной и описанной окружности?
Inna Zotova
Ученик
(175),
на голосовании
6 лет назад
Помогите, пожалуйста.
Как можно найти количество сторон и углы в правильном многоугольнике, зная только радиус вписанной и описанной окружности?
R – 2√3
r – 3
Голосование за лучший ответ
Вы здесь
-
Сторона правильного многоугольника
Правильные многоугольники часто фигурируют в задачах с вписанными или описанными окружностями. Отрезок, проведенный из центра окружности в угол или середину стороны, является радиусом описанной или вписанной окружности соответственно.
Зная количество сторон многоугольника, ключевой задачей является нахождение центрального угла между этими двумя радиусами, так как они с половиной стороны образуют прямоугольный треугольник. Такой угол будет равен 180 градусам, разделенным на количество сторон многоугольника n:
Из тригонометрических отношений в треугольнике, сторона будет равна удвоенному произведению радиуса описанной окружности на синус центрального угла или радиуса вписанной окружности на тангенс того же угла.