Как найти количество сторон н угольник

План урока:

Понятие правильного многоугольника

Описанная и вписанная окружности правильного многоугольника

Формулы для правильного многоугольника

Построение правильных многоугольников

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

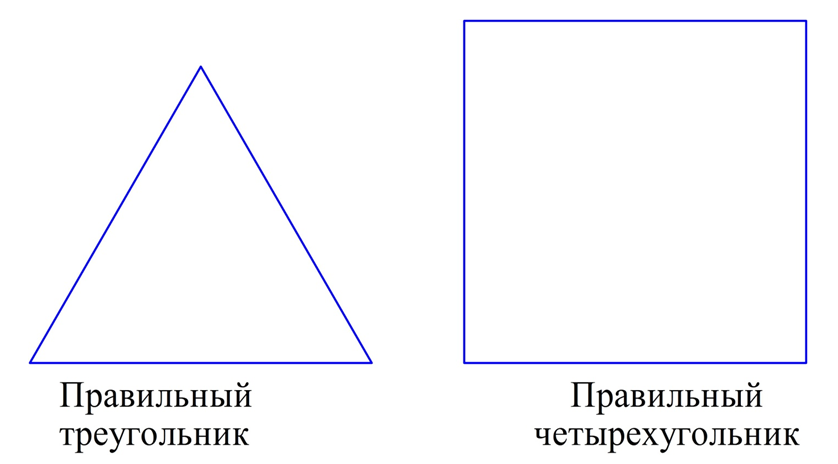
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

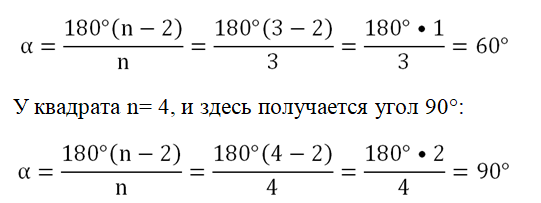
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу 

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

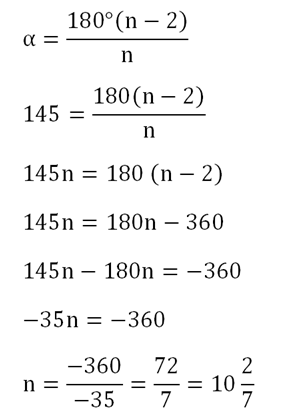
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Ответ: не может.

Описанная и вписанная окружности правильного многоугольника

Докажем важную теорему о правильном многоуг-ке.

Для доказательства обозначим вершины произвольного правильного n-угольника буквами А₁, А₂, А₃…А_n. Далее проведем биссектрисы углов ∠А₁ и ∠А₂. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА₃, ОА₄ и т. д.

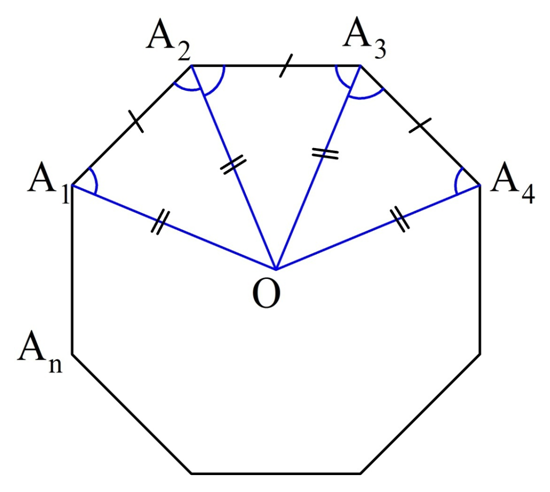
∠А₁ и ∠А₂ одинаковы по определению правильного многоуг-ка:

Из этого факта вытекает два равенства:

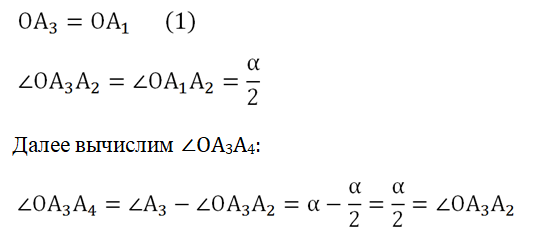
Получается, что ОА₃ – это также биссектриса ∠А₃. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):

Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:

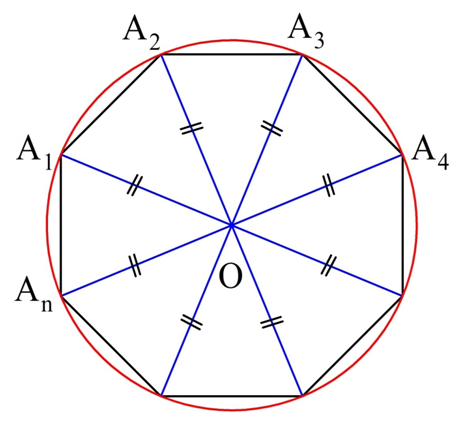
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А₁, А₂ и А₃, можно провести только одну окружность, ч. т. д.

Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН₁, ОН₂, ОН₃… на стороны многоуг-ка.

Так как высоты проведены в равных треуг-ках, то и сами они равны:

Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН₁. Он должен будет пройти и через точки Н₂, Н₃, … Н_n. Причем отрезки ОН₁, ОН₂, ОН₃ окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:

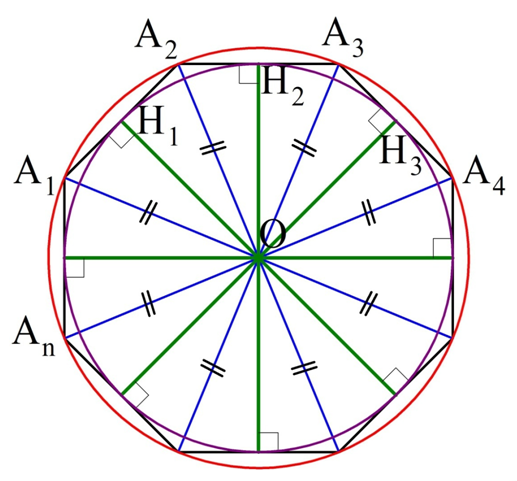
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А₁, ∠А₂, ∠А₃, то есть в точке О. Так как расстояние от О до А₁А₂ – это отрезок ОН₁, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.

Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.

Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН₁, ОН₂, ОН₃,… проведены в равнобедренных треуг-ках∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н₁, Н₂, Н₃,… – это середины сторон многоуг-ка.

Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?

Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.

Ответ: не могут.

Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.

Формулы для правильного многоугольника

Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой a_n, где n– число сторон у многоуг-ка. Например a₄– это сторона квадрата, a₆– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.

Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу

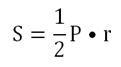
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.

Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:

Теперь можно найти и ∠А₁ОН₁, рассмотрев ∆А₁ОН₁:

Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:

С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).

Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.

Решение. Запишем следующую формулу:

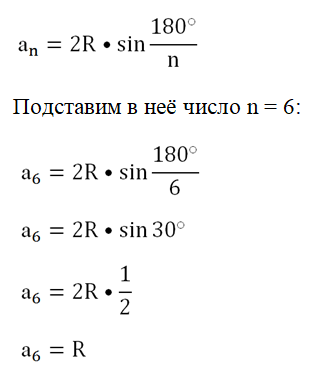
Это равенство как раз и надо было доказать в этом задании.

Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.

Решение. Запишем формулу:

Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.

Решение.

Найдем периметр шестиугольника:

Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?

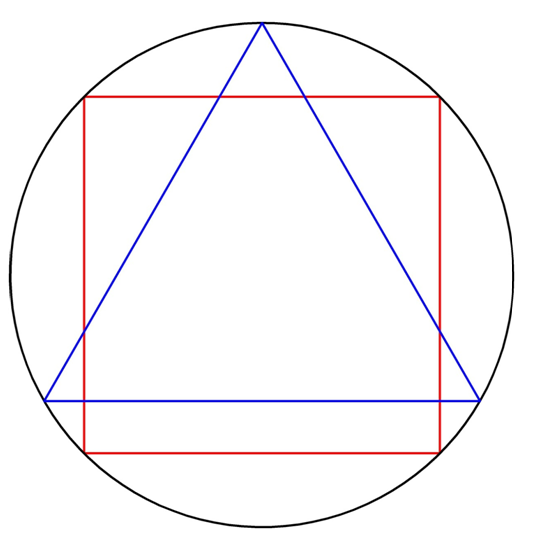
Решение. Зная периметр треуг-ка, легко найдем и его сторону:

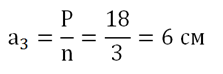
Далее вычисляется радиус описанной около треугольника окружности:

Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?

Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:

Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:

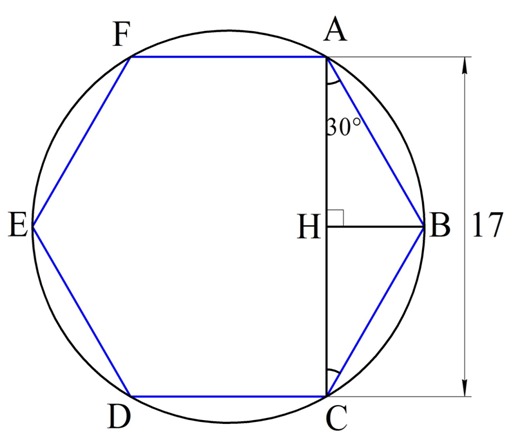
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:

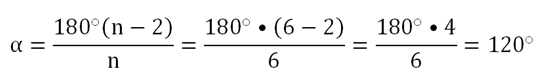
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:

Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:

AC = 17 мм

∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:

AH = AC/2 = 17/2 = 8,5 мм

Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:

Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.

Ответ: 20 мм.

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.

A polygon by definition is any geometric shape that is enclosed by a number of straight sides, and a polygon is considered regular if each side is equal in length. Polygons are classified by their number of sides. For example, a six-sided polygon is a hexagon, and a three-sided one is a triangle.

Regular Polygons

The number of sides of a regular polygon can be calculated by using the interior and exterior angles, which are, respectively, the inside and outside angles created by the connecting sides of the polygon. For a regular polygon the measure of each interior angle and each exterior angle is congruent. For example, a regular octagon has interior angles each equal to 125 degrees.

These relationships only hold true for convex polygons where the measure of each interior angle does not exceed 180 degrees.

Using Interior Angles

Subtract the interior angle from 180; then divide 360 by the difference of the angle and 180 degrees. For example, if the interior angle was 165, subtracting it from 180 would yield 15, and 360 divided by 15 equals 24, which is the number of sides of the polygon. Here is the general formula (it is important to note that this only works for the ‌interior‌ angles of a regular polygon):

text{# of sides}=frac{360^circ}{180^circ-text{interior angle}}

Using Exterior Angles

Divide 360 by the amount of the exterior angle to also find the number of sides of the polygon. For example, if the measurement of the exterior angle is 60 degrees, then dividing 360 by 60 yields 6. Six is the number of sides that the polygon has. This is a hexagon, so we can check this reasoning by finding the interior angle to be 120 degrees, which is the measure of the interior angle of a hexagon.

The general formula using the ‌exterior‌ angles of a regular polygon follows:

text{# of sides}=frac{360}{text{exterior angle}}

Irregular Polygons

Not all polygons have congruent angles and sides. The measure of the internal angles can vary depending on the measures of each side. Regardless of the polygon shape, the sum of exterior angles will always be 360 degrees. We can use this relationship to reason out a formula for an n-sided polygon with any side lengths.

The sum of the interior angles of a polygon can be related to the the number of sides through the polygon formula:

text{# of sides} = frac{text{sum of interior angles}}{180} + 2

We can try this formula with any quadrilateral. We know that the sum of the interior angles of any four sided polygon (like a square, rhombus, parallelogram, or trapezoid) is 360 degrees. Plugging this into the formula we can prove this known relationship:

text{# of sides} = frac{text{360}}{180} + 2 = 4 text{ sides}

Terminology of Polygons

As a helpful guide for reporting calculations, these are the general conventions for discussing polygons in geometry and trigonometry.

‌Naming polygons (3 – 10 sides):‌

Определение правильного многоугольника

Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.

Признаки правильного n-угольника

• a1 = a2 = a3 = … an-1 = an
• α1 = α2 = α3 = … αn-1 = αn

Примечание: n – количество сторон/углов фигуры.

Элементы правильного многоугольника

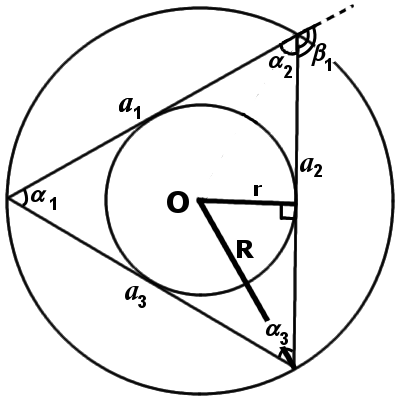
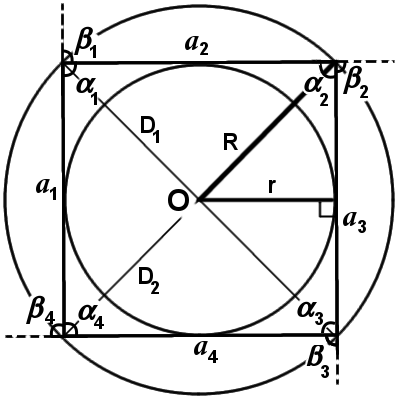
Для рисунка выше:

• a – сторона/ребро;
• α – угол между смежными сторонами;
• O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
• β – центральный угол описанной окружности, опирающийся на сторону многоугольника.

Диагонали n — угольника

Фигура	Рисунок	Описание
Диагональ многоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника		Число диагоналейn – угольника равно

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Внешний угол многоугольника

Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).

Рис.2

Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n — 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Виды правильных многоугольников

1. Правильный (равносторонний) треугольник
2. Правильный четырехугольник (квадрат)
3. Правильный пяти-, шести-, n-угольник

Основные свойства правильного многоугольника

• Все стороны равны:
  a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
  α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:

180° · (n — 2)

• Сумма всех внешних углов n-угольника равна 360°:

β1 + β2 + β3 + … + βn-1 + βn = 360°

• Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

• В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

• Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Свойство 1

Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:

где n – число сторон фигуры.

Свойство 2

Сумма всех углов правильного n-угольника равняется: 180° · (n-2).

Свойство 3

Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:

Свойство 4

В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.

В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.

Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:

Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:

Свойство 5

Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:

• Площадь (S):

• Периметр (P):
• Радиус описанной окружности (R):

• Радиус вписанной окружности (r):

Свойство 6

Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:

Доказательства свойств углов многоугольника

Теорема 1. В любом треугольнике сумма углов равна 180°.

Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).

Рис.3

Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.

Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).

Рис.4

Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.

Замечание. Теорема 1 является следствием теоремы 2.

Теорема 3. Сумма углов  – угольникаn равна

Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).

Рис.5

Получим n треугольников:

OA1A2,  OA2A3,  …  OAnA1

Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна

что и требовалось доказать.

Теорема 4. Сумма внешних углов  – угольникаn , взятых по одному у каждой вершины, равна 360°.

Доказательство. Рассмотрим рисунок 6.

Рис.6

В соответствии рисунком 6 справедливы равенства

Теорема доказана.

Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

• Формула стороны правильного n-угольника через радиус вписанной окружности:

• Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

• Формула площади n-угольника через длину стороны:

• Формула площади n-угольника через радиус вписанной окружности:

• Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

Рис.3

Формулы правильного треугольника:

• Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

• Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

• Формула радиуса вписанной окружности правильного треугольника через длину стороны:

• Формула радиуса описанной окружности правильного треугольника через длину стороны:

• Формула площади правильного треугольника через длину стороны:

• Формула площади правильного треугольника через радиус вписанной окружности:

S = r2 3√3

• Формула площади правильного треугольника через радиус описанной окружности:

• Угол между сторонами правильного треугольника:

α = 60°

Рис.4

Формулы правильного четырехугольника:

• Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

• Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

• Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

• Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

• Формула площади правильного четырехугольника через длину стороны:

S = a2

• Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r2

• Формула площади правильного четырехугольника через радиус описанной окружности:

S =  2 R2

• Угол между сторонами правильного четырехугольника:

α = 90°

Формулы правильного шестиугольника:

Формула стороны правильного шестиугольника через радиус вписанной окружности:

Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

Формула площади правильного шестиугольника через длину стороны:

Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r2 2√3

Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

Формулы правильного восьмиугольника:

Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 — 1)

Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 — √2

Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

Формула площади правильного восьмиугольника через длину стороны:

S = a2 2(√2 + 1)

Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r2 8(√2 — 1)

Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R2 2√2

Угол между сторонами правильного восьмиугольника:

α = 135°

Сторона правильного многоугольника через радиус описанной вокруг него окружности

Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле

Где:

a – длина его стороны;

R – радиус описанной окружности;

n – число сторон многоугольника.

Формула стороны правильного многоугольника

Шаг 1

Рассмотрим правильный многоугольник А1А2А3…Аn.

Пусть его сторона будет равна a.

Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.

Вывод формулы стороны правильного многоугольника.

Шаг 2

Соединим точку О с его вершинами. А1А2А3…Аn.

Рассмотрим треугольник ОА1А2.

Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.

Проведем в треугольнике А1ОА2 высоту ОК.

Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:

Вывод формулы стороны правильного многоугольника.

Шаг 3

Рассмотрим треугольник А1КО.

Этот треугольник прямоугольный, так как ОК – высота по построению.

Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.

Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:

По свойству углов правильного многоугольника, каждый угол равен:

Тогда угол ОА1К будет равен:

Из определения косинуса угла получим:

Отсюда:

Подставим в формулу значения, полученные выше и на шаге 2:

Умножим обе части уравнения на 2:

Воспользуемся формулами приведения

Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:

Вывод формулы стороны правильного многоугольника.

Правильный многоугольник

• формулы, признаки и свойства правильного многоугольника
• формулы правильного n-угольника
• правильный треугольник
• правильный четырехугольник
• правильный шестиугольник
• правильный восьмиугольник