Как найти кол-во теплоты, выделяемое при неупругом столкновении двух тел? Известны обе массы и обе скорости
Наталия Дмитриева
Ученик
(98),
закрыт
8 лет назад
ВиталийГорностаев
Мастер
(2365)
10 лет назад
Обозначим скорости тел до столкновения V1 V2
Общая скорость после столкновения U
Закон сохранения импульса m1*V1+m2*V2=U*(m1+m2)
Отсюда U=(m1*V1+m2*V2)/(m1+m2)
Кинетическая энергия до столкновения Ek1=m1*(V1)^2+m2*(V2)^2
Кинетическая энергия после столкновения Ek2=(m1+m2)*(U)^2
Количество теплоты Q=Ek2-Ek1
Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
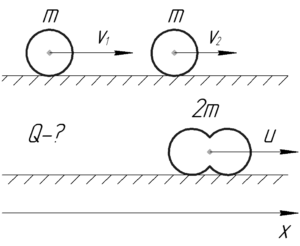 Запишем два закона:
Запишем два закона:
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
Брусок массой 400 г, движущийся по гладкой горизонтальной поверхности со скоростью ʋ = 10 м/с, ударяется о такой же, но неподвижный брусок и теряет половину своей скорости. Найдите количество теплоты, выделившейся при соударении брусков. Движение брусков считать поступательным.
Спрятать решение
Решение.
| Дано:
m=0,4 кг υ=10 м/c Q—? |
Решение:
Согласно закону сохранения импульса откуда скорость второго бруска после соударения Согласно закону сохранения энергии откуда количество теплоты, выделившееся при ударе, равно Подставляя числовые данные условия задачи и проверяя размерность найденной величины, получаем Ответ: 10 Дж. |
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное правильное решение, включающее следующие элементы:
1) верно записано краткое условие задачи; 2) записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом; 3) выполнены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение «по частям» (с промежуточными вычислениями). |
3 |
| Правильно записаны необходимые формулы, проведены вычисления, и получен ответ (верный или неверный), но допущена ошибка в записи краткого условия или переводе единиц в СИ.
ИЛИ Представлено правильное решение только в общем виде, без каких-либо числовых расчётов. ИЛИ Записаны уравнения и формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, но в математических преобразованиях или вычислениях допущена ошибка. |
2 |
| Записаны и использованы не все исходные формулы, необходимые для решения задачи.
ИЛИ Записаны все исходные формулы, но в одной из них допущена ошибка. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Условие задачи:
Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового шара массой 1 кг об очень тяжелую стенку, движущуюся со скоростью 5 см/с. Шар до удара двигался не вращаясь перпендикулярно стенке, навстречу ей со скоростью 10 см/с.
Задача №2.10.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(m=1) кг, (u=5) см/с, (upsilon=10) см/с, (M gg m), (Q-?)
Решение задачи:
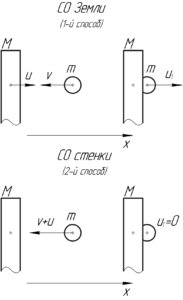 Эту задачу можно решать двумя способами.
Эту задачу можно решать двумя способами.
Первый способ. Запишем закон сохранения импульса в проекции на ось (x) и закон сохранения энергии для системы тел «шар — стенка» в системе отсчета (СО) Земли. Замечу, что этот способ достаточно трудоёмкий, по сравнению со вторым.
Из равенства (1) выразим скорость стенки с шаром (u_1) после удара:
Полученное выражение для скорости (u_1) подставим в (2).
Оставим искомое количество теплоты (Q) в одной стороне, все остальные члены перенесем в другую, где приведем их под общий знаменатель.
Раскроем в числителе скобки и квадрат разности:
Вынесем в числителе общий множитель (mM) за скобки:
Воспользуемся основным свойством дроби и поделим и числитель и знаменатель на (M).
Так как по условию стенка очень тяжелая, то есть (M gg m), то отношение (<frac>) стремится к нулю, значит им можно пренебречь. В итоге конечная формула такая:
Второй способ. Перейдем в систему отсчета (СО), связанную с массивной стенкой. В этой СО скорость свинцового шарика равна (upsilon + u) и направлена к стенке. После удара скорость шарика станет такой же, как и у стенки, то есть в этой СО станет равной нулю. Получается, что вся кинетическая энергия шарика в этой СО перейдет в теплоту:
Как Вы видите, второй способ решения этой задачи существенно короче.
Переведем скорости в систему СИ, а уже потом будет считать ответ:
Ответ: 11,25 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Вследствие изменения полной механической энергии системы может выделяться теплота.
Наличие сил трения (сопротивления) между телами замкнутой системы приводит к выделению энергии в виде теплоты:
где E 1 — полная механическая энергия системы в начальном состоянии; E 2 — полная механическая энергия системы в конечном состоянии.
Если теплота в механической системе выделяется в результате совершения работы силами трения, то количество выделившейся при этом теплоты может быть рассчитано по формуле
где A тр — работа, совершенная силами трения.
Превращение части механической энергии в теплоту происходит при абсолютно неупругом столкновении (ударе) двух и более тел.
Абсолютно неупругий удар — это столкновение тел, в результате которого тела объединяются и продолжают двигаться как единое целое.
Для абсолютно неупругого удара двух тел:
- выполняется закон сохранения импульса:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ;
- не выполняется закон сохранения полной механической (кинетической) энергии:
m 1 v 1 2 2 + m 2 v 2 2 2 ≠ ( m 1 + m 2 ) u 2 2 ,
где m 1 и m 2 — массы соударяющихся тел; v → 1 и v → 2 — скорости тел до столкновения; ( m 1 + m 2 ) — масса тела, образовавшегося в результате удара; u → — скорость тела, образовавшегося в результате удара.
Разность энергий до и после столкновения равна теплоте, выделившейся в процессе столкновения:
Q = m 1 v 1 2 2 + m 2 v 2 2 2 − ( m 1 + m 2 ) u 2 2 .
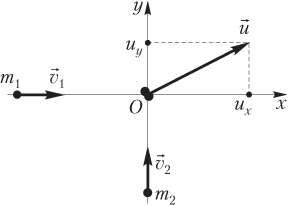
Пример 36. Какая доля энергии двух движущихся с равными по модулю скоростями тел, направленными под прямым углом друг к другу, перейдет в теплоту при абсолютно неупругом ударе? Массы тел относятся как 1:2.
Решение. На рисунке показаны два положения системы тел: до удара и сразу после удара. До удара тела движутся: первое — в положительном направлении оси Ox , второе — в положительном направлении оси Oy . Столкновение тел (абсолютно неупругий удар) происходит в начале системы координат. В результате абсолютно неупругого удара тела объединяются и движутся как единое целое со скоростью u → .
Полная механическая энергия системы является кинетической энергией:
E 1 = W k 1 + W k 2 ;
где W k 1 = m 1 v 1 2 2 — кинетическая энергия первого тела до удара; W k 2 = m 2 v 2 2 2 — кинетическая энергия второго тела до удара; m 1 — масса первого тела; m 2 — масса второго тела; v 1 — модуль скорости первого тела до удара; v 2 — модуль скорости второго тела до удара; W k = ( m 1 + m 2 ) u 2 2 — кинетическая энергия объединенного тела после удара; ( m 1 + m 2 ) — масса объединенного тела после удара; u — модуль скорости объединенного тела после удара.
Теплота, выделившаяся в результате абсолютно неупругого удара, определяется разностью полных механических энергий системы до удара и после него:
Для ее вычисления необходимо определить скорость объединенного тела.
Воспользуемся законом сохранения импульса, записав его в виде:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
или в проекциях на координатные оси,
O x : m 1 v 1 = ( m 1 + m 2 ) u x ; O y : m 2 v 2 = ( m 1 + m 2 ) u y . >
Выразим отсюда проекции скорости объединенного тела:
u x = m 1 v 1 m 1 + m 2 u y = m 2 v 2 m 1 + m 2 >
и подставим их в формулу, определяющую квадрат скорости объединенного тела:
u 2 = u x 2 + u y 2 = ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 .
Полная механическая энергия объединенного тела, таким образом, определяется формулой
E 2 = ( m 1 + m 2 ) u 2 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] .
- равенства модулей скоростей тел до удара:
- соотношения между массами тел:
запишем полные механические энергии системы:
E 1 = m 1 v 1 2 2 + m 2 v 2 2 2 = m v 2 2 + 2 m v 2 2 = 3 2 m v 2 ;
E 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] = 5 6 m v 2 .
Количество теплоты, выделившейся после абсолютно неупругого удара, определяется формулой
Q = E 1 − E 2 = 3 2 m v 2 − 5 6 m v 2 = 2 3 m v 2 .
Доля механической энергии, превратившейся в теплоту в результате абсолютно неупругого удара,
η = Q E 1 = 2 m v 2 3 2 3 m v 2 = 4 9 ≈ 0,44 .
При абсолютно неупругом ударе двух тел с заданными соотношениями масс и скоростей в теплоту перешло около 44 % механической энергии системы.
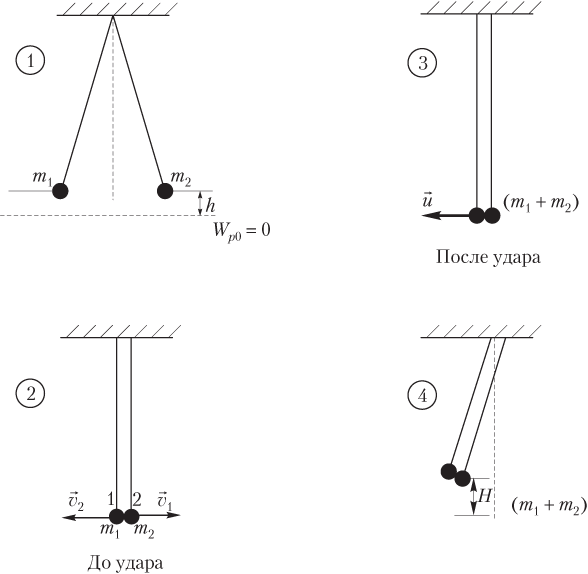
Пример 37. Два пластилиновых шарика, массы которых соотносятся как 1:5, подвешены на нитях одинаковой длины. Шарики симметрично разводят в противоположные стороны и отпускают. Какая часть механической энергии перейдет в теплоту при абсолютно неупругом ударе?
Решение. На рисунке показаны четыре состояния системы тел:
1) шарики симметрично разведены в стороны, при этом они подняты на высоту h над нулевым уровнем потенциальной энергии; полная механическая энергия системы является потенциальной:
E 1 = m 1 gh + m 2 gh ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где g — модуль ускорения свободного падения; h — первоначальная высота шариков над нулевым уровнем потенциальной энергии;
2) шарики подлетают друг к другу (но соударения еще не происходит); полная механическая энергия системы является кинетической:
E 2 = m 1 v 1 2 2 + m 2 v 2 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
E 2 = m 2 ( v 1 2 + 5 v 2 2 ) ,
где v 1 — модуль скорости первого шарика; v 2 — модуль скорости второго шарика;
3) шарики после абсолютно неупругого удара объединяются и движутся как единое целое с некоторой скоростью; полная механическая энергия системы является кинетической:
E 3 = ( m 1 + m 2 ) u 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где u — модуль скорости объединенного тела непосредственно после удара;
4) объединенное тело поднимается на некоторую высоту, полная механическая энергия системы является потенциальной:
E 4 = ( m 1 + m 2 ) gH ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где H — максимальная высота, на которую может подняться объединенное тело.
При переходе системы из первого состояния во второе полная механическая энергия сохраняется как для всей системы, так и для каждого шарика в отдельности:
m 1 g h = m 1 v 1 2 2 ; m 2 g h = m 2 v 2 2 2 . >
Отсюда следует равенство модулей скоростей шариков перед абсолютно неупругим ударом:
v = v 1 = v 2 = 2 g h .
С учетом этого равенства полная механическая энергия системы перед ударом определяется формулой
При переходе системы из второго состояния в третье полная механическая энергия системы не сохраняется (при абсолютно неупругом ударе часть энергии переходит в теплоту), однако импульс системы сохраняется:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
в проекции на направление скорости объединенного тела
− m 1 v 1 + m 2 v 2 = ( m 1 + m 2 ) u ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ) и равенства модулей скоростей ( v = v 1 = v 2 ):
Отсюда найдем отношение модулей скоростей шариков до и после удара:
Искомой величиной является доля механической энергии, которая перейдет в результате абсолютно неупругого удара в теплоту, т.е.
η = Q E 2 = E 2 − E 3 E 2 = 1 − E 3 E 2 ,
где E 2 — полная механическая энергия системы до удара (состояние 2); E 3 — полная механическая энергия системы после удара (состояние 3).
Подстановка в формулу соответствующих энергий и отношения скоростей ( u / v ) дает искомую долю:
η = 1 − 3 m u 2 3 m v 2 = 1 − u 2 v 2 = 1 − ( u v ) 2 = 1 − ( 2 3 ) 2 = 5 9 ≈ 0,56 .
Таким образом, при абсолютно неупругом ударе шариков с заданным соотношением масс в теплоту превращается около 56 % их суммарной механической энергии.
Пример 38. Тело массой 2,0 кг влетает в вязкую среду со скоростью 10 м/c. Определить кинетическую энергию тела при вылете из среды, если 30 % его механической энергии в среде превращается в теплоту.
Решение. На рисунке показаны два положения тела:
1) перед попаданием в вязкую среду; тело имеет полную механическую (кинетическую) энергию E 1 ;
2) после вылета из вязкой среды; тело имеет полную механическую (кинетическую) энергию E 2 .
Теплота, которая выделяется при движении тела в вязкой среде, определяется разностью
где Q = 0,3 E 1 — по условию задачи.
Выразим искомую кинетическую энергию тела при вылете из вязкой среды:
Замена Q = 0,3 E 1 преобразует формулу к виду:
E 2 = E 1 − 0,3 E 1 = 0,7 E 1 ,
где E 1 = m v 1 2 2 — кинетическая энергия тела перед его попаданием в вязкую среду; m — масса тела; v 1 — модуль первоначальной скорости тела.
Окончательная формула для расчета искомой кинетической энергии имеет следующий вид:
Скорость брошенного мяча непосредственно перед ударом об абсолютно гладкую стену была вдвое больше его скорости сразу после удара. Какое количество теплоты выделилось при ударе, если перед ударом кинетическая энергия мяча была равна 20 Дж? (Ответ дайте в джоулях.)
Кинетическая энергия пропорциональна квадрату скорости. Поскольку скорость после удара уменьшилась в 2 раза, кинетическая энергия мяча уменьшилась в 4 раза и стала равна 5 Дж. По закону сохранения, количество теплоты, выделившееся после удара равняется убыли кинетической энергии:
Для приведенного здесь решения задачи существенно, что стенка, о которую ударяется мяч, абсолютно гладкая. Действительно, в противном случае на мяч во время удара может дейстовать еще и сила трения со стороны стенки, которая приведет к тому, что мяч после удара будет вращаться поэтому кинетическая энергия шара после удара будет состоять из энергии поступательного и вращательного движений. Следовательно, судить о величине выделившегося тепла будет невозможно.
2014-05-31 ![]()
Какое количество тепла выделится при лобовом ударе двух свинцовых шаров массой m = 1 кг каждый, скользящих без вращении на абсолютно гладкой горизонтальной поверхности по одной прямой в одном направлении? Скорость первого шара $v_{1}=10 см/с$, скорость второго $v_{2} = 20 см/с$. Удар шаров считать абсолютно неупругим
Решение:
Так как удар абсолютно неупругий, то после удара оба шара будут двигаться с одинаковой скоростью $v$. Согласно закону сохранения импульса
$mv_{1}+mv_{2}=2mu$.
Отсюда
$v=frac{v_{1}+v_{2}}{2}$.
До столкновения шары обладали кинетической энергией
$W_{1}=frac{mv_{1}^{2}}{2}+frac{mv_{2}^{2}}{2}$.
После удара их кинетическая энергия равна
$W_{2}=2 frac{mv^{2}}{2}= frac{m(v_{1}+v_{2})^{2}}{4}$.
В результате удара кинетическая энергия системы уменьшается на величину
$Delta = W_{1} – W_{2}=frac{m}{4}(v_{1}-v_{2})^{2} = 0,0025 Дж$.
Эта энергия и переходит в тепло.