Содержание
- Как найти количество тепла отданное холодильнику
- Задачи на КПД теплового двигателя: примеры решений
- Задачи по физике на КПД теплового двигателя
- Задача на вычисление КПД теплового двигателя №1
- Задача на вычисление КПД теплового двигателя №2
- Задача на вычисление КПД теплового двигателя №3
- Задача на вычисление КПД теплового двигателя №4
- Задача на вычисление КПД теплового двигателя №5
- Вопросы на тему тепловые двигатели
- Задачи и вопросы на цикл Карно
- Задача на цикл Карно №1
- Задача на цикл Карно №2
- Задача на цикл Карно №3
- Вопрос на цикл Карно №1
- Вопрос на цикл Карно №2
- Тепловые машины
- Тепловые двигатели
- Холодильные машины
- Тепловая машина Карно
- Тепловые двигатели и охрана окружающей среды
Как найти количество тепла отданное холодильнику
Температуру холодильника идеальной тепловой машины увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины, количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Количество теплоты, отданное газом
холодильнику за цикл работы |
Работа газа за цикл |
Если повысить температуру холодильника при неизменной температуре нагревателя, КПД идеальной тепловой машины уменьшится: КПД связано с работой газа и количеством теплоты, полученным газом за цикл, соотношением
Таким образом, при повышении температуры холодильника работа газа за цикл уменьшится. Отданное холодильнику количество теплоты можно найти из закона сохранения энергии:
Так как после повышения температуры холодильника количество теплоты
останется неизменным, а работа уменьшится, количество теплоты, отданное холодильнику за цикл работы, увеличится.
Источник
Задачи на КПД теплового двигателя: примеры решений

- 10 марта 2022 г.
- 13 минут
- 78 200
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
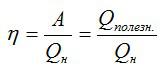
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
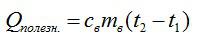
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
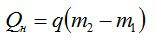
Подставляем значения и вычисляем:
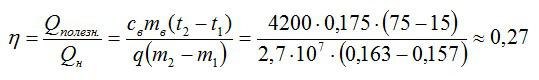
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
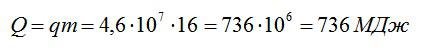
Теперь можно рассчитать КПД:
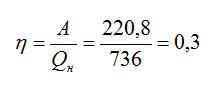
Или, умножая на 100, получаем значение КПД в процентах:
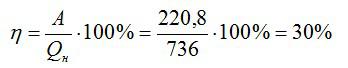
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
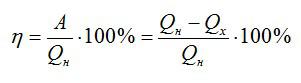
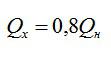
Вычислим сначала работу, а затем КПД:
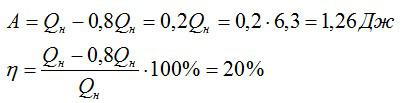
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
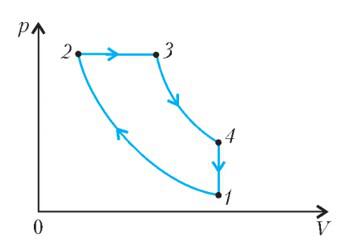
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
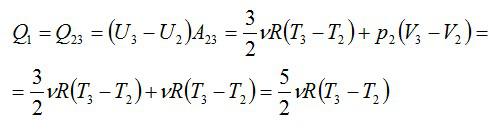
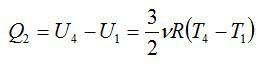
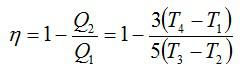
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
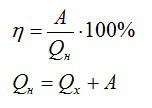
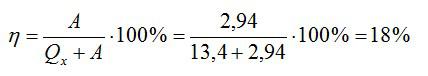
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
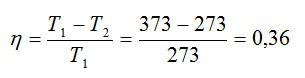
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
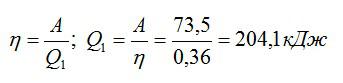
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
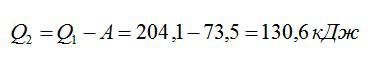
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
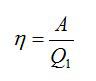
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
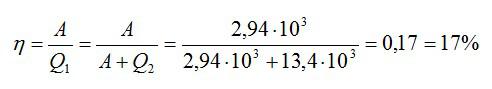
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
Тепловые машины
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: принципы действия тепловых машин, КПД тепловой машины, тепловые двигатели и охрана окружающей среды.
Коротко говоря, тепловые машины преобразуют теплоту в работу или, наоборот, работу в теплоту.
Тепловые машины бывают двух видов — в зависимости от направления протекающих в них процессов.
1. Тепловые двигатели преобразуют теплоту, поступающую от внешнего источника, в механическую работу.
2. Холодильные машины передают тепло от менее нагретого тела к более нагретому за счёт механической работы внешнего источника.
Рассмотрим эти виды тепловых машин более подробно.
Тепловые двигатели
Мы знаем, что совершение над телом работы есть один из способов изменения его внутренней энергии: совершённая работа как бы растворяется в теле, переходя в энергию беспорядочного движения и взаимодействия его частиц.

Рис. 1. Тепловой двигатель
Тепловой двигатель — это устройство, которое, наоборот, извлекает полезную работу из «хаотической» внутренней энергии тела. Изобретение теплового двигателя радикально изменило облик человеческой цивилизации.
Принципиальную схему теплового двигателя можно изобразить следующим образом (рис. 1 ). Давайте разбираться, что означают элементы данной схемы.
Рабочее тело двигателя — это газ. Он расширяется, двигает поршень и совершает тем самым полезную механическую работу.
Но чтобы заставить газ расширяться, преодолевая внешние силы, нужно нагреть его до температуры, которая существенно выше температуры окружающей среды. Для этого газ приводится в контакт с нагревателем — сгорающим топливом.
В процессе сгорания топлива выделяется значительная энергия, часть которой идёт на нагревание газа. Газ получает от нагревателя количество теплоты . Именно за счёт этого тепла двигатель совершает полезную работу .
Это всё понятно. Что такое холодильник и зачем он нужен?
При однократном расширении газа мы можем использовать поступающее тепло максимально эффективно и целиком превратить его в работу. Для этого надо расширять газ изотермически: первый закон термодинамики, как мы знаем, даёт нам в этом случае .
Но однократное расширение никому не нужно. Двигатель должен работать циклически, обеспечивая периодическую повторяемость движений поршня. Следовательно, по окончании расширения газ нужно сжимать, возвращая его в исходное состояние.
В процессе расширения газ совершает некоторую положительную работу . В процессе сжатия над газом совершается положительная работа (а сам газ совершает отрицательную работу ). В итоге полезная работа газа за цикл: .
Разумеется, должно быть 0′ alt=’A>0′/> , или (иначе никакого смысла в двигателе нет).
Сжимая газ, мы должны совершить меньшую работу, чем совершил газ при расширении.
Как этого достичь? Ответ: сжимать газ под меньшими давлениями, чем были в ходе расширения. Иными словами, на -диаграмме процесс сжатия должен идти ниже процесса расширения, т. е. цикл должен проходиться по часовой стрелке (рис. 2 ).

Рис. 2. Цикл теплового двигателя
Например, в цикле на рисунке работа газа при расширении равна площади криволинейной трапеции . Аналогично, работа газа при сжатии равна площади криволинейной трапеции со знаком минус. В результате работа газа за цикл оказывается положительной и равной площади цикла .
Хорошо, но как заставить газ возвращаться в исходное состояние по более низкой кривой, т. е. через состояния с меньшими давлениями? Вспомним, что при данном объёме давление газа тем меньше, чем ниже температура. Стало быть, при сжатии газ должен проходить состояния с меньшими температурами.
Вот именно для этого и нужен холодильник: чтобы охлаждать газ в процессе сжатия.
Холодильником может служить атмосфера (для двигателей внутреннего сгорания) или охлаждающая проточная вода (для паровых турбин). При охлаждении газ отдаёт холодильнику некоторое количество теплоты .
Суммарное количество теплоты, полученное газом за цикл, оказывается равным . Согласно первому закону термодинамики:
где — изменение внутренней энергии газа за цикл. Оно равно нулю: , так как газ вернулся в исходное состояние (а внутренняя энергия, как мы помним, является функцией состояния). В итоге работа газа за цикл получается равна:
Как видите, : не удаётся полностью превратить в работу поступающее от нагревателя тепло. Часть теплоты приходится отдавать холодильнику — для обеспечения цикличности процесса.
Показателем эффективности превращения энергии сгорающего топлива в механическую работу служит коэффициент полезного действия теплового двигателя.
КПД теплового двигателя — это отношение механической работы к количеству теплоты , поступившему от нагревателя:
С учётом соотношения (1) имеем также
КПД теплового двигателя, как видим, всегда меньше единицы. Например, КПД паровых турбин приблизительно , а КПД двигателей внутреннего сгорания около .
Холодильные машины
Житейский опыт и физические эксперименты говорят нам о том, что в процессе теплообмена теплота передаётся от более нагретого тела к менее нагретому, но не наоборот. Никогда не наблюдаются процессы, в которых за счёт теплообмена энергия самопроизвольно переходит от холодного тела к горячему, в результате чего холодное тело ещё больше остывало бы, а горячее тело — ещё больше нагревалось.

Рис. 3. Холодильная машина
Ключевое слово здесь — «самопроизвольно». Если использовать внешний источник энергии, то осуществить процесс передачи тепла от холодного тела к горячему оказывается вполне возможным. Это и делают холодильные
машины.
По сравнению с тепловым двигателем процессы в холодильной машине имеют противоположное направление (рис. 3 ).
Рабочее тело холодильной машины называют также хладагентом. Мы для простоты будем считать его газом, который поглощает теплоту при расширении и отдаёт при сжатии (в реальных холодильных установках хладагент — это летучий раствор с низкой температурой кипения, который забирает теплоту в процессе испарения и отдаёт при конденсации).
Холодильник в холодильной машине — это тело, от которого отводится теплота. Холодильник передаёт рабочему телу (газу) количество теплоты , в результате чего газ расширяется.
В ходе сжатия газ отдаёт теплоту более нагретому телу — нагревателю. Чтобы такая теплопередача осуществлялась, надо сжимать газ при более высоких температурах, чем были при расширении. Это возможно лишь за счёт работы , совершаемой внешним источником (например, электродвигателем (в реальных холодильных агрегатах электродвигатель создаёт в испарителе низкое давление, в результате чего хладагент вскипает и забирает тепло; наоборот, в конденсаторе электродвигатель создаёт высокое давление, под которым хладагент конденсируется и отдаёт тепло)). Поэтому количество теплоты, передаваемое нагревателю, оказывается больше количества теплоты, забираемого от холодильника, как раз на величину :
Таким образом, на -диаграмме рабочий цикл холодильной машины идёт против часовой стрелки. Площадь цикла — это работа , совершаемая внешним источником (рис. 4 ).

Рис. 4. Цикл холодильной машины
Основное назначение холодильной машины — охлаждение некоторого резервуара (например, морозильной камеры). В таком случае данный резервуар играет роль холодильника, а нагревателем служит окружающая среда — в неё рассеивается отводимое от резервуара тепло.
Показателем эффективности работы холодильной машины является холодильный коэффициент, равный отношению отведённого от холодильника тепла к работе внешнего источника:
Холодильный коэффициент может быть и больше единицы. В реальных холодильниках он принимает значения приблизительно от 1 до 3.
Имеется ещё одно интересное применение: холодильная машина может работать как тепловой насос. Тогда её назначение — нагревание некоторого резервуара (например, обогрев помещения) за счёт тепла, отводимого от окружающей среды. В данном случае этот резервуар будет нагревателем, а окружающая среда — холодильником.
Показателем эффективности работы теплового насоса служит отопительный коэффициент, равный отношению количества теплоты, переданного обогреваемому резервуару, к работе внешнего источника:
Значения отопительного коэффициента реальных тепловых насосов находятся обычно в диапазоне от 3 до 5.
Тепловая машина Карно
Важными характеристиками тепловой машины являются наибольшее и наименьшее значения температуры рабочего тела в ходе цикла. Эти значения называются соответственно температурой нагревателя и температурой холодильника.
Мы видели, что КПД теплового двигателя строго меньше единицы. Возникает естественный вопрос: каков наибольший возможный КПД теплового двигателя с фиксированными значениями температуры нагревателя и температуры холодильника ?
Пусть, например, максимальная температура рабочего тела двигателя равна , а минимальная — . Каков теоретический предел КПД такого двигателя?
Ответ на поставленный вопрос дал французский физик и инженер Сади Карно в 1824 году.
Он придумал и исследовал замечательную тепловую машину с идеальным газом в качестве рабочего тела. Эта машина работает по циклу Карно, состоящему из двух изотерм и двух адиабат.
Рассмотрим прямой цикл машины Карно, идущий по часовой стрелке (рис. 5 ). В этом случае машина функционирует как тепловой двигатель.

Рис. 5. Цикл Карно
Изотерма . На участке газ приводится в тепловой контакт с нагревателем температуры и расширяется изотермически. От нагревателя поступает количество теплоты и целиком превращается в работу на этом участке: .
Адиабата . В целях последующего сжатия нужно перевести газ в зону более низких температур. Для этого газ теплоизолируется, а затем расширяется адиабатно на учатке .
При расширении газ совершает положительную работу , и за счёт этого уменьшается его внутренняя энергия: .
Изотерма . Теплоизоляция снимается, газ приводится в тепловой контакт с холодильником температуры . Происходит изотермическое сжатие. Газ отдаёт холодильнику количество теплоты и совершает отрицательную работу .
Адиабата . Этот участок необходим для возврата газа в исходное состояние. В ходе адиабатного сжатия газ совершает отрицательную работу , а изменение внутренней энергии положительно: . Газ нагревается до исходной температуры .
Карно нашёл КПД этого цикла (вычисления, к сожалению, выходят за рамки школьной программы):
Кроме того, он доказал, что КПД цикла Карно является максимально возможным для всех тепловых двигателей с температурой нагревателя и температурой холодильника .
Так, в приведённом выше примере имеем:
В чём смысл использования именно изотерм и адиабат, а не каких-то других процессов?
Оказывается, изотермические и адиабатные процессы делают машину Карно обратимой. Её можно запустить по обратному циклу (против часовой стрелки) между теми же нагревателем и холодильником, не привлекая другие устройства. В таком случае машина Карно будет функционировать как холодильная машина.
Возможность запуска машины Карно в обоих направлениях играет очень большую роль в термодинамике. Например, данный факт служит звеном доказательства максимальности КПД цикла Карно. Мы ещё вернёмся к этому в следующей статье, посвящённой второму закону термодинамики.
Тепловые двигатели и охрана окружающей среды
Тепловые двигатели наносят серьёзный ущерб окружающей среде. Их повсеместное использование приводит к целому ряду негативных эффектов.
• Рассеяние в атмосферу огромного количества тепловой энергии приводит к повышению температуры на планете. Потепление климата грозит обернуться таянием ледников и катастрофическими бедствиями.
• К потеплению климата ведёт также накопление в атмосфере углекислого газа, который замедляет уход теплового излучения Земли в космос (парниковый эффект).
• Из-за высокой концентрации продуктов сгорания топлива ухудшается экологическая ситуация.
Это — проблемы в масштабе всей цивилизации. Для борьбы с вредными последствиями работы тепловых двигателей следует повышать их КПД, снижать выбросы токсичных веществ, разрабатывать новые виды топлива и экономно расходовать энергию.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Тепловые машины» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Источник
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
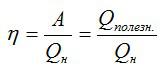
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
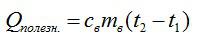
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
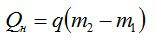
Подставляем значения и вычисляем:
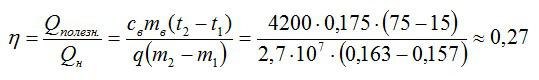
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
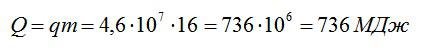
Теперь можно рассчитать КПД:
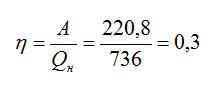
Или, умножая на 100, получаем значение КПД в процентах:
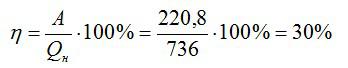
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
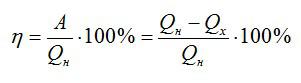
По условию:
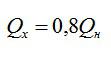
Вычислим сначала работу, а затем КПД:
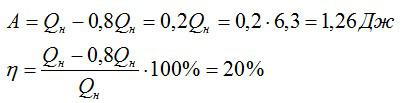
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
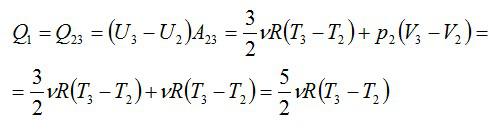
Аналогично:
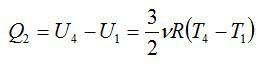
Получим результат:
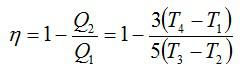
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
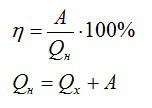
Отсюда:
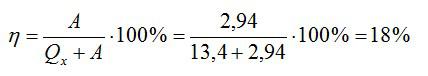
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
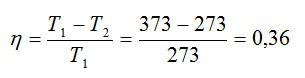
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
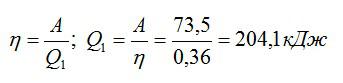
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
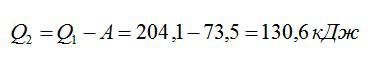
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
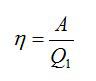
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
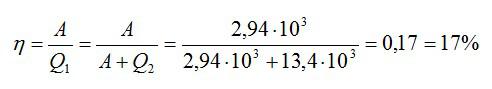
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
На
прошлых уроках мы с вами познакомились с понятием «внутренняя энергия тела» и
узнали, что изменить её можно двумя способами: либо путём совершения
механической работы, либо теплопередачей.
Также
мы с вами выяснили, что мерой изменения внутренней энергии тела при
теплопередаче является количество теплоты. Давайте вспомним, что количество
теплоты — это скалярная физическая величина, равная изменению внутренней
энергии тела в процессе теплопередачи без совершения механической работы.
А
ещё мы получили уравнение, по которому можно рассчитать количество теплоты,
которое необходимо подвести к телу для его нагревания, или выделяемое телом,
при его охлаждении:
Q
= cm(t
– t0).
Из
формулы видно, что количество теплоты зависит от массы тела, разности
температур в конечном и начальном состояниях, а также от удельной теплоёмкости
вещества, из которого это тело изготовлено.
Чтобы
вспомнить, же что же такое теплоёмкость, рассмотрим решение следующей задачи.
Задача
1.
В сосуд с горячей водой опустили алюминиевую и латунную болванки одинаковой
массы и температуры. Одинаковым ли будет изменение их температур?
В
жизненных ситуациях довольно часто возникает необходимость в тепловых расчётах.
Например, при строительстве жилых домов необходимо знать, какое количество
теплоты должна отдавать зданию система отопления. Или нужно определить
температуру после смешивания горячей и холодной воды. И на этом уроке мы
разберёмся, как проводятся такие расчёты.
Последовательность
действий при решении задач на расчёт теплообменных процессов:
Задача
2.
Для купания ребёнка температура воды в ванночке не должна превышать 38 оС.
Для этого родители смешали 40 кг холодной воды при температуре 12 оС
и 20 кг горячей воды при температуре 90 оС. Если потерями тепла
можно пренебречь, то какое количество теплоты получили холодная вода при
нагревании и отдала горячая вода при охлаждении?
Мы
получили, что количество теплоты, отданное горячей водой, равно количеству
теплоты, полученному водой холодной. И это не случайно. Вспомните: если
между телами происходит теплообмен, то внутренняя энергия всех нагревающихся
тел увеличивается ровно на столько, на сколько уменьшается внутренняя энергия
остывающих тел.
Конечно
в реальных условиях количество теплоты, отданное горячей водой, всегда будет
больше чем-то количество теплоты, которое получит холодная вода. Это
объясняется тем, что часть энергии идёт на нагревание сосуда, в котором
находилась вода, а ещё часть теряется на нагревание окружающего воздуха.
Теперь
мы можем внести дополнительный пункт в нашу последовательность действий при
решении задач — пункт о необходимости составления уравнения теплового
баланса.
Количество
теплоты, отданное или полученное телом, можно измерить с помощью прибора,
который называется калориметр.
Школьный калориметр
Школьный
калориметр состоит из двух стаканов, вставленных один в другой. Воздушная
прослойка и подставка между ними уменьшают теплопередачу между содержимым
внутреннего стакана и окружающим воздухом.
Задача
3.
Калориметр содержит 3 л воды при температуре 80 оС. В воду опускают
нагретый на плитке кирпич массой 1,5 кг. Определите начальную температуру
кирпича, если в результате теплообмена температура воды повысилась до 9 оС.
Теплопередачей калориметру и окружающему воздуху можно пренебречь.
Обратите
внимание на то, что в некоторых задачах теплоёмкостью калориметра пренебрегать
нельзя. В этом случае необходимо учитывать, что и вода, и калориметр будут
нагреваться или охлаждаться вместе. А их температуры можно считать одинаковыми.
Количество
теплоты ![]() ,
,
Дж,
отданное (воспринятое) телом за
время τ
в
процессе охлаждения (нагревания), равно
![]() ,
,
(4.11) где
![]() -количество
-количество
теплоты, переданное за время полного
охлаждения (нагревания), Дж; ![]()
— средняя по объему безразмерная
температура тела в момент времени τ
.
Для
пластины
толщиной
2δ и площадью поверхности F
теплота,
переданная за время полного охлаждения,
равна
![]() (4.12)
(4.12)
где m
—
масса пластины, кг; с
—
теплоемкость материала пластины,
Дж/(кг∙К); ![]() — его
— его
плотность, кг/м3.
Средняя
по объему безразмерная температура
пластины в момент времени τ:
при
Fо≥0,3
 .(4.13)
.(4.13)
Для
цилиндра
радиусом
![]()
и
длиной l
теплота,
отданная за время полного охлаждения,
равна
![]() .(4.14)
.(4.14)
Средняя
по объему безразмерная температура
цилиндра в момент времени τ
при Fо≥0,3
равна
 .(4.15)
.(4.15)
Средняя безразмерная
температура цилиндра конечной длины
![]() ,(4.16)
,(4.16)
где
функция ![]()
определяется
по формуле (4.13), а ![]()
— по (4.15).
Для
параллелепипеда
со
сторонами ![]() ,
,![]()
, ![]()
(рис. 7) теплота, отданная за время
полного охлаждения, равна
![]() .(4.17)
.(4.17)
Средняя безразмерная
температура параллелепипеда
![]() ,(4.18)
,(4.18)
где функции ![]() ,
,![]() ,
,![]()
определяются по формуле (4.14).
Если
Fо<0,3,
то для вычисления ![]()
используется ряд, члены которого
определяются формулами типа (4.14), (4.16),
причем величины ![]() ,
,![]() ,
,
…,![]()
определяются по таблицам, приведенным,
например, в [12].
Лекция
№12
Тема: Нестационарный
процесс теплопроводности.
План лекции
4.4. Регулярный
режим охлаждения (нагревания) тел
4.4. Регулярный режим охлаждения (нагревания) тел
Теорию
регулярного режима разработал Г. М.
Кондратьев. Процесс охлаждения тела в
среде с постоянной температурой tж
и постоянным коэффициентом теплоотдачи
α можно разделить на три режима:
1)
неупорядоченный
—
на процесс влияет начальное распределение
температуры в теле;
2)
регулярный
—
в любой точке тела относительная скорость
изменения температуры, называемая
темпом охлаждения (нагревания)
остается постоянной и не зависит от
времени;
3)
стационарный
—
температура во всех точках тела равна
температуре среды (тепловое равновесие).
В
регулярном режиме темп охлаждения
(нагревания), m,
![]() ,
,
определенный по двум моментам времени
![]()
и ![]() ,
,
равен
![]() ,(4.19)
,(4.19)
где
![]() и
и![]() —избыточные
—избыточные
температуры в любой точке тела в моменты
времени ![]()
и
![]()
.
Темп
охлаждения т
зависит
от физических свойств тела, его размеров
и формы, коэффициента теплоотдачи и не
зависит от времени и координат.
Первая
теорема Г. М. Кондратьева для регулярного
режима выражается формулой
![]() ,(4.20)
,(4.20)
где
F
и V
—
площадь поверхности и объем тела; ψ —
коэффициент неравномерности распределения
температуры в теле, определяемый
следующим образом:
![]() ,(4.21)
,(4.21)
где
![]() —
—
модифицированная форма числа Bi
; K
— коэффициент
формы
тела, м2.
Коэффициент
ψ зависит от условий процесса на
поверхности тела при Вi<0,1
ψ = 1 (температуры, усредненные по
поверхности и объему тела, одинаковы),
при Вi>100
ψ = 0 (температура поверхности тела
равна температуре среды).
Вторая
теорема Г. М. Кондратьева: при высокой
интенсивности
теплоотдачи
темп охлаждения пропорционален
коэффициенту температуропроводности
материала тела а,
м2/с:
![]() .(4.22)
.(4.22)
Коэффициент
формы К.
различных
тел:
для
шара радиусом ![]()
![]()
;
(4.23)
для
цилиндра
длиной l
и радиусом r0
 ;(4.24)
;(4.24)
для
параллелепипеда со сторонами a,
b,
c
![]()
.
(4.25)
Лекция
№ 13
Тема:
ТЕОРИЯ ПОДОБИЯ ПРИМЕНИТЕЛЬНО К ТЕПЛОВЫМ
ПРОЦЕССАМ
План лекции
5.1
Числа теплового и гидромеханического
подобия
процессов
При
экспериментальном изучении тепловых
процессов принято выражать математическое
описание процесса и расчетные уравнения
в виде зависимостей между числами
(критериями) подобия, представляющими
собой безразмерные комплексы.
Уравнения
подобия, выражая обобщенную зависимость
между величинами, характеризующими
процесс, справедливы для всех подобных
между собой процессов. Первая теорема
подобия: для подобных между собой
процессов все одноименные числа подобия
численно одинаковы, например Re
= idem,
Pr
= idem.
Согласно второй теореме подобия связь
между числами подобия выражается в
форме однозначной функциональной
зависимости, например Nu=f
(Rе,
Рr,
Gг,
…).
Третья
теорема подобия утверждает, что условия
подобия физических явлений, заключаются
в подобии условий однозначности и
равенстве одноименных чисел подобия,
составленных из величин, входящих в
эти условия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет количества теплоты при нагревании и охлаждении:
Вы уже знаете, что изменить внутреннюю энергию тела можно передачей ему количества теплоты. Как связано изменение внутренней энергии тела, т. е. количество теплоты, с характеристиками самого тела?
Внутренняя энергия тела есть суммарная энергия всех его частиц. Значит, если массу данного тела увеличить в два или три раза, то и количество теплоты, необходимое для его нагревания на одно и то же число градусов, увеличится в два или три раза. Например, на нагревание двух килограммов воды от 20 °C до 80 °C потребуется в два раза больше теплоты, чем на нагревание одного килограмма воды (рис. 40, а).
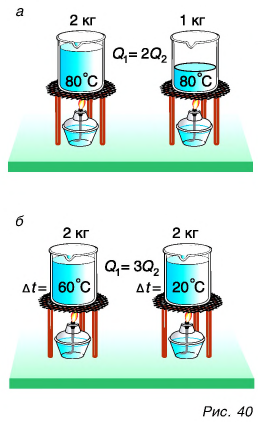
Очевидно также, что для нагревания воды на 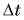
Из этих рассуждений следует подтвержденный опытами вывод. Количество теплоты, необходимое для нагревания тела, прямо пропорционально его массе и изменению температуры.
А зависит ли количество теплоты, идущее на нагревание, от рода вещества, которое нагревается?
Для ответа на этот вопрос проведем опыт. В два одинаковых стакана нальем по 150 г подсолнечного масла и воды. Поместим в них термометры и поставим на нагреватель (рис. 41).
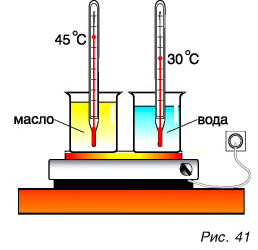
Получив за одинаковое время от нагревателя равное с водой количество теплоты, масло нагрелось больше, чем вода. Значит, для изменения температуры масла на одну и ту же величину требуется меньше теплоты, чем для изменения температуры такой же массы воды.
Поэтому для всех веществ вводят специальную величину — удельную теплоемкость вещества. Эту величину обозначают буквой с (от лат. capacite — емкость, вместимость). Теперь мы можем записать строгую формулу для количества теплоты, необходимого для нагревания:
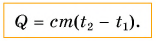
Выразим из этой формулы с: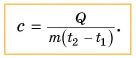
Удельная теплоемкость есть физическая величина, численно равная количеству теплоты, которое необходимо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C. Удельная теплоемкость измеряется в джоулях на килограмм-градус Цельсия 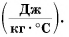
Для любознательных:
Часто формулу 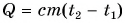 записывают в виде
записывают в виде 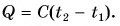 Здесь величина
Здесь величина 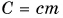 называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия
называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия 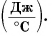
В таблице 1 представлены значения удельной теплоемкости различных веществ (в различных состояниях). Как следует из этой таблицы, среди жидкостей максимальное значение удельной теплоемкости имеет вода: для нагревания 1 кг воды на 1 °C требуется 4200 Дж теплоты — это почти в 2,5 раза больше, чем для нагревания 1 кг подсолнечного масла, и в 35 раз больше, чем для нагревания 1 кг ртути.
Формула 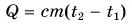 дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура
дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура 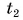 остывшего тела меньше начальной
остывшего тела меньше начальной 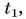 то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
В заключение заметим, что при теплообмене двух или нескольких тел абсолютное значение количества теплоты, которое отдано более нагретым телом (телами), равно количеству теплоты, которое получено более холодным телом (телами):
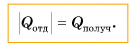
Это равенство называется уравнением теплового баланса и выражает, по сути, закон сохранения энергии. Оно справедливо при отсутствии потерь теплоты.
Таблица 1. Удельная теплоемкость некоторых веществ
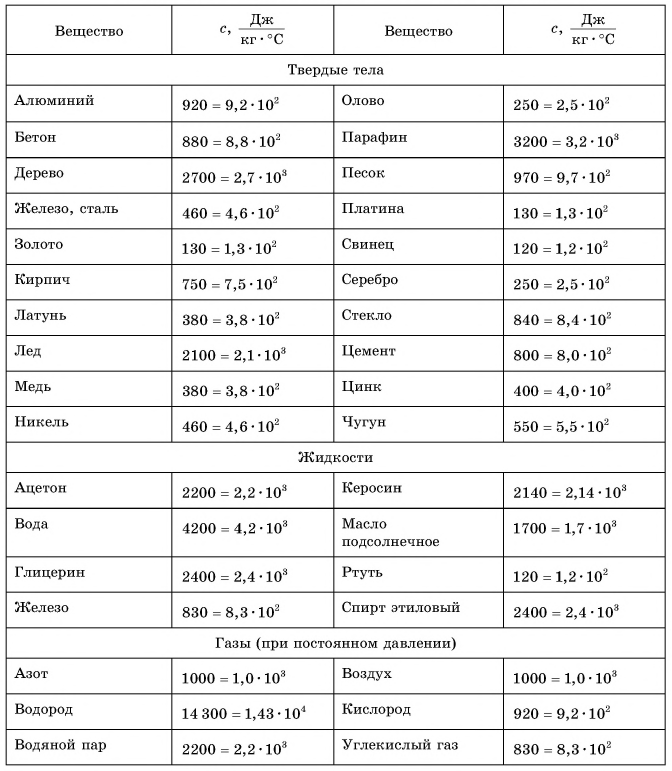
Главные выводы:
- Количество теплоты, необходимое для нагревания тела (выделившееся при охлаждении), прямо пропорционально его массе, изменению температуры тела и зависит от вещества тела.
- Удельная теплоемкость вещества численно равна количеству теплоты, которое надо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C.
- При теплообмене количество теплоты, отданное более горячим телом, равно по модулю количеству теплоты, полученному более холодным телом, если нет потерь теплоты.
- Заказать решение задач по физике
Пример решения задачи:
Для купания ребенка в ванночку влили холодную воду массой 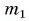 = 20 кг при температуре
= 20 кг при температуре 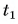 = 12 °C. Какую массу горячей воды при температуре
= 12 °C. Какую массу горячей воды при температуре 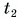 = 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала
= 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала 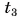 = 37 °C? Удельная теплоемкость воды с = 4200
= 37 °C? Удельная теплоемкость воды с = 4200 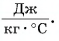
Дано:
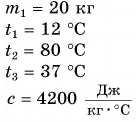
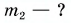
Решение
По закону сохранения энергии 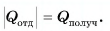
Отдавала теплоту горячая вода, изменяя свою температуру от 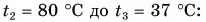
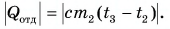
Холодная вода получила эту теплоту и нагрелась от 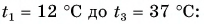
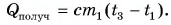
Так как нас интересует только модуль 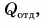 то можно записать:
то можно записать:
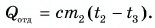
Тогда 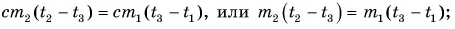
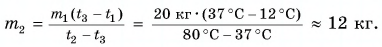
При решении мы пренебрегали потерями теплоты на нагревание ванночки, окружающего воздуха и т. д.
Возможен и другой вариант решения.
Рассчитаем сначала количество теплоты, которое было получено холодной водой:
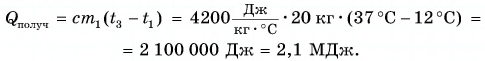
Полагая, что эта теплота отдана горячей водой, запишем: 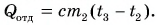 Выразим искомую массу:
Выразим искомую массу:
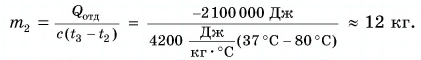
Ответ: 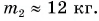
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
- Поверхностное натяжение жидкости
- Излучение тепла в физике
- Виды излучений в физике
- Инфракрасные излучения
- Количество теплоты в физике
