Расчет количества теплоты при нагревании и охлаждении:
Вы уже знаете, что изменить внутреннюю энергию тела можно передачей ему количества теплоты. Как связано изменение внутренней энергии тела, т. е. количество теплоты, с характеристиками самого тела?
Внутренняя энергия тела есть суммарная энергия всех его частиц. Значит, если массу данного тела увеличить в два или три раза, то и количество теплоты, необходимое для его нагревания на одно и то же число градусов, увеличится в два или три раза. Например, на нагревание двух килограммов воды от 20 °C до 80 °C потребуется в два раза больше теплоты, чем на нагревание одного килограмма воды (рис. 40, а).
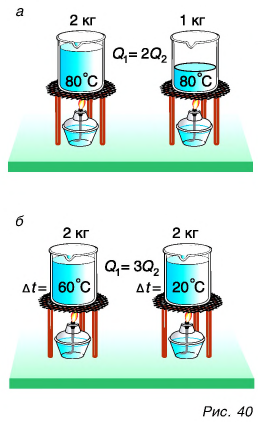
Очевидно также, что для нагревания воды на 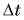
Из этих рассуждений следует подтвержденный опытами вывод. Количество теплоты, необходимое для нагревания тела, прямо пропорционально его массе и изменению температуры.
А зависит ли количество теплоты, идущее на нагревание, от рода вещества, которое нагревается?
Для ответа на этот вопрос проведем опыт. В два одинаковых стакана нальем по 150 г подсолнечного масла и воды. Поместим в них термометры и поставим на нагреватель (рис. 41).
Получив за одинаковое время от нагревателя равное с водой количество теплоты, масло нагрелось больше, чем вода. Значит, для изменения температуры масла на одну и ту же величину требуется меньше теплоты, чем для изменения температуры такой же массы воды.
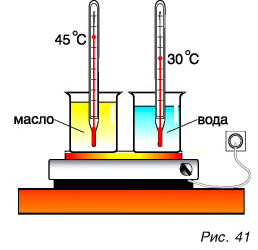
Поэтому для всех веществ вводят специальную величину — удельную теплоемкость вещества. Эту величину обозначают буквой с (от лат. capacite — емкость, вместимость). Теперь мы можем записать строгую формулу для количества теплоты, необходимого для нагревания:
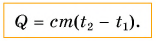
Выразим из этой формулы с: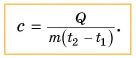
Удельная теплоемкость есть физическая величина, численно равная количеству теплоты, которое необходимо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C. Удельная теплоемкость измеряется в джоулях на килограмм-градус Цельсия 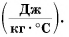
Для любознательных:
Часто формулу 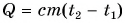 записывают в виде
записывают в виде 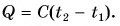 Здесь величина
Здесь величина 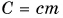 называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия
называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия 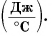
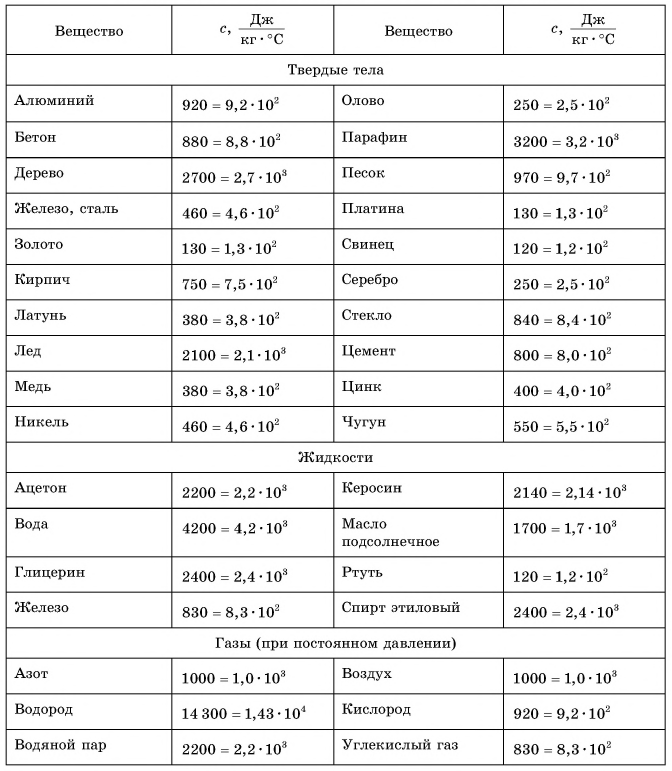
В таблице 1 представлены значения удельной теплоемкости различных веществ (в различных состояниях). Как следует из этой таблицы, среди жидкостей максимальное значение удельной теплоемкости имеет вода: для нагревания 1 кг воды на 1 °C требуется 4200 Дж теплоты — это почти в 2,5 раза больше, чем для нагревания 1 кг подсолнечного масла, и в 35 раз больше, чем для нагревания 1 кг ртути.
Формула 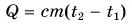 дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура
дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура 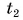 остывшего тела меньше начальной
остывшего тела меньше начальной 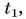 то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
В заключение заметим, что при теплообмене двух или нескольких тел абсолютное значение количества теплоты, которое отдано более нагретым телом (телами), равно количеству теплоты, которое получено более холодным телом (телами):
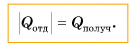
Это равенство называется уравнением теплового баланса и выражает, по сути, закон сохранения энергии. Оно справедливо при отсутствии потерь теплоты.
Таблица 1. Удельная теплоемкость некоторых веществ
Главные выводы:
- Количество теплоты, необходимое для нагревания тела (выделившееся при охлаждении), прямо пропорционально его массе, изменению температуры тела и зависит от вещества тела.
- Удельная теплоемкость вещества численно равна количеству теплоты, которое надо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C.
- При теплообмене количество теплоты, отданное более горячим телом, равно по модулю количеству теплоты, полученному более холодным телом, если нет потерь теплоты.
- Заказать решение задач по физике
Пример решения задачи:
Для купания ребенка в ванночку влили холодную воду массой 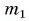 = 20 кг при температуре
= 20 кг при температуре 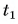 = 12 °C. Какую массу горячей воды при температуре
= 12 °C. Какую массу горячей воды при температуре 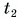 = 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала
= 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала 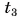 = 37 °C? Удельная теплоемкость воды с = 4200
= 37 °C? Удельная теплоемкость воды с = 4200 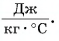
Дано:
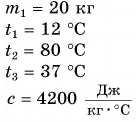
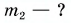
Решение
По закону сохранения энергии 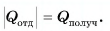
Отдавала теплоту горячая вода, изменяя свою температуру от 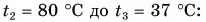
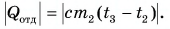
Холодная вода получила эту теплоту и нагрелась от 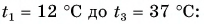
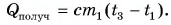
Так как нас интересует только модуль 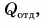 то можно записать:
то можно записать:
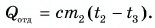
Тогда 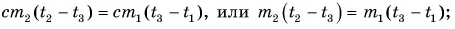
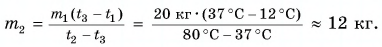
При решении мы пренебрегали потерями теплоты на нагревание ванночки, окружающего воздуха и т. д.
Возможен и другой вариант решения.
Рассчитаем сначала количество теплоты, которое было получено холодной водой:
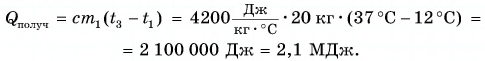
Полагая, что эта теплота отдана горячей водой, запишем: 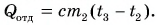 Выразим искомую массу:
Выразим искомую массу:
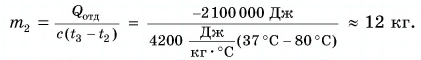
Ответ: 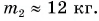
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
- Поверхностное натяжение жидкости
- Излучение тепла в физике
- Виды излучений в физике
- Инфракрасные излучения
- Количество теплоты в физике
Количество теплоты — еще один изученный нами вид энергии. Эту энергию тело получает или отдает при теплопередаче. Мы установили, что количество теплоты, необходимое для нагревания тела, зависит от массы тела, разности температур и рода вещества. Нам известен физический смысл удельной теплоемкости и некоторые ее табличные значения для разных веществ. В этом уроке мы перейдем к численному расчету количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении.
Зачем это нужно? На самом деле, на практике очень часто используют подобные расчеты.
При строительстве зданий и проектировании систем отопления важно знать, какое количество теплоты необходимо отдавать для полного обогрева всех помещений. С другой стороны, также необходима информация о том, какое количество теплоты будет уходить через окна, стены и двери.
Формула для расчета количества теплоты
Допустим, на нужно узнать, какое количество теплоты получила при нагревании железная деталь. Масса детали $3 space кг$. Деталь нагрелась от $20 degree C$ до $300 degree C$.
Возьмем значение теплоемкости железа из таблицы — $460 frac{Дж}{кг cdot degree C}$. Объясним смысл этой величины: на нагревание куска железа массой $1 space кг$ на $1 degree C$ необходимо затратить количество теплоты, равное $460 space Дж$.
- Масса детали у нас в 3 раза больше, значит, на ее нагрев потребуется в 3 раза большее количество теплоты — $1380 space Дж$
- Температура изменилась не на $1 degree C$, а на $280 degree C$
- Значит, необходимо в 280 раз большее количество теплоты: $1380 space Дж cdot 280 = 386 400 space Дж$
Тогда, формула для расчета количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении примет вид:
$Q = cm(t_2 — t_1)$,
где $Q$ — количество теплоты,
$c$ — удельная теплоемкость вещества, из которого состоит тело,
$m$ — масса тела,
$t_1$ — начальная температура тела,
$t_2$ — конечная температура тела.
Чтобы рассчитать количество теплоты, которое необходимо затратить для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость умножить на массу тела и на разность конечной и начальной температур.
Рассмотрим подробнее особенности расчета количества теплоты на примерах решения задач.
Расчет количества теплоты, затраченного на нагревание двух тел
В железный котелок массой $4 space кг$ налили воду массой $10 space кг$ (рисунок 1). Их температура $25 degree C$. Какое количество теплоты нужно затратить, чтобы нагреть котелок и воду до температуры $100 degree C$?
Обратите внимание, что нагреваться будут сразу два тела: и котелок, и вода в нем. Между постоянно будет происходить теплообмен. Поэтому их температуры мы можем считать одинаковыми.
Отметим, что массы котелка и воды различные. Также они имеют различные теплоемкости. Значит, полученные ими количества теплоты будет различными.
Теперь мы можем записать условие задачи и решить ее.
Дано:
$m_1 = 4 space кг$
$c_1 = 460 frac{Дж}{кг cdot degree C}$
$m_2 = 10 space кг$
$c_2 = 4200 frac{Дж}{кг cdot degree C}$
$t_1 = 25 degree C$
$t_2 = 100 degree C$
Q-?
Посмотреть решение и ответ
Скрыть
Решение:
Для расчета полученного количества теплоты используем формулу $Q = cm(t_2 — t_1)$.
Запишем эту формулу для количества теплоты, полученного котелком:
$Q_1 = c_1m_1(t_2 — t_1)$.
Рассчитаем это количество теплоты:
$Q_1 = 460 frac{Дж}{кг cdot degree C} cdot 4 space кг cdot (100 degree C — 25 degree C) = 1840 frac{Дж}{degree C} cdot 75 degree C = 138 000 space Дж = 138 space кДж$.
Количество теплоты, полученное водой при нагревании будет равно:
$Q_2 = c_2m_2(t_2 — t_1)$.
Подставим численные значения и рассчитаем:
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 10 space кг cdot (100 degree C — 25 degree C) = 42000 frac{Дж}{degree C} cdot 75 degree C = 3 150 000 space Дж = 3150 space кДж$.
Общее количество теплоты, затраченное на нагревание котелка и воды:
$Q = Q_1 +Q_2$,
$Q = 138 space кДж + 3150 space кДж = 3288 space кДж$.
Ответ: $Q = 3288 space кДж$.
Расчет количества теплоты при смешивании жидкостей
Горячую воду разбавили холодной и получили температуру смеси $30 degree C$. Горячей воды с температурой $100 degree C$ при этом было $0.3 space кг$. Холодная вода имела массу $1.4 space кг$ и температуру $15 degree C$. Рассчитайте, какое количество теплоты было отдано горячей водой при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Дано:
$c_1 = c_2 = c = 4200 frac{Дж}{кг cdot degree C}$
$m_1 = 0.3 space кг$
$m_2 = 1.4 space кг$
$t_1 = 100 degree C$
$t_2 = 15 degree C$
$t = 30 degree C$
$Q_1 — ?$
$Q_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Запишем формулу для расчета количества теплоты, отданного горячей водой при остывании от $100 degree C$ до $30 degree C$:
$Q_1 = cm_1(t_1 — t)$.
Рассчитаем эту величину:
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 0.3 space кг cdot (100 degree C — 30 degree C) = 1260 frac{Дж}{degree C} cdot 70 degree C = 88 200 space Дж = 88.2 space кДж$.
Запишем формулу для расчета количества теплоты, полученного холодной водой при нагревании от $15 degree C$ до $30 degree C$:
$Q_2 = cm_2(t — t_2)$.
Рассчитаем эту величину:
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 1.4 space кг cdot (30 degree C — 15 degree C) = 5880 frac{Дж}{degree C} cdot 15 degree C = 88 200 space Дж = 88.2 space кДж$.
$Q_1 = Q_2 = 88.2 space кДж$.
Ответ: $Q_1 = Q_2 = 88.2 space кДж$.
В ходе решения этой задачи мы увидели, что количество теплоты, отданное горячей водой, и количество теплоты, полученное холодной водой, равны. Другие опыты дают схожие результаты.
Значит,
Если между телами происходит теплоообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
На практике часто получается так, что отданная горячей водой энергия больше, чем полученная холодной. На самом деле, горячая вода при охлаждении передает какую-то часть своей внутренней энергии воздуху и сосуду, в котором происходит смешивание.
Есть 2 способа учесть этот фактор:
- Если мы максимально сократим потери энергии, то добьемся приблизительного равенства отданной и полученной энергий
- Если рассчитать и учесть потери энергии, то можно получить точное равенство
Расчет температуры при известной величине количества теплоты
При нагревании куска меди было затрачено $22 space кДж$. Масса этого куска составляет $300 space г$. Начальная температура была равна $20 degree C$. До какой температуры нагрели кусок меди?
Дано:
$m = 300 space г$
$t_1 = 20 degree C$
$c = 400 frac{Дж}{кг cdot degree C}$
$Q = 22 space кДж$
СИ:
$0.3 space кг$
$22 000 space Дж$
$t_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Запишем формулу для расчета количества теплоты:
$Q = cm(t_2 — t_1)$.
Постепенно выразим из этой формулы искомую температуру $t_2$:
$t_2 — t_1 = frac{Q}{cm}$,
$t_2 = frac{Q}{cm} + t_1$.
Рассчитаем $t_2$:
$t_2 = frac{22 000 space Дж}{400 frac{Дж}{кг cdot degree C} cdot 0.3 space кг} + 20 degree C approx 183 degree C + 20 degree C approx 203 degree C$.
Ответ: $t_2 approx 203 degree C$.
На этой странице вы узнаете
- В чем прелесть фазовых переходов?
- Что лучше выбрать: Mercedes или BMW?
Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне.
Тепловые машины и их КПД
Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.
Вспомним, что фазовые переходы — это переход из одного агрегатного состояния в другое. При этом может выделяться большое количество теплоты.
Именно благодаря этому они и стали такими полезными для нас. Например, в ядерных реакторах воду используют в качестве рабочего тела, то есть она нагревается вследствие энергии, полученной из ядерных реакций, доходит до температуры кипения, а затем под большим давлением уже в качестве водяного пара воздействует на ротор генератора, который вращается и дает нам электроэнергию! На этом основан принцип работы атомных электростанций.
А самый простой пример фазового перехода — образование льда на лужах в морозные ноябрьские дни. Правда о выделении тепла здесь речи не идет.
Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.
Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую.
Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:
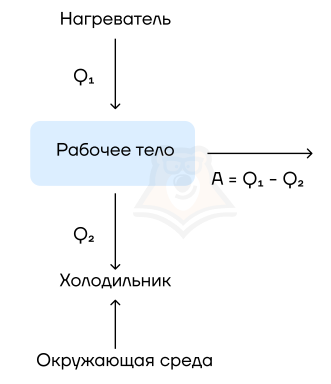
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q1, из которой A уходит на работу механизма. Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:
Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta) — КПД,
A — работа газа (Дж),
Q1 — количество теплоты, полученное от нагревателя (Дж).
Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери.
Полезную работу можно расписать как Q1 — Q2 (по закону сохранения энергии). Тогда формула примет вид:
(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})
Давайте попрактикуемся в применении данной формулы на задаче номер 9 из ЕГЭ.
Задача. Тепловая машина, КПД которой равен 60%, за цикл отдает холодильнику 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях).
Решение:
Давайте сначала вспомним нашу формулу для КПД:
(eta = frac{Q_1 — Q_2}{Q_1}),
где (Q_1) — это теплота, которую тело получает от нагревателя, (Q_2) — теплота, которая подводится к холодильнику.
Тогда отсюда можно вывести искомую теплоту нагревателя:
(eta Q_1 =Q_1-Q_2)
(eta Q_1 — Q_1= -Q_2)
(Q_1=frac{- Q_2}{eta-1}=frac{-100}{0,6-1}=250 Дж).
Ответ: 250 Дж
Цикл Карно
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).
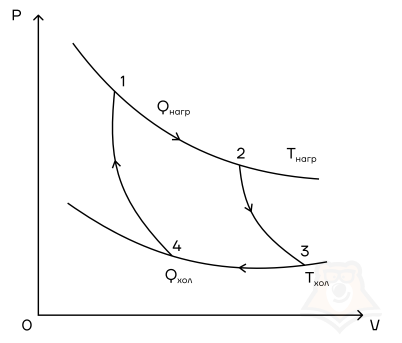
- Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
- Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
- 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.
Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД.
Формула, по которой можно рассчитать ее КПД выражается через температуры:
T1 — температура нагревателя,
T2 — температура холодильника.
Не то круто, что красиво, а то, что по Карно работает! Поэтому присматривайте такой автомобиль, у которого высокий КПД.
Интересно, что максимальный уровень КПД двигателя внутреннего сгорания автомобилей на данный момент всего около 43%. По официальным заявлениям компания Nissan Motor с 2021 года испытывает прообраз двигателя нового поколения с планируемым КПД 50%.
Приступим к задачам
Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.
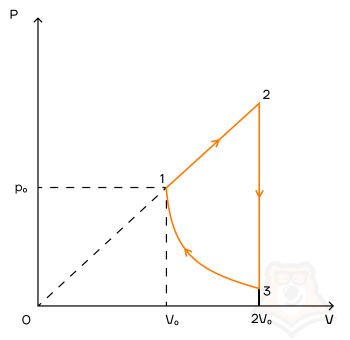
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A12 = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Qхол| = 4780 Дж. Найдите работу газа |A13| на адиабате, если количество вещества постоянно.
Решение:
Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов.
Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.
Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем.
Оформим все данные в таблицу.
Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.
Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде:
Q12 = ΔU12 + A12.
Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции:
(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}).
Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:
(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}).
Заметим, что это в 3 раза больше работы газа на этом участке:
(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).
Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A12 — |A31|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q12 — |Q31|.
Сравним эти формулы:
Q12 -|Q31| = A12 — |A31|,
подставим выражения из предыдущего пункта:
4A12 — |Q31| = A12 — |A31| (rightarrow) |A31| = -3A12 + |Q31| = -31520 + 4780 = 220 Дж.
Ответ: 220 Дж
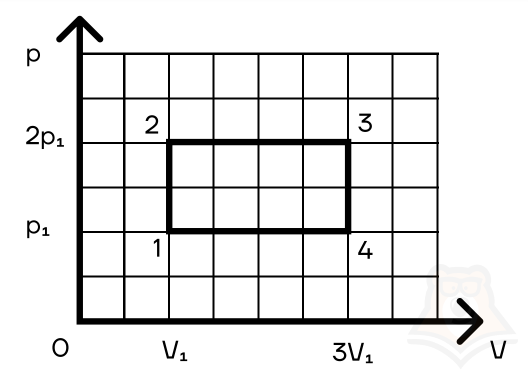
Задание 2. Найти КПД цикла для идеального одноатомного газа.
Решение:
Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p1 — p1)(3V1 — V1) = 2p1V1.
Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:
Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.
2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.
3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.
4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.
Оформим данные в таблицу:
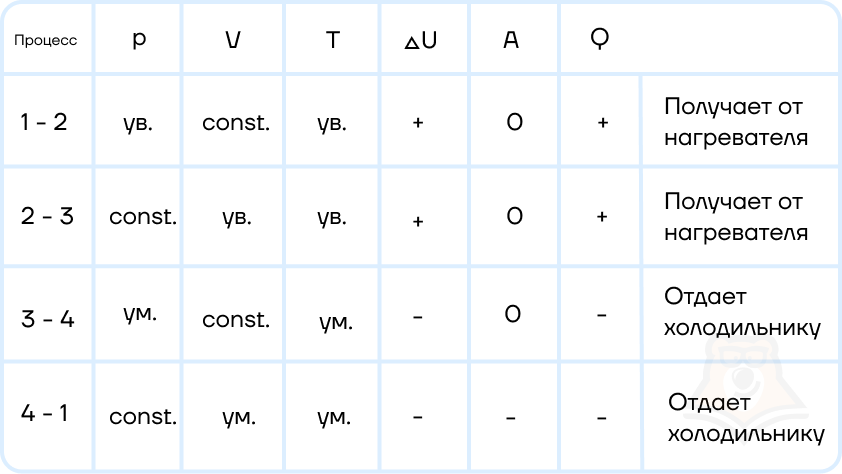
Отметим, что необходимое Q = Q12 + Q23.
Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:
(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A23 = 2p1(3V1 — V1) = 4p1V1.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).
Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).
Ответ: 17%
Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».
Фактчек
- Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую.
- Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
- Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1}) - Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
- Не забываем, что работа считается, как площадь фигуры под графиком.
Проверь себя
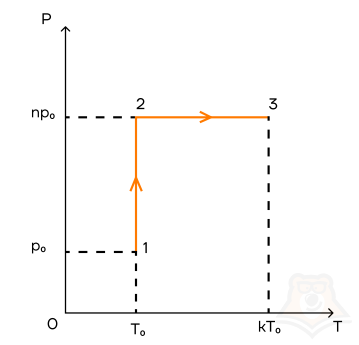
Задание 1.
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T0 = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.
- 5672 Дж
- 4731 Дж
- 5817 Дж
- 6393 Дж
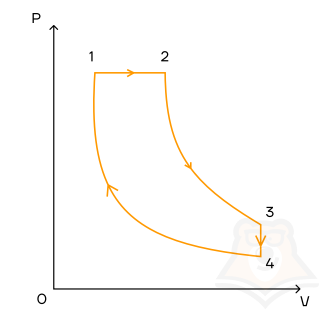
Задание 2.
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
- 0,6
- 0,5
- 0,8
- 1
Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.
- 6%
- 100%
- 22%
- 9%
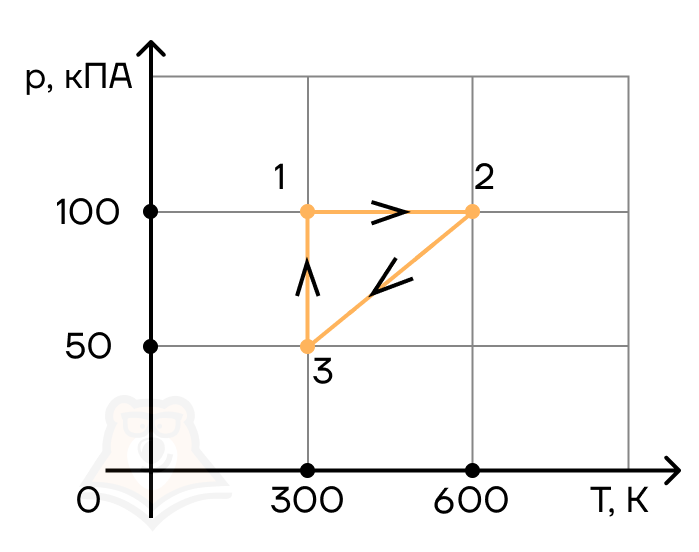
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?
- 4444 Дж
- 2891 Дж
- 4986 Дж
- 9355 Дж
Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.
На
прошлых уроках мы с вами познакомились с понятием «внутренняя энергия тела» и
узнали, что изменить её можно двумя способами: либо путём совершения
механической работы, либо теплопередачей.
Также
мы с вами выяснили, что мерой изменения внутренней энергии тела при
теплопередаче является количество теплоты. Давайте вспомним, что количество
теплоты — это скалярная физическая величина, равная изменению внутренней
энергии тела в процессе теплопередачи без совершения механической работы.
А
ещё мы получили уравнение, по которому можно рассчитать количество теплоты,
которое необходимо подвести к телу для его нагревания, или выделяемое телом,
при его охлаждении:
Q
= cm(t
– t0).
Из
формулы видно, что количество теплоты зависит от массы тела, разности
температур в конечном и начальном состояниях, а также от удельной теплоёмкости
вещества, из которого это тело изготовлено.
Чтобы
вспомнить, же что же такое теплоёмкость, рассмотрим решение следующей задачи.
Задача
1.
В сосуд с горячей водой опустили алюминиевую и латунную болванки одинаковой
массы и температуры. Одинаковым ли будет изменение их температур?
В
жизненных ситуациях довольно часто возникает необходимость в тепловых расчётах.
Например, при строительстве жилых домов необходимо знать, какое количество
теплоты должна отдавать зданию система отопления. Или нужно определить
температуру после смешивания горячей и холодной воды. И на этом уроке мы
разберёмся, как проводятся такие расчёты.
Последовательность
действий при решении задач на расчёт теплообменных процессов:
Задача
2.
Для купания ребёнка температура воды в ванночке не должна превышать 38 оС.
Для этого родители смешали 40 кг холодной воды при температуре 12 оС
и 20 кг горячей воды при температуре 90 оС. Если потерями тепла
можно пренебречь, то какое количество теплоты получили холодная вода при
нагревании и отдала горячая вода при охлаждении?
Мы
получили, что количество теплоты, отданное горячей водой, равно количеству
теплоты, полученному водой холодной. И это не случайно. Вспомните: если
между телами происходит теплообмен, то внутренняя энергия всех нагревающихся
тел увеличивается ровно на столько, на сколько уменьшается внутренняя энергия
остывающих тел.
Конечно
в реальных условиях количество теплоты, отданное горячей водой, всегда будет
больше чем-то количество теплоты, которое получит холодная вода. Это
объясняется тем, что часть энергии идёт на нагревание сосуда, в котором
находилась вода, а ещё часть теряется на нагревание окружающего воздуха.
Теперь
мы можем внести дополнительный пункт в нашу последовательность действий при
решении задач — пункт о необходимости составления уравнения теплового
баланса.
Количество
теплоты, отданное или полученное телом, можно измерить с помощью прибора,
который называется калориметр.
Школьный калориметр
Школьный
калориметр состоит из двух стаканов, вставленных один в другой. Воздушная
прослойка и подставка между ними уменьшают теплопередачу между содержимым
внутреннего стакана и окружающим воздухом.
Задача
3.
Калориметр содержит 3 л воды при температуре 80 оС. В воду опускают
нагретый на плитке кирпич массой 1,5 кг. Определите начальную температуру
кирпича, если в результате теплообмена температура воды повысилась до 9 оС.
Теплопередачей калориметру и окружающему воздуху можно пренебречь.
Обратите
внимание на то, что в некоторых задачах теплоёмкостью калориметра пренебрегать
нельзя. В этом случае необходимо учитывать, что и вода, и калориметр будут
нагреваться или охлаждаться вместе. А их температуры можно считать одинаковыми.
