Содержание:
Количество теплоты:
В чём причина изменения внутренней энергии макроскопического тела при теплообмене?
Теплообмен
Другим способом изменения внутренней энергии термодинамической системы является теплообмен.
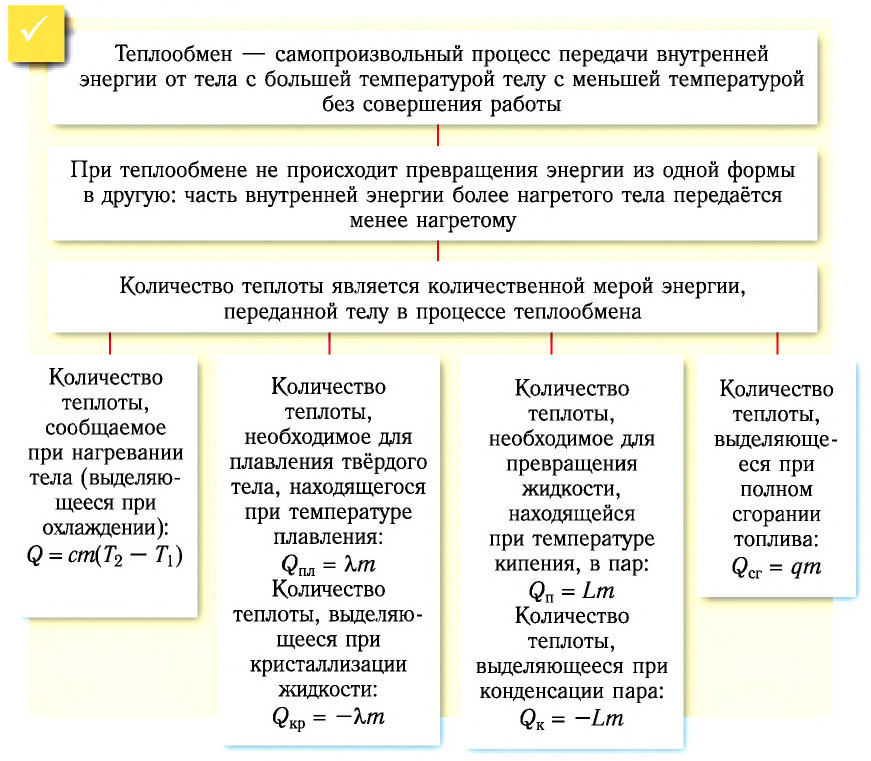
Теплообмен — самопроизвольный процесс передачи внутренней энергии от тела с большей температурой телу с меньшей температурой без совершения работы.
Теплообмен между контактирующими телами называют теплопередачей. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей кинетической энергии частицам менее нагретого тела. В результате внутренняя энергия одного тела уменьшается, а другого увеличивается.
Таким образом, при теплопередаче не происходит превращения энергии из одной формы в другую: часть внутренней энергии более нагретого тела передаётся менее нагретому.
Количество теплоты и удельная теплоёмкость
Количественной мерой энергии, сообщённой телу (или отданной им) в процессе теплообмена, является количество теплоты.
В СИ единицей количества теплоты Q является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию 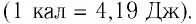
Если процесс теплообмена не сопровождается изменением агрегатного состояния вещества, то
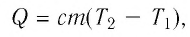
где 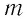 — масса тела;
— масса тела; 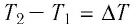 — разность температур в конце и в начале процесса теплообмена; с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает вещество массой 1 кг при увеличении его температуры на 1 К. Удельную теплоёмкость измеряют в джоулях, деленных на килограмм, кельвин
— разность температур в конце и в начале процесса теплообмена; с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает вещество массой 1 кг при увеличении его температуры на 1 К. Удельную теплоёмкость измеряют в джоулях, деленных на килограмм, кельвин 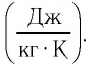
Удельная теплоёмкость зависит от свойств данного вещества и, как показывает опыт, в достаточно большом интервале температур практически не изменяется. Однако удельная теплоёмкость газа зависит от того, при каком процессе (изобарном или изохорном) осуществляется теплообмен.
Интересно знать:
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкость тела. Обозначают теплоёмкость С и измеряют в джоулях, деленных на кельвин 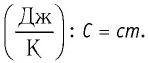 Теплоёмкость в отличии от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
Теплоёмкость в отличии от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 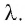 Эту величину измеряют в джоулях, делённых на килограмм
Эту величину измеряют в джоулях, делённых на килограмм 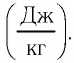 Для плавления тела массой
Для плавления тела массой 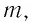 предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты
предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты 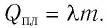 При кристаллизации тела такое же количество теплоты выделяется:
При кристаллизации тела такое же количество теплоты выделяется: 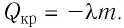
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Единицей измерения этой величины является джоуль, делённый на килограмм 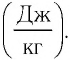 Количество теплоты, необходимое для превращения жидкости массой
Количество теплоты, необходимое для превращения жидкости массой 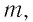 предварительно нагретой до температуры кипения, в пар, определяют по формуле
предварительно нагретой до температуры кипения, в пар, определяют по формуле 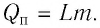 Конденсация пара сопровождается выделением количества теплоты
Конденсация пара сопровождается выделением количества теплоты 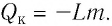
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания 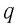 топлива и измеряют в джоулях, делённых на килограмм
топлива и измеряют в джоулях, делённых на килограмм 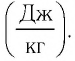 Количество теплоты, выделившееся при полном сгорании некоторой массы
Количество теплоты, выделившееся при полном сгорании некоторой массы 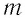 топлива, определяют по формуле
топлива, определяют по формуле
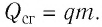
Это количество теплоты передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.
- Заказать решение задач по физике
Примеры решения задач
Пример №1
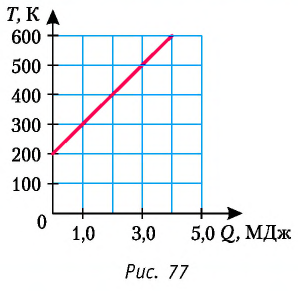
На рисунке 77 представлен график зависимости абсолютной температуры нагреваемого тела от переданного ему количества теплоты. Воспользовавшись таблицей на с. 84, определите вещество, из которого изготовлено тело, если его масса 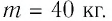
Решение:
Для того чтобы определить вещество, из которого изготовлено тело, найдём его удельную теплоёмкость с. Анализируя график, делаем вывод, что при нагревании тела от температуры 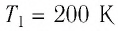 до температуры
до температуры 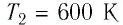 ему было передано количество теплоты
ему было передано количество теплоты 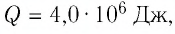 которое можно рассчитать по формуле
которое можно рассчитать по формуле 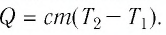
Следовательно, удельная теплоёмкость вещества 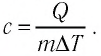
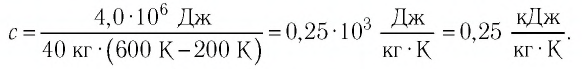
Полученное значение удельной теплоёмкости соответствует олову.
Ответ: 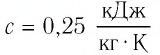 — олово.
— олово.
Пример №2
В налитую в сосуд воду, масса которой 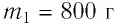 и температура
и температура 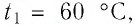 добавили некоторое количество льда при температуре
добавили некоторое количество льда при температуре 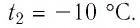 Определите массу льда, если после достижения теплового равновесия температура содержимого сосуда
Определите массу льда, если после достижения теплового равновесия температура содержимого сосуда 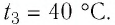 Теплоёмкостью сосуда и потерями тепла пренебречь. Удельная теплоёмкость воды
Теплоёмкостью сосуда и потерями тепла пренебречь. Удельная теплоёмкость воды 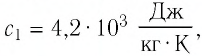 льда
льда 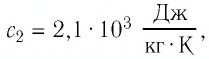 удельная теплота плавления льда
удельная теплота плавления льда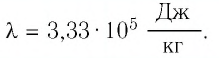

Решение:

Ответ: 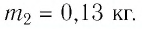
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
- Конвекция в физике
- Излучение тепла в физике
- Виды излучений в физике
- Инфракрасные излучения
При введении
понятия теплоемкости мы не обращали
внимание на одно существенное
обстоятельство: теплоемкости зависят
не только от свойств вещества, но и от
процесса, при котором осуществляется
теплопередача.
Если нагревать
тело при постоянном давлении, то оно
будет расширяться и совершать работу.
Для нагревания тела на 1 К при постоянном
давлении ему нужно передать большее
количество теплоты, чем при таком же
нагревании при постоянном объеме.
Жидкие и твердые
тела расширяются при нагревании
незначительно, и их теплоемкости при
постоянном объеме и постоянном давлении
мало различаются. Но для газов это
различие существенно. С помощью первого
закона термодинамики можно найти связь
между теплоемкостями газа при постоянном
объеме и постоянном давлении.
Теплоемкость газа при постоянном объеме Найдем молярную теплоемкость газа при постоянном объеме. Согласно определению теплоемкости
![]()
где
ΔT
—
изменение температуры. Если процесс
происходит при постоянном объеме, то
эту теплоемкость обозначим через Cv.
Тогда
![]() (5.6.1)
(5.6.1)
При постоянном
объеме работа не совершается. Поэтому
первый закон термодинамики запишется
так:
![]()
(5.6.2)
Изменение
энергии одного моля достаточно
разреженного (идеального) одноатомного
газа равно:
![]()
(см.
§ 4.8).
Следовательно,
молярная теплоемкость при постоянном
объеме одноатомного газа равна:
![]()
(5.6.3)
Теплоемкость газа при постоянном давлении
Согласно
определению теплоемкости при постоянном
давлении Ср
![]()
(5.6.4)
Работа, которую
совершит 1 моль идеального газа,
расширяющегося при постоянном давлении,
равна:
![]()
(5.6.5)
* Из формулы (5.6.5)
видно, что универсальная газовая
постоянная численно равна работе,
которую совершает 1 моль идеального
газа при постоянном давлении, если
температура его увеличивается на 1К.
Это
следует из выражения для работы газа
при постоянном давлении А’
= pΔV
и
уравнения состояния (для одного моля)
идеального газа pV
=
RT.
Внутренняя
энергия идеального газа от объема не
зависит. Поэтому и при постоянном
давлении изменение внутренней энергии
ΔU
= CVΔT,
как
и при постоянном объеме. Применяя первый
закон термодинамики, получим:
![]()
(5.6.6)
Следовательно,
молярные теплоемкости идеального газа
связаны соотношением
![]()
(5.6.7)
Впервые эта формула
была получена Р. Майером и носит его
имя.
В случае идеального
одноатомного газа
![]()
(5.6.8)
Теплоемкость идеального газа при изотермическом процессе
Можно формально
ввести понятие теплоемкости и при
изотермическом процессе. Так как при
этом процессе внутренняя энергия
идеального газа не меняется, какое бы
количество теплоты ему ни было передано,
то теплоемкость бесконечна.
Молярная
теплоемкость идеального газа при
постоянном давлении больше теплоемкости
при постоянном объеме на величину
универсальной газовой постоянной R.
§ 5.7. Адиабатный процесс
Мы
рассмотрели изотермический, изобарный
и изохорный процессы. После ознакомления
с первым законом термодинамики появляется
возможность изучить еще один процесс,
—
это
процесс, протекающий в системе при
отсутствии теплообмена с окружающими
телами. (Но работу над окружающими телами
система может совершать.)
Процесс в
теплоизолированной системе называют
адиабатным.
При
адиабатном процессе Q
=
0 и согласно закону (5.5.3) изменение
внутренней энергии происходит только
за счет совершения работы:
![]()
(5.7.1)
Конечно, нельзя
окружить систему оболочкой, абсолютно
исключающей теплообмен. Но в ряде случаев
реальные процессы очень близки к
адиабатным. Существуют оболочки,
обладающие малой теплопроводностью,
например двойные стенки с вакуумом
между ними. Так изготовляются термосы.
Процесс можно
считать адиабатным даже без теплоизолирующей
оболочки, если он происходит достаточно
быстро, т. е. так, чтобы за время процесса
не происходило заметного теплообмена
между системой и окружающими телами.
Согласно
выражению (5.7.1) при совершении над
системой положительной работы, например
при сжатии газа, внутренняя энергия его
увеличивается; газ нагревается. Наоборот,
при расширении газ сам совершает
положительную работу (А’ > 0), но А
< 0
и внутренняя энергия его уменьшается;
газ охлаждается.
Зависимость
давления газа от его объема при адиабатном
процессе изображается кривой, называемой
адиабатой
(рис. 5.9). Адиабата обязательно идет круче
изотермы. Ведь при адиабатном процессе
давление газа уменьшается не только за
счет увеличения объема, как при
изотермическом процессе, но и за счет
уменьшения его температуры.
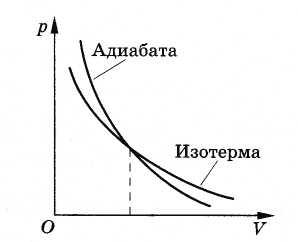
Рис. 5.9
Адиабатные процессы
широко используются в технике. Они
играют немалую роль в природе.
Нагревание воздуха
при быстром сжатии нашло применение в
двигателях Дизеля. В этих двигателях
отсутствуют системы приготовления и
зажигания горючей смеси, необходимые
для обычных бензиновых двигателей
внутреннего сгорания. В цилиндр
засасывается не горючая смесь, а
атмосферный воздух. К концу такта сжатия
в цилиндр с помощью специальной форсунки
впрыскивается жидкое топливо (рис.
5.10). К этому моменту температура сжатого
воздуха так велика, что горючее
воспламеняется.
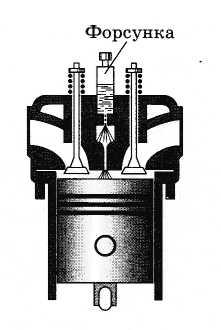
Рис. 5.10
Так как в двигателе
Дизеля сжимается не горючая смесь, а
воздух, то степень сжатия у этого
двигателя больше, а значит, коэффициент
полезного действия (КПД) двигателей
Дизеля выше, чем у обычных двигателей
внутреннего сгорания. Кроме того, они
могут работать на более дешевом
низкосортном топливе. Есть, однако, у
двигателя Дизеля и недостатки:
необходимость высоких степеней сжатия
и большое рабочее давление делают эти
двигатели массивными и вследствие этого
более инерционными — они медленнее
набирают мощность. Двигатели Дизеля
более сложны в изготовлении и эксплуатации,
тем не менее они постепенно вытесняют
обычные бензиновые двигатели, используемые
в автомобилях.
Охлаждение газа
при адиабатном расширении происходит
в грандиозных масштабах в атмосфере
Земли. Нагретый воздух поднимается
вверх и расширяется, так как атмосферное
давление падает с высотой. Это расширение
сопровождается значительным охлаждением.
В результате водяные пары конденсируются
и образуются облака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем,
что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом
случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система
микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии,
которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой).
Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание,
что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом.
Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$delta Q=c m d T=nu c_{mu} d T(2)$$
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{mu}=c cdot mu$ – молярная теплоемкость,
$mu$ – молярная масса вещества,
$nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты
($Delta Q$), которое получает тело при увеличении его температуры на величину
$Delta t = t_2 – t_1$ можно вычислить как:
$$Delta Q=c m Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности
($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты,
которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты
($delta Q$) равное:
$$delta Q=lambda d m$$
где $lambda$ – удельная теплота плавления, dm – элемент массы тела.
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура
одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 –
количество теплоты части воды температурой t1 и массой m1;
Q2=cm2t2– количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$
begin{array}{l}
mathrm{cmt}=mathrm{cm}_{1} t_{1}+mathrm{~cm}_{2} t_{2} rightarrow mathrm{mt}=mathrm{m}_{1} t_{1}+mathrm{~m}_{2} t_{2} rightarrow \
rightarrow rho mathrm{Vt}=rho V_{1} t_{1}+rho mathrm{V}_{2} t_{2} rightarrow mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2)
end{array}
$$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1.3)
$$$
Так, мы получаем систему уравнений:
$$
left{begin{array}{c}
V t=V_{1} t_{1}+V_{2} t_{2} \
V=V_{1}+V_{2}
end{array}right.
$$
Решив ее получим:
$$
begin{array}{l}
V_{1}=frac{left(t_{2}-tright)}{t_{2}-t_{1}} V \
V_{2}=frac{left(t-t_{1}right)}{t_{2}-t_{1}} V
end{array}
$$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$
begin{array}{l}
V_{1}=frac{(60-40)}{60-10} 200=80 text { (л) } \
V_{2}=frac{(40-10)}{60-10} 200=120 text { (л) }
end{array}
$$
Ответ. V1=80 л, V2=120 л.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
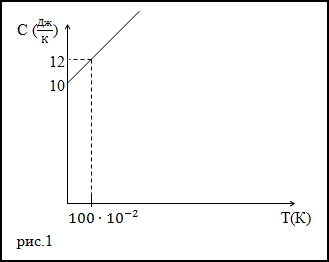
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в
рассматриваемом интервале $T_{1} leq T leq T_{2}$ .
Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:
$C(T)=10+2 cdot 10^{-2} T$ (Дж/К)
Основой для решения задачи послужит формула для количества теплоты в виде:
$$delta Q=C d T(2.2)$$
Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:
$$
begin{array}{c}
Delta Q=int_{300}^{400}left(10+2 cdot 10^{-2} Tright) d T=left.left(10 cdot T+10^{-2} T^{2}right)right|_{300} ^{400}= \
=left(10 cdot 400+10^{-2} cdot(400)^{2}right)-left(10 cdot 300+10^{-2} cdot(300)^{2}right)=1700left(mathrm{~A}^{*}right)
end{array}
$$
Ответ. $Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.
Количество теплоты. Удельная теплоемкость вещества
Количеством теплоты называют количественную меру изменения внутренней энергии тела при теплообмене.
Количество теплоты — это энергия, которую тело отдает при теплообмене (без совершения работы). Количество теплоты, как и энергия, измеряется в джоулях (Дж).
Удельная теплоемкость вещества
Теплоемкость — это количество теплоты, поглощаемой телом при нагревании на $1$ градус.
Теплоемкость тела обозначается заглавной латинской буквой С.
От чего зависит теплоемкость тела? Прежде всего, от его массы. Ясно, что для нагрева, например, $1$ килограмма воды потребуется больше тепла, чем для нагрева $200$ граммов.
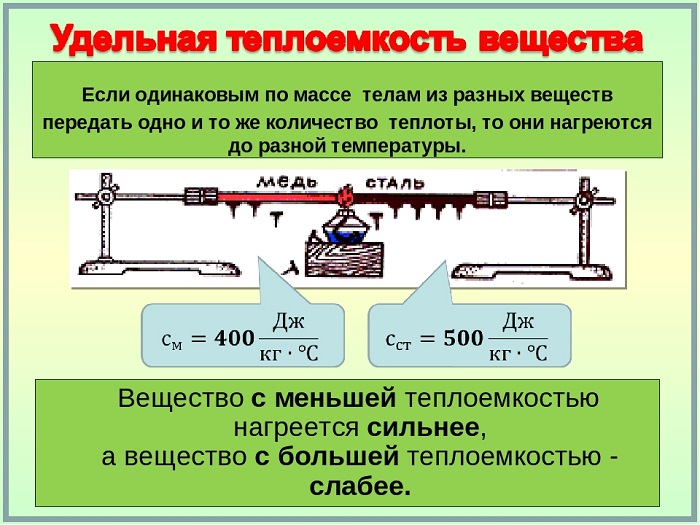
А от рода вещества? Проделаем опыт. Возьмем два одинаковых сосуда и, налив в один из них воду массой $400$ г, а в другой — растительное масло массой $400$ г, начнем их нагревать с помощью одинаковых горелок. Наблюдая за показаниями термометров, мы увидим, что масло нагревается быстрее. Чтобы нагреть воду и масло до одной и той же температуры, воду следует нагревать дольше. Но чем дольше мы нагреваем воду, тем большее количество теплоты она получает от горелки.
Таким образом, для нагревания одной и той же массы разных веществ до одинаковой температуры требуется разное количество теплоты. Количество теплоты, необходимое для нагревания тела и, следовательно, его теплоемкость зависят от рода вещества, из которого состоит это тело.
Так, например, чтобы увеличить на $1°$С температуру воды массой $1$ кг, требуется количество теплоты, равное $4200$ Дж, а для нагревания на $1°$С такой же массы подсолнечного масла необходимо количество теплоты, равное $1700$ Дж.
Физическая величина, показывающая, какое количество теплоты требуется для нагревания $1$ кг вещества на $1°$С, называется удельной теплоемкостью этого вещества.
У каждого вещества своя удельная теплоемкость, которая обозначается латинской буквой $с$ и измеряется в джоулях на килограмм-градус (Дж/(кг$·°$С)).
Удельная теплоемкость одного и того же вещества в разных агрегатных состояниях (твердом, жидком и газообразном) различна. Например, удельная теплоемкость воды равна $4200$ Дж/(кг$·°$С), а удельная теплоемкость льда $2100$ Дж/(кг$·°$С); алюминий в твердом состоянии имеет удельную теплоемкость, равную $920$ Дж/(кг$·°$С), а в жидком — $1080$ Дж/(кг$·°$С).
Заметим, что вода имеет очень большую удельную теплоемкость. Поэтому вода в морях и океанах, нагреваясь летом, поглощает из воздуха большое количество тепла. Благодаря этому в тех местах, которые расположены вблизи больших водоемов, лето не бывает таким жарким, как в местах, удаленных от воды.
Расчет количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении
Из вышеизложенного ясно, что количество теплоты, необходимое для нагревания тела, зависит от рода вещества, из которого состоит тело (т. е. его удельной теплоемкости), и от массы тела. Ясно также, что количество теплоты зависит от того, на сколько градусов мы собираемся увеличить температуру тела.
Итак, чтобы определить количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость тела умножить на его массу и на разность между его конечной и начальной температурами:
$Q=cm(t_2-t_1)$
где $Q$ — количество теплоты, $c$ — удельная теплоемкость, $m$ — масса тела, $t_1$ — начальная температура, $t_2$ — конечная температура.
При нагревании тела $t_2 > t_1$ и, следовательно, $Q > 0$. При охлаждении тела $t_2 < t_1$ и, следовательно, $Q < 0$.
В случае, если известна теплоемкость всего тела $С, Q$ определяется по формуле
$Q=C(t_2-t_1)$
Удельная теплота парообразования, плавления, сгорания
Теплота парообразования (теплота испарения) — количество теплоты, которое необходимо сообщить веществу (при постоянном давлении и постоянной температуре) для полного превращения жидкого вещества в пар.
Теплота парообразования равна количеству теплоты, выделяющемуся при конденсации пара в жидкость.
Превращение жидкости в пар при постоянной температуре не ведет к увеличению кинетической энергии молекул, но сопровождается увеличением их потенциальной энергии, т. к. расстояние между молекулами существенно увеличивается.
Удельная теплота парообразования и конденсации. Опытами установлено, что для полного обращения в пар $1$ кг воды (при температуре кипения) необходимо затратить $2.3$ МДж энергии. Для обращения в пар других жидкостей требуется иное количество теплоты. Например, для спирта оно составляет $0.9$ МДж.
Физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой $1$ кг в пар без изменения температуры, называется удельной теплотой парообразования.
Удельную теплоту парообразования обозначают буквой $r$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты, необходимое для парообразования (или выделяющееся при конденсации). Чтобы вычислить количество теплоты $Q$, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования $r$ умножить на массу $m$:
$Q=rm$
При конденсации пара происходит выделение такого же количества теплоты:
$Q=-rm$
Удельная теплота плавления
Теплота плавления — это количество теплоты, которое необходимо сообщить веществу при постоянном давлении и постоянной температуре, равной температуре плавления, чтобы полностью перевести его из твердого кристаллического состояния в жидкое.
Теплота плавления равна тому количеству теплоты, которое выделяется при кристаллизации вещества из жидкого состояния.
При плавлении вся подводимая к веществу теплота идет на увеличение потенциальной энергии его молекул. Кинетическая энергия не меняется, поскольку плавление идет при постоянной температуре.
Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить один килограмм льда, нужно затратить $332$ Дж энергии, а для того чтобы расплавить $1$ кг свинца — $25$ кДж.
Физическая величина, показывающая, какое количество теплоты необходимо сообщить кристаллическому телу массой $1$ кг, чтобы при температуре плавления полностью перевести его в жидкое состояние, называется удельной теплотой плавления.
Удельную теплоту плавления измеряют в джоулях на килограмм (Дж/кг) и обозначают греческой буквой $λ$ (лямбда).
Удельная теплота кристаллизации равна удельной теплоте плавления, поскольку при кристаллизации выделяется такое же количество теплоты, какое поглощается при плавлении. Так, например, при замерзании воды массой $1$ кг выделяются те же $332$ Дж энергии, которые нужны для превращения такой же массы льда в воду.
Чтобы найти количество теплоты, необходимое для плавления кристаллического тела произвольной массы, или теплоту плавления, надо удельную теплоту плавления этого тела умножить на его массу:
$Q=λm$
Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой $m$, следует пользоваться той же формулой, но со знаком «минус»:
$-Q=λm$
Удельная теплота сгорания
Теплота сгорания (или теплотворная способность, калорийность) — это количество теплоты, выделяющейся при полном сгорании топлива.
Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива. Обычное топливо (уголь, нефть, бензин) содержит углерод. При горении атомы углерода соединяются с атомами кислорода, содержащегося в воздухе, в результате чего образуются молекулы углекислого газа. Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.
Теплота сгорания топлива зависит от вида топлива и его массы. Чем больше масса топлива, тем больше количество теплоты, выделяющейся при его полном сгорании.
Физическая величина, показывающая, какое количество теплоты выделяется при полном сгорании топлива массой $1$ кг, называется удельной теплотой сгорания топлива.
Удельную теплоту сгорания обозначают буквой $q$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты $Q$, выделяющееся при сгорании $m$ кг топлива, определяют по формуле:
$Q=qm$
Чтобы найти количество теплоты, выделяющееся при полном сгорании топлива произвольной массы, нужно удельную теплоту сгорания этого топлива умножить на его массу.
Уравнение теплового баланса
В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы $∆U_i$ не может приводить к изменению внутренней энергии всей системы. Следовательно,
$∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$
Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: $∆U_i=Q_i$. Учитывая ($∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$), получим:
$Q_1+Q_2+Q_3+…+Q_n=∑↙{i}↖{n}Q_i=0$
Это уравнение называется уравнением теплового баланса. Здесь $Q_i$ — количество теплоты, полученное или отданное $i$-м телом. Любое из количеств теплоты $Q_i$ может означать теплоту, выделяемую или поглощаемую при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.
Уравнение теплового баланса является математическим выражением закона сохранения энергии при теплообмене.
Физика под удельной теплоемкостью понимает количество теплоты, которое термодинамическое вещество или система способно поглотить до повышения температуры.
Определение из учебника говорит, что это количество тепла, необходимое для создания температуры при нагревании.
Количество теплоты
Единица измерения – джоуль. Другой распространенной формой измерения является использование калорий.

Обозначается латинской буквой Q.
Удельная теплоемкость вещества
Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.
Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).
Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.
Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.
Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы. Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:
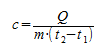
где:
Q – передача тепловой энергии между системой и средой (Дж);
m – масса системы (кг);
Δt или (t2 – t1) – повышение температуры, которой она подвергается (°C).
Формула для нахождения количества теплоты Q:
Q = c∗m(t2 – t1)
Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).
Уравнение теплового баланса:
Q отданное + Q полученное = 0.
Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:

Примеры решения задач
Следующие задачи покажут примеры расчета необходимого количества теплоты.
Задача №1
Сколько теплоты нужно, чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С?
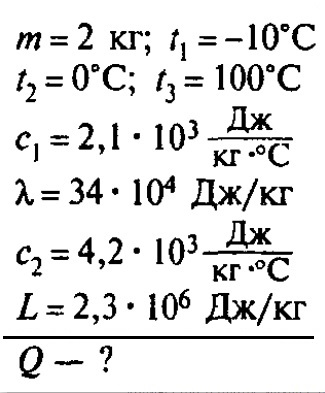
Решение:
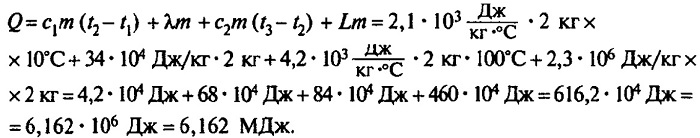
Ответ: чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С, нужно взять 6,162 мегаджоулей теплоты.
Задача №2
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100°С?
Начнем решение и отметим, что нагреваться будет и котёл, и вода. Разница температур составит 1000С — 100С = 900С. Т. е. и температура котла изменится на 90 градусов, и температура воды также изменится на 90 градусов.
Количества теплоты, которые получили оба объекта (Q1
– для котла и Q2 — для воды), не будут одинаковыми. Мы найдем общее количество теплоты по формуле теплового баланса Q = Q1 + Q2.