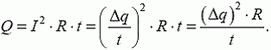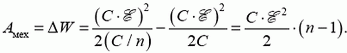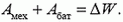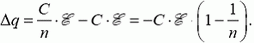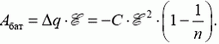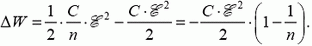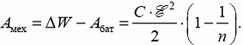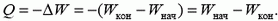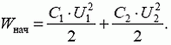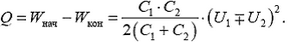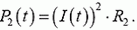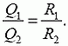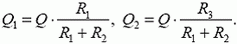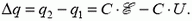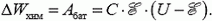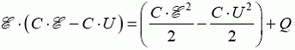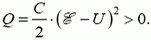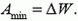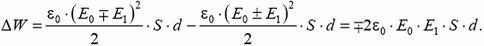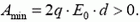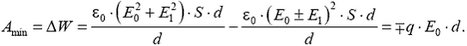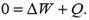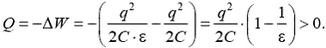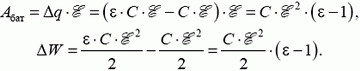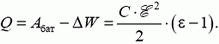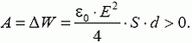§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
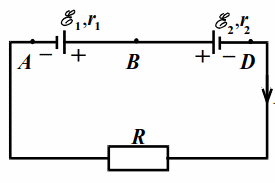 |
| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
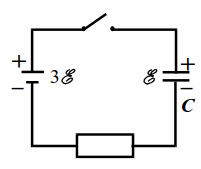 |
| Рис. 19.1 |
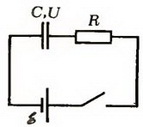
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
(A = U*I*T)
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
(Q = U*I*R*t)
или используя закон Ома (U = I*R), получим
(Q = {I^2}Rt)
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
На чтение 6 мин. Просмотров 2.9k. Опубликовано 27.07.2021
Практически все электроприборы содержат в своих схемах резисторы. Это объясняется тем, что для каждого прибора или проводника избирается своя сила тока для функционирования. Для того чтобы компенсировать значение между напряжением и движением заряженных частиц, в схемы вводят сопротивление. Основной параметр – это его мощность.
Что такое тепловая мощность резистора
Другое название – рассеивание. Этим понятием называют максимальные токи, которые без вреда могут протекать через него для осуществления работы и образования ЭДС в контактах и т.п.
Важно! Для каждой электрической схемы параметры рассеивания подбираются индивидуально.
Вычисляется по физической формуле с алгебраическими значениями: P = I * R.
В СИ:
- I – сила тока, Ампер.
- R – сопротивление, Ом.
- Р – мощность, Вт.
В физическом плане рассеивание – это способность проводника отдавать тепло в окружающую среду в том количестве, которое не вредит составным частям самого элемента. Это очень важный параметр, так как от него зависит исправность и долговечность электроприбора.
Важно! Все компоненты работают, подчиняясь закону Ома, но сам нагрев происходит из-за разности величин напряжения на входе и выходе. Это и является основным условием движения заряженных частиц через проводник.
Как определить и подобрать мощность
Данный параметр избирается от максимального значения силы заряженных частиц, которые будут протекать через проводник.
Для того чтобы подбирать тепловое рассеивание участков сопротивления для конкретных электроприборов, необходимо изучить параметры входного и выходного напряжения, а также силу электроцепи.
Важно! Необходимо понимать, что городские и промышленные цепи различаются по нагрузке и напряжению. Для бытовых используется 220V, для промышленных часто применяется значение в 380V.
Далее будет представлен стандартный ряд с графическим изображением мощностного отбора резистантов. Абсолютное большинство фабричных электроприборов оснащаются схемами, где указан конкретный диапазон элементов. Такие схемы незаменимы при ремонте и позволяют быстро подбирать необходимое.
Стандартный ряд мощностей и их обозначение на схемах
| Вт | Условное обозначение на электросхемах |
| 0,05 Вт |  |
| 0,125 Вт |  |
| 0,025 Вт |  |
| 0,5 Вт |  |
| 1 Вт |  |
| 2 Вт |  |
| 5 Вт |  |
В качестве графических обозначений используются римские цифры и черточки, раскрывающие диапазон от 0,05 до 25
Важно! Очень важно запомнить то, что слабые устройства обозначается косыми линиями.
Формула для расчета мощности тока в активном сопротивлении, как узнать сколько ватт
Как уже было упомянуто, классическая формула для расчета формируется так: квадрат силы движущихся заряженных частиц, помноженный на величину резистента.
Так показатели работоспособности напрямую зависят от напряжения. При работе и возникновении ЭДС частицы протекают через элемент, «осаживаясь» сопротивлением, и происходит нагрев элемента. Нагрев – это выделение тепла, который может быть измерен в Вт.
Важно! Что будет, если неправильно подобрать изделие? Если величина рассеивания слишком маленькая, то сопротивление перегорит, а если установить слишком «сильный» резистант, то движение заряженных частиц не начнется, и произойдет замыкание. Если из строя вышел элемент в 0,5 Вт, то он заменяется точным аналогом с соответствующими параметрами.
Действует еще одно правило подбора – оно касается не графических изображений на схеме, а самого типоразмера устройства. Чем больше элемент по габаритам, тем выше характеристика его параметров.
Как рассчитать рассеивание для сопротивления
Рассеиванием в физике и электромеханике называется процесс образования тепловой энергии, при чем это касается не только резисторов, но и прочих электрических элементов: кабелей, проводов, штекеров и катушек.
Главное не допускать перегрева, так как это кратно снижает долговечность электроприборов и их отдельных элементов. Следующий ряд является типовым в отборе характеристик зависимости производительности от напряжения:
- 0,125
- 0,25
- 0,5
- 1
- 2
- Более 2 Ватт.
Им соответствует значение для сопротивлений, Ом: 10, 20, 25, 50, 60, 100.
Приведем конкретный пример алгебраического вычисления.
Мы имеем изделие с параметром в 10 Ом и пропускаем через него поток заряда в 0,1 А. Используем значения для того, чтобы подставить их в известную формулу с переменными. Получаем P = 1
P(Ватт) – теплота, выделяемая на резисторе;
R(Ом) – сопротивление цепочки;
I(А) – движение заряженных частиц.
Как определить по внешнему виду
Если на схеме имеется конкретное обозначение, то тепловая мощность на резисторе определяется по символам, но как определить параметр по внешнему виду элементов на плате?
Известно, что чем больше площадь поверхности, тем больше она может поглощать или отдавать количества теплоты на резисторе.
Кроме того, существуют буквенные обозначения для российских и импортных устройств.
Для отечественных:
В – Маломощные от 0,125 до 0,25
Для импортных:
W — Маломощные от 0,125 до 0,25
V – Средний диапазон.
SW – Более 2
Важно! Существуют миниатюрные устройства, на корпусе которых невозможно нанести маркировку. Такие сопротивления окрашиваются в белый, желтый или красный цвет. Цвета в соответствии с диапазонами по возрастающей. В частности, это касается импортных изделий.
Как рассчитать мощность в схеме
Для схем также обязательны знания о силе тока и сопротивлении, без знания этих параметров расчет будет невозможен. Тепловые потери на резисторе формируются из квадрата силы тока, помноженного на сопротивление: P = I² * R (количество теплоты на резисторе формула). Актуальна только при расчетах готовой и известной схемы, во всех случаях предварительного расчета используется прямое значение силы тока, а не ее квадрат.
Величина указывается исключительно в Омах, если используются значения в кило- или мегаомах, то их необходимо округлять до классического значения в одну единицу сопротивления – Ом.
Схема с последовательным соединением элементов
Последовательное соединение означает тот факт, что через все элементы схемы проходит одно и то же значение силы тока. Это означает, что и рассеивание будет тождественным на всех резистантах. Для подсчета необходимо:
- Суммировать значения на всех участках, то есть: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Сила тока рассчитывается по закону: I = U/R. Алгебраически значение формируется в следующем виде: I = 100 В / 390 Ом = 0,256 А.
- Рассчитать параметр: P = 0,256² * 390 Ом = 25,549
Это ответ на вопрос о том, какая тепловая мощность будет выделяться на резисторе r1 в схеме.
Таким образом становится возможным подсчитать индивидуальное рассеивание на каждом участке, указанном в схеме.
Как подобрать резистор на замену
Для замены всегда подбирается точно такой же элемент. Допускается временное использование сопротивлений с параметром на 1 порядок выше, чем у перегоревшего или вышедшего из строя по другим причинам. Это основное условие замкнутого контура в цепи. Установить неисправный участок цепи – означает разомкнуть цепь.
Определить параметры можно приблизительно по маркировке и размерам.
Элементы для замены оснащены выводами с обоих концов – их паяют на плату. Рекомендуется не подрезать выводы, так как они тоже обладают дополнительным сопротивлением.
На резисторе внешней цепи аккумулятора выделяется тепловая мощность 10 Вт
Этот параметр и условие являются актуальными при последовательном подключении трех аккумуляторов. Если к концам подведена внешняя цепь с аккумулятором, то для каждого следующего аккумулятора значение будет увеличиваться в 2 раза. Но поскольку мощность зависит от напряжения через силу тока, то для третьего аккумулятора возрастание мощности составит значение в 25%. Тепловые потери составят 26,9Вт.
Используя сведения, которые были представлены в данной статье, можно самостоятельно и быстро подобрать необходимые элементы электроцепи в электроприборе для замены. Для этого в настоящее время существует множество магазинов электроники, которые удовлетворят запросы самых претенциозных клиентов.
Данную статью можно использовать в качестве конкретного руководства по выбору резисторов не только в бытовые электроприборы, но и в промышленные установки.
Закон сохранения энергии определяет в самом общем виде энергетический баланс при всевозможных изменениях в любой системе. Запишем его следующим образом:
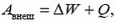
где Aвнеш — работа, совершенная над рассматриваемой системой внешними силами, ΔW — изменение энергии системы, Q — количество теплоты, выделяемое в системе. Договоримся, что если Aвнеш > 0, то над системой совершают положительную работу, а если Aвнеш < 0, положительную работу совершает система; если ΔW > 0, то энергия системы увеличивается, а если ΔW < 0, энергия уменьшается; наконец, если Q > 0, то в системе выделяется тепло, а если Q < 0, тепло системой поглощается.
В этой статье мы рассмотрим, как закон сохранения энергии «работает» в электростатике. В общем случае электростатическая система содержит взаимодействующие между собой заряды, находящиеся в электрическом поле.
Рассмотрим каждое слагаемое в уравнении (1) по отдельности.
Начнем с энергии. Энергия взаимодействия зарядов выражается через характеристики электрического поля этой системы зарядов. Так, например, энергия заряженного конденсатора емкостью C задается известным выражением
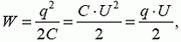
где q — заряд обкладок, U — напряжение между ними. Напомним, что конденсатор — это система двух проводников (обкладок, пластин), обладающая следующим свойством: если с одной обкладки на другую перенести заряд q (т. е. одну обкладку зарядить зарядом +q, а другую –q), то все силовые линии созданного таким образом поля будут начинаться на одной (положительно заряженной) обкладке и заканчиваться на другой. Поле конденсатора существует только внутри него.
Энергию заряженного конденсатора можно представить также как энергию поля, локализованного в пространстве между пластинами с плотностью энергии 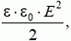
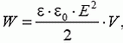
где V — объем конденсатора. Последней формулой легко пользоваться, конечно, только в случае однородного поля, но представление энергии в такой форме очень наглядно, а потому удобно.
Конечно, кроме энергии взаимодействия зарядов (энергии электрического поля) в энергию системы может входить и кинетическая энергия заряженных тел, и их потенциальная энергия в поле тяжести, и энергия пружин, прикрепленных к телам, и т. п.
Теперь о работе внешних сил. Помимо обычной механической работы Aмех (например, по раздвиганию пластин конденсатора), для электрической системы можно говорить о работе внешнего электрического поля. Например, о работе батареи, заряжающей или перезаряжающей конденсатор. Задача батареи — создать фиксированную, присущую данному источнику разность потенциалов между теми телами, к которым она присоединена. Делает она это единственно возможным способом — забирает заряд от одного тела и передает его другому. Источник никогда не создает заряды, а только перемещает их. Общий заряд системы при этом сохраняется — это один из краеугольных законов природы.
В источниках разных конструкций электрическое поле, необходимое для перемещения зарядов, создают различные «механизмы». В батареях и аккумуляторах — это электрохимические реакции, в динамомашинах — электромагнитная индукция. Существенно, что для выбранной системы зарядов (заряженных тел) это поле — внешнее, стороннее. Когда через источник с ЭДС от отрицательного полюса к положительному протекает заряд Δq, сторонние силы совершают работу
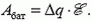
При этом если Δq > 0, то Aбат > 0 — батарея разряжается; если же Δq < 0, то Aбат < 0 — батарея заряжается и в ней накапливается химическая (или магнитная) энергия.
Наконец, о выделении тепла. Заметим только, что это джоулево тепло, т.е. тепло, связанное с протеканием тока через сопротивление.
Теперь обсудим несколько конкретных задач.
Задача 1. Два одинаковых плоских конденсатора емкостью C каждый присоединены к двум одинаковым батареям с ЭДС . В какой-то момент один конденсатор отключают от батареи, а другой оставляют присоединенным. Затем медленно разводят пластины обоих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае?
Если процесс изменения заряда на конденсаторе осуществляется все время медленно, тепло выделяться не будет. Действительно, если через резистор сопротивлением R протек заряд Δq за время t, то на резисторе за это время выделится количество теплоты
При достаточно больших t количество теплоты Q может оказаться сколь угодно малым.
В первом случае фиксирован заряд на пластинах (батарея отключена), равный Механическая работа определяется изменением энергии конденсатора:
Во втором случае фиксирована разность потенциалов на конденсаторе и работает батарея, поэтому
Через батарею протекает заряд
Этот заряд меньше нуля, значит, батарея заряжается и ее работа
Энергия поля в конденсаторе уменьшается:
Таким образом,
Зарядка батареи происходит за счет работы по раздвиганию пластин и за счет энергии конденсатора.
Заметим, что слова про раздвигание пластин существенной роли не играют. Такой же результат будет при любых других изменениях, приводящих к уменьшению емкости в n раз.
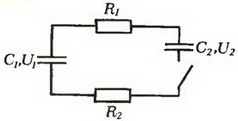
Задача 2. В схеме, изображенной на рисунке, найдите количество теплоты, выделившееся в каждом резисторе после замыкания ключа. Конденсатор емкостью C1 заряжен до напряжения U1, а конденсатор емкостью C2 — до напряжения U2. Сопротивления резисторов R1 и R2.
Рис. 1
Закон сохранения энергии (1) для данной системы имеет вид
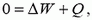
Начальная энергия конденсаторов равна
Для определения энергии в конечном состоянии воспользуемся тем, что суммарный заряд конденсаторов не может измениться. Он равен 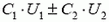
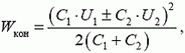
Как и должно быть, в обоих случаях выделяется тепло — есть джоулевы потери. Замечательно, что выделившееся количество теплоты не зависит от сопротивления цепи — при малых сопротивлениях текут большие токи и наоборот.
Теперь найдем, как количество теплоты Q распределяется между резисторами. Через сопротивления R1 и R2 в каждый момент процесса перезарядки текут одинаковые токи, значит, в каждый момент мощности, выделяемые на сопротивлениях, равны
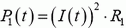
Следовательно,
Кроме того, 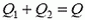
Задача 3. В схеме на рисунке 2 конденсатор емкостью C заряжен до напряжения U. Какое количество химической энергии запасется в аккумуляторе с ЭДС после замыкания ключа? Какое количество теплоты выделится в резисторе?
Рис. 2
Первоначальный заряд на конденсаторе 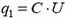
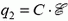
В противном случае 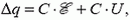
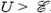
Теперь запишем закон сохранения энергии (1) –
– и найдем выделившееся количество теплоты:
Задача 4. Плоский конденсатор находится во внешнем однородном поле с напряженностью 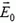
Работа будет минимальной, когда процесс проводится очень медленно — при этом не выделяется тепло. Тогда, согласно закону сохранения энергии,
Чтобы найти ΔW, воспользуемся формулой (3). Поле между пластинами представляет собой суперпозицию поля 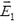
– и внешнего поля 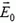
При перемене пластин местами поле 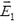
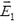
Если направления векторов 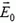
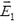
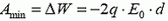
Когда пластины конденсатора расположены параллельно полю 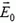
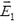
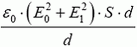
Когда конденсатор вынули из поля, в том месте, где он был, поле стало 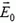
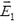
Задача 5. Конденсатор емкостью С без диэлектрика заряжен зарядом q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью ε? То же, но конденсатор присоединен к батарее с ЭДС .
При заливании диэлектрика емкость конденсатора увеличилась в ε раз.
В первом случае фиксирован заряд на пластинах, внешних сил нет, и закон сохранения энергии (1) имеет вид
Отсюда
Тепло выделяется за счет уменьшения энергии взаимодействия зарядов.
Во втором случае есть работа батареи и фиксировано напряжение на конденсаторе:
Тогда из уравнения (1) следует
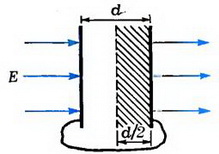
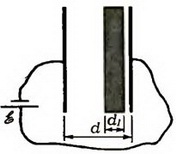
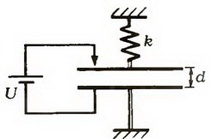
Задача 6. Две соединенные проводником пластины площадью S каждая находятся на расстоянии d друг от друга (это расстояние мало по сравнению с размерами пластин) во внешнем однородном поле с напряженностью , перпендикулярной пластинам (рис. 3). Какую работу надо совершить, чтобы сблизить их до расстояния d/2?
Рис. 3
Пластины эквипотенциальны, и между ними поля нет. Результатом работы по сближению является создание поля с напряженностью Е в объеме 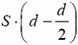
Упражнения
1. Два одинаковых плоских конденсатора емкостью С каждый соединены параллельно и заряжены до напряжения U. Пластины одного из конденсаторов медленно разводят на большое расстояние. Какая при этом совершается работа?
2. Два конденсатора, каждый емкостью С, заряжены до напряжения U и соединены через резистор (рис. 4). Пластины одного из конденсаторов быстро раздвигают, так что расстояние между ними увеличивается вдвое, а заряд на пластинах за время их перемещения не изменяется. Какое количество теплоты выделится в резисторе?
Рис. 4
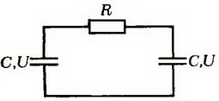
3. Плоский воздушный конденсатор присоединен к батарее с ЭДС . Площадь пластин S, расстояние между ними d. В конденсаторе находится металлическая плита толщиной d1, параллельная пластинам (рис. 5). Какую минимальную работу нужно затратить, чтобы удалить плиту из конденсатора?
Рис. 5
4. Большая тонкая проводящая пластина площадью S и толщиной d помещена в однородное электрическое поле с напряженностью , перпендикулярной поверхности пластины. Какое количество теплоты выделится в пластине, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы удалить пластину из поля?
5. Одна из пластин плоского конденсатора подвешена на пружине (рис. 6). Площадь каждой пластины S, расстояние между ними в начальный момент d. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть минимальная жесткость пружины, чтобы не произошло касание пластин? Смещением пластин за время зарядки пренебречь.
Рис. 6
Ответы.
1. 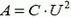
2. 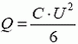
3. 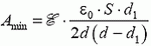
4. 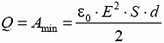
5. 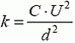
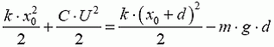
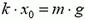
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Работа тока. Закон Джоуля – Ленца
В электронагревателе с неизменным сопротивлением спирали , через который течёт постоянный ток, за время (t) выделяется количество теплоты (Q). Если силу тока и время (t) увеличить вдвое, то во сколько раз увеличится количество теплоты, выделившееся в нагревателе?
Количество теплоты можно найти по формуле: [Q=I^2Rt] где (I) — сила тока, (R) — сопротивление спирали.
Если силу тока (I) и время (t) увеличить вдвое, количество теплоты увеличится в 8 раз.
Ответ: 8
К идеальному источнику тока с ЭДС 3 В подключили конденсатор ёмкостью 1 мкФ один раз через резистор 10(^7) Ом, а второй раз — через резистор 2(cdot)10(^7) Ом. Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым? Излучением пренебречь.
Энергия, запасенная в конденсаторе находится по формуле: [W=dfrac{C U^2}{2}=dfrac{C varepsilon^2}{2}] Вся энергия, запасенная в конденсаторе выделяется через резисторы в виде тепла. Энергия не зависит от сопротивления резистора, поэтому при замене резисторов, количество выделяемого тепла не изменяется.
Ответ: 1
Электрический чайник мощностью 4,4 кВт рассчитан на включение в электрическую сеть напряжением 220 В. Определите силу тока в нагревательном элементе чайника при его работе в такой сети. (Ответ дайте в амперах.)
Мощность можно найти по формуле: [P=UI] где (U) — напряжение, (I) — сила тока. Отсюда выразим силу тока: [I =dfrac{P}{U}=dfrac{4400text{ Вт}}{220text{ В}}=20 text{ А}]
Ответ: 20
Резистор 1 с электрическим сопротивлением (R_1) = 6 Ом и резистор 2 с электрическим сопротивлением (R_2) = 3 Ом включены последовательно в цепь постоянного тока. Чему равно отношение количества теплоты, выделяющегося на резисторе 1, к количеству теплоты, выделяющемуся на резисторе 2 за одинаковое время?
Кол-во теплоты можно найти по формуле: [Q=I^2Rt] где (I) — сила тока, (R) — сопротивление резистора, (t) — время.
Так как резисторы соединены последовательно, то через них протекает одинаковый ток за одинаковый промежуток времени: [dfrac{Q_1}{Q_2}=dfrac{I^2R_1t}{I^2R_2t}=dfrac{R_1}{R_2}] [dfrac{Q_1}{Q_2} = dfrac{6text{ Ом}}{3text{ Ом}}=2]
Ответ: 2
На корпусе электропечи-ростера имеется надпись: «220 В, 880 Вт». Найдите силу тока, потребляемого ростером. (Ответ дайте в амперах.)
Мощность можно найти по формуле: [P=UI] где (U) — напряжение, (I) — сила тока. Выразим отсюда силу тока: [I=dfrac{P}{U}=dfrac{880text{ Вт}}{220text{ В}}=4text{ А}]
Ответ: 4
Два последовательно соединённых резистора сопротивлениями 4 Ом и 8 Ом подключены к аккумулятору, напряжение на клеммах которого равно 24 В. Какая тепловая мощность выделяется в резисторе меньшего номинала? (Ответ дайте в ваттах.)
Запишем закон Ома для участка цепи с учетом того, что резисторы соединены последовательно: [I=frac{U}{R_1+R_2}] где (U) – напряжение, (I) – сила тока, (R_1) и (R_2) — сопротивление на резисторах 1 и 2 соответственно.
Так как резисторы соединены последовательно, то через них течет ток одинаковой силы, равной: [I = dfrac{24text{ В}}{4text{ Ом}+8text{ Ом}}=dfrac{24text{ В}}{12text{ Ом}}=2 text{ А}] Мощность на 1 резисторе найдем по формуле: [P=I^2R_1] [P=(2text{ А})^2cdot4text{ Ом}=16 text{ Вт}]
Ответ: 16
По проводнику с сопротивлением (R) = 12 Ом пропускали постоянный ток в течение 9 с. Какое количество теплоты выделилось в проводнике за это время, если через его сечение прошел заряд 3 Кл? (Ответ дайте в джоулях.)
Сила тока показывает, какой заряд прошел через поперечное сечение проводника за промежуток времени: [; ; ; ; ; ; ; ; ; ; I=dfrac{Delta q}{Delta t} ; ; ; ; ; ; ; ; ; ;(1)] Количество теплоты, выделяемое в проводнике, можно найти по формуле: [; ; ; ; ; ; ; ; Q=I^2RDelta t ; ; ; ; ; ; ; (2)] Подставим (1) в (2) и найдем количество теплоты: [Q=left(dfrac{Delta q}{Delta t}right)^2 RDelta t = dfrac{Delta q^2 R}{Delta t}] [Q = dfrac{(3text{ Кл})^2cdot12text{ Ом}}{9text{ с}}=12 text{ Дж}]
Ответ: 12

УСТАЛ? Просто отдохни