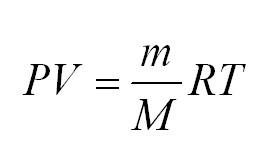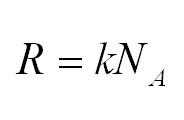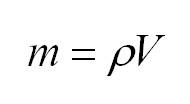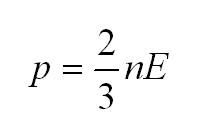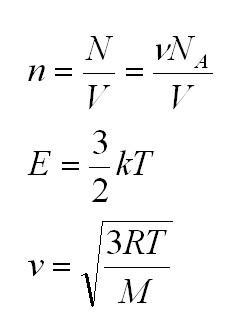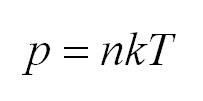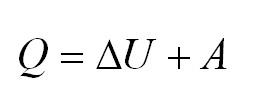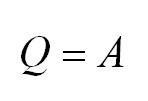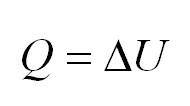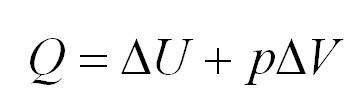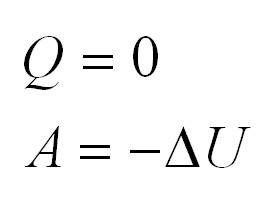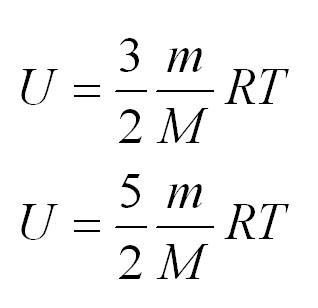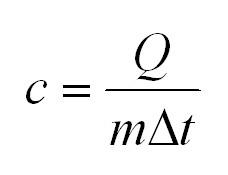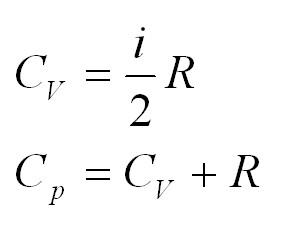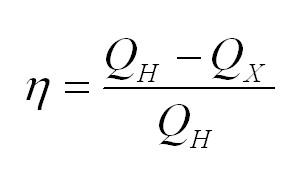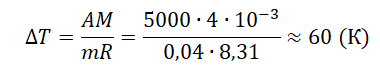Физика, 10 класс
Урок 23. Внутренняя энергия. Работа. Количество теплоты
Список вопросов, рассмотренных в уроке: внутренняя энергия; способы изменения внутренней энергии; различные виды теплообмена; уравнение теплового баланса; работа в термодинамике; нахождение численного значения работы в различных тепловых процессах.
Глоссарий по теме
Термодинамическая система представляет собой систему тел, которые взаимодействуют и обмениваются энергией и веществом.
Состояние равновесия – это состояние системы, в которой нет теплообмена между телами, составляющими систему.
Термодинамический процесс – процесс изменения состояния системы, который изменяет параметры системы.
Внутренняя энергия представляет собой сумму кинетической энергии хаотичного теплового движения и потенциальной энергии взаимодействия всех молекул, составляющих тело.
Теплоемкость представляет собой энергию, которая численно равна количеству тепла, которое выделяется или поглощается, когда температура тела изменяется на 1 К.
Теплопередача- это передача энергии от одного тела другому без выполнения работы.
Количество тепла является количественной мерой изменения внутренней энергии во время теплообмена.
Работа в термодинамике – это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.
Список литературы
Г.Я. Мякишев., Б. Буховцев., Н. Н. Соцкий. Физика.10. Учебник для образовательных организаций М .: Просвещение, 2017. – С. 243-254.
Рымкевич А.П. Сборник задач по физике. 10-11 класс М.: Дрофа, 2009.- с.75-84
Основное содержание урока
Внутренняя энергия тела – это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.
U = 3/2 · ν · R · T
Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.
Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.
Работа газа в изобарном процессе равна A = P · ΔV. Если газ расширяется, то А > 0, если газ сжимается, то А < 0.
Кроме того, работа газа может быть определена с использованием графика давления в зависимости от объема.
Работа газа численно равна площади под графиком давления.
Количество теплоты – это энергия, которую система получает или теряет во время теплообмена.
Количество тепла для различных термических процессов определяется по-разному.
При нагревании и охлаждении: Q = c_ ∙ m ∙ ΔT;
Во время плавления и кристаллизации: Q = ℷ ∙ m;
Во время испарения и конденсации; Q = r ∙ m;
При сжигании: Q = q ∙ m.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса: Q1 + Q2 + … + Qn = 0
Выражение для внутренней энергии одноатомного идеального или разреженного реального газа имеет следующий вид:
U = 3/2 ν ∙ R ∙ T
Для идеального газа из молекул с двумя, тремя или более атомами необходимо учитывать кинетическую энергию вращения молекул (они больше не могут считаться материальными точками), поэтому выражение для их внутренней энергии отличается от U = 3/2 ν ∙ R ∙ T числовым коэффициентом.
Для двухатомного газа (например, O2, CO и т. д.):
U = 5/2 ν ∙ R ∙ T
Для газа с тремя атомами или более (например, O3, CH4):
U = 3ν · R · T
Изменить внутреннюю энергию вещества можно, передав ему некоторое количество тепла или выполнить над ним работу.
Существует три типа теплопередачи:
1) Теплопроводность представляет собой процесс переноса энергии от более теплого тела к менее нагретому телу с прямым контактом или от более нагретых частей тела к менее нагретым, осуществляемый хаотично движущимися частицами тела (атомы, молекулы, электроны , и т.д.). Простым примером является нагревание чашки, в которую выливают горячий чай.
2) Конвекция – это своего рода передача тепла, в которой внутренняя энергия передается снизу вверх струями или потоками жидкости или газа. Пример: нагревание воды в чайнике, который стоит на горячей плите.
3) Лучистый обмен или излучение – это процесс передачи энергии через электромагнитное излучение. Простой пример: солнечный свет.
Механическая работа изменяет механическую энергию тела. Термодинамическая работа изменяет внутреннюю энергию газа.
Если газ расширяется, то работа газа считается положительной. Если он сжат, то отрицательной.
Формула для нахождения работы газа в изобарном процессе имеет следующий вид:
A = p · ΔV
Для изотермического процесса формула принимает следующий вид: A = ν ∙ R ∙ T ∙ ln (V_2 / V_1)
Разбор тренировочных заданий
1. Объём газа, расширяющегося при постоянном давлении 100 кПа, увеличился на 20 литров. Работа, выполняемая газом в этом процессе, – _____.
Варианты ответов:
2000 Дж;
20 000 Дж;
200 Дж;
50 МДж.
Правильный вариант / варианты (или правильные комбинации вариантов): 3) 2000 Дж.
Совет: используйте формулу работы.
2. Чтобы из 5 кг снега, при температуре 0ºС, получить воду при 20ºС, необходимо сжигать в печке с КПД 40% __ кг дров.
Решение: при сгорании дров выделится количество теплоты:

из этого количества на полезную работу пойдёт только:
Для плавления снега необходимо количество теплоты:

для нагревания воды понадобится:
Согласно уравнению теплового баланса:

Отсюда следует:
Подставим числовые значения в формулу:
Ответ: 0,5175 кг.
Количество теплоты:
Процесс передачи
энергии от одного тела к другому без
совершения работы называется теплообменом
или теплопередачей.
Теплообмен происходит между телами,
имеющими разную температуру. При
установлении контакта между телами с
различными температурами происходит
передача части внутренней энергии от
тела с более высокой температурой к
телу, у которого температура ниже.
Энергия, переданная телу в результате
теплообмена, называется количеством
теплоты.
Удельная теплоемкость вещества:
Если процесс
теплопередачи не сопровождается работой,
то на основании первого закона
термодинамики количество теплоты равно
изменению внутренней энергии тела:
.
Средняя энергия
беспорядочного поступательного движения
молекул пропорциональна абсолютной
температуре. Изменение внутренней
энергии тела равно алгебраической сумме
изменений энергии всех атомов или
молекул, число которых пропорционально
массе тела, поэтому изменение внутренней
энергии и, следовательно, количество
теплоты пропорционально массе и изменению
температуры:
Коэффициент
пропорциональности в этом уравнении
называется удельной
теплоемкостью вещества.
Удельная теплоемкость показывает, какое
количество теплоты необходимо для
нагревания 1 кг вещества на 1 К.
Работа в термодинамике:
В механике работа
определяется как произведение модулей
силы и перемещения и косинуса угла между
ними. Работа совершается при действии
силы на движущееся тело и равна изменению
его кинетической энергии.
В термодинамике
движение тела как целого не рассматривается,
речь идет о перемещении частей
макроскопического тела относительно
друг друга. В результате меняется объем
тела, а его скорость остается равной
нулю. Работа в термодинамике определяется
так же, как и в механике, но равна изменению
не кинетической энергии тела, а его
внутренней энергии.
При совершении
работы (сжатии или расширении) изменяется
внутренняя энергия газа. Причина этого
состоит в следующем: при
упругих соударениях молекул газа с
движущимся поршнем изменяется их
кинетическая энергия.
Вычислим работу
газа при расширении. Газ действует на
поршень с силой
,
где– давление газа, а
– площадь поверхности
поршня.
При расширении газа поршень смещается
в направлении силына малое расстояние
.
Если расстояние мало, то давление газа
можно считать постоянным. Работа газа
равна:
,
где
– изменение объема газа.
В процессе расширения
газа совершает положительную работу,
так как направление силы и перемещения
совпадают. В процессе расширения газ
отдает энергию окружающим телам.
Работа, совершаемая
внешними телами над газом, отличается
от работы газа только знаком
,
так как сила,
действующая на газ, противоположна силе,
с которой газ действует на поршень, и
равна ей по модулю (третий закон Ньютона);
а перемещение остается тем же самым.
Поэтому работа внешних сил равна:
.
Первый закон термодинамики:
Первый закон
термодинамики является законом сохранения
энергии, распространенным на тепловые
явления. Закон сохранения энергии:
энергия в
природе не возникает из ничего и не
исчезает: количество энергии неизменно,
она только переходит из одной формы в
другую.
В
термодинамике рассматриваются тела,
положение центра тяжести которых
практически не меняется. Механическая
энергия таких тел остается постоянной,
а изменяться может лишь внутренняя
энергия.
Внутренняя энергия
может изменяться двумя способами:
теплопередачей и совершением работы.
В общем случае внутренняя энергия
изменяется как за счет теплопередачи,
так и за счет совершения работы. Первый
закон термодинамики формулируется
именно для таких общих случаев:
Изменение
внутренней энергии системы при переходе
ее из одного состояния в другое равно
сумме работы внешних сил и количества
теплоты, переданного системе:
Если система
изолирована, то над ней не совершается
работа и она не обменивается теплотой
с окружающими телами. Согласно первому
закону термодинамики внутренняя
энергия изолированной системы остается
неизменной.
Учитывая, что
,
первый закон термодинамики можно
записать так:
Количество
теплоты, переданное системе, идет на
изменение ее внутренней энергии и на
совершение системой работы над внешними
телами.
Второй закон
термодинамики: невозможно
перевести теплоту от более холодной
системы к более горячей при отсутствии
других одновременных изменений в обеих
системах или в окружающих телах.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.
Идеальный газ
Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.
Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).
Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)
Массу, в свою очередь, можно вычислить, как произведение плотности и объема.
Основное уравнение молекулярно-кинетической теории (МКТ)
Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:
Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:
Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ
Первое начало термодинамики. Формулы для изопроцессов
Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:
Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:
Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.
Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:
Внутренняя энергия одноатомного и двухатомного идеального газа
Теплоемкость
Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.
Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.
Тепловые машины. Формула КПД в термодинамике
Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.
Коэффициент полезного действия тепловой машины вычисляется по формуле
Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.
Термодинамика – раздел физики, изучающий превращения энергии в макроскопических системах и основные свойства этих систем.
Термодинамика опирается на общие закономерности тепловых процессов и свойств макроскопических систем. Выводы термодинамики эмпирические, то есть опираются на факты, проверенные опытным путем с использованием молекулярно-кинетической модели.
Для описания термодинамических процессов в системах, состоящих из большого числа частиц, используются величины, не применимые к отдельным молекулам и атомам: температура, давление, концентрация, объем, энтропия)
Термодинамическое равновесие – состояние макросопической системы, когда описывающие ее макроскопические величины остаются неизменными.
В термодинамике рассматриваются изолированные системы тел, находящиеся в термодинамическом равновесии. То есть в системах с прекращением всех наблюдаемых макроскопических процессов. Особую важность представляет свойство, которое получило название выравнивания температуры всех ее частей.
При внешнем воздействии на термодинамическую систему наблюдается переход в другое равновесное состояние. Он получил название термодинамического процесса. Когда время его протекания достаточно медленное, система приближена к состоянию равновесия. Процессы, состоящие из последовательности равновесных состояний, называют квазистатическими.
Внутренняя энергия. Формулы
Внутренняя энергия считается важнейшим понятием термодинамики. Макроскопические тела (системы) имеют внутреннюю энергию, состящую из энергии каждой молекулы. Исходя из молекулярно-кинетической теории, внутренняя энергия состоит из кинетической энергии атомов и молекул, а также потенциальной энергии их взаимодействия.
Например, внутренняя энергия идеального газа равняется сумме кинетических энергий частиц газа, которые находятся в непрерывном беспорядочном тепловом движении. После подтверждений большим количеством экспериментов, был получен закон Джоуля:
Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема.
Применение молекулярно-кинетической теории говорит о том, что выражение для определения внутренней энергии 1 моля одноатомного газа, с поступательными движениями молекул записывается как:
U=32NАkT=32RT.
Зависимость от расстояния между молекулами у потенциальной энергии очевидна, поэтому внутренняя U и температура Т обусловлены изменениями V:
U=U(T, V).
Определение внутренней энергии U производится с помощью наличия макроскопических параметров, характеризующих состояние тела. Изменение внутренней энергии происходит по причине действия на тело внешних сил, совершающих работу. Внутренняя энергия является функцией состояния системы.
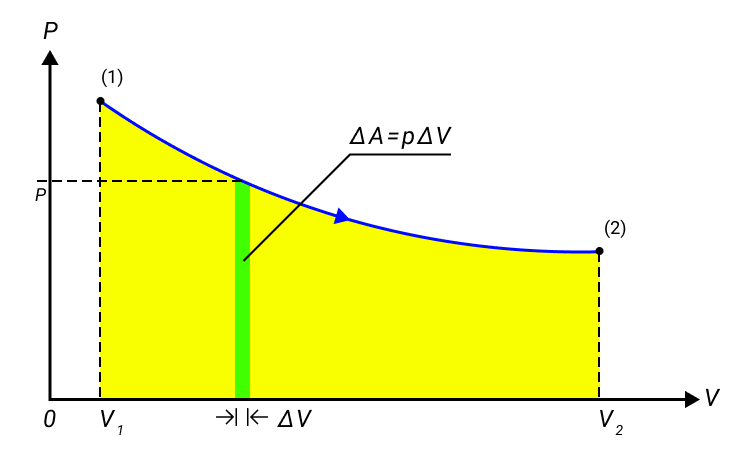
Когда газ в цилиндре сжимается под поршнем, то внешние силы совершают положительную работу A’. Силы давления газа на поршень также совершают работу, но равную A=-A’. При изменении объема газа на величину ∆V, говорят, что он совершает работу pS∆x=p∆V, где p – давление газа, S – площадь поршня, ∆x – его перемещение. Подробно показано в примере на рисунке 1.
Наличие знака перед работой говорит о работе газа в разных состояниях: положительная при расширении и отрицательная при сжатии. Переход из начального в конечное состояние работы газа может быть описан с помощью формулы:
A=∑pidVi или в пределе при ∆Vi→0:
A=∫V1V2pdV.
Рисунок 1. Работа газа при расширении.
Обратимые и необратимые процессы
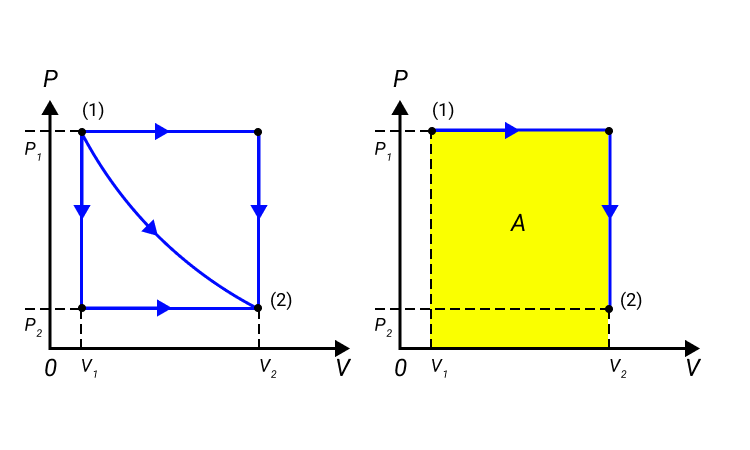
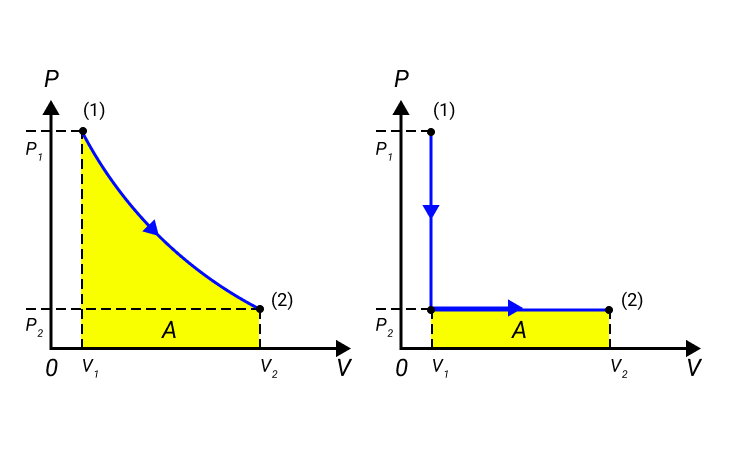
Работа численно равняется площади процесса, изображенного на диаграмме p, V. Величина А зависит от метода перехода от начального состояния в конечное. Рисунок 2 показывает 3 процесса, которые переводят газ из состояние (1) в состояние (2). Во всех случаях газ совершает работу.
Рисунок 2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.
Процессы из рисунка 2 возможно провести в обратном направлении. Тогда произойдет изменение знака А на противоположный.
Процессы, которые возможно проводить в обоих направлениях, получили название обратимых.
Жидкости и твердые тела могут незначительно изменять свой объем, поэтому при совершении работы разрешено им пренебречь. Но их внутренняя энергия подвергается изменениям посредствам совершения работы.
Механическая обработка деталей нагревает их. Это способствует изменению внутренней энергии. Имеется еще один пример опыта Джоуля 1843 года, служащий для определения механического эквивалента теплоты, изображенного на рисунке 3. Во время вращения катушки, находящейся в воде, внешние силы совершают положительную работу A’>0, тогда жидкость повышает температуру из-за наличия силы трения, то есть происходит увеличение внутренней энергии.
Процессы примеров не могут проводиться в противоположных направлениях, поэтому они получили название необратимых.
Рисунок 3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты.
Изменение внутренней энергии возможно при наличии совершаемой работы и при теплообмене. Тепловой контакт тел позволяет увеличиваться энергии одного тела с уменьшением энергии другого. Иначе это называется тепловым потоком.
Количество теплоты
Количество теплоты Q, полученное телом, называется его внутренней энергией, получаемой в результате теплообмена.
Рисунок 4. Модель работы газа.
Процесс передачи тепла тел возможен только при разности их температур.
Направление теплового потока всегда идет к холодному телу.
Количество теплоты Q считается энергетической величиной и измеряется в джоулях (Дж).
Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.
Первое начало термодинамики
Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.
±ΔU=±Q±A‘
Пояснение:
- +∆U — внутренняя энергия газа увеличивается.
- –∆U — внутренняя энергия газа уменьшается.
- +Q — газ нагревают (газу передают количество теплоты).
- –Q — газ охлаждается (газ отдает тепло окружающей среде).
- +A’ — газ сжимает внешняя сила.
- –A’ — газ расширяется, совершая работу.
Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.
Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?
Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:
Q = A – U = 500 – 300 = 200 (Дж)
Зависимость физических величин
Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:
ΔU=32νRΔT
Работа идеального газа зависит от изменения его объема:
A‘=pΔV
Первое начало термодинамики для изопроцессов
| Изотермический процесс (T = const) |
ΔU=0, Q=A‘ |
| Изохорный процесс (V = const) |
A‘=0, ΔU=Q |
| Изобарное расширение газа (p = const) |
ΔU=Q−pΔV ΔU=Q−νRΔT |
| Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0) |
Q=0, ΔU=A‘ |
Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?
18 кДж = 18000 Дж
Внутреннюю энергию газа можно определить по формуле:
ΔU=32νRΔT
Отсюда изменение температуры равно:
ΔT=2ΔU3νR
Уравнение состояния идеального газа для 1 и 2 состояния:
p1V=νRT1
p2V=νRT2
Отсюда давления равны:
p1=νRT1V
p2=νRT2V
Разность давлений:
p2−p1=νRT2V−νRT1V=νRVΔT=νRV·2ΔU3νR=2ΔU3V
p2−p1=2·180003·0,6=20000 (Па)=20 (кПа)
Графические задачи на первое начало термодинамики
Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.
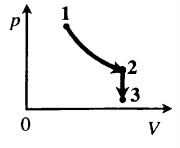
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?
Порядок решения:
1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.
T1 = T2 = 300 К; T3 = 100 К
2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.
Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.
3. Записать для него первое начало термодинамики.
В данном процессе:
ΔU=Q
4. Учитывая характер изменения величин, правильно расставить знаки: −ΔU=−Q.
5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.
Формула изменения внутренней энергии газа:
ΔU=32νRΔT
Формула работы газа:
A‘=pΔV
Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:
Изменение внутренней энергии равно:
Q23=32νRΔT23=32·1·8,31·200=2493 (Дж)
Задание EF17492
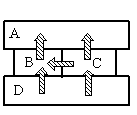
- A
- B
- C
- D
Алгоритм решения
- Определить тип теплопередачи.
- Вспомнить, как происходит этот тип теплопередачи.
- Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.
Решение
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.
На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 оС.
Ответ: A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17562
Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?
Ответ:
а) увеличилась на 300 Дж
б) уменьшилась на 300 Дж
в) увеличилась на 600 Дж
г) уменьшилась на 600 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 300 Дж.
Первое начало термодинамики:
ΔU=Q+A
Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:
ΔU=Q=300 (Дж)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17597
Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на
Ответ:
а) 5 кДж
б) 10 кДж
в) 15 кДж
г) 25 кДж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 10 кДж.
• Работа, совершенная газом: A = 15 кДж.
Первое начало термодинамики:
ΔU=Q+A
В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:
ΔU=Q−A=10−15=−5 (кДж)
Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17579
При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?
Ответ:
а) 60 К
б) 25 К
в) 15 К
г) 3 К
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать первое начало термодинамики.
3.Записать формулу для расчета работы газа.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и выполнить вычисления искомой величины.
Решение
Запишем исходные данные:
• Газ совершил работу: A = 5 кДж.
• Масса гелия: m = 0,04 кг.
5 кДж = 5000 Дж
Первое начало термодинамики:
ΔU=Q+A
Учтем, что не над газом совершают работу, а сам газ совершает ее:
Отсюда:
ΔU=Q−A
Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.
Работа, совершенная газом, равна:
A=pΔV=mMRΔT
Молярная масса гелия равна 4∙10–3 кг/моль.
Отсюда:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.9k