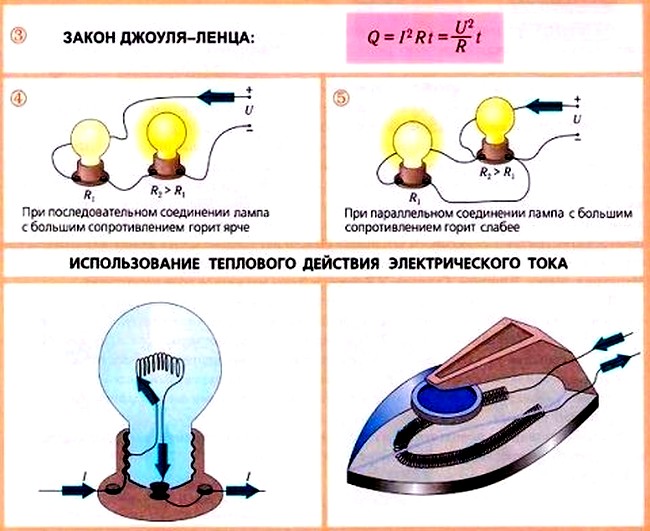
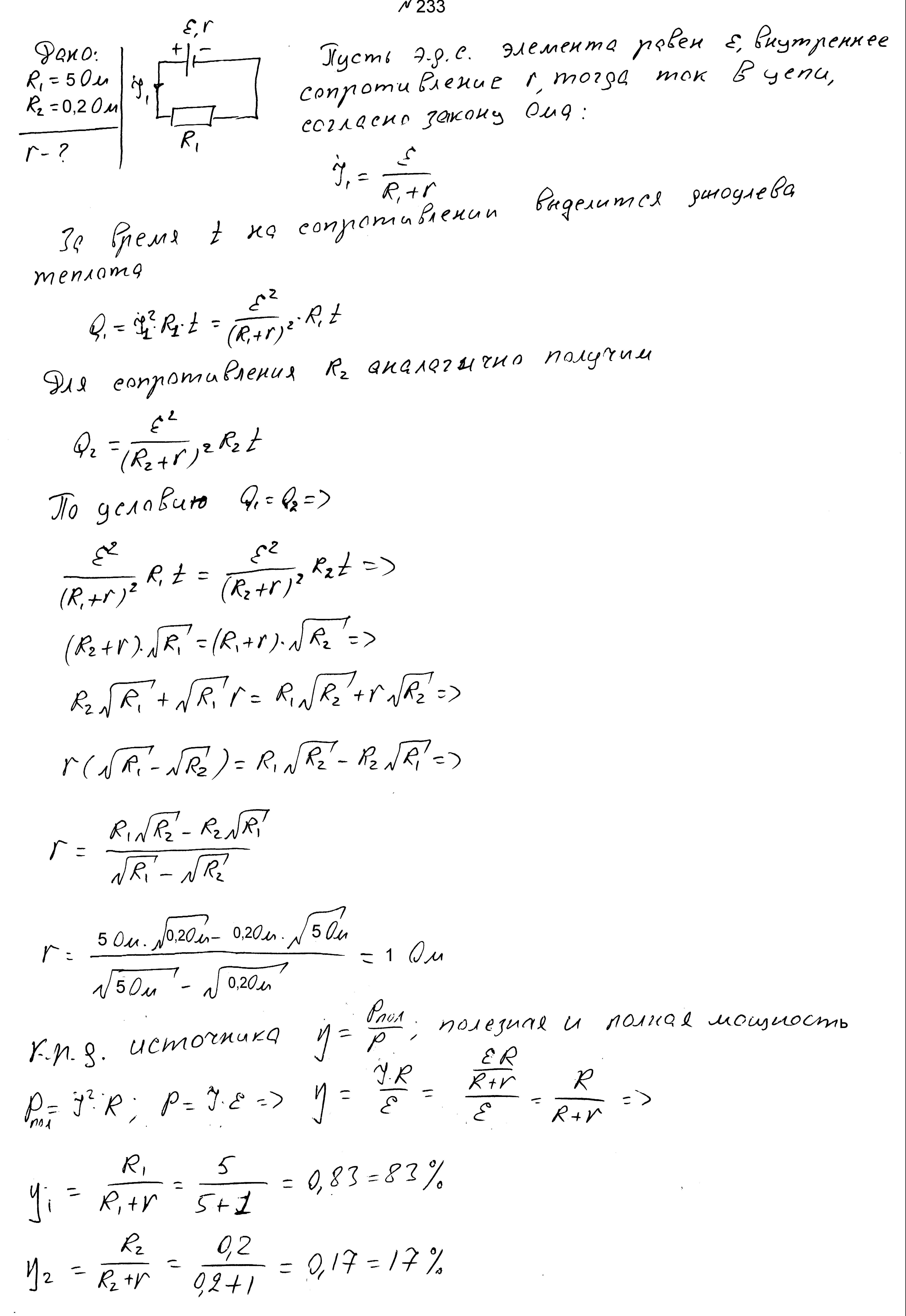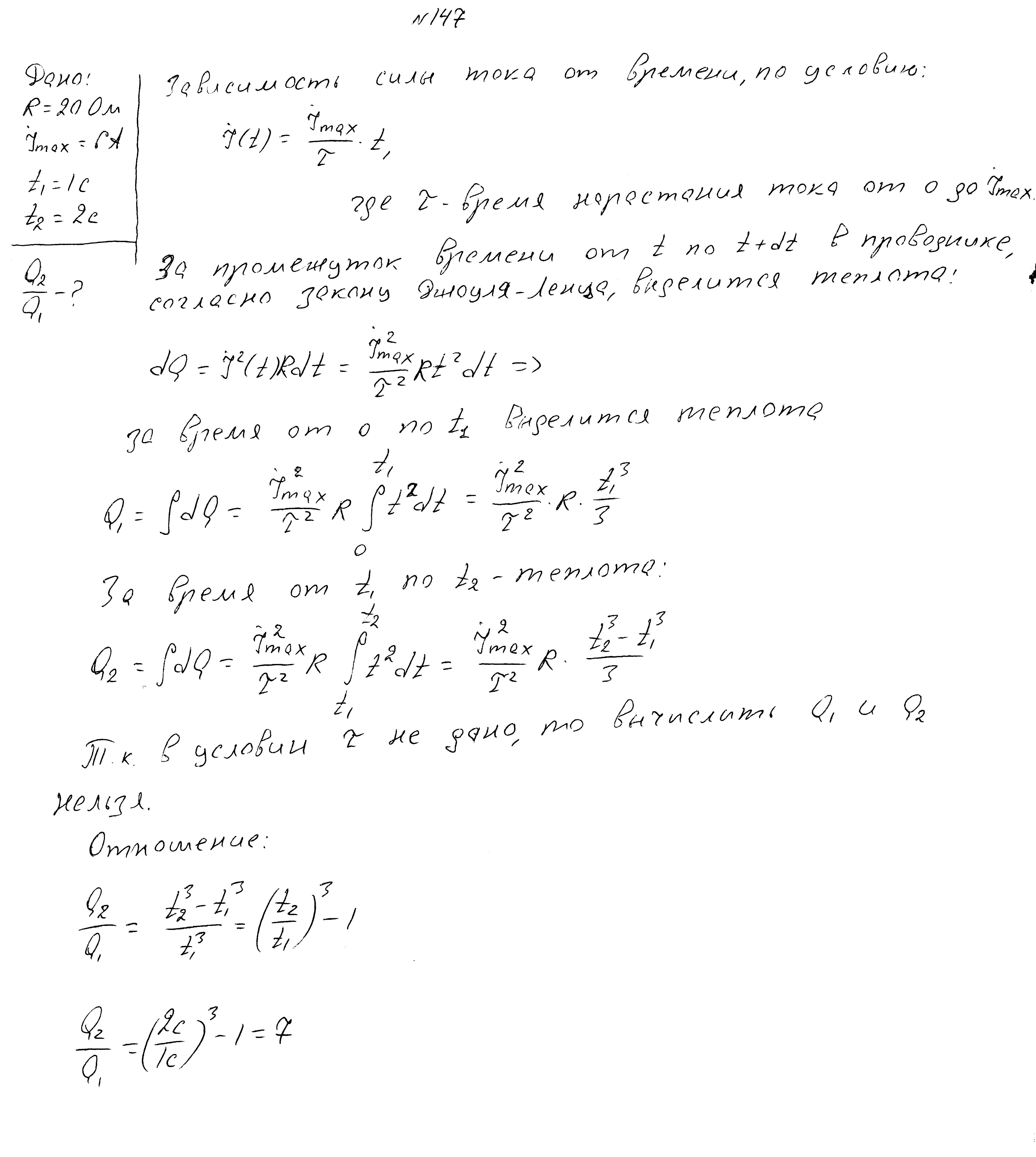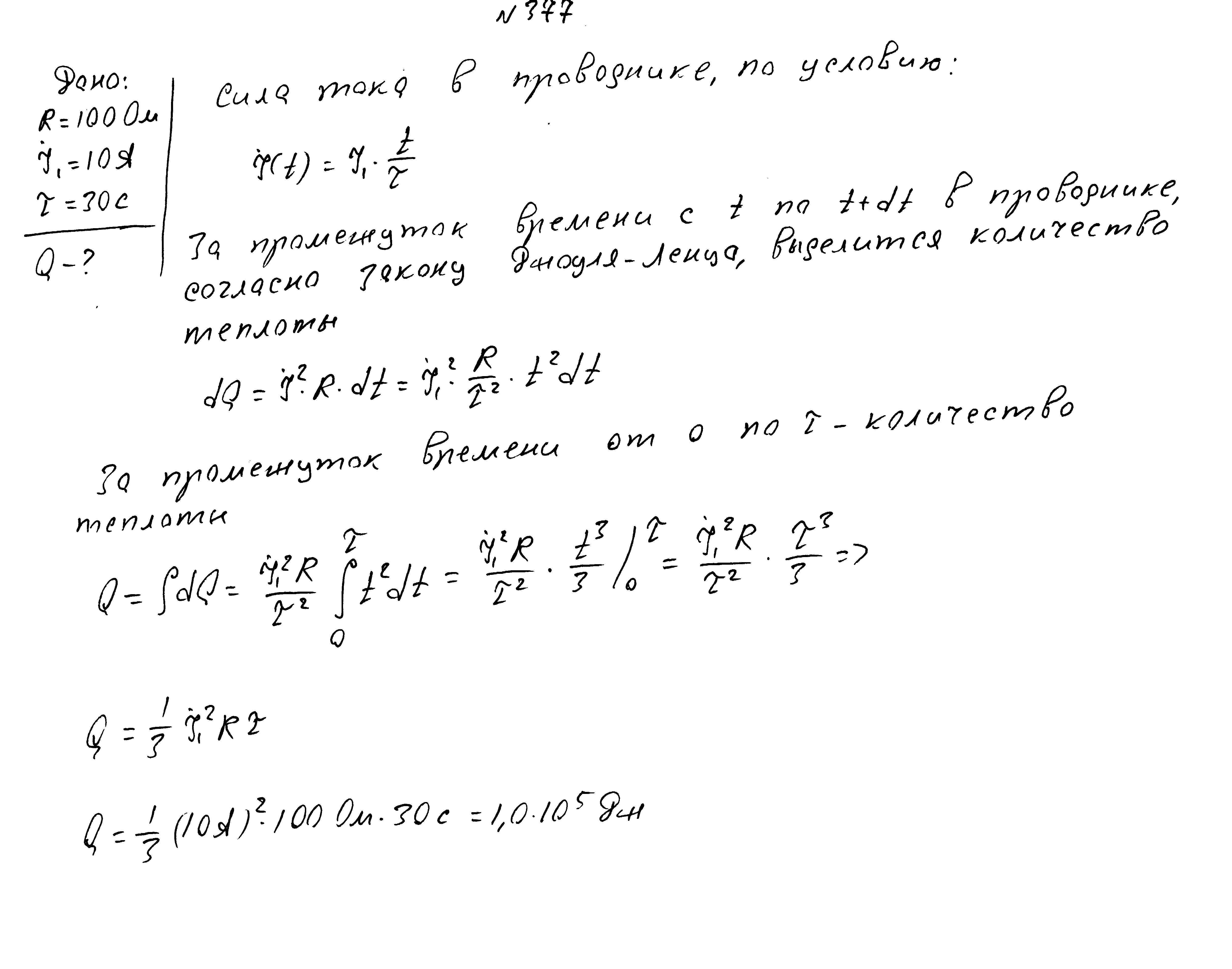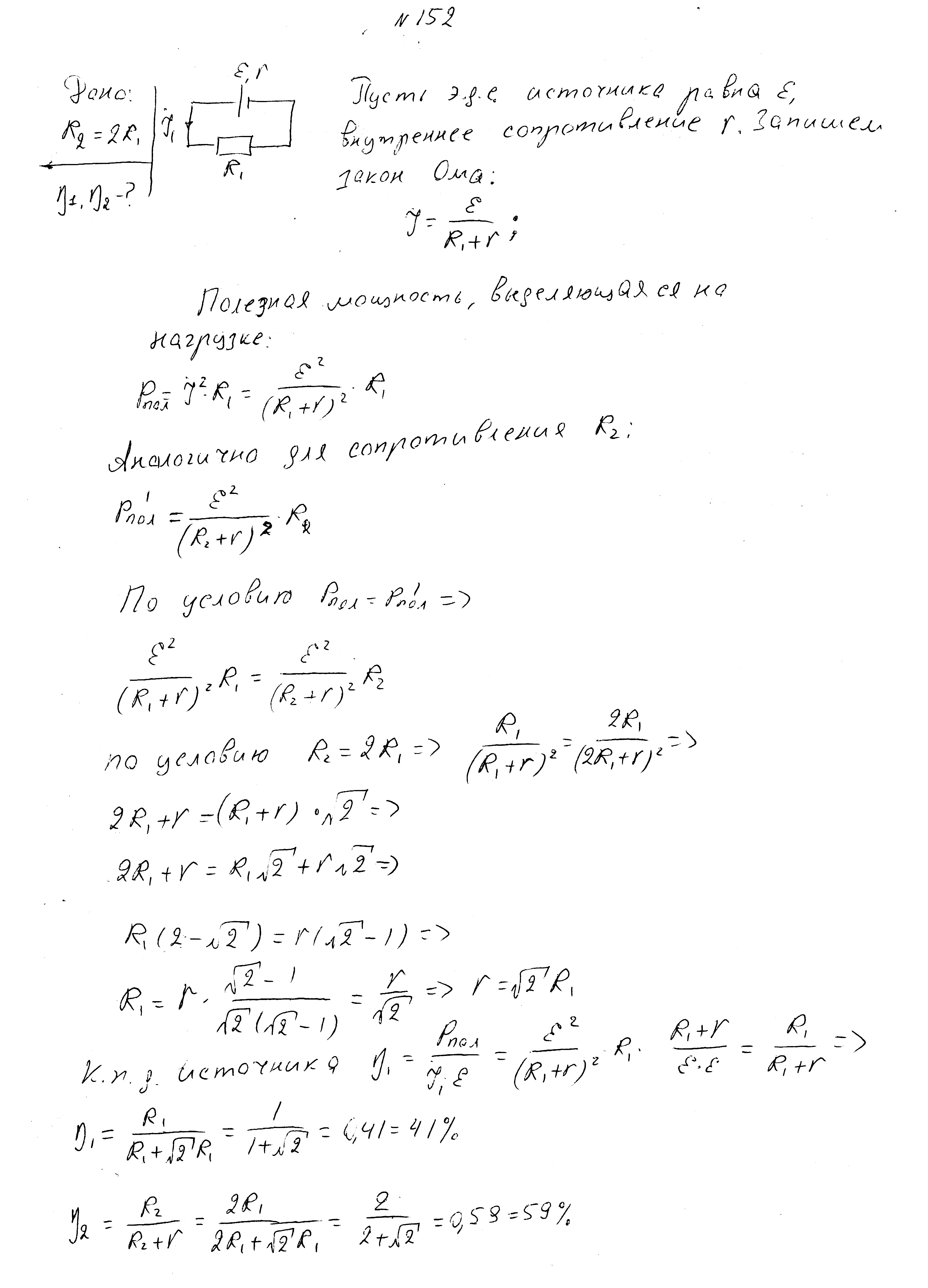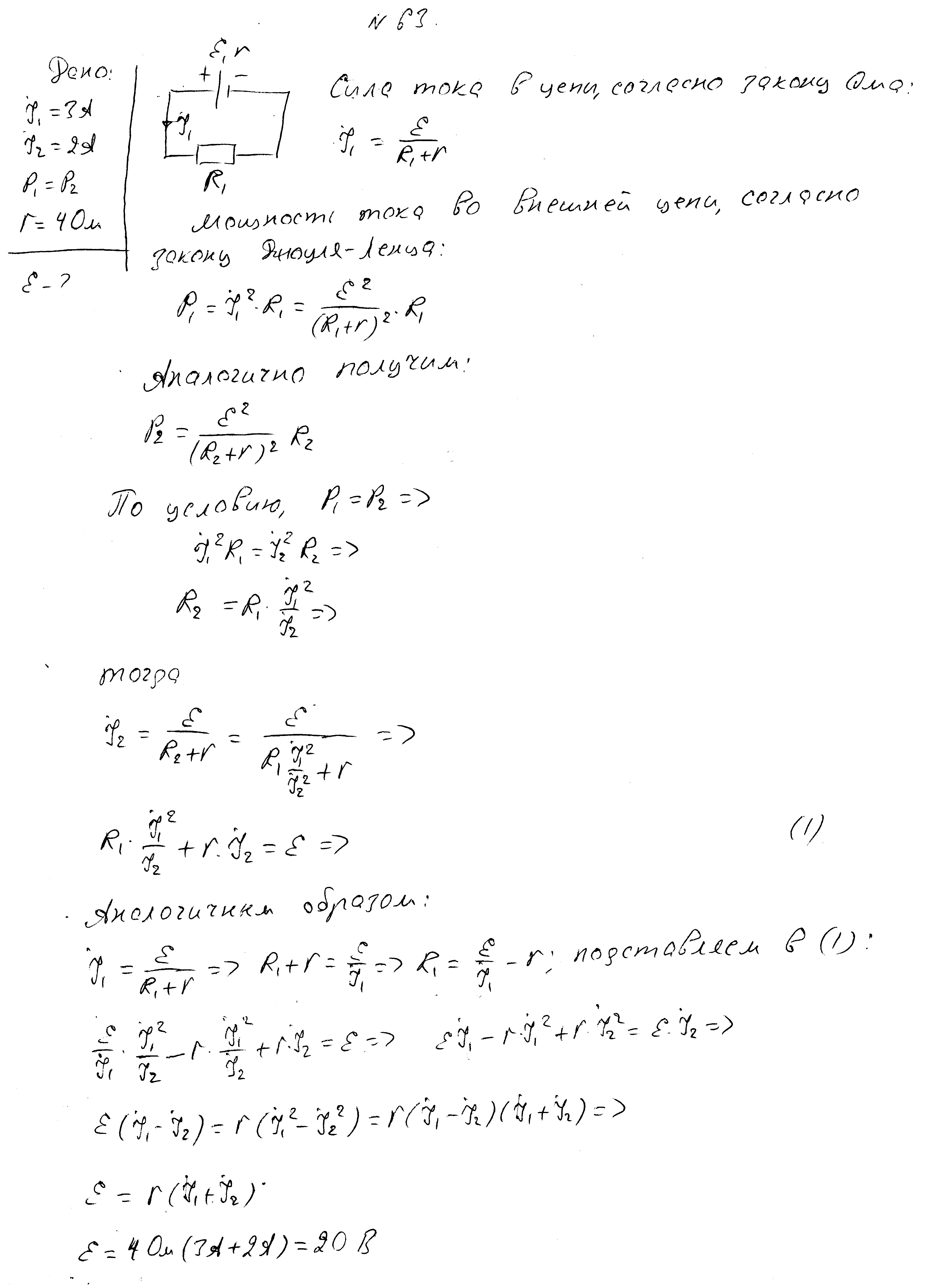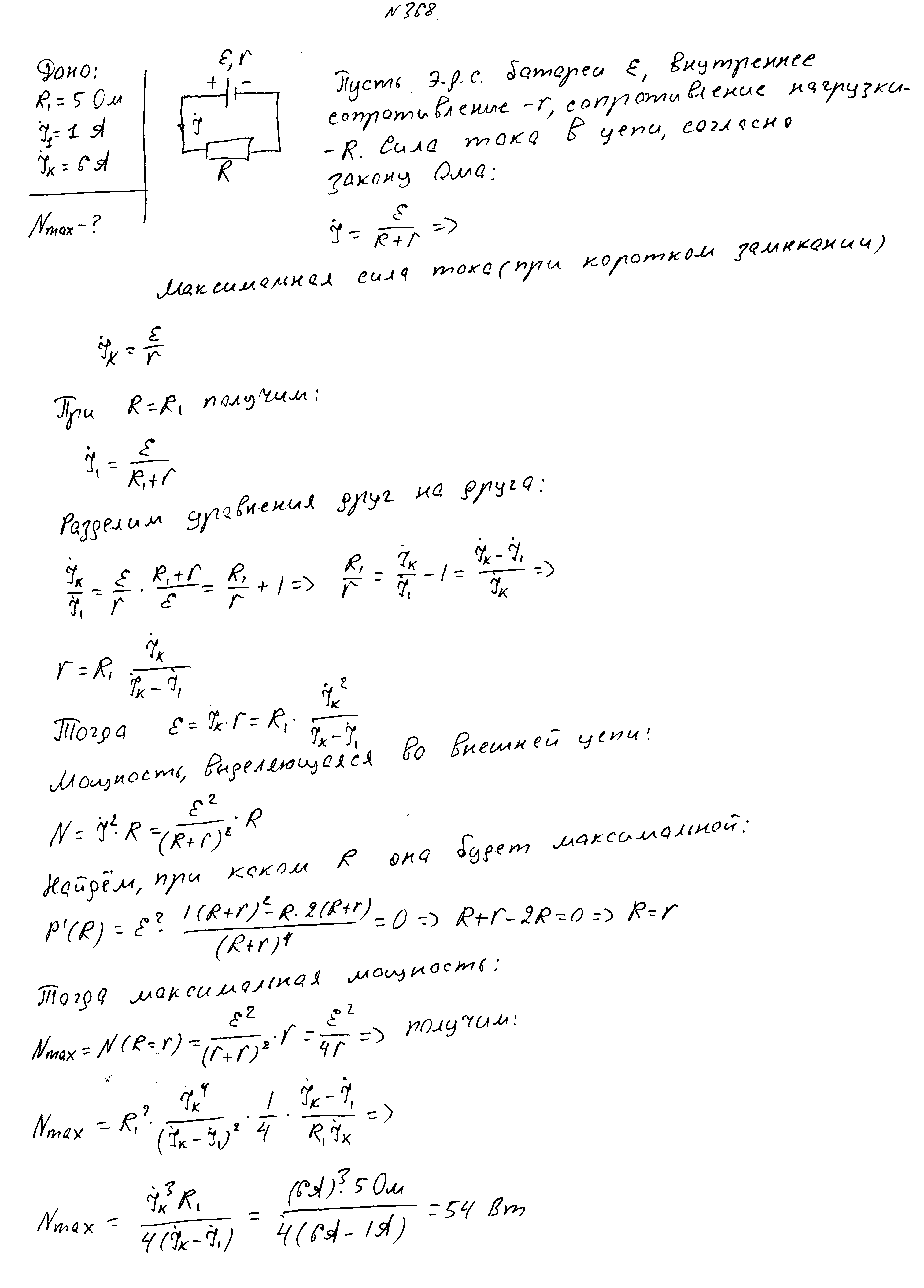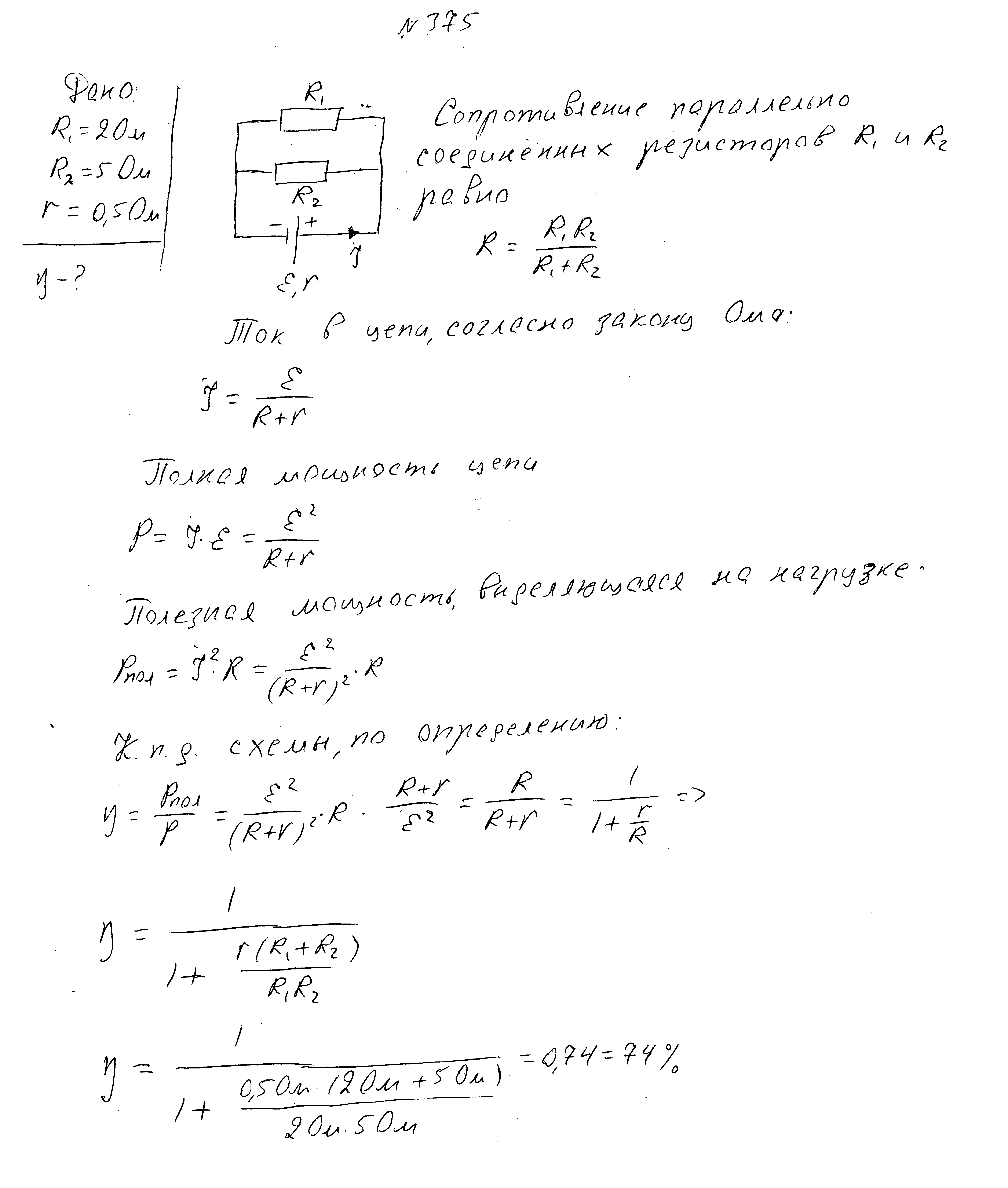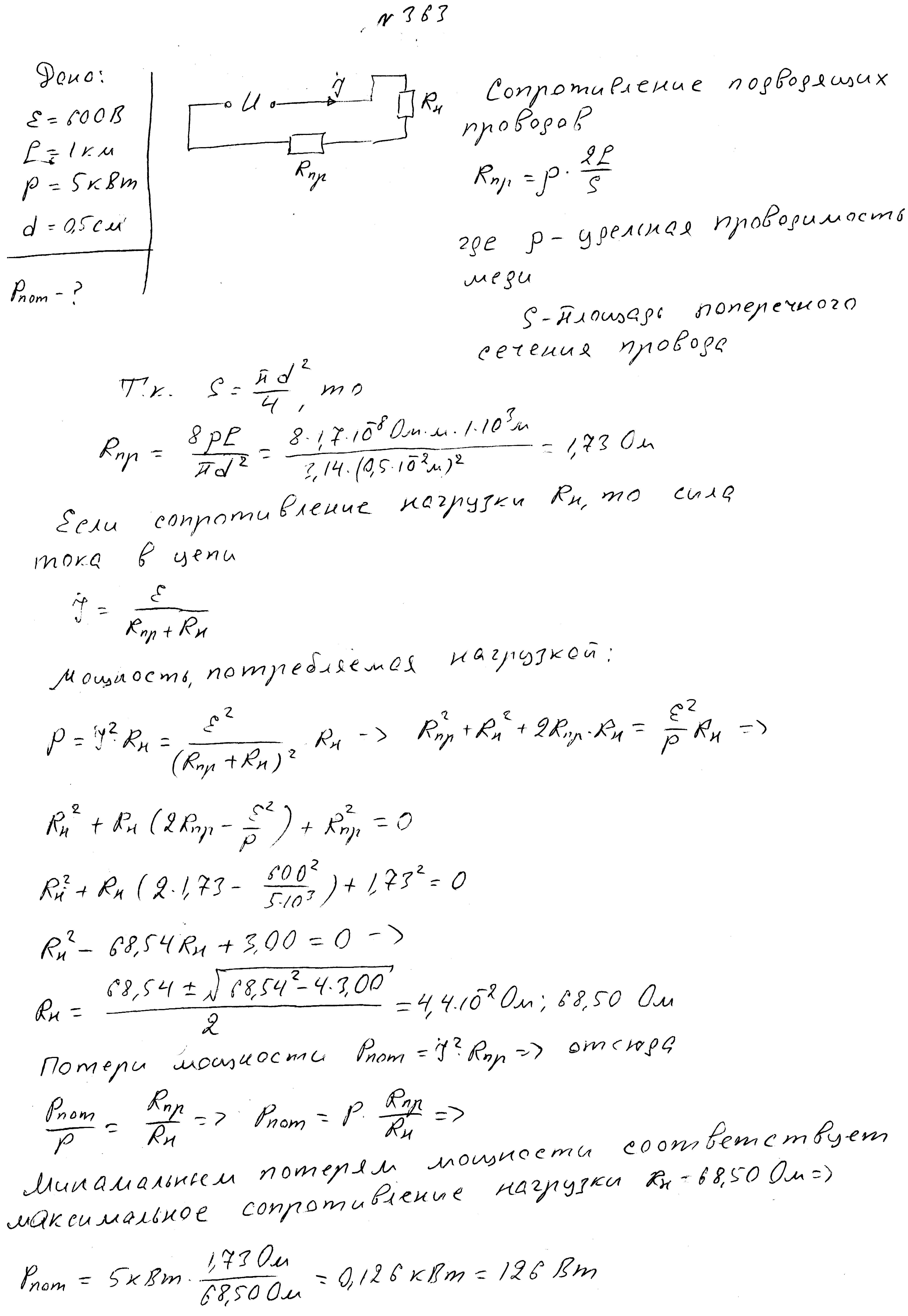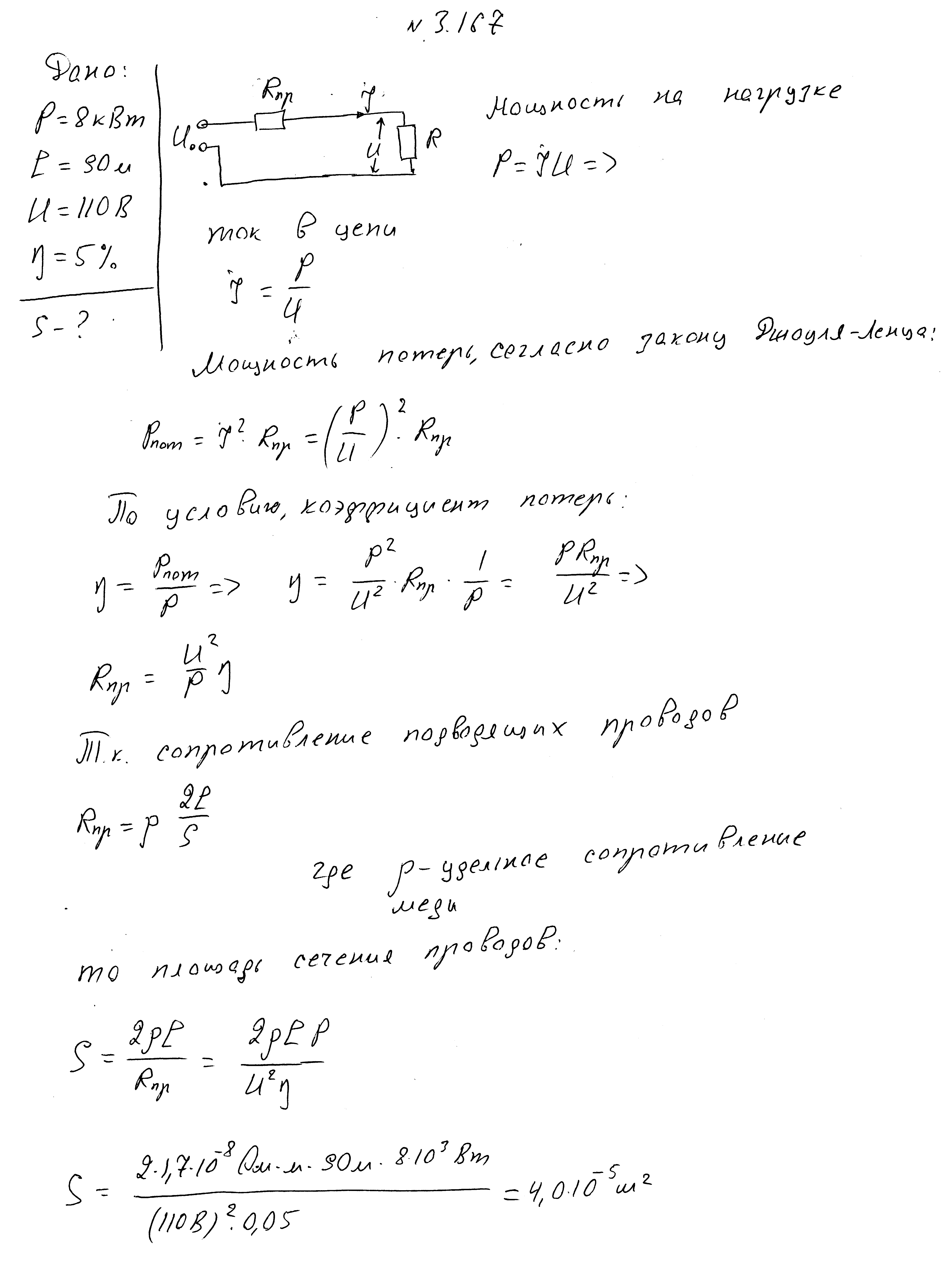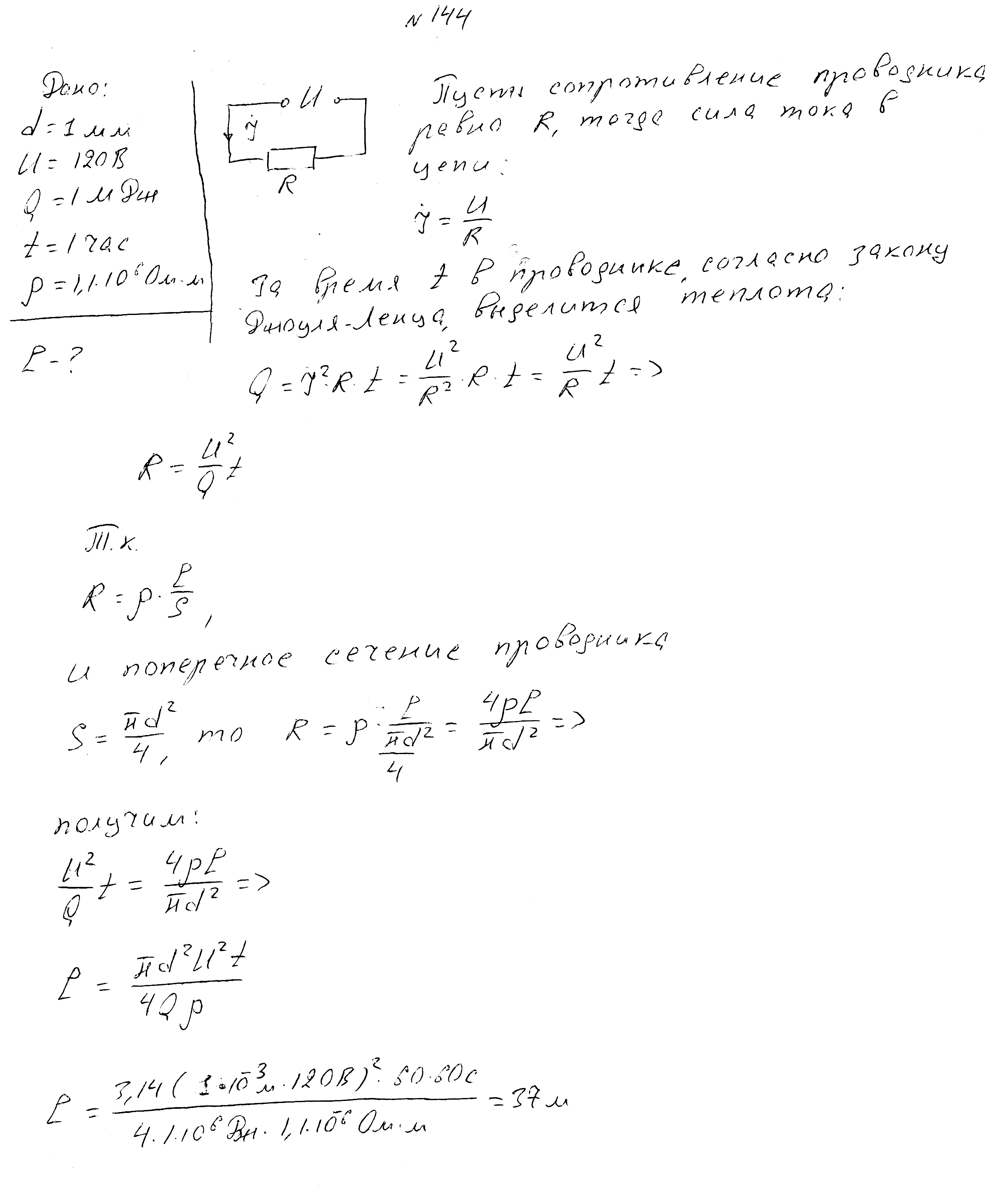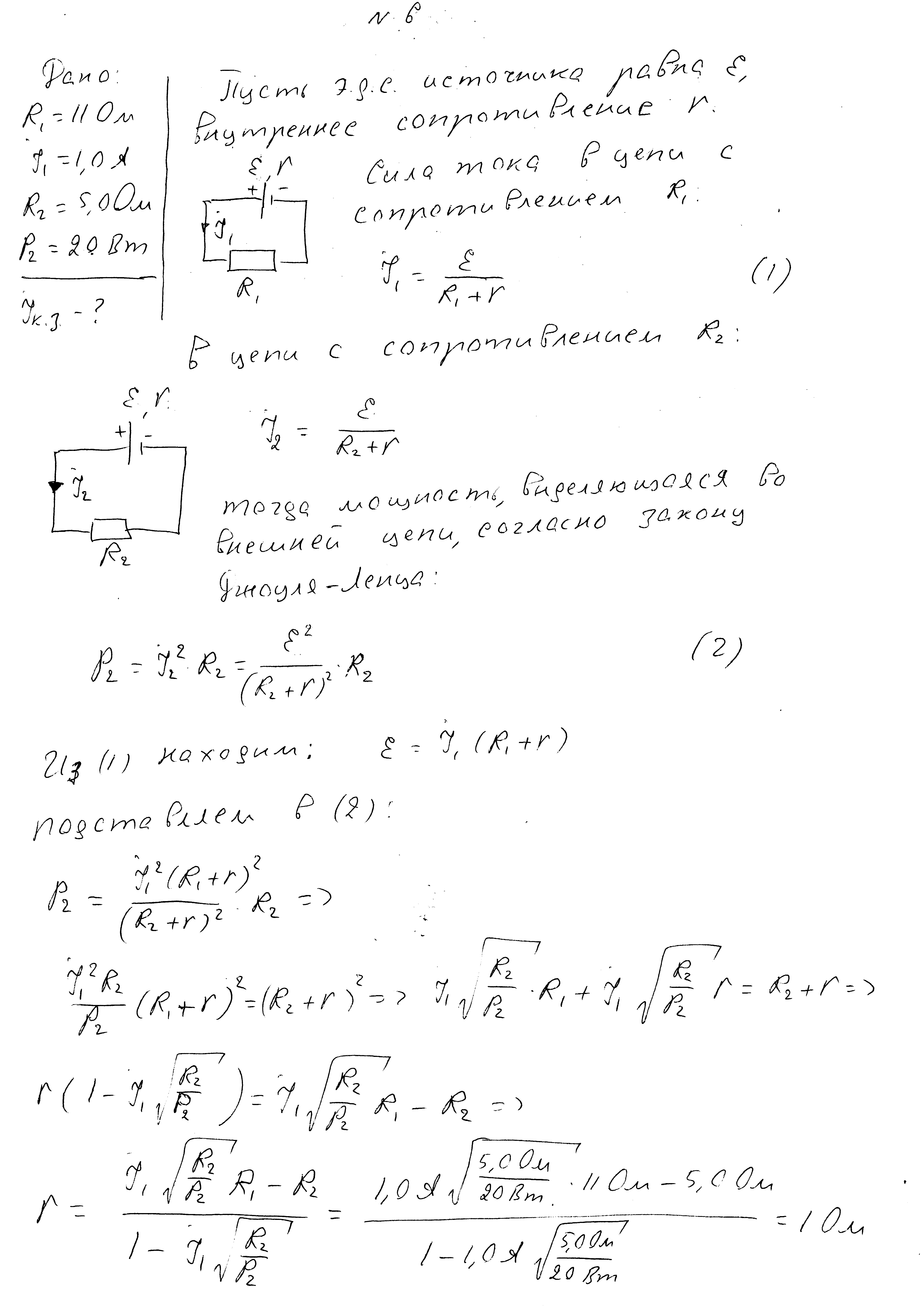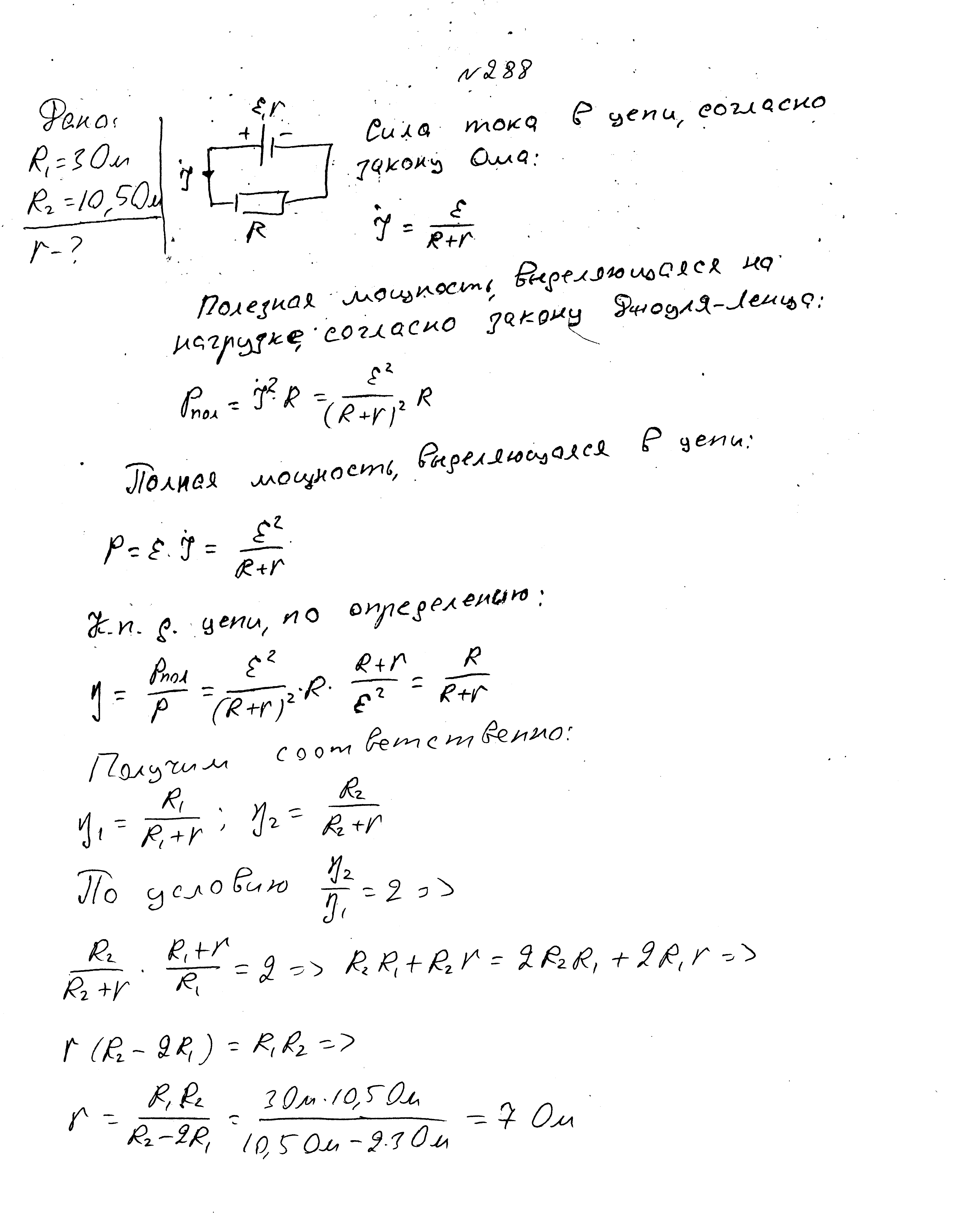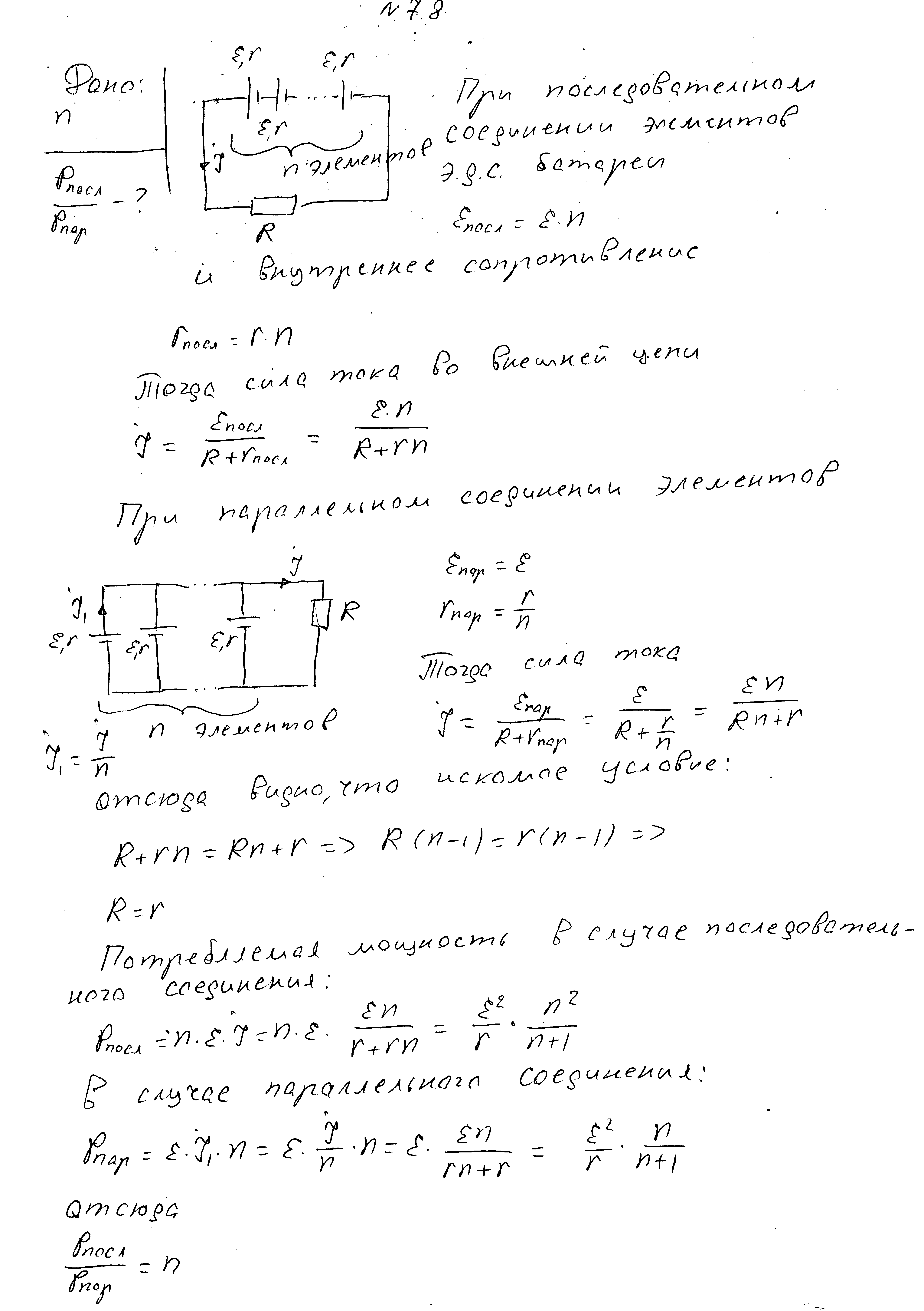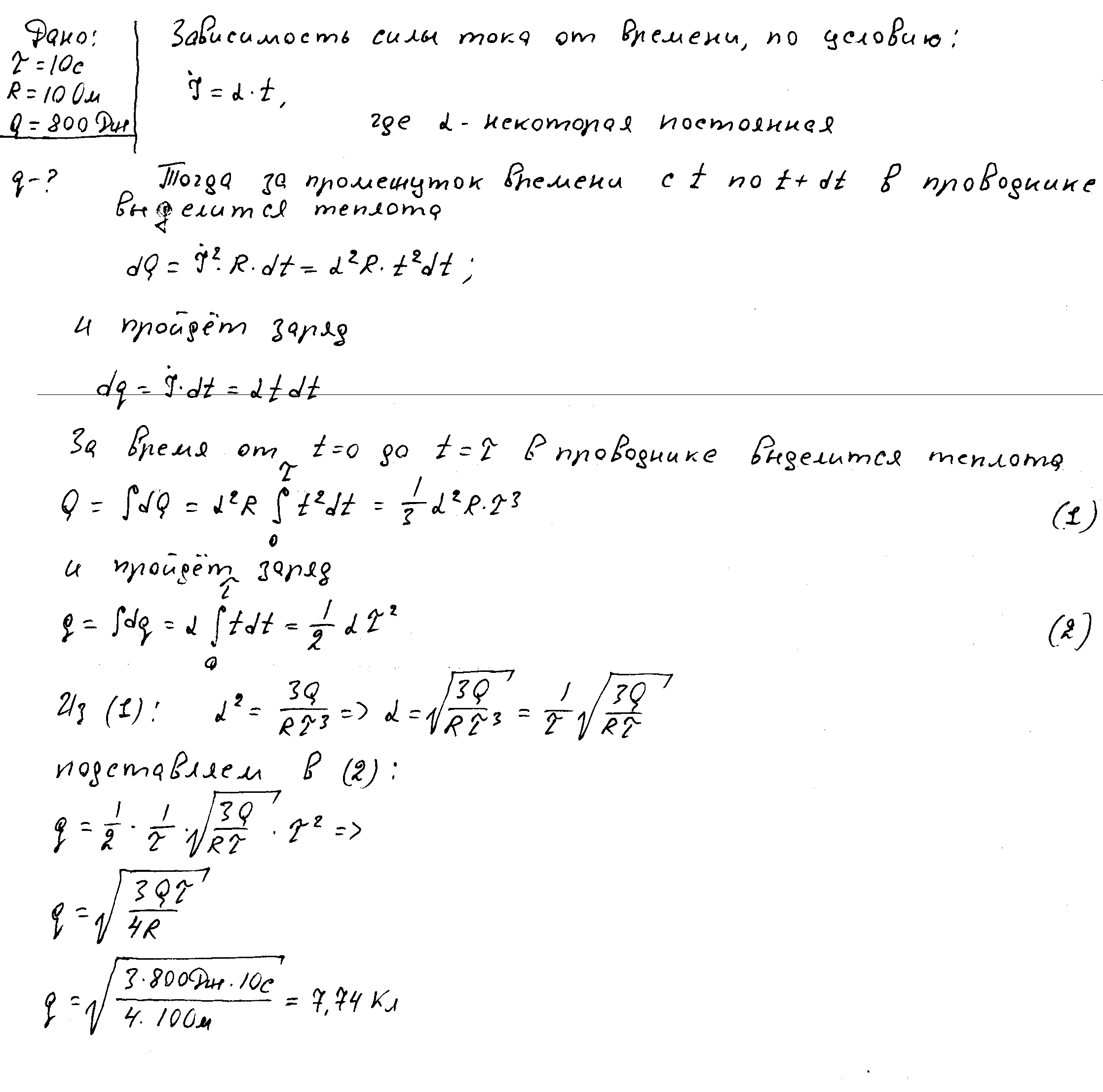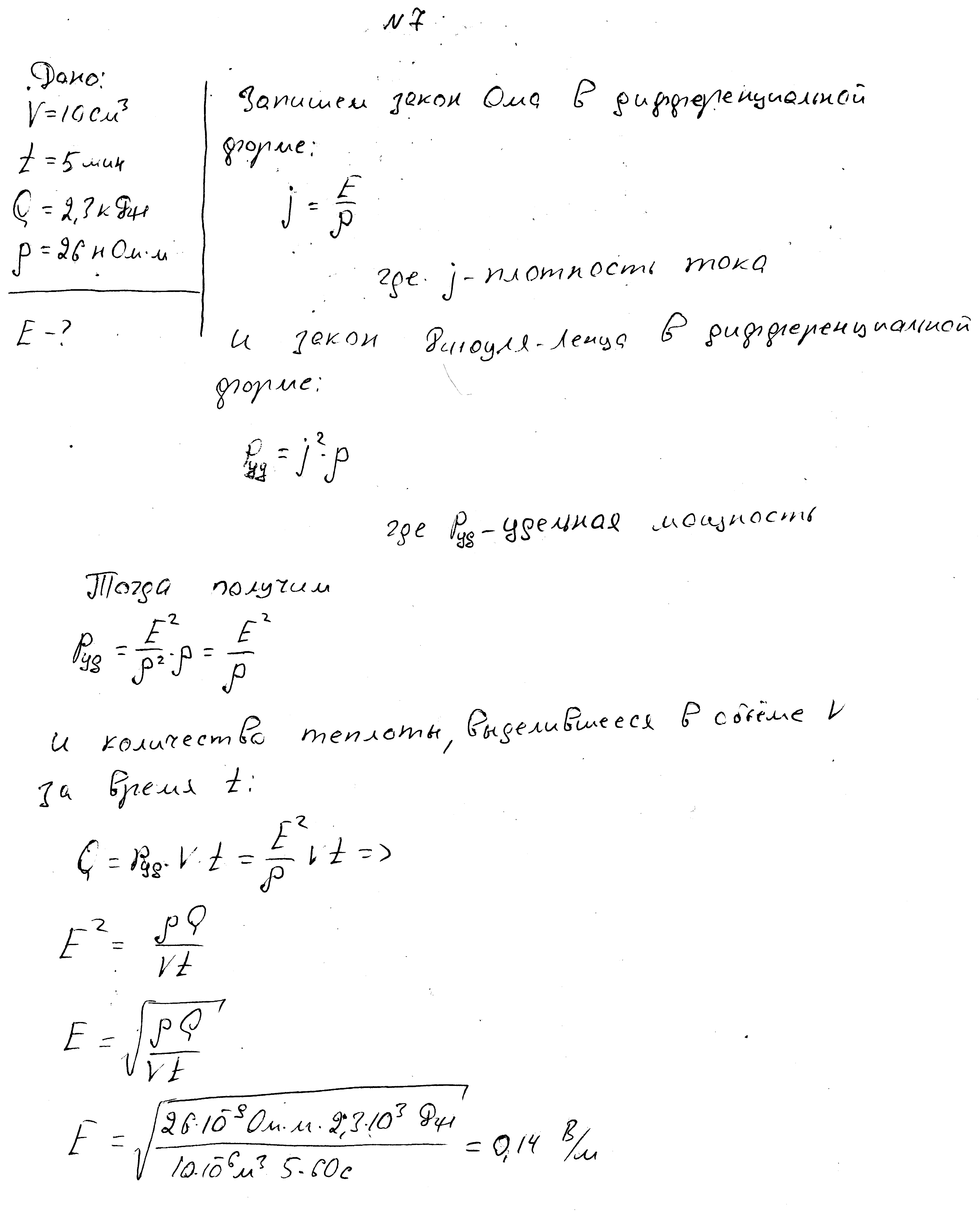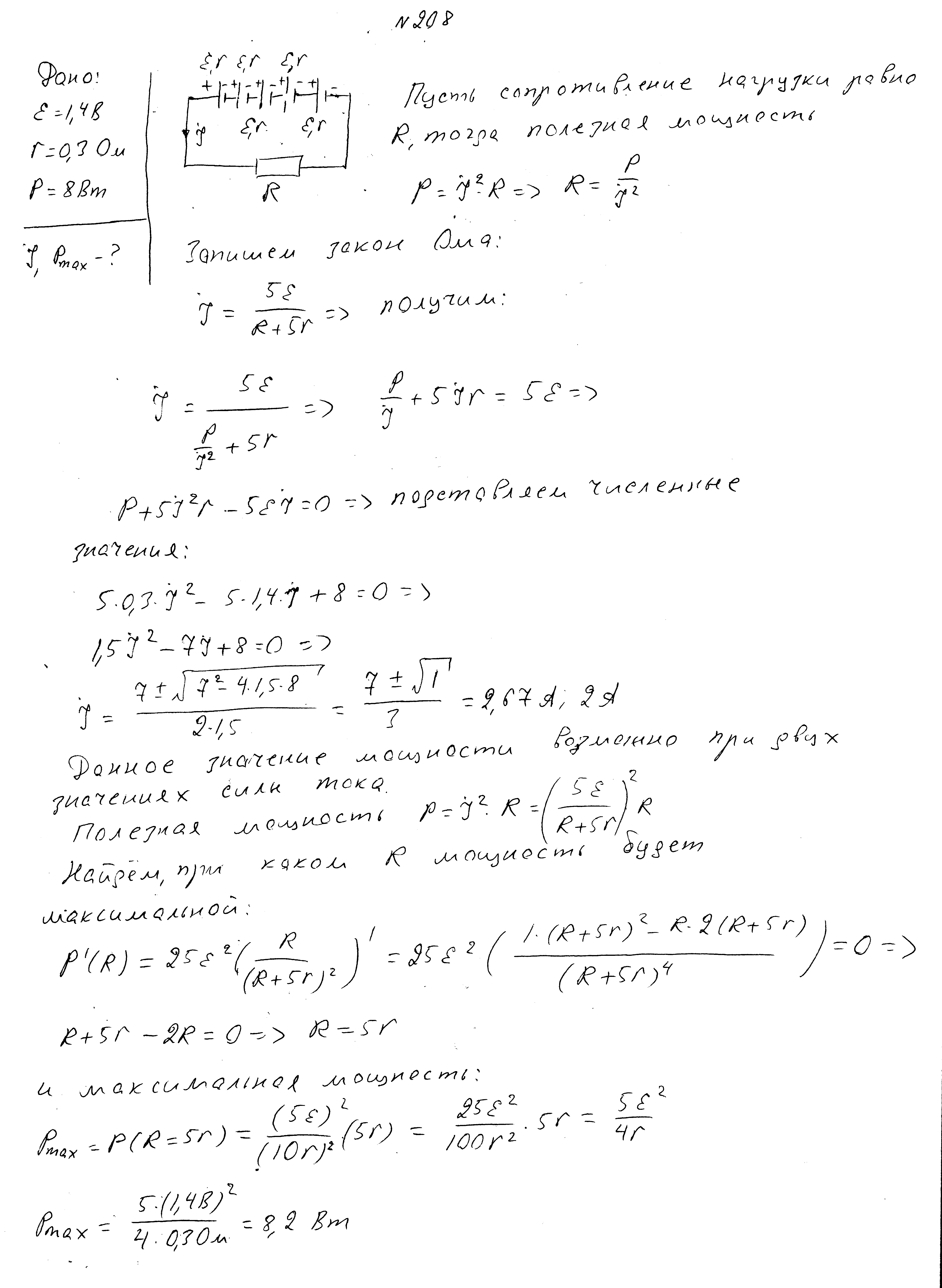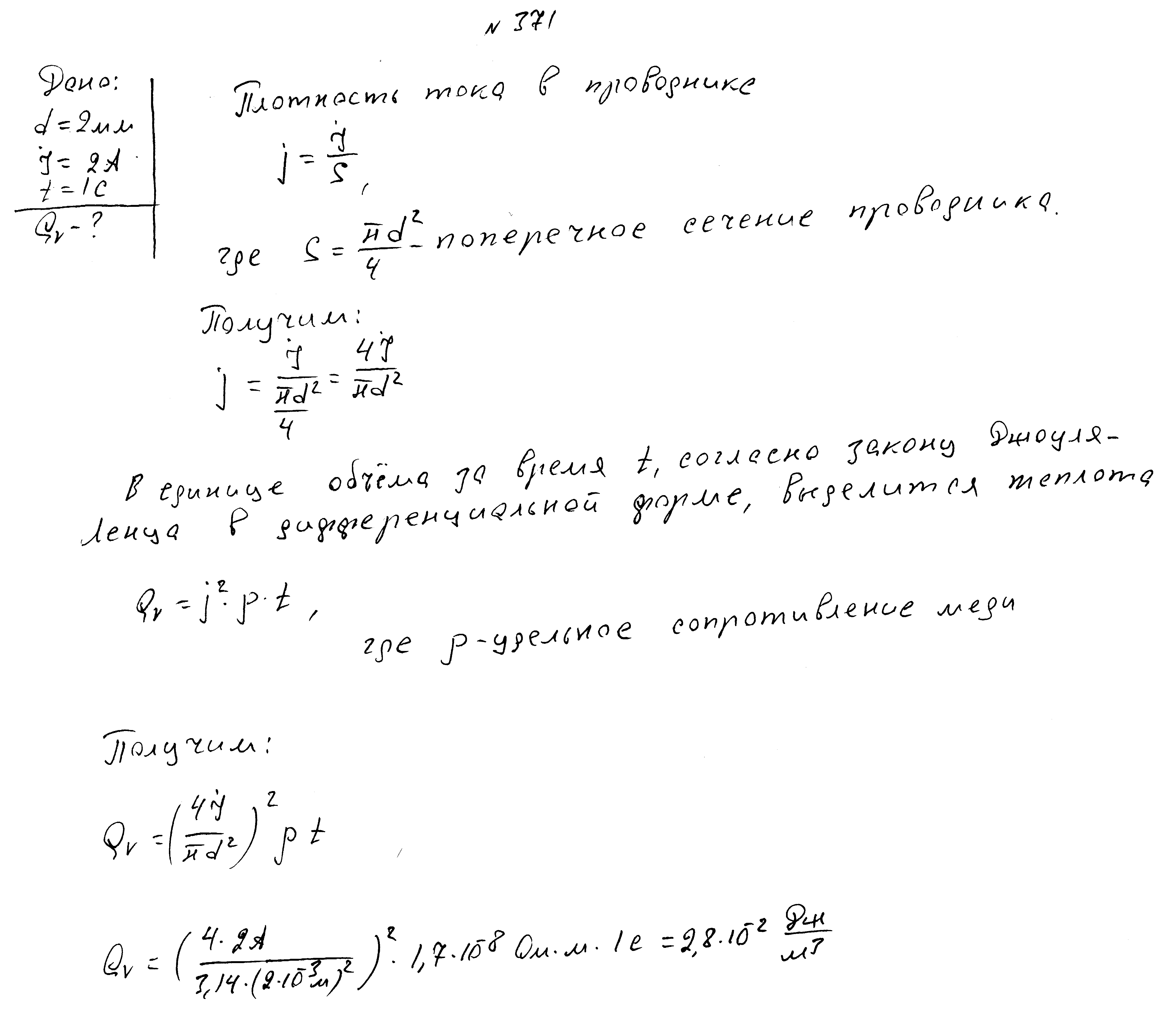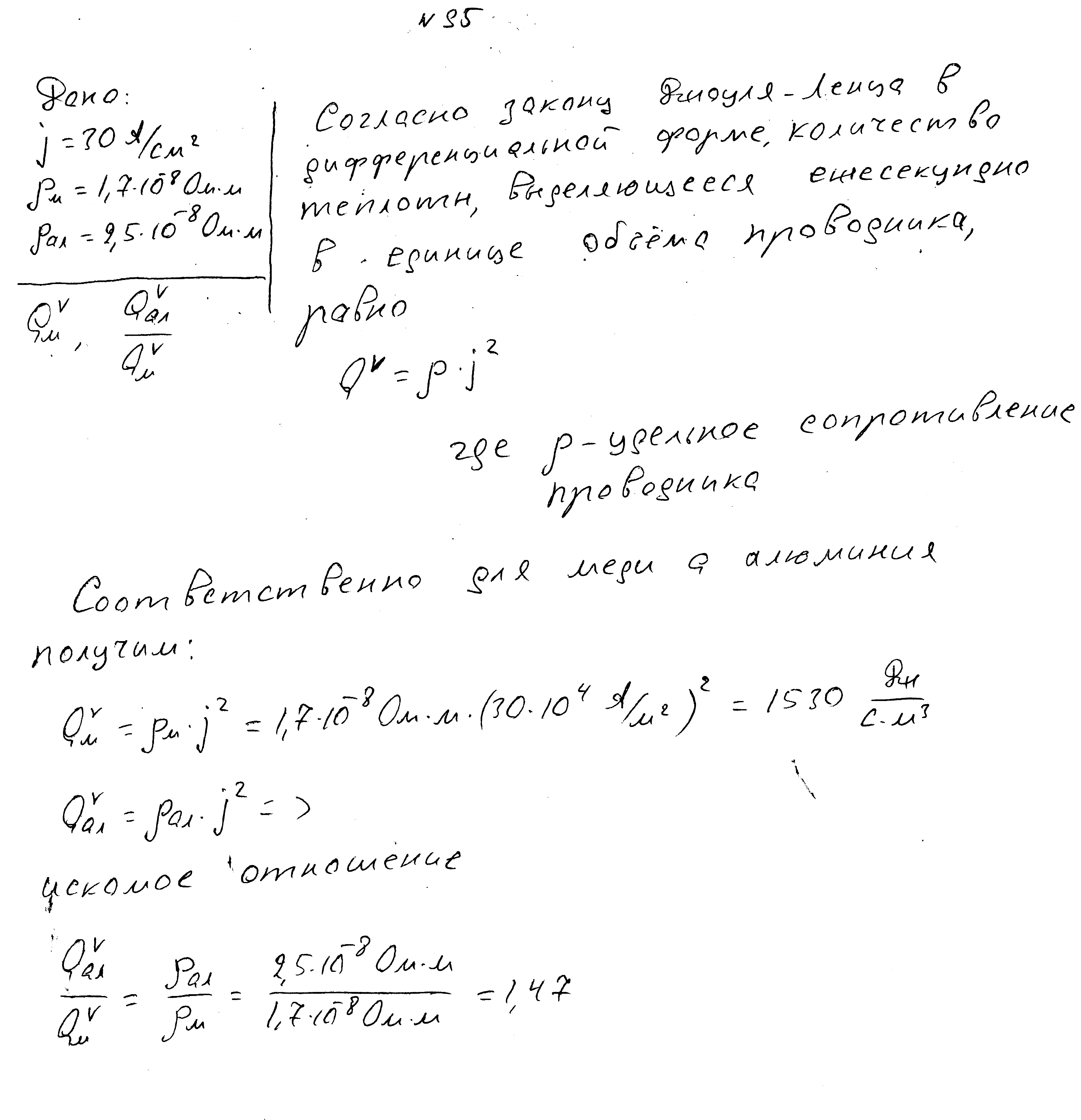§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
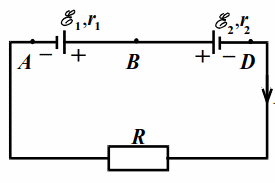 |
| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
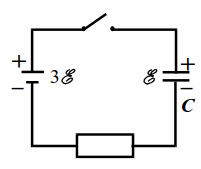 |
| Рис. 19.1 |
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
(A = U*I*T)
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
(Q = U*I*R*t)
или используя закон Ома (U = I*R), получим
(Q = {I^2}Rt)
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
Чтобы найти количество теплоты, выделяющееся на каждом резисторе за 1 минуту, необходимо знать мощность, потребляемую каждым резистором, поскольку теплота, выделяющаяся на резисторе, связана с мощностью как разность между потребляемой и отдаваемой мощностями.
Если два резистора подключены параллельно, то сопротивления схемы можно найти по формуле:
1/ R = 1/ R1 + 1/ R2
где R1 и R2 – сопротивления двух резисторов.
Поскольку резисторы имеют одинаковое сопротивление, то формула принимает вид:
1/ R = 1/ R1 + 1/ R2 = 2/ R
R = R1 = R2 / 2
С учетом того, что сила тока в цепи I = 10 А и напряжение U = 220 В, можно определить сопротивление каждого резистора по закону Ома:
R = U / I = 220 В / 10 А = 22 Ом
Тогда мощность, потребляемая каждым резистором, равна:
P = I^2 * R = 10^2 * 22 Ом = 2200 Вт
Количество теплоты, выделяющееся на каждом резисторе за 1 минуту, равно:
Q = P * t = 2200 Вт * 60 сек = 132000 Дж = 132 кДж
Таким образом, на каждом резисторе выделяется 132 кДж теплоты за 1 минуту.
Содержание
- Количество теплоты в электрической цепи: формула выделения теплоты
- Содержание:
- Формула выделения теплоты
- Снижение потерь
- Задача
- Тепло на резисторе через заряд
- § 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
- Тепловая мощность на резисторе формула
- Как рассчитать мощность резистора?
- Как рассчитать мощность резистора?
- Тепловая мощность, выделяемая на резисторе
- Зависимость количества теплоты от напряжения
- Закон Джоуля-Ленца
- Опыты Ленца
- Закон Джоуля-Ленца
- Почему греется проводник
- Применение закона Джоуля-Ленца в жизни
- Заключение
- Зависимость количества теплоты от напряжения
- Q = I 2 Rt , где
- ♦ Закон Джоуля–Ленца : количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока.
- Где применяется закон Джоуля-Ленца ?
- Закон Джоуля-Ленца и его применение
- Формулировка закона Джоуля-Ленца
- Физический смысл закона
- Уравнения закона в различных формах
- Уравнение в интегральной форме
- Уравнение в дифференциальной форме
- Видео по теме
Количество теплоты в электрической цепи: формула выделения теплоты
Содержание:
Эмилий Ленц – российский физик XIX века, вышедший из балтийских немцев, с английским коллегой Джеймсом Джоулем опытным путём установили зависимость количества выделяемой проводником тепловой энергии от его параметров. На интенсивность нагрева влияют: сила тока, время его протекания, сопротивление материала. Рассмотрим, по какой формуле вычисляется количество теплоты на резисторе, участке цепи.
Формула выделения теплоты
- Q измеряется в Джоулях (Дж);
- I – сила электричества (А);
- R – сопротивление участка цепи (Ом);
- t – время пропускания тока (с).
Для подтверждения закона Джоуля-Ленца используют калориметр. В него помещают проводник с известным сопротивлением, пропускают по нему определённой ток на протяжении времени t. Выделенное тепло определяется благодаря формуле теплового баланса, применяемой при калориметрических измерениях.
Прибегнув к закону Ома, выразим ток через сопротивление и напряжение:
После упрощения получим уравнение:
Полученные формулы позволяют вычислять нагрев отдельных участков цепи, подключённых параллельно либо последовательно. В первом случае компоненты схемы пропускают различный ток, напряжение на их клеммах одинаково. Целесообразно пользоваться формулой Q = (U 2 * R ) / t: количество тепловой энергии обратно пропорционально сопротивлению компонентов.
Во втором случае через компоненты схемы протекает одинаковый ток, поэтому генерируемое ими тепло зависит от электрического сопротивления материалов, из которых те изготовлены. Для расчётов актуальна формула: Q = I 2 Rt.
Снижение потерь
Не зря на дальние расстояния электричество транспортируется с низким током, но под высоким напряжением: 110, 220 и более кВ. При таком потенциале длина линии может достигать 150 и 250 км соответственно. Повышают и понижают напряжение трансформаторы.
Задача
Воспользуемся формулой вычисления количества выделенной электричеством теплоты: Q = I 2 Rt.
Минуты переведём в секунды: 20 * 60 = 1200 с.
Источник
Тепло на резисторе через заряд
§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W=^<2>Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ _<mathrm<Т>>=q(<varphi >_<1>—<varphi >_<2>)$$.
Работой источника с ЭДС $$ mathcal$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Если заряд переносится постоянным током $$ I$$, то $$ _<mathrm<ист>>=pm mathcalIt$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
Источник
Тепловая мощность на резисторе формула
Как рассчитать мощность резистора?
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
Как рассчитать мощность резистора?
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
- Главная
- Обучение
- Предварительный просмотр
- Мероприятия / ВИШР
- Обучение
- Тренажер ЕГЭ
- Учебные пособия
- Игры
- 120 лет ТПУ. Викторина онлайн
- Университетские субботы
- Высшая инженерная школа России
Физика
3.2.9.1. Тепловая мощность, выделяемая на резисторе
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
или используя закон Ома (U = I*R) , получим
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
Источник
Зависимость количества теплоты от напряжения
Закон Джоуля-Ленца
Электричество — неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.
При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Закон Джоуля-Ленца
В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.
Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:
Q — количество выделяемого тепла (Джоули)
I — сила тока, протекающего через проводник (Амперы)
R — сопротивление проводника (Омы)
t — время прохождения тока через проводник (Секунды)
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы «трётся», соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Из формулы также следует — чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом — будет неравномерный нагрев в месте скрутки. В итоге — подгорание с последующим пропаданием контакта.
Применение закона Джоуля-Ленца в жизни
Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины — первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.
Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку
Заключение
Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.
Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.
Раз уж заговорили про ДжОУля )) Читайте статья про ОУ — Операционный усилитель.
Зависимость количества теплоты от напряжения
Раздел ОГЭ по физике: 3.9.Закон Джоуля-Ленца
Раздел ЕГЭ по физике: 3.2.8. Работа электрического тока. Закон Джоуля–Ленца
Рассмотрим Закон Джоуля-Ленца и его применение.
При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: Q = А или Q = IUt . Учитывая, что U = IR, в результате получаем формулу:
Q = I 2 Rt , где
Q — количество выделяемой теплоты (в Джоулях)
I — сила тока (в Амперах)
R — сопротивление проводника (в Омах)
t — время прохождения (в секундах)
♦ Закон Джоуля–Ленца : количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока.
В XIX в. независимо друг от друга англичанин Д. Джоуль и россиянин Э. Ленц изучали нагревание проводников при прохождении электрического тока и опытным путём обнаружили закономерность: количество теплоты, выделяющееся при прохождении тока по проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени: Q = I 2 Rt (в случае постоянных силы тока и сопротивления). Эту закономерность называют законом Джоуля-Ленца. Данный закон дает количественную оценку теплового действия электрического тока.
Применяя закон Ома, можно получить эквивалентные формулы: Q = IUt , Q= U 2 t/R
Где применяется закон Джоуля-Ленца ?
1. Например, в лампах накаливания и в электронагревательных приборах применяется закон Джоуля-Ленца. В них используют нагревательный элемент, который является проводником с высоким сопротивлением. За счет этого элемента можно добиться локализованного выделения тепла на определенном участке. Выделение тепла будет появляться при повышении сопротивления, увеличении длины проводника, выбором определенного сплава.
2. Одной из областей применения закона Джоуля-Ленца является снижение потерь энергии. Тепловое действие силы тока ведет к потерям энергии. При передаче электроэнергии, передаваемая мощность линейно зависит от напряжения и силы тока, а сила нагрева зависит от силы тока квадратично, поэтому если повышать напряжение, при этом понижая силу тока перед подачей электроэнергии, то это будет более выгодно. Но повышение напряжения ведет к снижению электробезопасности. Для повышения уровня электробезопасности повышают сопротивление нагрузки соответственно повышению напряжения в сети.
3. Также закон Джоуля-Ленца влияет на выбор проводов для цепей. Потому что при неправильном подборе проводов возможен сильный нагрев проводника, а также его возгорание. Это происходит когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии.
Нагревание проводов является вредным, поскольку приводит к потерям электроэнергии при передаче ее от источника к потребителю. Для уменьшения этих потерь силу тока уменьшают, повышая напряжение источника с тем, чтобы передаваемая мощность осталась прежней. Чтобы избежать электрического пробоя изоляции проводов, их поднимают на большую высоту на мачтах высоковольтных линий электропередач, связывающих крупные электростанции с городами и поселками, отстоящими от них на десятки и сотни километров.
Вы смотрели конспект урока физики в 8 классе «Закон Джоуля-Ленца и его применение».
Выберите дальнейшие действия:
Закон Джоуля-Ленца и его применение
Современный человек привык к тому факту, что включив в розетку утюг, настольную лампу либо обычный кипятильник, техника сразу начнет отдавать тепловую энергию и свет. По какому же закону физики происходит данное действие? Объяснить это удалось Джеймсу Джоулю и Эмилю Ленцу. Результат их исследований получил название закона Джоуля-Ленца. На практике он помог достичь больших открытий в электромеханике.
Формулировка закона Джоуля-Ленца
Правило было обобщено и сформулировано на основе трудов двух физиков — британского и русского. Джоуль и Ленц свой закон вывели практически одновременно, но независимо друг от друга, поэтому он и был назван именами обоих ученых.
Формулировка закона хорошо иллюстрирует следующее: если на участок цепи пустить электричество, то провод начнет нагреваться. В бытовых условиях тепловое действие тока наблюдается в лампах накаливания и всех электроприборах. Если подключить устройство со спиралью на конце участка цепи в розетку, то она нагреется, и выделит тепло. Например, подключенный к электричеству сварочный аппарат начнет плавить электрод, электрический чайник или кипятильник нагреют воду, а настольная лампа наполнит комнату светом.
Кратко закон Джеймса Джоуля и Эмиля Ленца можно сформулировать так: количество выделяемой теплоты при нагревании полупроводника либо проводника прямо пропорционально определенному количеству времени, за которое происходит воздействие тока, плюс сопротивлению и квадрату рабочей силы электрического тока.
Физический смысл закона
Закон Джоуля-Ленца, с помощью которого определение количества тепла, выделяющегося при воздействии силы тока в проводнике, осуществляется достаточно просто, подтверждает также, что это количество напрямую зависит от сопротивления. Сам нагрев происходит в результате того, что свободные электроны, перемещаясь под действием электрополя, бомбардируют атомы молекул материала проводника. При этом они передают им собственную кинетическую энергию, преобразующуюся в тепловую.
Чем выше сила тока, тем большее количество электронов проходит через сечение проводника, и тем чаще происходят столкновения между ними и атомами. Соответственно, проводнику передается большое количество энергии, и он сильно нагревается.
В проводнике с большим сечением столкновений частиц будет намного меньше, следовательно, выделится меньше тепла. С учетом того, что между удельным сопротивлением любого проводника и его сечением существует обратно пропорциональная зависимость, можно сказать, что чем выше сопротивление проводника, тем сильнее он нагревается.
Как видим, руководствуясь законом Джоуля-Ленца, можно сделать два вывода:
- С увеличением сопротивления проводника, будет увеличиваться и количество выделяемой теплоэнергии. Иными словами, количество теплоты прямо пропорционально сопротивлению.
- Выделившееся количество теплоты в проводнике за время прохождения тока, зависит от мощности последнего. Иными словами, если увеличивается мощность тока, то количество свободных электронов, проходящих через проводник за единицу времени, тоже будет увеличиваться.
Согласно закону сохранения энергии в физике, в проводнике под воздействием тока происходит преобразование кинетической энергии свободных заряженных частиц в тепловую внутреннюю энергию.
Уравнения закона в различных формах
Формулы, выведенные для закона Джоуля-Ленца, наглядно демонстрируют зависимость количества теплоты от сопротивления и мощности тока. Согласно этому закону, любой участок локальной цепи, пребывающий под воздействием электроэнергии, должен выделять тепло.
Уравнение в интегральной форме
При отсутствии на участке цепи каких-либо механических или химических процессов, требующих затрат электрической энергии, теплота, выделенная проводником, будет равна работе тока. То есть, Q = A.
Формулу для количества теплоты можно записать в таком виде:
С учетом того, что уравнение для напряжения участка цепи можно записывать через силу тока и сопротивление (закон Ома U = I×R), формула для количества теплоты имеет вид:
С помощью этой формулы закон Джоуля-Ленца выражается в интегральной форме.
Математически ее еще можно выразить так:
Уравнение в дифференциальной форме
Иногда бывает так, что величина силы тока остается неизвестной, однако существуют точные данные о том, какое на участке цепи напряжение. В этом случае также стоит воспользоваться законом Ома. Исходя из того, что I = U/R, можно представить формулу Джоуля-Ленца в дифференциальной форме:
Следовательно, можно использовать два уравнения для определения количества тепла, выделяемого проводником, пребывающим под воздействием электротока. Но их применение возможно лишь для тех случаев, когда работа и мощность электрического тока расходуются исключительно на выделение тепла, а других потребителей энергии не существует. Единицей измерения выделенного тепла является джоуль: 1 Дж = 1 В × 1 А × 1 с.
Практическое применение закона в повседневной жизни человека
Закон Джоуля-Ленца наглядно применяется на практике при работе бытовых электрических приборов. Как всем известно, чтобы нагреть электрочайник, воспользоваться феном, утюгом или паяльником, необходимо превратить электричество в тепло. Свечение лампы накаливания происходит из-за наличия вольфрамовой нити, которая при высоком напряжении тока способна осветить все вокруг.
Стоит отметить, что получение теплоэнергии от электричества достаточно выгодно, так как помогает избежать энергопотерь. Достаточно лишь уменьшить силу тока, чтобы выровнять количество поступающего тепла от прибора. Также это повышает электробезопасность и регулирует нагрузку на сетевое напряжение.
Но нельзя допускать, чтобы проводник нагревался очень сильно. Под воздействием высокой температуры разрушается структура металла или, если говорить просто, он начинает плавиться. Это может стать причиной короткого замыкания, что в свою очередь приводит к выводу из строя элекрооборудования или даже пожару. Чтобы избежать коротких замыканий используются защитные блоки, предохранители и автоматические выключатели.
Применение закона на практике делает жизнь человека очень удобной, поэтому точно можно сделать вывод, что это в своем роде гениальное достижение, на котором держится вся электротехника. На сегодняшний день практически каждый бытовой прибор в любом доме работает на электричестве, и эта работа основывается на взаимосвязи силы тока и тепловой энергии. Главное, проводить правильные расчеты, чтобы не допускать перегрева деталей в устройстве.
Видео по теме
Источник
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свое задание по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
К источнику с внутренним сопротивлением 4 Ом подключена электроплитка с двумя спиралями с разными значениями сопротивлений. При подключении спирали сопротивлением 8 Ом чайник на плитке закипает за такое же время, как при подключении второй спирали. Найдите сопротивление второй спирали.
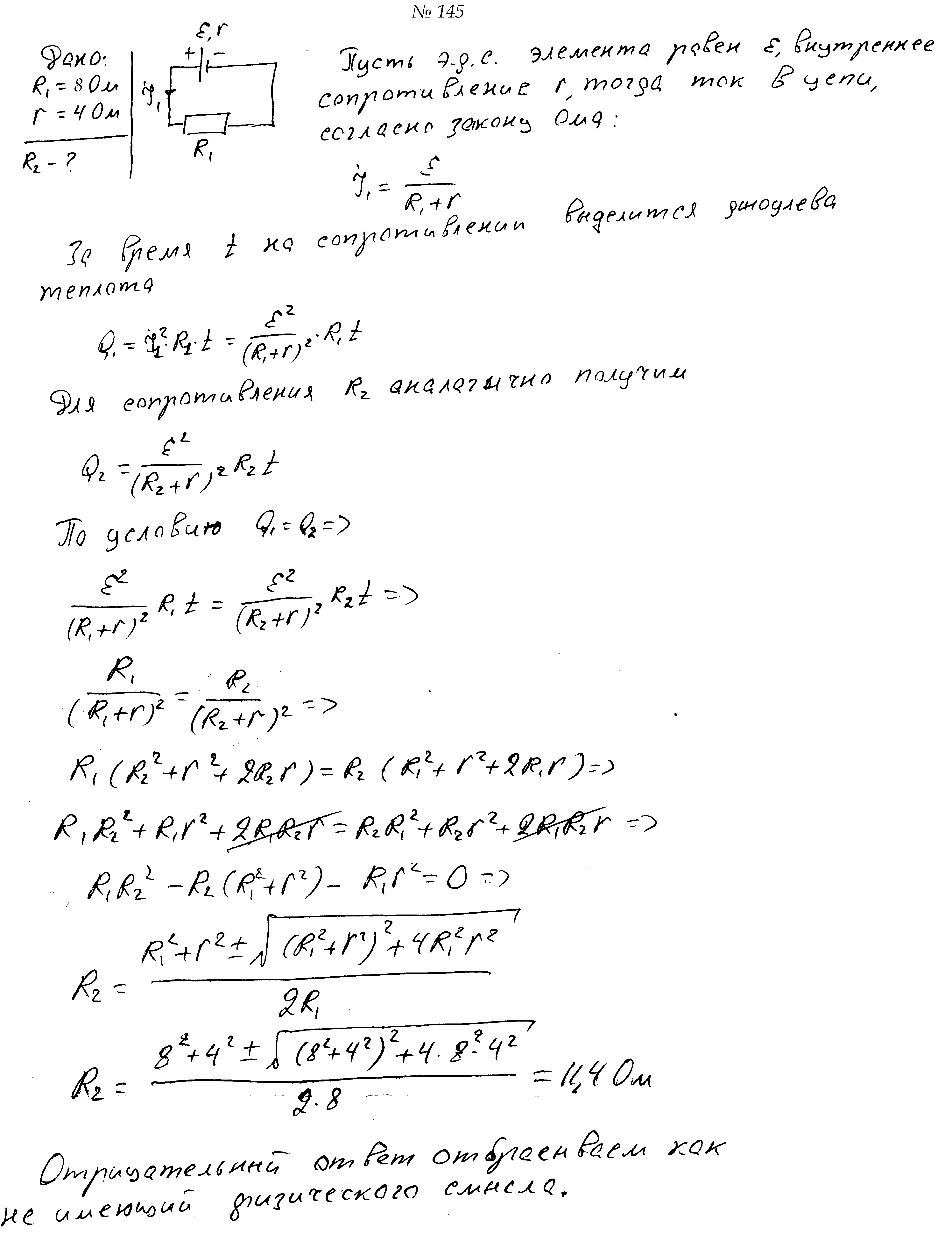
При сопротивлениях нагрузки, равных 5 Ом и 0,2 Ом, на нагрузке за одно и то же время выделяется одинаковое количество теплоты. Определите внутреннее сопротивление источника.
Ток через резистор 20 Ом за некоторое время линейно нарастает от нуля до максимального значения 6А. Найдите количество теплоты, выделившееся на резисторе за вторую секунду.
Сила тока через резистор сопротивлением 10 Ом линейно нарастает от нуля до значения 10А за время 30с. Найти количество выделившейся за это время теплоты.
При различных сопротивлениях нагрузки, одно из которых в два раза больше другого, выделяющаяся на нагрузке мощность одинакова. Определите КПД источника для обоих значений нагрузок.
При подключении одного сопротивления к источнику сила тока составляет 2А, при подключении второго – 3А. Выделяющаяся на сопротивлениях мощность при этом одинакова. Внутреннее сопротивлени источника равно 4 Ом. Найдите ЭДС источника.
Зависимость силы тока через сопротивление 10Ом от времени I=A+Bt, где А=4А, B=2А/с.Найдите выделившееся за промежуток времени с t=4 с по t=6 с количество теплоты.
Источник С ЭДС 24 В подключен к реостату. При этом максимально достижимая сила тока составляет 10 А. Какава максимально достижимая мощность, рассеиваемая на реостате?
В электроплитке имеются две обмотки. При подключении одной из них чайник закипает за 15 мин, при подключении другой – за 30 мин. За какое время закипит чайник при подключении обмоток а) последовательно б) параллельно? Потерями энергии пренебречь.
Источник с ЭДС 1,6 В и внутренним сопротивлением 0,5 Ом подключен к нагрузке. При этом ток в цепи равен 2,4 А. Определите КПД источника. Определите максимальное и минимальное значение КПД.
Источник с ЭДС 12 В подключен к нагрузке, при этом ток в цепи составляет 4А. КПД источника равен 60%.Определите внутреннее сопротивление источника и ток короткого замыкания.
При силе тока в цепи 3А мощность на нагрузке составляет 18 Вт, а при силе тока 1 А мощность равна 10 ВТ. Определите ЭДС источника, его внутреннее сопротивление и силу тока короткого замыкания.
Сила тока, протекающего через провод поперечным сечением 1,5 мм2, равна 30А. Какая мощность выделяется в объеме проводника 1 мм3?
Ток короткого замыкания батарее составляет 6А. При сопротивлении нагрузки 5 Ом ток в цепи равен 1А. Определить максимальную полуезную мощность.
Два резистора сопротивлениями 2 Ом и 5 Ом соединены параллельно и подсоединены к источнику с внутренним сопротивлением 0,5 Ом. Найдите КПД цепи.
Идеальный источник с ЭДС 600 В соединен с нагрузкой подводящими медными проводами длиной 1км и диаметром 0,5 см. Мощность, потребляемая нагрузкой, составляет 5 кВт. Определите мощность, рассеиваемую проводами.
Нагрузка, потребляющая мощность 8 кВт, соединена с идеальным источником с ЭДС 110 В медными проводами длиной 90м. Коэффициент потери мощности при этом равен 5%. Найдите площадь поперечного сечения проводов.
Провод диаметром 1 мм2 подключен с идеальному источнику с ЭДС 120 В. При этом за 1 час в проводе выделяется количество теплоты 1 Мдж. Найдите длину провода.
Элемент питания с ЭДС 1,1 В и внутренним сопротивлением 1 Ом подключен к резистору сопротивлением 9 Ом. Найдите напряжения на нагрузке и внутри элемента, мощности, рассеиваемые нагрузкой и элементом, КПД источника.
Источник подключен к нагрузке. При сопротивлении нагрузки 11 Ом ток в цепи 1,0 А. При сопротивлении нагрузки 5,0 Ом мощность, выделяющая во внешней цепи, составляет 20 Вт. Определите ток короткого замыкания источника.
При сопротивлении нагрузки 10,5 Ом КПД источника в два раза выше, чем при сопротивлении нагрузки 3 Ом. Найдите внутреннее сопротивление источника.
К резистору сопротивлением R могут быть подключено n источников тока с внутренним сопротивлением r. Найдите отношение мощностей, выделяющихся на нагрузке, при параллельном и последовательном соединении источников.
Ток через резистор сопротивлением 10 Ом линейно нарастает от нулевого значения. За время 10 с в резисторе выделилось количество теплоты 800 Дж. Какой заряд прошел через резистор за это время?
При протекании тока через провод в объеме 10 см3 за 5 мин выделяется количество теплоты 2,3 кДж. Определите напряженность электрического поля в проводе.
При подключении к резистору батареи из пяти последовательно соединенных источников с ЭДС 1,4 В и внутренними сопротивлениями 0,3 Ом на нем выделяется мощность 8 Вт. Найдите силу тока в цепи и максимальную полезную мощность батареи источников.
Напряжение на проводе длиной 0,2м составляет 4 В. Определите удельную тепловую мощность, выделяющуюся в единице объема провода.
Через провод диаметром 2 мм протекает ток 2А. Найдите количество теплоты, выделяющееся в единице объема провода за 1 с.
Плотность тока в медном проводе составляет 30 А/см2. Какое количество теплоты выделяется ежесекундно в единице объема проводника? Найдите отношение удельной мощности, выделяющейся в алюминиевом проводе, к удельной мощности, выделяющемуся в медном проводе, при одинакой плотности тока
Ток в проводнике сопротивлением 10 Ом линейно уменьшается от значения 10 А до нуля за время 10с. Какое количество теплоты выделится за это время в проводнике?
Ниже вы можете посмотреть видеоурок на данную тему: