Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
(A = U*I*T)
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
(Q = U*I*R*t)
или используя закон Ома (U = I*R), получим
(Q = {I^2}Rt)
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
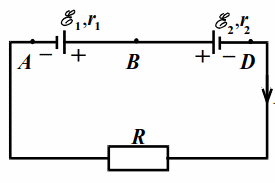 |
| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
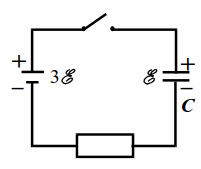 |
| Рис. 19.1 |
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.
Количество теплоты,выделяемой на резисторе
Prowling Tiger
Мастер
(1897),
закрыт
15 лет назад
Не подскажите формулу для вычисления?
Faustman
Мастер
(1650)
15 лет назад
Тебя интересует колличество тепла, выделяемого резистором. Вот формула:
Q = I (в квадрате) r t {ДЖ] . То есть, колличество тепла Q (Жд) выделяемого на резисторе прямо пропорционально квадрату тока I (А) , сопротивлению проводника r (Ом) и времени действия тока t.
Prowling TigerМастер (1897)
15 лет назад
Это количество теплоты,выделяемой на проводнике,а не на резисторе 🙂
Faustman
Мастер
(1650)
Вопрос был: “Количество теплоты,выделяемой на резисторе”
:), каждый из существующих ныне проводников является резистором, поскольку обладает каким-либо электр. сопротивлением, даже если незначительным. Закон джоуля-ленца для количества выделяемым проводником тепла, одинаково справедлив как для резистора с сопротивлением в 1 Мом так и для кусочка медной проволоки! Не исключено что вопрос тогда был сформулирован неверно.
Если ты меня переубедишь, то я даже буду рад
Закон сохранения энергии определяет в самом общем виде энергетический баланс при всевозможных изменениях в любой системе. Запишем его следующим образом:
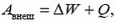 (1)
(1)
где Aвнеш — работа, совершенная над рассматриваемой системой внешними силами, ΔW — изменение энергии системы, Q — количество теплоты, выделяемое в системе. Договоримся, что если Aвнеш > 0, то над системой совершают положительную работу, а если Aвнеш < 0, положительную работу совершает система; если ΔW > 0, то энергия системы увеличивается, а если ΔW < 0, энергия уменьшается; наконец, если Q > 0, то в системе выделяется тепло, а если Q < 0, тепло системой поглощается.
В этой статье мы рассмотрим, как закон сохранения энергии «работает» в электростатике. В общем случае электростатическая система содержит взаимодействующие между собой заряды, находящиеся в электрическом поле.
Рассмотрим каждое слагаемое в уравнении (1) по отдельности.
Начнем с энергии. Энергия взаимодействия зарядов выражается через характеристики электрического поля этой системы зарядов. Так, например, энергия заряженного конденсатора емкостью C задается известным выражением
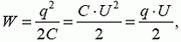 (2)
(2)
где q — заряд обкладок, U — напряжение между ними. Напомним, что конденсатор — это система двух проводников (обкладок, пластин), обладающая следующим свойством: если с одной обкладки на другую перенести заряд q (т. е. одну обкладку зарядить зарядом +q, а другую –q), то все силовые линии созданного таким образом поля будут начинаться на одной (положительно заряженной) обкладке и заканчиваться на другой. Поле конденсатора существует только внутри него.
Энергию заряженного конденсатора можно представить также как энергию поля, локализованного в пространстве между пластинами с плотностью энергии 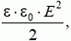 где E — напряженность поля. В сущности, именно этот факт дает основание говорить о поле как об объекте, реально существующем, — у этого объекта есть плотность энергии. Но надо помнить, что это просто эквивалентный способ определения энергии взаимодействия зарядов (которую теперь мы называем энергией электрического поля). Таким образом, мы можем считать энергию конденсатора как по формулам (2), так и по формуле
где E — напряженность поля. В сущности, именно этот факт дает основание говорить о поле как об объекте, реально существующем, — у этого объекта есть плотность энергии. Но надо помнить, что это просто эквивалентный способ определения энергии взаимодействия зарядов (которую теперь мы называем энергией электрического поля). Таким образом, мы можем считать энергию конденсатора как по формулам (2), так и по формуле
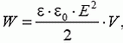 (3)
(3)
где V — объем конденсатора. Последней формулой легко пользоваться, конечно, только в случае однородного поля, но представление энергии в такой форме очень наглядно, а потому удобно.
Конечно, кроме энергии взаимодействия зарядов (энергии электрического поля) в энергию системы может входить и кинетическая энергия заряженных тел, и их потенциальная энергия в поле тяжести, и энергия пружин, прикрепленных к телам, и т. п.
Теперь о работе внешних сил. Помимо обычной механической работы Aмех (например, по раздвиганию пластин конденсатора), для электрической системы можно говорить о работе внешнего электрического поля. Например, о работе батареи, заряжающей или перезаряжающей конденсатор. Задача батареи — создать фиксированную, присущую данному источнику разность потенциалов между теми телами, к которым она присоединена. Делает она это единственно возможным способом — забирает заряд от одного тела и передает его другому. Источник никогда не создает заряды, а только перемещает их. Общий заряд системы при этом сохраняется — это один из краеугольных законов природы.
В источниках разных конструкций электрическое поле, необходимое для перемещения зарядов, создают различные «механизмы». В батареях и аккумуляторах — это электрохимические реакции, в динамомашинах — электромагнитная индукция. Существенно, что для выбранной системы зарядов (заряженных тел) это поле — внешнее, стороннее. Когда через источник с ЭДС ![]() от отрицательного полюса к положительному протекает заряд Δq, сторонние силы совершают работу
от отрицательного полюса к положительному протекает заряд Δq, сторонние силы совершают работу
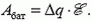 (4)
(4)
При этом если Δq > 0, то Aбат > 0 — батарея разряжается; если же Δq < 0, то Aбат < 0 — батарея заряжается и в ней накапливается химическая (или магнитная) энергия.
Наконец, о выделении тепла. Заметим только, что это джоулево тепло, т.е. тепло, связанное с протеканием тока через сопротивление.
Теперь обсудим несколько конкретных задач.
Задача 1. Два одинаковых плоских конденсатора емкостью C каждый присоединены к двум одинаковым батареям с ЭДС ![]() . В какой-то момент один конденсатор отключают от батареи, а другой оставляют присоединенным. Затем медленно разводят пластины обоих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае?
. В какой-то момент один конденсатор отключают от батареи, а другой оставляют присоединенным. Затем медленно разводят пластины обоих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае?
Если процесс изменения заряда на конденсаторе осуществляется все время медленно, тепло выделяться не будет. Действительно, если через резистор сопротивлением R протек заряд Δq за время t, то на резисторе за это время выделится количество теплоты
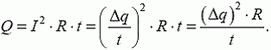
При достаточно больших t количество теплоты Q может оказаться сколь угодно малым.
В первом случае фиксирован заряд на пластинах (батарея отключена), равный ![]() Механическая работа определяется изменением энергии конденсатора:
Механическая работа определяется изменением энергии конденсатора:
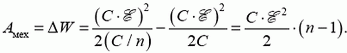
Во втором случае фиксирована разность потенциалов на конденсаторе и работает батарея, поэтому
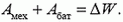
Через батарею протекает заряд
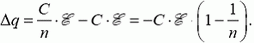
Этот заряд меньше нуля, значит, батарея заряжается и ее работа
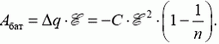
Энергия поля в конденсаторе уменьшается:
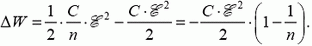
Таким образом,
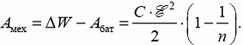
Зарядка батареи происходит за счет работы по раздвиганию пластин и за счет энергии конденсатора.
Заметим, что слова про раздвигание пластин существенной роли не играют. Такой же результат будет при любых других изменениях, приводящих к уменьшению емкости в n раз.
Задача 2. В схеме, изображенной на рисунке, найдите количество теплоты, выделившееся в каждом резисторе после замыкания ключа. Конденсатор емкостью C1 заряжен до напряжения U1, а конденсатор емкостью C2 — до напряжения U2. Сопротивления резисторов R1 и R2.
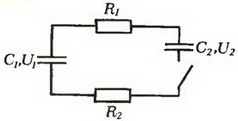
Рис. 1
Закон сохранения энергии (1) для данной системы имеет вид
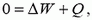 т. е.
т. е. 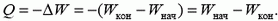
Начальная энергия конденсаторов равна
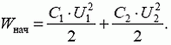
Для определения энергии в конечном состоянии воспользуемся тем, что суммарный заряд конденсаторов не может измениться. Он равен 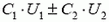 (для случаев, когда конденсаторы были соединены одноименно или разноименно заряженными пластинами соответственно). После замыкания ключа этим зарядом оказывается заряжен конденсатор емкостью C1 + C2 (конденсаторы емкостями C1 и C2 соединены параллельно). Таким образом,
(для случаев, когда конденсаторы были соединены одноименно или разноименно заряженными пластинами соответственно). После замыкания ключа этим зарядом оказывается заряжен конденсатор емкостью C1 + C2 (конденсаторы емкостями C1 и C2 соединены параллельно). Таким образом,
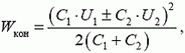 и
и 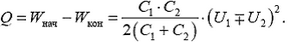
Как и должно быть, в обоих случаях выделяется тепло — есть джоулевы потери. Замечательно, что выделившееся количество теплоты не зависит от сопротивления цепи — при малых сопротивлениях текут большие токи и наоборот.
Теперь найдем, как количество теплоты Q распределяется между резисторами. Через сопротивления R1 и R2 в каждый момент процесса перезарядки текут одинаковые токи, значит, в каждый момент мощности, выделяемые на сопротивлениях, равны
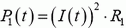 и
и 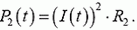
Следовательно,
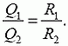
Кроме того, 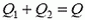 . Поэтому окончательно
. Поэтому окончательно
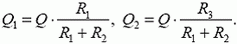
Задача 3. В схеме на рисунке 2 конденсатор емкостью C заряжен до напряжения U. Какое количество химической энергии запасется в аккумуляторе с ЭДС ![]() после замыкания ключа? Какое количество теплоты выделится в резисторе?
после замыкания ключа? Какое количество теплоты выделится в резисторе?
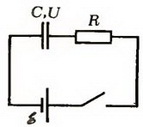
Рис. 2
Первоначальный заряд на конденсаторе 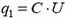 . После окончания перезарядки заряд на конденсаторе станет равным
. После окончания перезарядки заряд на конденсаторе станет равным 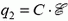 . Протекший через батарею заряд в случае, когда к минусу батареи подключена отрицательно заряженная обкладка конденсатора, будет равен
. Протекший через батарею заряд в случае, когда к минусу батареи подключена отрицательно заряженная обкладка конденсатора, будет равен
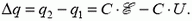
В противном случае 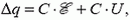 и при этом аккумулятор будет разряжаться (Δq > 0). А в первом случае при
и при этом аккумулятор будет разряжаться (Δq > 0). А в первом случае при 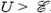 аккумулятор заряжается (Δq < 0), и количество химической энергии, запасенной в аккумуляторе после замыкания ключа, равно работе батареи:
аккумулятор заряжается (Δq < 0), и количество химической энергии, запасенной в аккумуляторе после замыкания ключа, равно работе батареи:
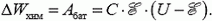
Теперь запишем закон сохранения энергии (1) –
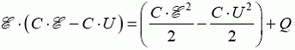
– и найдем выделившееся количество теплоты:
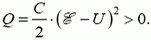
Задача 4. Плоский конденсатор находится во внешнем однородном поле с напряженностью 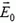 , перпендикулярной пластинам. На пластинах площадью S распределены заряды +q и –q. Расстояние между пластинами d. Какую минимальную работу надо совершить, чтобы поменять пластины местами? Расположить параллельно полю? Вынуть из поля?
, перпендикулярной пластинам. На пластинах площадью S распределены заряды +q и –q. Расстояние между пластинами d. Какую минимальную работу надо совершить, чтобы поменять пластины местами? Расположить параллельно полю? Вынуть из поля?
Работа будет минимальной, когда процесс проводится очень медленно — при этом не выделяется тепло. Тогда, согласно закону сохранения энергии, 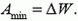
Чтобы найти ΔW, воспользуемся формулой (3). Поле между пластинами представляет собой суперпозицию поля 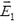 данного плоского конденсатора –
данного плоского конденсатора –
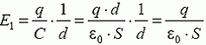
– и внешнего поля 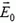 .
.
При перемене пластин местами поле 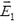 меняется на –
меняется на –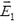 , а поле снаружи не меняется, т. е. изменение энергии системы связано с изменением ее плотности между пластинами конденсатора:
, а поле снаружи не меняется, т. е. изменение энергии системы связано с изменением ее плотности между пластинами конденсатора:
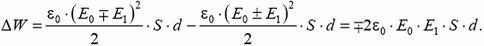
Если направления векторов 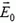 и
и 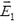 были одинаковы, то плотность энергии между пластинами уменьшилась после перемены пластин местами, а если направления были противоположны, то плотность энергии увеличилась. Таким образом, в первом случае
были одинаковы, то плотность энергии между пластинами уменьшилась после перемены пластин местами, а если направления были противоположны, то плотность энергии увеличилась. Таким образом, в первом случае 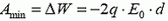 — конденсатор хочет сам развернуться и его надо удерживать (A < 0), а во втором случае
— конденсатор хочет сам развернуться и его надо удерживать (A < 0), а во втором случае 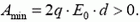
Когда пластины конденсатора расположены параллельно полю 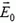 и
и 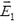 перпендикулярны друг другу. Энергия поля внутри конденсатора в этом случае равна
перпендикулярны друг другу. Энергия поля внутри конденсатора в этом случае равна 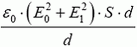 . Тогда
. Тогда
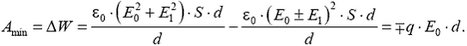
Когда конденсатор вынули из поля, в том месте, где он был, поле стало 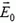 , а в нем самом теперь поле
, а в нем самом теперь поле 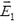 , т.е. ΔW и Amin оказываются такими же, как и в предыдущем случае.
, т.е. ΔW и Amin оказываются такими же, как и в предыдущем случае.
Задача 5. Конденсатор емкостью С без диэлектрика заряжен зарядом q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью ε? То же, но конденсатор присоединен к батарее с ЭДС ![]() .
.
При заливании диэлектрика емкость конденсатора увеличилась в ε раз.
В первом случае фиксирован заряд на пластинах, внешних сил нет, и закон сохранения энергии (1) имеет вид
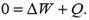
Отсюда
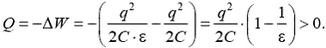
Тепло выделяется за счет уменьшения энергии взаимодействия зарядов.
Во втором случае есть работа батареи и фиксировано напряжение на конденсаторе:
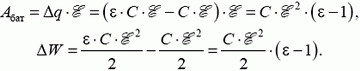
Тогда из уравнения (1) следует
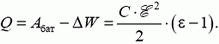
Задача 6. Две соединенные проводником пластины площадью S каждая находятся на расстоянии d друг от друга (это расстояние мало по сравнению с размерами пластин) во внешнем однородном поле с напряженностью ![]() , перпендикулярной пластинам (рис. 3). Какую работу надо совершить, чтобы сблизить их до расстояния d/2?
, перпендикулярной пластинам (рис. 3). Какую работу надо совершить, чтобы сблизить их до расстояния d/2?
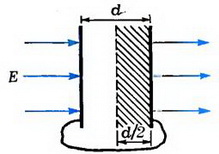
Рис. 3
Пластины эквипотенциальны, и между ними поля нет. Результатом работы по сближению является создание поля с напряженностью Е в объеме 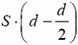 . Тогда, в соответствии с уравнениями (1) и (3),
. Тогда, в соответствии с уравнениями (1) и (3),
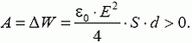
Упражнения
1. Два одинаковых плоских конденсатора емкостью С каждый соединены параллельно и заряжены до напряжения U. Пластины одного из конденсаторов медленно разводят на большое расстояние. Какая при этом совершается работа?
2. Два конденсатора, каждый емкостью С, заряжены до напряжения U и соединены через резистор (рис. 4). Пластины одного из конденсаторов быстро раздвигают, так что расстояние между ними увеличивается вдвое, а заряд на пластинах за время их перемещения не изменяется. Какое количество теплоты выделится в резисторе?
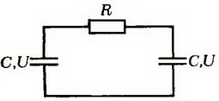
Рис. 4
3. Плоский воздушный конденсатор присоединен к батарее с ЭДС ![]() . Площадь пластин S, расстояние между ними d. В конденсаторе находится металлическая плита толщиной d1, параллельная пластинам (рис. 5). Какую минимальную работу нужно затратить, чтобы удалить плиту из конденсатора?
. Площадь пластин S, расстояние между ними d. В конденсаторе находится металлическая плита толщиной d1, параллельная пластинам (рис. 5). Какую минимальную работу нужно затратить, чтобы удалить плиту из конденсатора?
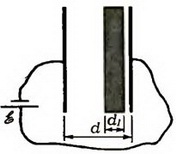
Рис. 5
4. Большая тонкая проводящая пластина площадью S и толщиной d помещена в однородное электрическое поле с напряженностью ![]() , перпендикулярной поверхности пластины. Какое количество теплоты выделится в пластине, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы удалить пластину из поля?
, перпендикулярной поверхности пластины. Какое количество теплоты выделится в пластине, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы удалить пластину из поля?
5. Одна из пластин плоского конденсатора подвешена на пружине (рис. 6). Площадь каждой пластины S, расстояние между ними в начальный момент d. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть минимальная жесткость пружины, чтобы не произошло касание пластин? Смещением пластин за время зарядки пренебречь.
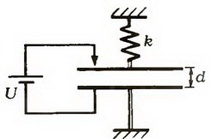
Рис. 6
Ответы.
1. 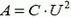 (весь заряд оказывается на конденсаторе, пластины которого не раздвигали).
(весь заряд оказывается на конденсаторе, пластины которого не раздвигали).
2. 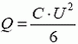 (в первый момент после разведения пластин замкнутыми друг на друга оказываются конденсатор емкостью С с напряжением U и конденсатор емкостью С/2 с напряжением 2U).
(в первый момент после разведения пластин замкнутыми друг на друга оказываются конденсатор емкостью С с напряжением U и конденсатор емкостью С/2 с напряжением 2U).
3. 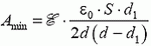 (минимальная работа по удалению плиты равна разности изменения энергии конденсатора и работы батареи).
(минимальная работа по удалению плиты равна разности изменения энергии конденсатора и работы батареи).
4. 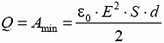 (сразу после выключения внешнего поля в пластине есть поле поляризационных зарядов, напряженность которого равна Е удаление пластины из поля эквивалентно созданию поля с напряженностью Е в объеме пластины).
(сразу после выключения внешнего поля в пластине есть поле поляризационных зарядов, напряженность которого равна Е удаление пластины из поля эквивалентно созданию поля с напряженностью Е в объеме пластины).
5. 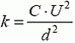 (результат получается из закона сохранения энергии
(результат получается из закона сохранения энергии 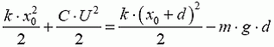 и из условия равновесия пластины
и из условия равновесия пластины 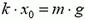 ).
).
