Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2021 года; проверки требуют 4 правки.
Закон Джоуля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
Определения[править | править код]
В словесной формулировке звучит следующим образом[2]:
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.
Математически может быть выражен в следующей форме:
где 


Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.
В интегральной форме этот закон имеет вид
где 






Применяя закон Ома, можно получить следующие эквивалентные формулы:
Практическое значение[править | править код]
Снижение потерь энергии[править | править код]
При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно — значит, ток в сети 
Откуда следует, что 

Выбор проводов для цепей[править | править код]
Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.
По этой причине для передачи необходимой мощности через современные магистральные воздушные линии электропередач, их проектируют под сверхвысокое напряжение (до 1150 кВ), чтобы обеспечить сверхнизкие токи в ЛЭП.
Электронагревательные приборы[править | править код]
Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.
За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.
Плавкие предохранители[править | править код]
Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.
См. также[править | править код]
- Закон Ома
Примечания[править | править код]
- ↑ Джоуля — Ленца закон // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 186. — 688 с.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 197—198. — 688 с.
Проходя по проводнику, ток может оказывать некоторые действия: тепловое, химическое и магнитное.
Тепловое действие тока обусловлено тем, что свободные электроны, двигаясь с большой скорость, взаимодействуют с ионами металлов, ионами солей в растворах кислот и щелочей. Ионы начинают усиленно колебаться, двигаться, вращаться, то есть их энергия тоже повышается. Проводник или электролит нагревается.
Например, спираль лампочки раскаляется до такой температуры, что начинает излучать свет.

Электрическая энергия превращается в тепловую энергию проводника; часть рассеивается, часть используется в бытовых целях (для нагревания).
Работа, которую совершает электрический ток, определяется количеством теплоты, выделяемой проводником:
Q = A
, где (A) — работа тока, (Q) — количество теплоты.
Работу тока рассчитывают по формуле:
A = U⋅I⋅t
. Тогда количество теплоты, исходя из закона сохранения энергии, также будет равно:
Q = U⋅I⋅t
.
Согласно закону Ома
U = IR
. Подставляя эту формулу в предыдущую, получим:
Q = I2⋅R⋅t
.
Количество теплоты, которое выделяется в проводнике с током, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока.
В процессе своих экспериментов получили такой же результат Джеймс Джоуль в Англии и Эмилий Христианович Ленц в России. В их честь закон имеет двойное название: закон Джоуля-Ленца.

Джоуль Джеймс Прескотт ((1818—1889)) — английский физик, член Лондонского королевского общества. Он внёс значительный вклад в исследование электромагнетизма и тепловых явлений, в создание физики низких температур, в обоснование закона сохранения и превращения энергии. Именем Джоуля назвали единицу измерения работы и энергии в системе СИ.

Эмилий Христианович Ленц ((1804—1865)) — российский физик и электротехник, академик Петербургской Академии наук ((1830)), ректор Санкт-Петербургского университета (с (1863)). Результатом его исследований стало открытие взаимосвязей (на «языке математики») между электрическими и термодинамическими параметрами, между электрическими и магнитными параметрами при протекании тока в проводнике.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах.
Состояние сети, когда по проводам и приборам проходит ток больше допустимого значения, называется перегрузкой. Опасность этого явления в тепловом действии тока, ведь при большой перегрузке изоляция проводников легко воспламеняется. Перегрузка может возникнуть при подключении устройств большой мощности через удлинитель (смотри рисунок и никогда так не делай!).

Для примера, перегрузка проводов на (25)% приводит к сокращению срока их службы где-то с (20) лет до (3—5) месяцев, а перегрузка проводов на (50)% — до нескольких часов.
Электричество — неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.


При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Закон Джоуля-Ленца
В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.
Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:
Q=I2Rt
где
Q — количество выделяемого тепла (Джоули)
I — сила тока, протекающего через проводник (Амперы)
R — сопротивление проводника (Омы)
t — время прохождения тока через проводник (Секунды)
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы «трётся», соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует — чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом — будет неравномерный нагрев в месте скрутки. В итоге — подгорание с последующим пропаданием контакта.
Применение закона Джоуля-Ленца в жизни
Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины — первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.
Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение
Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.
Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.
Раз уж заговорили про ДжОУля )) Читайте статья про ОУ — Операционный усилитель.
Закон Джоуля-Ленца
Знание законов и способов использования электричества — необходимый элемент школьного образования. Вместе с экспертом разберем задачи на закон Джоуля-Ленца и узнаем, где он применяется в жизни

Физики всегда искали способы практического применения электричества, чувствуя его гигантский потенциал. Первой ступенькой на этом пути стал закон Ома, связавший в один узел основные понятия новой науки. Эксперименты показали, что электричество можно преобразовать в теплоту. Это стало научным прорывом, нужен был только математический аппарат для инженерных расчетов. И вот от он найден.
Определение закона Джоуля-Ленца простыми словами
Джеймс Джоуль и Эмилий Ленц независимо установили опытным путем, что проводник, по которому течет электрический ток, выделяет тепло. И его количество прямо пропорционально квадрату силы тока, его сопротивлению и времени протекания тока. Это, собственно говоря, и есть самое простое определение закона Джоуля-Ленца
Формула закона Джоуля-Ленца
Определить количество теплоты, выделяемой проводником при прохождении через него электричества, можно по следующей формуле:
Q=I2⋅R⋅t
Где:
Q — количество теплоты в джоулях;
I — сила тока в амперах;
R — сопротивление проводника в омах;
t — время в секундах.
Задачи на закон Джоуля-Ленца
Наиболее ярко этот закон проявляется при расчетах тепловых приборов.
Задача 1
25 минут через спираль электроплитки сопротивлением 30 Ом протекает электрический ток силой 1,3 А. Какое количество теплоты выделится за это время?
Подставляем данные в формулу:
Q=1,32*30*25*60=76 050 дж
Ответ: 76,05 килоджоулей.
Закон Ома
Разбираем формулировку, формулу и задачи на закон Ома с решением
подробнее

Задача 2
Сколько времени нагревался проводник сопротивлением 25 Ом, если на нем выделилось 8 кДж теплоты при силе тока 2 А?
Преобразуем формулу закона Джоуля-Ленца к удобному для нас виду:
Q=I2⋅R⋅t → t=Q/(I2⋅R)
Подставляем исходные данные:
t=8000/(22*25)=80
Ответ: 80 секунд.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель физики проекта «ИнтернетУрок».
Как открыли закон Джоуля-Ленца?
В первой половине (в 30-х – 40-х годах) XIX века русский учёный Эмилий Христианович Ленц и английский физик Джеймс Прескотт Джоуль независимо друг от друга провели опыты, которые позволили выяснить зависимость выделяющегося в проводнике тепла от его сопротивления и силы тока, протекающей через этот проводник. В научном сообществе подобные зависимости принято называть именами первооткрывателей. Так и появился закон Джоуля-Ленца.
Где применяется закон Джоуля-Ленца?
Электрический ток при протекании через проводник или любой электрический прибор совершает работу. Эта работа может быть полезной. Например, нагревание утюга, свечение электрической лампы и так далее. А может быть и вредной: нагревание подводящих проводов, которое как минимум ведет к потерям в электрических цепях или может привести к пожару. Данный закон позволяет рассчитать, какими, например, должны быть провода, а какими спирали нагревательных приборов, чтобы потери были минимальны, а энергия выделялась там, где нам нужно.
Где и как применяется закон Джоуля-Ленца в жизни?
Нельзя сказать, что каждый человек применяет в жизни этот закон, но его знание позволяет понять, почему, например, соединение проводов электрической цепи в доме должно быть очень надежным. Если контакт плохой, то в этом месте сопротивление будет большим, и место контакта станет нагреваться, что может спровоцировать пожар. Конструкторы используют этот закон для расчета спиралей электронагревательных приборов или элементов предохранителей, которые отключают электричество в случае опасности.
§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
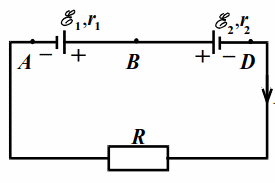
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
 |
| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
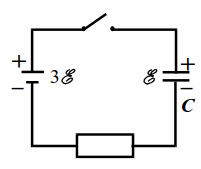 |
| Рис. 19.1 |
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.







