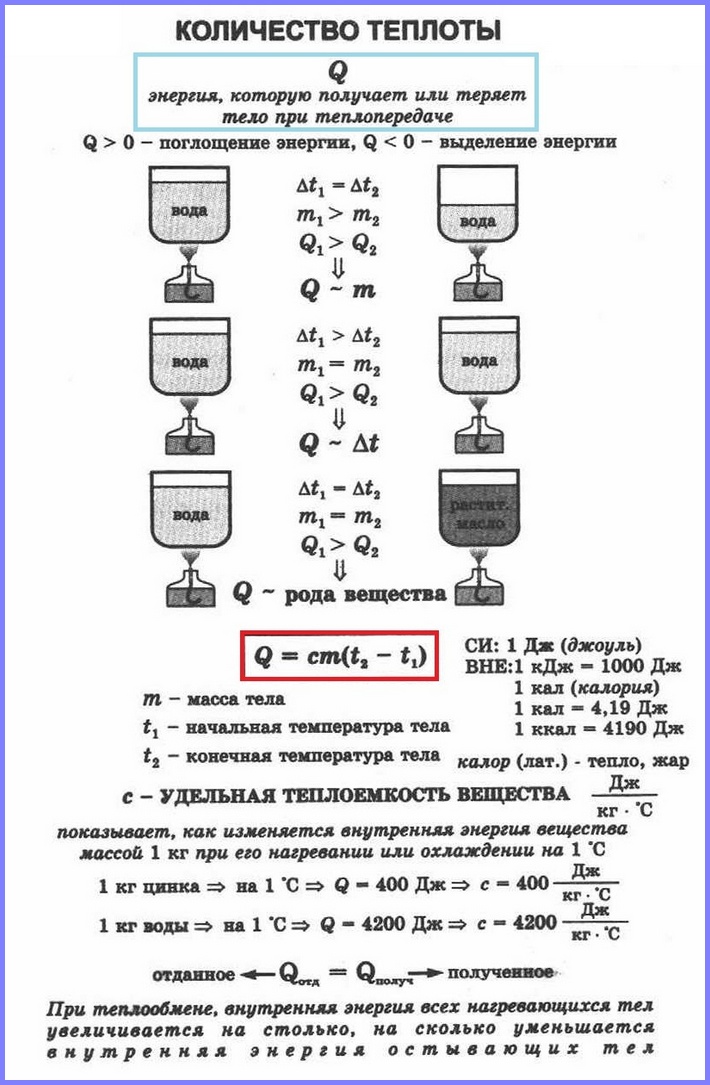
как вычисляется количество теплоты, если известна удельная теплоемкость вещества?
Ученик
(185),
закрыт
10 лет назад
Дополнен 10 лет назад
в каких случаях можно использовать это выражение?
Рустам Искендеров
Искусственный Интеллект
(133392)
10 лет назад
Это выражение, как правило, используется по отношению подводимой к телу или отводимой от него теплоты. А последние равны произведению массы тела, изменения температуры и удельной теплоемкости вещества тела. Если речь идет о “количестве теплоты”, содержащемся в теле, тут обычно используется понятие “внутренная энергия”, что равна тому же произведению – только в этом случае вместо разности температур берется абсолютная тепература тела.
На практике часто приходится проводить различные тепловые расчёты. Для увеличения эргономичности тепловой системы жилых домов измеряют количество тепловой энергии, рассеиваемой через вентиляцию, окна, расщелины.
Для расчёта количества тепловой энергии нужно измерить массу (m), разность температуры в начале и в конце процесса
Δt=tкон−tнач
, а также знать теплоёмкость (c) данного вещества.
Чтобы нагреть некоторое вещество массой (1) кг на (1°C), необходимо затратить количество теплоты, равное удельной теплоёмкости (c) данного вещества.
Количество теплоты, получаемое веществом при нагревании, прямо пропорционально удельной теплоёмкости вещества, его массе и разности температур, то есть:
Q=cmΔt
или
Данная формула даёт возможность найти и выделяемую при охлаждении вещества теплоту.
Чтобы рассчитать количество теплоты, необходимое для нагревания вещества (или выделяемое им при охлаждении), следует удельную теплоёмкость вещества умножить на его массу и на разность между конечной и начальной температурой вещества.
Так как конечная температура остывающего вещества меньше его начальной температуры:
то изменение температуры оказывается отрицательным числом:
Значит, и выделяемое веществом количество теплоты выражается отрицательным числом:
Последний факт обозначает не рост, а убыль внутренней энергии вещества.
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
«Количество теплоты. Удельная теплоёмкость»
Количество теплоты
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
Количество теплоты – это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q.
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах — джоулях (Дж), как и всякий вид энергии.
В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии — калория (кал), равная количеству теплоты, необходимому для нагревания 1 грамма воды на 1 градус Цельсия (точнее, от 19,5 до 20,5 °С). Данную единицу, в частности, используют в настоящее время при расчетах потребления тепла (тепловой энергии) в многоквартирных домах. Опытным путем установлен механический эквивалент теплоты — соотношение между калорией и джоулем: 1 кал = 4,2 Дж.
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.
Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Удельная теплоёмкость
Удельная теплоёмкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой с. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты Q, необходимое для нагревания тела массой m от температуры t1°С до температуры t2°С, равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
Q = c ∙ m (t2 — t1)
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
Это конспект по теме «Количество теплоты. Удельная теплоёмкость». Выберите дальнейшие действия:
- Перейти к следующему конспекту: «Уравнение теплового баланса»
- Вернуться к списку конспектов по Физике
- Посмотреть решение типовых задач на количество теплоты