Версия для печати и копирования в MS Word
1
2
3
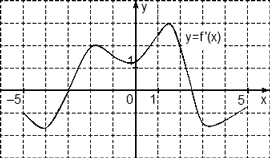
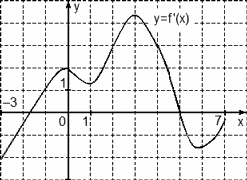
На рисунке изображен график производной функции f(x), определенной на интервале (−15; 2). Найдите количество точек максимума функции f(x) на отрезке [−11;0].
4
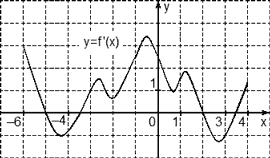
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].
5
6
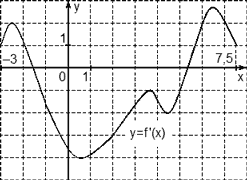
На рисунке изображен график y = f ‘(x) — производной функции f(x), определенной на интервале (−17; 5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−15; 0].
7
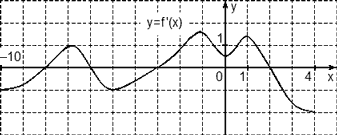
На рисунке изображен график y = f ‘(x) — производной функции f(x), определенной на интервале (−12; 11). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−8; 9].
8
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
9
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
10
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
11
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
12
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
13
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
14
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
15
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
16
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
17
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
18
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
19
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
20
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
21
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
22
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
23
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
24
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
25
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
26
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
27
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
28
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
29
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
30
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
31
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
32
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
33
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
34
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
35
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
36
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
37
На рисунке изображен график производной функции
определенной на интервале
Найдите количество точек
максимума функции на отрезке
Готовимся к ЕГЭ
Пособие для учащихся
Исследование функций по графику
производной
В данной статье рассматриваются задачи входящие в ЕГЭ по
математике, в которых дан график производной функции (задание 7). В этих
задачах ставятся следующие вопросы:
1. В какой точке заданного отрезка функция принимает наибольшее
(или наименьшее) значение.
2. Найти количество точек максимума (или минимума) функции,
принадлежащих заданному отрезку.
3. Найти количество точек экстремума функции, принадлежащих
заданному отрезку.
4. Найти точку экстремума функции, принадлежащую заданному
отрезку.
5. Найти промежутки возрастания (или убывания) функции и в ответе
указать сумму целых точек, входящих в эти промежутки.
6. Найти промежутки возрастания (или убывания) функции. В ответе
указать длину наибольшего из этих промежутков.
7. Найти количество точек, в которых касательная к графику функции
параллельна прямой вида у = kx + b или совпадает с ней.
8. Найти абсциссу точки, в которой касательная к графику функции
параллельна оси абсцисс или совпадает с ней.
Краткая теория
1. Производная на интервалах возрастания имеет положительный знак.
Если производная в определённой точке из некоторого интервала
имеет положительное значение, то график функции на этом интервале
возрастает.
2. На интервалах убывания производная имеет отрицательный знак.
Если производная в определённой точке из некоторого интервала
имеет отрицательное значение, то график функции на этом интервале
убывает.
3. Производная в точке х равна угловому коэффициенту касательной,
проведённой к графику функции в этой же точке.
4. В точках экстремума (максимума-минимума) функции производная
равна нулю. Касательная к графику функции в этой точке параллельна оси
ох.
Многие путают график производной и график функции. Поэтому в таких
зданиях, где дан график, сразу же нужно обратить своё внимание в условии на
том, что дано: график функции или график производной функции?
Если это график производной функции, то рассматривать его нужно
как бы «отражение» самой функции, которое просто даёт нам информацию об этой
функции.
Рассмотрим алгоритм решения задания.
Задача
На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–2;21).

Ответим на следующие вопросы:
1. В какой точке отрезка [7;15] функция f(х) принимает
наибольшее значение.
На заданном отрезке производная функции отрицательна, значит,
функция на этом отрезке убывает (она убывает от левой границы интервала к
правой). Таким образом, наибольшее значение функции достигается на левой
границе отрезка, т. е. в точке 7.
Ответ: 7.
2. В какой точке отрезка [3;6] функция f(х) принимает
наименьшее значение.
По данному графику производной можем сказать следующее. На
заданном отрезке производная функции положительна, значит, функция на
этом отрезке возрастает (она возрастает от левой границы интервала к правой).
Таким образом, наименьшее значение функции достигается на левой границе
отрезка, то есть в точке х = 3.
Ответ: 3.
3. Найдите количество точек максимума функции f(х),
принадлежащих отрезку [0;20].
Точки максимума соответствуют точкам смены знака производной с
положительного на отрицательный. Рассмотрим, где таким образом меняется знак.
На отрезке (3;6) производная положительна, на отрезке (6;16)
отрицательна.
На отрезке (16;18) производная положительна, на отрезке (18;20)
отрицательна.
Таким образом, на заданном отрезке [0;20] функция имеет две точки
максимума х = 6 и х = 18.
Ответ: 2.
4. Найдите количество точек минимума функции f(х),
принадлежащих отрезку [0;4].
Точки минимума соответствуют точкам смены знака производной с
отрицательного на положительный. У нас на интервале (0;3)
производная отрицательна, на интервале (3;4) положительна.
Таким образом, на отрезке [0;4] функция имеет только одну точку
минимума х = 3.
!!! Будьте внимательны при записи ответа – записывается количество
точек, а не значение х, такую ошибку можно допустить из-за
невнимательности.
Ответ: 1.
5. Найдите количество точек экстремума функции f(х),
принадлежащих отрезку [0;20].
Обратите внимание, что необходимо найти количество точек
экстремума (это и точки максимума и точки минимума).
Точки экстремума соответствуют точкам смены знака производной (с
положительного на отрицательный или наоборот). На данном в условии графике это
нули функции. Производная обращается в нуль
в точках 3, 6, 16, 18.
Таким образом, на отрезке [0;20] функция имеет 4 точки экстремума.
Ответ: 4.
6. Найдите промежутки возрастания функции f(х). В
ответе укажите сумму целых точек, входящих в эти промежутки.
Промежутки возрастания данной функции f(х) соответствуют
промежуткам, на которых ее производная положительна, то есть интервалам (3;6) и
(16;18). Обратите внимание, что границы интервала не входят в него (круглые
скобки – границы не включены в интервал, квадратные – включены). Данные
интервалы содержат целые точки 4, 5, 17. Их сумма равна: 4 + 5 + 17 = 26
Ответ: 26.
7. Найдите промежутки убывания функции f(х) на
заданном интервале. В ответе укажите сумму целых точек, входящих
в эти промежутки.
Промежутки убывания функции f(х) соответствуют
промежуткам, на которых производная функции отрицательна. В данной задаче это
интервалы (–2;3), (6;16), (18;21).
Данные интервалы содержат следующие целые точки: –1, 0, 1, 2, 7,
8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Их сумма равна:
( –1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +
+ 11 + 12 + 13 + 14 + 15 + 19 + 20 = 140
Ответ: 140.
!!! Необходимо обратить внимание в условии: включены ли границы в
интервал или нет. Если границы будут включены, то и в рассматриваемых в
процессе решения интервалах эти границы также необходимо учитывать.
8. Найдите промежутки возрастания функции f(х). В
ответе укажите длину наибольшего из них.
Промежутки возрастания функции f(х) соответствуют
промежуткам, на которых производная функции положительна. Мы уже указывали их:
(3;6) и (16;18). Наибольшим из них является интервал (3;6), его длина
равна 3.
Ответ: 3
9. Найдите промежутки убывания функции f(х). В ответе
укажите длину наибольшего из них.
Промежутки убывания функции f(х) соответствуют
промежуткам, на которых производная функции отрицательна. Мы уже указывали их,
это интервалы
(–2;3), (6;16), (18;21), их длины соответственно равны 5, 10, 3.
Длина наибольшего интервала равна 10.
Ответ: 10
10. Найдите количество точек, в которых касательная
к графику функции f(х) параллельна прямой у = 2х + 3 или
совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту
касательной. Так как касательная параллельна прямой у = 2х + 3 или совпадает с
ней, то их угловые коэффициенты равны 2. Значит, необходимо найти количество
точек, в которых у′(х0) = 2. Геометрически это соответствует
количеству точек пересечения графика производной с прямой у = 2. На
данном интервале таких точек 4.
Ответ: 4
11. Найдите точку экстремума функции f(х),
принадлежащую отрезку [0;5].
Точка экстремума функции это такая точка, в которой её производная
равна нулю, при чём в окрестности этой точки производная меняет знак (с
положительного на отрицательный или наоборот). На отрезке [0;5] график
производной пересекает ось абсцисс, производная меняет знак с отрицательного на
положительный. Следовательно, точка х = 3 является точкой экстремума.
Ответ: 3
12. Найдите абсциссы точек, в которых касательные к
графику у = f (x) параллельны оси абсцисс или совпадают с ней. В ответе укажите
наибольшую из них.
Касательная к графику у = f (x) может быть параллельна оси абсцисс
или совпадать с ней, только в точках, где производная равна нулю (это могут
быть точки экстремума или стационарные точки, в окрестностях которых
производная свой знак не меняет). По данному графику видно, что производная
равна нулю в точках 3, 6, 16,18. Наибольшая равна 18.
Можно построить рассуждение таким образом:
Значение производной в точке касания равно угловому коэффициенту
касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней,
её угловой коэффициент равен 0 (действительно тангенс угла в ноль
градусов равен нулю). Следовательно, мы ищем точку, в которой угловой
коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна
нулю в той точке, в которой её график пересекает ось абсцисс, а это точки
3, 6, 16,18.
Ответ: 18
Решите самостоятельно
Задача № 1.
На рисунке изображен график у= f′(х) — производной
функции f(х), определенной на интервале (–8;4). В какой точке
отрезка [–7;–3] функция f(х) принимает наименьшее значение.

Задача № 2.
На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–7;14).
Найдите количество точек максимума функции f(х),
принадлежащих отрезку [–6;9].

Задача № 3.
На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–18;6).
Найдите количество точек минимума функции f(х), принадлежащих
отрезку [–13;1].

Задача № 4.
На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–11; –11). Найдите количество
точек экстремума функции f(х), принадлежащих отрезку [–10;
–10].

Задача № 5.
На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–7;4). Найдите
промежутки возрастания функции f(х). В ответе укажите сумму целых
точек, входящих в эти промежутки.

Задача № 6.
На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–5;7). Найдите промежутки
убывания функции f(х). В ответе укажите сумму целых точек, входящих
в эти промежутки.

Задача № 7.
На рисунке изображен график у = f′(х) —
производной функцииf(х), определенной на интервале (–11;3). Найдите
промежутки возрастания функции f(х). В ответе укажите длину
наибольшего из них.

Задача № 8.
На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–2;12). Найдите промежутки
убывания функции f(х). В ответе укажите длину наибольшего из них.

Задача № 9.
На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–10;2). Найдите количество
точек, в которых касательная к графику функции f(х) параллельна
прямой у = –2х – 11 или совпадает с ней.

Задача № 10.
На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–4;8). Найдите точку
экстремума функции f(х), принадлежащую отрезку [–2;6].

Задача № 11.
На рисунке изображен график у = f′(х) —
производной функции f(х). Найдите абсциссу точки, в которой
касательная к графику у=f(х) параллельна прямой
у = 2х – 2 или совпадает с ней.

Задача № 12.
На рисунке изображен график у = f′(х) —
производной функции f(х). Найдите абсциссу точки, в которой касательная
к графику
у = f(х) параллельна оси абсцисс или
совпадает с ней.

Ответы:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
-7 |
1 |
1 |
5 |
-3 |
18 |
6 |
6 |
5 |
4 |
5 |
-3 |
09
Авг 2013
Категория: 07 Производная, ПО
07. Применение производной к исследованию функции
2013-08-09
2023-04-30
Cледующая таблица будет весьма полезна при работе с данной темой.
 Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции
Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции или ее производной
Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины», как в случае
не интересуют нас в принципе!
Задача 1. На рисунке изображен график функции , определенной на интервале
. Определите количество целых точек, в которых производная функции
отрицательна.

Решение: + показать
Задача 2. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.

Решение:+ показать
Задача 3. На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.

Решение: + показать
Задача 4. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых производная функции
равна 0.

Решение: + показать
Задача 5. На рисунке изображён график функции и одиннадцать точек на оси абсцисс:
. В скольких из этих точек производная функции
отрицательна?

Решение: + показать
Задача 6. На рисунке изображен график функции , определенной на интервале
. Найдите сумму точек экстремума функции
.

Решение: + показать
Задача 7. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: + показать
Задача 8. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите длину наибольшего из них.

Решение: + показать
Задача 9. На рисунке изображен график производной функции , определенной на интервале
. В какой точке отрезка
принимает наибольшее значение.
 Решение: + показать
Решение: + показать
Задача 10. На рисунке изображен график — производной функции
, определенной на интервале
. Найдите количество точек максимума функции
, принадлежащих отрезку
.

Решение: + показать
Задача 11. На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Решение: + показать
Задача 12. Функция определена на промежутке
На рисунке изображен график её производной. Найдите точку
в которой функция
принимает наименьшее значение, если

Решение: + показать
Задача 13. Функция определена и непрерывна на полуинтервале
На рисунке изображен график её производной. Найдите промежутки убывания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: + показать

Вы можете пройти тест «Применение производной к исследованию функции»
Автор: egeMax |
комментариев 29
Печать страницы
Рассмотрим задания, в которых требуется найти для функции точки максимума на графике производной.
Важно внимательно читать условие. Точки минимума и максимума функции на графике функции находим иначе!
№1
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-3;9 ). Найти точку максимума функции f(x).
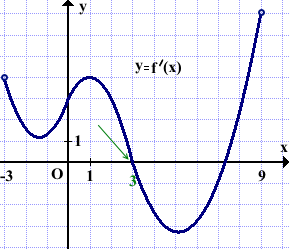
Решение:
В точке максимума производная непрерывной функции обращается в нуль и при переходе через точку максимума знак производной меняется с плюса на минус.
Соответственно, график производной в точке максимума пересекает ось абсцисс сверху вниз.
В данном случае точкой максимума функции f(x) является точка с абсциссой x=3.
Ответ: 3.
№2
На рисунке изображён график функции y=f'(x), определённой на интервале (-14;9). Определить количество точек максимума функции f(x).
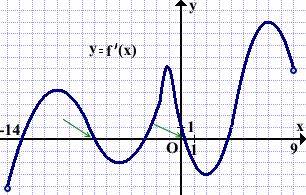
Решение:
В точках максимума производная меняет свой знак с плюса на минус.
График производной при переходе через точку максимума пересекает ось абсцисс сверху вниз.
График производной y=f'(x) данной функции пересекает ось Ox в двух точках. Значит, функция f(x) имеет две точки максимума.
Ответ: 2.
№3
На рисунке изображён график производной функции f(x), определённой на интервале (-9;14). Найти количество точек максимума функции f(x) на отрезке [-6;13].
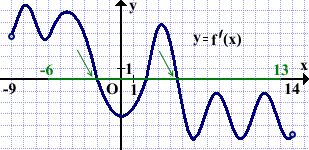
Решение:
Выделяем рассматриваемый отрезок [-6;13].
В точках максимума функции f(x) график её производной f'(x) пересекает ось Ox сверху вниз.
На отрезке [-6;13] график производной данной функции пересекает ось абсцисс в двух точках. Следовательно, на этом отрезке функция f(x) имеет две точки максимума.
Ответ: 2.
15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
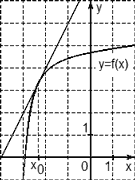
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
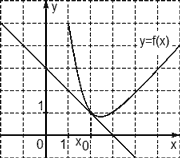
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
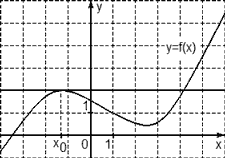
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
![]()
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
![]()
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
![]()
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
![]()
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
![]()
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции

- ЕГЭ 2022, задание 6. Касательная к графику функции

- Схема Бернулли. Примеры решения задач

- Решение задач B6: №362—377

- Четырехугольная пирамида: как найти координаты вершин

- Нестандартная задача B2: студенты, гонорары и налоги