Как найти количество точек пересечения окружности

Как найти количество точек пересечения окружности

Как найти количество точек пересечения окружности с другими фигурами

Окружности являются одной из наиболее фундаментальных геометрических фигур. Часто возникает задача определения количества точек пересечения окружности с другими фигурами, такими как прямые, окружности и многоугольники.

Определение

Окружность – это геометрическая фигура, представляющая собой множество точек, находящихся на одинаковом расстоянии от фиксированной точки на плоскости. Точка, от которой измеряется расстояние до окружности, называется центром окружности, а расстояние от центра окружности до любой ее точки называется ее радиусом.

Определение пересечения

Пересечение – это геометрическое свойство, при котором две фигуры имеют общие точки. Если окружность пересекает другую фигуру, то она имеет одну или несколько общих точек с этой фигурой.

Пересечение с прямой

Если окружность пересекает прямую, то количество точек пересечения зависит от того, как расположена прямая относительно окружности. В зависимости от относительных положений прямой и окружности, могут возникать следующие случаи:

  • Прямая пересекает окружность в двух точках.
  • Прямая касается окружности в одной точке.
  • Прямая не пересекает и не касается окружности.

Количество точек пересечения окружности с прямой можно определить с использованием алгоритмов геометрической аналитики.

Пересечение с окружностью

Если окружность пересекает другую окружность, то количество точек пересечения зависит от того, как расположены окружности относительно друг друга. В зависимости от относительных положений окружностей могут возникать следующие случаи:

  • Одна окружность содержится внутри другой, и точек пересечения нет.
  • Окружности пересекаются в двух точках.
  • Окружности касаются друг друга в одной точке.
  • Одинаковые окружности совпадают и имеют бесконечное количество точек пересечения.

Пересечение с многоугольником

Если окружность пересекает многоугольник, то количество точек пересечения также зависит от того, как расположены фигуры относительно друг друга. В зависимости от относительных положений окружности и многоугольника могут возникать следующие случаи:

  • Окружность не пересекает многоугольник.
  • Окружность пересекает многоугольник в нескольких точках.
  • Окружность состоит из ребер, которые пересекают многоугольник в нескольких точках.

Заключение

Количество точек пересечения окружности с другими фигурами зависит от относительных положений этих фигур. Эту задачу можно решать с помощью геометрической аналитики и алгоритмов. Однако требуется некоторый опыт и знания в области геометрии.

Источник

Пересечение двух окружностей

Даны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают).

Решение

Предположим, не теряя общности, что центр первой окружности – в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений:

Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных:

Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой:

А решение последней задачи описано в соответствующей статье.

Единственный вырожденный случай, который надо рассмотреть отдельно – когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C – некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ – бесконечность, иначе – точек пересечения нет.

Пересечение двух окружностей

Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют

Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.

Формулы для расчета приведены под калькулятором.

Точки пересечения двух окружностей

Первая окружность

Вторая окружность

Пересечение окружностей

Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.

При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):

Случай Описание Условие
Тривиальный случай – окружности совпадают (это одна и та же окружность)
Окружности не касаются друг друга r1 + r2″ />
Одна окружность содержится внутри другой и не касается ее
Окружности пересекаются в двух точках Не выполнено ни одно из условий выше
Окружности соприкасаются в одной точке Частный случай предыдущего

Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:

Сначала калькулятор находит отрезок a

Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):

И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:

Обратите внимание на разные знаки перед вторым слагаемым

По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres

Как определить количество точек пересечения окружностей

Мой порядок написания этой программы происходил так:
Функция main и стандартные строки инициализации и завершения графики.
Определение переменных, обозначающих точки и длины радиусов, определение внутри main
Написание функции input (функция ввода параметров) , в которую в качестве параметров принимаются ссылки. Так как любой хороший программист будет рекомендовать использовать локальные переменные, то поэтому сделано так. (напомню желающим: использование ссылок помогает использовать локальные переменные аналогично глобальным, но только внутри своих функций)
Написание функции возвращающей число точек.

Если пробовать воссоздать этот материал самостоятельно из теории, то это довольно легко, но кто-то может путаться во всех семи вариантах при проверке условий.

3 комментария на «“C++ для начинающих Узнать количество точек пересечения двух окружностей”»

Не пишите ничего для начинающих, это просто ужасно.

[spoiler title=”источники:”]

http://planetcalc.ru/8098/

C++ для начинающих Узнать количество точек пересечения двух окружностей

[/spoiler]

Источник

Dennis Ritchie

555 / 148 / 58

Регистрация: 27.07.2014

Сообщений: 2,446

1

Определить количество точек пересечения двух окружностей

22.02.2015, 21:07. Показов 13610. Ответов 4

Метки нет (Все метки)

Студворк — интернет-сервис помощи студентам

Две окружности

Определить количество точек пересечения двух окружностей.

Входные данные
6 чисел x1, y1, r1, x2, y2, r2, где x1, y1, x2, y2 – координаты центров окружностей, а r1, r2 – их радиусы. Все числа – действительные, не превышают по модулю 1000000000, заданы не более чем с 3-мя знаками после запятой.

Выходные данные
Количество точек пересечения. Если точек пересечения бесконечно много, то вывести -1.

Пример

Входные данные Выходные данные
0 0 5 5 0 5 2

Подскажите, пожалуйста, какой случай я не учёл? Программа проходит 5 тестов из 7:

C++ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <cmath>
#include <cstdio>
 
int main(void) {
    
    double x1, y1, r1, x2, y2, r2;
    
    scanf("%lf%lf%lf%lf%lf%lf", &x1, &y1, &r1, &x2, &y2, &r2);
    
    double dist = pow(((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)), 0.5);
    
    if (r2 > r1) {
        double tmp = r1;
        r1 = r2;
        r2 = tmp;
    }
    
    if (x1 == x2 && y1 == y2) {
        if (r1 == r2)
            puts("-1");
        else
            puts("0");
    }
    else
        if (dist == r1 + r2 || dist == r1 - r2)
            puts("1");
        else
            if (dist > r1 + r2 || dist + r2 < r1)
                puts("0");
            else
                puts("2");
 
    return 0;
}



0

ValeryS

Модератор

Эксперт по электронике

8802 / 6585 / 894

Регистрация: 14.02.2011

Сообщений: 23,147

22.02.2015, 21:22

2

Лучший ответ Сообщение было отмечено Dennis Ritchie как решение

Решение

Цитата
Сообщение от Dennis Ritchie
Посмотреть сообщение

double dist

я так понял, что это расстояния между точками

Цитата
Сообщение от Dennis Ritchie
Посмотреть сообщение

if (dist == r1 + r2 || dist == r1 – r2)

вот здесь может быть ошибка
плавающие так не сравнивают из за округления может не сработать, нужно вводить какую то дельту
поскольку

Цитата
Сообщение от Dennis Ritchie
Посмотреть сообщение

заданы не более чем с 3-мя знаками после запятой.

введем дельту 0.0001
получаем

C++ 
1

if (fabs(dist- (r1 + r2))<0.0001 || fabs(dist -( r1 - r2))<0.0001)

но решение это не совсем верное
если сравнивать радиусы 1000000000 и 0.01 то скорее всего комп сойдет с ума
дельту нужно рассчитывать исходя из порядков чисел



1

555 / 148 / 58

Регистрация: 27.07.2014

Сообщений: 2,446

22.02.2015, 21:35

 [ТС]

3

Цитата
Сообщение от ValeryS
Посмотреть сообщение

дельту нужно рассчитывать исходя из порядков чисел

Спасибо. Решение прошло все тесты. Работает даже с дельтой, равной 0.1. Я до этого ни туда дельту вставлял.



0

Модератор

Эксперт по электронике

8802 / 6585 / 894

Регистрация: 14.02.2011

Сообщений: 23,147

22.02.2015, 21:39

4

Цитата
Сообщение от Dennis Ritchie
Посмотреть сообщение

Работает даже с дельтой, равной 0.1.

чем больше дельта, тем грубее расчет
это так скажем округление, можно округлять до километров, а можно и до микрон
но этим занимается другая наука – метрология



0

Dennis Ritchie

555 / 148 / 58

Регистрация: 27.07.2014

Сообщений: 2,446

23.02.2015, 00:18

 [ТС]

5

Цитата
Сообщение от ValeryS
Посмотреть сообщение

чем больше дельта, тем грубее расчет

Прочитал я такую статью:
Что нужно знать про арифметику с плавающей запятой (лучший способ для сравнения вещественных чисел)
Увидел там алгоритм сравнения чисел с плавающей запятой преобразованием к целочисленным переменным:

C++ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

bool AlmostEqual2sComplement(float A, float B, int maxUlps) {
    // maxUlps не должен быть отрицательным и не слишком большим, чтобы
    // NaN не был равен ни одному числу
    assert(maxUlps > 0 && maxUlps < 4 * 1024 * 1024);
    int aInt = *(int*)&A;
    // Уберем знак в aInt, если есть, чтобы получить правильно упорядоченную последовательность
    if (aInt < 0) aInt = 0x80000000 - aInt;
    //aInt &= 0x7fffffff; //(см. комментарий пользователя Vayun)
    // Аналогично для bInt
    int bInt = *(int*)&B;
    if (bInt < 0) bInt = 0x80000000 - bInt;
    /*aInt &= 0x7fffffff;*/
    unsigned int intDiff = abs(aInt - bInt); /*(см. комментарий пользователя Vayun)*/
    if (intDiff <= maxUlps)
        return true;
    return false;
}

Не могли бы вы привести пример, как сравнить два вещественных числа с помощью этого алгоритма.



0
Источник

Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.

Формулы для расчета приведены под калькулятором.

PLANETCALC, Точки пересечения двух окружностей

Точки пересечения двух окружностей

Первая окружность

Вторая окружность

Точность вычисления

Знаков после запятой: 2

Проверка расстояния между окружностями

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Пересечение окружностей

Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.

При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):

Случай Описание Условие
Тривиальный случай – окружности совпадают (это одна и та же окружность) d = 0, r1 = r2
separate.png Окружности не касаются друг друга d > r1 + r2
contained.png Одна окружность содержится внутри другой и не касается ее d < abs(r1 - r2)
twopoints.pngtwopoints2.png Окружности пересекаются в двух точках Не выполнено ни одно из условий выше
onepoint.pngonepoint2.png Окружности соприкасаются в одной точке Частный случай предыдущего

Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:

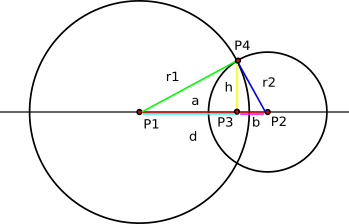
Two intersection points
Two intersection points

Сначала калькулятор находит отрезок a
a=frac{r^2_1-r^2_2+d^2}{2d}
и затем отрезок h
h=sqrt{r^2_1-a^2}

Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
P3=P1 + frac{a}{d}(P2-P1)

И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
x_4=x_3+frac{h}{d}(y_2-y_1)\y_4=y_3-frac{h}{d}(x2-x_1)
Вторая точка:
x_4=x_3-frac{h}{d}(y_2-y_1)\y_4=y_3+frac{h}{d}(x2-x_1)
Обратите внимание на разные знаки перед вторым слагаемым

По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres

Источник

 Если построить две окружности в одной плоскости, то относительно друг друга эти окружности могут не иметь общих точек, иметь одну общую точку или иметь две общие точки. Иногда требуется программно решать эту задачу. Сразу сообщу, что в этом обучающем материале, я решил лучше и нагляднее будет разбить весь код на отдельные небольшие функции, при этом старался совместить максимальную простоту с наглядностью. Здесь нет поиска координат пересечения, а просто определяется количество точек пересечения двух окружностей с заданными радиусами и центрами. Также я не считаю нужным запихивать сюда картинки и слова, слова, слова. Несмотря на мои плохие математические познания, мне 

Код С++ Определить количество точек пересечения двух окружностей

==================
#include <stdlib.h>
#include <iostream.h>
#include <graphics.h> //Для работы с графическими функциями
#include <math.h> //Для работы с математическими функцями

/*ФУНКЦИЯ ОПРЕДЕЛЯЮЩАЯ ЧИСЛО ОБЩИХ ТОЧЕК ДВУХ ОКРУЖНОСТЕЙ*/
int Tochek(double &x1,double &y1,double &R1,double &x2,double &y2, double &R2)
{
  double D=sqrt((x1–x2)*(x1–x2)+(y1–y2)*(y1–y2)); //Расстояние между центрами окружностей
//сущестует 7 ситуаций, в зависимости от которых можно говорить о числе общих точек
  if (D==0)
   {
    if (R1!=R2) return 0; else {cout<<“БЕСКОНЕЧНОЕ МНОЖЕСТВО ОБЩИХ ТОЧЕК”;return 8;}
   }
   else
    if (D>R1+R2)            {cout<<“ОТДАЛЕНЫ”<<endl; return 0;}
    else if (D==R1+R2)      {cout<<“СОПРИКАСАЮТСЯ”<<endl; return 1;}
    else if (abs(R1–R2)<D)  {cout<<“ПЕРЕСЕКАЮТСЯ”<<endl; return 2;}
    else if (abs(R1-R2)==D) {cout<<“СОПРИКАСАЮТСЯ”<<endl; return 1;}
   cout<<“ОДНА В ДРУГОЙ”<<endl;
  return 0;

}

/*ФУНКЦИЯ ВВОДА ПАРАМЕТРОВ ДЛЯ ОКРУЖНОСТЕЙ*/
void input(double &x1,double &y1,double &R1,double &x2,double &y2, double &R2)
{
//переписать способ ввода параметров не должно составлять труда
cout<<“ПАРАМЕТРЫ ПЕРВОЙ ОКРУЖНОСТИ : “; cin>>x1>>y1>>R1; cout<<“ПАРАМЕТРЫ ВТОРОЙ ОКРУЖНОСТИ: “;  cin>>x2>>y2>>R2;
}

void main()
{
 system(“CLS”);

  int gdriver=DETECT,gm;
  initgraph(&gdriver,&gm,“”); //Инициализация для работы с графикой
      double x1,y1,R1,x2,y2,R2; //Точки центра окружностей и длины их радиусов
      input(x1,y1,R1,x2,y2,R2); //Ввод параметров
//Выводим окружности на экран для визуальной наглядности
    circle(x1,y1,R1);
    circle(x2,y2,R2);

    cout<<Tochek(x1,y1,R1,x2,y2,R2)<<endl; //Выводим количество общих точек

   system(“PAUSE”);
   closegraph(); //Заканчиваем работу в графическом режиме
 return;
}
==================
 Мой порядок написания этой программы происходил так:
  Функция main и стандартные строки инициализации и завершения графики.
  Определение переменных, обозначающих точки и длины радиусов, определение внутри main
  Написание функции input (функция ввода параметров) , в которую в качестве параметров принимаются ссылки. Так как любой хороший программист будет рекомендовать использовать локальные переменные, то поэтому сделано так. (напомню желающим: использование ссылок помогает использовать локальные переменные аналогично глобальным, но только внутри своих функций)
  Написание функции возвращающей число точек.

Если пробовать воссоздать этот материал самостоятельно из теории, то это довольно легко, но кто-то может путаться во всех семи вариантах при проверке условий.

Published
August 19, 2012

Источник

Добавить комментарий