Как найти количество точек пересечения прямых

Как найти количество точек пересечения прямых

Инфоурок

›

Математика

›Презентации›Комбинаторная задача о числе точек пересечения прямых

Комбинаторная задача о числе точек пересечения прямых

Скачать материал

Комбинаторная задачао числе точек пересечения прямых

Скачать материал

  • Сейчас обучается 47 человек из 25 регионов

  • Сейчас обучается 24 человека из 17 регионов

  • Сейчас обучается 353 человека из 70 регионов

Описание презентации по отдельным слайдам:

  • Комбинаторная задачао числе точек пересечения прямых

    1 слайд

    Комбинаторная задача
    о числе точек пересечения прямых

  • Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А....

    2 слайд

    Известная комбинаторная задача
    1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика.
    – М.: МЦНМО, 2006.
    2) Смирнова И.М., Смирнов В.А.  Комбинаторные задачи по геометрии (Библиотечка “Первого сентября”. Математика. Вып. 5 (11)).
    – М.: Чистые пруды, 2006.

  • Задача о количестве точек пересечения n прямыхНа плоскости проведены n прямых...

    3 слайд

    Задача о количестве точек пересечения n прямых
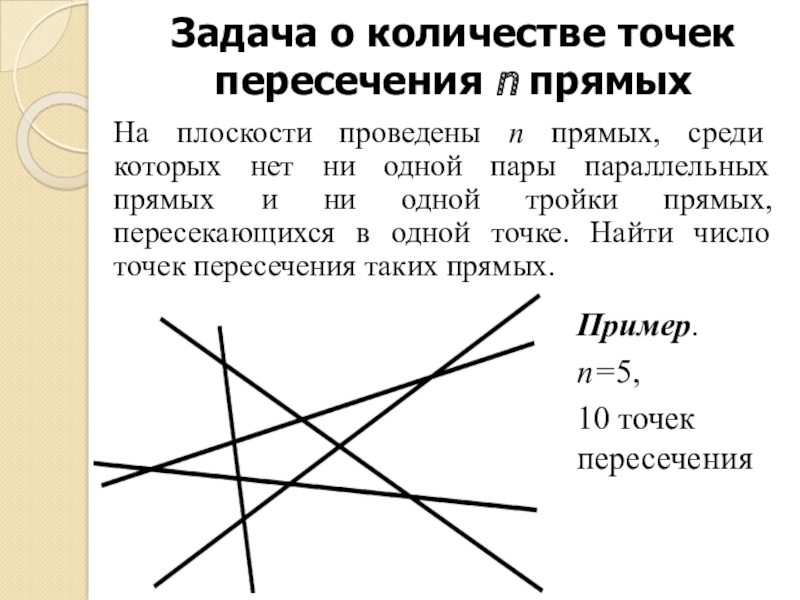
    На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых.

    Пример.
    n=5,
    10 точек пересечения

  • Цели работы 1) обобщить одну из известных комбинаторных задач по геометрии и...

    4 слайд

    Цели работы
    1) обобщить одну из известных комбинаторных задач по геометрии и получить полное решение новых задач;
    2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.

  • Задача 1. Наличие параллельных прямых На плоскости провели n прямых, среди ко...

    5 слайд

    Задача 1. Наличие параллельных прямых
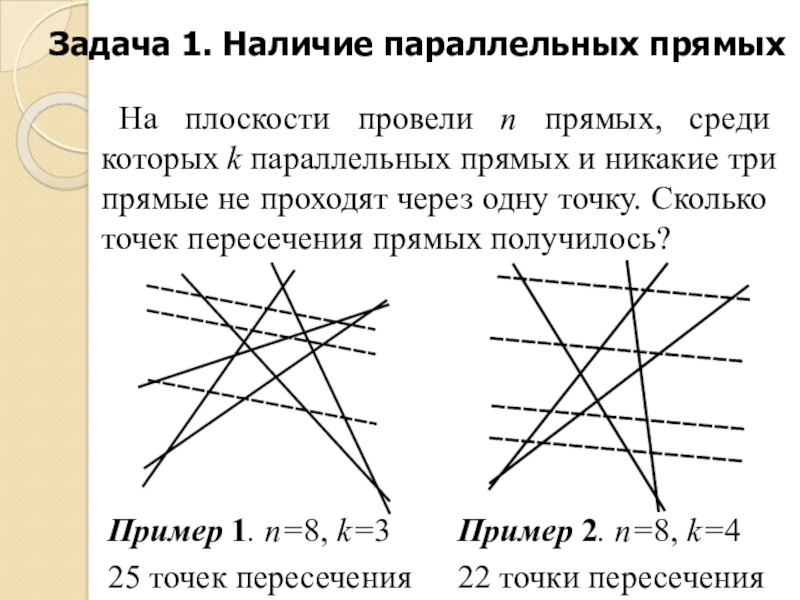
    На плоскости провели n прямых, среди которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?
    Пример 1. n=8, k=3
    25 точек пересечения
    Пример 2. n=8, k=4
    22 точки пересечения

  • О методе рекуррентных соотношений Метод сведения комбинаторной задачи к анало...

    6 слайд

    О методе рекуррентных соотношений
    Метод сведения комбинаторной задачи к аналогичной задаче для меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений.
    Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д.
    Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.

  • Решение задачи №11) Наглядное нахождение закономерностей 2) Нахождение формул...

    7 слайд

    Решение задачи №1
    1) Наглядное нахождение закономерностей
    2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

  • Нахождение числа точек пересечения

    8 слайд

    Нахождение числа точек пересечения

  • Таблица и рекуррентные соотношения

    9 слайд

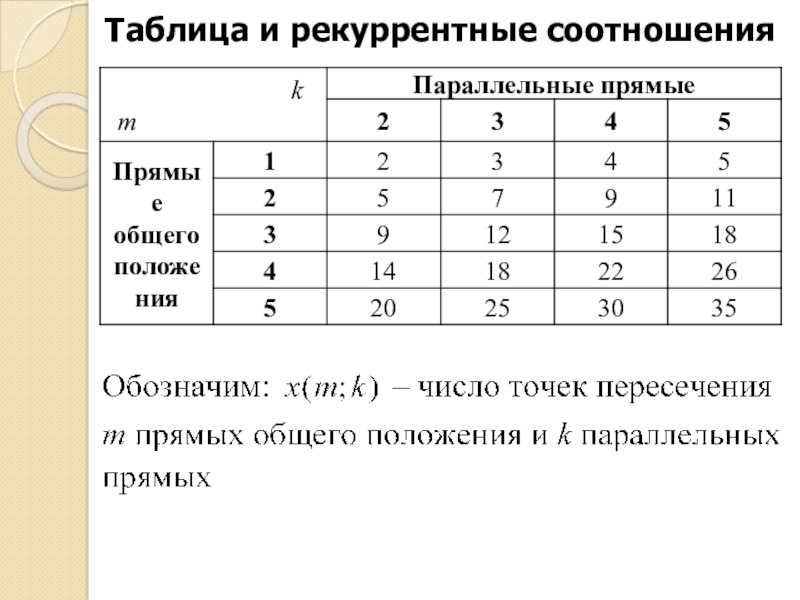
    Таблица и рекуррентные соотношения

  • Рекуррентные соотношения

    10 слайд

    Рекуррентные соотношения

  • Нахождение формулы

    11 слайд

    Нахождение формулы

  • Задача 2. Наличие пар параллельных прямыхНа плоскости провели n прямых, среди...

    12 слайд

    Задача 2. Наличие пар параллельных прямых
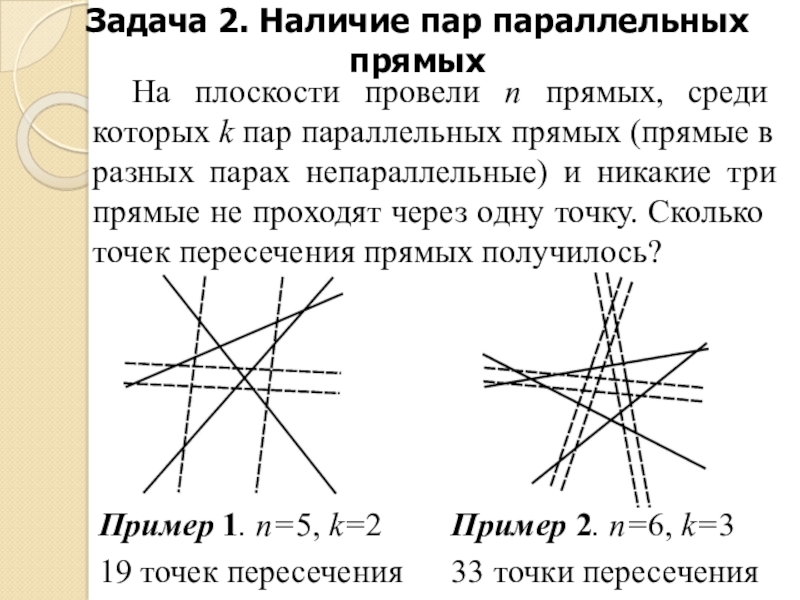
    На плоскости провели n прямых, среди которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?
    Пример 1. n=5, k=2
    19 точек пересечения
    Пример 2. n=6, k=3
    33 точки пересечения

  • Решение задачи №21) Наглядное нахождение закономерностей 2) Нахождение формул...

    13 слайд

    Решение задачи №2
    1) Наглядное нахождение закономерностей
    2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

  • Нахождение числа точек пересечения

    14 слайд

    Нахождение числа точек пересечения

  • Таблица и рекуррентные соотношения

    15 слайд

    Таблица и рекуррентные соотношения

  • Рекуррентные соотношения

    16 слайд

    Рекуррентные соотношения

  • Нахождение формулы

    17 слайд

    Нахождение формулы

  • Выводы

  • Выводы

  • СПАСИБО ЗА ВНИМАНИЕ!

    20 слайд

    СПАСИБО ЗА ВНИМАНИЕ!

Краткое описание документа:

Именно учебная деятельность как универсальный способ учения определяет особую деятельностную образовательную технологию: переход от «ситуации успеха» к «ситуации разрыва» через рефлексивную оценку (постановку учебной задачи); моделирование и конструирование (этап решения учебной задачи); продвижение от диагностической работы на «входе» через коррекцию к диагностической работе на «выходе» (этап решения частных задач); проверочная работа как переход от одной учебной задачи к другой (констатирующая оценка); перенос способов действий и средств в квазиреальные ситуации (этап решения проектных задач).

Основной принцип построения деятельностной технологии — цикличность (ритмичность) разворачивания образовательного процесса, в котором выделяются три цикла: пятилетний, годовой и тематический.

В рамках реализации деятельностной технологии необходимо особое внимание уделять контрольно-оценочной деятельности. Целесообразно развести контроль и оценку как учебные действия младших школьников и контроль и оценку как педагогические действия.

При деятельностной технологии педагогом создаются разные образовательные пространства:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 260 832 материала в базе

  • Выберите категорию:

  • Выберите учебник и тему

  • Выберите класс:

  • Тип материала:

    • Все материалы

    • Статьи

    • Научные работы

    • Видеоуроки

    • Презентации

    • Конспекты

    • Тесты

    • Рабочие программы

    • Другие методич. материалы

Найти материалы

Материал подходит для УМК

  • «Математика», Виленкин Н.Я., Жохов В.И. и др.

Другие материалы

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

Реферат “Мне не нужен калькулятор”

  • Учебник: «Математика», Виленкин Н.Я., Жохов В.И. и др.
  • Тема: 11. Умножение натуральных чисел и его свойства

Рейтинг:
5 из 5

  • 26.03.2018
  • 885
  • 3

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

«Математика», Виленкин Н.Я., Жохов В.И. и др.

Вам будут интересны эти курсы:

  • Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

  • Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

  • Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

  • Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

  • Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

  • Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

  • Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

  • Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

  • Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

  • Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

  • Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

  • Скачать материал


    • 22.04.2018


      14620
    • PPTX
      2.1 мбайт
    • 139
      скачиваний
    • Рейтинг:
      5 из 5
    • Оцените материал:





  • Настоящий материал опубликован пользователем Тележинская Елена Леонидовна. Инфоурок является
    информационным посредником и предоставляет пользователям возможность размещать на сайте
    методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
    сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
    сайта, Вы можете оставить жалобу на материал.

    Удалить материал

  • Тележинская Елена Леонидовна

    • На сайте: 6 лет и 3 месяца
    • Подписчики: 177
    • Всего просмотров: 6644322
    • Всего материалов:

      4416

Источник
  • Главная
  • Разное
  • Образование
  • Спорт
  • Естествознание
  • Природоведение
  • Религиоведение
  • Французский язык
  • Черчение
  • Английский язык
  • Астрономия
  • Алгебра
  • Биология
  • География
  • Геометрия
  • Детские презентации
  • Информатика
  • История
  • Литература
  • Математика
  • Музыка
  • МХК
  • Немецкий язык
  • ОБЖ
  • Обществознание
  • Окружающий мир
  • Педагогика
  • Русский язык
  • Технология
  • Физика
  • Философия
  • Химия
  • Шаблоны, фоны, картинки для презентаций
  • Экология
  • Экономика

Презентация, доклад на тему Комбинаторная задача о числе точек пересечения прямых

Содержание

  • 1.

    Комбинаторная задача о числе точек пересечения прямых

  • 2.

    Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н.,

  • 3.

    Задача о количестве точек пересечения n прямыхНа

  • 4.

    Цели работы 1) обобщить одну из

  • 5.

    Задача 1. Наличие параллельных прямых На плоскости

  • 6.

    О методе рекуррентных соотношений Метод сведения комбинаторной задачи

  • 7.

    Решение задачи №11) Наглядное нахождение закономерностей2) Нахождение

  • 8.

    Нахождение числа точек пересечения

  • 9.

    Таблица и рекуррентные соотношения

  • 10.

    Рекуррентные соотношения

  • 11.

    Нахождение формулы

  • 12.

    Задача 2. Наличие пар параллельных прямыхНа плоскости

  • 13.

    Решение задачи №21) Наглядное нахождение закономерностей2) Нахождение

  • 14.

    Нахождение числа точек пересечения

  • 15.

    Таблица и рекуррентные соотношения

  • 16.

    Рекуррентные соотношения

  • 17.

    Нахождение формулы

  • 18.

    Выводы

  • 19.

    Выводы

  • 20.

    СПАСИБО ЗА ВНИМАНИЕ!

Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006.2) Смирнова И.М., Смирнов В.А.  Комбинаторные задачи по геометрии (Библиотечка “Первого сентября”. Математика. Вып. 5 (11)).– М.: Чистые пруды, 2006.

Слайд 1Комбинаторная задача
о числе точек пересечения прямых

Комбинаторная задача о числе точек пересечения прямых

Слайд 2Известная комбинаторная задача
1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика.
–

М.: МЦНМО, 2006.
2) Смирнова И.М., Смирнов В.А.  Комбинаторные задачи по геометрии (Библиотечка “Первого сентября”. Математика. Вып. 5 (11)).
– М.: Чистые пруды, 2006.

Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006.2) Смирнова И.М., Смирнов

Слайд 3Задача о количестве точек пересечения n прямых
На плоскости проведены n прямых,

среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых.

Пример.
n=5,
10 точек пересечения

Задача о количестве точек пересечения n прямыхНа плоскости проведены n прямых, среди которых нет ни одной пары

Слайд 4 Цели работы
1) обобщить одну из известных комбинаторных задач по

геометрии и получить полное решение новых задач;
2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.

Цели работы 1) обобщить одну из известных комбинаторных задач по геометрии и получить полное решение новых

Слайд 5Задача 1. Наличие параллельных прямых
На плоскости провели n прямых, среди

которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?

Пример 1. n=8, k=3
25 точек пересечения

Пример 2. n=8, k=4
22 точки пересечения

Задача 1. Наличие параллельных прямых На плоскости провели n прямых, среди которых k параллельных прямых и никакие

Слайд 6О методе рекуррентных соотношений
Метод сведения комбинаторной задачи к аналогичной задаче для

меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений.
Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д.
Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.

О методе рекуррентных соотношений Метод сведения комбинаторной задачи к аналогичной задаче для меньшего числа предметов с помощью некоторого

Слайд 7Решение задачи №1
1) Наглядное нахождение закономерностей
2) Нахождение формулы, позволяющей найти количество

точек пересечения по любым значениям n и k

Решение задачи №11) Наглядное нахождение закономерностей2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n

Слайд 8Нахождение числа точек пересечения

Нахождение числа точек пересечения

Слайд 9Таблица и рекуррентные соотношения

Таблица и рекуррентные соотношения

Слайд 12Задача 2. Наличие пар параллельных прямых
На плоскости провели n прямых, среди

которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?

Пример 1. n=5, k=2
19 точек пересечения

Пример 2. n=6, k=3
33 точки пересечения

Задача 2. Наличие пар параллельных прямыхНа плоскости провели n прямых, среди которых k пар параллельных прямых (прямые

Слайд 13Решение задачи №2
1) Наглядное нахождение закономерностей
2) Нахождение формулы, позволяющей найти количество

точек пересечения по любым значениям n и k

Решение задачи №21) Наглядное нахождение закономерностей2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n

Слайд 14Нахождение числа точек пересечения

Нахождение числа точек пересечения

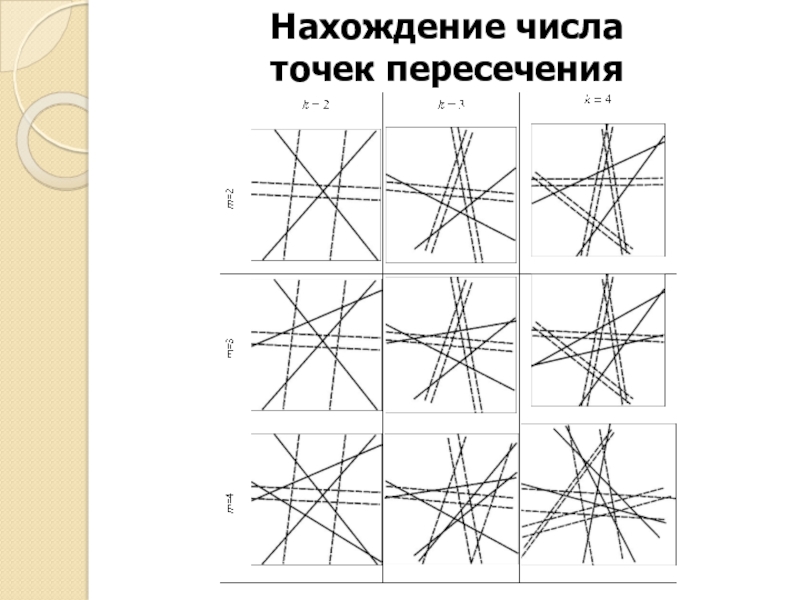
Слайд 15Таблица и рекуррентные соотношения

Таблица и рекуррентные соотношения

Источник

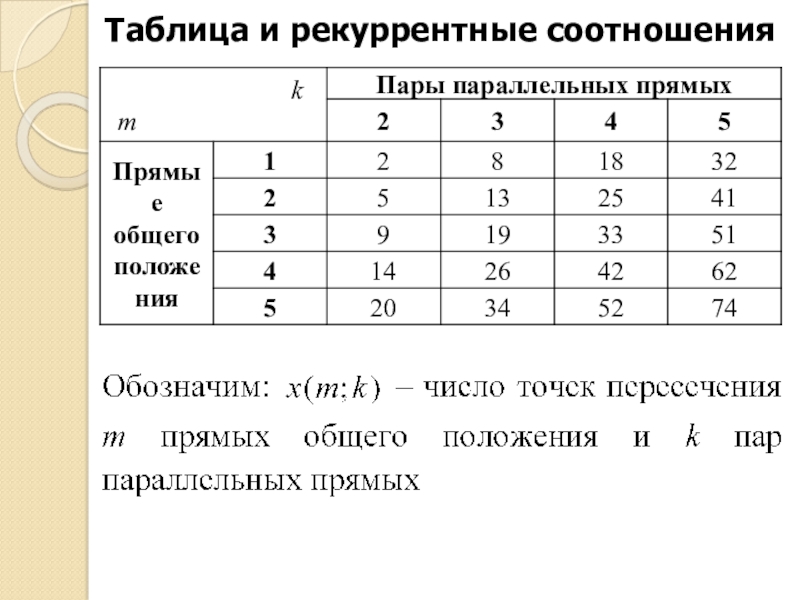
Решим следующим образом.

Посчитаем общее количество точек пересечения, если бы прямы пересекались в каждой уникальной точке.

1-я прямая пересекается с 19-ю (19 точек)

2-я прямая пересекается с 18-ю (+ еще 18 точек)

и т.д.

19-я прямая пересекается с 1-й (+ 1 точка)

20-я прямая – больше не с чем не пересекается

Итого точек пересечения 1 + 2 + … + 19 (Сумма арифметической прогрессии из 19 элементов с разностью 1 от 1 до 19): S = (1+19)/2 • 19 = 190

Итого было бы 190 точек.

Теперь аналогично считаем количество пересечений у 6 прямых: S = (1+5)/2 • 5 = 15

Должно было быть 15 точек, но вместо этого 1 точка A

Теперь аналогично считаем количество пересечений у 5 прямых: S = (1+4)/2 • 4 = 10

Должно было быть 10 точек, но вместо этого 1 точка B

Теперь аналогично считаем количество пересечений у 4 прямых: S = (1+3)/2 • 3 = 6

Должно было быть 6 точек, но вместо этого 1 точка C

Таким образом всего пересечений при таких условиях будет: 190 – 15 + 1 – 10 + 1 – 6 + 1 = 190 – 14 – 9 – 5 = 190 – 28 = 162

Ответ: 162

П.С. Условие в очередной раз безобразное.

Прямые в любом случае пересекаются по две. Имелось ввиду, что через остальные точки пересечения проходят только 2 прямые. Но звучит фраза безграмотно.

Равно как и далее:

У этих – это у каких? Такое предложение уместно, когда описывается однозначно один случай. Тут же идет описание сначала про 20 прямых, потом про 6, про 5, про 4, про оставшиеся. И так писать вопрос тоже безграмотно

Источник

Тема: Признак пересечения прямых?  (Прочитано 5115 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Если задано 5 прямых коэффициентами их уравнений: Ax+By+C=0, то каким образом определить сколько точек пересечения имеют эти прямые? Каков признак пересечения?

Признак пересечения двух прямых один – у них одна общая точка. К стати при пересечении с другими прямыми тоже…

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.

Это понятно, что у них одна общая точка… Я хочу узнать, что происходит с коэффициентами, когда прямые пересекаются? Ну скажем, если A1/A2=B1/B2, то прямые параллельны… А когда они пересекаются? Ну что-то кроме A1/A2<>B1/B2

ну если прямые не параллельны, то они пересекаются.

Если задано N (N>2) прямых, то при проверке такого условия каждой прямой (с исключением проверенных), то количество точек пересечения между ними, найденное таким способом, не соответствует количеству точек пересечений при использовании графического способа

Источник

“Великий” математик в треде и сейчас будет учить геометрии за 8-й класс школы.

Цитата
Сообщение от unveez
Посмотреть сообщение

Подсчитать количество точек пересечений этих прямых

Прямые на плоскости не пересекаются только если они параллельные.

Цитата
Сообщение от unveez
Посмотреть сообщение

определить номер прямой, имеющий минимальное количество точек пересечения

Если на плоскости нет взаимно параллельных прямых, то они пересекаются друг с другом равное колчесво раз. И количество таких пересечений = https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{{n}^{2}-n}{2}, где n – колличество прямых.
Если же есть, то меньше всего пересечений будет у тех прямых, которые взаимно параллельны. И опять же их будет несколько, а не одна.
Чтобы вообще было возможно существование такой прямой, которая имеет наименьшее количество пересечений с другими на плоскости, нужно ввести ограничение, например “плоскость ограничена квадратом со стороной = a”.

Добавлено через 3 минуты
Да, это полностью верно для евклидовой геометрии. Но даже так если нужно было использовать геометрию Лобачевского, например, об этом нужно заранее говорить.

Добавлено через 2 часа 28 минут

C 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

#include <stdio.h>
#include <stdlib.h>
 
typedef struct line{
    int angle;
    int pos;
} line;
 
void swap(line* ptr, int pos1, int pos2){
    line tmp = ptr[pos1];
    ptr[pos1] = ptr[pos2];
    ptr[pos2] = tmp;
}
 
#define N 5
 
int main(){
    line lines[N];
    // put input for lines.
    
    int sec = 0;
 
    int i = N;
    while(--i){
        int j = i;
        int parallel = 1;
        while(j--){
            if(lines[i].angle == lines[j].angle){
                ++parallel;
                swap(lines, j, i-1);
                --i;
            }
        }
        sec += parallel * i;
    }
    
    printf("There is %d intersectionsn", sec);
    
    int maxParallel = 0, currentParallel = 0, maxPos = N-1;
 
    i = N-1;
    while(i--){
        if(lines[i+1].angle == lines[i].angle) ++currentParallel;
        else{
            if(maxParallel < currentParallel){
                maxParallel = currentParallel;
                maxPos = i+1;
            }
            currentParallel = 0;
        }
    }
    
    printf("min intersections count founded for lines of y = %d*x + B groupn", lines[maxPos].angle);
}
Источник

Добавить комментарий