Функция
является непрерывной в некоторой точке
,
если выполняются следующие условия:
Т.е.
предел функции
при стремлении
(слева), равен пределу функции при стремлении
(справа) и равен значению функции в точке
.
Если хотя бы одно из условий нарушается, тогда говорят, что функция
имеет разрыв в точке
.
Все
точки разрыва функции
делят на точки разрыва первого рода и точки разрыва второго рода.
Eсли существуют конечные односторонние пределы
и
, тогда точка
называется точкой разрыва
первого рода.
Точки разрыва первого рода в свою очередь подразделяются на точки устранимого разрыва и скачки.
Если
– является точкой разрыва первого рода и при этом
, точка
называется точкой
устранимого разрыва.
График соответствующей функции приведён на рисунке ниже:
Eсли же
, тогда в точке
.
происходит скачок функции
Величина скачка определяется по формуле
. Соответствующий график приведён на рисунке:
Если хотя бы один из пределов
или
равен
, точка
называется точкой разрыва
второго рода. Пример соответствующего графика функции представлен на рисунке ниже:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha вычисляет точки разрыва заданной функции с описанием подробного хода решения.
Точки разрыва функции
Назначение
Сервис предназначен для определения типа точек разрыва функции.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение сохраняется в формате MS Word
Классификация точек разрыва
Для точек разрыва принята следующая классификация.
Если в точке имеются конечные пределы, но они не равны
f(x0+0)≠f(x0-0), то x0 называется точкой разрыва первого рода, при этом разрыв называют скачком функции.Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
Точка x=x0 называется точкой устранимого разрыва, если
f(x0+0)=f(x0-0)≠f(x0). Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) функцию и функция станет непрерывной в точке x0.
см. также Непрерывность функции: основные понятия и свойства (разрывы функции и их классификации с подробными примерами).
Пример №1. Установить непрерывность или определить характер точек разрыва. Нарисовать график функции f(x) в окрестностях этих точек:
Решение. Найдем точки разрыва функции внутри указанной области.
Находим переделы в точке x=1.
В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.
Находим переделы в точке x=0
В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.
Ответ: точка x1=1 является точкой разрыва II-го рода, точка x2=0 является точкой разрыва I-го рода.
Пример №2. Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение. Исследуем точку стыка промежутков x=π/2
В этой точке пределы существуют и они равны, поэтому функция в этой точке непрерывна.
Исследуем поведение функции на отрезке (π/2;π).
Пределы существуют, на указанном промежутке функция непрерывна.
Исследуем точку стыка промежутков x=π
В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода.
Исследуем поведение функции на отрезке (pi;∞).
Пределы существуют, на указанном промежутке функция непрерывна.
Ответ: Точка x=π является точкой разрыва I-го рода.
Пример №3. Найти точки разрыва функции и определить их тип.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Данный калькулятор предназначен для нахождения точек разрыва функции онлайн.
Точки разрыва функции – это точки, в которых функция имеет разрыв, при этом функция в этих точках не является непрерывной.
Существует определенная классификация точек разрыва функции. Точки разрыва функции (нули знаменателя) делятся на точки разрыва первого рода и точки разрыва второго рода.
Точки разрыва первого рода при x=a имеют место быть, если существуют левосторонний и правосторонний пределы: lim(x→a-0)f(x) и lim(x→a+0)f(x). Эти пределы должны быть конечны. Если хотя бы один из односторонних пределов равен нулю или бесконечности, то в таком случае функция имеет точки разрыва второго рода.
Для того чтобы найти точки разрыва функции онлайн, необходимо указать функцию и значение аргумента.
Для получения полного хода решения нажимаем в ответе Step-by-step.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
прерывистый:frac{x^{2}+3x-4}{x^{2}+x-12}
-
прерывистый:frac{4x^{2}-36x}{x-9}
-
прерывистый:left|3-frac{3x^{2}}{49}right|
-
прерывистый:frac{left|xright|}{x},x=0
- Показать больше
Описание
Найдите пошагово, является ли функция разрывной
function-discontinuity-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Классификация точек разрыва функцииВсе точки разрыва функции разделяются на точки разрыва первого и второго рода. 1) Функция f (x) имеет точку разрыва первого рода при x=a, если в этой точке 2) Функция f (x) имеет точку разрыва второго рода при x=a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. Калькулятор для исследования точек разрыва функции.
|
Категория: Исследовать функцию,построить график | Просмотров: 73228 | | Теги: построить график, экстремумы функции, исследовать функциию | Рейтинг: 4.5/4 |
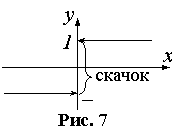 Если в точке имеются конечные пределы, но они не равны
Если в точке имеются конечные пределы, но они не равны 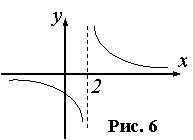 Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.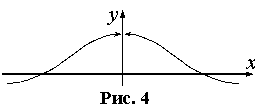 Точка x=x0 называется точкой устранимого разрыва, если
Точка x=x0 называется точкой устранимого разрыва, если 


