Привет! Сегодня разберём новый тип 6 задания из ЕГЭ по информатике 2023! Добавим недостающий пазл в видеокурс по подготовке к ЕГЭ по информатике.
Так же Вы можете посмотреть разбор 6 задания из ДЕМОВЕРСИИ 2023.
На мой взгляд, на экзамене скорее всего будет задача, похожая именно на демонстрационный вариант. Т.к. это задание нового образца, то выпускникам необходимо привыкнуть к нему.
Вспомним, когда в прошлом году была введена новая формулировка для 3 задания, то на экзамене дали очень похожую задачу на ту, которая была в демоверсии.
Рассмотрим первую тренировочную задачу из 6 задания ЕГЭ по информатике 2023.
Задача (Элегантный способ)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 15 [Вперёд 15 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Решение:
В начале нужно понять, какая фигура получится в результате действий Исполнителя Черепахи.
Черепаха идёт вверх на 15 единиц. Потом поворачивает направо на 120 градусов. Потом идёт на 15 единиц по заданному курсу и снова поворачивает на 120 градусов, идёт на 15 единиц ещё и попадает в исходную точку. В итоге получается равносторонний треугольник! Дальнейшие повторения не имеют смысла, т.к. нового больше ничего не нарисуется.
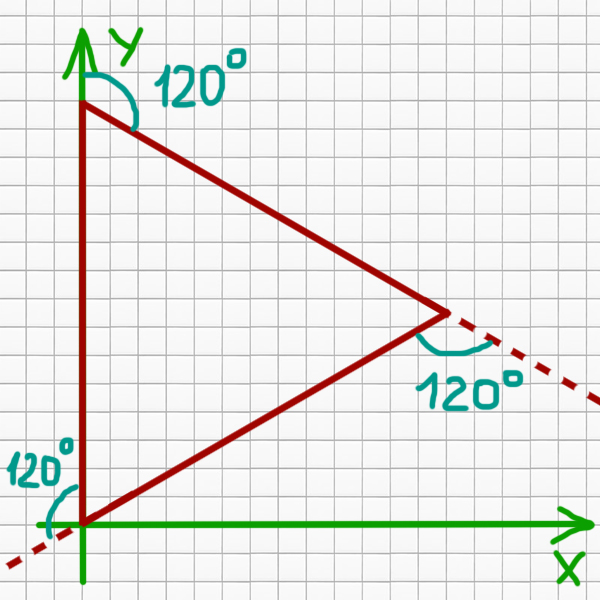
Проведём перпендикуляры от каждой точки с целыми координатами на оси Y внутри треугольника.
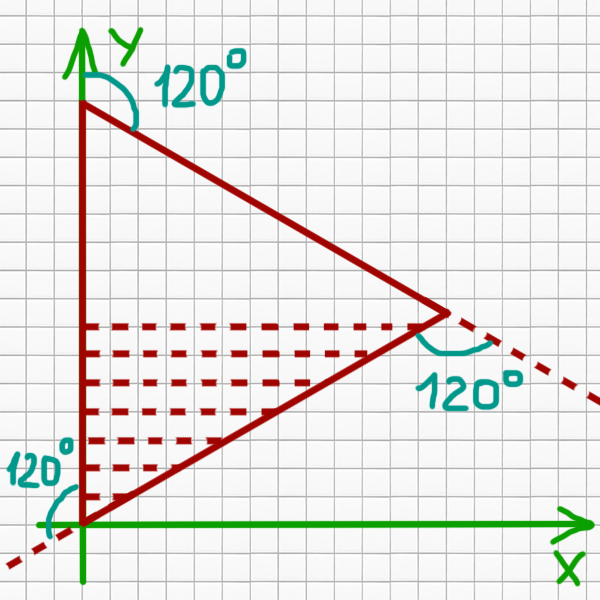
Для каждой точки на оси Y мы можем найти этот перпендикуляр. Это и есть искомое количество точек на каждой такой линии, если округлить это значение в меньшую сторону.
Посмотрим, как найти такой перпендикуляр, если точка на оси Y находится до середины стороны. Пусть есть точка (0, yn), а dn – это перпендикуляр для этой точки. Тогда
tg(60o) = dn / yn
dn = tg(60o) * yn
Для второй половины длины перпендикуляров будут такие же.
Напишем программу на Питоне, которая подсчитает все точки.
import math s=0 for y in range(0, 8): s = s + int(math.tan(math.pi / 3) * y ) s = 2*s print(s)
Нам необходимо взять первые 7 точек, дальше ситуация симметричная. Пишем в цикле for 8, потому что последнее число не проходится в Питоне.
Вычисляем по формуле длину каждого перпендикуляра. Тангенс вычисляется с помощью функции math.tan. Для неё нужна математическая библиотека math. Функция должна получить градусы в радианах, поэтому ей передаём π/3 = 60o.
В цикле суммируем все точки для каждой линии. Результат нужно умножить на 2, чтобы учесть вторую половину треугольника.
Ответ: 90
Задача(Считаем точки вручную)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 16 [Налево 36 Вперёд 4 Налево 36]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии следует учитывать.
Решение:
В это задачке достаточно не просто составить уравнения прямых полученной фигуры. В таких случаях можно попробовать вручную посчитать точки с помощью известной программы Кумир от НИИСИ РАН. Скачать её можно с официального сайта НИИСИ РАН.
Вероятно, это программа окажется на компьютере на экзамене.
Запустим программу Кумир-Стандарт. В начале нужно подключить модуль Черепаха.
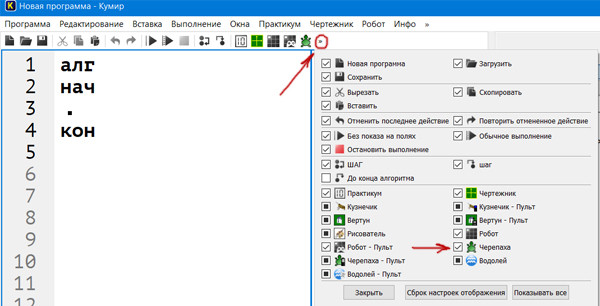
После того, как модуль Черепаха подключён, можно написать программу на языке Кумир.
использовать Черепаха
алг
нач
опустить хвост
нц 16 раз
влево(36)
вперед(4)
влево(36)
кц
кон
В начале нужно подключить модуль Черепаха. Слово алг обозначает начало алгоритма. Слово нач – это начало программы.
Опускаем хвост у Черепахи. Цикл пишем с помощью команды нц – начало цикла. Команда кц – это конец цикла. Команда влево – это аналог команды Налево (видим, что эти команды пишутся по-разному). Аналогично есть команда вправо в программе Кумир. Команда вперед пишется без буквы ё.
После того, как алгоритм перенесли в программу Кумир, запускаем программу, нажав на кнопку F9 (или кнопка плей в виде треугольника).
После этого появится окно в правом нижнем углу. Это окно можно расширить до приемлемых размеров, чтобы нам было удобно анализировать рисунок.
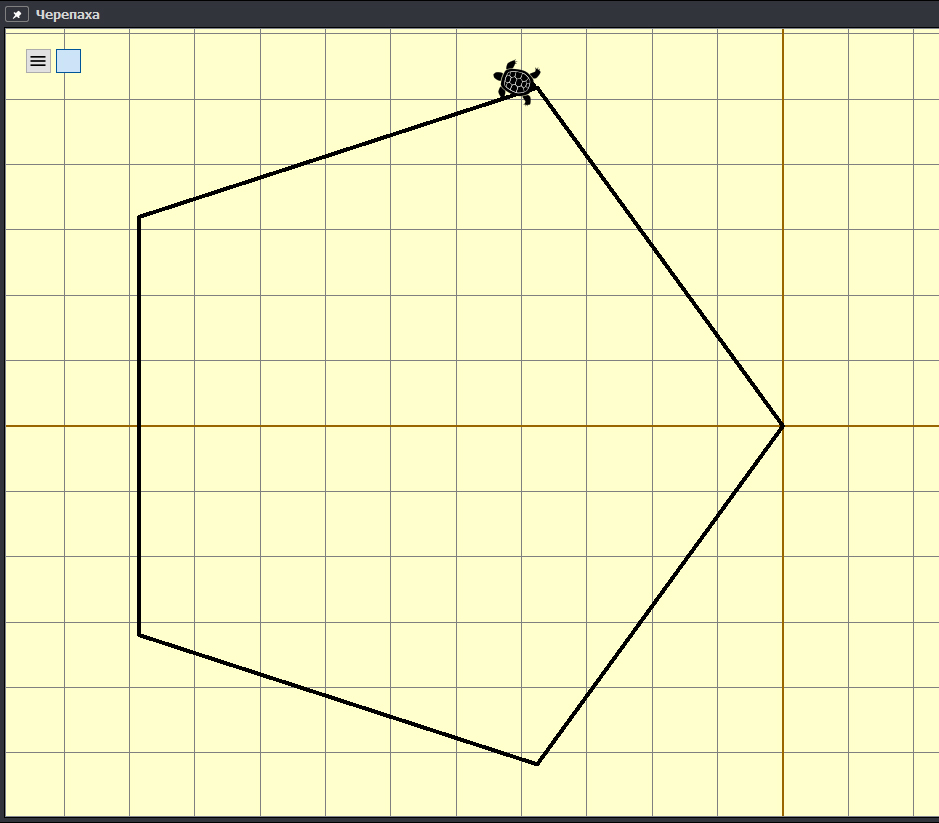
Необходимо настроить масштабирование на 1.
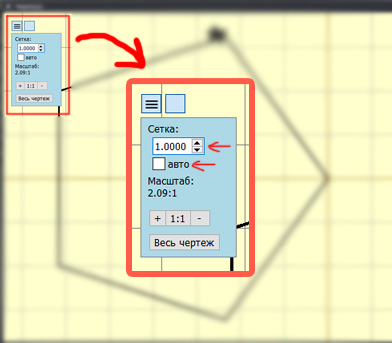
После этого можно сделать скриншот и перенести рисунок в программу Paint, где и посчитать точки вручную.
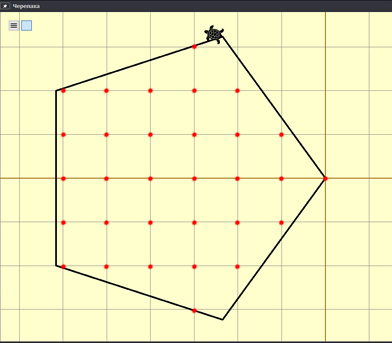
Получается в ответе 31 точка. Обратите внимание, что в этой задачи просили подсчитать точки, которые находятся на линиях в том числе.
Даже если нет программы Кумир, можно подсчитать точки вручную через Python. Напишем программу.
from turtle import * left(90) for i in range(16): left(36) forward(4*40) left(36) penup() for x in range(-10, 10): for y in range(-10, 10): setpos(x*40, y*40) dot(4, 'red')
Программа выведет такую картину.
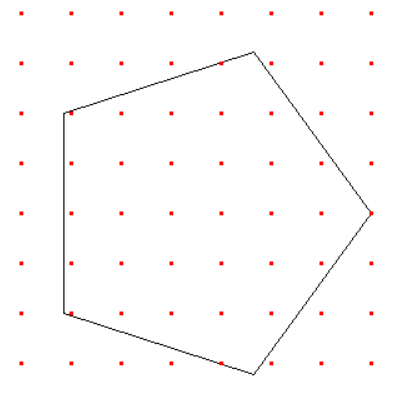
В программе подключаем модуль turtle. В начале повернём Черепаху на 90 градусов налево, с помощью команды left. Это делается из-за того, в Python Черепаха смотрит вдоль положительного направления оси абсцисс.
Далее идёт цикл, который указан в задаче. Он должен повторится 16 раз. Внутри цикла пишем программу для Черепахи. Команда left() – поворот налево (аналогично right() – поворот направо), команда forward() – это движение верёд.
4 единицы внутри команды forward() умножаются на 40. Число 40 – это коэффициент размера нашего рисунка. Попробуйте “поиграть” с этим числом, чтобы посмотреть эффект уменьшения или увеличения рисунка.
Команда penup() позволяет поднять кисть, чтобы проставить точки, которые будут символизировать точки с целыми координатами.
Далее идут вложенные циклы, с помощью них мы проставим точки с целыми координатами. Выбираем диапазон, чтобы наша фигура точно уместилась.
Команда setpos() ставим точки. Умножаем координаты x и y на тот же коэффициент, что использовали ранее.
Команда dot() устанавливает жирность и цвет точки.
Ответ: 31
Задача (Составляем уравнения)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост поднят. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.
Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Вперёд 100 Направо 90 Вперёд 100 Направо 30 Опусти Повтори 10 [Вперёд 25 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Решение:
Нарисуем общий рисунок.
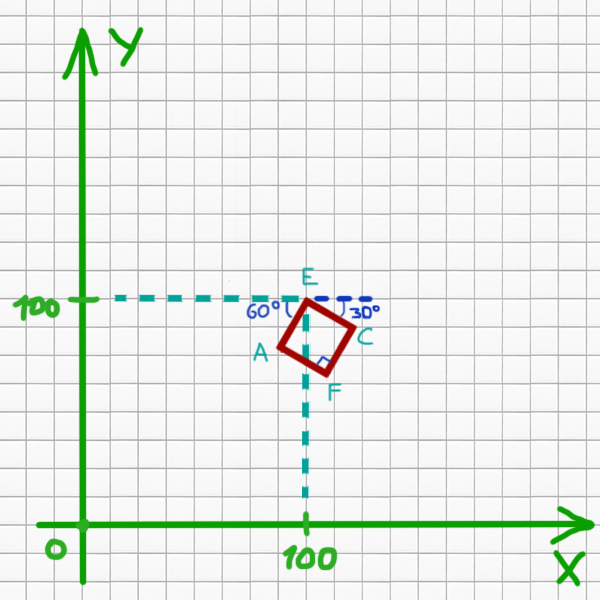
Здесь уже не очень удобно пользоваться элегантным способом. Составим уравнения прямых, которые образуют квадрат. Общий вид уравнения прямой выглядит так:
y=k*x+b
Коэффициент k – это тангенс угла наклона α к оси X ( 0 ≤ α < π, но α ≠ π/2). Число b – это смещение прямой по оси Y относительно нуля.
Для прямой AE k1=tan(60o)=√3. Так же она проходит через точку (100, 100).
Найдём число b. Подставим в общее уравнение координаты точки (100, 100):
y = k*x+b = √3*100 + b = 100
b=100*(1 – √3)
Получается уравнение прямой AE:
y= √3*x + 100(1 – √3)
Найдём на сколько смещена FC по оси Y относительно AE.
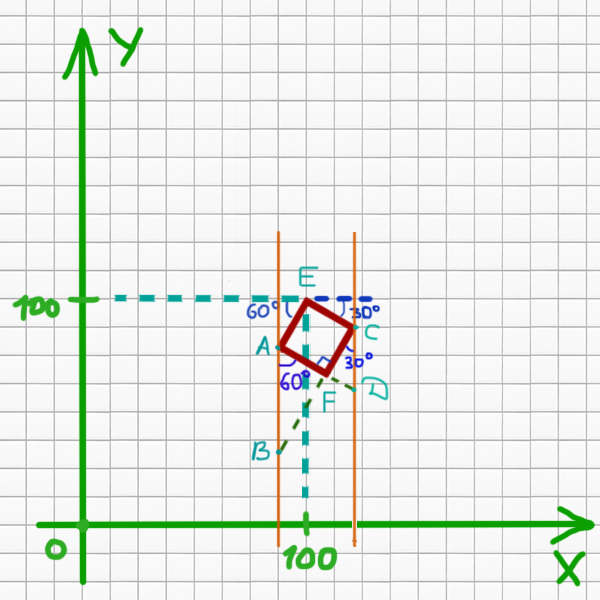
cos(60o) = 25 (сторона квадрата) / AB
AB = 25 / cos(60o) = 25 / 0,5 = 50
Получается, что уравнение для прямой FC:
y=√3*x + 100(1 – √3) – 50
Для прямой EC k2=-tan(30o) = – √3/3. Эта прямая тоже проходит через точку (100, 100). Подставим эти координаты в уравнение и найдём b.
y = (-√3/3) * x + b = (-√3/3) * 100 + b = 100
b = 100(1 + √3/3)
Тогда уравнение для прямой EC получается:
y = (-√3/3) * x + 100(1 + √3/3)
Найдём на сколько смещена прямая AF относительно EC по оси Y.
cos(30o) = 25 (длина стороны) / CD
CD = 25 / cos(30o) = 25 / (√3/2) = 50/√3
Тогда для прямой AF:
y = (- √3/3) * x + 100(1 + √3/3) – 50/√3
Пробежимся с помощью Питона для переменной x от 0 до 150. Для переменной y от 0 до 100. Чтобы получить точку, используем вложенные циклы!
s=0
for x in range(1, 200):
for y in range(1, 200):
if (y < (3**0.5)*x + 100*(1-3**0.5)) and (y > (3**0.5)*x + 100*(1-3**0.5) - 50) and (y < (- 3**0.5 / 3)*x + 100*(1+ 3**0.5 / 3)) and (y > (-3**0.5/3)*x + 100*(1 + 3**0.5 /3) - 50 / 3**0.5 ):
s=s+1
print(s)
Точки, которые лежат в квадрате должны удовлетворять следующим условиям:
Точки должны быть ниже прямых AE и EC, но выше AF и FC
Проверить выше или ниже некоторая точка M(xm, ym), чем прямая y=k*x+b, можно следующим образом:
Если ym > k*xm + b, то точка лежит выше прямой.
Если ym < k*xm + b, то точка лежит ниже прямой.
Данный принцип и был использован в программе.
Ответ: 625
Задача (Закрепление)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.
Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 21 [Вперёд 31 Направо 60]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Копирование прямо
Решение:
Попробуем понять, какая фигура получится в итоге.
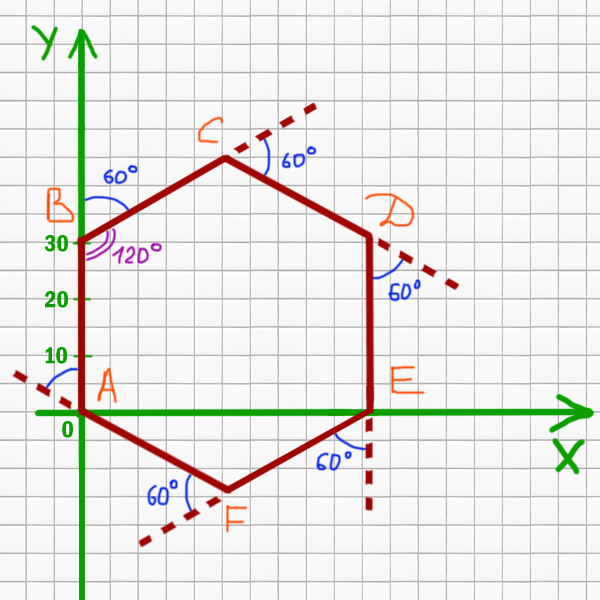
Получается правильный шестиугольник. Угол ∠СВА = 120o. Как раз угол правильного n-угольника равен (n-2)*180o/n. Для шестиугольника получается (6-2)*180o/6 = 120o.
Будем решать методом составления уравнений.
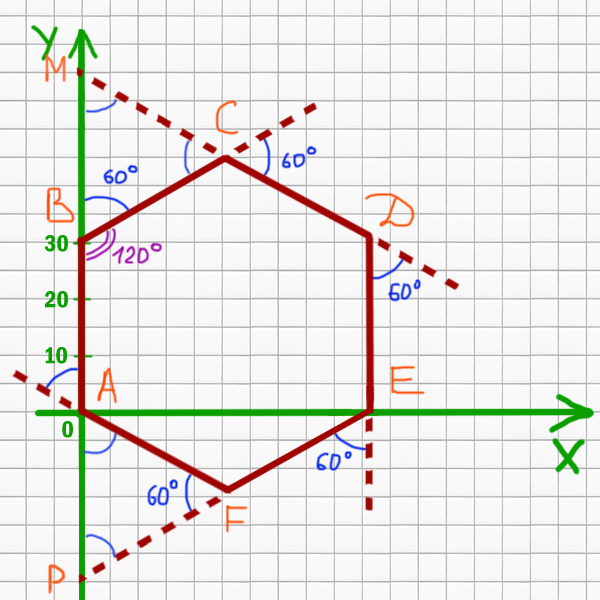
Рассмотрим прямую BC. Если провести от точки B прямую параллельную оси X, то мы увидим, что угол наклона прямой BC равен 30o.
y = tan(30o)*x + 31
y = (√3/3) * x + 31
Прямая DC имеет угол наклона -30o к оси X. Она расположена выше, чем BC на МВ. Треугольник BCM равносторонний. Значит, МВ=31. Тогда уравнение для DC будет:
y = -(√3/3) * x + 62
Уравнение для AF будет:
y = -(√3/3) * x
Прямая EF имеет угол наклона 30o относительно оси X. Смещена она вниз на AP. Треугольник AFP так же является равносторонним. Следовательно, AP = 31. Тогда для EF получается:
y=tan(30o)*x – 31
y=(√3/3)*x – 31
Прямая AB это x=0. Найдём так же ED.
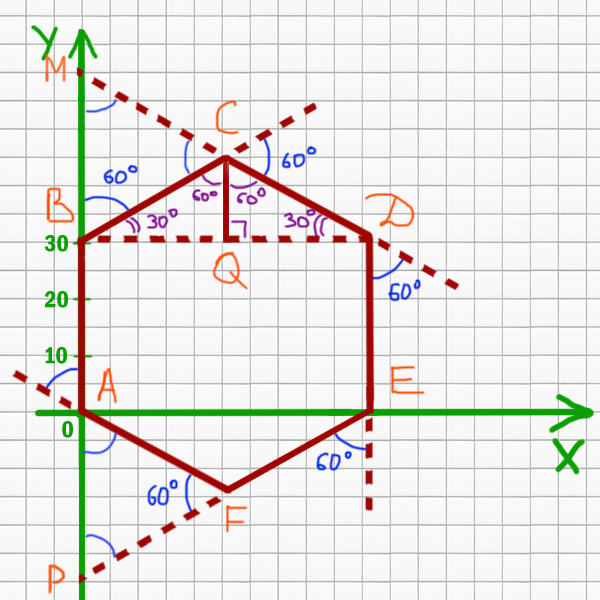
cos(30o) = BQ / BC
BQ = BC * cos(30o)
BQ = 31 * (√3/2)
BD = 2 * BQ = 2 * 31 * (√3/2) = 31 * √3
Значит, уравнение для ED: x = 31 * √3.
Когда уравнения готовы, можно написать программу.
k=0
for x in range(-100, 100):
for y in range(-100, 100):
if (y < 3**0.5 / 3 * x + 31) and (y < -(3**0.5) / 3 * x + 62) and (y > -(3**0.5) / 3 * x) and (y > 3**0.5 / 3 * x - 31) and (x > 0) and (x < 31 * 3**0.5):
k=k+1
print(k)
Точки должны быть ниже прямых BC и CD, но выше прямых AF и EF. Так же координаты x должны быть 0 < x < 31 * √3.
Важно не забыть для y пробежаться и по отрицательным значениям, т.к. фигура находится меньше оси X.
Ответ: 2476
На сегодня всё. Удачи при решение 6 задания из ЕГЭ по информатике 2023.
Зачем это делать? Авторы задания предполагают, что ученики просто воспользуются КуМир и все там получат.
В Кумире не удобно считать.
В данном задании ЕГЭ №6 по информатике можно применить своё воображение или творчество для нахождения расстояния между точками или посчитать количество точек, ограниченные контуром, на плоскости XY.
Само по себе задание представляет алгоритм движения “черепашки”. У неё существует определённое количество команд для движения и она способна оставлять за собой “след” при движении.
Среди команд есть следующие:
- Вперёд [количество шагов];
- Направо [поворот направо на заданный угол];
- Налево [поворот налево на заданный угол]
В самом задании ещё применяют цикл, который повторяет эти действия определённое количество раз. К примеру, Повтори 4 [Вперёд 10 Направо 90]. Данный алгоритм строит квадрат со стороной 10.
К счастью, не обязательно искать полотно с клеточками и аккуратно чертить линии, заданной длины и соблюдать заданный угол поворота. В Python была давным-давно добавлена библиотека, помогающая детям в изучении программирования.
Библиотека очень похожа на текущее задание и во многом способна помочь. Называется похоже на главного персонажа этой истории — turtle (что в переводе означает “черепаха”).
Сама по себе библиотека воспроизводит команды “черепашки” и визуализирует их. Команды, которые потребуются следующие:
- forward(Количество шагов) — движение вперёд на заданное количество шагов;
- backward(Количество шагов) — движение назад на заданное количество шагов;
- right(Угол) — поворот направо на заданный угол;
- left(Угол) — поворот налево на заданный угол;
- color(Цвет пера, Цвет заливки) — устанавливает цвет пера и заливки;
- goto(X, Y) — перемещается на точку с координатами X, Y;
- dot(Размер, Цвет) — рисует точку в текущей позиции;
- speed(Скорость) — устанавливает скорость перемещения главного героя (от 0 до 10);
- xcor() — возвращает текущую координату по X;
- ycor() — возвразает текущую координату по Y;
- up() — поднимает “перо” (другими словами, перестаёт оставлять за собой след);
- down() — опускает “перо” (другими словами, начинает оставлять за собой след);
- begin_fill() — начинает заливку контура;
- end_fill() — прекращает заливку контура;
- done() — завершает работу программы.
Теперь, когда с командами разобрались, можно приступить к практике. Разберём несколько заданий.
Задание №1
Задание:
Определите сколько точек с целочисленными координатами будут находиться в области после работы алгоритма: Повтори 10 [Вперёд 5 Направо 60].
Решение:
Напишем программу с использованием алгоритма из задания.
В программе сначала подключаем библиотеку turtle, затем устанавливаем необходимые параметры: коэффициент и скорость перемещения (можно установить 10 для получения более быстрого результата).
Коэффициент масштабируемости необходим для увеличения рисунка и более удобного счёта в дальнейшем (можете его убрать и посмотреть, что из этого получится). Запустим и посмотрим на результат работы программы.
Получился шестиугольник, осталось посчитать количество точек внутри данной фигуры. Как можно это сделать? Для этого воспользуемся командой, которая оставляет точки в текущей позиции. Допишем программу.
Для нанесения точек на координаты используем два цикла (один для X, второй для Y). Важным являются параметры в цикле. Здесь также происходит умножение параметров на коэффициент масштабируемости и есть ещё третий параметр — шаг цикла. Он добавляется как раз из-за коэффициента. Результат будет следующим.
Останется лишь посчитать количество точек внутри фигуры. Важным моментом при подсчёте является то, что точки на контуре фигуры не считаются. Остаётся аккуратно посчитать точки — 62. Существуют и способы автоматического подсчёта точек внутри фигуры (но они не всегда хорошо работают).
Задание №2
Задание:
Определите расстояние между начальной позицией и после работы алгоритма: Повтори 11 [Вперёд 36 Направо 72].
Решение:
Решение данной задачи может сводиться к расчётам в голове после некоторого анализа. Но можно и написать программу. Для начала перепишем алгоритм из задания.
Очень похоже на первое задание, но тут уже необходимо посчитать расстояние от начальной точки до позиции после остановки алгоритма. Для этого стоит записывать координаты и при помощи формулы нахождения расстояния между двумя точками найти расстояние. Добавим это в программу.
Особое внимание стоит уделить формуле нахождения расстояния, вот её математический вид:
Команда round округляет полученное значение.
В этом номере отсутствует коэффициент, т.к. он бы только испортил расчёт.
Понравилась статья? Хочешь разбираться в информатике, программировании и уметь работать в разных программах? Тогда ставь лайк, подпишись на канал и поделись статьей с друзьями! Остались или появились вопросы — спроси в комментариях!
Читайте также:
Круги Эйлера в информатике
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.
Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.
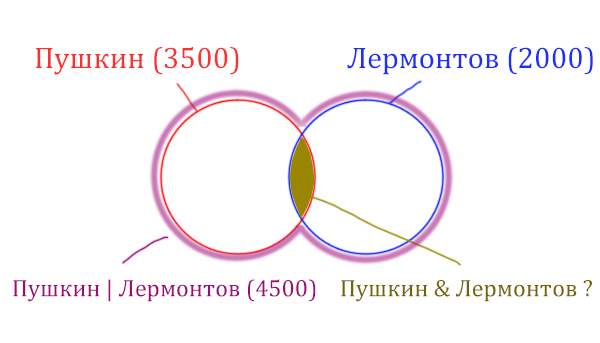
Объединение двух кругов в общую фигуру ( показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
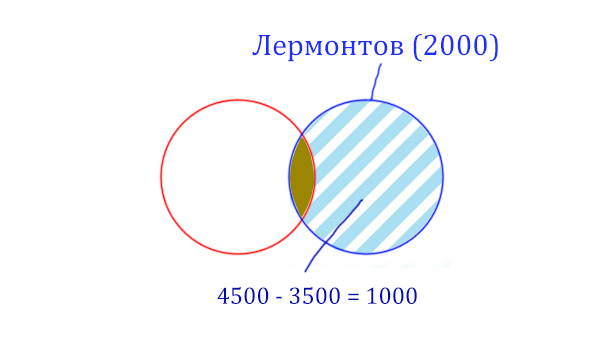
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Рассмотрим ещё одну не сложную разминочную задачу.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
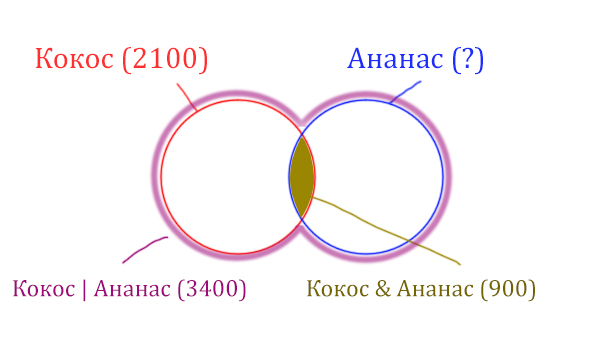
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.
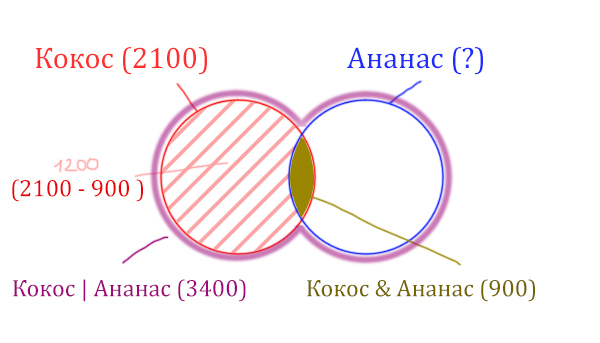
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.
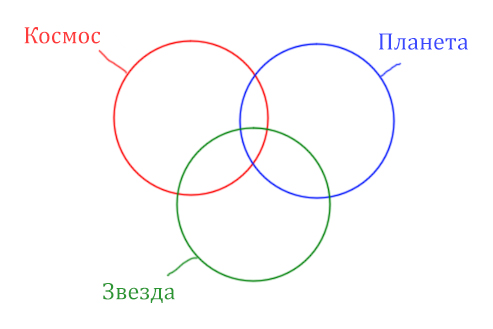
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
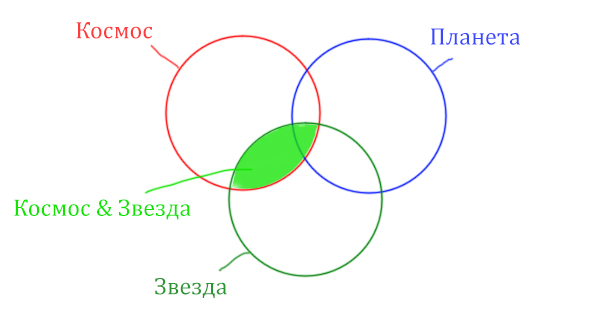
Теперь отметим вторую скобку Космос & Планета.
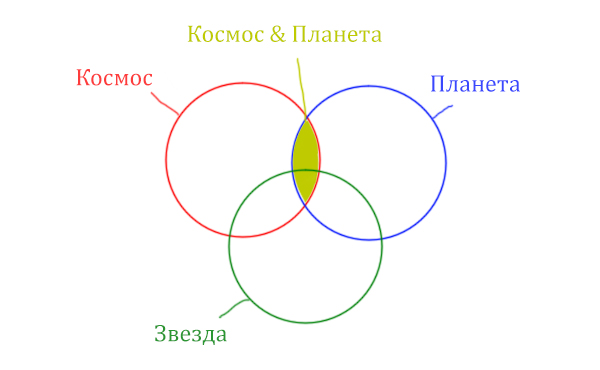
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
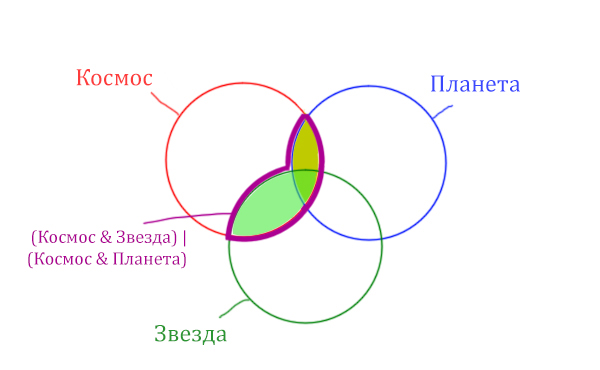
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
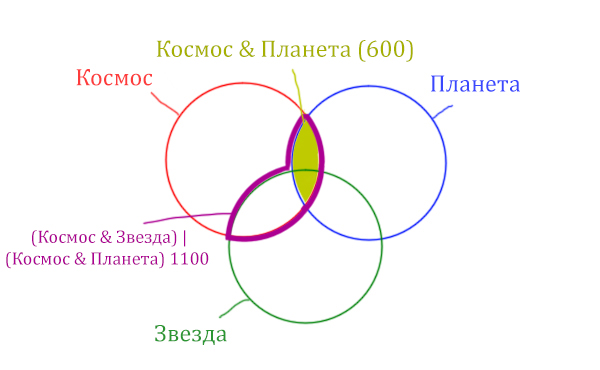
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
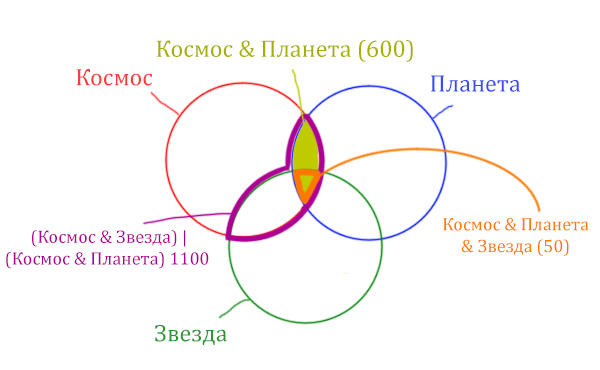
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
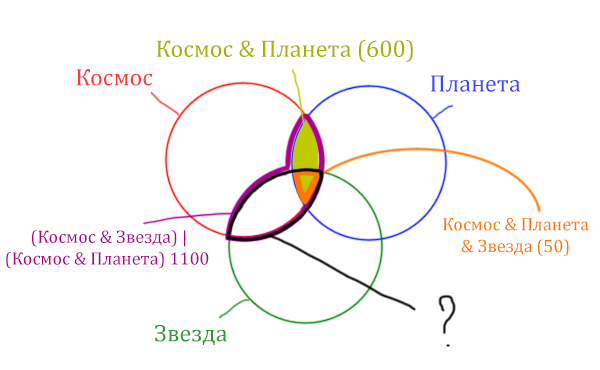
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
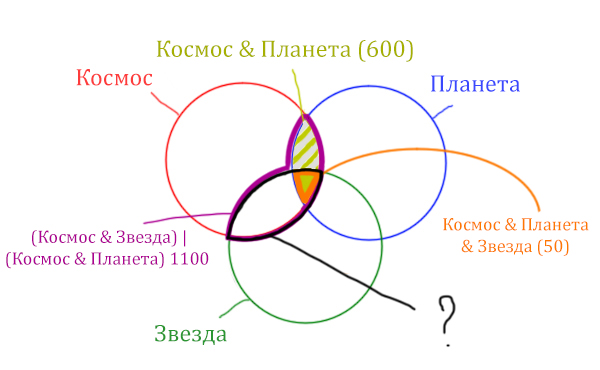
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
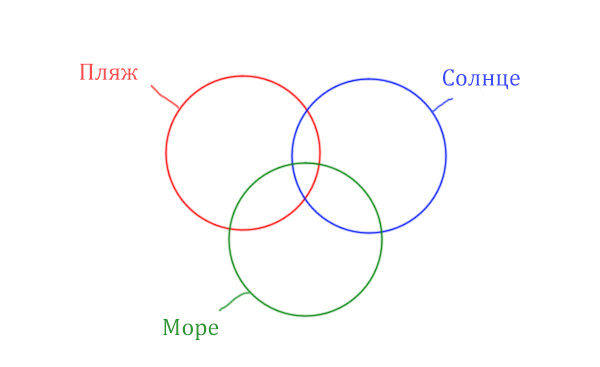
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце) 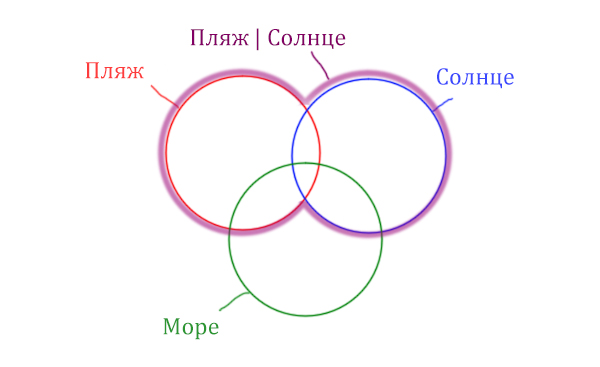
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
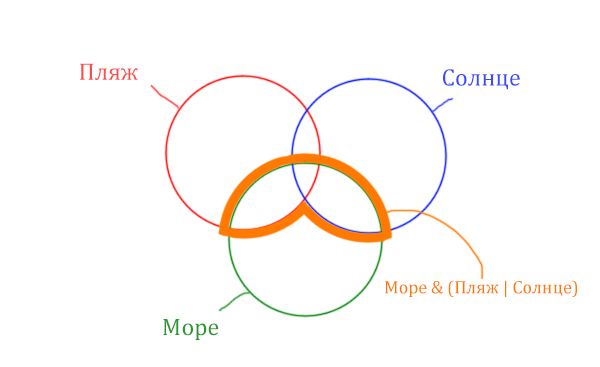
Теперь отметим Море & Пляж.
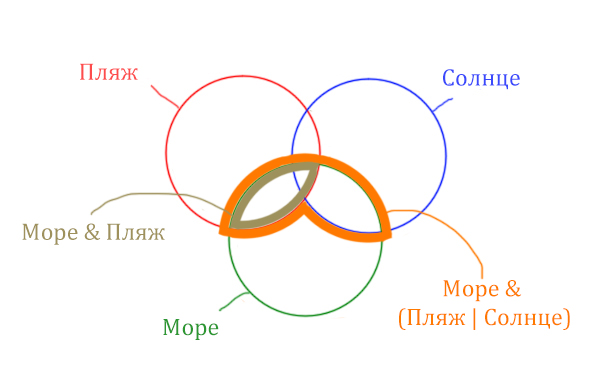
Теперь отметим Море & Солнце.
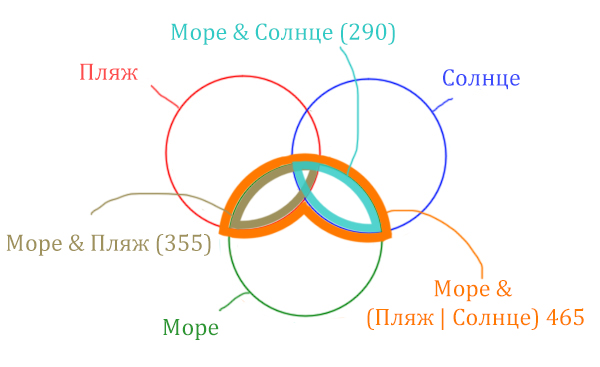
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
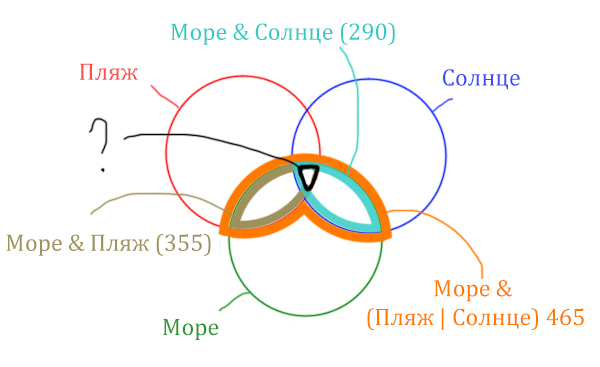
Найдём заштрихованную область!
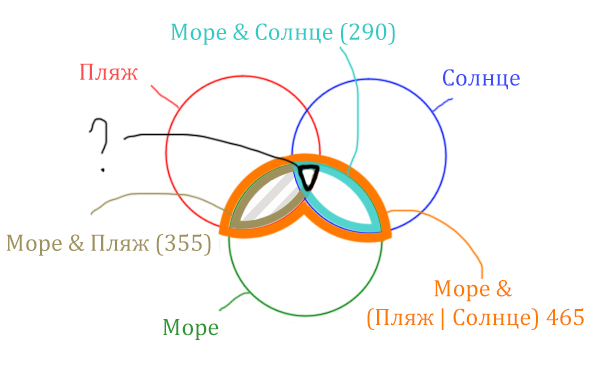
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
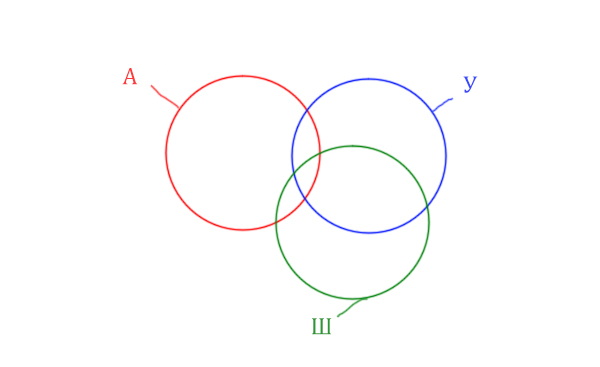
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
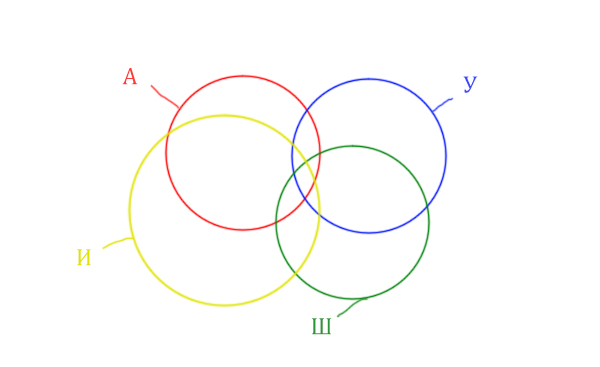
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
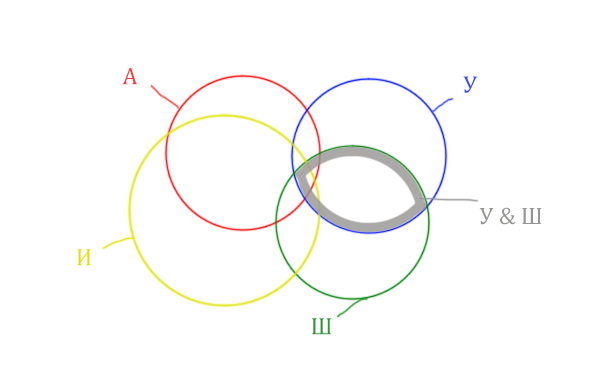
Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
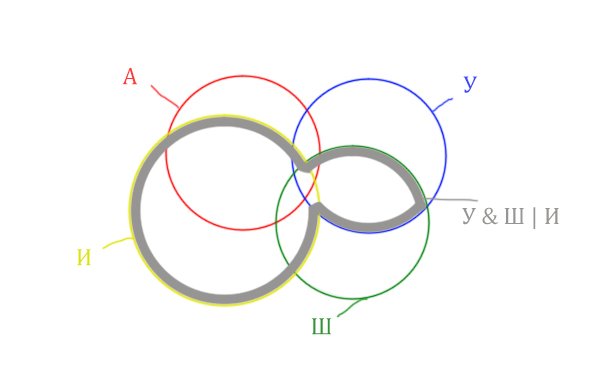
Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
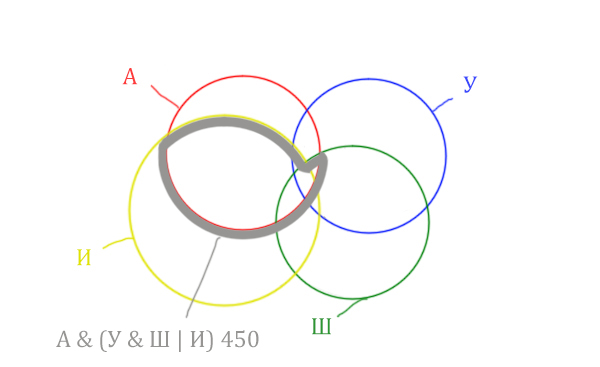
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
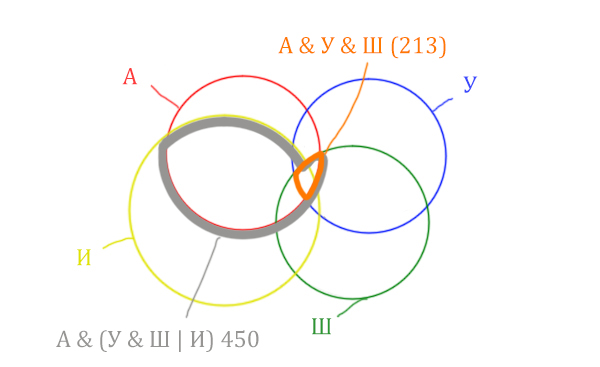
Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
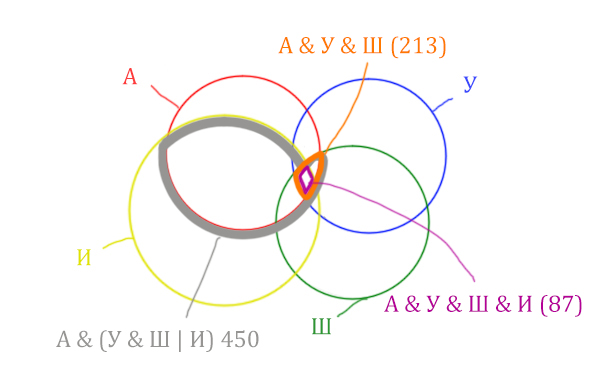
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
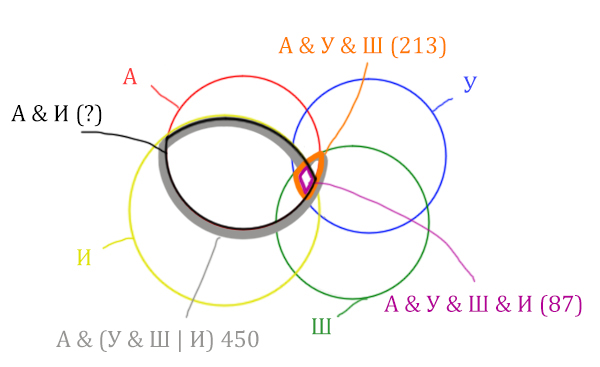
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
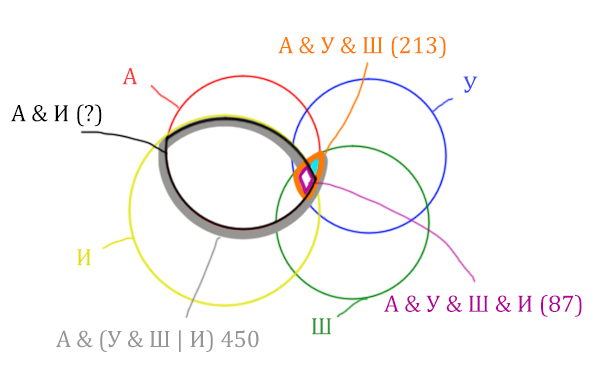
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.
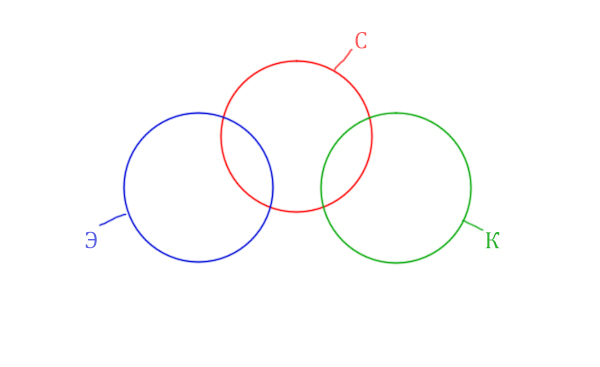
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
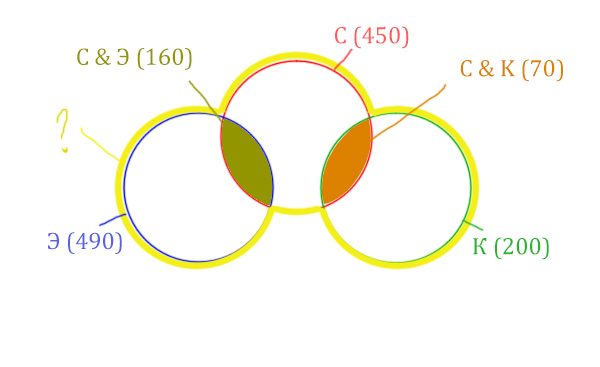
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
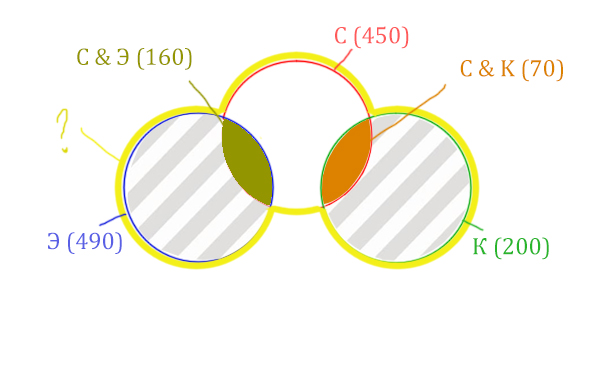
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
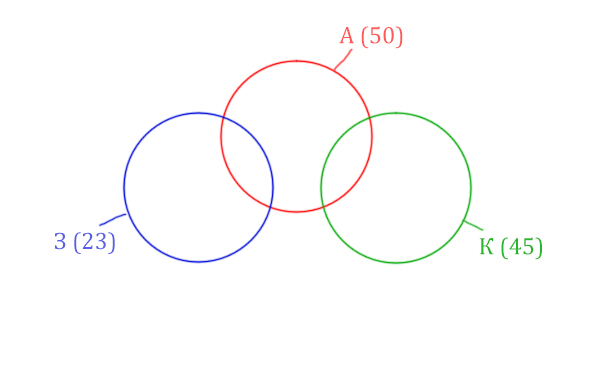
Нарисуем все данные на рисунке.
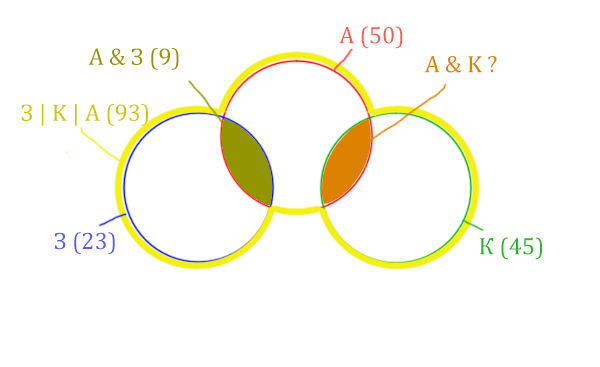
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43
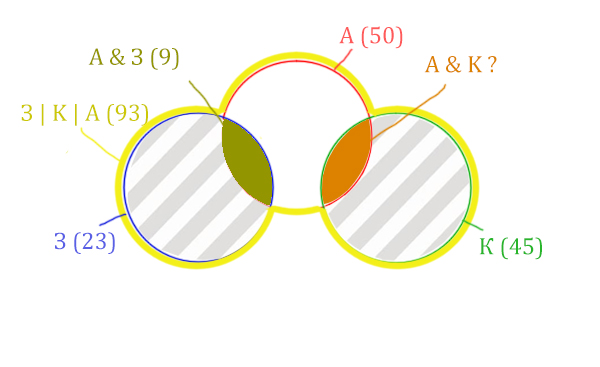
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Решение задач с окружностями информатика
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (x, y — действительные числа) и определяет принадлежность точки заштрихованной области, включая её границы. Программист торопился и написал программу неправильно.
Последовательно выполните следующее.
1. Перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (A, B, C, D, E, F, G и H).
Точки, лежащие на границах областей, отдельно не рассматривать. В столбцах условий укажите “да”, если условие выполнится, “нет”, если условие не выполнится, “—” (прочерк), если условие не будет проверяться, “не изв.”, если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце “Программа выведет” укажите, что программа выведет на экран. Если программа ничего не выводит, напишите “—” (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите “не изв”. В последнем столбце укажите “да” или “нет”.
2. Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, достаточно указать любой способ доработки исходной программы.)
| Паскаль | Бейсик |
|---|---|
| Си++ | Алгоритмический |
| Область | Условие 1
(x*x+y*y>=4) |
Условие 2
(x>= –2) |
Условие 3
(y =4) |
Условие 2
(x>= –2) |
Условие 3
(y if (x*x+y*y>=4) and (x>= –2) and (y =0) then (могут быть и другие способы доработки). Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно. if x*x+y*y >= 4 then IF x*x+y*y >= 4 THEN если x*x+y*y >= 4 то Последовательно выполните следующее: 1. Перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (A, B, C, D, E, F, G и H). Точки, лежащие на границах областей, отдельно не рассматривать. В столбцах условий укажите “да”, если условие выполнится, “нет”, если условие не выполнится, “—” (прочерк), если условие не будет проверяться, “не изв.”, если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце “Программа выведет” укажите, что программа выведет на экран. Если программа ничего не выводит, напишите “—” (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите “не изв”. В последнем столбце укажите “да” или “нет”. 2. Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, достаточно указать любой способ доработки исходной программы.)
Предварительный просмотр:«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС » учитель математики информатики ВведениеОдна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования – готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи. В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования. Основная частьТема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг». Задания, которые рассматриваются на занятии:
Для решения задач используем линейные структуры, ветвления и циклы. Проверяемые элементы содержанияФормальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд. Знание основных конструкций языка программирования, понятия переменной, оператора присваивания. Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд. Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление. Умение анализировать результат исполнения алгоритма. Основное содержание теоретической частиАлгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных. Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов. Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование. Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ. Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными. Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат. Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии). Задания на этапе первичного закрепленияРассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот). Задача 1. Вычислить длину окружности по заданному радиусу.
Математическая модель. Вычислить длину окружности по формуле Описать переменные. Ввести данные. Вычислить по формуле длины окружности C= 2*π*R. Write( ‘Введите радиус окружности R= ‘ ); WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 ); Скриншот программы с результатами решения Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно. Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= . Описать переменные. Ввести данные. Выразить радиус R из формулы длины окружности. Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= . Write( ‘Введите длину окружности С= ‘ ); WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 ); Скриншот программы с результатами решения Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна. Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).
Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R – внешний радиус, r-внутренний радиуc, (R> r). Описать переменные. Ввести данные. Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r). Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ ); S := pi * (R2 * R2 – R1 * R1); WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 ); Скриншот программы с результатами решения Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно. Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.
Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости. Из точек A и B опустим перпендикуляры на оси координат. Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны: AC = x b – x a ; Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB: Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = . Описать переменные. Ввести данные. Вычислить расстояние между точками по формуле R= . Напишем алгоритм на псевдокоде * вывод (‘Введите координаты (x и y) точки 1’) * вывод (‘Введите координаты (x и y) точки 2’) * R := Sqrt(Sqr(X2 – X1) + Sqr(Y2 – Y1)); * вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3); X1, X2, Y1, Y2, R: Real ; Writeln( ‘Введите координаты (x и y) точки 1’ ); Writeln( ‘Введите координаты (x и y) точки 2’ ); R := Sqrt(Sqr(X2 – X1) + Sqr(Y2 – Y1)); Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 ); Скриншот программы с результатами решения Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно. Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .
Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга. Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна = * вывод (‘Введите величину дуги кругового сектора (в радианах)’) * вывод (‘Площадь кругового сектора =’, S:8:2) write(‘Введите величину дуги кругового сектора (в радианах) ‘); writeln(‘Площадь кругового сектора = ‘, S:8:2) Скриншот программы с результатами решения Вывод. Программа работоспособна. Проверим результат с помощью калькулятора. Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок. АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром. [spoiler title=”источники:”] http://inf-ege.sdamgia.ru/test?theme=194 http://nsportal.ru/shkola/informatika-i-ikt/library/2017/09/28/razrabotka-algoritmov-i-programm-dlya-resheniya-zadach-s [/spoiler] |

Решение задач по кодированию графической информации

Определить требуемый объем видеопамяти для различных графических режимов экрана монитора, если известна глубина цвета на одну точку.
Режим экрана
Глубина цвета (бит на точку)
4
640 на 480
8
800 на 600
16
1024 на 768
24
1280 на 1024
32

Задача
- Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10 10 точек. Какой объем памяти займет это изображение?

Решение:
- Количество точек -100
- Так как всего 2 цвета черный и белый. то глубина цвета равна 1 ( 2 1 =2)
- Объем видеопамяти равен 100*1=100 бит

Задача
Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 КБ памяти. Каково максимально возможное число цветов в палитре изображения

Решение
- Определим количество точек изображения. 128*128=16384 точек или пикселей.
- Объем памяти на изображение 4 Кб выразим в битах, так как V=I*X*Y вычисляется в битах. 4 Кб=4*1024=4 096 байт = 4096*8 бит =32768 бит
- Найдем глубину цвета I =V/(X*Y)=32768:16384=2
- N=2 I , где N – число цветов в палитре. N=4
- Ответ: 4

Задача
- Сколько бит видеопамяти занимает информация об одном пикселе на ч/б экране (без полутонов)?

Решение
- Если изображение Ч/Б без полутонов, то используется всего два цвета –черный и белый, т.е. К=2, 2 i =2, I= 1 бит на пиксель.
Ответ: 1 пиксель

Задача
Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея- 800 х 600 пикселей?

Решение
- Найдем объем видеопамяти для одной страницы: 800*600*24=11520000 бит =1440000 байт =1406,25 Кб ≈1, 37 Мб
- 1,37*4 =5,48 Мб ≈5.5 Мб для хранения 4 страниц.
Ответ: 5.5 Мб

Задача
Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора High Color с разрешающей способностью 1024 х 768 точек и палитрой цветов из 65536 цветов.

Решение
- 1. По формуле K=2 I , где K – количество цветов, I – глубина цвета определим глубину цвета. 2 I =65536
- Глубина цвета составляет: I = log 2 65 536 = 16 бит (вычисляем с помощью программы Wise Calculator)
- 2.. Количество точек изображения равно: 1024 768 = 786 432
- 3. Требуемый объем видеопамяти равен: 16 бит 786 432 = 12 582 912 бит = 1572864 байт = 1536 Кб =1,5 Мб ( 1,2 Мбайта. Ответ дан в практикуме Угринович). Приучаем учеников, переводя в другие единицы, делить на 1024, а не на 1000.
- Ответ: 1,5 Мб

Задача
В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится объем занимаемой им памяти?

Решение
Чтобы закодировать 65536 различных цветов для каждой точки, необходимо 16 бит. Чтобы закодировать 16 цветов, необходимо всего 4 бита. Следовательно, объем занимаемой памяти уменьшился в 16:4=4 раза.
Ответ: в 4 раза
![Задача Достаточно ли видеопамяти объемом 256 Кбайт для работы монитора в режиме 640 480 и палитрой из 16 цветов? (2.77 [3]) Решение:](https://fsd.multiurok.ru/html/2019/01/04/s_5c2f6f3813fd2/img14.jpg)
Задача
- Достаточно ли видеопамяти объемом 256 Кбайт для работы монитора в режиме 640 480 и палитрой из 16 цветов? (2.77 [3])
- Решение:

решение
- Узнаем объем видеопамяти, которая потребуется для работы монитора в режиме 640х480 и палитрой в 16 цветов. V=I*X*Y=640*480*4 (2 4 =16, глубина цвета равна 4),
- V= 1228800 бит = 153600 байт =150 Кб.
- 150
- Ответ: достаточно

Задача
Укажите минимальный объем памяти (в килобайтах), достаточный для хранения любого растрового изображения размером 256 х 256 пикселей, если известно, что в изображении используется палитра из 2 16 цветов. Саму палитру хранить не нужно.
- 128
- 512
- 1024
- 2048

Решение
Найдем минимальный объем памяти, необходимый для хранения одного пикселя. В изображении используется палитра из 2 16 цветов, следовательно, одному пикселю может быть сопоставлен любой из 2 16 возможных номеров цвета в палитре. Поэтому, минимальный объем памяти, для одного пикселя будет равен log 2 2 16 =16 битам. Минимальный объем памяти, достаточный для хранения всего изображения будет равен 16*256*256 =2 4 * 2 8 * 2 8 =2 20 бит=2 20 : 2 3 =2 17 байт = 2 17 : 2 10 =2 7 Кбайт =128 Кбайт, что соответствует пункту под номером 1.
Ответ: 1

Задача
Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640 х 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами?

Решение
- Определим объем изображения в битах:
- 3 байт = 3*8 = 24 бит,
- V=I*X*Y=640*480*24 бит =7372800 бит
- Найдем число секунд на передачу изображения: 7372800 : 28800=256 секунд
Ответ: 256.

Задача
Сколько секунд потребуется модему, передающему сообщения со скоростью 14400 бит/сек, чтобы передать цветное растровое изображение размером 800 х 600 пикселей, при условии, что в палитре 16 миллионов цветов?

Решение
Для кодирования 16 млн. цветов требуется 3 байта или 24 бита (Графический режим True Color). Общее количество пикселей в изображении 800 х 600 =480000. Так как на 1 пиксель приходится 3 байта, то на 480000 пикселей приходится 480000*3=1 440 000 байт или 11520000 бит. 11520000 : 14400 = 800 секунд.
Ответ: 800 секунд.

Задача
Современный монитор позволяет получать на экране 16777216 различных цветов. Сколько бит памяти занимает 1 пиксель?

Решение
- Один пиксель кодируется комбинацией двух знаков «0» и «1». Надо узнать длину кода пикселя.
- 2 х =16777216, log 2 16777216 =24 бит
Ответ: 24.

Задача
Каков минимальный объем памяти ( в байтах), достаточный для хранения черно-белого растрового изображения размером 32 х 32 пикселя, если известно, что в изображении используется не более 16 градаций серого цвета

Решение
- Глубина цвета равна 4, т.к. 16 градаций цвета используется.
- 32*32*4=4096 бит памяти для хранения черно-белого изображения
- 4096 : 8 = 512 байт.
Ответ: 512 байт

Задача
Монитор работает с 16 цветной палитрой в режиме 640*400 пикселей. Для кодирования изображения требуется 1250 Кбайт. Сколько страниц видеопамяти оно занимает?

Решение
- Т.к. страница –раздел видеопамяти, вмещающий информацию об одном образе экрана одной «картинки» на экране, т.е. в видеопамяти могут размещаться одновременно несколько страниц, то, чтобы узнать число страниц надо поделить объем видеопамяти для всего изображения на объем памяти на 1 страницу. К-число страниц, К=V изобр /V 1 стр
- V изобр =1250 Кб по условию
- Для этого вычислим объем видеопамяти для одной страницы изображения с 16 цветовой палитрой и разрешающей способностью 640*400.
- V 1 стр = 640*400*4 , где 4- глубина цвета (2 4 =16)
- V 1 стр = 1024000 бит = 128000 байт =125 Кб
- 3. К=1250 : 125 =10 страниц
Ответ: 10 страниц

Задача
Страница видеопамяти составляет 16000 байтов. Дисплей работает в режиме 320*400 пикселей. Сколько цветов в палитре?

Решение
- 1. V=I*X*Y – объем одной страницы, V=16000 байт = 128000 бит по условию. Найдем глубину цвета I.
- I=V/(X*Y).
- I= 128000 / (320*400)=1.
- 2. Определим теперь, сколько цветов в палитре. K=2 I , где K – количество цветов, I – глубина цвета. K=2
Ответ: 2 цвета.

Задача
Сканируется цветное изображение размером 10 10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл

Решение
- Разрешающая способность сканера 600 dpi (dot per inch — точек на дюйм) означает, что на отрезке длиной 1 дюйм сканер способен различить 600 точек. Переведем разрешающую способность сканера из точек на дюйм в точки на сантиметр:
- 600 dpi : 2,54 236 точек/см (1 дюйм = 2.54 см.)
- 2. Следовательно, размер изображения в точках составит 2360 2360 точек. (умножили на 10 см.)
- 3. Общее количество точек изображения равно:
- 2360 2360 = 5 569 600
- 4. Информационный объем файла равен:
- 32 бит 5569600 = 178 227 200 бит 21 Мбайт
Ответ: 21 Мбайт

Задача
Сколько цветов будет использоваться, если для каждого цвета пикселя взято 2 уровня градации яркости? 64 уровня яркости каждого цвета?

Решение
- 1. Всего для каждого пикселя используется набор из трех цветов (красный, зеленый, синий) со своими уровнями яркости (0-горит, 1-не горит). Значит, K=2 3 =8 цветов.
- 2.64 3 =262144
Ответ: 8; 262 144 цвета.

Решить дома следующие задачи:
- Объем страницы видеопамяти -125 Кбайт. Монитор работает с 16 цветной палитрой. Какова разрешающая способность экрана
- Достаточно ли видеопамяти объемом 256 Кбайт для работы монитора в режиме 640 ´ 480 и палитрой из 16 цветов?
Урок информатики в 9 классе на тему «Количество отчек»
-
«Сфера – 15 баллов».
Дан шар радиуса R, центр которого находится в центре координат. Определить количество точек с целочисленными координатами, находящихся на его поверхности.
Ваша программа должна
-
запросить целое число R (0R1000) – радиус шара;
-
подсчитать и сообщить число точек с целочисленными координатами, лежащих на поверхности шара.
Пример 1.
Если R=13, то K=78
Пример 2.
Если R=16, то K=6
Примечание. Ограничение времени на прохождение одного теста – 20 секунд.
-
«Предложение – 20 баллов».
В заданном предложении, не содержащем знаки препинания, тире, двоеточия и т.д., заменить каждое слово перевернутым. Например, если исходное предложение А роза упала на лапу Азора, то результатом должно быть предложение А азор алапу ан упал арозА. Слова в предложении разделаются одним пробелом, других пробелов в предложении нет, предложение может состоять из одного слова, общая длина предложения не более 128 символов.
Ваша программа должна
-
принять исходное предложение с клавиатуры или файла;
-
составить и сообщить предложение, образованное заменой каждого слова введенного предложения на перевернутое.
Примечание. Ограничение времени на прохождение одного теста – 5 секунд.
-
«Популяция – 25 баллов». На планете Серобуромалиновая звезды SBR-2008 обитает n серых, k бурых и m малиновых хамеликов. Известна их особенность, если встречаются два хамелика разного цвета, то они сливаются, образуя особь третьего цвета. Известно, что через несколько подобных встреч на планете остались только особи одного цвета. Какого именно цвета и после какого числа встреч? Из всех вариантов такой эволюции нужно выбрать ту, изменения в которой произошли за минимальное количество встреч.
Программа должна
-
запросить целые числа (не превосходящие 32000) n, k и m;
-
найти и сообщить наименьшее число встреч, приводящих к нужному результату (все особи одного цвета);
-
найти и сообщить особи какого цвета остались (если вариантов ответов несколько, то все возможные варианты).
Например:
Если n=13, k=13, m=13, то встреч 13, цвет – серый, бурый или малиновый
Если n=22, k=1, m=7, то встреч 7, цвет – серый
Примечание. Ограничение времени на прохождение одного теста – 5 секунд.
Тесты и рекомендации по оценке
Задание 1. «Сфера – 15 баллов».
Тест
|
R |
Ответ |
|
|
1 |
5 |
30 |
|
2 |
32 |
6 |
|
3 |
481 |
2886 |
|
4 |
987 |
13230 |
Оценка: 1 тест – 1 балл, 2 теста – 3 балла, 3 теста – 6 баллов, все – 15 баллов
Задание 2. « Предложение – 20 баллов ».
Тест
|
Исходное предложение |
Результат |
|
|
1 |
Смеркалось |
ьсолакремС |
|
2 |
Взлет разрешаю |
телзВ юашерзар |
|
3 |
А азор алапу ан упал арозА |
А роза упала на лапу Азора |
|
4 |
Тот кок еще и казак |
тоТ кок еще и казак |
Оценка: 1 тест – 2 балла, 2 теста – 6 баллов, 3 теста – 12 баллов, все – 20 баллов
Задание 3. « Популяция – 25 баллов ».
Тест
|
Количество |
Ответ |
|
|
1 |
0,5,7 |
встреч 7, цвет –серый |
|
2 |
8,7,26 |
встреч 26, цвет –бурый |
|
3 |
13,15,25 |
встреч 15, цвет – малиновый |
|
4 |
8,4,8 |
встреч 8, цвет – серый, бурый или малиновый |
Оценка: 1 тест – 3 балла, 2 теста – 8 баллов, 3 теста – 16 баллов, все – 25 баллов
Здесь представлен конспект к уроку на тему «Количество точек», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Информатика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые,
Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

