Теорема
(о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).
(n — количество сторон многоугольника).
Другой вариант формулировки этой теоремы:
Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).
Дано:
— выпуклый n -угольник.
Доказать:
Доказательство:

Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
Так как сумма углов при вершине O составляет 360º
то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
Сумма углов каждого треугольника равна 180º.
Таким образом, искомая сумма углов n угольника равна
Что и требовалось доказать.

Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.
Сумма всех углов этих треугольников равна сумме углов многоугольника.
Сумма углов углов каждого из треугольников равна 180º.
Следовательно, сумма углов многоугольника
Что и требовалось доказать.
Углы многоугольника
- Сумма внутренних углов
- Сумма внешних углов
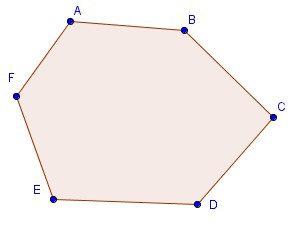
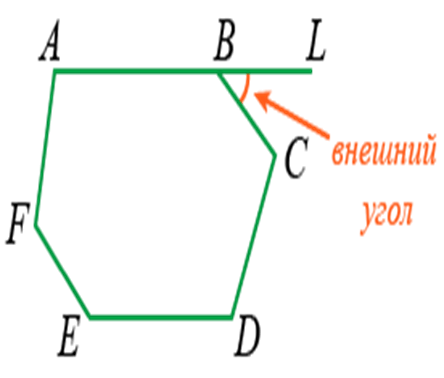
Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.
Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.
Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n – 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n – 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n – 2):
s = 2dn – 2d(n – 2) = 2dn – 2dn + 4d = 4d.
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.
Поговорим подробнее о видах многоугольников и их характеристиках.
Определение
Многоугольник — это замкнутая ломаная линия.
Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.
При изучении темы, что такое многоугольники, применяются следующие термины:
- Вершины многоугольника.
- Стороны замкнутой ломаной.
- Углы, образованные между смежными сторонами.
- Отрезки между несмежными вершинами называются диагоналями.
- Сумма длин всех сторон фигуры является периметром.
- Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.
Наименования данных фигур зависят от количества сторон:
- Треугольник – это 3 стороны.
- Четырехугольник имеет 4 стороны.
- Пятиугольник – это 5 сторон и пр.
Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.
Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.
Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.
Виды многоугольников
Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.
Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.
Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.
Что такое правильные многоугольники
Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.
На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
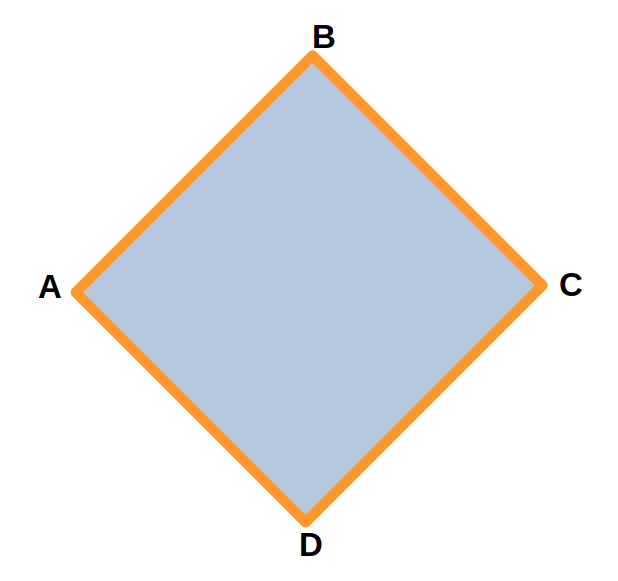
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Пример
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
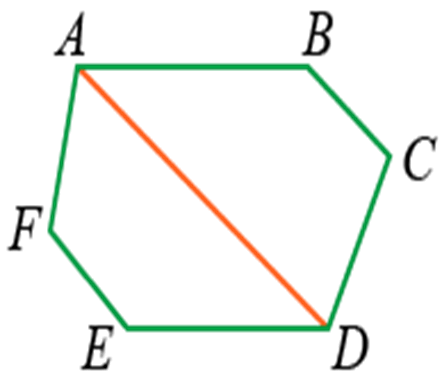
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
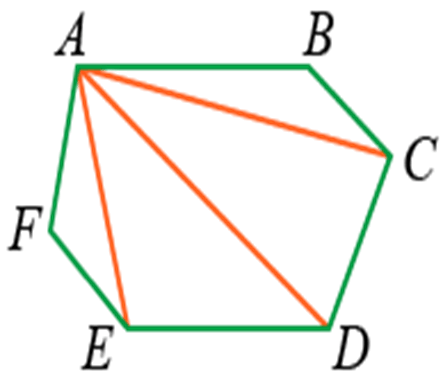
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Сумма углов выпуклого многоугольника
Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.
Внутренним называется угол между смежными сторонами.
Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.
Например, ∠LBC является внешним углом для ABCDEF.
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.
Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.
Сумма внутренних углов
Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.
Обозначения выглядят следующим образом:
- сумма углов – s;
- число сторон – n;
- два прямых угла (2 · 90 = 180°) – 2d.
Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).
Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).
Пример:
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.
Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.
Нет времени решать самому?
Наши эксперты помогут!
Сумма внешних углов
Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.
Где:
- s — сумма внешних углов;
- 4d — четыре прямых угла (4 · 90 = 360°).
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).
Например, ∠1 и ∠2:
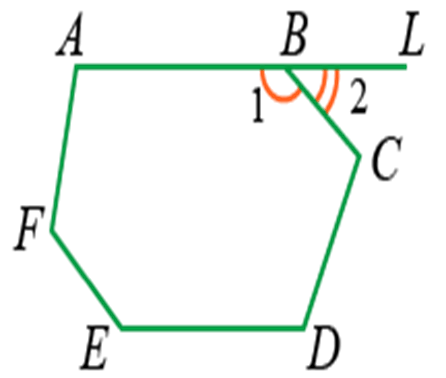
Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.
Пример
Задание: Найдите сумму углов выпуклого двенадцатиугольника.
Решение: Для выпуклого n-угольника сумма углов равна 180° (n -2).
Если имеется 12 вершин, то сумма всех углов будет рассчитываться следующим образом: 2 · 90 · (12 – 2) = 1800°.
Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.
Выпуклый многоугольник
Определение
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.
Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.
Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.
В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.
Выпуклые многоугольники. Определение выпуклого многоугольника. Диагонали выпуклого многоугольника
Данные геометрические фигуры окружают нас повсюду. Выпуклые многоугольники бывают природными, например, пчелиные соты или искусственными (созданными человеком). Эти фигуры используются в производстве различных видов покрытий, в живописи, архитектуре, украшениях и т.д. Выпуклые многоугольники обладают тем свойством, что все их точки располагаются по одну сторону от прямой, что проходит через пару соседних вершин этой геометрической фигуры. Существуют и другие определения. Выпуклым называется тот многоугольник, который расположен в единой полуплоскости относительно любой прямой, содержащей одну из его сторон.
Выпуклые многоугольники
Вершины многоугольника называют соседними, в том случае если они представляют собой концы одной из его сторон. Геометрическая фигура, у которой имеется n-е число вершин, а значит, и n-е количество сторон, называется n-угольником. Саму ломаную линию называют границей или контуром этой геометрической фигуры. Многоугольной плоскостью или плоским многоугольником называют конечную часть любой плоскости, им ограниченной. Соседними сторонами этой геометрической фигуры называют отрезки ломаной линии, исходящие из одной вершины. Они будут не соседними, если исходят их разных вершин многоугольника.
Другие определения выпуклых многоугольников
• каждый отрезок, что соединяет две любые точки внутри него, полностью лежит в нем;
• внутри него лежат все его диагонали;
• любой внутренний угол не превышает 180°.
Многоугольник всегда разбивает плоскость на 2 части. Одна из них – ограниченная (она может быть заключена в круг), а другая – неограниченная. Первую называют внутренней областью, а вторую – внешней областью этой геометрической фигуры. Данный многоугольник является пересечением (иными словами – общей составляющей) нескольких полуплоскостей. При этом каждый отрезок, имеющий концы в точках, которые принадлежат многоугольнику, полностью принадлежит ему.
Разновидности выпуклых многоугольников
Правильные выпуклые многоугольники
Правильный четырехугольник – квадрат. Правильный треугольник называют равносторонним. Для таких фигур существует следующее правило: каждый угол выпуклого многоугольника равен 180° * (n-2)/ n,
где n – число вершин этой выпуклой геометрической фигуры.
Площадь любого правильного многоугольника определяют по формуле:
где p равно половине суммы всех сторон данного многоугольника, а h равно длине апофемы.
Свойства выпуклых многоугольников
Предположим, что Р – данный выпуклый многоугольник. Берем 2 произвольные точки, например, А, В , которые принадлежат Р. По существующему определению выпуклого многоугольника эти точки расположены в одной стороне от прямой, что содержит любую сторону Р. Следовательно, АВ также имеет это свойство и содержится в Р. Выпуклый многоугольник всегда возможно разбить на несколько треугольников абсолютно всеми диагоналями, которые проведены из одной его вершины.
Углы выпуклых геометрических фигур
Углы выпуклого многоугольника – это углы, что образованы его сторонами. Внутренние углы находятся во внутренней области данной геометрической фигуры. Угол, что образован его сторонами, которые сходятся в одной вершине, называют углом выпуклого многоугольника. Углы, смежные с внутренними углами данной геометрической фигуры, называют внешними. Каждый угол выпуклого многоугольника, расположенный внутри него, равен:
где х – величина внешнего угла. Эта простая формула действует в отношении любых геометрических фигур такого типа.
В общем случае, для внешних углов существует следующие правило: каждый угол выпуклого многоугольника равен разности между 180° и величиной внутреннего угла. Он может иметь значения в пределах от -180° до 180°. Следовательно, когда внутренний угол составляет 120°, внешний будет иметь величину в 60°.
Сумма углов выпуклых многоугольников
где n – число вершин n-угольника.
Сумма углов выпуклого многоугольника вычисляется довольно просто. Рассмотрим любую такую геометрическую фигуру. Для определения суммы углов внутри выпуклого многоугольника необходимо соединить одну из его вершин с другими вершинами. В результате такого действия получается (n-2) треугольника. Известно, что сумма углов любых треугольников всегда равна 180°. Поскольку их количество в любом многоугольнике равняется (n-2), сумма внутренних углов такой фигуры равняется 180° х (n-2).
Сумма углов выпуклого многоугольника, а именно любых двух внутренних и смежных с ними внешних углов, у данной выпуклой геометрической фигуры всегда будет равна 180°. Исходя из этого, можно определить сумму всех ее углов:
Сумма внутренних углов составляет 180° * (n-2). Исходя из этого, сумму всех внешних углов данной фигуры устанавливают по формуле:
180° * n-180°-(n-2)= 360°.
Сумма внешних углов любого выпуклого многоугольника всегда будет равна 360° (независимо от количества его сторон).
Внешний угол выпуклого многоугольника в общем случае представляется разностью между 180° и величиной внутреннего угла.
Другие свойства выпуклого многоугольника
Помимо основных свойств данных геометрических фигур, у них есть и другие, которые возникают при манипуляциях с ними. Так, любой из многоугольников может быть разделен на несколько выпуклых n-угольников. Для этого необходимо продолжить каждую из его сторон и разрезать эту геометрическую фигуру вдоль этих прямых линий. Разбить любой многоугольник на несколько выпуклых частей можно и таким образом, чтобы вершины каждого из кусков совпадали со всеми его вершинами. Из такой геометрической фигуры можно очень просто сделать треугольники путем проведения всех диагоналей из одной вершины. Таким образом, любой многоугольник, в конечном счете, можно разбить на определенное количество треугольников, что оказывается весьма полезным при решении различных задач, связанных с такими геометрическими фигурами.
Периметр выпуклого многоугольника
Отрезки ломаной линии, называемые сторонами многоугольника, чаще всего обозначаются следующими буквами: ab, bc, cd, de, ea. Это стороны геометрической фигуры с вершинами a, b, c, d, e. Сумма длины всех сторон этого выпуклого многоугольника называют его периметром.
Окружность многоугольника
Выпуклые многоугольники могут быть вписанными и описанными. Окружность, касающаяся всех сторон этой геометрической фигуры, называется вписанной в нее. Такой многоугольник называют описанным. Центр окружности, которая вписана в многоугольник, представляет собой точку пересечения биссектрис всех углов внутри данной геометрической фигуры. Площадь такого многоугольника равняется:
где r – радиус вписанной окружности, а p – полупериметр данного многоугольника.
Окружность, содержащую вершины многоугольника, называют описанной около него. При этом данная выпуклая геометрическая фигура называется вписанной. Центр окружности, которая описана около такого многоугольника, представляет собой точку пересечения так называемых серединных перпендикуляров всех сторон.
Диагонали выпуклых геометрических фигур
Число диагоналей выпуклого многоугольника играет важную роль в элементарной геометрии. Число треугольников (К), на которые возможно разбить каждый выпуклый многоугольник, вычисляется по следующей формуле:
Количество диагоналей выпуклого многоугольника всегда зависит от числа его вершин.
Разбиение выпуклого многоугольника
В некоторых случаях для решения геометрических задач необходимо разбить выпуклый многоугольник на несколько треугольников с непересекающимися диагоналями. Эту проблему можно решить путем выведения определенной формулы.
Определение задачи: назовем правильным некое разбиение выпуклого n-угольника на несколько треугольников диагоналями, пересекающимися только в вершинах этой геометрической фигуры.
Решение: Предположим, что Р1, Р2 , Р3 … , Pn – вершины этого n-угольника. Число Xn – количество его разбиений. Внимательно рассмотрим полученную диагональ геометрической фигуры Pi Pn. В любом из правильных разбиений Р1 Pn принадлежит определенному треугольнику Р1 Pi Pn, у которого 1 17 апреля, 2014
Выпуклый многоугольник: определение, элементы, свойства, примеры
Выпуклый многоугольник: определение, элементы, свойства, примеры – Наука
Содержание:
А выпуклый многоугольник Это геометрическая фигура, содержащаяся в плоскости, которая характеризуется тем, что все ее диагонали находятся внутри, а ее углы составляют менее 180 °. Среди его свойств можно выделить следующие:
1) Он состоит из n последовательных сегментов, в которых последний из сегментов соединяется с первым. 2) Ни один из сегментов не пересекается таким образом, чтобы ограничить плоскость во внутренней и внешней областях. 3) Каждый угол во внутренней области строго меньше плоского угла.
Простой способ определить, является ли многоугольник выпуклым или нет, – это рассмотреть линию, проходящую через одну из его сторон, которая определяет две полуплоскости. Если на каждой линии, проходящей через одну сторону, другие стороны многоугольника находятся в одной полуплоскости, то это выпуклый многоугольник.
Элементы многоугольника
Каждый многоугольник состоит из следующих элементов:
Стороны – это каждый из последовательных сегментов, составляющих многоугольник. В многоугольнике ни один из составляющих его сегментов не может иметь открытого конца, в этом случае будет многоугольная линия, но не многоугольник.
Вершины – это точки соединения двух последовательных отрезков. В многоугольнике количество вершин всегда равно количеству сторон.
Если две стороны или сегменты многоугольника пересекаются, значит, у вас есть перекрещенный многоугольник. Точка пересечения не считается вершиной. Поперечный многоугольник – это невыпуклый многоугольник. Звездообразные многоугольники являются перекрестными многоугольниками и поэтому не являются выпуклыми.
Когда у многоугольника все стороны одинаковой длины, мы получаем правильный многоугольник. Все правильные многоугольники выпуклые.
Выпуклые и невыпуклые многоугольники
На рисунке 1 показано несколько многоугольников, некоторые из них выпуклые, а некоторые – нет. Разберем их:
Номер 1 – это трехсторонний многоугольник (треугольник), а все внутренние углы меньше 180 °, поэтому это выпуклый многоугольник. Все треугольники – выпуклые многоугольники.
Число 2 – это четырехсторонний многоугольник (четырехугольник), в котором ни одна из сторон не пересекается, а каждый внутренний угол меньше 180 °. Тогда это будет выпуклый многоугольник с четырьмя сторонами (выпуклый четырехугольник).
С другой стороны, число 3 представляет собой многоугольник с четырьмя сторонами, но один из его внутренних углов больше 180 °, поэтому он не удовлетворяет условию выпуклости. То есть это невыпуклый четырехсторонний многоугольник, называемый вогнутым четырехугольником.
Число 4 представляет собой многоугольник с четырьмя отрезками (сторонами), два из которых пересекаются. Четыре внутренних угла меньше 180 °, но поскольку две стороны пересекаются, получается невыпуклый перекрещенный многоугольник (перекрещенный четырехугольник).
Другой случай – число 5. Это многоугольник с пятью сторонами, но поскольку один из его внутренних углов больше 180 °, мы получаем вогнутый многоугольник.
Наконец, число 6, у которого также есть пять сторон, имеет все внутренние углы меньше 180º, поэтому это выпуклый многоугольник с пятью сторонами (выпуклый пятиугольник).
Свойства выпуклого многоугольника
1. Непересекающийся многоугольник или простой многоугольник делит содержащую его плоскость на две области. Внутренняя область и внешняя область, многоугольник является границей между двумя областями.
Но если многоугольник дополнительно выпуклый, тогда у нас есть внутренняя область, которая является односвязной, что означает, что, взяв любые две точки из внутренней области, он всегда может быть соединен сегментом, который полностью принадлежит внутренней области.
2- Каждый внутренний угол выпуклого многоугольника меньше плоского угла (180º).
3- Все внутренние точки выпуклого многоугольника всегда принадлежат одной из полуплоскостей, определяемых линией, проходящей через две последовательные вершины.
4- В выпуклом многоугольнике все диагонали полностью содержатся во внутренней многоугольной области.
5- Внутренние точки выпуклого многоугольника полностью принадлежат выпуклому угловому сектору, определяемому каждым внутренним углом.
6. Каждый многоугольник, все вершины которого находятся на окружности, является выпуклым многоугольником, который называется циклическим многоугольником.
7- Каждый циклический многоугольник является выпуклым, но не каждый выпуклый многоугольник является циклическим.
8- Каждый непересекающийся многоугольник (простой многоугольник), все стороны которого равны, является выпуклым и известен как правильный многоугольник.
Диагонали и углы в выпуклых многоугольниках
9- Общее количество N диагоналей выпуклого многоугольника с n сторонами определяется по следующей формуле:
Доказательство. В выпуклом многоугольнике с n сторонами каждой вершины нарисовано n – 3 диагоналей, так как сама вершина и две соседние вершины исключены. Поскольку имеется n вершин, всего нарисовано n (n – 2) диагоналей, но каждая диагональ была нарисована дважды, поэтому количество диагоналей (без повторения) равно n (n-2) / 2.
10- Сумма S внутренних углов выпуклого многоугольника с n сторонами определяется следующим соотношением:
Доказательство. Из вершины выводятся n-3 диагонали, определяющие n-2 треугольника. Сумма внутренних углов каждого треугольника составляет 180º. Общая сумма углов n-2 треугольников равна (n-2) * 180º, что совпадает с суммой внутренних углов многоугольника.
Примеры
Пример 1
Циклический шестиугольник – это многоугольник с шестью сторонами и шестью вершинами, но все вершины находятся на одной окружности. Каждый циклический многоугольник выпуклый.
Пример 2
Определите значение внутренних углов обычного энегона.
Решение: enegon – это 9-сторонний многоугольник, но если он также правильный, все его стороны и углы равны.
Сумма всех внутренних углов 9-стороннего многоугольника равна:
S = (9 – 2) 180º = 7 * 180º = 1260º
Но существует 9 внутренних углов одинаковой меры α, поэтому должно выполняться равенство:
Отсюда следует, что мера α каждого внутреннего угла правильного ребра равна:
[spoiler title=”источники:”]
http://fb.ru/article/137593/vyipuklyie-mnogougolniki-opredelenie-vyipuklogo-mnogougolnika-diagonali-vyipuklogo-mnogougolnika
http://ru1.warbletoncouncil.org/poligono-convexo-15533
[/spoiler]
Загрузить PDF
Загрузить PDF
Многоугольник – это любая замкнутая фигура с тремя и более сторонами, которые представляют собой прямые отрезки. Каждая вершина многоугольника содержит как внутренний, так и внешний угол (изнутри и снаружи фигуры, соответственно). Для решения разных геометрических задач полезно знать, как соотносятся эти углы. В частности, необходимо уметь вычислять сумму внутренних углов многоугольника. Это можно сделать по формуле или через разбиение многоугольника на треугольники.
-
1
-
2
Найдите число сторон многоугольника. Помните, что у многоугольника должно быть не менее трех сторон.
- Например, если дан шестиугольник, то число сторон равно 6.
-
3
Подставьте число сторон в формулу. Найденное значение подставьте в формулу вместо
. Помните, что
– это число сторон многоугольника.
-
4
Вычислите сумму углов. Для этого из числа сторон вычтите 2, а затем результат умножьте на 180. Вы получите суммe внутренних углов многоугольника (в градусах).
Реклама
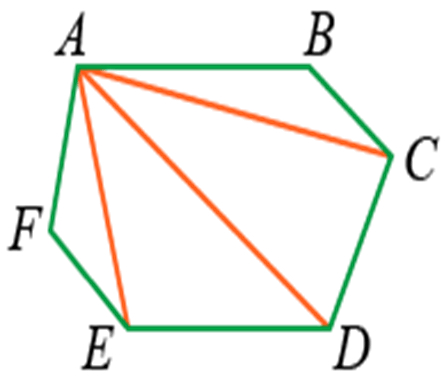
-
1
Нарисуйте многоугольник, сумму углов которого нужно вычислить. У многоугольника может быть сколько угодно сторон (но не менее трех), и он может быть правильной или неправильной формы.
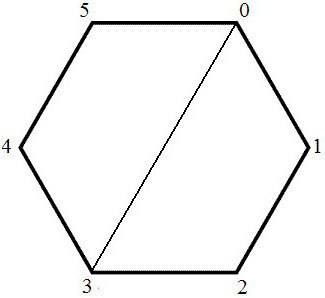
- Например, нужно вычислить сумму внутренних углов шестиугольника. Нарисуйте шестиугольник.
-
2
Выберите любую вершину. Обозначьте ее как A.
- Вершина – это точка, в которой сходятся две стороны многоугольника.
-
3
Соедините точку А с определенными вершинами многоугольника. Линии, соединяющие вершины, не должны пересекаться. Так вы разобьете многоугольник на треугольники.
- Выбранную вершину не нужно соединять со смежными ей вершинами, так как они соединены сторонами многоугольника.
- Например, в случае шестиугольника выбранную вершину нужно соединить с тремя другими вершинами, чтобы получить 4 треугольника.
-
4
Умножьте число треугольников на 180. Так как сумма углов треугольника равна 180, умножив количество треугольников на 180, вы найдете сумму внутренних углов многоугольника.
- В нашем примере шестигранник разбивается на 4 треугольника. Таким образом,
, то есть сумма внутренних углов шестиугольника равна 720 градусов.
Реклама
- В нашем примере шестигранник разбивается на 4 треугольника. Таким образом,
Советы
- Проверьте ответ при помощи транспортира, измерив каждый угол вручную. Для этого аккуратно нарисуйте прямые стороны многоугольника.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Транспортир (по желанию)
- Ручка
- Ластик
- Линейка
Похожие статьи
Об этой статье
Эту страницу просматривали 38 347 раз.