Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания
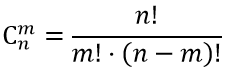
Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
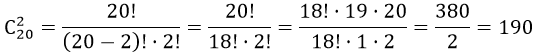
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =frac{{4!}}{{left( {4 — 3} right)!cdot3!}} = frac{{4!}}{{3!}} = frac{{1cdot2cdot3cdot4}}{{1cdot2cdot3}} = 4$
Пример 3
В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?
Решение
$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{9}^3$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{9}^3=frac{{6!}}{{(6-2)!2!}}·frac{{9!}}{{(9-3)!3!}}=15·84=1260$
Пример 4
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
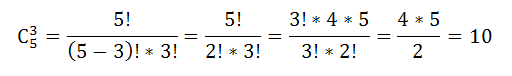
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
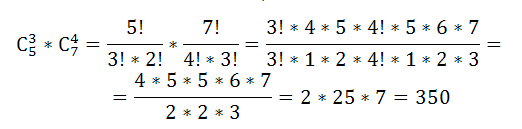
Пример 6
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
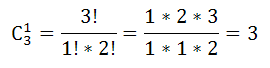
сержантов $С_6^2$
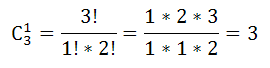
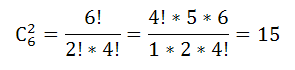
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
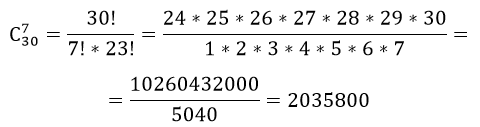
Итак, получаем число способов составления суточного наряда
$$C_3^1cdot{C_6^2}cdot{C_{30}^7}=3cdot15cdot2035800=91611000$$
Сочетания
- Сочетания без повторений
- Сочетания с повторениями
- Биномиальные коэффициенты и их свойства
- Примеры
п.1. Сочетания без повторений
Сочетаниe без повторений – это неупорядоченная ⟨n,k⟩-выборка без повторений, k ≤ n. Общее количество сочетаний без повторений: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$
Внимание! Главным отличием сочетаний от размещений является неупорядоченность выборок. Если для размещения выборки (a,b)≠(b,a) не равны, то для сочетания (a,b)=(b,a) – одна и та же выборка.
Сочетания используются тогда, когда порядок выборки не важен.
Например:
Из 10 программистов нужно отобрать 4 для участия в проекте. Сколькими способами это можно сделать?
$$mathrm{ n = 10, k=4 }$$ В данном случае, порядок отбора не важен (выборка неупорядоченная); каждый кандидат может войти только один раз в выборку (выборка без повторений). Поэтому рассматриваем неупорядоченные ⟨10,4⟩ –выборки без повторений. Количество способов отбора равно: $$mathrm{ C_{10}^4=frac{10!}{6! 4!}=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 }$$ Ответ: 210.
п.2. Сочетания с повторениями
Сочетаниe с повторениями – это неупорядоченная ⟨n,k⟩-выборка с повторениями. Общее количество сочетаний с повторениями: $$ mathrm{ overline{C}_n^k=frac{(n+k-1)!}{(n-1)k!} } $$
$$ mathrm{ overline{C}_n^k=C_{n+k-1}{k} } $$
Например:
Нужно отобрать 4 программистов для участия в проекте. Многочисленных претендентов можно разделить на две категории: желающих работать удаленно и предпочитающих работу в офисе. Сколько всего комбинаций из любителей офиса и удалёнки может оказаться в выбранной четвёрке? $$mathrm{ n = 2, k=4 }$$ Порядок отбора не важен; кандидатов из каждой категории может быть несколько или ни одного. Поэтому рассматриваем неупорядоченные ⟨2,4⟩ –выборки с повторениями: $$ mathrm{ overline{C}_2^4=frac{(2+4-1)!}{(2-1)4!}=frac{5!}{4!}=5 } $$ Всего – 5 комбинаций: OOOO,OOOD,OODD,ODDD,DDDD
где O – любитель офиса; D – любитель удалёнки. Напоминаем, что порядок не важен – важен только состав группы.
Ответ: 5.
п.3. Биномиальные коэффициенты и их свойства
Подробно о биноме – см. §28 справочника для 7 класса.
Для n-й степени бинома справедливо выражение: $$ mathrm{ (apm b)^n=a^n+C_n^1a^{n-1}bpm C_n^2a^{n-2}b^2+…+C_n^{n-1}b^n } $$ где (mathrm{C_n^k}) – биномиальные коэффициенты, к оторые одновременно являются количествами сочетаний без повторений из n по k: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$ Таким образом, биномиальные коэффициенты можно определять как с помощью треугольника Паскаля, так и с помощью данной формулы.
Заметим, что в литературе также часто встречается обозначение (mathrm{left(_k^nright)}) для биномиальных коэффициентов (mathrm{left(C_n^kright)}).
Свойства биномиальных коэффициентов
Свойство симметрии
$$mathrm{ C_n^k=C_n^{n-k} }$$
Свойство Паскаля
$$mathrm{ C_n^k=C_{n-1}^{k-1}+C_{n-1}^k }$$
Замена индексов
$$mathrm{ C_n^mC_m^{n-k}=C_{n}^{k}C_{k}^{n-m} }$$
Вынесение за скобки
$$mathrm{ C_n^k=frac{n}{k}C_{n-1}^{k-1} }$$
Рекуррентные формулы
begin{gather*}mathrm{ C_n^k=frac{n-k+1}{k}C_{n}^{k-1} }\ mathrm{ C_n^k=frac{n}{n-k}C_{n-1}^k } end{gather*}
Свойство суммы
$$mathrm{ C_n^0+C_n^1+C_n^2+…+ C_n^n=sum_{k=0}^nC_n^k=2^n }$$
Свойство разности
$$mathrm{ C_n^0-C_n^1+C_n^2-…+(-1)^nC_n^n=sum_{k=0}^n(-1)^kC_n^k=0 }$$
Свойства максимума
Если n – четное, то максимальное значение (mathrm{C_n^k}) имеет при (mathrm{k=frac{n}{2}}).
Если n – нечетное, то максимальное значение имеют два коэффициента (mathrm{C_n^k}), при (mathrm{k=frac{n-1}{2}}) и (mathrm{k=frac{n+1}{2}})
Свёртка Вандермонда
$$mathrm{ sum_{r=0}^kC_n^rC_m^{k-r}=C_{n+m}^k }$$
Сумма квадратов
$$mathrm{ sum_{k=0}^n(C_n^k)^2=C_{2n}^n }$$
Взвешенное суммирование
begin{gather*} mathrm{ sum_{k=0}^nnC_n^k=n2^{n-1} }\ mathrm{ sum_{k=0}^nn^2C_n^k=n(n+1)2^{n-2} } end{gather*}
Связь с числами Фибоначчи
$$mathrm{ C_n^0+C_{n-1}^1+…+C_{n-k}^{k}+…+C_{0}^{n}=F_{n+1} }$$
п.4. Примеры
Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?
1) Всего у нас n = 10 + 5 = 15 фруктов. Нужно выбрать k = 7 фруктов.
Порядок выбора не важен, т.е. выборка неупорядоченная. Находим: $$ mathrm{ C_n^k=C_{15}^7=frac{15cdot 14cdot 13cdot 12cdot 11cdot 10cdot 9}{1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7}=6435 } $$ Существует 6435 способов выбрать 7 фруктов из 15.
2) Выбираем 4 яблока из 10 и 3 груши из 5.
Для яблок: $$ mathrm{ C_{10}^4=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 } $$ Для груш: $$ mathrm{ C_3^5=C_{5}^2=frac{5cdot 4}{1cdot 2}=10 } $$ По правилу произведения, общее количество способов выбрать 4 яблока и 3 груши: $$ mathrm{ C_{10}^3cdot C_{5}^3=210cdot 10=2100 } $$ Ответ: 1) 6435; 2) 2100.
Пример 2. В кондитерском магазине продаётся 4 вида пирожных. Сколькими способами можно купить 7 пирожных? $$ mathrm{ n=4, k=7 } $$ Порядок выбора пирожных неважен – выборка неупорядоченная; пирожные одного вида могут повторяться. Значит, находим количество сочетаний с повторениями: $$ mathrm{ overline{C}_4^7=C_{7+4-1}^7=C_{10}^7=C_{10}^3=frac{10cdot 9cdot 8}{1cdot 2cdot 3}=120 } $$ Ответ: 120
Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?
По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: (mathrm{C_3^1=frac31=3})
Выбираем сержантов: (mathrm{C_6^2=frac{6cdot 5}{1cdot 2}=15})
Выбираем рядовых: (mathrm{C_{15}^6=frac{15cdot 14cdot 13cdot 12cdot 11}{1cdot 2cdot 3cdot 4cdot 5}=3003})
По правилу произведения, отряд можно выбрать:
(mathrm{3cdot 15cdot 3003=135135}) способами.
Ответ: 135135.
Пример 4. Найдите сумму
a) (mathrm{C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6})
По свойству суммы (mathrm{sum_{k=0}^6C_6^k=2^6}). Получаем: $$ mathrm{ C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=sum_{k=0}^6C_6^k-C_6^0=2^6-1=64-1=63 } $$
б) (mathrm{C_n^1+6C_n^2+6C_n^3}) $$ mathrm{ C_n^1=n, C_n^2=frac{n(n-1)}{2}, C_n^3=frac{n(n-1)(n-2)}{6} } $$ Получаем begin{gather*} mathrm{ C_n^1+6C_n^2+6C_n^3=n+6cdot frac{n(n-1)}{2}+6cdot frac{n(n-1)(n-2)}{6}=}\ mathrm{ =n(1+3(n-1)+(n-1)(n-2))=n(3n-2+n^2-3n+2)=n^3 } end{gather*} Ответ: а) 63; б) n3.
Пример 5. Рассчитайте все (mathrm{C_{10}^k}) по рекуррентной формуле (mathrm{C_{n}^k=frac{n-k+1}{k}C_n^{k-1}}).
Постройте график (mathrm{C_{10}^k(k)}). Сделайте выводы.
Начальное значение (mathrm{C_{10}^0=1}).
|
0 $$mathrm{ C_{10}^0=1 }$$ 1 $$mathrm{ C_{10}^1=frac{10-1+1}{1}C_{10}^0=10 }$$ 2 $$mathrm{ C_{10}^2=frac{10-2+1}{2}C_{10}^1=45 }$$ 3 $$mathrm{ C_{10}^3=frac{10-3+1}{3}C_{10}^2=120 }$$ 4 $$mathrm{ C_{10}^4=frac{10-4+1}{4}C_{10}^3=210 }$$ 5 $$mathrm{ C_{10}^4=frac{10-5+1}{5}C_{10}^4=252 }$$ 6 $$mathrm{ C_{10}^6=frac{10-6+1}{6}C_{10}^5=210 }$$ 7 $$mathrm{ C_{10}^7=frac{10-7+1}{7}C_{10}^6=120 }$$ 8 $$mathrm{ C_{10}^6=frac{10-8+1}{8}C_{10}^7=45 }$$ 9 $$mathrm{ C_{10}^9=frac{10-9+1}{9}C_{10}^8=10 }$$ 10 $$mathrm{ C_{10}^{10}=frac{10-10+1}{10}C_{10}^9=1 }$$ |
 |
На графике видно симметрию коэффициентов: (mathrm{C_{10}^k=C_{10}^{10-k}}).
Т.к. n = 10 – чётное, максимальный коэффициент при (mathrm{k=frac{n}{2}=5, C_{10}^5=252}).
Можем также проверить свойство суммы: (mathrm{sum_{k=0}^{10}C_{10}^k=1024=2^{10}}).

Рейтинг пользователей
Сочетания без повторений
Калькулятор рассчитывает количество сочетаний без повторений из n различных элементов по k элементам.
Например есть 3 фрукта(яблоко, мандарин и апельсин), сколькими способами можно разложить эти фрукты в коробку по 2 шт – яблоко и мандарин, яблоко и апельсин, мандарин и апельсин – получится всего 3 способа(3 сочетания).
В данном случае в калькулятор вводим в поле n=3, в поле k=2.
Общее количество различных элементов n
Количество элементов в сочетании k
Формула вычисления числа сочетаний без повторений из n по k
n>=k
Где n – количество различных элементов,
k – количество элементов в сочетании
Примеры задач на сочетания без повторений
Задача 1: Сколькими способами можно распределить 2 путёвки между 5 желающими. В данном случае общее количество n=5, количество путёвок k=2.
Задача 2: В магазине продаётся 8 книг по информатике, нужно в подарок купить 4 книги. Сколькими способами можно это сделать ? В данном случае общее количество книг n=8, количество книг в размещении k=4.
Похожие калькуляторы
Как найти общее количество исходов?
Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n! (n−k)!
Как подсчитать количество возможных вариантов?
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.
Как посчитать количество возможных комбинаций без повторений?
Подсчет количества Сочетаний Число всех Сочетаний из n элементов по k можно вычислить по формуле: Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!( 6-4)!)
Сколько комбинаций из 3 цифр без повторений?
Всего – 27 комбинаций.
Как рассчитать вероятность?
Так как в задаче происходит только одно испытание и оно связано с отбором/выбором по определенному условию, речь идет о классическом определении вероятности. Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Когда события независимы?
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Как посчитать количество комбинаций в коде?
если код из 4 символов А, В, С, Д, то 256. Количество вариантов четырехзначных кодов (при отсутствии условия, что все символы должны быть разными) равно N^4, где N — количество символов в том наборе, которым ты пользуешься. Так если код только из цифр, то N=10, а количество разных кодов 10^4=10000.
Сколько комбинаций из 3 цифр от 0 до 9?
Количество комбинаций из 3 цифр В разделе Естественные науки на вопрос Сколько чисел можно составить из комбинации трёх цифр, включая ноль (трёхзначных автомобильных номеров)? заданный автором Недосолить лучший ответ это Если не учитывать число 000, то вы правы, ровно 999!
Как посчитать количество возможных комбинаций из 4 цифр?
Количество вариантов четырехзначных кодов (при отсутствии условия, что все символы должны быть разными) равно N^4, где N — количество символов в том наборе, которым ты пользуешься. Так если код только из цифр, то N=10, а количество разных кодов 10^4=10000.
Сколько уникальных комбинаций из 3 цифр?
Количество комбинаций из 3 цифр В разделе Естественные науки на вопрос Сколько чисел можно составить из комбинации трёх цифр, включая ноль (трёхзначных автомобильных номеров)? заданный автором Недосолить лучший ответ это Если не учитывать число 000, то вы правы, ровно 999!
Сколько комбинаций можно составить из 3 цифр?
Количество комбинаций из 3 цифр В разделе Естественные науки на вопрос Сколько чисел можно составить из комбинации трёх цифр, включая ноль (трёхзначных автомобильных номеров)? заданный автором Недосолить лучший ответ это Если не учитывать число 000, то вы правы, ровно 999!
Сколько комбинаций можно сделать из 3 чисел?
Количество комбинаций можно посчитать по формуле I^n, где n — количество позиций, а I — количество цифр, букв в одной позиции. 10^3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.
Как посчитать вероятность в процентах?
По определению: P=m/n, m-кол-во благоприятных исходов, n-кол-во всех возможных исходов. Например. Есть 50 билетов из них 3 выигрышных. m=50, n=3, p=3/50=0,06, чтобы найти в процентах нужно это число умножить на 100%, т.
Как рассчитать вероятность совпадения?
Перемножьте вероятности каждого отдельного события. Например, стоит задача Найти вероятность того, что при бросании кубика два раза подряд выпадет 5. Это два независимых события, вероятность каждого из которых равна 1/6. Таким образом, вероятность обоих событий составляет 1/6 x 1/6 = 1/36, то есть 0,027, или 2,7 %.
Как понять что события независимы?
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Как понять что события зависимы?
События A и B называются зависимыми, если вероятность одного из них зависит от того, произошло или не произошло другое событие.
Сколько комбинаций можно составить из 3 символов?
Количество комбинаций из 3 цифр В разделе Естественные науки на вопрос Сколько чисел можно составить из комбинации трёх цифр, включая ноль (трёхзначных автомобильных номеров)? заданный автором Недосолить лучший ответ это Если не учитывать число 000, то вы правы, ровно 999!
Для
построения соответствующих математических
моделей комбинаторных задач будем
использовать математический
аппарат теории множеств.
Может случиться, что в данном множестве
порядок следования элементов не важен,
а важен только состав множества. Но есть
задачи, в которых прядок элементов
является существенным.
Определение
1: Порядок
во множестве
![]() из
из![]() элементов – это нумерация его элементов
элементов – это нумерация его элементов
натуральными числами, т.е. отображение
множества![]() на множество
на множество![]() .
.
Определение
2: Множество
с заданным на нем порядком называется
упорядоченным
множеством.
Очевидно,
что множество, содержащее более одного
элемента, можно упорядочить не единственным
способом.
Например,
из двух букв
![]() и
и![]() можно построить упорядоченное множество
можно построить упорядоченное множество
двумя различными способами:
![]() и
и
![]() .
.
Три
буквы
![]() ,
,![]() и
и![]() можно расположить в виде последовательности
можно расположить в виде последовательности
шестью способами:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Для четырех букв
путем перебора получим уже 24 различных
упорядоченных последовательностей.
Упорядоченные
последовательности элементов некоторого
множества можно рассматривать как
распределения или расстановки этих
элементов в последовательности.
Определение
3: Пусть
дано конечное множество
![]() из
из![]() элементов. Всякий набор из
элементов. Всякий набор из![]() элементов данного множества (при этом
элементов данного множества (при этом
элементы в наборе могут и повторяться)
будем называть![]() –расстановками.
–расстановками.
Через
понятие расстановки вводятся основные
определения комбинаторики: сочетания,
размещения и перестановки.
При этом каждое из этих понятий может
быть с повторениями и без повторений.
В данном параграфе будут рассмотрены
комбинаторные формулы без повторений.
Перестановки
без повторений.
Определение
4: Пусть
![]() – конечное множество из
– конечное множество из![]() элементов.Перестановками
элементов.Перестановками
из
![]() различных элементов множества
различных элементов множества![]() называются все расположения
называются все расположения![]() элементов в определенном порядке.
элементов в определенном порядке.
Обозначается:![]() (от французского словаpermutation
(от французского словаpermutation
– перестановка).
Упорядоченные
множества считаются различными, если
они отличаются либо своими элементами,
либо их порядком.
Определение
5: Различные
упорядоченные множества, которые
отличаются лишь порядком элементов,
называются перестановками
этого множества.
Последнее определение
сформулировано с позиции теории множеств.
Определение
6: Произведение
![]() последовательных натуральных чисел в
последовательных натуральных чисел в
математике обозначают![]() и называютфакториалом.
и называютфакториалом.
Выбор
для обозначения
![]() восклицательного знака, возможно, связан
восклицательного знака, возможно, связан
с тем, что даже для сравнительно небольших
значений![]() число
число![]() очень велико. Например,
очень велико. Например,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и т.д.
и т.д.
Теорема
1: Число
перестановок из
![]() различных элементов вычисляется по
различных элементов вычисляется по
формуле:
![]() (1)
(1)
Доказательство.
Рассмотрим произвольное множество из
![]() элементов. Построим всевозможные
элементов. Построим всевозможные
расстановки из этих![]() элементов.
элементов.
На первое
место
расстановки можно поставить любой из
![]() элементов (
элементов (![]() способов выбора первого элемента). После
способов выбора первого элемента). После
того, как первый элемент выбран и
независимо как он выбран, второй элемент
можно выбрать![]() способом. Для выбора третьего элемента
способом. Для выбора третьего элемента
остается![]() способа и т.д. Последний элемент выбирается
способа и т.д. Последний элемент выбирается
соответственно одним способом. Тогда,
в силу комбинаторного принципа умножения,
количество таких расстановок будет
равно:
![]()
Теорема доказана.
Пример
1: Сколькими
способами трое друзей могут занять в
кинотеатре места с номерами 1, 2 и 3.
Решение.
Количество искомых способов будет равно
числу перестановок без повторений из
трех элементов:
![]() способов. При необходимости эти способы
способов. При необходимости эти способы
можно перебрать.
Перестановки
букв некоторого слова называют
анаграммами.
Открытые еще в ІІІ
веке до
нашей эры греческим грамматиком
Ликофроном анаграммы до сих пор привлекают
внимание языковедов, поэтов и любителей
словесности. Мастера словесных игр
помимо эрудиции и большого запаса слов
знают много секретов, связанных с
комбинаторными навыками, один из которых
– анаграммы. Часто требуется среди всех
перестановок выбрать те, которые обладают
определенным свойством. Например, среди
анаграмм слова «крот»,
которых всего
![]() ,
,
только одна, не считая самого слова«крот»,
имеет смысл в русском языке – «корт».
Кроме линейных
перестановок, можно рассматривать
перестановки круговые (или циклические).
В этом случае перестановки, переходящие
друг в друга при вращении, считаются
одинаковыми и не должны засчитываться.
Теорема
2: Число
круговых перестановок из
![]() различных элементов равно
различных элементов равно![]()
Пример
2: Сколькими
способами 7 детей могут стать в хоровод?
Решение.
Число линейных перестановок 7 детей
будет равно
![]() .
.
Если хоровод уже сформирован, тогда для
него существует 7 круговых перестановок,
переходящих друг в друга при повороте.
Эти перестановки не должны быть засчитаны,
поэтому круговых перестановок из 7
элементов будет![]() .
.
Размещения без
повторений.
Определение
7: Пусть
имеется
![]() различных предметов. Расстановки из
различных предметов. Расстановки из![]() элементов по
элементов по![]() элементов (
элементов (![]() )
)
называютсяразмещениями
без повторений.
Обозначают:
![]() .
.
Здесь имеется в виду, что элементы в
расстановках не повторяются.
В
данном определении существенной является
следующая позиция: две расстановки
различны, если
они отличаются хотя бы одним элементом
или порядком элементов.
Приведем
еще одно определение размещений,
эквивалентное исходному, более простое
для понимания.
Определение
8: Конечные
упорядоченные множества называются
размещениями.
Теорема
3: Количество
всех размещений из
![]() элементов по
элементов по![]() элементов без повторений вычисляется
элементов без повторений вычисляется
по формуле:
![]() . (2)
. (2)
Доказательство.
Пусть имеется произвольное множество
![]() ,
,
состоящее из![]() элементов. Необходимо выбрать из этого
элементов. Необходимо выбрать из этого
множества![]() различных элементов. Причем, важен
различных элементов. Причем, важен
порядок выбора.
Выбор
элементов осуществляется поэтапно.
Первый элемент расстановки можно выбрать
![]() различными способами. Тогда из оставшихся
различными способами. Тогда из оставшихся
элементов множества![]() второй элемент расстановки выбирается
второй элемент расстановки выбирается![]() способом. Для выбора третьего элемента
способом. Для выбора третьего элемента
возможно![]() способа и т.д. Тогда для выбора
способа и т.д. Тогда для выбора![]() –
–
го элемента имеем![]() способ. Следовательно, согласно правилу
способ. Следовательно, согласно правилу
умножения, количество таких расстановок
будет равно:
![]() .
.
По
определению, такие расстановки являются
размещениями. Что и требовалось доказать.
Пример
3: Собрание
из 25 человек выбирает президиум из 3
человек: 1) председатель, 2) заместитель,
3) секретарь. Сколько возможно вариантов
выбора президиума?
Решение.
Выбирая трех человек из 25, замечаем, что
важен порядок выбора, поэтому количество
президиумов будет равно:
![]() .
.
Замечание:
Число размещений без повторений можно
также находить по формуле:
 . (3)
. (3)
Если
в знаменателе дроби из формулы (3)
![]() ,
,
то принято считать![]() .
.
Замечание:
Формула (3) отличается компактностью,
но при решении задач удобнее использовать
формулу (2). Дробь, стоящая в правой части
формулы (3), может быть сокращена до
целого числа. Это число равно числу из
правой части формулы (2).
Пример
4: Сколько
можно составить двухбуквенных слов
(буквы не повторяются) из 33 букв русского
алфавита?
Решение.
В данном случае мы имеем дело не со
словами в лингвистическом понимании,
а с буквенными комбинациями произвольного
состава.
Тогда количество
различных комбинаций из 2 букв, выбранных
из 33 букв алфавита, будет равно:
 .
.
В
данном случае важен порядок букв. Если
поменять 2 буквы в слове, то получим
новое слово.
Замечание:
Перестановка без повторений – это
частный случай размещений без повторений
при
![]() .
.
Можно сказать, что перестановка из![]() элементов – это размещение из
элементов – это размещение из![]() элементов по
элементов по![]() элементов:
элементов:
![]()
В
некоторых задачах по комбинаторике не
имеет значения порядок расположения
объектов в той или иной совокупности.
Важно лишь то, какие именно элементы ее
составляют. В таких ситуациях мы имеем
дело с сочетаниями.
Сочетания без
повторений.
Определение
9: Сочетания
без
повторений из
![]() элементов некоторого множества по
элементов некоторого множества по![]() элементов (
элементов (![]() )
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком
элементов. Обозначают:
![]() (от французского словаcombinaison
(от французского словаcombinaison
– сочетание).
В
данном случае в расстановках важен
состав, а не порядок элементов
в подмножестве. Если две расстановки
отличаются только порядком следования
элементов, то с точки зрения сочетаний
они не различимы. Элементы в этих
расстановках не повторяются.
С
точки зрения теории множеств определение
сочетаний можно сформулировать иначе.
Определение
10: Конечные
неупорядоченные множества называются
сочетаниями.
Таким образом,
сочетания – это такая выборка элементов,
при которой их порядок совершенно не
важен.
Сочетаний
из
![]() элементов по
элементов по![]() элементов должно быть меньше, чем
элементов должно быть меньше, чем
соответствующих размещений. Это следует
из того, что не надо засчитывать
расстановки одинакового состава.
Теорема
4: Число
сочетаний
![]() находится по следующей формуле:
находится по следующей формуле:
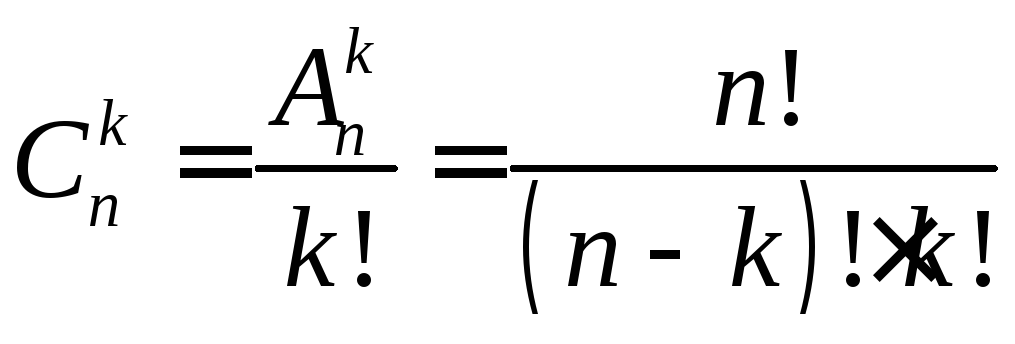 . (4)
. (4)
Доказательство.
Если из произвольного
![]() -элементного
-элементного
множества выбраны![]() элементов, то их можно пронумеровать
элементов, то их можно пронумеровать
номерами![]() числом способов, равным
числом способов, равным![]() .
.
Оставшиеся![]() элементов можно занумеровать номерами
элементов можно занумеровать номерами![]() ,
,![]() ,
,
…,![]() всего
всего![]() способами. Кроме того, сам отбор
способами. Кроме того, сам отбор![]() элементов из
элементов из![]() элементов можно осуществить
элементов можно осуществить![]() способами. Таким образом, мы получили
способами. Таким образом, мы получили
![]()
вариантов нумерации полного множества
из
![]() элементов, которых всего
элементов, которых всего![]() .
.
Поэтому имеем![]() ,
,
откуда получаем:
 .
.
Теорема доказана.
Замечание:
Дробь, стоящая в правой части (4), может
быть сокращена до целого числа.
Из формулы числа
сочетаний следует:
![]() ,
,
![]() ,
,![]() .
.
Формула
(4) может быть преобразована к виду:
![]() .
.
Отсюда видно, что число размещений![]() в
в![]() раз больше числа соответствующих
раз больше числа соответствующих
сочетаний![]() .
.
Другими словами, чтобы посчитать все
сочетания![]() ,
,
нужно исключить из всех размещений![]() подмножества, отличающиеся порядком
подмножества, отличающиеся порядком
(их будет![]() штук), т.е.
штук), т.е.![]() делят на
делят на![]() .
.
Пример
5: Сколькими
способами можно выбрать 3 различные
краски из имеющихся пяти.
Решение.
Порядок выбора красок не важен. Важно
только какие краски выбраны. Поэтому
количество вариантов равно:
![]() .
.
Пример
6: Сколькими
способами можно пошить трехцветные
полосатые флаги, если имеется материал
пяти различных цветов.
Решение.
Порядок выбора полос важен, поэтому
количество таких флагов равно:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
