Как найти количество верных знаков

Как найти количество верных знаков

Приближенное
число можно
представить в виде:

,
(1.1.1)

где
m–
величина старшего разряда, n–
текущий номер знака, отсчитываемый
слева направо.
Говорят, что

первых знаков приближенного числа
верные, если абсолютная погрешность

удовлетворяют условию:
,
то есть меньше половины соответствующего
разряда. Подбирается минимальное число
вида

большее,
чем

и сравниваются разряды.

1.2. Погрешность функций



Пусть дана функция

от n
приближенных значений
,
погрешности которых известны. Требуется
определить погрешность функции
.
,
где
–
абсолютная погрешность приближенной
величины
.
Если
,
то разность, стоящую в формуле можно
оценить в линейном приближении:

Отсюда следует
оценка погрешности:

,

(1.2.1)

1.3. Погрешность простейших функций двух переменных

Погрешность суммы:


Погрешность
разности:

При

качество измерений разности ухудшается.

Замечание:
Абсолютная
погрешность суммы и разности n
приближенных
величин равна сумме их абсолютных
погрешностей.

Погрешность
произведения:


То
есть предпочтительней сначала найти
относительную погрешность, а затем
искать абсолютную:

Замечания:

  • Относительная
    погрешность степени есть произведение
    модуля показателя на относительную
    погрешность основания степени:.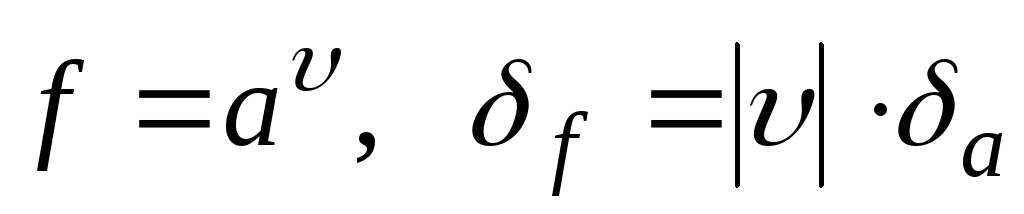

  • Относительная
    погрешность произведения n
    сомножителей
    приближенных величин равна сумме
    относительных погрешностей
    сомножителей:
    .
    Погрешность
    частного:


Все
замечания сделанные для произведения
справедливы и в этом случае.

1.4. Примеры и задания

Пример:
дано приближенное число 3457,0
погрешность
– 0,6.
Найти число верных знаков. Цифра 3 входит
в число с весом 103,
(1.3) то есть m=3.
,
минимальное k=1,

,
то есть верны три знака

Пример:
Дан куб, сторона которого
,
измерена с точностью
.
Определить погрешности измерения
поверхности и объема куба:

Пример.
Расчет погрешности функции трех
переменных (1.2.1):

,
,
.

.

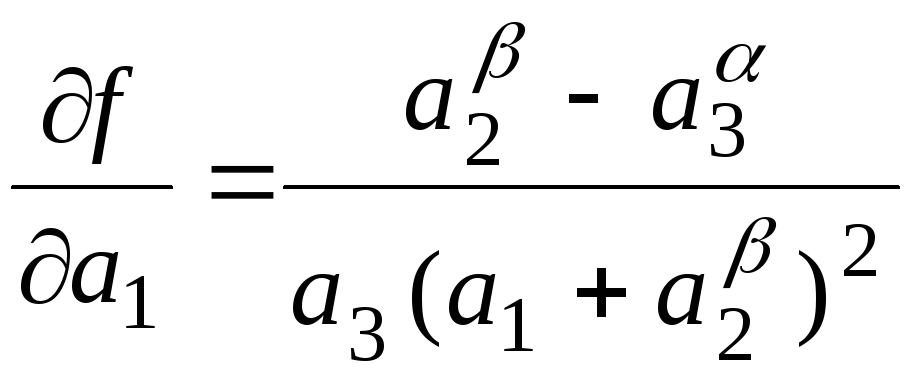Пример.
Катеты прямоугольного треугольника
см.
и
см.
измерены с погрешностью
см.
Определить погрешность измерения
гипотенузы с.

см.,
,

,
см.

В
каждом варианте задания три задачи,
ниже приведены последовательно первая,
вторая и третья задачи вариантов.

А.
Найти абсолютную и относительную ошибки
выражения , где
,

и

– приближенные величины данные с
погрешностями

– соответственно:

1),.
2)
,.

3)
,

.

4)

,.

5)

,.
6)
,

7)

,.
8)
,

.
9)
,

.

10)

,

.
11)
,

.
12)
,.

13)

,.
14)
,.

15)

,.
16.
,

.

Б.
Дано приближенное число и его погрешность.
Найти количество верных знаков:

  1. 23,587;
    0,08 . 2) 13,58; 0,07. 3) 103,58; 0,03. 4) 1655; 6.

5) 323,07; 0,06. 6) 43,837;
0,008. 7) 16,402; 0,009. 8) 13,540; 0,006.

9) 31,541; 0,003. 10) 13,42;
0,03. 11) 137,5; 0,08. 12) 134; 20.

13) 3457,0; 0,6. 14) 4657; 8.
15) 16,47; 0,07. 16) 130,6; 0,06.

В.
Дана геометрическая фигура. Определить
в трехмерном случае объем и полную
поверхность, а в плоском случае площадь
и периметр. Погрешность определения
размеров линейных элементов равна 1см:

  1. Равнобедренная
    трапеция со сторонами основания, равными
    20 и 30см. и высотой равной 12см.

  2. Правильная
    четырехугольная пирамида со стороной
    основания равной 10см. и высотой равной
    12см.

  3. Конус с высотой
    равной 30см. и радиусом равным 40см.

  4. Прямоугольный
    параллелепипед с высотой 30см стороной
    основания 60см и диагональю основания
    100см.

  5. Цилиндр с главной
    диагональю равной 100см. и радиусом
    равным 40см.

  6. Равнобедренная
    трапеция со сторонами основания, равными
    20 и 80см. и высотой равной 40см.

  7. Правильная
    четырехугольная пирамида со стороной
    основания равной 60см. и высотой равной
    40см.

  8. Прямоугольный
    параллелепипед с высотой 25см, стороной
    основания 60 и диагональю основания
    100см.

  9. Равнобедренная
    трапеция со сторонами основания, равными
    34 и 58см. и высотой равной 5см.

  10. Правильная
    четырехугольная пирамида со стороной
    основания равной 120см. и высотой равной
    80см.

  11. Конус
    с высотой равной 12см. и радиусом
    основания, равным 5см.

  12. Прямоугольный
    параллелепипед с высотой 20см стороной
    основания 50 и диагональю основания
    130см.

  13. Цилиндр с образующей
    равной 60см. и главной диагональю равной
    100см.

  14. Равнобедренная
    трапеция со сторонами основания, равными
    20 и 32см. и высотой равной 8см.

  15. Правильная
    четырехугольная пирамида со стороной
    основания равной 24см. и высотой равной
    5см.

  16. Прямоугольный
    параллелепипед со стороной основания
    12см, его диагональю 13см и высотой 40см.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Лабораторная работа №1

Методы оценки погрешностей

  I.  Описание работы

Тема: Методы оценки погрешностей приближенных величин.

Задание 1. Округляя точные числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближенных чисел.

Дано:

Найти:

Решение:

– приближенное значение числа A

Абсолютная погрешность:

Относительная погрешность:

Ответ: ;

Задание 2. Определить абсолютную погрешность приближенных чисел по их относительной погрешности .

Дано:

Найти:

Решение:

Абсолютная погрешность:

Ответ:

Задание 3. Решить задачу.

При измерении длины с точностью до 5 м получено км, а при определении другой длины с точностью до 0.5 см, получено метров. Какое измерение по своему качеству лучше?

Дано: Км, М, М, См

Сравнить: и

Решение: Итак, по 1-му измерению, результат Км = М с точностью до М ( – абсолютная погрешность величины ).

Тогда относительная погрешность: %

По 2-му измерению, результат Км с точностью до См =М ( – абсолютная погрешность величины ).

Тогда относительная погрешность: %

Так как , то измерение можно считать по качеству лучше, чем .

Ответ: измерение по качеству лучше, чем .

Задание 4. а) Определить количество верных знаков в числе , если известна его предельная абсолютная погрешность

Дано:

Найти:

Решение:

По определению, n первые значащие цифры являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда младшей цифры, считая слева направо.

Абсолютная погрешность: , поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.

Ответ: число X имеет две верных цифры в узком смысле (8 и 4), то есть

Б) Определить количество верных знаков в числе , если известна его предельная относительная погрешность .

Дано: %

Найти:

Решение:

Предельная абсолютная погрешность:

Только первая значащая цифра 1 числа A верна в узком смысле.

Ответ: число A имеет одну верную цифру в узком смысле (1), то есть

Задание 5. Найти предельные относительные погрешности, допускаемые при взятии вместо чисел 3.1, 3.14, 3.1416:

А) считая, что у них все записанные знаки являются верными;

Б) зная, что

Провести сравнения погрешностей и сделать необходимые выводы.

Дано: , ,

Найти:

Решение:

А) :

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

%

:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

%

:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

%

Б) Пусть (прервем запись числа на 7-м знаке после запятой и считаем полученное число точным значением числа ).

Тогда абсолютная погрешность первого представления числа : .

Относительная погрешность: %

Абсолютная погрешность второго представления числа : .

Относительная погрешность: %

Абсолютная погрешность третьего представления числа : %.

Относительная погрешность: %

Выводы:

1) Можно заметить, что , то есть ;

, то есть ;

, то есть

Иными словами, для трех чисел их «истинная» относительная погрешность ограничена предельной относительной погрешностью, определенной из условия верности знаков чисел. Причем, для каждого числа две оценки отличаются меньше, чем на порядок. Значит, предположение о верности всех знаков чисел Обосновано.

2) Сравнение относительных погрешностей чисел :

показывает,

Что числа Перечислены

В порядке увеличения точности представления числа ,

То есть точнее , точнее .

Ответ: а)

б)

Задание 6. Найти сумму приближенных чисел , , считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.

Дано: , ,

Найти:

Решение:

1) Считаем, что в числах , , все знаки верны в узком смысле, то есть

Число с наибольшей абсолютной погрешностью .

2) Остальные числа округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :

, абсолютная погрешность округления

, абсолютная погрешность округления

3) Сложим все эти числа, учитывая все сохраненные знаки:

4) Полученный результат округлим на один знак (формально):

, абсолютная погрешность округления

5) Полную абсолютную погрешность суммы будем складывать из трех компонентов:

A)  суммы предельных абсолютных погрешностей исходных чисел;

B)  абсолютной величины суммы ошибок округления слагаемых;

C)  заключительной погрешности округления результата.

– абсолютная погрешность суммы.

% – относительная погрешность суммы.

Ответ: ; %.

Задание 7. Найти предельную абсолютную и относительную погрешности при вычислении объема прямого кругового цилиндра, если значения его высоты и радиуса основания имеют все верные знаки.

Дано: ,

Найти:

Решение:

,

Примем

1) Так как в числах и все числа верны, то их абсолютные погрешности:

Число с наибольшей абсолютной погрешностью .

Число R округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :

, абсолютная погрешность округления (округления не требуется)

2) перемножим числа, учитывая все сохраненные знаки:

3) Полученный результат округляем, сохраняя столько значащих цифр, сколько верных цифр имеется в числе H, то есть 2 значащих цифры:

;

Абсолютная погрешность округления

4) Полную абсолютную погрешность произведения будем складывать из двух слагаемых:

A) предельной абсолютной погрешности произведения до его округления;

B) заключительной погрешности округления произведения.

Абсолютную погрешность произведения до округления вычислим на основе предварительно найденной относительной погрешности произведения округленных сомножителей:

%.

Полная абсолютная погрешность

Теперь перейдем к искомому объему.

(Здесь полученный результат округляем до трех значащих цифр).

– предельная абсолютная погрешность объема.

% – предельная относительная погрешность объема.

Ответ: , , %

Задание 8. Привести пример потери точности при вычитании двух близких чисел.

Решение:

Пусть и – два близких числа; примем, что у них одинаковое число знаков после запятой.

Считаем, что все знаки в числах и верны в узком смысле. Тогда абсолютные погрешности:

Относительные погрешности:

%

%

Так как , то

Абсолютная погрешность результата:

Относительная погрешность результата: %

При вычитании двух близких чисел и относительная погрешность возросла на 3 порядка!

Лабораторная работа №2

Метод Гаусса

  I.  Описание работы

Тема: Решение системы линейных неоднородных алгебраических уравнений методом Гаусса (схема единственного деления).

Задание. Решить систему трех уравнений с тремя неизвестными с точностью искомых неизвестных до .

Промежуточные вычисления вести с двумя запасными знаками.

,

Решение:

Исходные данные и все результаты вычислений запишем в таблицу 1.

Прямой ход

1.  Записываем коэффициенты данной системы в трех строках и четырех столбцах раздела 1 таблицы 1.

2.  Суммируем все коэффициенты по строке и записываем сумму в столбце (столбец контроля), например .

3.  Делим все числа, стоящие в первой строке, на и результаты записываем в 4-й строке раздела 1.

4.  Вычисляем и делаем проверку, если вычисления ведутся с 6 и более знаками после запятой, то числа и не должны отличаться более, чем на единицу последнего разряда:

5.  По формулам вычисляем коэффициенты :

Результаты записываем в первые две строки раздела:

6.  Делаем проверку. Сумма элементов каждой строки не должна отличаться от более, чем на 1-2 единицы последнего разряда. Заметим, что ,

,

,

7.  Делим все элементы 1 строки раздела 2 на и результаты записываем в 3 строке раздела 2.

8.  Делаем проверку:

9.  По формулам вычисляем :

Результаты записываем в 1 строку раздела 3.

10. Делаем проверку:

,

11. Делим все элементы 1 строки раздела 3 на и результаты записываем в следующей (второй) строке этого раздела.

12.  Делаем проверку:

Обратный ход

1.  В разделе 4 записываем единицы

2.  Записываем .

3.  Для вычисления и используем лишь строки разделов, содержащие 1.

4.  Вычислим по формуле: .

5.  Вычислим по формуле:

.

6.  Аналогично проводим обратный ход в контрольной системе. Записываем ,

вычисляем и с заменой и на и соответственно:

Делаем обычную проверку по строкам – должно быть , с точностью до 1-2 единиц последнего разряда.

Действительно:

Заполним таблицу 1 результатами вычислений:

Таблица 1

Раз

Дел

1

1

2

3

2

2

3

3

3

4

1

1

1

1

1

Округлим полученное решение до , по требованию задачи:

Окончательную проверку точности полученного решения системы выполним подстановкой этого решения в систему. Должно получиться приближенное тождество с точностью до .

Ответ:

< Предыдущая   Следующая >
Источник

Значащие цифры  десятичного числа – это все его цифры, начиная с первой ненулевой слева.

Пример 1

x = 0.002036,    цифры 2036 являются значащими;

x = 2.27×106,     значащими цифрами являются цифры 2, 2, 7;

x = 2270000,     все цифры этого числа являются значащими.

Значащая цифра в записи числа верна, если абсолютная погрешность числа меньше или равна пяти единицам разряда, следующего за этой цифрой.

Пример 2

Определить, сколько верных значащих цифр содержит число:

x = 0.002306 ± 0.00001.

Для определения числа верных значащих цифр запишем x и Dx таким образом, чтобы легко было сравнить разряды этих чисел:

x     = 0.002306, абсолютная погрешность Dx = 0.00001.

x     = 0.002306,

Dx  = 0.00001.

Третья значащая цифра (0) не может быть верной, так как она одного порядка с погрешностью. Верными могут быть цифры, которые стоят перед ней (2, 3). Цифра 3 будет верной, если Dx £ 0.00005. В нашем случае это условие выполнено, следовательно, 2, 3 – верные значащие цифры.

Цифры в записи числа, следующие за верными, называются сомнительными.

Пример 3

x     = 1.121 ± 0.003;

x     = 1.121;

Dx  = 0.003.

В числе x = 1.121 три верные значащие цифры (1, 1, 2) и одна сомнительная (1).

Пример 4

x     = 0.002306 ± 0.00007;

x     = 0.002306;

Dx  = 0.00007.

В числе x = 0.002306 одна верная значащая цифра (2), три сомнительные (3, 0, 6).

Пример 5

x     = 12.3 ± 0.5;

x     = 12.3;

Dx  =   0.5.

В числе x = 12.3 три значащие цифры, две верные значащие цифры (1, 2), одна сомнительная (3).

Пример 6

x     = 12.3 ± 0.8;

x     = 12.3;

Dx  =   0.8.

В числе x = 12.3 одна верная значащая цифра (1), две сомнительные (2, 3).

При записи абсолютной и относительной погрешностей используют, как правило, одну-две значащие цифры. Приближенные числа принято записывать следующим образом: сначала записывают все верные значащие цифры, затем одну-две сомнительные. То есть в записи приближенного числа, как правило, число значащих цифр на одну-две больше, чем число верных значащих цифр.

Практическое правило. Одна верная значащая цифра в записи числа соответствует приблизительно относительной погрешности 10 %. И наоборот, относительная погрешность 10 % соответствует приблизительно одной верной значащей цифре. Две верные значащие цифры соответствуют относительной погрешности 1 %, три верные значащие цифры – относительной погрешности 0.1 %.

Источник

Добавить комментарий