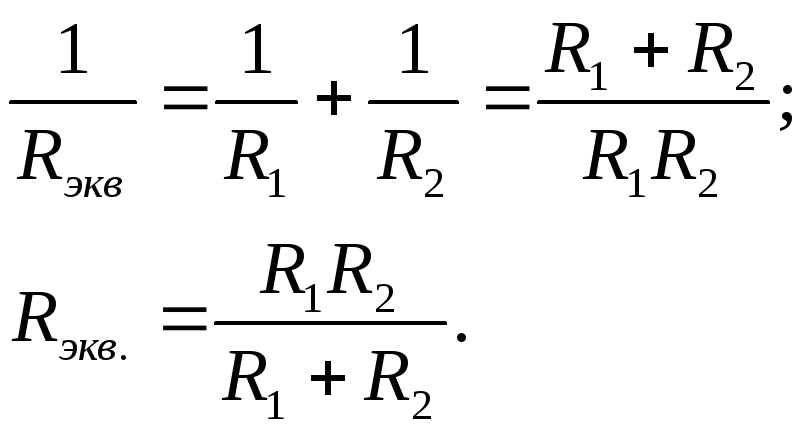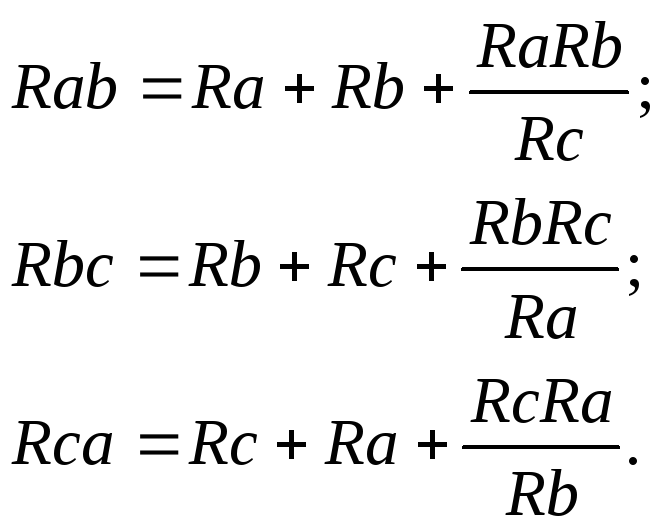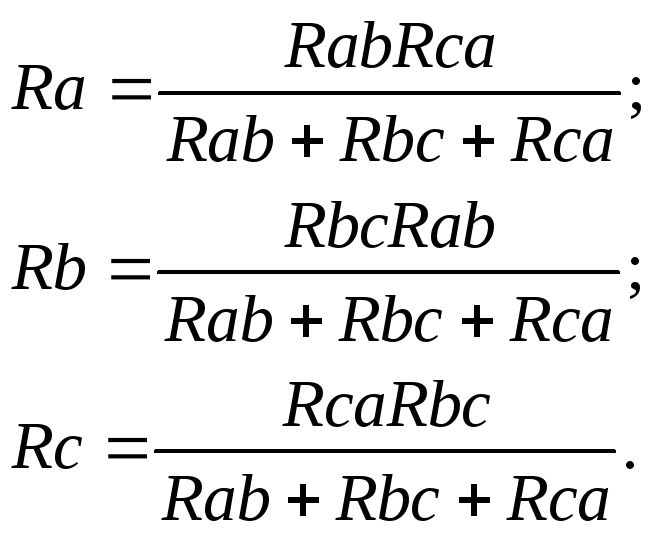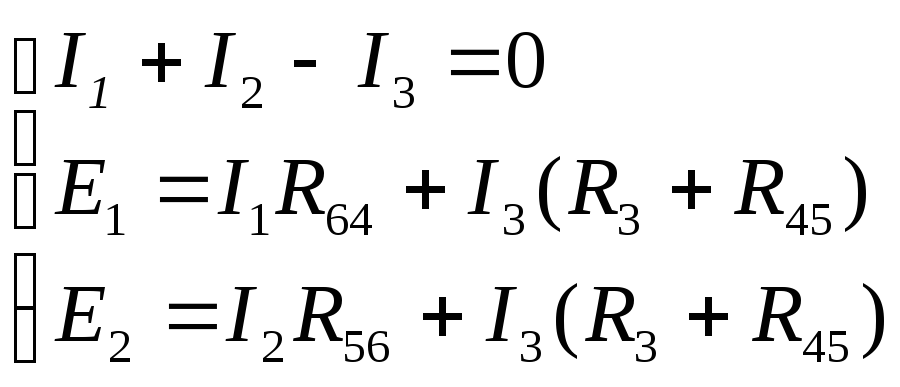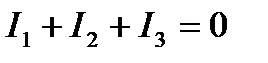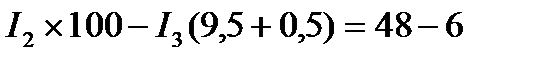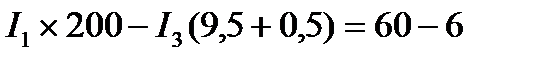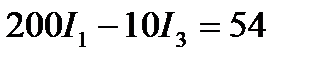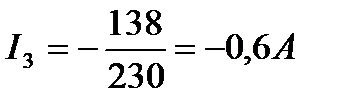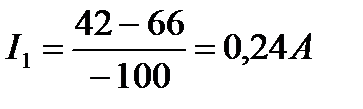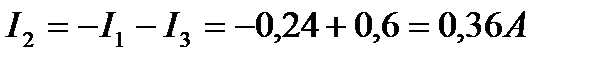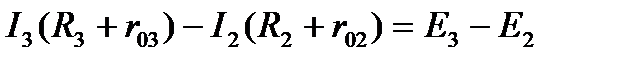Как найти количество ветвей в цепи

Электрическая цепь

Определение

Электрической цепью называется совокупность электротехнических устройств, создающих замкнутый путь электрическому току. Она состоит из источников (генераторов) энергии, приемников энергии (нагрузки) и соединительных проводов. В цепи могут быть также различные преобразователи (играют роль как роль источников, так и приемников), защитная и коммутационная аппаратура.

В источниках неэлектрические виды энергии преобразуются (в соответствии с законом сохранения энергии) в энергию электромагнитного поля. Так, например, на гидроэлектростанциях энергия падающей воды (энергия гравитационного поля) преобразуется в энергию электромагнитного поля. В приемниках энергия электромагнитного поля преобразуется в тепловую и другие виды энергии. Кроме того, некоторая часть энергии запасается в электрических и магнитных полях цепи.

Электромагнитные процессы в электрической цепи описываются с помощью понятий о токе, напряжении, электродвижущей силе (ЭДС), сопротивлении, индуктивности и емкости. Буквенные обозначения этих, а также других величин, используемых в этом учебном пособии представлены в табл.1.1. Там же дана их русская транскрипция и единицы измерений. Заметим здесь, что ЭДС, токи и напряжения, изменяющиеся во времени, обозначаются строчными латинскими буквами е, i, u, а ЭДС, токи и напряжения, неизменные во времени, обозначаются заглавными латинскими буквами E, I, U.

Графическое изображение электрической цепи и ее элементов

Графическое изображение электрической цепи называется ее схемой. В схеме различают ветви, узлы и контуры. Ветвь – это часть схемы, состоящая только из последовательно соединенных источников и приемников. Узел – точка схемы, в которой сходятся не менее трех ветвей (ветви начинаются и заканчиваются на узлах цепи). Контур – часть схемы, образованная ветвями; число контуров определяется числом вариантов обходов по ветвям цепи. На рис.1.1 даны структурные схемы трех электрических цепей и указано количество ветвей узлов и контуров в каждой из них.

Принятые в настоящем учебном пособии графические обозначения основных элементов цепи, показаны на рис.1.2.

На этом рисунке : 1 — источник ЭДС; 2 — источник тока; 3 — соединительный провод; 4 — сопротивление R цепи; 5 — индуктивность L цепи; 6 — емкость С цепи; 7 — двухполюсник (цепь с неизвестной структурой, имеющая два входных зажима).

В цепях постоянного тока (рис.1.3,а) направление действия ЭДС источника принято указывать в сторону того зажима, на котором образуются положительные заряды. Направление тока во внешней цепи принято указывать от положительно заряженного полюса (зажима) источника к отрицательно заряженному. Направление действия напряжения в приемнике всегда указывают в ту же сторону, что и направление действия тока.
В цепях синусоидального тока (рис.1.3,б) принято обозначать направления ЭДС тока и напряжения, используя положительный полупериод тока, при котором ток не изменяет своего направления. При этом картина этих направлений получается аналогичной с цепью постоянного тока.

Законы электрических цепей

Законы электрических цепей

Ими являются первый и второй законы Кирхгофа.
Первый закон Кирхгофа относится к узлам цепи: в любой момент времени алгебраическая сумма токов в узле равна нулю

где К – число ветвей, подходящих к узлу (три и более).
Токи, подходящие к узлу, и токи, отходящие от узла, имеют противоположные знаки. Будем считать подходящие к узлу токи положительными и брать их в уравнениях первого закона Кирхгофа со знаком (+), а отходящие от узла, – отрицательными и брать их со знаком (−) . Первый закон Кирхгофа фактически является следствием известного из курса физики принципа непрерывности электрического тока, согласно которому линии тока всегда замкнуты и не имеют ни начала, ни конца.

Пример 1.1. На рис.1.4,а показан узел цепи с пятью подходящими к нему ветвями. Требуется составить для этого узла уравнение по первому закону Кирхгофа.
Решение. На основании формулы (1.1) имеем

Таким образом, всегда сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла.

Второй закон Кирхгофа относится к контурам цепи: в любой момент времени алгебраическая сумма ЭДС всех источников энергии контура равна алгебраической сумме напряжений на всех приемниках этого контура.

где Q – число источников ЭДС в контуре; N – число приемников контура.
Для составления уравнения по второму закону Кирхгофа необходимо предварительно (произвольно) выбрать направление обхода этого контура. Те ЭДС и напряжения, направления которых совпадают с выбранным 9
направлением обхода, считаются положительными и берутся в уравнении со знаком (+), а остальные − со знаком (−).

Пример 1.2. На рис.1.4,б показан один из контуров сложной электрической цепи. Направления действия ЭДС источников и напряжений на приемниках известны. Требуется составить для этого контура уравнение по второму закону Кирхгофа.
Решение. Для этого предварительно выбираем (произвольно) направление обхода контура и в соответствии с формулой (1.2) составляем следующее уравнение:

Здесь е₂ и е₃ , u₁ и u₂ взяты со знаком (−), так как их направление действия не совпадает с направлением обхода контура; е₁, u₄ и u₃ взяты со знаком (+), так как их направление действия совпадает с направлением обхода контура.

Параметры электрических цепей

Параметры электрических цепей

Любая электрическая цепь и каждый ее элемент в отдельности обладают тремя параметрами: сопротивлением R, индуктивностью L и емкостью С.
Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую. Количество тепловой энергии W_Т , выделяющееся в сопротивлении R при протекании тока i в течение времени t, определяется соотношением (1.3) и измеряется в джоулях (Дж):

Величина сопротивления любого элемента цепи определяется как отношение постоянного напряжения на этом элементе к постоянному току в нем и измеряется в омах (Ом):

Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладает любой проводник с током или система проводов. Количество этой энергии W_M , накопленной в цепи, зависит от величины тока i и измеряется в джоулях (Дж):

Эта энергия не преобразуется в тепло, а существует в цепи в виде некоторого запаса. Когда ток в цепи равен нулю, запаса энергии магнитного поля в ней нет.
Величина индуктивности определяется как отношение потокосцепления цепи ψ к току i и измеряется в генри (Гн)

Потокосцеплением называется сумма магнитных потоков всех витков катушки. В простейшем случае для катушки на замкнутом стальном сердечнике можно считать, что ее потокосцепление есть магнитный поток Ф, умноженный на число витков w: Ψ = Ф w.

Емкость С характеризует способность цепи накапливать энергию электрического поля. Такой способностью обладают любые два провода, разделенные диэлектриком, например провод, висящий над землей, любые два провода линии передачи.
Количество энергии электрического поля W _Э , накопленной в цепи с емкостью С , зависит от величины напряжения между проводами и измеряется в джоулях (Дж):

Эта энергия не может преобразовываться в тепловую, а существует в цепи в виде некоторого запаса. Если напряжение между проводами отсутствует, то и запаса энергии электрического поля в цепи нет.
Величина емкости С определяется как отношение электрического заряда q одного из проводов к напряжению u между ними и измеряется в фарадах (Ф):

В табл.1.2 представлены конструкции некоторых простейших электротехнических устройств и формулы для расчета их параметров. В этой табл.: γ − удельная электрическая проводимость провода (1/Ом⋅м); μ _a − абсолютная магнитная проницаемость стали (Гн/м); ε _a абсолютная диэлектрическая проницаемость диэлектрика (Ф/м); l −длина провода, средняя длина стального сердечника, расстояние между пластинами конденсатора (м); S – площадь поперечного сечения провода, площадь поперечного сечения стального сердечника, площадь пластины конденсатора (м 2 ); w – число витков обмотки; Ф – магнитный поток в сердечнике, измеряемый в веберах (Вб).

Понятие о линейных и нелинейных электрических цепях

Если γ, μ_a и ε_a (и следовательно R, L и С ) являются постоянными величинами и не зависят от тока (или напряжения), то такие устройства, называются линейными, а цепи, их содержащие, называются линейными цепями. Именно такие цепи рассматриваются в данном учебном пособии.
Существует, однако, целый ряд устройств, у которых γ, μ_a и ε_a зависят от величин токов (или напряжений). Таковыми, в частности, являются все полупроводниковые приборы, катушки на насыщенных стальных сердечниках, нагревательные устройства с большим диапазоном изменения температур (электрическая дуга, лампы накаливания), конденсаторы с сегнетодиэлектриками. Цепи, содержащие такие устройства, называются нелинейными.

Свойства нелинейного элемента электрической цепи не могут быть выражены одним постоянным числом и поэтому описываются его характеристикой. Для сопротивлений это зависимости напряжения от тока (вольтамперные характеристики); для индуктивностей это зависимости потокосцепления от тока (веберамперные характеристики); для емкостей это зависимости электрического заряда от напряжения (кулонвольтные характеристики). На рис.1.5 показаны примеры характеристик некоторых линейных (ЛЭ) и нелинейных (НЭ) элементов цепи. Заметим, что характеристики всех линейных элементов цепи являются прямыми линиями, а нелинейных элементов – кривыми.

Идеальные элементы электрической цепи

Идеальные элементы электрической цепи

Любое электротехническое устройство содержит все три параметра: сопротивление R , индуктивность L и емкость С. Рассмотрим (рис.1.6), катушку, выполненную из провода с конечной проводимостью (это может быть и нить лампы накаливания, и обмотка трансформатора или электродвигателя).

При подаче на ее зажимы напряжения u на концах катушки появляются разноименные заряды (+)q и (−)q и в обмотке начинает протекать ток i. При этом вокруг витков обмотки возникает магнитное поле, характеризуемое потокосцеплением ψ. Таким образом, в соответствии с формулами (1.4), (1.6) и (1.8) рассматриваемая катушка обладает всеми тремя вышеуказанными параметрами.

Для удобства анализа и расчета электрических цепей вводят в рассмотрение такие элементы, которые при всех условиях обладают только одним параметром: только сопротивлением, только индуктивностью, только емкостью. Они называются идеальными.

Графическое изображение идеальных элементов электрической цепи показано на рис.1.2 позициями 4, 5 и 6. В природе таких элементов не существует, но есть устройства, по своим свойствам близкие к идеальным. Реостат (резистор) при низких частотах обладает практически только сопротивлением R, а индуктивностью L и емкостью С этого устройства можно пренебречь. Катушка индуктивности на замкнутом ферромагнитном сердечнике с малыми тепловыми потерями в нем обладает на низких частотах практически только индуктивностью L, а сопротивлением R и емкостью С такой катушки можно пренебречь. Конденсатор с малыми внутренними тепловыми потерями обладает практически только емкостью С, а его активной проводимостью G и индуктивностью L можно пренебречь.

Заметим, что реостат, катушку индуктивности и конденсатор широко используют для имитации (моделирования) идеальных элементов при проведении лабораторного практикума по теории цепей.

Любое реальное электротехническое устройство можно изобразить в виде электрической схемы, состоящей из комбинации идеальных элементов и, следовательно, произвести его электрический расчет. В табл.1.3 приведено несколько примеров изображения реальных устройств в виде электрических схем.

Соотношение между током и напряжением в идеальных элементах цепи

Прежде чем приступать к расчету сколько-нибудь сложных электрических цепей, следует выяснить, каким образом связаны между собой ток и напряжение в каждом из идеальных элементов цепи. Эти соотношения, известные из курса физики, приведены в табл.1.4. Они имеют всеобщий характер и справедливы для цепей, у которых ток и напряжение изменяются во времени по любому закону. Это важнейшие формулы теории цепей, которые встретятся нам много раз в этом учебном пособии ∗. Заметим здесь, что формулы позиции 1 соответствуют закону Ома, формулы позиции 2 вытекают из закона электромагнитной индукции, а формулы позиции 3 следуют из определения электрической емкости.

Из табл.1.4 видно, что только в сопротивлении R ток и напряжение связаны между собой алгебраическим соотношением. Между током и напряжением в индуктивности и емкости имеют место интегро-дифференциальные соотношения.
Пример 1.3. В цепи с идеальной индуктивностью (рис.1.7,а) действует пилообразный периодический ток (рис.1.7,б). Требуется определить форму приложенного напряжения.

Решение. Для нахождения графика напряжения используем соотношение u = di/dt (поз.2 табл.1.4), из которого следует, что форма кривой напряжения соответствует производной от тока по времени. Из курса математики известно, что графически производная di/dt определяется в каждой точке кривой тока, как тангенс угла наклона касательной к этой кривой относительно оси t.
В нашем примере на участке от 0 до T/2 кривая тока представляет собой прямую, проходящую через начало координат под острым углом α 1 90°, и поэтому производная di/dt на этом участке есть постоянная и отрицательная величина. tgα ₂ = tg(180 — α ₁) = -tgα ₁
Таким образом, график искомого напряжения представляет собой отрезки прямых, меняющих каждую половину периода свой знак, как это показано на рис.1.7,б.

Основная задача анализа электрической цепи

Анализ электрических цепей осуществляется с помощью законов Кирхгофа. При этом можно преследовать различные цели. Например, определять напряжения во всех ветвях цепи по их известным параметрам. Можно также определять необходимые ЭДС всех источников энергии по известным токам и параметрам приемников и источников. Для придания нашему курсу логической стройности основной задачей анализа (расчета) будем считать определение токов во всех ветвях цепи по известным параметрам всех источников и известным параметрам всех приемников. Научившись решать эту задачу, мы сможем решать и другие задачи, связанные с анализом и расчетом электрических цепей.

Источник

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.

Простым языком электрическая схема это упрощенное изображение электрической цепи.

Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.  

Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.

В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.

  Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.

Ветви присоединённые к одной паре узлов называются параллельными.

Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.

Узел – место соединения трёх и более ветвей. 

• Узел A
• Узел B
• Узел C
• Узел D

Точки К и Е не являются узлами.

Методы расчета электрических цепей

Постановка
задачи: в известной схеме цепи с заданными
параметрами необходимо рассчитать
токи, напряжения, мощности на отдельных
участках. Для этого можно использовать
следующие методы:

• преобразования цепи;

• непосредственного применения законов
  Кирхгофа;

• контурных токов;

• узловых потенциалов;

• наложения;

• эквивалентного генератора.

Будем
рассматривать первых два метода.

1. Метод
   преобразования цепи. Суть метода: если
   несколько последовательно или (и)
   параллельно включенных сопротивлений
   заменить одним, то распределение токов
   в электрической цепи не изменится.

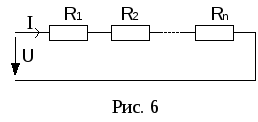
а)
Последовательное соединение резисторов.
Сопротивления включены таким образом,
что начало следующего сопротивления
подключается к концу предыдущего (рис.
6).

Ток
во всех последовательно соединенных
элементах одинаков.

З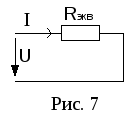аменим
все последовательно соединенные
резисторы одним эквивалентным(рис. 7.).

По
IIзакону Кирхгофа:

;

;

т.е.
при последовательном соединении
резисторов эквивалентное сопротивление
участка цепи равно сумме всех
последовательно включенных сопротивлений.

б)
Параллельное соединение резисторов.
При этом соединении соединяются вместе
одноименные зажимы резисторов (рис. 8).

В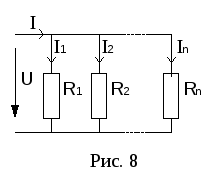се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.

По Iзакону Кирхгофа:.

По
закону Ома
.
Тогда.

Для
эквивалентной схемы (см рис. 7):
;
.

Величина
,
обратная сопротивлению, называется
проводимостьюG.

;=
Сименс (См).

Ч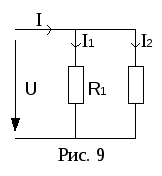астный
случай: параллельно соединены два
резистора (рис. 9).

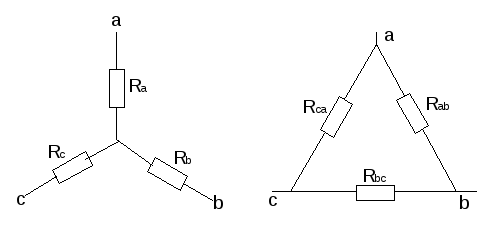
в)
Взаимное преобразование звезды (рис.10а)
и треугольник сопротивлений (рис. 10б).

–
преобразование звезды сопротивлений
в треугольник:

а)	б)
Рис. 10

–
преобразование “треугольника”
сопротивлений в “звезду”:

1. Метод
   непосредственного применения законов
   Кирхгофа. Порядок расчета:

• Определить
  число ветвей (т.е. токов) и узлов в схеме.

• Произвольно
  выбрать условно-положительные направления
  токов. Общее число уравнений должно
  быть равно числу неизвестных токов.

• Определить,
  сколько уравнений должно быть составлено
  по Iзакону Кирхгофа, а
  сколько – поIIзакону
  Кирхгофа.

• Составить
  уравнения для
  узлов
  поIзакону Кирхгофа и
  длянезависимых
  контуров (отличающихся друг от друга
  хотя бы на одну ветвь) – поIIзакону Кирхгофа.

• Решить
  система уравнений относительно токов.
  Если в результате ток получился
  отрицательным, то его действительное
  направление противоположно выбранному.

• Проверить
  правильность решения задачи, составив
  уравнение баланса мощности и смоделировав
  электрическую цепь средствами
  моделирующего пакета ElectronicsWorkbench.

Примечание:
если есть возможность, то перед
составлением системы уравнений по
законам Кирхгофа, следует преобразовать
“треугольник” сопротивлений в
соответствующую “звезду”.

Пример расчет электрических цепей постоянного тока

Расчет будем выполнять с применением
законов Кирхгофа, предварительно
преобразовав треугольник сопротивлений
в звезду.

П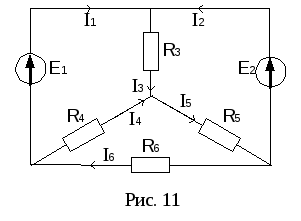ример.
Определить токи в цепи рис. 11, еслиE₁=160
В,E₂=100 В,R₃=100 Ом,R₄=100 Ом,R₅=150 Ом,R₆=40
Ом.

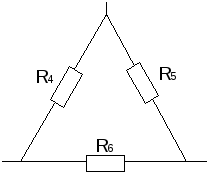
Преобразуем
треугольник сопротивлений R₄
R₅ R₆в звезду сопротивленийR₄₅
R₅₆ R₆₄,
предварительно указав условные
положительные направления токов в цепи
(рис. 12).

Ом;

Ом;

Ом.

а)	б)
Рис. 12

После
преобразования электрическая цепь
примет вид рис. 13 (в непреобразованной
части электрической цепи направления
токов не изменятся).

В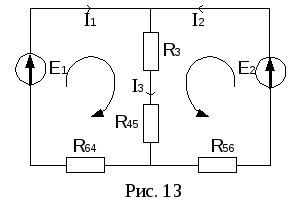полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:

Подставим
в полученную систему уравнений известные
значения ЭДС и сопротивлений:

Решая
систему уравнений любым способом,
определяем токи схемы электрической
цепи рис. 13:

А;А;А.

Переходим
к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:

;

А.

По Iзакону Кирхгофа:

;

А;

;

А.

Т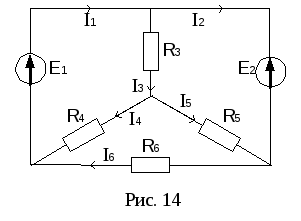окииполучились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).

Правильность
решения проверяем, составив уравнение
баланса мощности. Мощность источников
(учтем, что ЭДС источника E₂направленно встречно токуI₂,
протекающему через него):

Вт.

Мощность
потребителей:

Погрешность
вычислений в пределах допустимого
(меньше 5%).

Смоделируем
электрическую цепь рис. 11 средствами
моделирующего пакета ElectronicsWorkbench(рис. 15):

Рис.
15

При
сравнении расчетных результатов и
результатов моделирования, можно
увидеть, что они отличаются (различия
не превышают 5%), т.к. измерительные
приборы имеют внутренние сопротивления,
которые моделирующая система учитывает

Соседние файлы в папке Все что скинул препод

• #
• #
• #

  25.03.20169.01 Кб111Задача 1.xlsx

• #

  25.03.201610.02 Кб63зАДАЧА 2.xlsx

• #

  25.03.20168.97 Кб42Звезда с нулем.xlsx

• #
• #
• #

Расчёт электрической цепи постоянного тока методом узловых и контурных уравнений.

Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.

Порядок расчёта:

1. Произвольно задаёмся направлением токов в ветвях.

Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.

Красным выделены изменения после первого действия

Синим выделены изменения после третьего пункта

2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:

1. Обозначаем узлы буквами.
2. Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
   0=I1-I4-I6 (Полученное уравнение)
3. Повторяем пункт B ещё для двух узлов.
   0=-I3+I4+I5(Узел В)
   0=I3-I1-I2(Узел D)

3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы. Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.

3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)

3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)

3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.

Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3

Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5

Контур ABCA 0=I6*R6-I4*R4+I5*R5

4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.

Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.

Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.

I3=I1+I2(Узел D)

I5=I3-I4(Узел В)

I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:

Заменим токи I3 I5 I6 и получим уравнения с тремя токами :

Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:

40 = 71*I1 + 24*I2 + 14*I4

20 = 55*I1 + 93*I2 — 61*I4

0 = 60*I1 + 16*I2 — 81*I4

Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.

Правильность решения можно проверить с помощью баланса мощностей.

Метод узловых и контурных уравнений

Данный метод является одним из самых простейших методов расчёта электрических цепей постоянного тока любой сложности. Основывается на составлении уравнений по I и II законам Кирхгофа.

1. Определяем число ветвей m, узлов и контуров в электрической цепи. Число токов в цепи равно числу ветвей. Для каждой ветви выбираем условное направление тока и укажем их на схеме.

2. По первому закону Кирхгофа составляем уравнение для узлов в количестве n-1, где n – число узлов.

3. На основании II закона Кирхгофа составляем m-n+1 уравнений, где m-число ветвей,n-число узлов. Для обхода выбираем контуры с меньшим числом ветвей и содержащих хотя бы одну новую ветвь. Контур обходим по часовой стрелке.

4. Полученные уравнения объединяем в систему и решаем любым способом, известным из математики.

Дано: (рис. 14) Е₁=60 В; Е₂=48 В; Е₃=6 В; R₁=200 Ом; R₂=100 Ом; R₃=9,5 Ом; r₀₃=0,5 Ом; r₀₁=r₀₂ 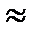0.

1. Сущность метода. Этот метод основан на применении первого и второго закона Кирхгофа, не требует никаких преобразований схемы и пригоден для расчёта любой цепи; в этом его преимущество.

Сколько же нужно составить уравнений для расчёта цепи? Очевидно, столько, сколько неизвестных величин, в нашем случае – токов. Поэтому начнём решение задачи с определения числа неизвестных токов.

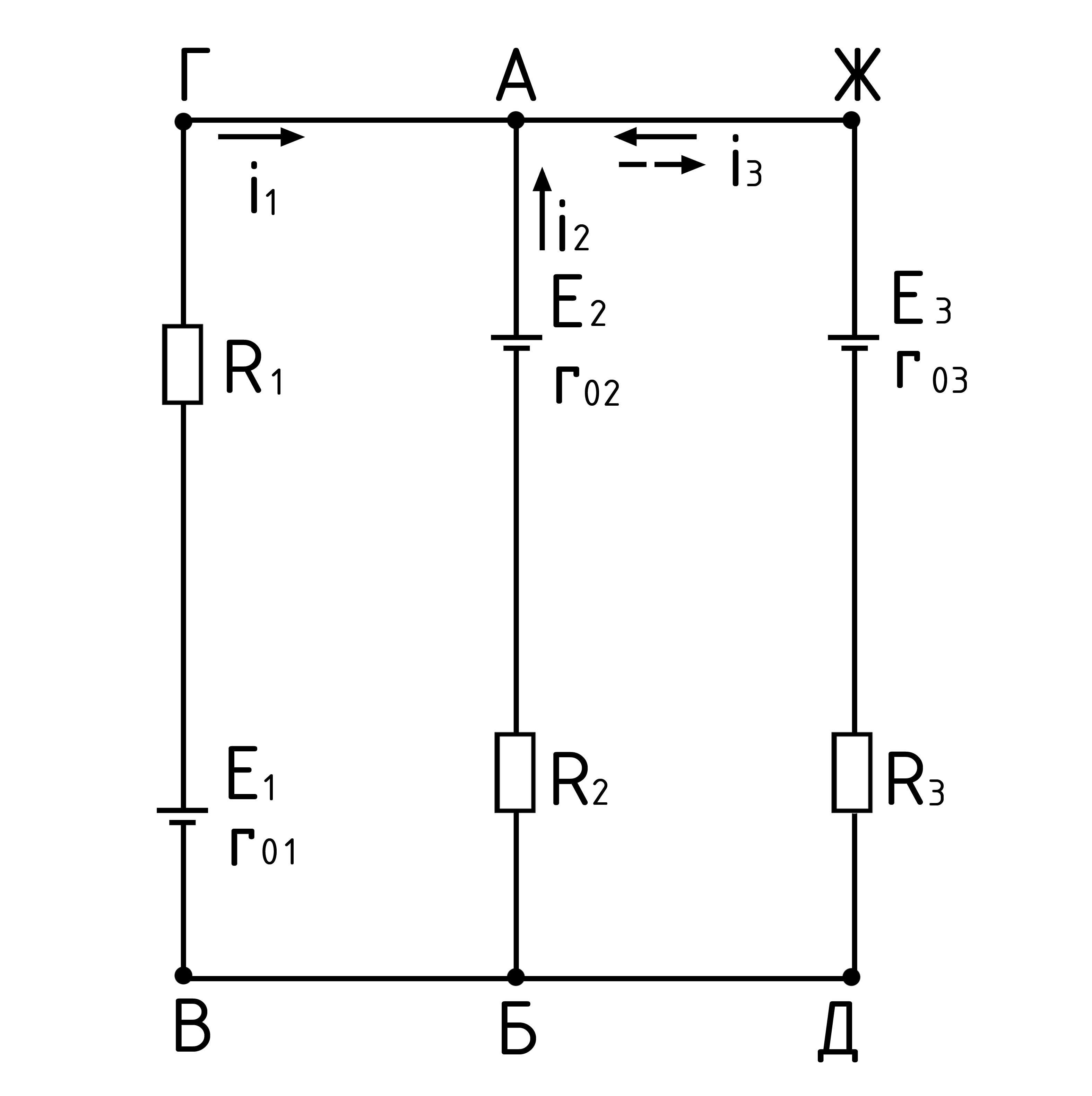
2. Определение числа неизвестных токов и выбор их направлений. Как известно, в каждом неразветвлённом участке цепи (ветви) ток имеет одно и тоже значение от начала до конца участка. В рассматриваемой цепи к узловым точкам А и Б присоединены три ветви: БВГА с током I₁, БА с током I₂, БДЖА с током I₃

Итак, число различных токов равно числу ветвей электрической цепи.

Как определить направления токов?

Нам уже известно, что в сложной цепи до её расчёта узнать направления всех токов нельзя. Поэтому в начале направления токов выбирают произвольно (положительные направления токов) и при выбранных направлениях составляют уравнения. Затем решают эти уравнения и определяют истинные направления токов по их алгебраическим знакам, а именно: токи, действительные направления которых обратны выбранным, выражаются отрицательными числами.

Так, в нашем случае можно заранее сказать, что не все выбранные направления токов (рис. 14, сплошные стрелки) совпадают с действительными, так как не могут все токи притекать к узлу А. Очевидно, что один или два тока выразятся отрицательными числами.

Итак, токи в уравнениях Кирхгофа являются алгебраическими величинами, знаки которых зависят от направлений токов.

3. Составление уравнений по законам Кирхгофа. В нашей задаче – три неизвестных тока I₁, I₂, I₃, для определения которых составим три уравнения.

Начнём с уравнений по первому закону Кирхгофа как более простых. Для цепи с n узлами можно составить n-1 независимое уравнение; для одного (любого) узла цепи уравнение не следует составлять, так как оно было бы следствием предыдущих.

В цепи на рис. 14 два узла, поэтому составим одно уравнение по первому закону Кирхгофа, например для узла А:

Два недостающих уравнения составим по второму закону Кирхгофа, выбрав для этого, например, контуры БАЖДБ и ВГЖДВ (чтобы уравнения были независимы, в каждый следующий контур должна входить одна новая ветвь, не входившая в предыдущий).

Приняв обход каждого контура по направлению движения часовой стрелки и учитывая правила знаков, получим:

;

.

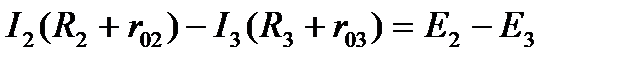
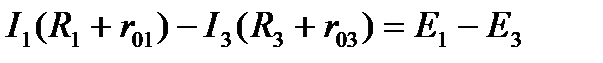
4. Вычисление токов. Подставив в уравнения значения сопротивлений и ЭДС, получим:

Итак, вычисление токов сводится к решению системы трёх уравнений с тремя неизвестными. Для этого, например, определим ток I₂ из уравнения и подставим его значение в уравнение:

;

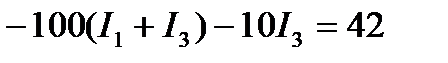
приведя подобные члены, получим:

.

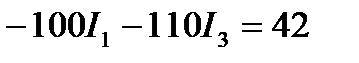
Получились два уравнения с двумя неизвестными: I₁ и I₃.

Умножив второе уравнение на и сложив его с уравнением с первым, получим:

,

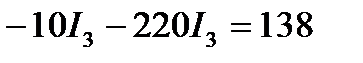
Подставив значение тока I₃ в уравнение , получим:

,

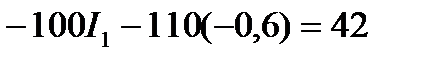
Ток I₂ определим из:

Ток I₁ и I₂ имеют положительные значения, а I₃ – отрицательное, следовательно, направления первых двух токов были выбраны правильно, а тока I₃ – неправильно.

Действительное направление тока I₃ указано пунктирной стрелкой на рис. 14. При этом сумма притекающих к узлу А токов I₁+I₂=0,24+0,36=0,6 А равна оттекающему току I₃=0,6 А.

*Дополнительные вопросы к задаче

1. Сколько электрических контуров имеют цепи, показанные на рис.14 ?

Электрическая цепь (рис.14) имеет три контура: ГАБВГ, ГЖДВГ и АЖДБА. Для составления двух уравнений по второму закону Кирхгофа необходимо и достаточно выбрать два контура. Проще всего выбрать контуры, образующие отдельные ячейки, в нашем случае ГАБВГ и АЖДБА. Число ячеек всегда равно числу независимых уравнений, которые надо составить по второму закону Кирхгофа.

Для расчёта цепи на рис.14 при помощи законов Кирхгофа надо составить пять независимых уравнений (цепь состоит из пяти ветвей). Цепь имеет (А, Б, В), значит, по первому закону Кирхгофа можно составить два независимых уравнения. Недостающие три уравнения нужно составить по второму закону Кирхгофа.

В цепи по рис.14 можно наметить шесть контуров (АВКА, АБВКА, АБМКА, АБВА, АБМВА и БМВБ), но независимые уравнения получаются только для трёх контуров, например для трёх ячеек: АВКА, АБВА, и БМВБ, в каждую из которых входит новая ветвь.

Итак, разветвлённая цепь электрическая цепь имеет больше контуров, чем нужно и можно использовать для составления уравнений.

2. Как вести расчёт, если заданы значения токов, но неизвестны другие параметры цепи?

Очевидно, что из трёх независимых уравнений , составленных для цепи на рис.14 , можно определить любые три неизвестные величины. например, при заданных значениях токов и сопротивлений можно определить ЭДС Е₁, Е₂ и Е₃, а по известным токам и ЭДС – величины трёх сопротивлений.

Итак, порядок расчёта цепи по методу уравнений Кирхгофа не зависит от того, какие величины заданы и какие неизвестны. Число неизвестных величин не должно быть больше числа независимых уравнений, которые можно составить по первому и второму закону Кирхгофа.

3. Следует ли принимать одинаковое направление обхода для всех контуров?

При составлении уравнений было выбрано одно и то же направление обхода этих контуров (по направлению движения часовой стрелки). Приняв для одного из них, например АЖДБА (рис. 14), противоположное направление обхода, получим:

Сравнивая уравнение (4.2) и (4.7), легко убедится, что они тождественны, так как различают только противоположными знаками всех членов уравнения.

Итак, для каждого контура направление обхода может быть выбрано произвольно.

4. Целесообразно ли предыдущую задачу решать методом уравнений Кирхгофа?

Электрическая цепь по рис. 15 имеет пять неизвестных токов, и для их вычисления потребовалась бы пять уравнений (два по первому и три по второму закону Кирхгофа).

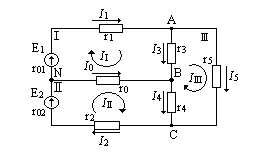
Решение системы из пяти не проще, чем вычисление токов в двух простых цепях по методу наложения.

В схеме (рис. 15) трехпроводной линии постоянного тока ЭДС источников Е₁ = 253в и Е₂ = 225в, их внутренние сопротивление r₀₁ = r₀₂ = 0,5 ом, сопротивления главных проводов r₁ = r₂ = 0,5 ом и нейтрального провода r₀ = 1 ом, сопротивления пассивных приемников энергии r₃ = 40 ом, r₄ = 20 ом и r₅ = 40 ом.

Определить токи, применив законы Кирхгофа.

В схеме имеются шесть ветвей и, следовательно, число неизвестных токов равно шести. Число узлов равно четырем.

Намечаем на схеме предполагаемые направления токов в ветвях. После этого составляем, основываясь на первый закон Кирхгофа, три независимых уравнения:

;

;

;

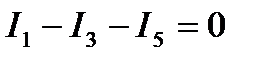
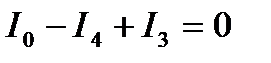
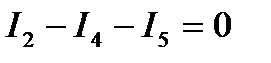
Недостающее уравнение для трех замкнутых контуров I, II и III составляем на основании второго закона Кирхгофа. Направление обхода контуров выбираем по часовой стрелке.

;

;

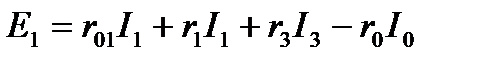
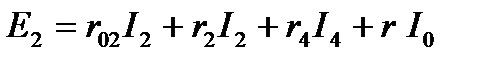
для контура III

.

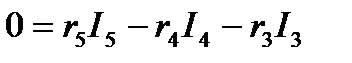
Решение системы уравнений с шестью неизвестными дает: I₃ = 6 a, I₅ = 11 a, I₄ = 10 a, I₂ = 21 a, I₁ = 17 a и I₀ = 4 a.

Найденные токи проверим, подставив их значения в уравнения, составленные на основании первого закона Кирхгофа:

Метод узловых и контурных уравнений

Вы будете перенаправлены на Автор24

Алгоритм расчета электрической цепи методом контурных и узловых уравнений

Метод узловых и контурных уравнений — самый простой метод расчета электрической цепи, который основан на составлении уравнений по первому и второму законам Кирхгофа.

Первый закон Кирхгофа звучит следующим образом: алгебраическая сумма токов в ветвях цепи, которые сходятся в каждом узле, равна нулю. При этом ток, направленный к узлу считается положительным, а направленный от него отрицательным. Сумма токов, которые направлены к узлу цепи равняется сумме токов, направленных от него. Таким образом получается, что в узел втекает столько же тока, сколько и вытекает из него (правило фундаментального закона сохранения заряда.

Второй закон Кирхгофа гласит — алгебраическая сумма напряжений на резистивных составляющих замкнутого контура цепи равняется сумме электродвижущих сил в составе данного контура. В том случае, когда источник электродвижущей силы отсутствует в контуре, суммарное падение напряжений равно нулю.

Порядок расчета электрической цепи методом узловых и контурных уравнений выглядит следующим образом:

1. Определяют количество неизвестных токов (количество ветвей цепи равняется число токов в ней).
2. Произвольно выбираются направление определенных токов и обозначаются на рассматриваемой схеме.
3. Составляется система уравнений согласно первому закону Кирхгофа, количество которых на единицу меньше количества узлов в рассматриваемой схеме.
4. Составляются недостающие, до общего количества, уравнения по второму закону Кирхгофа. Направления обхода тока, как правило, выбираются одинаковыми.
5. Определяются неизвестные токи, после чего решается получившаяся система уравнений. В том случае, когда рассчитанный (определенный) ток имеет отрицательную величину, это значит, что его направление противоположно направлению, которое было выбрано в пункте 2.
6. Осуществляется проверка посредством составления баланса мощностей или расчет рассматриваемой цепи производится другим методом.

Готовые работы на аналогичную тему

Баланс мощностей электрической цепи — это суммарная генерируемая источниками электроэнергии мощность, равная сумме мощностей, которые потребляются в цепи.

Примеры расчета методом узловых и контурных уравнений

Рассмотрим схему, которая представлена на рисунке ниже

Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ

Допустим, что E1 = 50 В; Е2 = 30 В; Е3=3 В; R1 = 100 Ом; R2 = 50 Ом; R3 = 8 Ом; r03 = 0,5 Ом; r01 = r02 = 0 Ом. Нам необходимо рассчитать все токи цепи.

Решение задачи следует начинать с определения количества неизвестных токов и выбора их направления. В каждом неразветвленном участке цепи (ветвь) электрический ток одно и тоже значение от его начала и до конца. К узловым точкам (А и Б) присоединены три ветви:

1. БВГА с током I1
2. БА с током I2
3. БДЖА с током I3

Таким образом количество разных токов равняется количеству ветвей рассматриваемой цепи. Направление токов выбирается произвольно и при них составляются уравнения. После чего они решаются и определяются их истинные направления (по алгебраическим знакам). В рассматриваемой задаче три неизвестны — I1, I2, I3, для них и составляется система уравнения по законам Кирхгофа. Уравнения на основе первого закона более простые, поэтому следует начинать с них. Известно, что для электрической цепи с n узлами можно составить n-1 независимых уравнений. Уравнение по первому закону Кирхгофа для узла А будет выглядеть следующим образом:

Уравнения, которых не хватает составляются по второму закону Кирхгофа. Для этого выбираем контуры БАЖДБ и ВГЖДВ. Принимаем, что обход контуров цепи осуществляется по часовой стрелке и учитывая правила знаков получаем следующие уравнения:

Подставив численные значения в третьем уравнение получаем:

$I1*(100+0) – I3*(8+0,5) = 50-30$

Таким образом вычисление токов сводится к решению системы из трех уравнений с тремя неизвестными. Рассчитаем I2 из уравнения и подставим значение в уравнение:

$-50*(I1+I3) – 8,5*I3 = 27$

Приводя подобные числа получим:

В результате у нас получилось два уравнения с двумя неизвестными (I1, I3). Уравнение (-50I1-58,5I3 = 27) умножается на два, в результате чего получается:

$-100*I1- 117*I3 = 54$ Получившееся уравнение складывается с уравнение (100I1-8,5I3 = 20):

$I3 = – (64/125,5) =- 0,5 A$

Теперь подставляем получившееся значение I3 в уравнение, где неизвестно I1:

$I1 = -24,5/-100 = 0,245A$

Теперь получившиеся значения подставляются в первое уравнение, составленное по первому закону Кирхгофа:

$I2 = 0,245+0,5 = 0,745A$

Проверка результата осуществляет при помощи составления баланса мощностей или решения задачи другим способом.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 08 2021

Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет

[spoiler title=”источники:”]

http://mydocx.ru/3-70624.html

http://spravochnick.ru/elektronika_elektrotehnika_radiotehnika/metod_uzlovyh_i_konturnyh_uravneniy/

[/spoiler]