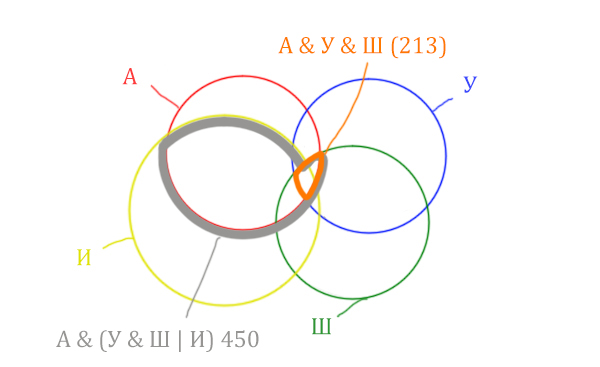Автор – Лада Борисовна Есакова.
Для быстрого поиска информации в Интернете используют поисковые запросы. Поисковый запрос – это набор ключевых слов, соединенных знаками логических операций И, ИЛИ, НЕ.
Приоритет выполнения операций, если нет специально поставленных скобок, следующий: сначала НЕ, затем И, затем ИЛИ.
Нужно понимать, что операция И (одновременное выполнение условий) сокращает объем получаемого результата, а операция ИЛИ (выполнение хотя бы одного из условий) наоборот увеличивает объем.
Если в запросе стоит фраза в кавычках, система будет искать точно такую фразу целиком.
1. Расположение запросов по возрастанию (убыванию)
Операция «И» (&) обозначает одновременное присутствие ключевых слов в искомых документах, а потому уменьшает количество найденной информации. Чем больше ключевых слов соединены операцией «И», тем меньше количество найденной информации. И наоборот, операция «ИЛИ» (|) обозначает присутствие хотя бы одного ключевого слова в искомых документах, а потому увеличивает количество найденной информации.
Пример 1.
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
А) реферат | математика | Гаусс
Б) реферат | математика | Гаусс | метод
В) реферат | математика
Г) реферат & математика & Гаусс
Решение:
Самое маленькое количество страниц будет отобрано по запросу с наибольшим количеством операций «И» (запрос Г), Самое большое количество страниц будет отобрано по запросу с наибольшим количеством операций «ИЛИ» (запрос Б). По запросу А будет отобрано больше страниц, чем по запросу В, т.к. запрос А содержит больше ключевых слов, связанных операцией «ИЛИ».
Ответ: ГВАБ
2. Подсчет найденных по запросу страниц
Такой тип задач обычно решают системой уравнений. Предложу более наглядный и простой способ.
Принцип отбора информации по поисковым запросам хорошо иллюстрирует диаграмма Эйлера-Венна (круги Эйлера). На диаграмме множества изображаются пересекающимися кругами. Операция «И» (&) – это пересечение кругов, а операция «ИЛИ» (|) – это объединение кругов.
Например, обозначим кругами множества Яблоки, Груши, Бананы. По запросу Яблоки & Груши & Бананы будет отобрано пересечение (общая часть) всех трех кругов:
По запросу Яблоки | Груши будет отобрано объединение двух кругов:
Пример 2.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу шахматы?
Решение:
Нарисуем диаграмму Эйлера-Венна. Прием решения задачи состоит в подсчете количества страниц, соответствующего каждой области, ограниченной линиями:
Запросу шахматы & теннис соответствует средняя область (1000 тыс. страниц), а запросу теннис – весь правый круг (5500 тыс. страниц).
Тогда правый «обрезанный круг» – это 5500-1000=4500:
Запросу шахматы | теннис соответствуют оба круга (7770), тогда левый «обрезанный круг» – это 7770-5500=2270

Итак, мы посчитали количества страниц для каждой ограниченной линиями области:
Несложно увидеть, что по запросу шахматы будет найдено 2270+1000=3270 тыс. страниц.
Ответ: 3270
Пример 3.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу
Москва & (Париж | Лондон)
Решение:
Как и в предыдущей задаче, нарисуем диаграмму Эйлера-Венна и посчитаем количество страниц, соответствующее каждой известной области, ограниченной линиями:
Несложно увидеть, что запросу Москва & (Париж | Лондон) соответствует область:
Ответ: 427
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №17. Построение запросов для поисковых систем. Расположение запросов по возрастанию (убыванию). Подсчет количества страниц.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
На уроке рассмотрен материал для подготовки к ОГЭ (ГИА) по информатике, разбор 8 задания. Объясняется тема об осуществлении поиска информации в Интернете, логических выражениях и запросах.
Содержание:
- ОГЭ по информатике 8 задания объяснение
- 8 задание как решать
- Актуальное
- Тренировочные
8-е задание: «Поиск информации в Интернете»
Уровень сложности — повышенный,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.
* до 2020 г — это было задание № 18 ОГЭ
- Поисковые запросы:
-
- операция «И» (
&) в поисковом запросе всегда ограничивает поиск (уменьшает количество страниц в выдаче), т. е., в ответ на запрос яблоко И груша поисковый сервер выдаст меньше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствуют оба этих слова;
- операция «И» (
чем больше в запросе операций «И», тем меньше результатов
-
- операция «ИЛИ» (
|) в поисковом запросе всегда расширяет поиск (увеличивает количество страниц в выдаче), т. е., в ответ на запрос яблоко ИЛИ груша поисковик выдаст больше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствует хотя бы одно из этих слов (или сразу оба слова).
- операция «ИЛИ» (
чем больше в запросе «ИЛИ», тем больше результатов
- Круги Эйлера-Вена:
Решать 8 задание также можно, представляя запрос в виде кругов Эйлера-Вена:
- Операция «И» представляется как умножение (пересечение).
- Операция «ИЛИ» представляется как сложение (объединение).
- Заштрихованная область при объединении больше, чем при пересечении.
Пример использования кругов Эйлера:
Пример:
Известно количество сайтов, которых находит поисковый сервер по следующим запросам :
| Ключевое слово | Количество сайтов, для которых данное слово является ключевым |
|---|---|
| Глинка & Лист | 320 |
| Бах & Лист | 280 |
| (Глинка | Бах) & Лист | 430 |
Сколько сайтов будет найдено по запросу
Глинка & Бах & Лист
- Упрощение логических выражений:
(A & B) | C = (A | C) & (B | C)
(A | B) & C = (A & C) | (B & C)
8 задание как решать
Актуальное
Разбор задания 8.1: Демонстрационный вариант ОГЭ 2022 г.:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Рыбка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Рыбак | Рыбка | 780 |
| Рыбак | 260 |
| Рыбак & Рыбка | 50 |
✍ Решение:
-
✎ Решим задание с помощью кругов Эйлера-Вена.
- Сначала отобразим первую строку таблицы — т.е. операцию
ИЛИ(|), которая обозначает объединение одновременно двух кругов: - Для второй строки таблицы отобразим отдельный круг, соответствующий количеству страниц для слова
Рыбак: - В третьей строке наблюдаем операцию И (
&), что соответствует области пересечения кругов: - Поскольку в задании требуется найти запрос
Рыбка, то для начала нам необходимо из общего объединения, т.е. из первого изображения, «вычесть» результат второго изображения, т.е.Рыбак; получим: - Теперь, чтобы получить полностью число страниц для запроса
Рыбка, необходимо добавить область пересечения кругов, которая равна 50 (вычисление для третьей строки); т.е. получим:
520 + 50 = 570
Ответ: 570
Тренировочные
Разбор задания 8.2:
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код — соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые нашёл поисковый сервер по каждому запросу. По всем запросам было найдено разное количество страниц.
Для обозначения логической операции «ИЛИ» в запросе используется символ «|», а для логической операции «И» — «&»:
| Код | Запрос |
|---|---|
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
✍ Решение:
✎
Способ 1:
(Муха & Денежка) | Самовар = (Муха | Самовар) & (Денежка | Самовар)
Ответ: ВАГБ
✎ Способ 2:
- Для начала отобразим все 4 объекта задания в виде пересеченных кругов одинакового размера:
- Рассмотрим строку с кодом А. Сначала необходимо выполнить действие в скобках: (Муха & Денежка). Логическое «И» представляется, как область пересечения двух кругов:
- Теперь выполним операцию «ИЛИ» — результат пересечения | Самовар. Для этого нам необходимо к полученной области «добавить» круг для объекта Самовар:
- Таким образом, мы получили область для кода А.
- Рассмотрим строку для кода Б: операция «И» — Муха & Денежка & Базар & Самовар — обозначает область пересечения одновременно всех кругов:
- Рассмотрим строку для кода Б:
- Рассмотрим строку для кода В: операция «ИЛИ» — Муха | Денежка | Самовар — обозначает объединение одновременно всех трех кругов:
- Рассмотрим строку для кода Г: операция «И» — Муха & Денежка & Самовар — обозначает область пересечения одновременно всех трех кругов:
- То есть выделенная область одновременно принадлежит и кругу Муха, и кругу Денежка, и кругу Самовар.
- Сравним все четыре полученных области и расположим их в порядке убывания, то есть с самой большой области до самой маленькой: ВАГБ
Решим задание с помощью кругов Эйлера-Вена.
Ответ: ВАГБ
Разбор задания 8.3:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пьер & Наука | 180 |
| Пьер & (Наука | Кюри) | 410 |
| Пьер & Кюри | 320 |
Какое количество страниц (в тысячах) будет найдено по запросу:
Пьер & Наука & Кюри
✍ Решение:
- Везде присутствует сомножитель «Пьер &» (и в искомом запросе!), сократим его:
- Используем круги Эйлера для решения, обозначив цифрами каждую составляющую:
- Из схемы и исходных данных получим:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Наука | 180 |
| Наука | Кюри | 410 |
| Кюри | 320 |
Искомый запрос: Наука & Кюри
1. №1 + №2 = 180 (Наука) 2. №2 + №3 = 320 (Кюри) 3. №1 + №2 + №3 = 410 (Наука | Кюри)
№1 + №2 + №3 = 180 + №3 = 410 №3 = 410 - 180 = 230
№2 + №3 = №2 + 230 = 320 №2 = 320 - 230 = 90
Результат: 90
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Рыбак | Рыбка | 780 |
| Рыбак | 260 |
| Рыбак & Рыбка | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу
Рыбка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Угол | Прямая | 180 |
| Угол | 60 |
| Угол & Прямая | 20 |
Какое количество страниц (в тысячах) будет найдено по запросу
Прямая?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
3
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Угол | Прямая | 180 |
| Угол | 60 |
| Прямая | 140 |
Какое количество страниц (в тысячах) будет найдено по запросу
Угол & Прямая?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
4
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Линкор | Корвет | 3320 |
| Линкор & Корвет | 1300 |
| Линкор | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Корвет?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
5
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Крейсер | Линкор | 3700 |
| Крейсер & Линкор | 400 |
| Линкор | 1800 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пройти тестирование по этим заданиям
Добрый день, сегодня научимся решать задание №8 ОГЭ по информатике. Данное задание основано на знании такой темы как, круги Эйлера. В текущем задании есть такие понятия как “запрос” и “количество страниц”.
Для начала попробуем разобраться с понятиями, которые используются в данном задании.
Поисковая система (поисковик) – сайт, которые постоянно просматривает огромное количество различных сайтов в интернете. Он их фильтрует и определяет, по какому запросу можно показать тот или иной сайт. Поисковик может и добавить сайт в “чёрный список” (удалить из выдачи системы), если он нарушает какие-либо правила.
Запрос – сообщение, которое помогает найти определённую информацию в поисковой системе. В запросы могут добавлять специальные символы для более конкретного поиска информации.
Количество страниц – количество страниц в поисковой системе, найденных по определённому запросу.
Множество – группа объектов, связанные каким-либо свойством. Например, деревья, машины, дома, натуральные числа.
В самом задании делаются запросы в поисковую систему. Указывается количество найденных страниц по разным запросам. И нужно найти, сколько будет найдено страниц с определённым запросом. Запросы могут быть связаны двумя логическими операциями: конъюнкцией (логическое И), дизъюнкцией (логическое ИЛИ). Также может использоваться инверсия (логическое отрицание).
Для того чтобы разобраться с примерами, нам осталось понять, как работают круги Эйлера. Как при помощи их можно находить количество страниц при поисковом запросе. И как на них влияют логические операции.
На данном изображении нарисованы два круга, которые пересекаются (общая площадь). Следовательно, можно разделить два круга на три условные зоны (для удобства они помечены цветами). Два круга олицетворяют два множества, а зоны различные запросы с этими множествами. Попробуем подробнее разобраться.
Например, есть у нас два множества: стихи и рассказы. Стихи — это зелёная зона и синяя, а рассказы синяя и красная. Другими словами, у каждого множество полностью свой круг. Запросы обстоят чуть сложнее. Для удобства дальше будем применять логические знаки. Знак | (вертикальный слэш) для логического ИЛИ и & (амперсанд) для логического И.
- Стихи & Рассказы – синяя зона
- Стихи | Рассказы – зелёная, синяя и красная зона
- Стихи – зелёная и синяя зона
- Рассказы – синяя и красная зона
Теперь можем попробовать разобрать задания.
Задание №1
Даны три поисковых запроса с количеством выданных страниц. Необходимо определить, сколько будет найдено страниц по запросу “Соль”.
Для начала нарисуем круги Эйлера для наглядности.
Посмотрим на таблицу и на диаграмму (круги) и попробуем распределить запросы по зонам.
- Соль | Перец (Зелёная, синяя и красная) – 4000
- Перец (Синяя и красная) – 1600
- Соль & Перец (Синяя) – 300
- Соль (Зелёная и синяя) – ?
Решение
С зонами мы можем совершать лишь два действия: сложение и вычитание. При сложении зоны добавляются в группу, при вычитании из группы убирает зоны. Найти зелёную и синюю зону можно из других:
- Соль | Перец – Перец = 2400 (Зелёная) – здесь из зелёной, синей и красной вычитается синяя и красная
- Соль & Перец + “Зелёная” = 2700
Задание №2
Даны три поисковых запроса. Необходимо найти количество страниц при запросе “Вега & Арктур”.
В данном задание уже три множества, значит необходимо добавить ещё один круг. Добавление круга влечёт за собой добавление и дополнительных зон. Попробуем изобразить.
Сейчас мы замечаем, что тут уже целых 7 различных зон. Исходя из табличных данных нужно распределить запросы по цветам (по зонам):
- Сириус & Вега (малиновый и бирюзовый) – 260
- Вега & ( Сириус | Арктур) (малиновый, бирюзовый и жёлтый) – 467
- Сириус & Вега & Арктур (бирюзовый) – 119
- Вега & Арктур (бирюзовый и жёлтый) – ?
Решение
Попробуем найти малиновый цвет, а после найдём нужные цвета из Вега & ( Сириус | Арктур). Для этого сделаем следующие действия:
- Сириус & Вега – Сириус & Вега & Арктур = 260 – 119 = 141 (малиновый)
- Вега & ( Сириус | Арктур) – “Малиновый” = 467 – 141 = 326 (Вега & Арктур)
Понравилась статья? Хочешь разбираться в информатике, программировании и уметь работать в разных программах? Тогда ставь лайк, подпишись на канал и поделись статьей с друзьями!
Читайте также:
#информатика #огэ #разбор #задания #решение #экзамен
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
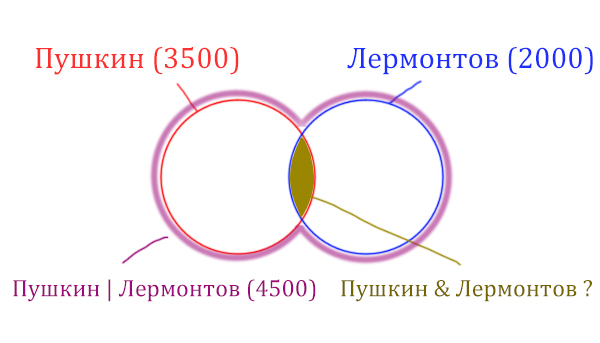
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
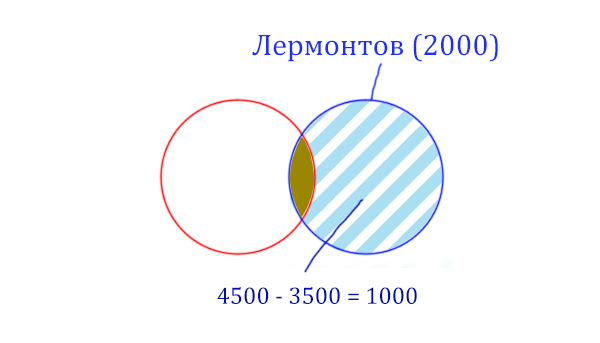
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
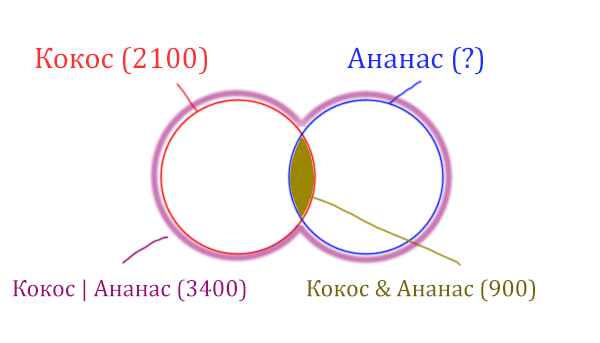
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
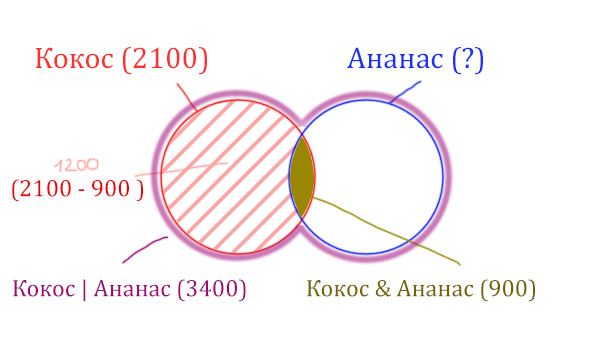
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
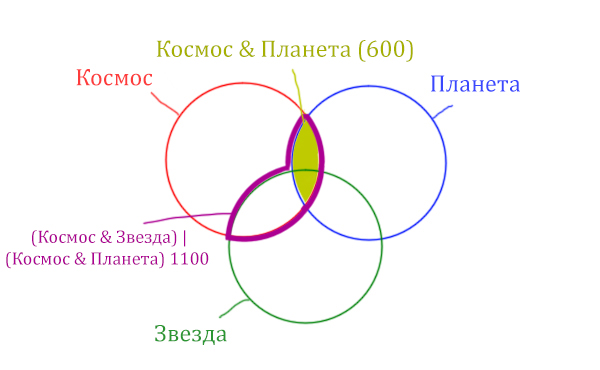
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.
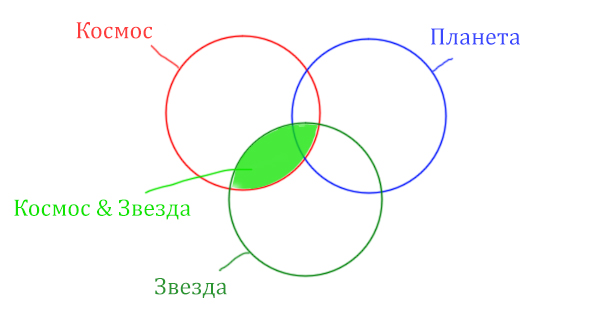
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
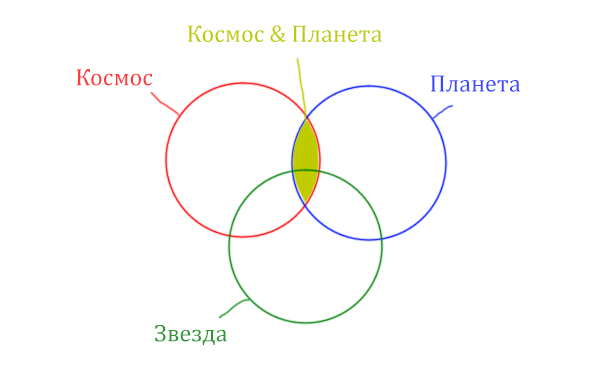
Теперь отметим вторую скобку Космос & Планета.
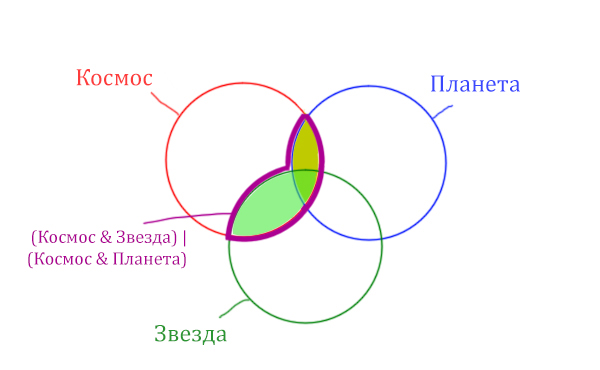
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
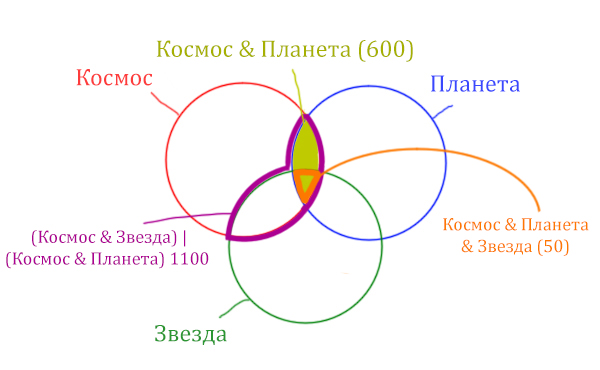
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
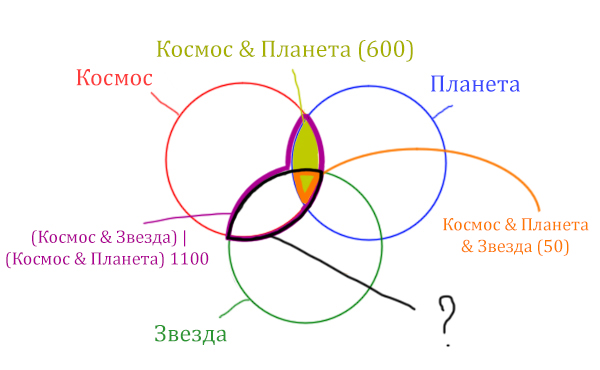
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
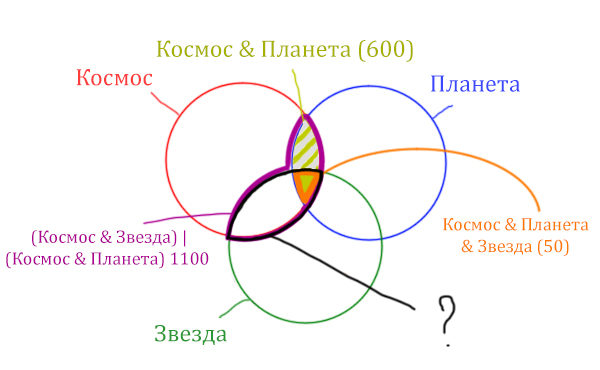
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
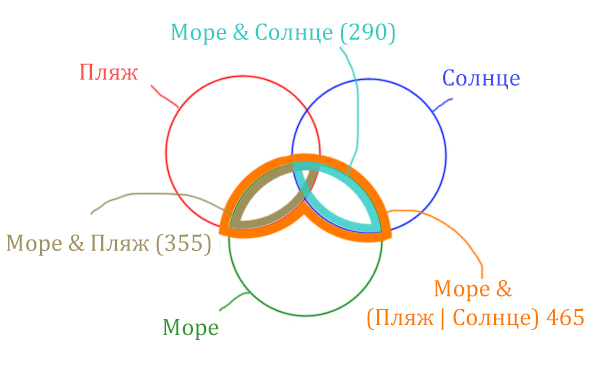
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
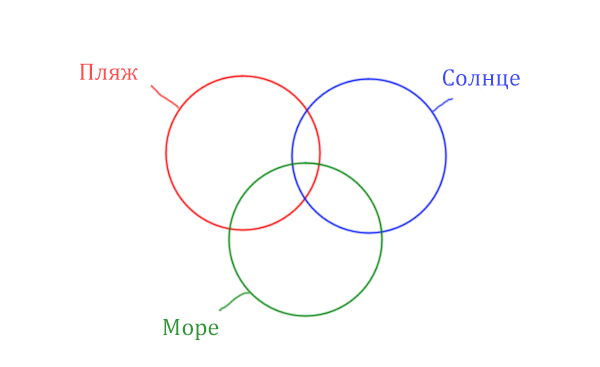
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
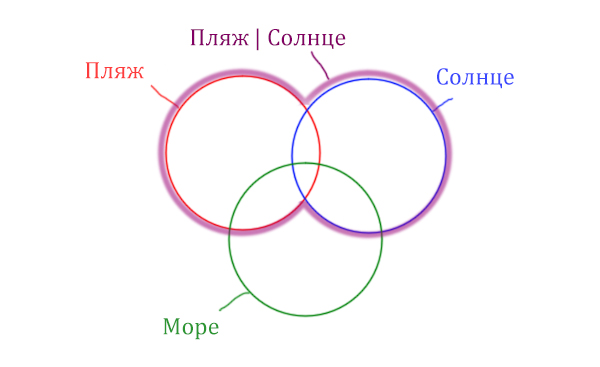
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
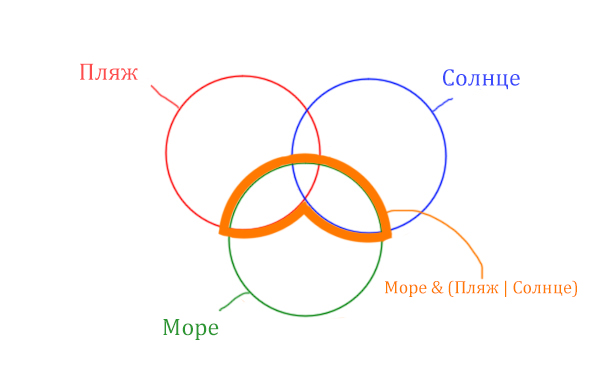
Теперь отметим Море & Пляж.
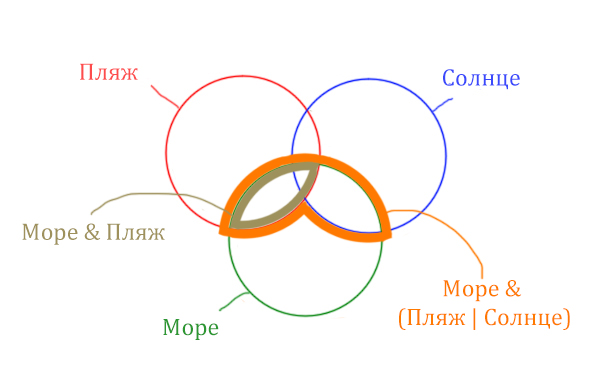
Теперь отметим Море & Солнце.
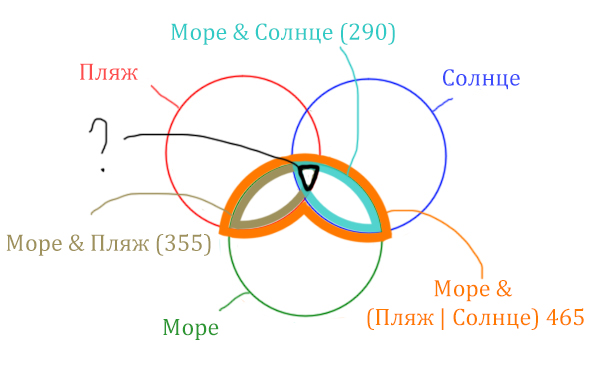
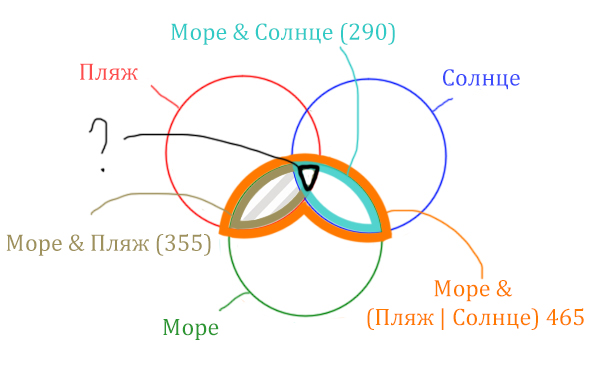
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
Задача (с 4 сущностями)
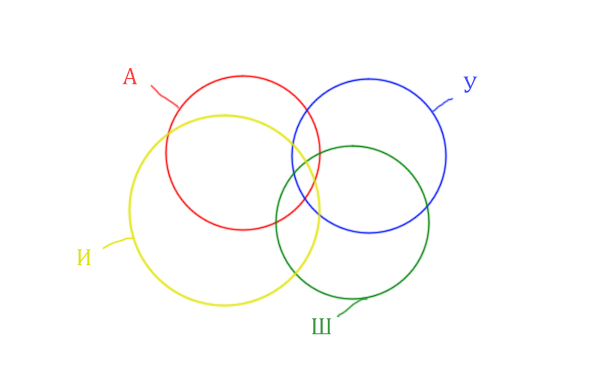
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
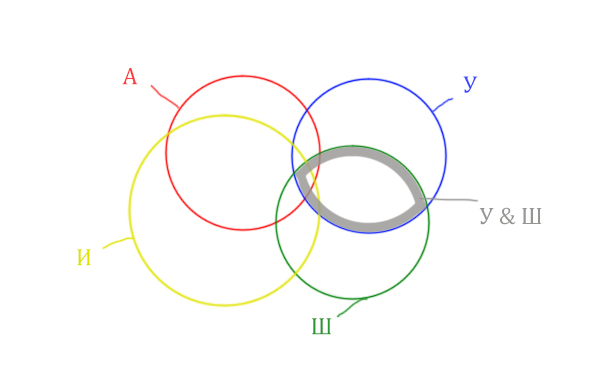
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
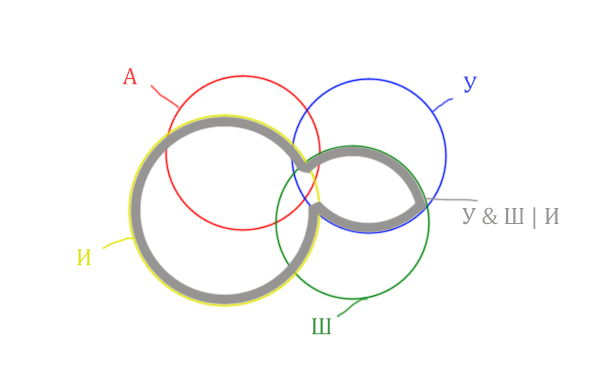
Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
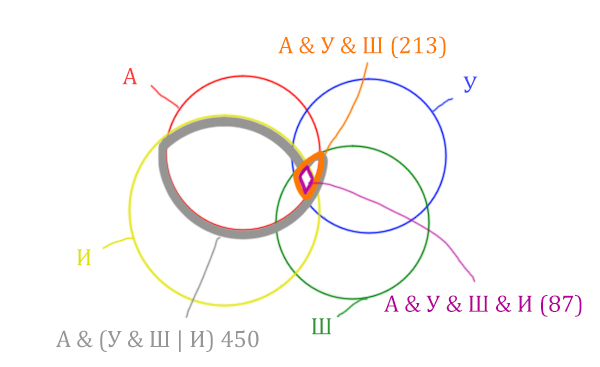
Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
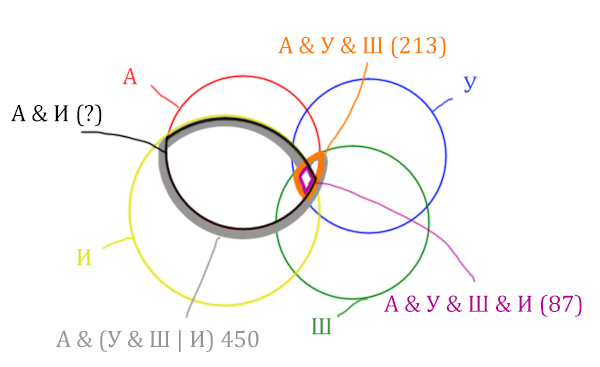
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
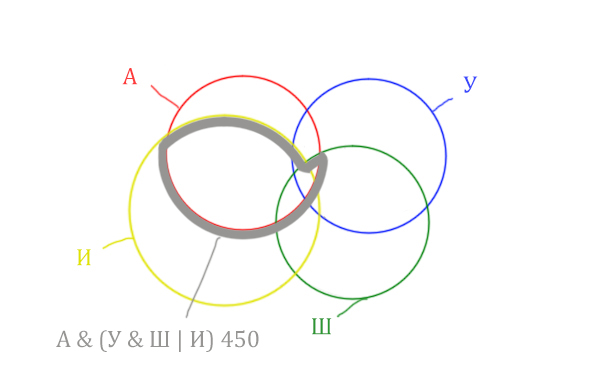
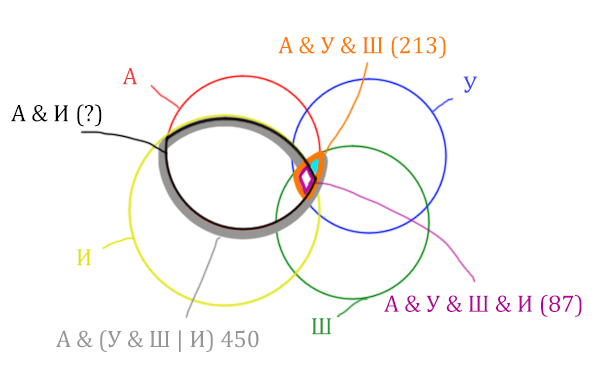
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Ответ: 324.
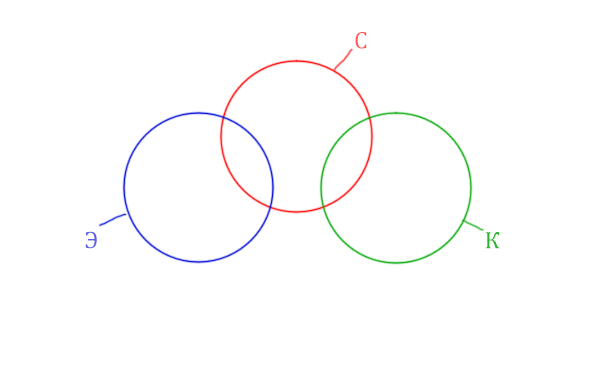
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
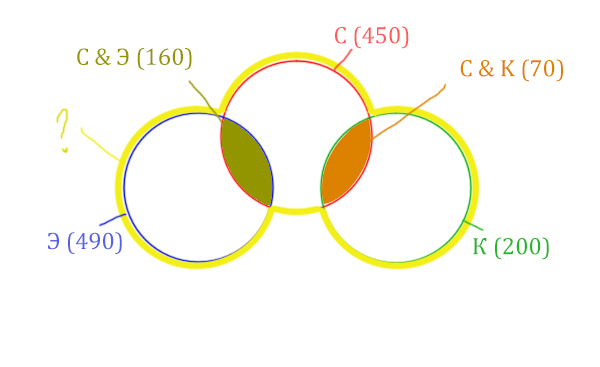
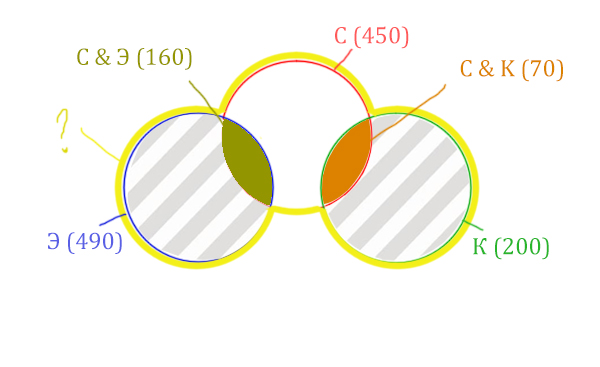
Отметим всё, что нам дано в условии.
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
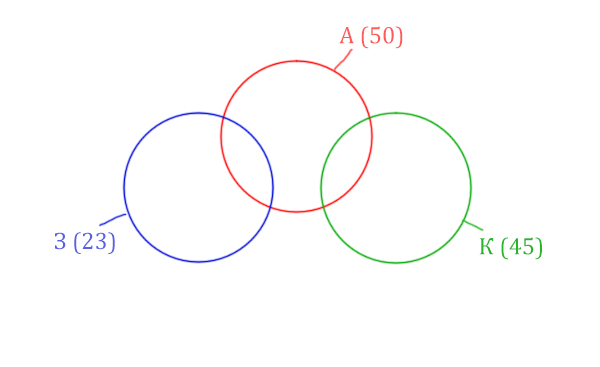
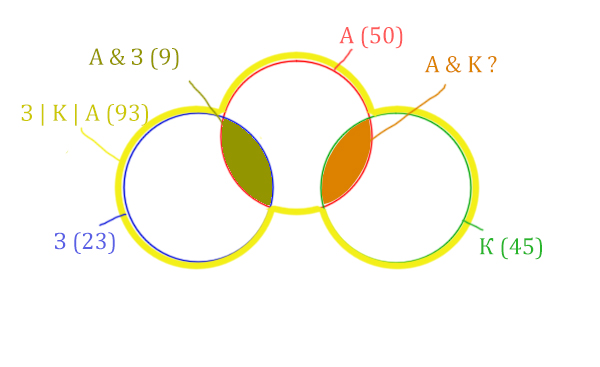
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
Нарисуем все данные на рисунке.
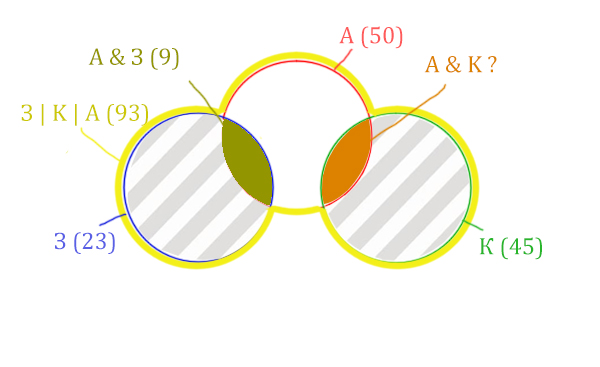
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++