Найти коммутатор матриц
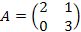 и
и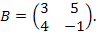
Решение:
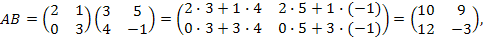
и
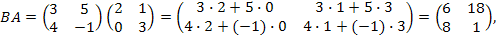
Тогда
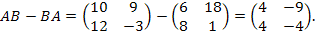
***
Найти A2010, если
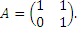
Решение:
…
***
Пусть
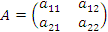 – матрица пторого порядка с произвольными элементами. Покажем непосредственным вычислением, что матрица вида
– матрица пторого порядка с произвольными элементами. Покажем непосредственным вычислением, что матрица вида 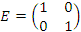 играет в матричной алгебре роль единицы.
играет в матричной алгебре роль единицы.
Действительно,
***
Аналогично, матрица
 не изменяется при умножении слева или справа на матрицу
не изменяется при умножении слева или справа на матрицу 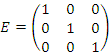 :
:

***
В условиях Примера 1 найти антикоммутатор матриц A и B.
Решение:
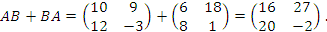
***
Пример 6.
Пусть 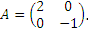
Решение:
…
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 ноября 2021 года; проверки требуют 3 правки.
Говорят, что две матрицы 


![{displaystyle [A,B]=AB-BA}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a3b93b316dd0b6b0ab2c71e486c901ddfe6e79a)

Описание и свойства[править | править код]
- Однако если квадрат коммутатора двух матриц равен нулю, то есть
, то обратное верно[2].
, но
не диагонализируема
- Если, однако, обе матрицы диагонализируемы, то они могут быть диагонализируемы одновременно.
- Если одна из матриц обладает свойством, что её минимальный многочлен совпадает с характеристическим многочленом (то есть он имеет максимальную степень), что случается, в частности, когда характеристический многочлен имеет только простые корни, то вторая матрица может быть записана в виде полинома от первой матрицы.
- Как прямое следствие одновременной триангуляризации, собственные значения двух перестановочных комплексных матриц A и B с их алгебраическими кратными (мультимножествами корней их характеристических многочленов) можно сопоставить
так, что множества собственных значений любого многочлена
двух матриц является мультимножеством значений
. Эта теорема принадлежит Фробениусу[3].
- Две эрмитовы матрицы коммутируют, если их собственные подпространства совпадают. В частности, две эрмитовы матрицы без кратных собственных значений коммутируют, если их множества собственных векторов совпадают. Это следует из рассмотрения собственных значений обоих матриц. Пусть
и
будут двумя эрмитовыми матрицами.
и
имеют общие собственные подпространства, если они могут быть записаны как
и
. Следует также
- Свойство двух матриц быть перестановочными не транзитивно — матрица
может коммутировать как с
, так и с
, но матрицы
и
друг с другом не коммутируют. Как пример, единичная матрица коммутирует со всеми остальными матрицами, которые не всегда коммутируют между собой. Если множество рассматриваемых матриц ограничено эрмитовыми матрицами без кратных собственных значений, то коммутативность транзитивна, как следствие характеризации в терминах собственных векторов.
- Теорема Ли, которая показывает, что любое представление разрешимой алгебры Ли[en] одновременно триангуляризуемо к верхней треугольной, можно рассматривать как обобщение.
- Матрица
коммутирует с любой другой матрицей тогда и только тогда, когда она является скалярной матрицей, то есть матрицей вида
, где
представляет единичную матрицу, а
является скаляром.
Примеры[править | править код]
- Единичная матрица коммутирует со всеми матрицами.
- Жордановы клетки коммутируют с верхнетреугольными матрицами, которые имеют одинаковые значения на каждой из диагоналей.
- Если произведение двух симметричных матриц является симметричной матрицей, то эти матрицы коммутируют.
История[править | править код]
Понятие коммутирования (перестановки) матриц ввёл Кэли в своих мемуарах по теории матриц, в которых была приведена также аксиоматизация матриц. Первым существенным доказанным результатом по коммутированию был представленный выше результат Фробениуса (1878)[4].
Примечания[править | править код]
- ↑ Horn, Johnson, 2012, с. 70.
- ↑ Horn, Johnson, 2012, с. 127.
- ↑ Frobenius, 1877, с. 1–63.
- ↑ Drazin, 1951, с. 222–231.
Ошибка в сносках?: Тег <ref> с именем «SE», определённый в <references>, не используется в предшествующем тексте.
Литература[править | править код]
- Roger A. Horn, Charles R. Johnson. Matrix Analysis. — Cambridge University Press, 2012. — ISBN 9780521839402.
- Хорн Р., Джонсон Ч. Матричный анализ. — М.: «Мир», 1989.
- Frobenius G. Ueber lineare Substitutionen und bilineare Formen // Journal für die reine und angewandte Mathematik. — 1877. — Т. 84.
- Drazin M. Some Generalizations of Matrix Commutativity // Proceedings of the London Mathematical Society. — 1951. — Т. 1, вып. 1. — doi:10.1112/plms/s3-1.1.222.
Коммутатором операторов [math]displaystyle{ hat A }[/math] и [math]displaystyle{ hat B }[/math] в алгебре, а также квантовой механике называется оператор [math]displaystyle{ [hat A, hat B] = hat A hat B – hat B hat A }[/math]. В общем случае он не равен нулю.
Понятие коммутатора распространяется также на произвольные ассоциативные алгебры (не обязательно операторные). В квантовой механике за коммутатором операторов также закрепилось название квантовая скобка Пуассона.
Если коммутатор двух операторов равен нулю, то они называются коммутирующими, иначе — некоммутирующими.
Коммутатор матриц
Коммутатор определяется для пары квадратных матриц одинакового размера. В этом случае его называют матричным коммутатором.
Коммутатор векторных полей
Гладкому векторному полю [math]displaystyle{ mathbf{v} }[/math] можно сопоставить дифференциальный оператор (математики часто считают, что векторные поля — это и есть дифференциальный операторы первого порядка):
[math]displaystyle{ hat v=v^ifrac{~partial}{partial X^i}. }[/math]
По повторяющемуся индексу подразумевается сумма.
Мы можем определить коммутатор двух таких дифференциальных операторов
[math]displaystyle{ [hat v,hat w]varphi=left(v^ifrac{~partial}{partial X^i}w^jfrac{~partial}{partial X^j}
-w^ifrac{~partial}{partial X^i}v^jfrac{~partial}{partial X^j}right)varphi
=left(v^ifrac{partial w^j}{partial X^i}
-w^ifrac{partial v^j}{partial X^i}right)frac{partialvarphi}{partial X^j}.
}[/math]
Коммутатору дифференциальных операторов [math]displaystyle{ [hat v,hat w] }[/math] можно сопоставить векторное поле с компонентами
[math]displaystyle{ [hat v,hat w]^j
=v^ifrac{partial w^j}{partial X^i}
-w^ifrac{partial v^j}{partial X^i}.
}[/math]
Это поле называется коммутатором векторных полей и обозначают как [math]displaystyle{ [mathbf{v},mathbf{w}] }[/math].
Тождества с коммутатором
- Антикоммутативность: [math]displaystyle{ [A,B] = -[B,A]. }[/math] Из этого тождества следует что [math]displaystyle{ [A,A]=0 }[/math] для любого оператора [math]displaystyle{ A }[/math].
В ассоциативной алгебре верны также следующие тождества:
- [math]displaystyle{ [A,BC] = [A,B]C + B [A,C] }[/math]. Это тождество представляет собой правило Лейбница для оператора [math]displaystyle{ D_A = [A,cdot]. }[/math] По этой причине оператор [math]displaystyle{ D_A }[/math] называют внутренним дифференцированием в алгебре. Аналогичным свойством обладает оператор [math]displaystyle{ tilde D_A = [cdot,A]. }[/math]
- Тождество Якоби: [math]displaystyle{ [A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0. }[/math] Алгебра, удовлетворяющая тождеству Якоби, называется алгеброй Ли. Таким образом, из любой ассоциативной алгебры можно получить алгебру Ли, если определить умножение в новой алгебре как коммутатор элементов старой алгебры.
- [math]displaystyle{ [AB,C]+[BC,A]+[CA,B]=0. }[/math] Это тождество представляет собой другую запись тождества Якоби.
- [math]displaystyle{ [AB,C] = A[B,C] + [A,C]B }[/math]
- [math]displaystyle{ [ABC,D] = AB[C,D] + A[B,D]C + [A,D]BC }[/math]
- [math]displaystyle{ [AB,CD] = A[B,CD] +[A,CD]B = A[B,C]D + AC[B,D] +[A,C]DB + C[A,D]B }[/math]
- [math]displaystyle{ [A,BCD] = [A,B]CD + B[A,C]D + BC[A,D] }[/math]
- [math]displaystyle{ [A,BCDE] = [A,B]CDE + B[A,C]DE + BC[A,D]E + BCD[A,E] }[/math]
- [math]displaystyle{ [ABCD,E] = ABC[D,E] + AB[C,E]D + A[B,E]CD + [A,E]BCD }[/math]
- [math]displaystyle{ [[[A,B], C], D] + [[[B,C], D], A] + [[[C, D], A], B] + [[[D, A], B], C] = [[A, C], [B, D]] }[/math]
- [math]displaystyle{ e^{A}Be^{-A}=B+[A,B]+frac{1}{2!}[A,[A,B]]+frac{1}{3!}[A,[A,[A,B]]]+cdots equiv e^{operatorname{ad}(A)} B. }[/math] Эта формула справедлива в алгебрах, где может быть определена матричная экспонента, например, в Банаховой алгебре или в кольце формальных степенных рядов. Она также играет важнейшую роль в квантовой механике и квантовой теории поля при построении теории возмущений для операторов в представлении Гейзенберга и представлении взаимодействия.
- [math]displaystyle{ ln left( e^{A} e^Be^{-A} e^{-B}right)= [A,B]+frac{1}{2!}[(A+B),[A,B]]+frac{1}{3!}left( [A,[B,[B,A]]]/2 + [(A+B),[(A+B),[A,B]]] right)+cdots . }[/math]
Коммутатор в квантовой механике
Как известно, физическое измерение в квантовой механике соответствует действию оператора [math]displaystyle{ hat F }[/math] физической величины [math]displaystyle{ f }[/math] на вектор состояния системы. Так называемые чистые состояния, в которых физическая величина имеет строго определённое значение, соответствуют собственным векторам [math]displaystyle{ hat F }[/math], при этом значение величины в данном состоянии — это собственное число вектора чистого состояния:
- [math]displaystyle{ hat F psi_i= f psi_i }[/math]
Если две квантовомеханические величины одновременно измеримы, то в чистых состояниях они обе будут иметь определённое значение, то есть множества собственных векторов операторов величин совпадают. Но тогда они будут коммутировать:
- [math]displaystyle{ hat F hat G psi_i = g hat F psi_i = g f psi_i = hat G hat F psi_i }[/math]
Соответственно, некоммутирующие операторы соответствуют физическим величинам, не имеющим одновременно определённого значения. Типичный пример — операторы импульса (компоненты импульса) [math]displaystyle{ hat p_x = – i hbar frac {partial}{partial x} }[/math] и соответствующей координаты [math]displaystyle{ hat x = x }[/math] (см. соотношение неопределённостей).
Законы сохранения
Собственные значения гамильтониана квантовой системы — это значения энергии в стационарных состояниях. Очевидным следствием вышеизложенного является то, что физическая величина, оператор которой коммутирует с гамильтонианом, может быть измерена одновременно с энергией системы. Однако, в квантовой механике энергия приобретает особую роль. Из уравнения Шрёдингера
- [math]displaystyle{ i hbar frac {partial psi}{partial t} = hat H psi }[/math]
и определения полной производной оператора по времени
- [math]displaystyle{ dot {hat f} = hat {dot f} }[/math]
можно получить выражение для полной производной по времени от физической величины, а именно:
- [math]displaystyle{ dot {hat f} = {i over hbar} [hat H, hat f]+ frac {partial hat f}{partial t} }[/math]
Следовательно, если оператор физической величины коммутирует с гамильтонианом, то эта величина не изменяется с течением времени. Это соотношение является квантовым аналогом тождества
- [math]displaystyle{ dot f = mathcal{{} H,f mathcal{}} + frac {partial f}{partial t} }[/math]
из классической механики, где {,} — скобка Пуассона функций. Аналогично классическому случаю, оно выражает наличие у системы определённых симметрий, порождающих интегралы движения. Именно свойство сохранения при определённых симметриях пространства кладётся в основу определения многих квантовых аналогов классических величин, например, импульс определяется как величина, сохраняющаяся при всех трансляциях системы, а момент импульса определяется как величина, сохраняющаяся при вращениях.
Некоторые соотношения коммутации
Укажем значения некоторых часто встречающихся коммутаторов.
- [math]displaystyle{ hat r_i, hat p_i, hat L_i }[/math] — оператор i-ой компоненты, соответственно, радиус-вектора, импульса и момента импульса; [math]displaystyle{ delta_{i j} }[/math] — дельта Кронекера; [math]displaystyle{ e_{i j k} }[/math] — абсолютно антисимметричный псевдотензор 3-го ранга.
- [math]displaystyle{ [hat r_i, hat p_j] = i hbar delta_{i j} }[/math]
- [math]displaystyle{ [hat p, f(vec r)] = – i hbar nabla f }[/math]
- [math]displaystyle{ [hat L_i, hat r_j] = i hbar e_{i j k}hat r_k }[/math]
- [math]displaystyle{ [hat L_i, hat p_j] = i hbar e_{i j k}hat p_k }[/math]
- [math]displaystyle{ [hat L_i, hat L_j] = i hbar e_{i j k}hat L_k }[/math]
- [math]displaystyle{ [hat L^2, hat L_i] = 0 }[/math]
Как правило, необходимы соотношения для нормированного момента: [math]displaystyle{ hat L_j = hbar hat l_j }[/math]
- [math]displaystyle{ [hat l_i, hat r_j] = i e_{i j k}hat r_k }[/math]
- [math]displaystyle{ [hat l_i, hat p_j] = i e_{i j k}hat p_k }[/math]
- [math]displaystyle{ [hat l_i, hat l_j] = i e_{i j k}hat l_k }[/math]
- [math]displaystyle{ [hat l^2, hat l_i] = 0 }[/math]
Из этих соотношений видно, что момент импульса частицы не измерим одновременно с её координатами или импульсом. Более того, за исключением случая, когда момент равен нулю, различные его компоненты не измеримы одновременно. Этим момент импульса принципиально отличается от импульса и радиус-вектора, у которых все три компоненты могут быть одновременно определены. Для момента импульса можно измерить лишь его проекцию на некоторую ось (обычно [math]displaystyle{ z }[/math]) и квадрат его длины.
Алгебра Ли физических величин
Коммутатор является квантовым аналогом скобки Пуассона в классической механике.
Операция коммутатора вводит на операторах (или элементах алгебры) структуру алгебры Ли,
поэтому антикоммутативное умножение в алгебре Ли также называют коммутатором.
Некоммутирующие величины
Некоммутирующими величинами [math]displaystyle{ A }[/math] и [math]displaystyle{ B }[/math] называются величины, коммутатор которых [math]displaystyle{ [A,B] = AB – BA neq 0 }[/math].
Две физические величины одновременно измеримы тогда и только тогда, когда их операторы коммутируют[1].
Антикоммутатор
Антикоммутатор — симметризующий оператор над элементами кольца, определяющий степень «антикоммутативности» умножения в кольце:
- [math]displaystyle{ [x, y]_+ := xy + yx }[/math]
Через антикоммутатор вводится коммутативное «йорданово умножение». Алгебра Клиффорда всегда естественным образом связывает антикоммутатор с задающей её билинейной формой.
Примеры
- Антикоммутатор пары различных мнимых единиц у кватернионов равен нулю.
- При помощи антикоммутатора определяются гамма-матрицы Дирака.
Литература
- Блохинцев Д. И. Основы квантовой механики. — 5-е изд. — М.: Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720c.
- Дирак П. Принципы квантовой механики. — 2-е изд. — М.: Наука, 1979. — 480 с.
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
См. также
- Теория операторов
- Поле Киллинга
Примечания
- ↑ 3.7. Одновременное измерение разных физических величин. Дата обращения: 15 апреля 2016. Архивировано 24 апреля 2016 года.
Здравствуйте, подскажите пожалуйста, как бы вы решали следующую задачку:
Даны две квадратные матрицы A и B поядка n*n. Их коммутатор, то есть матрица C=AB-BA представляет собой матрицу xI – то есть матрицу, кратную единчной. Нужно доказать, что x = 0. С первого прочтения может показаться сочетание условия и того, что нужно доказать нелепым (по крайней мере мне так показалось), так что я попытаюсь по своему сформулировать эту задачу: доказать, что если у коммутатора матриц A и B известно, что все элементы, не стоящие на главной диагонали равны нулю, то и на главной диагонали все элементы будут равны нулю (однако в своей формулировке задачи я не упомянул ещё что элементы стоящие на главной диагонали равны x)
Думал я над этой задачкой дня 3, усердной думал… хотя по сложности она помечена на 5 баллов (по 10-ти бальной шкале) так чо решение её не очень сложным должно быть… Вроде как минут 10 назад я придумал кое-какое доказательство, но не очень уверен в применении его правильности. Подскажие, действительно ли так просто доказывается эта “теорема”? Лучше, конечно, не смотрите сразу моё доказательство, вдруг вы на нём зациклитесь, а у меня какое-то предчувствие, что решать надо по другому.
Вообщем доказательство такое:
Вычисляем след этого коммутатора: с одной стороны он будет равен Tr(AB)-Tr(BA), т. е. = 0 (свойство такое есть =)) а сдругой стороны Tr(xI)=x*n Приравнивая эти части получаем 0=xn, т. е. либо n=0 (странная матрица, я таких ещё не встречал =0), ну или, что нам и надо доказать x=0
Написал много, по делу наверное мало, но всё-таки… буду рад любой помощи. Заранее большое спасибо…
В линейной алгебре две матрицы и называются коммутирующими, если или, что эквивалентно, если их коммутатор равен нулю. Набор матриц называется коммутируют , если они попарно коммутируют, что означает , что каждая пара матриц в множестве коммутируют друг с другом.

Характеристики и свойства
- Однако если квадрат коммутатора двух матриц равен нулю, то есть , то верно обратное.
- Если же обе матрицы диагонализуемы, то они могут быть диагонализованы одновременно.
- Если одна из матриц обладает тем свойством, что ее минимальный многочлен совпадает с ее характеристическим многочленом (т. Е. Имеет максимальную степень), что, в частности, происходит, когда характеристический многочлен имеет только простые корни , тогда другая матрица может быть записана как полином в первом.
- Как прямое следствие одновременной триангулируемости, собственные значения двух коммутирующих комплексных матриц A , B с их алгебраическими кратностями ( мультимножества корней их характеристических многочленов) могут быть сопоставлены таким образом, что мультимножество собственных значений любого многочлена из две матрицы – это мультимножество значений . Эта теорема принадлежит Фробениусу .
- Две эрмитовы матрицы коммутируют, если их собственные подпространства совпадают. В частности, две эрмитовы матрицы без нескольких собственных значений коммутируют, если они имеют один и тот же набор собственных векторов. Это следует из рассмотрения разложения по собственным значениям обеих матриц. Позвольте и быть две эрмитовы матрицы. и имеют общие собственные подпространства, когда их можно записать как и . Отсюда следует, что
- Свойство коммутации двух матриц не является транзитивным : матрица может коммутировать как с, так и с и по-прежнему и не коммутировать друг с другом. Например, единичная матрица коммутирует со всеми матрицами, которые между ними не коммутируют. Если набор рассматриваемых матриц ограничен эрмитовыми матрицами без кратных собственных значений, то коммутативность транзитивна как следствие характеризации в терминах собственных векторов.
- Теорема Ли , которая показывает , что любое представление о разрешимой алгебры Ли одновременно верхний triangularizable можно рассматривать как обобщение.
- П × п матрица коммутирует с любым другим п × п матрицей тогда и только тогда , когда она является скалярной матрицей, то есть матрица вида , где является п × п единичной матрицей , и является скаляром. Другими словами, центр из группы из п × п матриц относительно умножения является подгруппой скалярных матриц.
Примеры
- Единичная матрица коммутирует со всеми матрицами.
- Каждая диагональная матрица коммутирует со всеми другими диагональными матрицами.
- Жордановы блоки коммутируют с верхнетреугольными матрицами, которые имеют одинаковое значение вдоль лент.
- Если произведение двух симметричных матриц симметрично, они должны коммутировать.
- Циркулянтные матрицы коммутируют. Они образуют коммутативное кольцо, поскольку сумма двух циркулянтных матриц циркулянтна.
История
Понятие коммутирующих матриц было введено Кэли в его мемуарах по теории матриц, которые также обеспечили первую аксиоматизацию матриц. Первым значительным результатом, доказанным на них, был приведенный выше результат Фробениуса 1878 года.
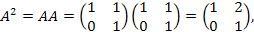
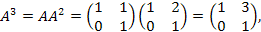
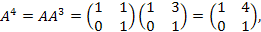
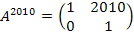
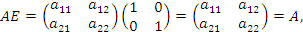
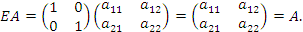
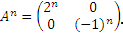
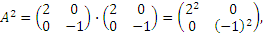
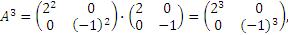

![{displaystyle [A,B]^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9f27c489a28c29b688ebd0cfebf64ee6834c6ac)














