Как найти комплексное число сопряженное данному числу

Операция
деления

Операция
комплексного сопряжения– это
изменение знака перед мнимой частью.
Еслиz=x+iy, то числоx–iyназывается сопряжен­ным
числуzи обозначается
:

=
= х –iy.

Пример
4.1 Найти
числа, сопряженные

а)
z₁
= i;
б) z₂
= 5; в) z₃
= 1 – 2i;
г) z₄
= 7i
+ 1.

Решение.

а)
z₁
= 0 + 1i , то

₁
= –i;

б)
z₂
=
5
+ 0 · i , то

₂
= 5 – 0 · i = 5;

в)

₃=
1 + 2i;

г)

_4
= –_{7 i +
1.}

_{Свойства
комплексно-сопряженных чисел:}

1)
z +

= x + iy + x – iy = 2x = 2Re z;

2)
z –

= x + iy – (x – iy) = 2iy = 2i lm z;

3)
z ·

= (x + iy) (x – iy) = x²
+ y².

Таким
образом, сумма и произведение комплексно
сопряженных чисел являются действительными
числами, а
их разность – число мнимое.

4)

=

=

= x + iy = z
С;

5)
z =


lm z = 0 

;

6)

=
;

7)

;

8)

.

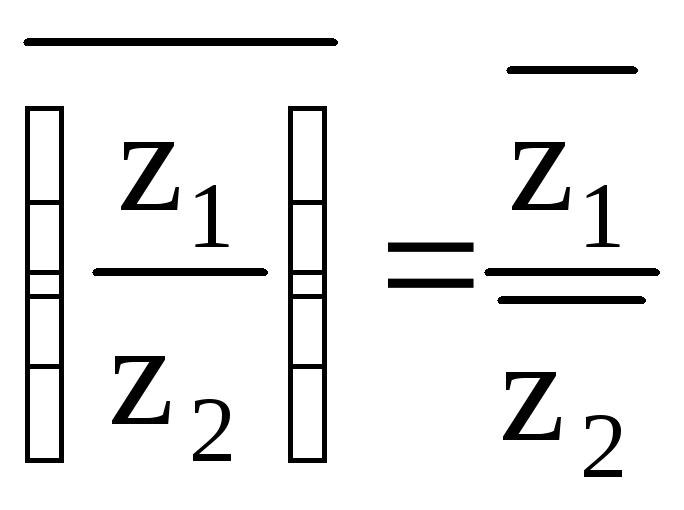Операция
деления
определяется как действие, обратное
умноже­нию. Частное

двух комплексных чисел z₁
и z₂

0 – это такое ком­плексное число z,
которое удовлетворяет условию z₂
· z = z₁.

Частное
получается путем умножения числителя
и знаменателя на число
,
сопряженное знаменателю.

=

=

Пример
4.2 Найти
,
если z₁
= 2 – 5i
, z₂
= –3 – 2i
.

Решение.

Пример
4.3 Записать
в алгебраической форме число

Решение.

Выполняем
последовательно все операции:

Re(1
+ 2i)²
= Re(–3
+ 4i) = –3;

(3
– 2i)(5
+ i) = 15 + 3i – 10i + 2 = 17 – 7i;

–3
– (17 – 7i) = –3
– 17 + 7i = –20
+ 7i;

;

1
+ 5i – (4 + i) = 1 + 5i – 4 – i = –3
+ 4i;

;

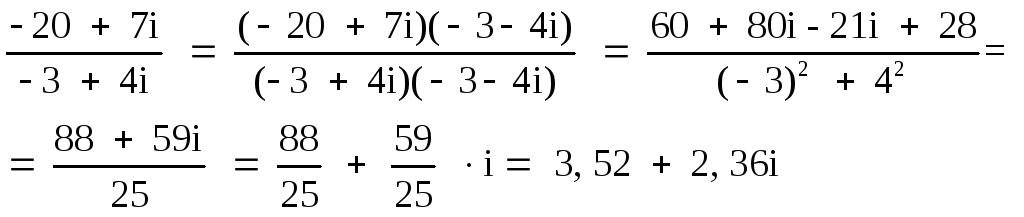
35,2
+ 2,36i – (– i) = 3,52 + 2,36i + i = 3,52 + 3,36i.

Упражнения

1 Вычислить:

а)
i⁴;
i⁸¹;
б)

в)
i²³¹;
i²⁰²⁴.

2
Найти
число, сопряженное данному:

а)
2i ; –3i; б)
(1 + i)(2 + 3i); (2 – i)(3 + i);

в)

г) (1 + i)²;
(2 – i)².

3
Представить
число в алгебраической форме:

а)

б)

в)

;
г)
;

д)

;
е)
;

ж)

;
з)

4 Выполнить действия:

а)

;
б)

;

в)
(1 – i)(4 + 3i)(2 + i)(3 + i) ; г)

;

д)

;
е)
;

ж)

.

5
Найти
значение выражения:

а)

z²
+ 3z + 1 + 3i при
z = 2 + 3i;

б)
(z – z²
+ 2z³)(2
– z + z²)
при
z =.

6
Найти
решение уравнений, где x
и y
– действительные числа:

а)
(1 + i)
∙ x
+ (2 + i)
∙ y
= 5 + 3i;

б)
2x
+ (1 + i)(x
+ y)
= 7 + i;

в)
(3 – y
+ x)(1
+ i)
+ (x
– y)(2
+ i)
= 6 – 3i;

г)
(i
– z)(1
+ 2i)
+ (1 – iz)(3
– 4i)
= 1 + 7i.

§5 Геометрическая интерпретация комплексных чисел

Определение
комплексного числа как упорядоченной
пары чисел (х; у) позволяет установить
взаимно однозначное соответст- вие
между комплексным числом

z
= x
+ iy
и точкой М(х; у) в декартовой системе
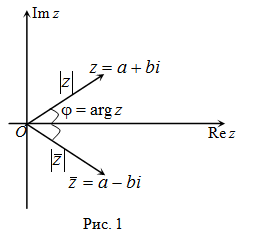
координат ОХУ (рисунок 1). Числовую
плоскость в этом случае называют
комплекс–

Рисунок
1 ной
плоскостью.

Ось
абсцисс называют действительной
осью, а ось ординат – мнимой
осью. С другой стороны, комплексное
число z
= x
+ iy
можно взаимно однозначно поставить в
соответствие вектору с координатами х
и у и началом в точке О (радиус-вектор).
Поэтому понятия “комплексное число”,
“точка z”
и “вектор z”
употребляются как синонимы.

Пример
5.1 Изобразить
на комплексной плоскости числа

а)
z
и
;
б) z
= 1 + 2i.

Решение:
а) – рисунок
2; б) – рисунок 3.

Рисунок 2
Рисунок 3

Соседние файлы в папке КЧ

• #
• #

Сопряжённые числа (комплексно-сопряжённые числа) — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине, но противоположными по знаку, мнимыми частями^[1]. Например, сопряжёнными являются числа и . Число, сопряжённое к числу , обозначается . В общем случае, сопряжённым к числу (где и  — действительные числа) является .

Например:

На комплексной плоскости сопряжённые числа представлены точками, симметричными относительно действительной оси. В полярной системе координат сопряжённые числа имеют вид и , что непосредственно следует из формулы Эйлера.

Сопряжёнными числами являются корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом.

Свойства[править | править код]

Для произвольных комплексных чисел и :

Если является голоморфной функцией, сужение которой на множество действительных чисел является действительной функцией, и определены , то:

.

В частности:

Определение координат числа и сопряжения[править | править код]

Прямоугольные и полярные координаты комплексного числа могут быть определены с помощью формул:

Примечания[править | править код]

Литература[править | править код]

• Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.

Содержание:

• Определение
• Свойства комплексно-сопряженных чисел

То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.

Например. Комплексно сопряженным к числу
$z=2-i$ есть число
$overline{z}=2+i$ .

На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.

Свойства комплексно сопряженных чисел

1) Если $z=overline{z}$, то можно сделать вывод,
что рассматриваемое число $z$ является действительным.

Например. $z=2 in R Rightarrow overline{z}=2$ и
$z=overline{z}$

2) Для любого комплексного числа
$z$ сумма
$z+overline{z}=2 operatorname{Re} z$ –
действительное число.

Например. Пусть
$z=2-3 i$, тогда
$overline{z}=2+3 i$, а тогда

$z+overline{z}=2-3 i+(2+3 i)=2-3 i+2+3 i=2+2=4 in R$

3) Для произвольного комплексного числа
$z=a+b i$ произведение
$z cdot overline{z}=|z|^{2} in R$ .

Например. Пусть
$z=2-3 i$, комплексно сопряженное к нему число
$overline{z}=2+3 i$, тогда произведение

$z cdot overline{z}=(2-3 i)(2+3 i)=2^{2}-(3 i)^{2}=2^{2}-3^{2} cdot i^{2}=$

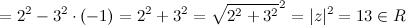
4) Модули комплексно сопряженных чисел равны:
$|z|=|overline{z}|$, а аргументы отличаются знаком (рис. 1).

5)  $overline{z_{1} pm z_{2}}=overline{z}_{1} pm overline{z}_{2}$

6)  $overline{z_{1} cdot z_{2}}=overline{z_{1}} cdot overline{z}_{2}$

7)  $frac{overline{z_{1}}}{z_{2}}=frac{overline{z}_{1}}{overline{z}_{2}}$

8)  $overline{(overline{z})}=z$

9) Если $z=a+b i$ и
$overline{z}=a-b i$ – комплексно сопряженные числа, то

$a=operatorname{Re} z=frac{z+overline{z}}{2}, b=operatorname{Im} z=frac{z-overline{z}}{2 i}$

Читать дальше: формы записи комплексного числа.

В данной публикации мы рассмотрим, что такое комплексно сопряженные числа, а также перечислим их основные свойства. Представленная теоретическая информация сопровождается практическими примерами для лучшего понимания.

Определение комплексно сопряженных чисел

Дано комплексное число z = a + bi. Комплексно сопряженным к нему является число z = a – bi (для обозначения используется черточка сверху).

Таким образом, у комплексно сопряженных чисел действительные части одинаковые, а мнимые отличаются по знаку.

Пример:
Для числа z = 3 + 2i комплексно сопряженным является z = 3 – 2i.

Геометрическая интерпретация

Если перенести комплексно сопряженные числа на комплексную плоскость, то они будут зеркальным отражением друг друга относительно действительной оси (RE).

Свойства комплексно сопряженных чисел

1. Если z = z, значит число z является действительным.

Пример:
z = 2, значит z ∈ R, следовательно z = 2, т.е. z = z.

2. Модули комплексно сопряженных чисел равны, т.е. |z| = |z|. А так как такие числа на комплексной плоскости зеркальны, то их аргументы отличаются по знаку.

3. Сумма комплексно сопряженных чисел – это действительное число: z + z = 2 RE z.

Пример:
z = 5 + 2i
z = 5 – 2i
z + z = 5 + 2i + 5 – 2i = 5 + 5 = 10, а 10 ∈ R.

4. Произведение комплексно сопряженных чисел равняется квадрату их модуля и является действительным числом: z ⋅ z = |z|² ∈ R.

Пример:
z = 6 – 4i
z = 6 + 4i
z ⋅ z = (6 – 4i)(6 + 4i) = 36 + 24i – 24i – 16i² = 36 – 16 ⋅ (-1) = 52, а 52 ∈ R.

Модуль считается так:

5. Для z = a + bi и z = a – bi справедливо:

6. Для произвольных комплексных чисел z₁ и z₂: