Что такое комплексное сопротивление или импеданс
Содержание
- 1 Что такое импеданс и его составляющие
- 2 Последовательность расчета компонентов импеданса
- 3 Определение импеданса
- 4 Видео по теме
Электрический импеданс — это термин, относящийся к цепям переменного тока. Слово происходит от латинского impedіо (сопротивляться). Расчёт комплексного сопротивления или импеданса представляет собой важный этап разработки различных электрических и электронных устройств.
Электронные устройства, требующие определения импеданса
Что такое импеданс и его составляющие
Импеданс электрических цепей — это векторная (двумерная) величина, состоящая из двух независимых скалярных (одномерных) компонентов: активного и реактивного сопротивления. Он обозначается буквой Z и выражает противодействие, которое электронный элемент, схема или система оказывает переменному электротоку. Измеряется в омах.
Виды сопротивлений в электроцепи
Активное сопротивление (R) является мерой интенсивности противодействия движению электронов между атомами. Чем легче атомы отдают/принимают электроны, тем ниже этот параметр, выражающийся в положительных действительных числах. Реактивное сопротивление, обозначаемое буквой Х, представляет собой выражение степени, с которой электронный компонент, схема или система накапливает или высвобождает энергию при колебаниях тока и напряжения за каждый единичный цикл переменного тока. Импедансом часто называют модуль комплексного сопротивления, поэтому реактивное сопротивление выражается в так называемых «мнимых» омах. Оно характерно только для линий переменного тока.
Когда переменный электроток проходит через катушку индуктивности, накапливаемая энергия высвобождается в виде магнитного поля. В этом случае реактивная составляющая импеданса является индуктивной (обозначается +jXL). Чем быстрее меняется направление тока, тем ХL больше.
Однако энергия может запасаться и высвобождаться в виде электрического поля, тогда данный параметр будет емкостным (обозначается –jXC ). Когда ток меняет направление, конденсатор многократно заряжается и разряжается. Чем больше времени конденсатор заряжается, тем сильнее он противодействует электротоку. Поэтому чем быстрее меняется направление электротока, тем ниже емкостное сопротивление.
Реактивное сопротивление обычно умножается на положительный квадратный корень из –1, который представляет собой единичное мнимое число j. Тогда комплексное сопротивление Z выражается как R + jXL или R – jXC. Следовательно, активное сопротивление R — это действительная часть комплексного импеданса, а реактивное Х — мнимая.
Графическая интерпретация составляющих импеданса
Левая половина координатной плоскости, представленной на рисунке выше, обычно не используется, поскольку на практике отрицательные сопротивления не встречаются. Индуктивное сопротивление указывается на положительной части линии мнимой оси, а ёмкостное — на отрицательной части линии.
Комплексное электрическое сопротивление фаз может быть определено как отношение электронапряжения к амплитуде электротока, что идентично закону Ома. Фаза импеданса является фазовым сдвигом, соответствующим отставанию электротока от электронапряжения.
Последовательность расчета компонентов импеданса
Найти импеданс или полное сопротивление последовательной цепи довольно просто, если в ней присутствует только какой-то один вид элементов. Импеданс идеального резистора соответствует его активному сопротивлению R, которое называется еще резистивным. Импеданс для катушки индуктивности — это мнимое реактивное сопротивление XL, а для конденсатора —ХС.
Если имеется активное сопротивление и один тип реактивного, тогда вычисления выполняются по формуле:
Формула импеданса при наличии активного и одного вида реактивного сопротивления
При наличии всех составляющих полное сопротивление или импеданс находим с помощью такого выражения:
Формула импеданса при наличии всех видов сопротивления в электроцепи
Таким образом, комплексное входное сопротивление цепи выражается как R + jX, где j — мнимое число √(–1).
Векторная диаграмма импеданса
Для расчетов всех составляющих импеданса используются формулы:
Формулы для расчета составляющих импеданса
Комплексное сопротивление и проводимости участков характеризуют замедление тока, которое связано с влиянием материала и формой резистора. Реактивное сопротивление X — это замедление тока из-за электрических и магнитных полей, противодействующих изменениям тока или напряжения. Этот параметр важен для конденсаторов и катушек индуктивности.
Импеданс в цепи переменного электротока
Определение импеданса
Рассчитать импеданс проще всего, если в цепи есть n резисторов, но нет катушек индуктивности или конденсаторов. Сначала измеряется сопротивление на каждом резисторе (или любом аналогичном компоненте). Найденные значения суммируются, если элементы соединены последовательно: R = R1 + R2 + … + Rn.
Результирующая величина для n резисторов, включённых параллельно, определяется следующим образом: 1/R = 1/R1 + 1/R2 + … + 1/Rn.
Если в цепи есть только индуктивная нагрузка или емкостная, импеданс будет соответствовать реактивному сопротивлению:
- Для последовательно соединенных катушек индуктивности X = XL1+ XL2 + …
- Для последовательно соединенных конденсаторов C =XC1 + XC2 + …
- Для катушек индуктивности, соединенных параллельно X = 1/(1/XL1+ 1/XL2 …)
- Для конденсаторов, соединенных параллельно: C = 1/(1/XC1+ 1/XC2 …)
С ростом частоты электротока сопротивление индуктивностей увеличивается, а конденсаторов уменьшается. Поэтому при их совместном использовании в электрической линии они уравновешивают друг друга. Чтобы найти общее реактивное сопротивление, надо вычесть одно значение из другого: X = |XC – XL|.
Величину импеданса можно вычислить для любой электроцепи переменного тока, состоящей из таких линейных пассивных элементов, как резисторы, индуктивности и конденсаторы. Для электроцепи с постоянным током не существует различия между импедансом и сопротивлением. Последний параметр можно рассматривать как импеданс, фазовый угол которого равняется нулю.
Видео по теме
Содержание
- Комплексные сопротивления и проводимости
- Комплексные числа. Основные законы электрических цепей в комплексной форме
- Готовые работы на аналогичную тему
- Комплексное сопротивление. Физический смысл
- Комплексная проводимость
- Комплексное сопротивление
Комплексные сопротивления и проводимости
Вы будете перенаправлены на Автор24
- Telegram
- Вконтакте
- Одноклассники
Комплексные числа. Основные законы электрических цепей в комплексной форме
Комплексное число – это число вида а + сi, где а и с — вещественные числа, а i — мнимая единица, то есть число для которого выполняется равенство i(2) = -1.
Множество комплексных чисел может обозначаться С. Вещественные числа рассматриваются как частный случай комплексных чисел и имеют следующий вид а + 0i. Главное свойство комплексного числа заключается в том, что в нем выполняется основная теорема алгебры, то есть многочлен n-ой степени (n ⩾ 1) имеет n корней. Также доказано, что система комплексных чисел логически непротиворечива.
Основная теорема алгебры представляет собой утверждение, что поле комплексных чисел алгебраически замкнуто, то есть любой многочлен, который отличен от константы, с комплексными коэффициентами имеет минимум один корень в поле комплексных чисел. Такое утверждение справедливо для многочленов с вещественными коэффициентами, потому что всякое вещественное число является комплексным с нулевой мнимой частью.
Необходимость применения комплексных чисел появилась в результате решения кубических уравнений, так как в формуле Кардано под квадратным корнем получалось отрицательное число. В изучение комплексных чисел большой вклад внесли такие ученые, как Эйлер, Гаусс и Декарт. Свойства комплексных чисел позволяют использовать их в решении разнообразных задач в области теории упругости, математики, обработке сигналов, теории колебаний, электромагнетизме, теории управления и т.п.
Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как цепи постоянного электрического тока, с заменой постоянных величин следующим образом:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
К основным законам электроцепей относятся:
- Закон Ома.
- Первый закон Кирхгофа.
- Второй закон Кирхгофа.
В комплексной форме закон Ома будет иметь следующий вид:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Первый закон Кирхгофа в применении к узлу в комплексной форме выглядит следующим образом:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Второй закон Кирхгофа, применительно к контуру цепи, в комплексной форме можно записать следующим образом:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Достоинство выражения законов электрических цепей в комплексной форме заключается в том, что в них учитываются связь между действующими значениями напряжения и тока, а также сдвиг фаз между ними.
Комплексное сопротивление. Физический смысл
Комплексное электрическое сопротивление (электрические импеданс) – это комплексное сопротивление между двумя узлами электрической цепи или двухполюсника для гармонического колебания.
Комплексное сопротивление представляет собой отношение комплексной амплитуды напряжение гармонического сигнала, которое прилагается к двухполюснику, к комплексной амплитуде электрического тока, который протекает через двухполюсник при установившемся режиме (то есть по окончании переходных процессов в цепи). Для пассивных линейных цепей, обладающих постоянными параметрами, в установившемся режиме комплексное электрическое сопротивление никак не зависит от времени. В том случае, когда время в математическом выражения для комплексного сопротивления не сокращается, понятие комплексного сопротивления для двухполюсника неприменимо. Сама формула для электрического импеданса выглядит следующим образом:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где: j — мнимая единица; w — круговая частота; U(w). I(w) — амплитуды напряжения и электрического тока на частоте w; фu(w), фi(w) — фазы напряжения и тока гармонического сигнала на частоте w; U(jw), I(jw) — комплексные амплитуды напряжения и электрического тока гармонического сигнала на частоте w.
Если рассматривать комплексное электрическое сопротивление в алгебраической форме, то его действительная часть соответствует активному сопротивлению, а мнимая реактивному. То есть двухполюсник с импедансом z(jw) представляет собой последовательно соединенные резистор с сопротивлением R (z(jw)) и реактивный элемент с комплексным сопротивлением J(z(jw)).
Когда комплексное сопротивление рассматривается в тригонометрической форме, то его модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент соответствует сдвигу фазы между электрическим током и напряжением.
Для резистора комплексное электрическое сопротивление всегда равно его собственном и при этом никак не зависит от частоты, то есть:
Напряжение и электрический ток в конденсаторе связаны соотношением:
Следовательно, при напряжении
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Электрический ток, который протекает через конденсатор, может быть рассчитан следующим образом:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Отсюда комплексное сопротивление конденсатора рассчитывается по формуле:
Аналогично расчету комплексного сопротивления для конденсатора получают формулу расчета для катушки индуктивности:
Комплексная проводимость
Комплексная проводимость какого-либо участка электрической цепи представляет собой отношение комплекса электрического тока к комплексу напряжения рассматриваемого участка, таким образом выражение проводимости в комплексной форме будет иметь следующий вид:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
где: У — полная проводимость (модуль комплексной проводимости; ф — аргумент разности фаз напряжения и тока; j — мнимая единица.
Выразить комплексную проводимость можно в следующих формах:
- Показательная.
- Тригонометрическая.
- Алгебраическая.
Показательная форма комплексной проводимости выглядит следующим образом:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
В тригонометрической форме ее можно выразить так:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
В алгебраической форме комплексная проводимость имеет следующий вид:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
где: g = Ycosф — активная проводимость; b = Ysinф — реактивная проводимость.
Пример треугольника проводимостей на комплексной плоскости изображен на рисунке ниже.
Рисунок 12. Треугольник проводимостей. Автор24 — интернет-биржа студенческих работ
Полную проводимость в данном случае можно рассчитать по формуле:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Формула для расчета аргумента, таким образом, будет иметь следующий вид:
Комплексная проводимость может быть также определена как величина обратная комплексному сопротивлению:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
Так как Y = g-jb, то
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 19.09.2022
Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет
Источник
Комплексное сопротивление



Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме — Z.
Хороши известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то
Но на предыдущей лекции было установлено, что 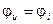
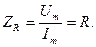
Таким образом видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между токами и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.
Комплексное сопротивление емкости определяется отношением
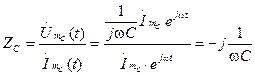
Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90 о . Это хорошо согласуется с ее максимальным значением
Поэтому на емкости напряжение отстает от тока на 90 о . Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.
Коэффициент 1/ 
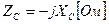
Комплексное сопротивление индуктивности определяется отношением
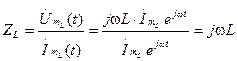
И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90 о .
Коэффициент wL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.
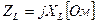
Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность — реактивными элементами цепи.
Определим теперь комплексное сопротивление электрической цепи, содержащей активные и реактивне элементы, например последовательно включенные R, L и С элементы (рис.3.1). Такая цепь представляет замкнутый 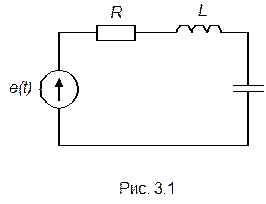
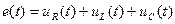
В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 1.2. Такой прием получил название символического метода. Так как ток протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду
Преобразуем это выражение к виду
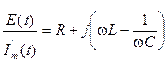
По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.3.1, т.е.
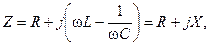
где R — действительная часть или активное сопротивление цепи.
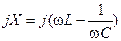
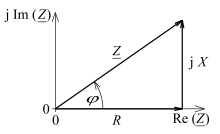
Выражение (3.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится понятие треугольника сопротивления (рис.3.2).

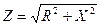
Противолежащий катет — реактивным сопротивлением X, причем
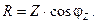
Угол 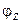
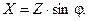
Учитывая выражения (3.8) ¸ (3.11) легко перейти от алгебраической к тригонометрической форме комплексного сопротивления
Z 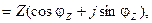
a применив формулу Эйлера получить показательную форму
Z 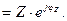
Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении
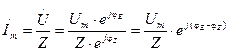
Выражение (3.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение
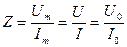
Источник
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Комплексные числа. Основные законы электрических цепей в комплексной форме
Определение 1
Комплексное число – это число вида а + сi, где а и с – вещественные числа, а i – мнимая единица, то есть число для которого выполняется равенство i(2) = -1.
Множество комплексных чисел может обозначаться С. Вещественные числа рассматриваются как частный случай комплексных чисел и имеют следующий вид а + 0i. Главное свойство комплексного числа заключается в том, что в нем выполняется основная теорема алгебры, то есть многочлен n-ой степени (n ⩾ 1) имеет n корней. Также доказано, что система комплексных чисел логически непротиворечива.
Замечание 1
Основная теорема алгебры представляет собой утверждение, что поле комплексных чисел алгебраически замкнуто, то есть любой многочлен, который отличен от константы, с комплексными коэффициентами имеет минимум один корень в поле комплексных чисел. Такое утверждение справедливо для многочленов с вещественными коэффициентами, потому что всякое вещественное число является комплексным с нулевой мнимой частью.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Необходимость применения комплексных чисел появилась в результате решения кубических уравнений, так как в формуле Кардано под квадратным корнем получалось отрицательное число. В изучение комплексных чисел большой вклад внесли такие ученые, как Эйлер, Гаусс и Декарт. Свойства комплексных чисел позволяют использовать их в решении разнообразных задач в области теории упругости, математики, обработке сигналов, теории колебаний, электромагнетизме, теории управления и т.п.
Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как цепи постоянного электрического тока, с заменой постоянных величин следующим образом:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
«Комплексные сопротивления и проводимости» 👇
К основным законам электроцепей относятся:
- Закон Ома.
- Первый закон Кирхгофа.
- Второй закон Кирхгофа.
В комплексной форме закон Ома будет иметь следующий вид:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Первый закон Кирхгофа в применении к узлу в комплексной форме выглядит следующим образом:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Второй закон Кирхгофа, применительно к контуру цепи, в комплексной форме можно записать следующим образом:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Достоинство выражения законов электрических цепей в комплексной форме заключается в том, что в них учитываются связь между действующими значениями напряжения и тока, а также сдвиг фаз между ними.
Комплексное сопротивление. Физический смысл
Комплексное сопротивление представляет собой отношение комплексной амплитуды напряжение гармонического сигнала, которое прилагается к двухполюснику, к комплексной амплитуде электрического тока, который протекает через двухполюсник при установившемся режиме (то есть по окончании переходных процессов в цепи). Для пассивных линейных цепей, обладающих постоянными параметрами, в установившемся режиме комплексное электрическое сопротивление никак не зависит от времени. В том случае, когда время в математическом выражения для комплексного сопротивления не сокращается, понятие комплексного сопротивления для двухполюсника неприменимо. Сама формула для электрического импеданса выглядит следующим образом:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где: j – мнимая единица; w – круговая частота; U(w). I(w) – амплитуды напряжения и электрического тока на частоте w; фu(w), фi(w) – фазы напряжения и тока гармонического сигнала на частоте w; U(jw), I(jw) – комплексные амплитуды напряжения и электрического тока гармонического сигнала на частоте w.
Если рассматривать комплексное электрическое сопротивление в алгебраической форме, то его действительная часть соответствует активному сопротивлению, а мнимая реактивному. То есть двухполюсник с импедансом z(jw) представляет собой последовательно соединенные резистор с сопротивлением R (z(jw)) и реактивный элемент с комплексным сопротивлением J(z(jw)).
Когда комплексное сопротивление рассматривается в тригонометрической форме, то его модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент соответствует сдвигу фазы между электрическим током и напряжением.
Для резистора комплексное электрическое сопротивление всегда равно его собственном и при этом никак не зависит от частоты, то есть:
$zR=R$
Напряжение и электрический ток в конденсаторе связаны соотношением:
$i(t) = C*(dU/dt)$
Следовательно, при напряжении
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Электрический ток, который протекает через конденсатор, может быть рассчитан следующим образом:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Отсюда комплексное сопротивление конденсатора рассчитывается по формуле:
$zC(jw) = 1/(jwC) = -(j/(wC).$
Аналогично расчету комплексного сопротивления для конденсатора получают формулу расчета для катушки индуктивности:
$zL(jw)=jwL$
Комплексная проводимость
Комплексная проводимость какого-либо участка электрической цепи представляет собой отношение комплекса электрического тока к комплексу напряжения рассматриваемого участка, таким образом выражение проводимости в комплексной форме будет иметь следующий вид:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
где: У – полная проводимость (модуль комплексной проводимости; ф – аргумент разности фаз напряжения и тока; j – мнимая единица.
Выразить комплексную проводимость можно в следующих формах:
- Показательная.
- Тригонометрическая.
- Алгебраическая.
Показательная форма комплексной проводимости выглядит следующим образом:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
В тригонометрической форме ее можно выразить так:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
В алгебраической форме комплексная проводимость имеет следующий вид:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
где: g = Ycosф – активная проводимость; b = Ysinф – реактивная проводимость.
Пример треугольника проводимостей на комплексной плоскости изображен на рисунке ниже.
Рисунок 12. Треугольник проводимостей. Автор24 — интернет-биржа студенческих работ
Полную проводимость в данном случае можно рассчитать по формуле:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Формула для расчета аргумента, таким образом, будет иметь следующий вид:
$ф = arctg(b/g)$
Комплексная проводимость может быть также определена как величина обратная комплексному сопротивлению:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
Так как Y = g-jb, то
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние[1][2]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Понятие и термин ввёл физик и математик О. Хевисайд в 1886 году[3][4].
Аналогия с электрическим сопротивлением проводника на примере резистора[править | править код]
Резистор — пассивный элемент, обладающий исключительно активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а также из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение 





Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:
- сопротивление идеальной катушки индуктивности стремится к нулю:
- если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:
- сопротивление идеального конденсатора стремится к бесконечности:
- если приложить к конденсатору некоторое постоянное напряжение
то при любом значении
ток через конденсатор будет нулевым:
Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:
- напряжение между выводами катушки индуктивности не равно нулю;
- ток, протекающий через конденсатор, не будет равен нулю.
Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.
Было бы удобно иметь некоторый параметр, аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитываются и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.
Определение[править | править код]
Импедансом 


|
(1) |
- Здесь:
Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как 



Физический смысл[править | править код]
Алгебраическая форма[править | править код]
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом 


Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма[править | править код]
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.
Ограничения[править | править код]
Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени 

- Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.
Обобщенный импеданс в s-плоскости и преобразование Лапласа[править | править код]
Импедансы, определённые через комплексную частоту 



Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы 
| Двухполюсник | Обобщённый импеданс |
|---|---|
| Резистор | 
|
| Катушка индуктивности |

|
| Конденсатор | 
|
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет 
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
- где
— некоторое вещественное число, выбираемое из условий сходимости интеграла.
- Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение
Пассивный RС-фильтр нижних частот 1-го порядка
Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи 
- где обозначено
— постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда 
- где
— амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
![{displaystyle F_{in}(s)={mathcal {L}}[U_{0} h(t)]=int limits _{0}^{infty }e^{-st},U_{0},h(t),dt=U_{0}/s.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17ae29a5b09e0fcaa003350e6a466d83535d3953)
Таким образом, получен отклик цепи при нулевом начальном условии (

Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.
Вычисление импеданса[править | править код]
Идеальные элементы[править | править код]
Резистор[править | править код]
Для резистора импеданс всегда равен его сопротивлению 

|
(2) |
Конденсатор[править | править код]
Ток и напряжение для конденсатора связаны соотношением:

|
(3) |
Отсюда следует, что при напряжении

|
(4) |
ток, текущий через конденсатор, будет равен:

|
(5) |
После подстановки (4) и (5) в (1) получаем:

|
(6) |
Катушка индуктивности[править | править код]
Аналогичное рассмотрение для катушки индуктивности приводит к результату:

|
(7) |
Общий случай[править | править код]
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:

|
(8) |
Экспериментальное измерение импеданса[править | править код]
Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.
Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.
В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.
Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.
Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.
Активная и реактивная составляющие импеданса обычно выражают в омах. Однако, для характеризации антенн, линиях передачи, СВЧ электронных устройств обычно более удобно использовать связанные с ним S-параметры, коэффициент стоячей волны или коэффициент отражения.
Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса[6].
Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств[6].
LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.
Применение понятия импеданса[править | править код]
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого применяется преобразование Лапласа, либо сигнал раскладывается на спектральные компоненты при помощи ряда Фурье (или преобразования Фурье) и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал .
См. также[править | править код]
- Внутреннее сопротивление
- Адмиттанс
- АФЧХ
Примечания[править | править код]
Литература[править | править код]
- Бессонов Л. А. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
- Графов Б. М., Укше Е. А. Электрохимические цепи переменного тока. — М.: Наука, 1983.

Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и тогда
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как .
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
где
При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
а угол
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
-
-
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
-
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида при φ = 0° равно
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Ток в цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство
Проверяем
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
-
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи
Откуда
— нагрузка носит активно-индуктивный характер
2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:











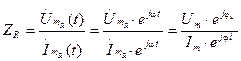
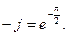
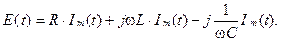























![{displaystyle f_{F,H}(t)={mathcal {L}}^{-1}[H(s) F_{t}(s)]={frac {1}{2pi j}}int limits _{sigma _{1}-jcdot infty }^{sigma _{1}+jcdot infty }e^{st}H(s) F_{t}(s),ds,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39a2cc1925670bb01a4d2af0cbd70bb0ace7ef6d)






![{displaystyle U_{out}(t)={mathcal {L}}^{-1}[H_{RC}(s) F_{in}(s)]={frac {1}{2pi j}}int limits _{sigma _{1}-jcdot infty }^{sigma _{1}+jcdot infty }e^{st}{frac {1}{sT+1}}cdot {frac {U_{0}}{s}},ds=U_{0}(1-e^{-t/T}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a379e2b89a1978a1b8ad8e0be3f3cc80ac7ac5a)






















