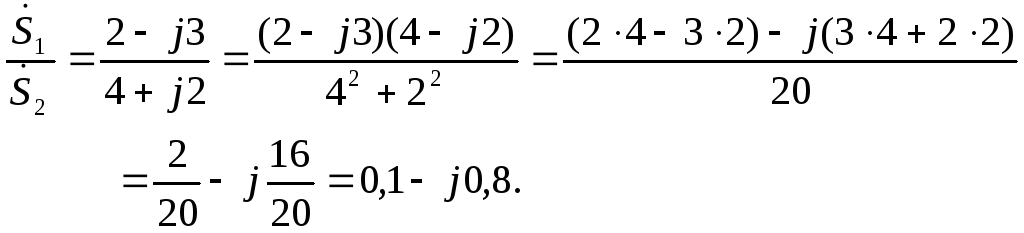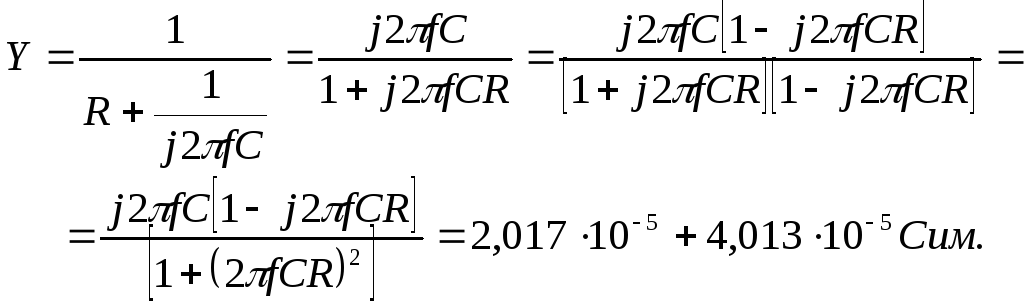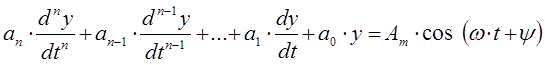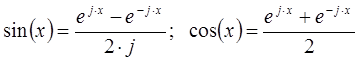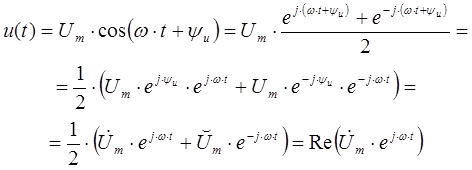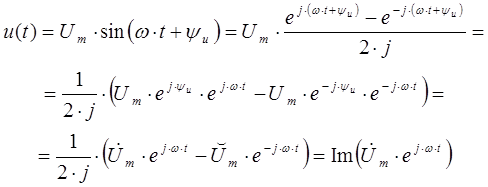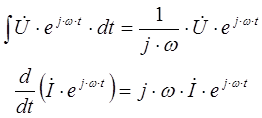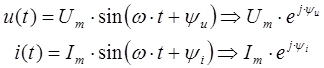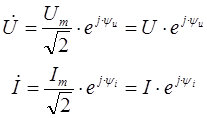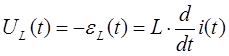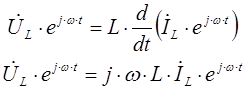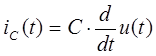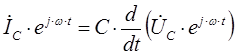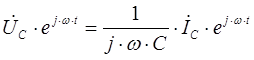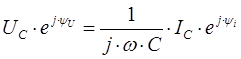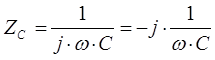5.1. Комплексная амплитуда гармонического
сигнала
Комплексная амплитуда является
комплексным числом (–мнимая единица), определяется
толькоамплитудой и начальной фазойсигнала и не зависит от его частоты.
Комплексная амплитуда обозначается
тем же символом, что и амплитуда сигнала,
но с точкой сверху (в литературе
используются и другие маркирующие
отметки, например, горизонтальная черта
сверху символа).
Например, если мгновенное значение
гармонического напряжения равно
В,
то его комплексная амплитуда имеет видВ
илиВ.
Если запись сигнала отличается от формы
(5.1) то необходимо провести соответствующие
тригонометрические преобразования,
представленные в табл. 5.1.
Таблица 5.1
|
|
|
|
91
Если гармоническое напряжение имеет
вид
мВ,
то после преобразования получиммВ,
а комплексная амплитуда будет равнамВ.
5.2. Операции с комплексными числами
Комплексные числа могут быть записаны
в двух формах: алгебраической и
показательной.
В алгебраической формекомплексное
числозаписывается в виде
,
(5.2)
где
–действительная, а
–мнимаячасти комплексного числа,
.
В показательной формекомплексное
число представляется выражением
,
(5.3)
величину
называютмодулем, а
–аргументомкомплексного числа.
От алгебраической формы можно перейти
к показательной, модуль комплексного
числа равен
,
(5.4)
а аргумент
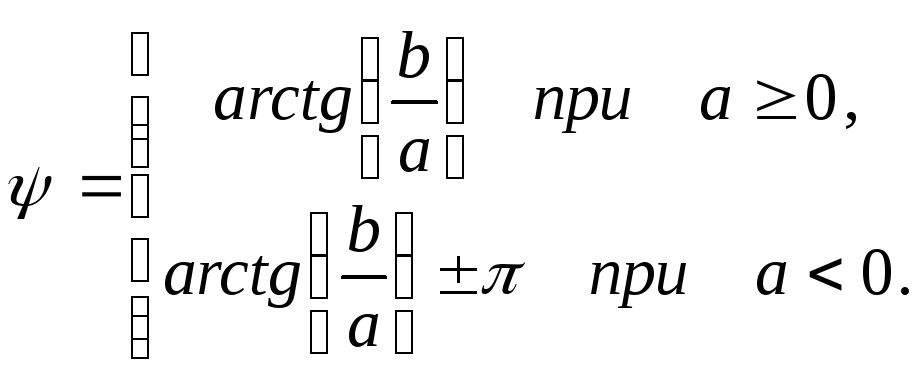
92
Аргумент комплексного числа, как и
начальная фаза гармонического сигнала
(подраздел 2.2), величина многозначная,
к ней можно добавить (или вычесть)
любое число раз. Для обеспечения
однозначности аргумента комплексного
числа его значения выбирают в диапазоне,
например, отдо
или от 0 до
.
Показательную форму комплексного числа
можно заменить алгебраической с помощью
соотношений
(5.6)
Они вытекают из известной в математике
формулы Эйлера,
(5.7)
Например, если комплексное число в
алгебраической форме равно
,
то в показательной форме его можно
записать в виде
.
Если комплексное число равно
,
то в показательной форме получим
.
Для комплексного числа в показательной
форме в виде
его алгебраическая форма имеет вид
.
93
С комплексными числами проводятся все
четыре арифметические действия.
При сложении и вычитании комплексных
чисел
и
в алгебраической форме получим
.
(5.8)
Если числа заданы в показательной форме,
то перед сложением или вычитанием их
необходимо преобразовать в алгебраическую
форму.
Операции умножения и деления удобнее
выполнять в показательной форме, когда
и
,
при этом при умножении комплексных
чисел их модули перемножаются, а аргументы
складываются,
,
(5.9)
а при делении делятся модули и вычитаются
аргументы,
.
(5.10)
Умножение можно провести и с алгебраической
формой сомножителей по известным
правилам с учетом того, что
,
.
(5.11)
При делении комплексных чисел в
алгебраической форме используется
операция устранения комплексности в
знаменателепутем умножения числителя
и знаменателя дроби на число,комплексно
сопряженноезнаменателю. Для заданного
числакомплексно сопряженное число
94
равно
,
то есть отличается отпротивоположным знаком примнимой
части. Произведение двух комплексно
сопряженных чисел всегда равно квадрату
их модуля,
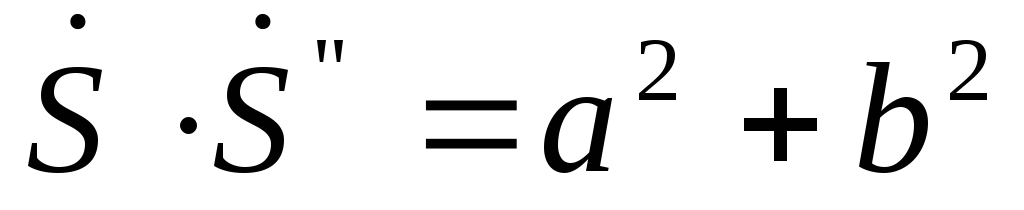
(5.12)
Тогда при делении в алгебраической
форме получим
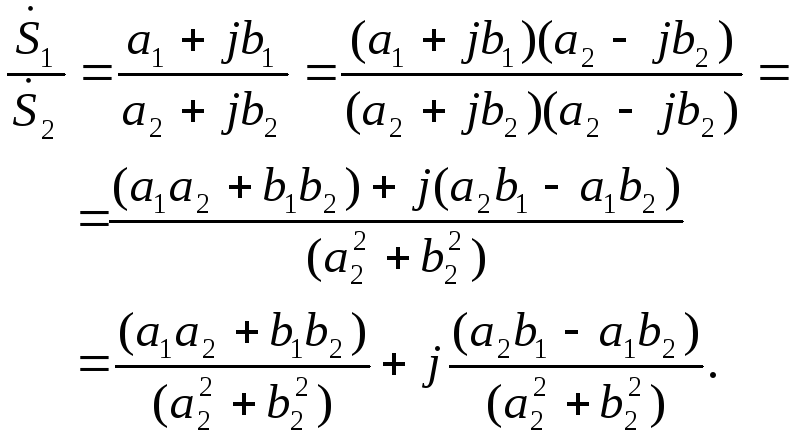
Рассмотрим пример
и
,
тогда
,
Эти операции можно провести и в
показательной форме, тогда
,
,
95
,

Как видно, полученные результаты
совпадают.
Полезно запомнитьследующие
равенства, вытекающие из формулы Эйлера
(5.7),
|
|
|
|
|
Вычисления с комплексными числами
удобно проводить на персональной ЭВМ
с помощью пакета программ MathCAD.
5.3. Законы Ома и Кирхгофа для комплексных
амплитуд
токов и напряжений
Законы Ома и Кирхгофа применимы в своих
классических формулировках для
комплексных амплитуд токов и напряжений.
96
Знаки в алгебраических суммах определяются
выбранными положительными направлениями
токов и напряжений и направлением обхода
контура.
5.4. Комплексные сопротивления
и проводимости
элементов цепи
Значения комплексных сопротивлений
и проводимостей
элементов цепиR,LиCприведены в табл. 5.2
(запомните эти формулы).
Таблица 5.2
|
R |
L |
C |
|
|
Комплексное
сопротивление |
|
|
|
|
Комплексная проводимость |
|
|
|
97
Комплексные сопротивление и проводимость
сопротивления
всегдадействительны(мнимая часть
равна нулю), а индуктивности и емкости
–мнимые (действительная часть
равна нулю).
Для комплексного сопротивления
из закона Ома (5.14) можно записать
,
(5.17)
где
– сдвиг фаз между напряжением и током в
элементе. Для сопротивлениянапряжение и ток совпадают по фазе, то
естьи из (5.17) величина
действительна.
В индуктивности напряжение опережает
по фазе ток на 900(нарадиан), следовательно
,
тогдаи величина комплексного сопротивления
индуктивностиоказывается снулевойдействительной
иположительноймнимой частями. В
емкости,
и ее комплексное сопротивление имеетнулевуюдействительную иотрицательнуюмнимую части.
Аналогичный анализ проводимости
элементов цепи проведите самостоятельно.
5.5. Комплексные сопротивление и
проводимость
участка цепи
Полные комплексные сопротивления (и
проводимости) двухполюсного участка
цепи с произвольным соединением элементов
определяются по тем же правилам, что и
для цепи постоянного тока:
– комплексное сопротивление
последовательногосоединения
двухполюсников равносуммеих
комплексных сопротивлений;
98
– комплексная проводимость параллельногосоединения двухполюсников равнасуммеих комплексных проводимостей.
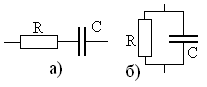
сопротивление последовательной цепи,
показанной на рис. 5.1а прикОм
ипФ
на частотекГц равно
кОм,
а проводимость параллельной
Рис. 5.1.
цепи на рис 5.1б –
Сим.
Зная комплексное сопротивление цепи,
можно определить ее комплексную
проводимость и наоборот,
(5.18)
Например, для последовательной цепи
на рис. 5.1а ее проводимость равна
Расчет проведен методом устранения
комплексности знаменателя путем
умножения числителя и знаменателя дроби
на множитель, комплексно-сопряженный
знаменателю.
99
Можно провести вычисление проводимости
путем преобразования комплексного
сопротивления из алгебраической формы
в показательную,
.
Тогда для проводимости получим
Комплексное сопротивление цепи со
смешанным соединением элементов
определяется следующим образом:
– в цепи выделяется фрагмент с простым
(последовательным или параллельным)
соединением элементов и определяется
его сопротивление или проводимость;
– фрагмент заменяется эквивалентным
элементом, в полученной цепи вновь
выделяется простой фрагмент и повторяется
предыдущее действие;
– эти действия повторяются до тех пор,
пока цепь не трансформируется в один
элемент с соответствующим сопротивлением
или проводимостью.
100
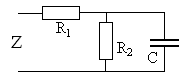
цепь, схема которой показана на рис. 5.2
прикОм,
нФ,
рад/с
и определим ее комплексное сопротивление.
В цепи выделяется простой параллельный
фрагмент из элементов
и определяется его сопро-
тивление
,
равное Рис. 5.2
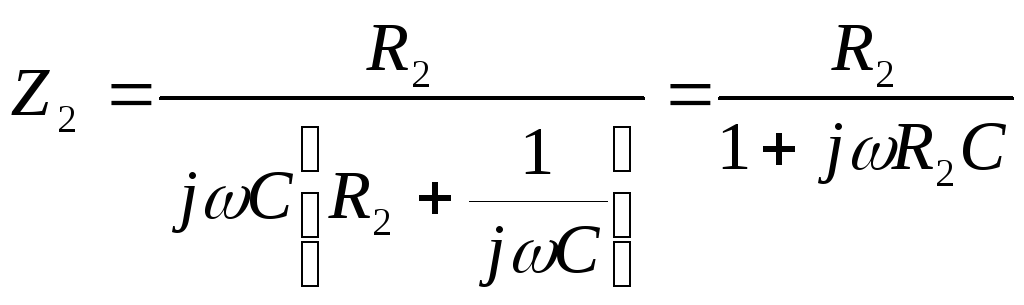
Тогда параллельный фрагмент
заменяется эквивалентным элементом с
сопротивлениеми схема цепи принимает вид, показанный
на рис. 5.3.
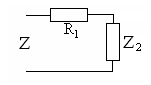
полученной последовательной цепи ее
сопротивлениеравно
.
.
Подставляя исходные данные, получим
Рис. 5.3
Ом.
5.6. Характеристики комплексного
сопротивления
и проводимости
Полное комплексное сопротивление
в показательной форме можно записать
в виде
101
.
(5.19)
Модулькомплексного сопротивления
равен отношению амплитуд (действующих
значений) напряжения и тока,
.
(5.20)
Аргументкомплексного сопротивления
равенсдвигу фазмежду напряжением
и током,
,
(5.21)
Комплексная проводимость в показательной
форме имеет вид
,
(5.22)
ее модульравен отношению амплитуд
(действующих значений) тока и напряжения,
,
(5.23)
а аргумент– сдвигу фаз между током
и напряжением,
.
(5.24)
Таким образом, комплексное сопротивление
и проводимость характеризуют взаимосвязь
амплитуд и начальных фаз напряжения и
тока.
102
Представим комплексное
сопротивление в алгебраической форме,
,
(5.25)
где
–активнаяа,
–реактивнаясоставляющие комплексного
сопротивления. Все величины в (5.25)
измеряются в Омах.
Рассмотрим в качестве примера
сопротивление цепи, показанной на рис.
5.2.
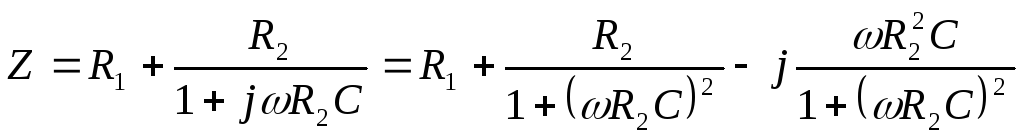
(5.26)
Как видно, активная
составляющая сопротивления
равна
,
(5.27)
а реактивная
–
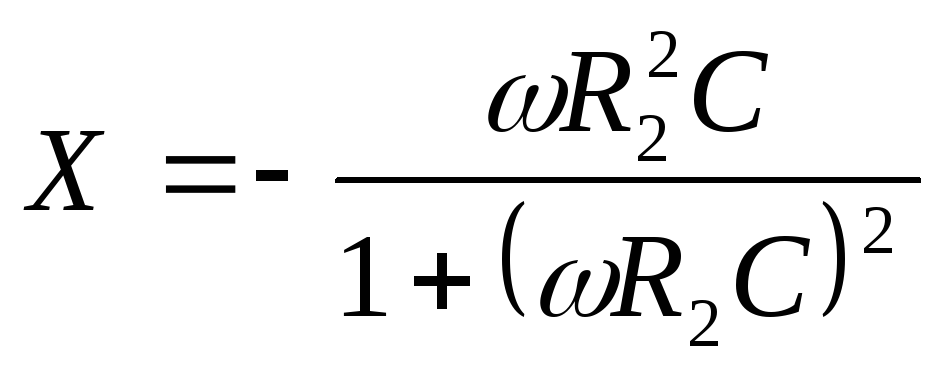
(5.28)
и обе зависят от частоты сигнала.
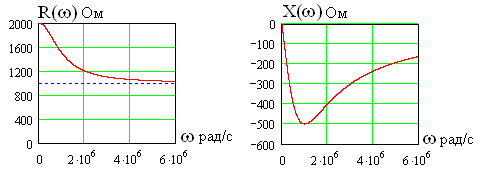
Зависимости от частоты
активной
и реактивной
составляющих сопротивления для цепи
рис. 5.2 показаны на рис. 5.4. На низких
частотахемкость является разрывом цепи и
сопротивлениеОм.
На высоких частотахемкость представляет собой короткое
замыкание (ее сопротивление стремится
к нулю) и сопротивление цепи равноОм.
И в том и другом случаях реактивное
сопротивление стремится к нулю.
103
При
рад/с
получается ранее вычисленное значениеОм.
Рис. 5.4.
Аналогичный анализ проводимости цепи,
показанной на рис. 5.2, проведите
самостоятельно.
5.7. Комплексная мощность
Это комплексная величина с действительной
и мнимой частями,
.
(5.30)
Комплексная мощность измеряется в ВА(вольт-амперах).
104
Как видно, действительная(активная)
составляющая
комплексной мощности представляет
собой среднюю мощность
,потребляемуюдвухполюсником,
.
(5.31)
Как уже отмечалось, активная мощность
измеряется в ваттах.
Мнимая(реактивная) составляющаякомплексной мощности равна
(5.32)
и характеризует процессы накопления и
обмена энергией с источником в реактивных
элементах цепи. Эта мощность не расходуется
цепью и измеряется в ВАр(вольт-амперы
реактивные), она численно равна
максимальной скорости запасания энергии
в цепи. Реактивная мощность может быть
положительной (при),
при этом энергия запасается в магнитном
поле индуктивностей, или отрицательной
(при)
при накоплении энергии в электрическом
поле емкостных элементов.
Модуль комплексной мощности равен
(5.33)
и измеряется в ВА. Величину
называютполной мощностью,она
определяется активной и реактивной
мощностями,
.
(5.34)
Можно записать
105
,
(5.35)
величину
называюткоэффициентом мощности.
Припотребляемая мощность
максимальнаи равна полной мощности
,
а реактивная мощностьравна нулю.
Если для вычисления мощности используются
действующие значениянапряжения и
тока, то в приведенных соотношениях
удаляется множитель.
5.8. Расчет мощности, потребляемой
двухполюсником
Зная комплексные амплитуды напряжения
и тока, согласно (5.29), можно определить
комплексную мощность, например, при
В
иА
получим, что сдвиг фаз между напряжением
и током равен.
Тогда комплексная мощность равна
ВА,
активная составляющая (потребляемая
мощность) –
Вт,
реактивная мощность –
ВАр,
а полная мощность –
ВА.
106
Отрицательная реактивная мощность
свидетельствует о том, что цепь накапливает
энергию в емкостном элементе. Так как
коэффициент мощности равен
,
то потребляемая мощность существенно
меньше полной.
Мощности можно определить, зная
комплексную амплитуду напряжения (или
тока) и комплексное сопротивление
(проводимость) цепи.

цепь на рис. 5.2 с подключенным к ней
идеальным источником гармонического
напряжения,
показанную на рис. 5.5.прикОм,
нФ,
В.
Ком-
плексная амплитуда
ЭДС Рис. 5.5
источника равна
В,
а комплексное сопротивление цепи было
определено ранее,
Ом.
По закону Ома найдем комплексную
амплитуду тока
,
мА,
а полная комплексная мощность равна
ВА,
или в алгебраической форме
107
ВА.
Таким образом, потребляемая цепью
мощность равна
Вт,
реактивная мощность –ВАр, а полная мощность –
ВА.
На практике наибольший интерес
представляет определение мощности,
которую потребляет цепь от одного или
нескольких источников. Необходимо
помнить, что в электрической цепи
мощность потребляется только активными
элементами – сопротивлениями.
Потребляемую мощность в цепи, содержащей
несколько сопротивлений, можно определить,
если известны амплитуды (действующие
значения) токов или напряжений на этих
элементах.
Расчет токов и напряжений на элементах
цепи будет рассмотрен в дальнейшем.
В цепи с комплексным
сопротивлениемпри протекании через нее тока с амплитудой
потребляемая мощность равна
.
(5.36)
Аналогично в цепи с комплексной
проводимостью
при наличии на ней напряжения с амплитудой
потребляемая мощность будет равна
.
(5.37)
108
5.9. Максимизация потребляемой мощности
В инженерной практике часто возникает
необходимость обеспечить максимум
активной мощности, передаваемой от
источника сигнала в нагрузку.
В качестве примеров можно выделить
задачу максимизации мощности на валу
электродвигателя при питании его от
силовой сети. Аналогичная проблема
возникает при передаче высокочастотной
мощности от выходного усилителя
радиопередатчика в антенну для излучения
электромагнитных волн (высокочастотная
мощность стоит очень дорого как с
экономической, так и с технической точки
зрения).
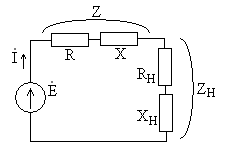
электрической цепи показана на рис.
5.6. В цепь включен реальный источник
напряжения с комплексной амплитудой
ЭДСи внутренним комплексным сопротивлением
,
к которому подключена нагрузка с
комплексным сопротивлением.
Необходимо подоб- Рис. 5.6.
Рать такое сопротивление
нагрузки, при котором она потребляла
бы от источника максимальную мощность.
Комплексная амплитуда тока в цепи
равна
,
тогда для амплитуды тока получим
109
,
(5.38)
в выражение для потребляемой мощности
примет вид

(5.39)
так как мощность потребляется только
в активном сопротивлении
.
Необходимо определить максимум (5.39) по
двум независимым переменным – активному
и
реактивномусопротивлениям нагрузки. Как видно,
величинаприсутствует только в знаменателе дроби
и суммавозводится в квадрат. Минимум знаменателя
будет иметь место при условии
или
.
(5.40)
Таким образом, реактивное сопротивление
нагрузки должно быть по модулю равно
реактивному сопротивлению источника
и иметь противоположный характер(если у источника сопротивление
индуктивно, то у нагрузки оно должно
быть емкостным и наоборот). В результате
получим
.
(5.41)
Максимум (5.41) по
можно найти, вычислив производную этой
функции и приравняв ее нулю. В результате
получим (проделайте это самостоятельно)условия, при которых
110
потребляемая нагрузкой мощность
максимальна,
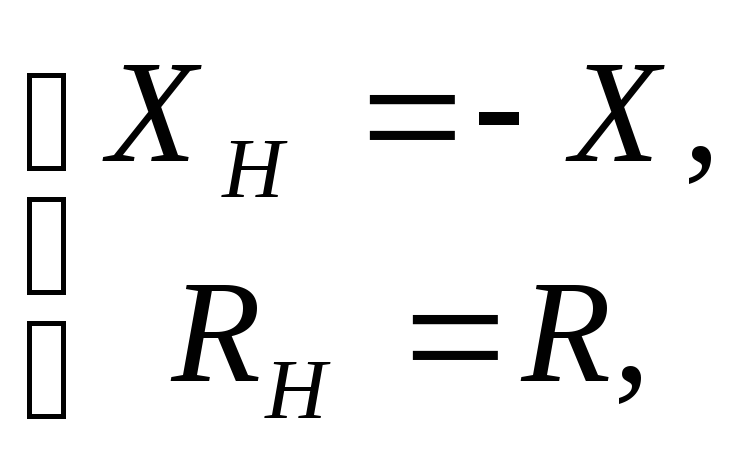
и соответствующую величину мощности
.
(5.43)
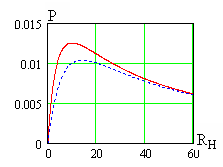
мощности в нагрузкеот
при
(сплошная линия) и
Ом
(пунктирная линия) показаны на рис. 5.7
приОм
иВ.
Как видно, при отклонении от оптимальных
условий (5.42) потребляемая нагрузкой
мощность замет но снижается.
Рис. 5.7
Рассмотрим коэффи-
циент полезного действия (КПД) – отношение
мощности в нагрузке к мощности,
потребляемой от источника сигнала,
при условии (5.40) равной
.
(5.44)
тогда КПД
равен
.
(5.45)
111

КПД от активной составляющей сопротивления
нагрузки показана на рис. 5.8. Как видно,
при условии передачи максимума мощности
в нагрузку КПД равен 0,5 (50%), то есть
половина мощности источника потребляется
его же внутренним со-
Рис. 5.8 противлением
(происходит на-
грев
источника). При повышении
КПД увеличивается, однако при этом
снижается мощность, передаваемая в
нагрузку.
5.10. Задания для самостоятельного решения
Задание 5.1.Определите комплексные
амплитуды гармонических сигналов
В,
мВ
мА,
А.
Задание 5.2.По заданной комплексной
амплитуде определите мгновенные значения
сигналов, их амплитуды и начальные фазы
В,
мВ,
В,
мВ,
мА,
А,
мА,
мкА.
Задание 5.3.Вычислите сумму, разность,
произведение и частное комплексных
чисели
,
результаты запишите в алгебраической
и показательной формах.
|
|
4-j3 |
7-j4 |
-j |
2 |
|
20+j3 |
|
|
|
-8+j2 |
-j5 |
j |
-1-j |
5+j2 |
|
|
112
Задание 5.4.Для чисел из задания 5.3
вычислите их модуль и аргумент, а также
обратную величину.
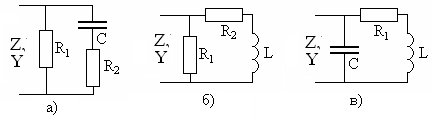
Задание 5.5.Найдите полное комплексное
сопротивлениеи проводимость
показанных на рис. 5.9 цепей при
кОм,
мГн
ипФ
на частотерад/c.
Рис. 5.9
Задание 5.6.Получите общие формулы
для полного комплексного сопротивления
цепей из задания 5.5. Найдите формулы его
модуля, аргумента, активной и реактивной
составляющих, постройте их графики в
зависимости от частоты сигнала.
Задание 5.7.Вычислите мощность,
потребляемую показанной на рис.5.10 цепью
при ЭДС источникаВ,
кОм
инФ.
Рис. 5.10
Задание 5.8.Определите мощность,
потребляемую показанной на рисунке
цепью от источника токамА
прикОм,
мГн
инФ.
Рис. 5.11
113
Главная
→
Теория электрических цепей
→
Комплексные амплитуды, комплексные действующие значения, комплексы действующих значений
Комплексные амплитуды, комплексные действующие значения, комплексы действующих значений
Комплексные амплитуды
Комплексные амплитуды напряжения
U ˙ m = U m e j α u
и тока
I ˙ m = I m e j α i
при анализе установившегося синусоидального режима соответствуют сигналам синусоидальной формы напряжения
купить 1с бухгалтерия купить. твердосплавные насадки – вся подробная информация у нас на сайте.
u(t) = Umcos(ωt + αu)
и тока
i(t) = Imcos(ωt + αi).
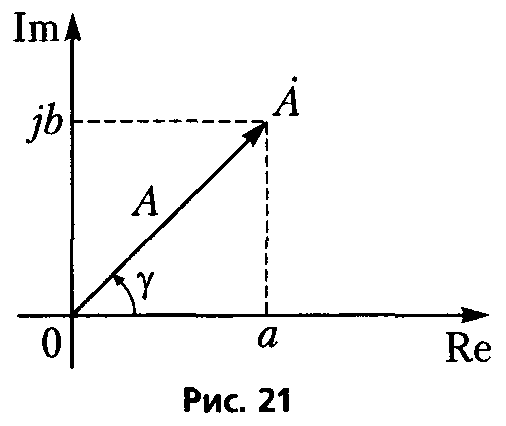
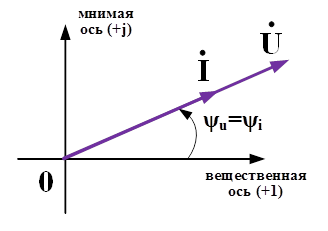
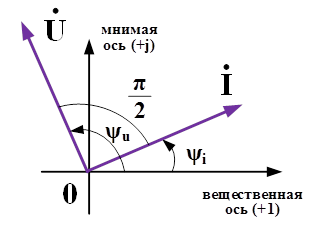
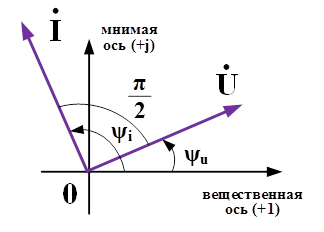
Комплексные амплитуды представляют векторами на комплексной плоскости, как комплексное число (рис. 21)
A ˙ =A e jγ =Acosγ+jAsinγ=a+jb,
где модуль (длина вектора)
A=| A ˙ |= a 2 + b 2 ,
фаза
γ=arctg b a ,
действительная часть комплексного числа
Re A ˙ =Acosγ=a,
мнимая часть комплексного числа
Im A ˙ =Asinγ=b,
мнимая единица
j= −1 ,
здесь
j 2 =−1, j⋅( −j )=− j 2 =−( −1 )=1, 1 j = j j 2 = j −1 =−j.
Сопряженное комплексное число
A * =A e −jγ =Acos( −γ )+jAsin( −γ )=Acosγ−jAsinγ=a−jb,
где положительный отсчет угла γ производят против часовой стрелки от «правого горизонта».
Комплексные амплитуды используют при обосновании метода комплексных амплитуд для расчета установившегося синусоидального режима
u( t )=Re U ˙ m e jωt =Re U m e j α u e jωt =Re U m e j( ωt+ α u ) = U m cos( ωt+ α u ); i( t )=Re I ˙ m e jωt =Re I m e j α i e jωt =Re I m e j( ωt+ α i ) = I m cos( ωt+ α i ),
где ejωt — оператор вращения, U ˙ m e jωt , I ˙ m e jωt – вращающиеся векторы, поскольку их суммарная фаза γ = ωt + α равномерно увеличивается с увеличением времени t.
Комплексные действующие значения или комплексы действующих значений:
комплексное действующее напряжение или комплекс действующего напряжения
U ˙ =U e j α u = U ˙ m 2 = U m 2 e j α u ,
комплексный действующий ток или комплекс действующего тока
I ˙ =I e j α i = I ˙ m 2 = I m 2 e j α i .

комплексные действующие значения,
Комплексные амплитуды

Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и тогда
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как .
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
где
При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
а угол
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
-
-
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
-
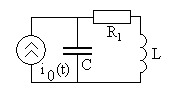
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида при φ = 0° равно
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Ток в цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство
Проверяем
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
-
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи
Откуда
— нагрузка носит активно-индуктивный характер
2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
Рассмотрим линейную электрическую цепь с сосредоточенными параметрами, находящуюся под гармоническим воздействием ЭДС (синусоидальная функция от времени). Определение значений токов и напряжений в рассматриваемой схеме сводится к составлению и решению системы дифференциальных уравнений с постоянными коэффициентами, которые могут быть записаны в следующем виде:
В общем виде решение данного дифференциального уравнения будет определяться суммой двух составляющих: свободной и вынужденной составляющей.
Свободная составляющая представляет собой общее решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Свободная составляющая определяет процессы, которые возникают в электрической цепи, выведенной из состояния покоя некоторым воздействием. Свободная составляющая характеризует процесс обмена энергией между индуктивными и емкостными элементами электрической цепи, частота колебаний свободной составляющей определяется параметрами расчетной цепи. В линейных электрических цепях свободные составляющие затухают во времени по экспоненциальному закону.
Вынужденная составляющая представляет собой частное решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Вынужденная составляющая определяет установившийся режим работы системы после окончания переходного процесса. Данная составляющая может также называться установившейся составляющей.
В большинстве решаемых задач рассматривают только квазистационарные режимы работы энергосистемы (установившийся режим работы), в связи с этим рассматривают только вынужденную составляющую, а свободной составляющей пренебрегают. В таком случае для расчёта сложной электрической цепи с гармоническими источниками ЭДС широко применяется метод комплексных амплитуд. Данный метод в технической литературе может встречаться под другими названиями: символический метод или комплексный метод, так как он основан на символическом изображении действительных синусоидальных функций времени комплексными числами. Данный метод разработан в конце XIX века американскими инженерами – электротехниками Ч.П.Штейнметцем и А.Е.Кеннели.
Метод комплексных амплитуд, основан на идее функционального преобразования, при котором гармоническая функция из временной области (оригинал функции) заменяется функцией, которая определена на комплексной области (изображение исходной функции). Переход от реальных гармонических токов и напряжений к комплексным амплитудам осуществляется с помощью формулы Эйлера, которая связывает комплексную экспоненту с тригонометрическими функциями.
Формула Эйлера позволяет определить тригонометрические функции через комплексные величины, которые записываются через экспоненты с мнимыми аргументами:
- Рассмотрим случай, когда гармонический сигнал представлен в виде косинусоидальной функции. В рассматриваемом случае в соответствиис представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:
Таким образом, оригинал косинусоидальной функции определяется проекцией комплексного числа на вещественную ось. В представленном выражении используются следующие обозначения:
– комплексная амплитуда, которая определяется по формуле:
– сопряженная комплексная амплитуда, которая определяется по формуле:
– оператор вращения, который имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью
. Всякий неподвижный вектор, будучи умноженным на оператор вращения, начинает вращаться в комплексной плоскости против часовой стрелки с заданной угловой скоростью.
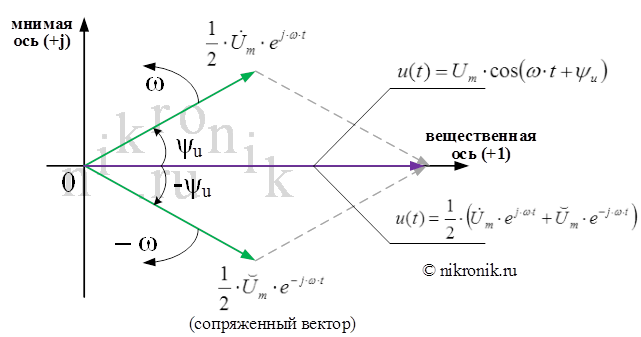
Рис.1. Разложение косинусоидальной функции в виде двух векторов
Таким образом, символическое изображение косинусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами – амплитудой и начальной фазой.
- Рассмотрим другой случай, когда гармонический сигнал представлен в виде синусоидальной функции. В рассматриваемом случае в соответствиис представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:
Таким образом, оригинал синусоидальной функции определяется проекцией комплексного числа на мнимую ось. В представленном выражении используются следующие обозначения:
– комплексная амплитуда, которая определяется по формуле:
– сопряженная комплексная амплитуда, которая определяется по формуле:
– оператор вращения, который имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью
. Всякий неподвижный вектор, будучи умноженным на оператор вращения, начинает вращаться в комплексной плоскости против часовой стрелки с заданной угловой скоростью.
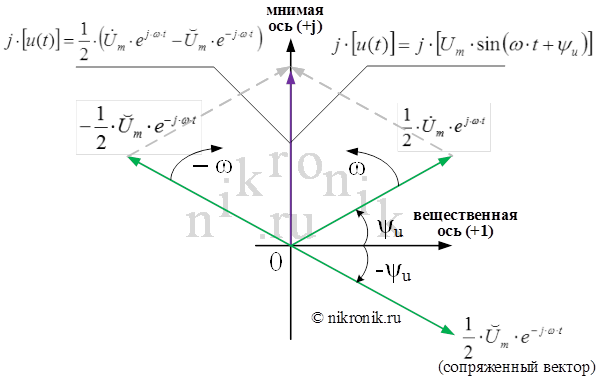
Рис.2.Разложение синусоидальной функции в виде двух векторов
Таким образом, символическое изображение синусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами – амплитудой и начальной фазой.
Использование метода комплексных амплитуд значительно упрощает расчет линейной электрической цепи, так как операции дифференцирования и интегрирования сводятся к задаче решения системы алгебраических уравнений: операция дифференцирование гармонической функции соответствует умножение комплексного числа на переменную «jω»,а операция интегрирование гармонической функции соответствует делению комплексного числа на «jω».
Объединяя полученные результаты можно сделать вывод, что любую гармоническую функцию с заданной частой ω можно представить в виде вектора на комплексной плоскости, который вращается с угловой скоростью ω. С целью единообразия выполнения расчетов в соответствии с методом комплексных амплитуд было принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для нулевого момента времени . Таким образом, символическое изображение синусоидальной функции определяется в следующем виде:
Для определения интенсивности действия электрических параметров (тока или напряжения) используют действующие комплексные значения, которые определяются следующим образом:
Расчет цепи синусоидального тока методом комплексных амплитуд проводится в следующем порядке:
– На первом этапе гармоническая функция, заданная во временной области, заменяется изображением данной функции на комплексной плоскости.
– На втором этапе составляется система уравнений, которая описывает рассматриваемую электрическую цепь, в соответствии с любым методом расчета электрических цепей. Далее выполняется расчет данной системы уравнений с определением комплексных значений искомых токов и напряжений.
– На третьем этапе выполняют обратное преобразование, с помощью которого переходят от изображения функции на комплексной плоскости к оригиналам функции во временной области. Чтобы восстановить исходное гармоническое колебание по известной комплексной амплитуде и частоте ω, необходимо комплексную амплитуду умножить на , а затем выделить мнимую часть (для синусоидальной функции).
Комплексное сопротивление электрической цепи
Определим комплексное сопротивление пассивных элементов электрической цепи, которые находятся под гармоническим воздействием. Для этого рассмотрим связь между током и напряжением на активном, индуктивном и емкостном элементах.
- Рассмотрим активное сопротивление, по которому протекает синусоидальный ток. Данный ток создает в активном напряжении падение напряжение на элементе, которое определяется в следующем виде:
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
Для нулевого момента времени данное выражение записывается в следующем виде:
Из полученного выражения видно, что ток на индуктивности совпадает по фазе с напряжением. Сопротивление на индуктивности носит активный характер и определяется в следующем виде:
Рис.3. Векторная диаграмма токов и напряжений на резистивном элементе
- Рассмотрим индуктивный элемент, по которому протекает синусоидальный ток. Данный ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции. Таким образом, падение напряжение на элементе определяется в следующем виде:
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
Для нулевого момента времени данное выражение записывается в следующем виде:
Из полученного выражения видно, что ток на индуктивности отстает от напряжения на угол 90 градусов. Сопротивление на индуктивности носит реактивный характер и определяется в следующем виде:
Рис.4. Векторная диаграмма токов и напряжений на индуктивном элементе
- Рассмотрим емкостной элемент, к которому приложено синусоидальное напряжение. Под действием синусоидального напряжения конденсатор будет периодически заряжаться и разряжаться. Периодическая перезарядка конденсатора будет сопровождаться протеканием тока. Таким образом, ток, протекающий между обкладками конденсатора, будет определяться следующим образом:
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
Для нулевого момента времени данное выражение записывается в следующем виде:
Из полученного выражения видно, что ток на емкости опережает напряжение на угол 90 градусов. Сопротивление на емкости носит реактивный характер и определяется в следующем виде:
Рис.5. Векторная диаграмма токов и напряжений на емкостном элементе
Следует отметить, что для определения изображений синусоидальных функции (токов и напряжений) в электрической цепи необходимо составить систему уравнений любым доступным методом:
– с помощью первого и второго закона Кирхгофа, который записывается для изображений синусоидальных функции;
– с помощью метода контурных токов, который записывается для изображений синусоидальных функции;
– с помощью метода узловых потенциалов, который записывается для изображений синусоидальных функции.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 сентября 2015 года; проверки требуют 2 правки.
Компле́ксная амплитуда (фазор) — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе гармонического сигнала.
Определение[править | править код]
Пусть имеется гармонический сигнал:

Сумма двух комплексных амплитуд в виде вращающихся векторов
Над сигналами, записанными в подобной форме, алгебраически неудобно производить такие арифметические операции, как сложение двух сигналов, вычитание из одного сигнала другого сигнала. С целью облегчения этих операций гармонические сигналы представляют в виде комплексного числа, модуль которого равен амплитуде сигнала, а аргумент — фазе сигнала. При этом оригинальный сигнал a(t) равен действительной части данного комплексного числа b(t):

где 
здесь комплексной амплитудой гармонического сигнала является следующее выражение:

Физический смысл[править | править код]
Алгебраическая форма[править | править код]
Если рассматривать комплексную амплитуду как комплексное число в алгебраической форме, то действительная часть соответствует амплитуде косинусной (синфазной) компоненты, а мнимая — амплитуде синусной (квадратурной) компоненты исходного сигнала. Так, для сигнала (1) имеем:

где

Тригонометрическая форма[править | править код]
Если рассматривать комплексную амплитуду как комплексное число в тригонометрической форме, то модуль соответствует амплитуде исходного гармонического сигнала, а аргумент — сдвигу фазы исходного гармонического сигнала относительно сигнала 
Операции над комплексной амплитудой[править | править код]
К сигналам в пространстве комплексных амплитуд могут быть применены линейные операции. Другими словами, перечисленные ниже операции над комплексными амплитудами:
- умножение комплексной амплитуды на константу
- сложение комплексных амплитуд (соответствующих одной и той же частоте)
- вычитание комплексных амплитуд (соответствующих одной и той же частоте)
- интегрирование комплексной амплитуды по времени
- дифференцирование комплексной амплитуды по времени
приводят к такому же результату, как если бы они были проделаны над соответствующими гармоническими сигналами, а затем от них взята комплексная амплитуда.
Ограничения[править | править код]
Несмотря на то, что в выражение для комплексной амплитуды не входит частота ω гармонического сигнала, следует помнить, что комплексная амплитуда описывает гармонический сигнал конкретной частоты. Поэтому в пространстве комплексных амплитуд недопустимы операции, которые:
- принимают в качестве операндов комплексные амплитуды, описывающие гармонические сигналы разных частот.
- меняют частоту гармонического сигнала или порождают новые частоты (все нелинейные операции, например, перемножение двух сигналов).
Применение[править | править код]
Комплексная амплитуда является полным и очень удобным способом описания гармонических сигналов, поскольку:
- Характеризует и амплитуду, и фазу
- Не содержит зависимости от времени
- Позволяет использовать векторные диаграммы для анализа цепей на переменном токе
Использование комплексных амплитуд и импедансов позволяет свести задачу прохождения гармонического сигнала через линейную цепь (описывается системой дифференциальных уравнений) к более простой задаче, эквивалентной анализу цепи из резисторов на постоянном токе (описывается системой алгебраических уравнений).
См. также[править | править код]
- Метод комплексных амплитуд
- Формула Эйлера