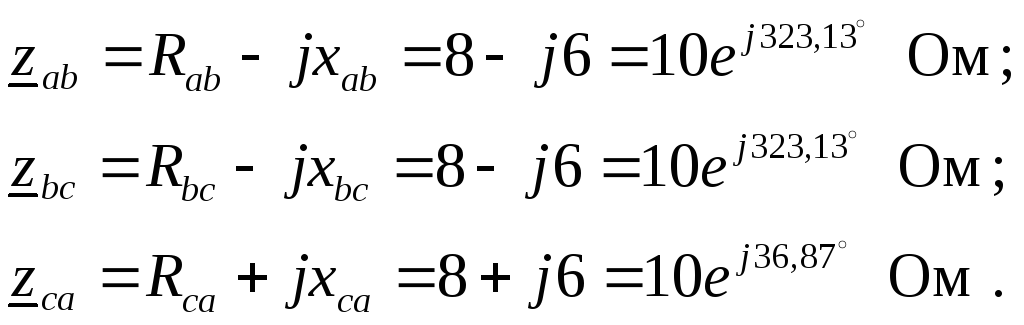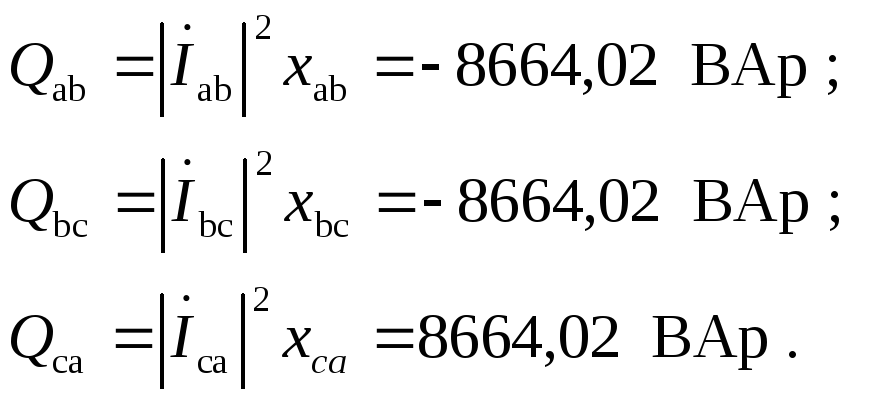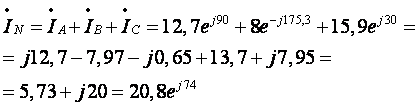Как найти комплексные сопротивления фаз приемника

Как найти комплексные сопротивления фаз приемника

  1. По закону Ома
    определяем фазные токи

5. Рассчитываем
линейные токи, используя первый закон
Кирхгофа

6. Определяем
полные комплексные, полные активные и
реактивные мощности каждой фазы и эти
же мощности на всем трехфазном приемнике

При этом

Без специальной
проверки видно, что баланс мощностей
подтверждается. Следовательно расчеты
проведены корректно.

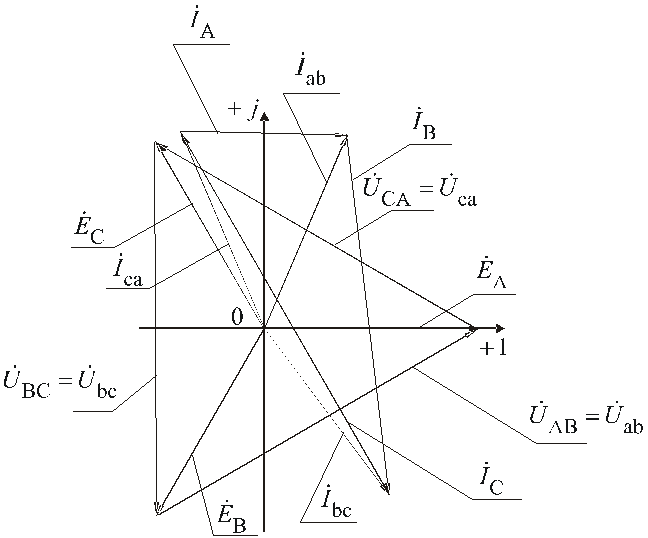
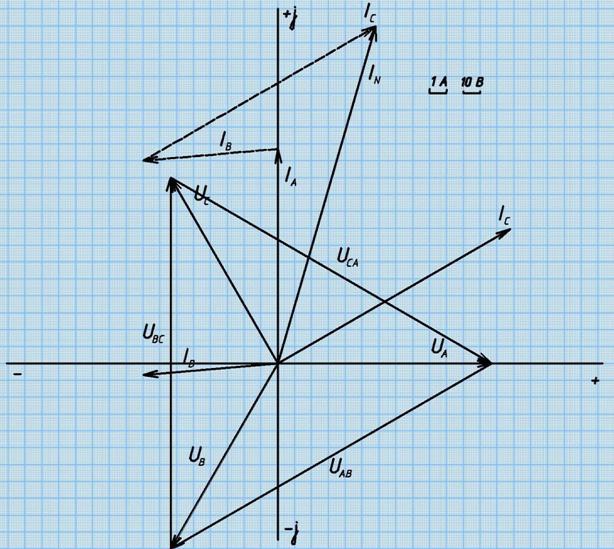
7. Строим векторную
диаграмму токов, напряжений и ЭДС.
Задаемся масштабами по току и по
напряжению:

Рис.
13.

Третий пункт и
все задание выполнены.

При выполнении
задания №3 можно воспользоваться
рекомендуемой литературой [2, 3, 6,7].

Пример 2 . Расчет
трехфазной цепи с несимметричной
нагрузкой (звезда)

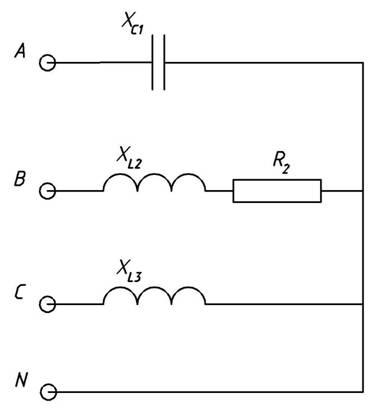
К трехфазному
источнику подключена цепь (рис. 1).
Значения линейного напряжения, активных,
индуктивных и емкостных сопротивлений
приемников приведены ниже.
Требуется:

  1. Определить фазные
    и линейные токи для заданной схемы
    соединения, а также ток в нейтральном
    проводе для схемы «звезда».

  2. Определить активную
    и реактивную мощности, потребляемые
    цепью.

  3. Построить векторную
    диаграмму напряжений и токов.

Исходные данные:
UЛ
= 220 В, XC1 = 10 Ом, R2 = 9 Ом, XL2 = 13 Ом, XL3 = 8
Ом
Рис.
1Решение

1. Определим фазные
напряжения для данной схемы типа
«звезда»:


2. Определим
комплексные эквивалентные сопротивления
каждой фазы:

(Ом)
(Ом)(Ом)

3. Определим фазные
токи (для соединения типа «звезда»
фазные токи равны линейным):

(А)
(А)(А)

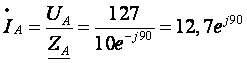
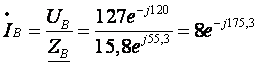
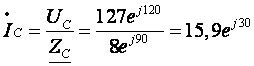
4. Определим комплекс
действующего значения тока в нейтральном
проводе:

5. Определим активную
мощность

(Вт)

6. Определим
реактивную мощность.

(вар)

7. Построим векторную
диаграмму

Пример 3.
Расчет
трехфазной цепи с несимметричной
нагрузкой (треугольник)
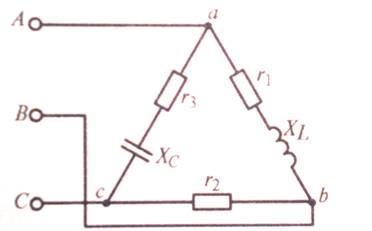
К
трехфазному источнику подключен
несимметричный трехфазный приемник
(рис. 1). Значения линейного напряжения,
активных, индуктивных и емкостных
сопротивлений приемников приведены
ниже.
Требуется:

  1. Определить фазные
    и линейные токи для заданной схемы
    соединения, а также ток в нейтральном
    проводе для схемы «звезда».

  2. Определить
    активную, реактивную и полную мощности,
    потребляемые цепью.

  3. Построить векторную
    диаграмму напряжений и токов.

Исходные данные:
UЛ
= 220 В, R1 = 25 Ом, XC = 18 Ом, XL = 28 Ом, R2 = 30 Ом, R3
= 30 Ом.

Рис. 1
Решение.

1. Определим фазные
напряжения для данной схемы типа
«треугольник»:


2. Определим
комплексные эквивалентные сопротивления
каждой фазы:

(Ом)
(Ом)(Ом)

3. Определим фазные
токи:

4. Определим
комплексы действующих значений линейных
токов:

(A)
 
(A)(A)

5. Определим активную
мощность цепи:

(Вт)

6. Определим
реактивную мощность цепи:

(вар)

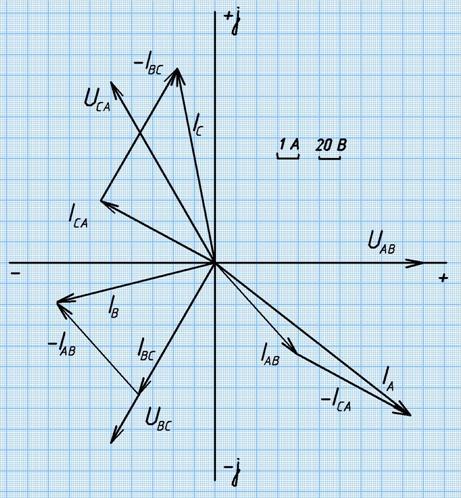
7. Построим векторную
диаграмму.

Контрольные
вопросы к экзамену (зачету) по разделу
Электротехника

Контрольные вопросы к зачету
(экзамену ) по разделу “Основы
электротехники”.

  1. Электрическая цепь постоянного тока,
    электрический ток и напряжение.

  2. Линейные и нелинейные элементы
    электрической цепи их свойства.

  3. Пассивные элементы электрической цепи:
    сопротивление, индуктивность, емкость.

  4. Активные элементы электрической цепи:
    источники ЭДС и источники тока.

  5. Закон Ома для замкнутой электрической
    цепи.

  6. Закон Ома для участка цепи без источника
    ЭДС.

  7. Первый закон Кирхгофа.

  8. Второй закон Кирхгофа.

  9. Баланс мощностей в цепях постоянного
    тока.

  10. Тепловое действие тока. Закон Джоуля-Ленца.

  11. Переменный ток. Параметры переменного
    синусоидального тока.

  12. Представление синусоидального тока
    проекциями вращающегося вектора.
    Векторная диаграмма.

  13. Представление синусоидального тока
    комплексными величинами.

  14. Метод комплексных амплитуд. Закон Ома
    для участка цепи без источников ЭДС в
    комплексной форме.

  15. Метод комплексных амплитуд. Законы
    Кирхгофа в комплексной форме.

  16. Катушка индуктивности в цепи
    синусоидального тока.

  17. Конденсатор емкостью С в цепи
    синусоидального тока.

  18. Цепь с последовательным соединением
    R, L и C. Резонанс напряжений и условия
    его возникновения.

  19. Цепь с параллельным соединением R, L и
    C. Резонанс токов и условия его
    возникновения.

  20. Последовательное соединение элементов
    R, L и C. Треугольники напряжений и
    сопротивлений.

  21. Параллельное соединение элементов R,
    L и C. Треугольники токов и проводимостей.

  22. Мощность в цепи синусоидального тока.
    Мгновенная мощность.

  23. Мощность в цепи синусоидального тока.
    Активная, реактивная, полная и комплексная
    мощность.

  24. Мощность в цепи синусоидального тока.
    Баланс мощностей в цепи синусоидального
    тока.

  25. Мощность в цепи синусоидального тока.
    Коэффициент мощности и способы его
    улучшения.

  26. .Трехфазные электрические цепи. Основные
    определения. Линейные и фазные токи и
    напряжения. Маркировка фазы. Способы
    соединения генераторов и приемников
    типа звезда и треугольник. Трехпроводные
    и четырехпроводные цепи. Нейтральный
    провод.

  27. Нелинейные электрические
    цепи. Аппроксимация нелинейных
    характеристик.

  28. Электрические фильтры. Низкочастотные
    сглаживающие фильтры.

  29. Электрические фильтры. Резонансные
    полосовые и заградительные фильтры.

  30. Понятие о многофазных цепях и системах.

  31. Линейные и фазные величины в трехфазных
    электрических цепях.

  32. Трехфазные цепи типа «звезда-звезда»
    с нулевым проводом.

  33. Трехфазные цепи типа «звезда-треугольник».

  34. Переходные процессы. Первый закон
    коммутации.

  35. Переходные процессы. Второй закон
    коммутации.

  36. Переходные процессы. Включение RL-цепи
    в источник постоянного тока.

  37. Переходные процессы. Включение RC-цепи
    в источник постоянного тока.

  38. . Расчет цепей постоянного
    тока с одним или несколькими нелинейными
    элементами.

  39. Основные магнитные величины. Магнитные
    цепи постоянного тока.

  40. Магнитные цепи переменного
    тока. Ферромагнитные материалы.

  41. Расчет катушки с
    магнитопроводом и воздушным зазором.

  42. . Энергия и основные потери в магнитопроводе.

  43. Трансформаторы. Конструкция и параметры.
    Схема замещения. Основные
    режимы работы.

  44. Асинхронные электродвигатели. Конструкция
    и параметры. Схемы замещения.

  45. Синхронные электрические машины
    переменного тока.

  46. Электрические машины постоянного тока.

  47. Электробезопасность. Характеристики
    поражения человека электрическим
    током.

Второй спсок

Темы
рефератов.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Самостоятельная работа студентов
состоит в изучении ряда теоретических
вопросов по темам дисциплины, перечень
которых приведен в таблице 5 и составления
рефератов..

Таблица 5

№

п/п

Тема
дисциплины

1

2

1

Тема 1.
Электрические цепи.

Основные
определения, топологические параметры

2

Тема 2. Методы расчета линейных
электрических цепей

3

Тема З. Однофазный переменный ток

4

Тема
4. Электрические цепи трехфазного
тока.

5

Тема 5. Магнитные цепи и электромагнитные
устройства.

6

Тема 6. Трансформаторы

7

Тема 7. Асинхронные машины

8

Тема 8. Машины постоянного тока (МПТ)

9

Тема 9. Синхронные машины

10

Тема 10. Электрические измерения и
приборы

11

Тема 11. Основы электроники и элементной
базы современных электронных устройств

12

Тема 12. Источники вторичного
электропитания

13

Тема 13. Усилители электрических
сигналов

14

Тема 14. Импульсные и автогенераторные
устройства

15

Тема 15. Основы цифровой электроники

16

Тема 16. Микропроцессорные средства

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно,
все рассмотренные ранее методы расчета и анализа в символической форме в полной
мере распространяются на них. Анализ трехфазных систем удобно осуществлять с
использованием векторных диаграмм, позволяющих достаточно просто определять
фазовые сдвиги между переменными. Однако определенная специфика многофазных
цепей вносит характерные особенности в их расчет, что, в первую очередь, касается
анализа их работы в симметричных режимах.

Расчет симметричных режимов работы трехфазных систем

Многофазный приемник и вообще многофазная цепь называются симметричными,
если в них комплексные сопротивления соответствующих фаз одинаковы, т.е.
если . В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии: .

Если к симметричной трехфазной цепи приложена симметричная трехфазная система
напряжений генератора, то в ней будет иметь место симметричная система токов.
Такой режим работы трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол . Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.

Так для симметричного режима работы цепи на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз можно записать

,

где
определяется характером нагрузки .

Тогда на основании вышесказанного

;

.

Комплексы линейных токов можно найти с использованием векторной диаграммы на
рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется
с помощью двух основных приемов:

Все треугольники заменяются эквивалентными звездами. Поскольку треугольники
симметричны, то в соответствии с формулами преобразования «треугольник-звезда»
.

Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы
их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи
их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется
базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам
которого определяются соответствующие величины в других фазах.

Пусть, например, при заданном фазном напряжении необходимо определить линейные
токи и в схеме на рис. 3, все сопротивления
в которой известны.

В соответствии с указанной методикой выделим расчетную фазу А, которая представлена
на рис. 4. Здесь , .

Тогда для тока можно записать

,

и соответственно .

Расчет несимметричных режимов работы трехфазных систем

Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет
место несимметричный режим работы. Такие режимы при наличии в цепи только статической
нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для
всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные
напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить,
что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес
также потенциалы узлов, чаще других для расчета сложных схем применяется метод
узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей
с электрическими машинами в основном применяется метод симметричных составляющих,
который будет рассмотрен далее.

При заданных линейных напряжениях наиболее просто рассчитываются трехфазные
цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома

; ; .

По найденным фазным токам приемника на основании первого закона Кирхгофа определяются
линейные токи:

.

Обычно на практике известны не комплексы линейных напряжений, а их модули.
В этом случае необходимо предварительное определение начальных фаз этих напряжений,
что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.

Тогда

Искомые углы a и b могут быть также найдены аналитически
на основании теоремы косинусов:

При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода
с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям
на фазах источника. В этом случае фазные токи легко определяются по закону Ома,
т.е. путем деления известных напряжений на фазах потребителя на соответствующие
сопротивления. Однако, если сопротивление нейтрального провода велико или он
отсутствует, требуется более сложный расчет.

Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной
нагрузке ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е. .

Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением
смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.

Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали.
Если оно известно, то напряжения на фазах нагрузки равны:

.

Тогда для искомых токов можно записать:

.

Соотношение для напряжения смещения нейтрали, записанное на основании метода
узловых потенциалов, имеет вид

. (1)

При наличии нейтрального провода с нулевым сопротивлением , и из (1) . В случае отсутствия нейтрального
провода . При симметричной нагрузке с учетом того, что , из (1) вытекает .

В качестве примера анализа несимметричного
режима работы цепи с использованием соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
.

Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь

Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника
опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.

В заключение отметим, что если при соединении в звезду задаются линейные напряжения
(что обычно имеет место на практике), то с учетом того, что сумма последних
равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
и . Тогда, поскольку при этом , соотношение (1) трансформируется
в формулу

. (2)

Литература

  1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
    С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
  2. Бессонов Л.А. Теоретические основы электротехники: Электрические
    цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
    специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

  1. Какой многофазный приемник является симметричным?
  2. Какой режим работы трехфазной цепи называется симметричным?
  3. В чем заключается специфика расчета симметричных режимов работы трехфазных
    цепей?
  4. С помощью каких приемов трехфазная симметричная схема сводится к расчетной
    однофазной?
  5. Что такое напряжение смещения нейтрали, как оно определяется?
  6. Как можно определить комплексы линейных напряжений, если заданы их модули?
  7. Что обеспечивает нейтральный провод с нулевым сопротивлением?
  8. В цепи на рис. 6,а ; ; ; . Линейное напряжение равно 380
    В.

    9. Определить ток в нейтральном проводе.

    Ответ: .

  9. В схеме предыдущей задачи ; . Остальные параметры те же.

    10. Определить ток в нейтральном проводе.

    Ответ: .

  10. В задаче 8 нейтральный провод оборван.

    11. Определить фазные напряжения на нагрузке.

    Ответ: ; ; .

  11. В задаче 9 нейтральный провод оборван.

    12. Определить фазные напряжения на нагрузке.

    Ответ: ; ; .

Источник

Основные определения

Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.

Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.

Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.

Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.

Соответственно

На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы – последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.

Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.

Соединение в звезду. Схема, определения

Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рисунке:

Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N’ называют нейтральным (нулевым) проводом.

Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.

Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах – линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.

Iл = Iф.

ZN – сопротивление нейтрального провода.

Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений:

Векторная диаграмма фазных и линейных напряжений симметричного источника.

Из векторной диаграммы видно, что

При симметричной системе ЭДС источника линейное напряжение больше фазного

в √3 раз.

Uл = √3 Uф

Соединение в треугольник. Схема, определения

Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.

На рис. 6.3 изображена трехфазная цепь, соединенная треугольником. Как видно

из рис. 6.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.

Uл = Uф

IA, IB, IC – линейные токи;

Iab, Ibc, Ica– фазные токи.

Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.

Линейный ток равен геометрической разности соответствующих фазных токов.

На следующем рисунке изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.

Из векторной диаграммы видно, что,

Iл = √3 Iф- при симметричной нагрузке.

Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме “звезда”. Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.

Мощность в трехфазных цепях

Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.

Активная мощность трехфазной цепи равна сумме активных мощностей фаз.

Данная формула используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.

При симметричной нагрузке:

При соединении в треугольник симметричной нагрузки:

Фазное и линейное напряжение

Фазным напряжением называется напряжение, измеренное между любым из фазных проводников и нейтралью.

Линейным напряжением называется напряжение, измеренное между любыми парами фаз.

Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными.

К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д.

К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Причем, способ соединения фаз приемника не зависит от способа соединения фаз трехфазного генератора.

Приемники делятся на

• симметричные Z a = Z b = Z c = Ze. Комплексные сопротивления фаз трехфазных приемников равны между собой.

• несимметричные Z a ≠ Z b ≠ Z c ≠ Ze (в общем случае). Комплексные сопротивления фаз трехфазных приемников разные.

Источник

Добавить комментарий