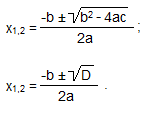Алгоритм вычисления комплексного корня полинома произвольной степени
Время на прочтение
10 мин
Количество просмотров 9.4K
Это завершение моей первой статьи: “Алгоритм расчёта вещественных корней полиномов”.
Спасибо комментаторам, сделавшим более ясным мое слишком уж конспективное изложение метода Лобачевского. В самом деле, мне следовало явно написать, что квадрированный полином надо рассматривать как полином от аргумента x^2, где x — аргумент исходного полинома.
Главное же, там был описан простой алгоритм вычисления всех вещественных корней полинома произвольной степени.
Теперь на этом фундаменте будет построен вполне элементарный алгоритм вычисления комплексного корня полинома, не имеющего вещественных корней.
Сначала нормируем полином так, чтобы его свободный член стал равным единице. Тогда при значении аргумента x=0 значение полинома будет вещественным и равным единице. Это широко известная математикам отправная точка рассуждений.
Представим аргумент x полинома в виде:
x=r*exp(i*fi)
Здесь i — это мнимая единица.
При изменении fi от нуля до 2*pi (=6.28318…) значение полинома p опишет некоторую замкнутую кривую. Назовём эту кривую эпициклоидой.
При исчезающе малом r эпициклоида будет похожа на маленькое колечко вокруг точки p=1. Не будем отвлекаться на ситуации, когда линейный член нашего полинома равен нулю.
При бесконечно большом значении r эпициклоида опишет несколько петель вокруг точки p=1. Количество петель равно степени полинома, форма близка к окружности большого радиуса.
Было бы полезно научиться вычислять все значения fi, при которых мнимая часть полинома обращается в нуль. Это позволит каждому значению r конструктивно поставить в соответствие минимальное значение координаты x, при которой эпициклоида пересекает ось абсцисс.
Это значение положительно при малых r и отрицательно при больших r.
Методом деления отрезка пополам можно найти такое r, при котором это значение будет в точности равно нулю. Соответствующие значения r и fi определят искомый комплексный корень полинома.
Перейдём к реализации намеченного плана.
Мнимая часть полинома с коэффициентами kf0, kf1, kf2,…, kfn представится в виде:
Im=kf1*r*sin(fi)+kf2*r^2*sin(2*fi)+...+kfn*r^n*sin(n*fi)
Хотелось бы представить её в виде какого-нибудь полинома, поскольку вещественные корни полиномов мы умеем вычислять. И действительно, эту мнимую часть можно представить как произведение синуса fi, на некоторый полином от косинуса fi. При небольшой степени полинома это можно непосредственно проверить.
Используем метод математической индукции для доказательства этого утверждения в общем виде.
Пусть
cos(n*x)=polynomC(cos(x))
sin(n*x)=sin(x)*polynomS(cos(x))
Тогда
cos(n*x+x)=cos(n*x)*cos(x)-sin(n*x)*sin(x)=
=polynomC(cos(x))*cos(x)-sin^2(x)*polynomS(cos(x))
Поскольку sin^2(x)=1-cos^2(x), ясно, что последнее выражение является некоторым полиномом от cos(x).
Аналогично:
sin(n*x+x)=sin(n*x)*cos(x)+cos(n*x)*sin(x)=
=sin(x)*(polynomS(cos(x)*cos(x)+polynomC(cos(x))))
И здесь очевидно, что сомножитель при sin(x) в последнем выражении является полиномом от cos(x).
Понятно, что тщательное выписывание приведенных соотношений позволяет получить рекуррентные формулы для коэффициентов нужных нам полиномов.
Дальнейшие подробности реализации намеченного плана удобнее проследить по приведенным ниже комментированным текстам соответствующей программы.
Полный комплект этой демонстрационной программы состоит из приведенных ниже трех файлов и двух файлов, описанных в предыдущей публикации.
Текст файла polynomComplexRoot.h
Содержимое
//*************************************************************************
class polinomComplexRoot
{
public:
//тело класса определяется степенью исследуемого полинома и набором его коэффициентов
polinomComplexRoot(int _degree,double* _kf);
~polinomComplexRoot();
//основная процедура внешнего интерфейса класса
//возвращает код ошибки
//при успешном завершении код ошибки равен нулю,
//а значения параметров rootRe и rootIm станут равны соответственно
//вещественной и мнимой части комплексного корня исследуемого полинома
int run(double& rootRe,double& rootIm);
private:
int degree,errorCode;
double *kf;
double *ki;
double *cosRootsArray;
double *rpw;
int **ck;
int **sk;
//основная рабочая процедура
//при заданном r находит минимальное значение вещественной части
//исследуемого полинома от аргумента r*exp(i*fi)
//при том значении fi, которое обеспечивает равенство нулю
//его мнимой части. Это значение fi
//будет присвоено второму аргументу процедуры по окончании вызова
double minAxeXcrossVal(double r,double& fi);
};//class polinomComplexRoot
//*************************************************************************
Текст файла polynomComplexRoot.cpp
Содержимое
//*************************************************************************
#include <math.h>
#include <polynomComplexRoot.h>
#include <polynomRealRoots.h>
const double cPI=3.14159265358979323846;
polinomComplexRoot::polinomComplexRoot(int _degree,double* _kf)
{
degree=_degree;errorCode=0;
//предварительная инициализация
kf=0;ck=0;sk=0;rpw=0;ki=0;cosRootsArray=0;
//отбраковка неприемлемых значений коэффициентов исходного полинома
if(_kf[0]==0){errorCode=1;return;}
if(_kf[degree]==0){errorCode=2;return;}
if(degree<2){errorCode=3;return;}
kf=new double[1+degree];
ki=new double[1+degree];
cosRootsArray=new double[1+degree];
rpw=new double[degree+1];
ck=new int*[1+degree];
sk=new int*[1+degree];
for(int i=0;i<=degree;i++)
{
ck[i]=new int[1+degree];
sk[i]=new int[1+degree];
}
//отбраковка исходного полинома, имеющего вещественные корни
polynomRealRoots(degree,_kf,kf,errorCode);
if(errorCode>0){errorCode=4;return;}
for(int i=0;i<=degree;i++)kf[i]=_kf[i]/_kf[0];
for(int i=0;i<=degree;i++)
for(int j=0;j<=degree;j++)
{ck[i][j]=0;sk[i][j]=0;}
//коэффициенты косинусных полиномов для представления
//кратных синусов и косинусов по формулам
//cos(n*x)=ck[n,0]+ck[n,1]*cos(x)+ck[n,2]*cos^2(x)+...+ck[n,n]*cos^n(x)
//sin(n*x)=sin(x)*(sk[n,0]+sk[n,1]*cos(x)+sk[n,2]*cos^2(x)+...+sk[n,n]*cos^n(x))
ck[1][1]=1;
sk[1][0]=1;
//расчёт ck и sk по рекуррентным формулам
//здесь np1=n+1
for(int n=1,np1=2;n<degree;n=np1,np1++)
for(int k=0;k<=np1;k++)
{//реализация рекуррентных формул
//ck[n+1,k]=ck[n,k-1]+sk[n,k-2]-sk[n,k];
//sk[n+1,k]=sk[n,k-1]+ck[n,k];
if(k>=1)ck[np1][k]+=ck[n][k-1];
if(k>=2)ck[np1][k]+=sk[n][k-2];
if(k>=1)sk[np1][k]+=sk[n][k-1];
if(k<=n){ck[np1][k]-=sk[n][k];sk[np1][k]+=ck[n][k];}
}//реализация рекуррентных формул
return;
}//constructor
polinomComplexRoot::~polinomComplexRoot()
{
if(kf)delete[] kf;
if(ki)delete[] ki;
if(cosRootsArray)delete[] cosRootsArray;
if(rpw)delete[] rpw;
if(ck)
{
for(int i=0;i<=degree;i++)delete[] ck[i];
delete[] ck;
}
if(sk)
{
for(int i=0;i<=degree;i++)delete[] sk[i];
delete[] sk;
}
}//destructor
int polinomComplexRoot::run(double& rootRe,double& rootIm)
{
rootRe=0;rootIm=0;
if(errorCode>0)return errorCode;
//верхняя rup и нижняя rdn границы поиска для r
double fidn=0,rdn=0,fiup=0,rup=1;
//удваиваем rup пока оно недостаточно велико
for(;minAxeXcrossVal(rup,fiup)>0;)rup+=rup;
for(;;)
{//цикл деления пополам интервала (rdn, rup)
double fit,rt=0.5*(rdn+rup);
if(rt==rdn||rt==rup)break;
if(minAxeXcrossVal(rt,fit)>0){rdn=rt;fidn=fit;}else {rup=rt;fiup=fit;}
}//цикл деления пополам интервала (rdn, rup)
//формальный выбор для выдачи результата одного из двух
//практически одинаковых решений (rdn, fidn) или (rup, fiup)
//будет вычислен модуль исследуемого полинома в каждой из этих двух точек
//и в качестве результата решения будет выдана та из этих точек,
//которой соответствует вычислительно меньшее значение этого модуля
double minmod; //минимальное значение модуля полинома
bool mindn=true; //минимум достигнут в точке с суффиксом dn
for(int c=0;c<2;c++)
{//контрольный расчёт в точках up и dn
double rc,fic;
if(c==0){rc=rdn;fic=fidn;}
else {rc=rup;fic=fiup;}
//rec - вещественная часть исследуемого полинома в пробной точке
//imc - мнимая часть исследуемого полинома в пробной точке
double rec=kf[degree]*cos(degree*fic),
imc=kf[degree]*sin(degree*fic);
for(int i=degree-1;i>0;i--)
{//gorner
rec=rc*rec+kf[i]*cos(i*fic);
imc=rc*imc+kf[i]*sin(i*fic);
}//gorner
rec=rc*rec+kf[0];
imc=rc*imc;
//mc - квадрат модуля исследуемого полинома в пробной точке
double mc=rec*rec+imc*imc;
if(c==0)minmod=mc;
else if(mc<minmod)
{//точка up лучше точки dn
minmod=mc;
mindn=false;
}//точка up лучше точки dn
}//контрольный расчёт в точках up и dn
//формирование результата
if(mindn)
{//выбор точки dn в качестве результата
rootRe=rdn*cos(fidn);
rootIm=rdn*sin(fidn);
}//выбор точки dn в качестве результата
else
{//выбор точки up в качестве результата
rootRe=rup*cos(fiup);
rootIm=rup*sin(fiup);
}//выбор точки up в качестве результата
return errorCode;
}//run
//основная рабочая процедура
//при заданном r находит минимальное значение вещественной части
//исследуемого полинома от аргумента r*exp(i*fi)
//при том значении fi, которое обеспечивает равенство нулю его мнимой части
//это значение fi будет присвоено второму аргументу процедуры по окончании вызова
double polinomComplexRoot::minAxeXcrossVal(double r,double& fi)
{
//предварительно формируем вспомогательный массив rpw[k]=r^k
double rb=1;
for(int i=0;i<=degree;i++){rpw[i]=rb;rb*=r;}
//значение исследуемого полинома от вещественного аргумента r
rb=kf[0];for(int i=1;i<=degree;i++)rb+=rpw[i]*kf[i];
double rez=rb;fi=0;
//значение исследуемого полинома от вещественного аргумента -r
rb=kf[0];
for(int i=1,od=1;i<=degree;i++,od=1-od)if(od)rb-=rpw[i]*kf[i];else rb+=rpw[i]*kf[i];
//мы ищем минимальное значение абсциссы эпициклоиды
if(rb<rez){rez=rb;fi=cPI;}
//мнимая часть исследуемого полинома от комплексного аргумента,
//представленного параметрами r и fi, выражается так
//im=r*kf[1]*sin(fi)+r^2*kf[2]*sin(2*fi)+...+r^n*kf[n]*sin(n*fi)
//она будет представлена с участием некоторого полинома от cos(fi)
//коэффициенты этого полинома обозначены идентификатором ki
//im=sin(fi)*(ki[0]+ki[1]*cos(fi)+ki[2]*cos^2(fi)+...+ki[n]*cos^n(fi))
//коэффициенты ki выражаются через коэффициенты исследуемого полинома kf
//и коэффициенты ck и sk, вычисленные в конструкторе класса по формулам
//ki[0]=r*kf[1]*sk[1][0]+r^2*kf[2]*sk[2][0]+...+r^n*kf[n]*sk[n][0]
//ki[1]=r*kf[1]*sk[1][1]+r^2*kf[2]*sk[2][1]+...+r^n*kf[n]*sk[n][1]
//...
//ki[n]=r*kf[1]*sk[1][n]+r^2*kf[2]*sk[2][n]+...+r^n*kf[n]*sk[n][n]
for(int i=0;i<=degree;i++)
{//вычисление коэффициентов ki
rb=0;
for(int j=i+1;j<=degree;j++)rb+=(rpw[j]*kf[j]*sk[j][i]);
ki[i]=rb;
}//вычисление коэффициентов ki
//cosDegree это степень косинусного полинома, представленного коэффициентами ki
//страхуемся от возможности равенства нулю старших коэффициентов
int cosDegree=0,cosRootsCount=0;
for(int i=degree-1;i>0;i--)if(fabs(ki[i])>0){cosDegree=i;break;}
//интерпретируем ситуацию вырождения ki-полинома как внутреннюю ошибку
if(cosDegree<1){errorCode=5;return rez;}
//находим все вещественные корни ki-полинома
polynomRealRoots(cosDegree,ki,cosRootsArray,cosRootsCount);
//обследование найденных корней ki-полинома
for(int i=0;i<cosRootsCount;i++)if(fabs(cosRootsArray[i])<1)
{//расчёт fi и коррекция rez
double x=acos(cosRootsArray[i]),
im=0,re=kf[0];
//расчёт вещественной (re) и мнимой (im) части исследуемого полинома
//при очередном значении найденного корня
for(int j=1;j<=degree;j++)
{
re+=(kf[j]*rpw[j]*cos(j*x));
im+=(kf[j]*rpw[j]*sin(j*x));
}
//существенно ненулевое значение im интерпретируем как внутреннюю ошибку
if(fabs(im)>1e-6)errorCode+=6;
//мы ищем минимальное значение абсциссы эпициклоиды
if(re<rez){rez=re;fi=x;}
}//расчёт fi и коррекция rez
//интерпретируем невероятный случай fi=0 или fi=cPI
//как внутреннюю ошибку
if(fi==0||fi==cPI)errorCode+=7;
return rez;
}//minAxeXcrossVal
//*************************************************************************
Текст файла main.cpp
//*************************************************************************
//демонстрация расчёта комплексного корня полинома
#include <stdio.h>
#include <math.h>
#include <polynomComplexRoot.h>
int main()
{
//задание степени и коэффициентов исходного полинома
int degree=4;
//double kf[5]={24,24,12,4,1};
//double kf[5]={2,-2,3,-2,1};
double kf[5]={4,0,0,0,1};
//запуск процесса расчёта комплексного корня
double re,im;
int ret=polinomComplexRoot(degree,kf).run(re,im);
//распечатка результата расчёта корня
if(ret==0||ret>4)
{//успешное завершение процедуры расчёта корня
//распечатка результата расчёта корня
if(ret==0)printf("успешное решениеn");
else
{
printf("ПРЕДУПРЕЖДЕНИЕnбыли странные ситуацииn");
printf("возможно из-за недостаточной точности аппаратного представления вещественных чиселn");
}
printf("кореньВещт=%fnкореньМним=%fn",re,im);
//проверка достоверности найденного корня
//используется следующая формула для полинома от суммы аргументов:
//p0(x+y)=p0(x)+p1(x)*y+p2(x)*y^2/2!+...+pn*y^n/n!
//представляющая собой конечную сумму ряда Тейлора по приращению y
//для исходного полинома p0 в точке x
//здесь p1, p2, ... , pn - производные 1-го, 2-го, ... , n-го порядка от исходного полинома
//в тексте программы далее использован обратный порядок индексации исходного и производных полиномов
//там индекс полинома равен его степени
double** kfx=new double*[degree+1];
for(int i=0;i<=degree;i++)kfx[i]=new double[degree+1];
double* kfy=new double[degree+1];
for(int i=degree;i>=0;i--)
{//исходные присвоения
for(int j=0;j<=degree;j++)kfx[i][j]=0;
kfy[i]=0;
kfx[degree][i]=kf[i];
}//исходные присвоения
//расчёт коэффициентов производных полиномов
for(int i=degree;i>0;i--)
for(int j=i;j>0;j--)kfx[i-1][j-1]=kfx[i][j]*j;
double fact=1;
for(int i=0,dmi=degree;i<=degree;i++,dmi--)
{//расчёт коэффициентов полинома по y
//вычисляется по схеме Горнера значение производного полинома от аргумента re
kfy[i]=kfx[dmi][dmi];
for(int j=dmi-1;j>=0;j--)kfy[i]=re*kfy[i]+kfx[dmi][j];
kfy[i]/=fact;
fact*=(i+1);
}//расчёт коэффициентов полинома по y
//массив степеней мнимой единицы
const int ipw[4]={1,1,-1,-1};
double ypw=1;
//вещественная и мнимая части значения исходного полинома
//при значении комплексного аргумента re+i*im
double fre=0,fim=0;
for(int i=0,od=0;i<=degree;i++,od=1-od)
{//расчёт значения исходного полинома
if(od==0)fre+=(ypw*kfy[i]*ipw[i%4]);
else fim+=(ypw*kfy[i]*ipw[i%4]);
ypw*=im;
}//расчёт значения исходного полинома
//печать погрешности расчёта корня исходного полинома
//это модуль полинома в найденном корне,
//нормированный на значение свободного члена
printf("погрешность=%7.1en",sqrt(fre*fre+fim*fim)/kf[0]);
//заключительное освобождение занимаемой памяти
for(int i=0;i<=degree;i++)delete[] kfx[i];
delete[] kfx;
delete[] kfy;
}//успешное решение
if(ret>0)switch(ret)
{//печать краткой диагностики произошедшей ошибки
case 1:
printf("#ошибка 1:нулевое значение свободного члена исходного полиномаn");
break;
case 2:
printf("#ошибка 2:нулевое значение старшего коэффициента полиномаn");
break;
case 3:
printf("#ошибка 3:степень исходного полинома слишком малаn");
break;
case 4:
printf("#ошибка 4:исходный полином имеет вещественные корниn");
break;
default:printf("#код ошибки=%dn",ret);
}//печать краткой диагностики произошедшей ошибки
return 0;
}//main
//*************************************************************************
132 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
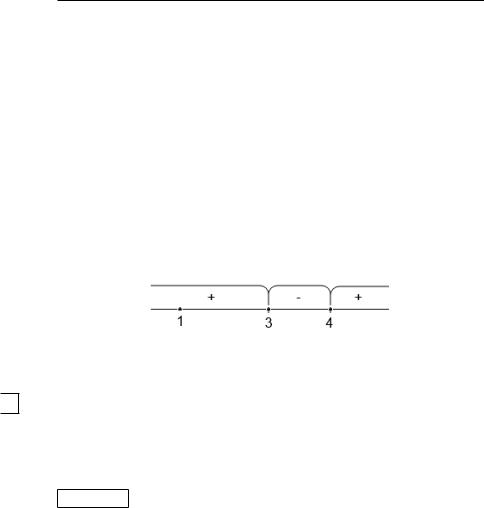
ными точками (рис. 24). Квадратный трехчлен ( 2 + + 1)
при всех вещественных сохраняет знак «+». Два корня –
3 и 4 – нечетной кратности, в них многочлен меняет знак. Таким образом, точки 3 и 4 разбивают вещественную ось на три промежутка знакопостоянства. Расставим на схеме (рис. 24) знаки и запишем ответ. Ответ включает подмножество, состоящее из изолированной точки 1, которая расположена внутри «знакоположительного» интервала.
Ответ: {1} [3; 4].
Рис. 24. Промежутки знакопостоянства из примера 7
Задачи к параграфу на с. 200, п. 27–28.
125 149 На протяжении всей истории развития человеческого общества развивалось и понятие «число». В ряде открытых европейскими путешественниками первобытных племен Африки и Океании люди знали только натуральные числа: 1, 2 и 3. Все, что больше, – это «много». Наверное, также обстояло дело с арифметикой и у наших далеких предков. Сейчас это может показаться смешным, но

|
§ 3.4. Комплексные корни многочлена |
133 |
такая числовая система вполне удовлетворяла потребности их общественной практики. Древние греки уже рассматривали не только натуральные числа, но и их отношения, т. е. положительные рациональные числа, а в школе Пифагора знали о существовании величин, которые нельзя измерить и
вэтой числовой системе. Так, диагональ единичного квадрата не может быть измерена рациональной дробью. Сейчас мы сказали бы, что уравнение 2 = 2 не имеет решения
на множестве рациональных чисел или не существует таких целых чисел и , что ( )2 = 2 . В средневековой Европе величины, не измеряемые отношением целых чисел,
называли иррациональными, т. е. «неразумными». Только
вXVI веке эти числа несколько реабилитировал Симон Стевин, внедривший в обиход десятичные дроби. Наконец, в XIX веке благодаря трудам Георга Кантора, Карла Вейерштрасса и Юлиуса Вильгельма Рихарда Дедекинда иррациональные числа получили строгое определение, а следовательно, прописку на числовой оси. Множество рациональных чисел, дополненное иррациональными, назвали множеством вещественных чисел. Оказалось, что иррациональные числа «заткнули» все дыры на числовой оси и теперь любая величина может быть измерена. На этом в истории развития «числа» можно было бы поставить жирную точку, если бы не одна беда. Еще Кардано при нахождении корней многочленов третьей степени, даже если они были вещественны-

134 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
√
ми, использовал вспомогательные величины вида + −1. Существование таких величин не укладывалось в традиционное мировоззрение, и сам Кардано считал их лишенными какого-либо смысла, однако совсем отказаться от их использования не получалось. Декарт также рассматривал их как
нечто нереальное, и с его легкой руки в XVI–XVII веках ве-
√
личины вида + −1 стали называть мнимыми. Впрочем, как мы заметили выше, тогда даже иррациональные числа еще «не добились равноправия» на вещественной оси да и на отрицательные нередко посматривали неодобрительно даже математики. И все-таки практическая польза по-
степенно теснила «эстетику». В XVIII веке Леонард Эйлер
√
ввел мнимую единицу = −1, а в XIX веке Карл Фридрих Гаусс доказал алгебраическую замкнутость множества комплексных чисел, т. е. чисел вида + . Последнее означает, что любой многочлен степени выше нулевой имеет хотя бы один комплесный корень. Если степень многочлена ( )
больше единицы и 1 его комплексный корень, то, разделив многочлен на линейный член ( − 1), мы получим многочлен степени на единицу меньшей (с. 102), который также должен иметь по крайней мере один комплексный корень. Продолжим процесс понижения степени многочлена до тех пор, пока в результате деления не получим многочлен нулевой степени 0. Теперь мы можем утверждать, что любой

|
§ 3.4. Комплексные корни многочлена |
135 |
многочлен -й степени имеет комплексных корней и
( ) = 0( − 1)( − 2) . . . ( − ).
Сейчас мнимую единицу определяют как некую величину (не являющуюся вещественным числом), для которой верно утверждение 2 = −1, а комплексное число как выражение вида + , где , . Если = + , то вещественное число = ( ) называют действительной частью, а = ( ) – мнимой частью.
Сразу сделаем два важных замечания. Иногда мнимую единицу определяют как решение уравнения 2 = −1. Такое определение некорректно, поскольку точно также решением будет и (− ). И второе. Поначалу сложилась практика в записи комплексного числа ставить отрицательное число под знак квадратного корня. Тогда
√ √ √ √
−1 · −1 = (−1)(−1) = 1 = 1.
Но, с другой стороны,
√√
−1 · −1 = · = 2 = −1.
|
Подобных недоразумений можно избежать, если, например, |
||||
|
√ |
√ |
|||
|
вместо |
−3 писать 3, т. е. не допускать записи отрица- |
тельного числа под корнем. Дело в том, что обычно сим-

|
136 |
ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА |
|
|
волом √ |
мы обозначаем арифметический квадратный ко- |
|
рень, определяемый как положительное вещественное число, квадрат которого равен подкоренному выражению. Данное определение исключает возможность нахождения под знаком квадратного корня отрицательного числа. В более широком смысле под квадратным корнем подразумевают решение уравнения 2 = . Уравнение имеет два корня. Определенный таким образом «корень» сложно использовать в выражениях.
Пусть 1 = 1 + 1 и 2 = 2 + 2. Тогда основные арифметические операции с комплексными числами определяются так:
1)1 ± 2 = ( 1 ± 2) + ( 1 ± 2);
2)1 2 = ( 1 + 1)( 2 + 2) = ( 1 2 − 1 2) + ( 1 2 + 2 1);
3)1 = 1 + 1 = ( 1 + 1)( 2 − 2) =2 2 + 2 ( 2 + 2)( 2 − 2)
|
= |
1 2 + 1 2 |
+ |
· |
2 1 − 1 2 |
. |
|
22 + 22 |
|||||
|
22 + 22 |
Имеет место равенство ( + ) = + . Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:
( 1) = ( 2) и ( 1) = ( 2).

|
§ 3.4. Комплексные корни многочлена |
137 |
Иначе говоря, ( 1 = 2)&( 1 = 2). Отношение неравенства для комплексных чисел не определено. Теперь обобщим алгоритм нахождения корней квадратного трехчлена
2 + + (с. 59) на случай произвольного дискриминанта. Пусть ̸= 0. Тогда квадратный трехчлен имеет два комплексных корня. Дискриминант = 2 − 4 . Корни
√
|
± |
, если ≥ 0; |
|||
|
2 |
||||
|
± 2 − , если < 0. |
||||
|
1,2 = |
√ |
Таким образом, мы избегаем ситуаций, когда под знаком квадратного корня может оказаться отрицательное число.
Пример 1. Найти корни квадратного трехчлена 2 2+2 +3. 200
|
Решение. На с. 61 мы установили, что этот трехчлен не име- |
||||||||||||||||||
|
ет вещественных корней. Найдем комплексные: |
||||||||||||||||||
|
√ |
√ |
|||||||||||||||||
|
= 4 |
− |
24 = 20 < 0 |
= |
−2 ± 20 |
= |
−1 ± 5 |
. |
|||||||||||
|
− |
1,2 |
4 |
2 |
|||||||||||||||
|
Ответ: |
√ |
√ |
||||||||||||||||
|
1 = |
−1 − |
5 |
и 2 = |
−1 + 5 |
. |
|||||||||||||
|
2 |
||||||||||||||||||
|
2 |
||||||||||||||||||
|
Пример 2. Найти корни многочлена 2 3 + 2 |
+ 4 − 15. |
|||||||||||||||||
|
201 |
||||||||||||||||||
|
Решение. В примере на с. 116 мы разложили этот много- |
||||||||||||||||||
|
член на множители: |
2 3 + 2 + 4 − 15 = (2 − 3)( 2 + 5).

|
138 |
ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА |
|||||||||
|
Корни неполного квадратного трехчлена 2+5: 2,3 = ± √ |
. |
|||||||||
|
5 |
||||||||||
|
√ |
√ |
|||||||||
|
Ответ: 1 = 1, 5; 2 = − 5 и 3 = |
5. |
|||||||||
|
201 |
Пример 3. |
Найти корни многочленаа 2 4 + 3 +4 2 + +2. |
Решение. В примере на с. 120 мы разложили многочлен в произведение двух квадратных трехчленов:
2 4 + 3 + 4 2 + + 2 = (2 2 + + 2)( 2 + 1).
Рассмотрим первый квадратный трехчлен 2 2 + + 2.
|
√ |
. |
||
|
= 1 − 16 = −15 < 0 1,2 = |
−1± 15 |
||
|
4 |
Корни неполного квадратного трехчлена: 3,4 = ± .
Ответ:
√√
|
1 |
= |
−1 − |
15 |
; |
2 |
= |
−1 + |
15 |
; |
3 |
= |
− |
и |
4 |
= . |
|||
|
4 |
4 |
|||||||||||||||||
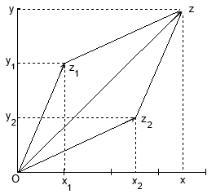
Комплексному числу + можно поставить в соответствие точку плоскости с координатами ( ; ). Таким образом, если раньше мы говорили о вещественной оси, то теперь можем говорить о комплексной плоскости. Комплексные числа образуют векторное пространство, базисом которого являются вещественная единица 1 и мнимая единица , и складываются по правилу сложения векторов (с. 136): если 1 = 1+ 1 и
2 = 2 + 2, то 1 + 2 = ( 1 + 2) + ( 1 + 2) (рис. 25). Также = + .
Для задания точки на плоскости, кроме декартовых прямо-
|
§ 3.4. Комплексные корни многочлена |
139 |
Рис. 25. Сумма комплексных чисел
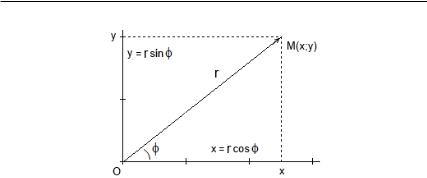
угольных координат, в математике часто используют и так называемые полярные координаты. Причем в повседневной жизни последние нам гораздо привычней. Действительно, если человек в лесу спросит у вас: «Как пройти в Ольховку?», то что вы ответите? Назовете координаты квадрата, в котором находится село? Нет! Вы скажете, что «это в двух километрах на северо-западе», т. е. укажете направление и расстояние относительно вашего текущего местонахождения. Это и есть полярные координаты. Мы введем их, отталкиваясь от декартовых. Пусть – точка плоскости с кординатами ( ; ) (рис. 26). Проведем из начала коорди-
|
нат в точку радиус-вектор −−→. Пусть радиус-вектор |
|||||
|
– длина |
|||||
|
2 |
+ |
2 |
|||
|
образует с осью угол , а = |−−→|= |
|||||
|
вектора. Направление и расстояние |
образуют пару поляр- |
||||
|
√ |
ных координат ( ; ), задающих положение точки . Для
140 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Рис. 26. Тригонометрическое представление комплексного числа
всех точек плоскости, кроме начала координат, имеет место взаимнооднозначное соответствие между парами координат
( ; ) и ( ; ), задаваемое уравнениями
= · cos ;
= · sin .
|
Комплексное |
число можно представить в тригонометри- |
||||
|
ческой форме: |
|||||
|
= + = (cos + · sin ), |
|||||
|
где = | |= |
2 + 2 |
называют модулем, а = ( ) |
|||
|
– |
аргументом |
. Леонард Эйлер расширил область |
|||
|
√числа |
определения элементарных и ряда других функций на комплексную плоскость и установил тождество
= cos + sin ,
которое называют формулой Эйлера. Таким образом, в
теории функций комплексной переменной экспонен-
|
§ 3.4. Комплексные корни многочлена |
141 |
та выражается через тригонометрические функции и наоборот:
Отсюда еще одна форма представления комплексного числа
–экспоненциальная:
= + = (cos + · sin ) = = ln + .
Из формулы Эйлера следует интересное отношение
= −1.
На множестве вещественных чисел мы лишены возможности видеть эти связи, как человек, рассматривающий с берега моря живописные острова, не подозревает, что они всего лишь вершины сложной горной системы подводного царства. На комплексной плоскости «в порядке вещей» многое из того, что категорически запрещено на вещественной оси. Здесь существуют решения уравнений ( ) = 5, 2 = −3
и т. д. Конечно, и теперь мы рассматриваем комплексное число как некую абстракцию, но не в большей мере, чем число «три». Ведь числа «три» также в природе не существует! Естественно возникает вопрос: не придется ли для решения других уравнений, например 4 + 1 = 0, и даль-
142 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
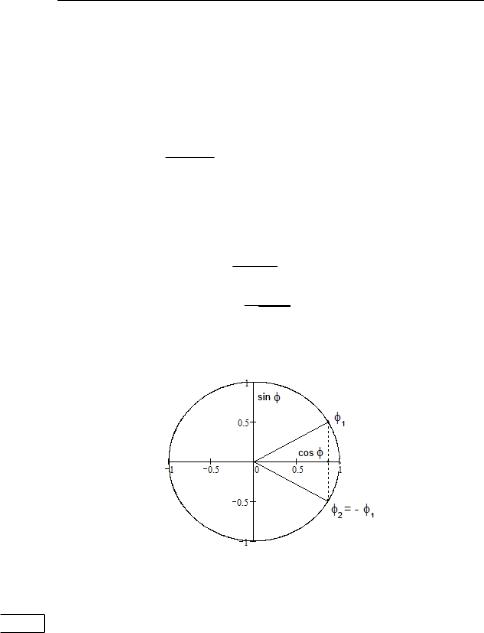
ше расширять понятие «число». Оказывается, на множестве комплексных чисел любой многочлен, как с действительными, так и с комплексными коэффициентами, имеет корни. Однако вернемся к тригонометрической форме. Как найти аргумент и модуль комплексного числа? Если = + ,
√
то = | |= 2 + 2, а аргумет = ( ) можно определить, приняв во внимание, что (0; ), следующим образом (рис. 27):
|
( |
|||||||
|
= |
√ |
), |
если ≥ 0; |
||||
|
2+ 2 |
|||||||
|
, |
< 0. |
||||||
|
(√ 2+ 2 ) |
если |
||||||
|
− |
Рис. 27. Аргумент комплексного числа
202 Пример 4. Преобразовать комплексное число
= 2 + 2 в тригонометрическую форму.

|
§ 3.4. Комплексные корни многочлена |
143 |
||||||||||||||||||||||||||||||||||||||
|
Решение: |
√ |
√ |
√ |
√ |
|||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
Ответ: |
2√2 |
cos ( |
). |
( |
) |
||||||||||||||||||||||||||||||||||
|
+ sin |
4 |
||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
+ |
= 2 2 |
||||||||||||||||||||||||||||||||||||
|
= 2 + 2 = 2 |
2 |
2 |
cos 4 + sin 4 . |
||||||||||||||||||||||||||||||||||||
|
( |
) |
||||||||||||||||||||||||||||||||||||||
|
Пример 5. Преобразовать комплексное число |
202 |
||||||||||||||||||||||||||||||||||||||
|
= 3 + 4 в тригонометрическую форму. |
|||||||||||||||||||||||||||||||||||||||
|
Решение: | |= |
√ |
= 5 = 3 + 4 = 5 53 |
+ 54 |
. |
|||||||||||||||||||||||||||||||||||
|
32 + 42 |
|||||||||||||||||||||||||||||||||||||||
|
Ответ: 5(cos + · sin ), где = 53 . |
( |
) |
|||||||||||||||||||||||||||||||||||||
|
Пример 6. Преобразовать комплексное число = 5 − 7 |
202 |
||||||||||||||||||||||||||||||||||||||
|
в тригонометрическую форму. |
|||||||||||||||||||||||||||||||||||||||
|
Решение: |
√ |
√ |
|||||||||||||||||||||||||||||||||||||
|
√ |
5 |
−7 |
|||||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
74(cos + |
sin ) |
= |
( |
) |
|||||||||||||||||||||||||||||||||||
|
| |= 5 + 7 = |
74 = 5 |
− 7 = |
74 √74 + √74 . |
||||||||||||||||||||||||||||||||||||
|
Ответ: |
√ |
· |
, где |
− |
5 |
. |
|||||||||||||||||||||||||||||||||
|
√ |
|||||||||||||||||||||||||||||||||||||||
|
74 |
|||||||||||||||||||||||||||||||||||||||
|
Операции сложения и вычитания комплексных чисел подчи- |
|||||||||||||||||||||||||||||||||||||||
|
няются правилу сложения и вычитания векторов (рис. 25). |
|||||||||||||||||||||||||||||||||||||||
|
Но формулы умножения и деления комплексных чисел вы- |
|||||||||||||||||||||||||||||||||||||||
|
глядят сложновато (с. 136). |
|||||||||||||||||||||||||||||||||||||||
|
Попробуем теперь выполнить эти операции с числами в три- |
|||||||||||||||||||||||||||||||||||||||
|
гонометрическом представлении. Пусть |
|||||||||||||||||||||||||||||||||||||||
|
1 = 1(cos + · sin ), |
2 |
= 2(cos + · sin ). |
Тогда 1 2 = 1 2(cos + · sin )(cos + · sin ) =
=1 2[(cos cos − sin sin )(cos sin + sin cos )] =
=| 1|| 2|(cos( + ) + sin( + )).

144 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются (рис. 28).
Рис. 28. Умножение комплексных чисел
Аналогично
|
1 |
= |
1 |
(cos + · sin ) |
= |
1 |
(cos + · sin )(cos − · sin ) |
= |
||||||||
|
2 |
2 |
(cos + · sin ) |
2 |
(cos + · sin )(cos − · sin ) |
|||||||||||
|
= |
| 1 |
| |
[cos( |
− |
) + sin( |
− |
)]. |
||||||||
|
| 2 |
| |
||||||||||||||
Следовательно,
| 1 2|= | 1|| 2|, ( 1 2) = ( 1) + ( 2),
|
2 |
= |
| 2 |
|, |
( 2 ) |
= ( 1) − ( 2). |
|||||
|
1 |
1 |
| |
1 |
|||||||
|
| |
||||||||||
В частности,
1
cos + · sin = cos − · sin .

|
§ 3.4. Комплексные корни многочлена |
145 |
Поскольку целая степень числа означает многократное произведение,
= [ (cos + · sin )] = (cos + · sin ).
Последнее тождество известно как формула Муавра. Отрицательная степень
− = [ (cos + · sin )]− = 1 (cos − · sin ).
|
Пример 7. Найти девятую степень числа cos + sin . |
202 |
||||||||||||||
|
Решение: |
6 |
6 |
|||||||||||||
|
9 |
|||||||||||||||
|
(cos |
+ sin |
) |
= cos |
9 |
+ sin |
9 |
= cos |
3 |
+ sin |
3 |
= − . |
||||
|
6 |
6 |
6 |
6 |
2 |
2 |
Ответ: − .
Пусть = (cos + · sin ) и требуется найти все решения
уравнения = (cos + · sin ).
(cos + sin ) = (cos( + 2 ) + · sin( + 2 ))
|
+ 2 |
||||||||||||
|
= , = + 2 |
= |
√ , = |
||||||||||
|
, |
||||||||||||
|
где k=0,1,. . . , n-1. Следовательно, |
). |
|||||||||||
|
0,1,··· −1 |
= √ (cos |
+ · sin |
||||||||||
|
+ 2 |
+ 2 |
146 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
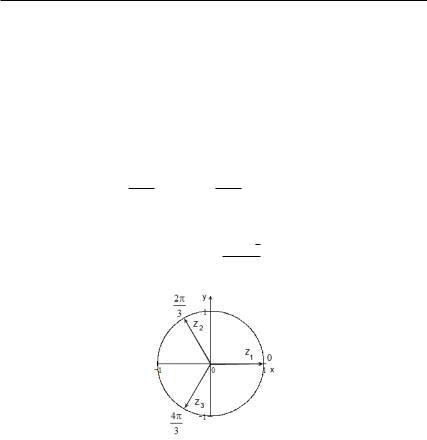
Если принимает значения 0, 1, . . . −1, то – принимает различных значений. В следующем параграфе нам понадобятся все кубические корни из 1, т. е. все решения уравнения
= 1. Представим вещественную единицу в тригонометрической форме: = cos 2 + · sin 2 . Тогда
= cos 23 + · sin 23 , где = 0, 1, 2.
Кубические корни из единицы показаны на диаграмме (рис. 29).
√
Таким образом, 1 = 1, 2,3 = −1±2 3 .
Рис. 29. Кубические корни единицы
|
202 |
Пример 8. |
Решить уравнение 3 |
= 5 + · 5. |
|||||||||||||||||
|
Решение: |
||||||||||||||||||||
|
√ |
√ |
|||||||||||||||||||
|
3 = 5√ |
( |
) |
= 5√ |
(cos |
+ 2 |
+ 2 |
), |
|||||||||||||
|
2 |
+ |
2 |
4 |
+ · sin |
4 |
|||||||||||||||
|
2 |
2 |
|||||||||||||||||||
|
2 |
2 |
3 |
3 |
где = 0, 1, 2. Подставляя поочередно в правую часть ра-
венства значения , получим
|
§ 3.4. Комплексные корни многочлена |
147 |
||||||||||||||||||||||||||||||||||
|
Ответ: |
|||||||||||||||||||||||||||||||||||
|
√3 |
|||||||||||||||||||||||||||||||||||
|
20 |
|||||||||||||||||||||||||||||||||||
|
1 = √6 50 |
(cos |
+ · sin |
) |
= |
[1 +3 |
√3 + · (−1 + √3)]; |
|||||||||||||||||||||||||||||
|
12 |
12 |
4 |
|||||||||||||||||||||||||||||||||
|
2 |
= √6 |
(cos 34 |
+ · sin |
4 |
) = |
2 (−1 + ) ; |
|||||||||||||||||||||||||||||
|
50 |
|||||||||||||||||||||||||||||||||||
|
3 |
√20 |
||||||||||||||||||||||||||||||||||
|
√3 |
|||||||||||||||||||||||||||||||||||
|
20 |
|||||||||||||||||||||||||||||||||||
|
3 = √6 50 |
(cos |
+ · sin |
) |
= |
[1 − |
√3 + · (−1 − √3)]. |
|||||||||||||||||||||||||||||
|
12 |
12 |
4 |
Прежде чем перейти к следующему вопросу, коротко коснемся проблемы графического представления многочлена, определенного на комплексной плоскости. Пусть дан многочлен с вещественными коэффициентами ( ) = 3 + 2 + +1
от комплексной переменной = + . Его график для действительных значений , т. е. для = , изображен на рис. 30г. Как видно на графике, многочлен имеет один вещественный корень = −1. Теперь рассмотрим комплексные значения = + . В таком случае и ( ) – комплексное число. Для построения графика функции, отображающей комплексную плоскость на комплексную плоскость, нам пришлось бы выйти в четырехмерное пространство, но мы поступим проще, рассмотрев отдельно графики [ ( )]
и [ ( )], т. е. графики действительной и мнимой частей функции ( ). Каждый график – это поверхность в трехмерном пространстве, а поверхность можно задать линиями уровня, как на географической карте. Такой график мы уже видели на рис. 13а (с. 73). График вещественной части
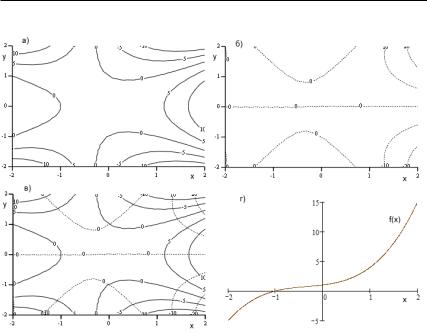
148 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Рис. 30. Графики многочлена 3 + 2 + + 1
( ) показан на рис. 30а, комплексной – на рис. 30б. Обратите внимание на нулевые линии уровня. На рис. 30б одна из таких линий задана уравнением = 0, поскольку действительным значениям соответствуют действительные значения функции. Корнями многочлена будут те значения , для которых одновременно [ ( )] = 0 и [ ( )] = 0, т. е. точки пересечения нулевых линий уровня, представленных на рис. 30а и 30б. На рис. 30в мы разместили оба графика на одной комплексной плоскости. Сплошные линии уровня соответствуют действительной, а пунктирные – комплексной
Комплексные корни
Решение уравнений
При решении многих задач в математике, физике, электротехнике часто возникает необходимость в решении уравнений с комплексными корнями, извлечении корней из комплексных чисел.
Пусть дано комплексное число z, из которого надо извлечь корень n. Для этого находим модуль |z| и аргумент (ф) комплексного числа.
Корень числа находим по формуле:
Результатом решения квадратных уравнений вида ах2 + by + с = 0 с комплексными коэффициентами являются комплексные корни 2-го порядка.
Для решения квадратного трехчлена необходимо вычислить дискриминант (D):
D = b2 — 4ac, затем найти корни, которые зависят от знака D. Квадратное уравнение имеет 2 корня.
- если D больше 0, уравнение имеет 2 вещественных корня;
- при D = 0 у уравнения 1 корень х = -b / 2а;
- при D меньше 0 — 2 мнимых корня (вещественных корней нет).
Общая формула:
Любое уравнение вида имеет п комплексных корней. Часть из них, возможно и все, — действительные.
Существует универсальный способ извлечения корней из любого комплексного числа.
Пусть дано уравнение , где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, …z n-1) можно по формуле:
|w| — модуль комплексного числа w, ф — его аргумент, k = 0, 1, 2, …n-1
С помощью онлайн калькулятора вы сможете быстро вычислять комплексные корни заданного многочлена.
Из графика многочлена 
Корень многочлена (не равного тождественно нулю)
над полем 


в тождество, то есть значение многочлена становится равным нулю.
Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.
Говорят, что корень 






Говорят, что многочлен имеет 
Свойства[править | править код]
-
- где
— (в общем случае комплексные) корни многочлена
, возможно с повторениями, при этом если среди корней
многочлена
встречаются равные, то их общее значение называется кратным корнем, а количество — кратностью этого корня.
Нахождение корней[править | править код]
Способ нахождения корней линейных и квадратичных многочленов в общем виде, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время, пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.
То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов (то есть то, что сами уравнения не являются разрешимыми в радикалах), было доказано норвежским математиком Нильсом Абелем в 1826 году[1]. Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, при некоторых особых комбинациях коэффициентов корни уравнения всё же могут быть определены (см., например, возвратное уравнение). Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие специальные функции — эллиптические или гипергеометрические (см., например, корень Бринга).
В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера, причем при нахождении целых корней перебор может быть существенно уменьшен приемом чистки корней. Также в этом случае можно использовать полиномиальный LLL -алгоритм.
Для приблизительного нахождения (с любой требуемой точностью) вещественных корней многочлена с вещественными коэффициентами используются итерационные методы, например, метод секущих, метод бисекции, метод Ньютона, Метод Лобачевского — Греффе. Количество вещественных корней многочлена на интервале может быть определено при помощи теоремы Штурма.
См. также[править | править код]
- Схема Горнера
- Метод Лиля — графический метод нахождения вещественных корней многочленов произвольной степени.
- Нуль функции
Примечания[править | править код]
- ↑ Теорема Абеля в задачах и решениях — М.: МЦНМО, 2001. — 192 с. Дата обращения: 9 ноября 2011. Архивировано 22 января 2021 года.
Литература[править | править код]
- Винберг Э. Б. Алгебра многочленов. — М.: Просвещение, 1980. — 176 с.
- Прасолов В. В. Многочлены. — М.: МЦНМО, 2003. — 336 с. — ISBN 5-94057-077-1.