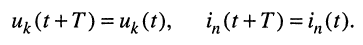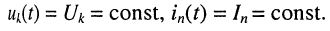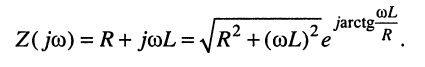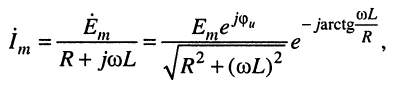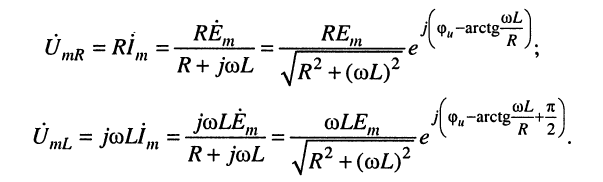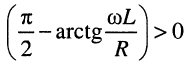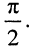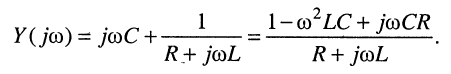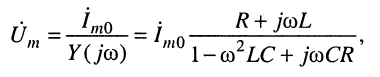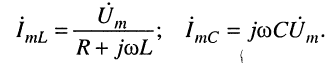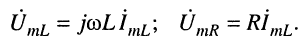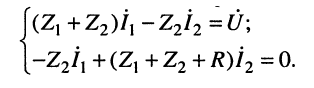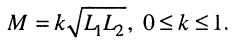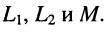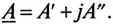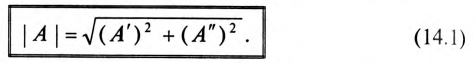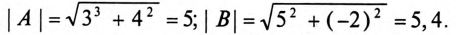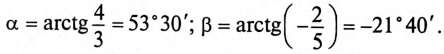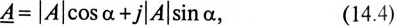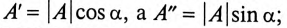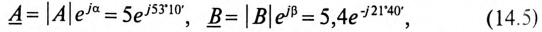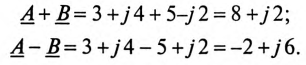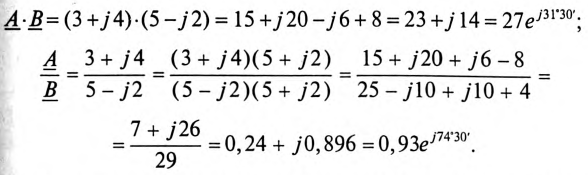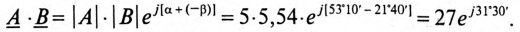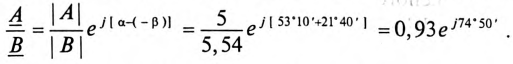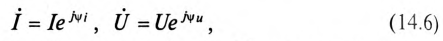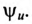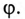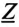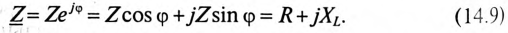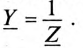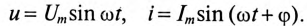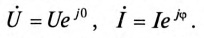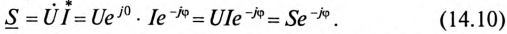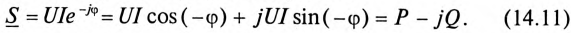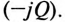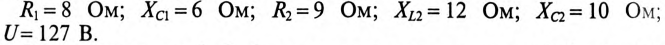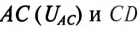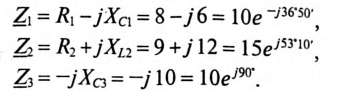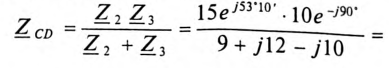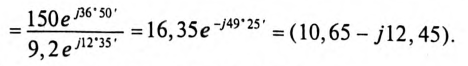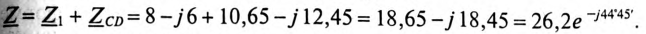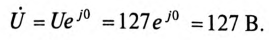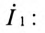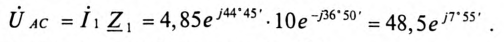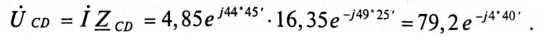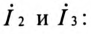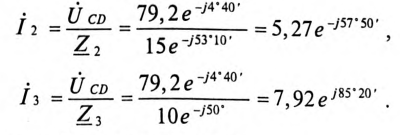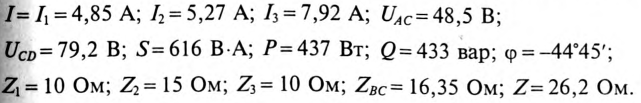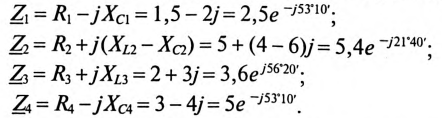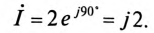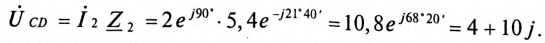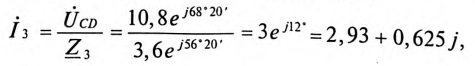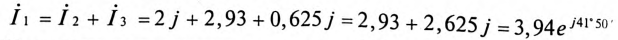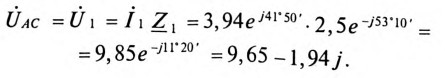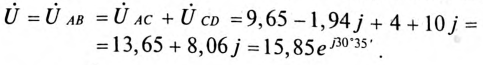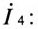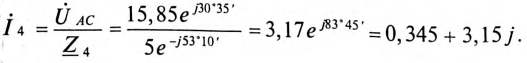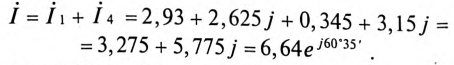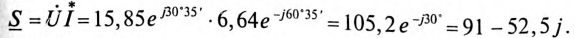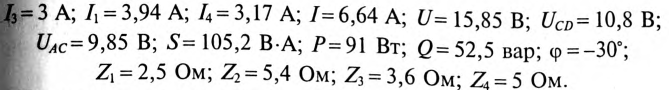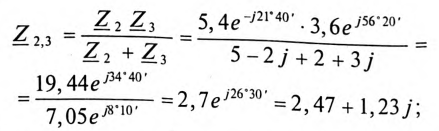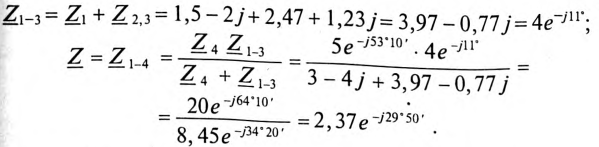Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и тогда
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как .
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
где
При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
а угол
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
-
-
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
-
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида при φ = 0° равно
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Ток в цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство
Проверяем
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
-
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи
Откуда
— нагрузка носит активно-индуктивный характер
2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
Комплексный
(символический)
метод расчета
электрических цепей
при периодическом
синусоидальном воздействии.
И
курса “Математики” известно, что
комплексное число можно представить в
виде вектора на комплексной плоскости,
а действительная и мнимая части
комплексного числа есть проекции вектора
на вещественную и мнимую оси.
(В
электротехнике, т.к. буква i
изображает ток, за признак мнимости
принята буква j,
а само число или сверху точка, или снизу
подчеркнуто
,
).
;
А – модуль;
– аргумент или
фаза.
Если
допустить, что вектор А на комплексной
плоскости вращается против часовой
стрелки с угловой скоростью ,
то это комплексное число запишется:
Величину
назвали – оператор вращения.
Можно
видеть, что мгновенное значение
периодического синусоидального тока
и напряжения
,
похоже на мнимую часть нашего вращающегося
комплексного числа, т.е. можно утверждать:
,
.
Комплексное число
назвали комплексной амплитудой тока,
а
– комплексном действующего значения
тока.
Комплексное число
назвали комплексной амплитудой
напряжения,
–
комплексом действующего значения
напряжения (как мы помним
,
).
Можно видеть, что
мгновенное значение периодического
синусоидального тока и напряжения есть
мнимая часть произведения комплексной
амплитуды тока или напряжения на оператор
вращения
.
Пример:
А,
А,
А.
;
,
В.
Таким образом,
реальные мгновенные значения
синусоидального тока и напряжения мы
можем заменить неким символом –
комплексной амплитудой или комплексом
действующего значения тока и напряжения,
помня все время об операторе
и
(отсюда и название метода – комплексный
или символический).
Посмотрим
на расчете простейшей электрической
схемы, что нам это даст.
Последовательное
соединение R,
L,
C.
По
2-му закону Кирхгофа:
(1)
Тогда
(1) можно записать:
(2)
В
математике давно доказано, что операции
над мнимыми частями комплексных чисел
равноценны операциям над комплексным
числом с выделением из результата мнимой
части.
Тогда
(2) примет вид:
Решили данное
уравнение:
.
Видим,
что на
можно сократить, и помня, что
,
,
,
в результате получим:
где
– назвали комплексным сопротивлением,
–комплексным индуктивным сопротивлением,
–комплексным
емкостным сопротивлением,
–комплексным
реактивным сопротивлением (знак
показывает, какое сопротивление больше
– индуктивное или емкостное).
Следует
помнить:
,
,
,
,
.
В
результате получим, что нашу исходную
схему с реальными мгновенными
синусоидальными токами и напряжениями
можно заменить схемой с комплексным
сопротивлением
,
в которой есть комплексные амплитуды
или комплексы действующих значений
токов или напряжений.
,
Получили
закон Ома в комплексной форме, а также
переход от комплексной величины тока
и напряжения к мгновенному значению
имеет только одно решение, можно записать
законы Кирхгофа в комплексной форме:
1-й
закон (в узле электрической цепи)
2-й
закон (в замкнутом контуре цепи)
.
Используя
при расчетах схемы с комплексными
сопротивлениями, комплексами токов и
напряжений мы от интегрально-дифференциальных
уравнений для мгновенных значений токов
и напряжений в реальной схеме, имеем
уравнения обычной алгебры, но с
комплексными числами. В этом основное
преимущество данного метода.
Комплексное
число всегда можно представить в виде
вектора на комплексной плоскости.
Диаграмма, отражающая совокупность
векторов токов и напряжений с учетом
их фаз по 1 и 2 законам Кирхгофа на
комплексной плоскости называется
векторной диаграммой (она широко
используется при расчетах).
Для
нашей схемы:

,
(надо
помнить, что
)
Параллельное
соединение R,
L,
С.
Примем
Оперируем
комплексом тока и напряжения и отбросим
.
,
где
,
,
,
,
,
.
– комплексная
полная проводимость;
– комплексная
индуктивная проводимость;
– комплексная
емкостная проводимость;
– комплексная
реактивная проводимость.
Связь
между комплексными сопротивлениями и
проводимостями:
;
;
;
;
;
;
;
;
;
;
.
Комплексная
мощность
За
комплексную мощность
приняли произведение комплекса
действующего значения напряжения
на сопряженный комплекс действующего
значения тока
(сопряженный комплекс изменен на обратный
()
знак прямого комплексного числа (,
)).
Если
,
,
тогда учитывая известные ранее полную
мощность
,
активную мощность
,
реактивную мощность
,
имеем:
В
электрических цепях при периодическом
синусоидальном воздействии имеет место
баланс мощностей источников и нагрузок,
т.е. комплексная мощность источников
энергии должна быть ровна комплексной
мощности нагрузок и активные и реактивные
мощности источников равны активной и
реактивной мощностям нагрузок.
,
,
,
,
.
Знак реактивной мощности означает
преимущество индуктивного (+) или
емкостного (–) сопротивлений.
Соседние файлы в папке Конспект 2
- #
- #
- #
- #
- #
- #
- #
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Основы комплексного расчета электрических цепей
Одним из основных способов расчета электрических цепей переменного тока является символический или комплексный метод. Как правило, он используется при анализе электрических схем с гармоническими токами, напряжениями и электродвижущей силой. В результате решения получается комплексное значение напряжений и токов. Синусоидальная величина может быть представлена:
- В форме вращающегося вектора.
- В виде комплексного числа.
Пример вращающегося вектора изображен на рисунке ниже.
Рисунок 1. Пример вращающегося вектора. Автор24 — интернет-биржа студенческих работ
По данному рисунку видно, что синусоидальная величина а изменяется с течением времени, которая может быть входным напряжением или любым другим параметром электрической сети. Величина имеет некоторое начальное значение (t=0) при начальной фазе ф:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
При угле Wt3, когда сумма Wt3+ф=90 и соответственно:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
«Комплексный расчет электрических сетей» 👇
Синусоидальная величина при угле Wt7, когда сумма Wt7 + ф = 270 будет иметь отрицательное значение:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Величина будет иметь отрицательное значение при углах Wtn + ф = 0, когда Wtn = –ф (данная область на рисунке не отмечена), таким образом:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
Также нулевое значение у синусоидальной величины будет при угле Wt11, когда Wt11+ ф = 360:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Именно по такому закону может меняться синусоидальная величина, например напряжение, изменяясь от 0 до максимального значения и обратно.
Другая форма представления — комплексная
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Для этого строится график (комплексная плоскость) зависимости двух величин, как на рисунке ниже.
Рисунок 8. График. Автор24 — интернет-биржа студенческих работ
Длина вектора Аm равна максимальному значению амплитуды рассматриваемой величины. Если учитывать начальную фазу (ф), то это число записывается следующим образом.
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
В практических расчетах комплексного метода применяют не амплитудное значение, а действующее, которое меньше в корень из 2 амплитудного:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
При работе с комплексными числами применяется один из трех способов записи комплексного числа: тригонометрическая форма, алгебраическая форма, показательная форма. Например, имеется комплексное число в показательной форме:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
В тригонометрической форме оно будет иметь следующий вид:
Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ
В итоге при переходе в алгебраическую форму, учитывая, что:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
получаем:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
где, ReA = 8,66 – действительная составляющая комплексного числа; ImA = 5 – мнимая составляющая комплексного числа.
При переходе от алгебраической формы к показательной получаем число следующего вида
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Оно переходит к показательной форме следующим преобразованием:
Рисунок 16. Формула. Автор24 — интернет-биржа студенческих работ
А угол рассчитывается по формуле
Рисунок 17. Формула. Автор24 — интернет-биржа студенческих работ
И в итоге получается:
Рисунок 18. Формула. Автор24 — интернет-биржа студенческих работ
Пример расчета электрической цепи комплексным методом
Алгоритм комплексного расчета электрической цепи выглядит следующим образом:
- Составляется комплексная схема электрической цепи, в которой мгновенные значения токов, напряжений и электродвижущей силы заменяются на комплексные.
- Выбираются и обозначаются направления токов.
- Составляется комплексное уравнение.
- Решается уравнение относительно комплексного значения искомой величины.
- При необходимости записываются мгновенные значения полученных комплексных величин.
Рассмотрим схему электрической цепи с последовательным соединением (рисунок ниже), в которой нам известны сопротивления — R1, R2 и R3, емкость — С, индуктивность — L и частота — f, электродвижущая сила е = 141sin*Wt (закон изменения ЭДС)
Рисунок 19. Схема электрической цепи. Автор24 — интернет-биржа студенческих работ
Сначала составляется комплексная схема, на которой обозначаются комплексные токи и напряжения.
Рисунок 20. Комплексная схема. Автор24 — интернет-биржа студенческих работ
Ток в цепи равен:
Рисунок 21. Формула. Автор24 — интернет-биржа студенческих работ
где, U – входное комплексное напряжение; Z – полное сопротивление всей электрической цепи.
Комплексное напряжение рассчитывается по формуле:
Рисунок 22. Формула. Автор24 — интернет-биржа студенческих работ
В данном случае начальная фаза ф=0, потому что для мгновенного значения напряжения вида
Рисунок 23. Формула. Автор24 — интернет-биржа студенческих работ
при ф =0 получаем:
Рисунок 24. Формула. Автор24 — интернет-биржа студенческих работ
Таким образом в показательной форме напряжение записывается:
Рисунок 25. Формула. Автор24 — интернет-биржа студенческих работ
Комплексное сопротивление имеет следующий общий вид:
Рисунок 26. Формула. Автор24 — интернет-биржа студенческих работ
Комплексное сопротивление емкости имеет следующий вид
Рисунок 27. Формула. Автор24 — интернет-биржа студенческих работ
Откуда общее комплексное сопротивление электрической сети рассчитывается по формуле:
Рисунок 28. Формула. Автор24 — интернет-биржа студенческих работ
Таким образом, после нахождения комплексного сопротивления становится возможным найти комплексный ток по второму закону Ома. Далее находятся комплексные напряжения на элементах цепи:
Рисунок 29. Формула. Автор24 — интернет-биржа студенческих работ
Для проверки результатов можно использовать второй закон Кирхгофа, согласно которому должно выполняться равенство:
Рисунок 30. Формула. Автор24 — интернет-биржа студенческих работ
В результате проверки допускается небольшое расхождение, которое может получиться в результате промежуточных округлений при расчете комплексных величин, а также преобразовании их из одной формы в другую.
Комплексный метод расчета электрических сетей уже давно доказал свою эффективность на практике. Его активно применяют на промышленных предприятиях, при строительстве объектов различного назначения, в том числе и объектах электроснабжения. Один из недостатков метода заключается в его большом объеме вычислительных и преобразовательных действий, поэтому для ускорения процесса используют электронно-вычислительные процессы и специальные программы.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Вращающиеся векторы, а следовательно, и изображаемые ими синусоидальные величины можно выражать комплексными числами.
Допустим, что требуется представить комплексом ток, амплитуда которого 


Изобразим на комплексной плоскости под углом 

длиной 



Рис. 2.11. Вектор тока на комплексной плоскости
Взаимное расположение векторов на векторной диаграмме с течением времени не изменяется; поэтому нет необходимости вращать векторы при изображении синусоидально изменяющихся величин на комплексной плоскости. Достаточно изобразить векторы в начальный момент времени, т.е. представить их комплексами. Например, ток i (2.34) можно представить в символической записи (2.35).
С учетом того, что на векторных диаграммах обычно откладывают не амплитуды, а действующие значения синусоидальных величин, комплексное значение тока, или комплекс тока, запишется в виде
(отсутствие индекса m указывает на то, что записано действующее значение комплексной величины).
Аналогично выполняется символическая запись напряжения.
Если

то комплекс напряжения

Частное от деления комплекса напряжения на выводах цепи (ветви) на комплекс тока называется комплексным сопротивлением цепи и обозначается 

или

где 


Переписав выражение (2.38), получим закон Ома в комплексной форме:

Комплексное сопротивление и его действительная и мнимая составляющие могут быть представлены на комплексной плоскости (рис. 2.12) в виде треугольника сопротивлений, в данном случае для rL – цепи.
Рис. 2.12. Треугольник сопротивлений rL – цепи
Модуль комплексного сопротивления, обозначенный строчной буквой z, определяется по формуле

а аргумент – через его синус или тангенс:
т.е. φ>0.
Из (2.40) напряжение на выводах цепи

Первое слагаемое этого выражения представляет собой комплексное напряжение на активном сопротивлении. Это напряжение совпадает по фазе с током (рис. 2.13), и, естественно, комплексы 

Рис. 2.13. Векторная диаграмма rL – цепи
Второе слагаемое – комплексное напряжение на индуктивности 

Для неразветвленной цепи с активным сопротивлением и емкостью (рис. 2.14) при 



где x= –xC; 


Рис. 2.14. Цепь с сопротивлением и емкостью
Треугольник сопротивлений показан на рис. 2.15.
Напряжение на емкости
отстает по фазе от тока на 90° (рис. 2.16).
Напряжение на выводах цепи:
Рис. 2.15. Треугольник сопротивлений rC – цепи
Рис. 2.16. Векторная диаграмма rC – цепи
Необходимо обратить внимание на то, что комплекс 





При расчетах разветвленных цепей часто вводят комплексную проводимость 

где 

Например, для последовательной rL–цeпи комплексная проводимость (рис. 2.17)

где активная проводимость 
Рис. 2.17. Треугольник проводимостей rL – цепи
Модуль комплексной проводимости можно определить по формуле

а аргумент – через его синус или тангенс:
откуда видно, что φ>0, т.е. напряжение опережает по фазе ток.
Для последовательной rC–цепи комплексная проводимость (рис. 2.18):

где активная проводимость g и емкостная bC определяются по следующим выражениям:
Модуль комплексной проводимости

а аргумент определяется через синус или тангенс:
откуда следует, что φ<0, т. е. ток опережает по фазе напряжение.
Наконец, для rLC-цeпи можно написать
где активная и реактивная проводимости
угол φ >0 при х>0 или при b>0;
угол φ <0 при x<0 или при b<0.
Пример 2.1. Неразветвленная цепь с активным сопротивлением r= 80 Ом и емкостным сопротивлением хС = 60 Ом находится под напряжением 
Решение.
Комплексное сопротивление

Модуль и аргумент этого сопротивления:

То же сопротивление в показательной форме

Ток в цепи


Если ток и напряжение цепи выражены в комплексной форме, то активную и реактивную мощности цепи определяют, умножая комплексное напряжение на сопряженный комплексный ток (комплексные величины, имеющие одинаковые модули и равные по абсолютному значению, но противоположные по знаку аргументы, называются сопряженными).
Допустим, что 

Произведение комплекса напряжения и сопряженного комплекса тока представляет мощность в комплексной форме или, комплексную мощность.

Таким образом, действительная часть полученного комплекса выражает активную мощность, а мнимая – реактивную мощность цепи. При емкостной нагрузке, т.е. при φ<0, мнимая часть комплексной мощности имеет отрицательный знак (sinφ<0).
Пример 2.2. Определить активную и реактивную мощности цепи, если ток. 

Решение.

Р = 1,760 [кВт];
Q= –1,320 [кBар].
Содержание:
Символический метод расчета цепей:
Символический метол, введенный в теорию переменных токов Штейнмецом, является аналитическим развитием векторных диаграмм. Он основан на изображении векторов в комплексной плоскости и на их записи комплексными числами. Это приводит к применению для цепей синусоидального переменного тока законов Ома и Кирхгофа и вытекающих из них методов расчета цепей в той же форме, что и для цепей постоянного тока. В России символический метод был введен В. Ф. Миткевичем.
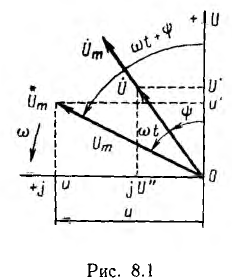
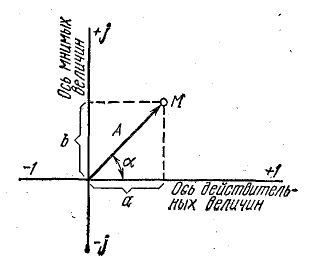
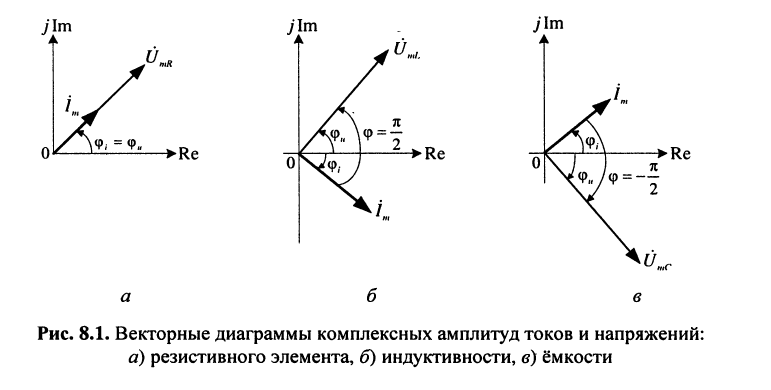
В символическом методе принято исходную ось направлять вертикально и на ней откладывать вверх положительные вещественные числа, а по горизонтальной оси влево — положительные мнимые числа (рис. 8.1). В дальнейшем эти оси называются осью и осью мнимых. Тогда, например, вращающийся вектор Um, изображающий синусоидальное напряжение
и составляющий с осью вещественных угол 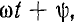
здесь 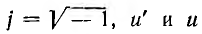
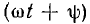
Комплекс 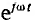
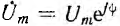
называют комплексным действующим значением, в данном примере — напряжения, или комплексным напряжением. На комплексной плоскости оно изображается неподвижным вектором.
*
Для обратного перехода от комплекса 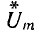
Тогда
Таким образом, комплекс 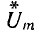
Геометрическому сложению и вычитанию векторов соответствует алгебраическое сложение и вычитание их проекций на оси комплексной плоскости, т. е. их вещественных и мнимых составляющих. Поэтому геометрическое сложение и вычитание векторов должно быть заменено вновь алгебраическим сложением и вычитанием их комплексов. Таким образом, алгебраический характер сложения и вычитания мгновенных значений синусоидальных величин сохраняется при замене оригиналов комплексными изображениями.
Так как проекция произведения двух векторов не равна произведению проекций этих векторов, изображение произведения двух синусоидальных функций не равно произведению их изображений, поэтому прч умножении таких функций нельзя применять символический метод.
Производная синусоидальной функции
имеет изображение
так как 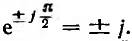
Интеграл той же синусоидальной функции
имеет изображение
равное интегралу изображения исходной функции:
Таким образом, однозначное соответствие имеет место также между производными и интегралами оригинала и комплексного изображения.
Здесь получен еще один важный результат: дифференцированию оригинала соответствует, умножение на 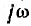
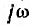
Применение символического метода для расчета цепей переменного тока
Применение символического метода можно показать на примере. Так, для цепи с последовательным соединением r, L и С уравнению по второму закону Кирхгофа
при синусоидальном законе изменения напряжения и тока соответствует алгебраическое уравнение
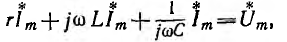
откуда комплексное изображение тока
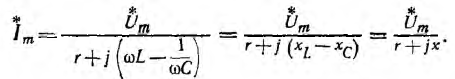
От изображения можно сделать переход к оригиналу — мгновенному значению тока.
Выражение (8.2) можно рассматривать как закон Ома в символической форме. Тогда знаменатель
может рассматриваться как комплексное полное сопротивление. Его модуль z равен полному сопротивлению цепи, его аргумент 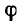
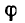
Необходимо заметить, что знак плюс, стоящий в общем выражении комплексного сопротивления Z =г + jx, сохраняется в конкретном числовом выражении при преобладании индуктивного сопротивления (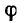
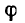
Величина, обратная полному сопротивлению
является комплексной полной проводимостью с модулем у, равным полной проводимости, и аргументом 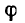
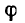
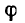
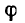
Если в символические выражения (8.1) для второго закона Кирхгофа и (8.2) для закона Ома подставить значения
множитель вращения 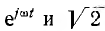
Следовательно, вместо комплексных изображений 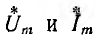
и комплексный ток I, т. е. оперировать с неподвижными векторами. Это, очевидно, в равной степени относится к первому закону Кирхгофа, и его можно применять в виде:
Таким образом, время t из уравнений выпадает, а закон Ома и оба закона Кирхгофа в символической форме для комплексных напряжений, токов, полных сопротивлений и полных проводимостей цепей синусоидального тока
получают алгебраическую форму, как и для цепей постоянного тока. Необходимо подчеркнуть, что этот вывод сделан для цепи без взаимной индукции.
Отсюда следует, что для расчета линейных цепей синусоидального переменного тока без взаимной индукции можно применить все изложенные в гл. III методы расчета цепей постоянного тока, вытекающие из законов Ома и Кирхгофа; метод преобразования, метод уравнений Кирхгофа, метод наложения, методы контурных токов и узловых напряжений и метод эквивалентных источников напряжения или тока. При этом, как указывалось, необходимо оперировать с комплексными напряжениями, токами, полными сопротивлениями и проводимостями.
Алгебраические действия над этими комплексами следует производить в соответствии с выбранными для напряжений и токов положительными направлениями, совпадающими с положительными направлениями их мгновенных значений и изображающих их векторов. По окончании расчетов следует перейти к действующим значениям, равным, очевидно, модулям соответствующих комплексов и, если это необходимо, к мгновенным значениям искомых величин.
Символический метод применим также для цепей1 с взаимной индукцией. Особенности их расчета рассмотрены в гл. IX.
Развитие методов расчета цепей постоянного и переменного синусоидального тока может быть проиллюстрировано табл. 8.1.
Таблица 8.1
| Род тока | Значения напряжений и токов | Учитываемые э. д. с. | Используемые сопротивления и проводимости | Операции |
|
Постоянный Синусоидальный То же > |
Действительные Мгновенные Действующие Комплексные | Внешние Внешние и внутренние Внешние > | Омические Активные Полные Комплексные | Алгебраические > Геометрические Алгебраические |
Непосредственное применение символического метода к вычислению по напряжению и току мощности, мгновенное значение которой является произведением их мгновенных значений (р = ui), невозможно. Однако для вычисления активной, реактивной и полной мощности по символическим изображениям напряжения и тока может быть использован искусственный прием. Для этого комплексное напряжение 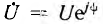
Таким образом, вещественная часть комплексной мощности S равна активной мощности Р, а мнимая — реактивной Q. При этом положительный знак сохраняется для индуктивной мощности и изменяется на отрицательный для емкостной. Полная мощность вычисляется, как модуль комплексной мощности:
Расчет цепей переменного тока символическим методом
При расчете цепей по законам Кирхгофа методика составления уравнений остается той же, что и при постоянном токе. Для заданных комплексных э. д. с. и токов должны быть также указаны их положительные направления, для искомых — ими надо задаться.
Например, для цени рис. 7.21, а с двумя узлами и двумя элементарными контурами по первому закону Кирхгофа должно быть составлено одно уравнение
Два уравнения, составляемые по второму закону Кирхгофа, при обходе элементарных контуров А и В по часовой стрелке, будут
При постоянном токе ответ со знаком минус указывал на встречное направление по сравнению с предположенным, а при переменном токе ответ в виде комплекса является окончательным для принятого направления искомой величины — напряжения или тока. При выборе обратного направления фаза (аргумент) искомого комплекса изменилась бы на угол π.
Аналогичным образом составляются и решаются уравнения при применении остальных методов, вытекающих из законов Кирхгофа. Так, уравнения по методу контурных токов для цепи рис. 7.21, а при обходе контуров A и В по часовой стрелке имеют вид:
где
Символический метод весьма удобен также для решения задач в общем виде.
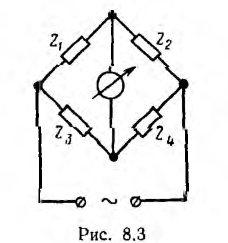
В электроизмерительной технике широко применяется мост переменного тока (рис. 8.3). Условие равновесия моста постоянного тока имеет вид:
По аналогии условие равновесия моста переменного тока:
Это условие распадается на два — равенство модулей и аргументов левой и правой частей:
Если модули и аргументы полных сопротивлений трех ветвей известны, из этих уравнений могут быть определены модуль и аргумент полного сопротивления четвертой ветви.
Вторым примером применения символического метода для решения задач в общем виде может служить задача поддержания в цепи изменяющейся нагрузки неизменного по величине и фазе тока. Например, при последовательном соединении ламп, применяемом при освещении аэродромов, должны автоматически замыкаться накоротко зажимы перегоревшей лампы, чтобы избежать разрыва цепи при этом ток остальных не должен измениться.
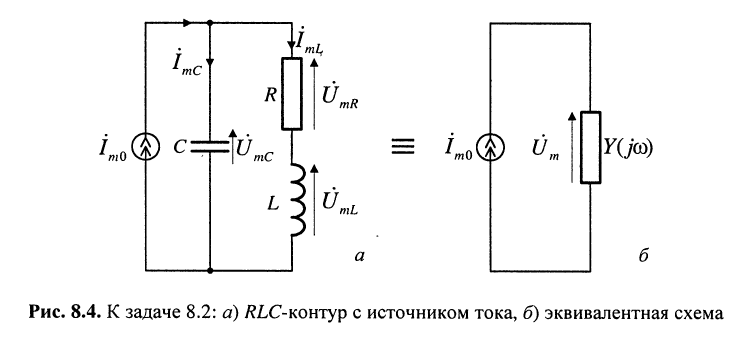
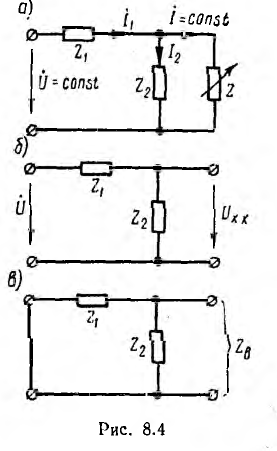
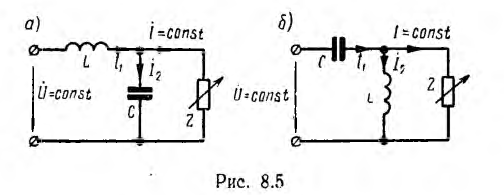
Пусть для схемы рис. 8.4, а, питаемой напряжением U = const, требуется найти условие, при выполнении которого ток I в правой параллельной ветви не будет меняться по величине и по фазе при любом изменении сопротивления Z этой ветви.
Общее выражение для комплекса тока I может быть найдено методом эквивалентного источника напряжения. По аналогии с цепью постоянного тока
Здесь комплекс напряжения 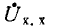
а искомый ток
Для того чтобы ток I не зависел от сопротивления Z нагрузки, коэффициент при Z в выражении I должен быть равен нулю:
Это будет выполнено, если
т. е. сопротивления Z1 и Z2 должны быть чисто реактивными, равными
по величине и противоположными по знаку. Одно из них будет индуктивным, а другое — емкостным:
причем
При этом ток нагрузки
Если в цепь до разветвления включено индуктивное сопротивление, а потом — емкостное (рис. 8.5, а), то ток
отстает по фазе от приложенного к цепи напряжения на угол π2. Если индуктивное и емкостное сопротивления поменять местами (рис. 8.5, б), то
- т. е. ток I опережает приложенное к цепи напряжение на угол π/2. При изменении Z ток I1 до разветвления изменяется и по величине
и по фазе от значения 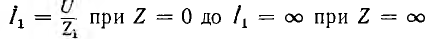
Метод дуальных цепей
Метод дуальных цепей, рассмотренный в для частного случая резонансных цепей, является общим методом. Взаимная замена величин при их символической записи должна осуществляться по табл. 8.2, вытекающей из табл. 7.1.
Таблица 8.2
| Последовательное соединение | Параллельное соединение | ω | U | I | L | C | r | g | Z | Y |
| Параллельное соединение | Последовательное соединение | ω | I | U | C | L | g | r | Y | Z |
Отсюда можно получить соотношения для дуальной цепи, если они даны для цепи исходной. Так, если для исходной цепи в какой-либо вегви имеет место короткое замыкание (Z = 0), то в дуальной цепи это соответствует холостому ходу (У = 0), и наоборот. При переходе от исходной цепи к дуальной уравнения по первому и второму законам Кирхгофа меняются местами.
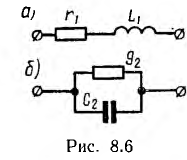
Основным свойством дуальных цепей является неизменность их параметров r, L и С при переменной частоте. Например, в дуальных цепях рис. 8.6, а и б численное равенство сопротивления 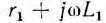
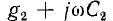
Это свойство дуальных цепей позволяет, произведя исследование поведения какой-либо цепи при переменной частоте, перенести результаты на дуальную цепь, заменив напряжения токами и т. д., что и было сделано для резонансных цепей.
При переходе к дуальной цепи не изменяют своей величины мощности S, Р и Q, так как в их выражения входят произведение напряження и тока, и лишь у реактивной мощности Q = VI sin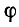
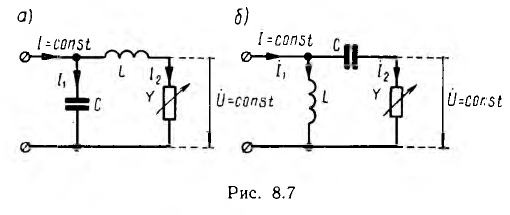
В качестве примера может быть решена задача создания схем преобразования неизменного по величине и фазе тока в неизменное по величине и фазе напряжение, т. е. схем, дуальных со схемами. При замене схем и величин по табл. 8.2 получается схема рис. 8.7, а, дуальная схеме рис. 8.5, а, и схема рис. 8.7, б, дуальная схеме рис. 8.5, б. Если
то при неизменном токе I напряжение О на изменяющейся проводимости Y будет постоянным, т. е.
что получается путем перехода от формул для токов I исходных цепей.
Символический метод электрических цепей переменного тока
Методы расчета электрических цепей переменного тока при помощи векторных диаграмм, рассмотренные в предыдущих главах, основаны на изображении синусоидальных величин векторами.
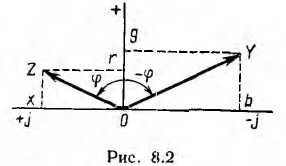
Из курса математики известно, что каждому вектору А в комплексной плоскости (рис. 15.1) соответствует комплексное число А, которое можно выразить в форме:
алгебраической —
Рис. 15.1. К вопросу о выражении вектора комплексным числом
тригонометрической —
показательной —
Это дает основание от графического (векторного) выражения синусоидальных напряжений и токов перейти к аналитическому выражению их комплексными числами, а операции с векторами заменить алгебраическими действиями.
Выражение характеристик электрических цепей комплексными числами
При расчете электрических цепей переменного тока используют или определяют следующие величины: э.д.с. напряжения, токи, сопротивления и проводимости, мощность. Все эти величины должны быть выражены в символической форме, т. е. комплексными числами.
Напряжения и токи
Подобно тому как на векторных диаграммах длины векторов выражают действующие величины, комплексные выражения э. д. с. .напряжений и токов записывают так, что модули их также равны действующим величинам (комплексы синусоидально изменяющихся величин принято отмечать точками над их буквенными обозначениями (например, комплексы напряжения 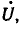
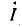
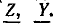
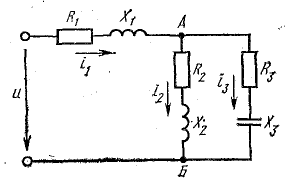
Для примера рассмотрим схему электрической цепи параллельного соединения катушки и конденсатора (рис. 15.2).
Напряжение на зажимах цепи выражается уравнением
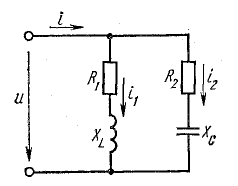
Этому напряжению соответствуют вектор U в комплексной плоскости (рис. 15.3) и комплексное число в показательной форме
Ток i1 в катушке отстает от напряжения на угол φ1:
угол 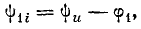
Вектору тока I1 соответствует комплексное число
Ток в конденсаторе опережает напряжение на угол φ2. Вектору тока I2 соответствуют уравнение
и комплекс
где
Согласно первому закону Кирхгофа, ток в неразветвленной части цепи складывается из токов в параллельных ветвях:
Для определения этого тока сложение векторов I1 и I2 можно заменить сложением комплексов:
Следует обратить внимание на различие между действительной или мнимой частями комплекса, с одной стороны, и активной или реактивной составляющими вектора тока — с другой.
Действительная и мнимая части комплекса тока равны проекциям вектора тока на оси комплексной плоскости (ось действительных и ось мнимых величин).
Активная и реактивная составляющие вектора тока в данном участке цепи равны его проекциям на взаимно перпендикулярные оси, одна из которых направлена вдоль вектора напряжения этого же участка цепи. Действительная и мнимая части комплекса тока равны соответственно активной и реактивной составляющим вектора тока только в том случае, если вектор напряжения направлен вдоль оси действительных чисел, т. е. комплекс напряжения выражается действительным числом.
Рис. 15.2. К вопросу о выражении токов, напряжений, сопротивлений проводимостей комплексными числами
Рис. 15.3. Векторная диаграмма к схеме цепи рис. 15.2
Сопротивления
Для выражения сопротивлений в комплексной форме продолжим рассмотрение схемы рис. 15.2, где каждый из элементов (катушка и конденсатор) представлен активным и реактивным сопротивлениями, соединенными последовательно.
Разделив комплекс напряжения 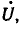
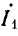
где 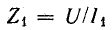
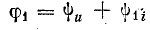
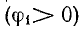
Выразим комплекс сопротивления катушки в тригонометрической и алгебраической форме:
Но 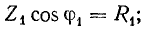
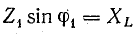
Аналогично, для второй ветви
где 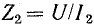
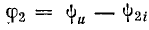
или
Если в ветвях схемы рис. 15.2 реактивных сопротивлений нет 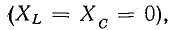
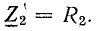
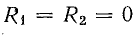
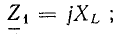
Из приведенных рассуждений следует:
- Активное сопротивление в комплексной форме выражается действительным положительным числом.
- Реактивные сопротивления в комплексной форме выражаются мнимыми числами, причем индуктивное сопротивление (ХL) положительно, а емкостное (ХC) отрицательно.
- Полное сопротивление участка цепи при последовательном соединении R и X выражается комплексным числом, действительная часть которого равна активному сопротивлению, а мнимая часть равна реактивному сопротивлению этого участка.
Проводимости
Выражения проводимостей ветвей в комплексной форме можно получить, представив каждый элемент (катушку и конденсатор) схемой параллельного соединения активной и реактивной проводимостей (см. рис. 14.1, б)
Из этих формул видно, что выражения проводимостей комплексными числами можно получить в таком же порядке, как для сопротивлений. Для того чтобы не повторять аналогичных рассуждений, полные проводимости в символической форме можно найти как величины, обратные комплексам полных сопротивлений:
Для первой ветви (катушки)
где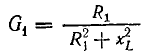
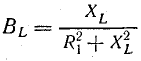
Для второй ветви (конденсатора)
где 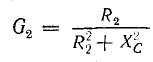
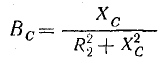
Результаты этих преобразований показывают, что полная проводимость ветви электрической цепи в комплексной форме выражается комплексным числом, действительная часть которого равна активной проводимости, а мнимая часть равна реактивной проводимости этой ветви, причем индуктивная проводимость отрицательна, а емкостная — положительна.
Мощность
Комплекс мощности в данной цепи определяется умножением комплекса напряжения на сопряженный комплекс тока этой цепи.
Для ветви с активным сопротивлением и индуктивностью (см. рис. 15.2), согласно векторной диаграмме (см. рис. 15.3),
Произведение комплекса напряжения и сопряженного комплекса тока
В алгебраической форме
Действительная часть полученного комплекса выражает активную мощность, а мнимая часть без множителя 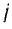
Для ветви с активным сопротивлением и емкостью
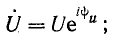
В алгебраической форме
Реактивная мощность в цепи с емкостью имеет отрицательный знак в отличие от положительного знака реактивной мощности в цепи с индуктивностью. Модуль комплекса мощности в той и другой ветви равен полной мощности:
Рис. 15.4. К вопросу о преобразовании схем с применением комплексных чисел
Основные уравнения электрических цепей в комплексной форме
Представление векторов напряжений и токов комплексами, выражение сопротивлений и проводимостей комплексными числами, а также замена операций с векторами алгебраическими действиями с комплексными числами позволяют значительно упростить расчет сложных цепей переменного тока. Кроме того, применение комплексных чисел обеспечивает единство методов расчета электрических цепей постоянного и переменного токов. Это значит, что все методы расчета и вытекающие из них соотношения для цепей постоянного тока можно применить и для цепей переменного тока, если величины выражены в комплексной форме. В этом практический смысл применения комплексных чисел для решения задач электротехники.
Законы Кирхгофа
Согласно первому закону Кирхгофа, алгебраическая сумма комплексов токов в электрическом узле равна нулю:
Для составления уравнения в символической форме по первому закону Кирхгофа нужно выбрать условно-положительные направления токов. В уравнении (15.15) ток записывают со знаком плюс, если он направлен к узлу. Для схемы рис. 14.15, а
или
а в комплексной форме
или
Согласно второму закону Кирхгофа, в контуре электрической цепи алгебраическая сумма комплексов э. д. с. источников равна алгебраической сумме комплексов падений напряжения:
Для схемы рис. 14.10
а в комплексной форме
Преобразование схем
На примере цепи смешанного соединения сопротивлений (рис. 15.4) рассмотрим расчет методом преобразования и упрощения схемы. Параллельно соединенные ветви, имеющие полные сопротивления
заменяются одной ветвью с эквивалентным сопротивлением
Сопротивление в неразветвленной части цепи 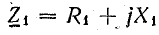
Общее сопротивление цепи
Ток в неразветвленной части цепи
Напряжения на участках, цепи:
Токи в параллельных ветвях:
Преобразованием можно упростить и более сложные схемы с последовательным и параллельным соединениями участков, а также схемы, которые содержат треугольники или трехлучевые звезды сопротивлений.
Метод узлового напряжения
Схему с двумя узлами можно рассчитать, определив узловое напряжение по формуле
Эта формула аналогична формуле (4.21). В числителе ее записана алгебраическая сумма произведений комплексов э. д. с. и проводимости всех ветвей, а в знаменателе — сумма комплексов проводимостей ветвей.
Комплекс тока определяют по формуле
Правило выбора знаков э.д. с. в формулах (15.16) — (15.18) такое же, как и в цепи постоянного тока, с той лишь разницей, что условно-положительные направления э. д. с. выбираются при расчете, а в цепи постоянного тока направления э. д. с. обычно заданы.
Метод эквивалентного генератора
Порядок расчета по методу эквивалентного генератора, для цепей постоянного тока, пригоден и для цепей переменного тока, если э.д. с., токи и сопротивления их выражены в комплексной форме.
Ток 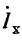
где 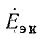
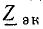
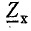
Задача 15.3.
Выполнить символическим методом расчет цепи (см. рис. 14.8). Дано:
= 8 Ом; Х21 = 6 Ом; Х1С — 15 Ом; Х2С = 10 Ом.
Определить ток в цепи и напряжения
Решение. Выразим заданные э. д. с. и сопротивления комплексными числами.
Э. д. с. в комплексной форме:
Сопротивления в комплексной форме:
При последовательном соединении общее сопротивление цепи
Сопротивление цепи в показательной форме:
модуль
аргумент
Угол φ можно определить, найдя
Ток в цепи
Для удобства деления выразим числитель и знаменатель в показательной форме:
Из сравнения комплексов 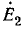
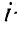
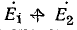
Напряжение
Угол сдвига фаз между током и напряжением
Напряжение
Между током и напряжением 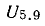
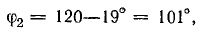
Задача 15.5.
Определить символическим методом напряжения ка зажимах источника, токи и мощность в цепи рис. 14.13, для которой известны R1 = 8 Ом; ХL = 6 Ом; R2 = 9 Ом; ХC = 12 Ом; I1 = 9А.
Решение. Выразим сопротивления ветвей в символической форме:
Предположим, что комплекс тока 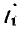
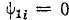
(начальную фазу тока можно выбрать произвольно, т.е. угол 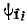
Напряжение в первой ветви, равное напряжению на зажимах источника,
Ток во второй ветви
Ток в источнике
Мощность цепи
Комплексные сопротивления и проводимости элементов электрических цепей
Вычисление комплексных сопротивлений и проводимостей последовательных и параллельных двухполюсников, содержащих различные элементы электрических цепей, осуществляются по тем же правилам, которые были получены для резистивных цепей, поскольку, как это было показано в лекции 7, для комплексных амплитуд справедливы законы Ома и Кирхгофа.
Комплексные сопротивления и проводимости полностью характеризуют свойства соответствующего элемента. Будем рассматривать только пассивные элементы, через которые проходит гармонический ток
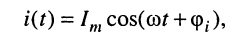
комплексная амплитуда которого равна 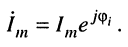
Резистивный элемент
Для резистивного элемента, обладающего активным сопротивлением, имеем
где 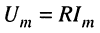
По определению комплексного сопротивления двухполюсника (7.38) имеем:
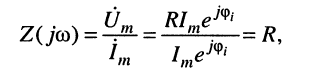
а комплексная проводимость
Средняя мощность, выделяемая в активном сопротивлении, согласно (7.15) при 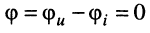
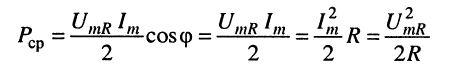
или, переходя к действующим значениям (7.18) напряжения и тока,
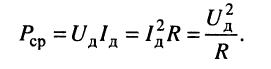
Выводы:
Индуктивность
Напряжение на зажимах индуктивности изменяется по закону
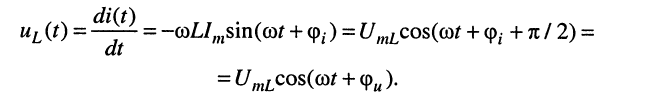
Операции дифференцирования гармонического колебания (см. лекцию 7) соответствует умножение символического изображения на оператор 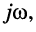
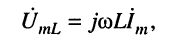
причём зависимость между амплитудами гармонических колебаний напряжения на зажимах индуктивности и тока в индуктивности определяется выражением:
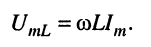
Из (8.7) для индуктивности получаем: комплексное сопротивление (индуктивное сопротивление)
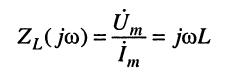
и комплексную проводимость (индуктивную проводимость)
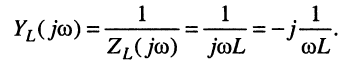
Выводы:
Комплексные сопротивление (8.9) и проводимость (8.10) индуктивности имеют только реактивные составляющие и зависят от частоты:
поэтому элемент индуктивности называют реактивным;
гармоническое напряжение на индуктивности опережает ток на 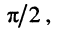
что следует из (8.6), т. е. ток и напряжение находятся в квадратуре (рис. 8.1, б);
значение средней мощности в элементе индуктивности равно нулю:
это объясняется тем, что в элементе индуктивности энергия не рассеивается; в режиме гармонических колебаний происходит обмен энергией между индуктивностью и подключённой к ней внешней цепью.
Ёмкость
Напряжение на зажимах ёмкости определяется соотношением
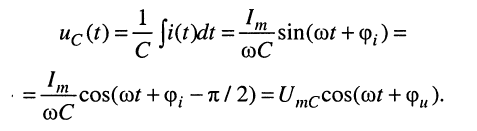
Операции интегрирования гармонического колебания (см. лекцию 7) соответствует деление символического изображения на оператору’со, т. е.
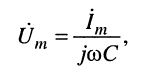
причём зависимость между амплитудами гармонических колебаний напряжения на зажимах ёмкости и тока в ёмкости определяется выражением:
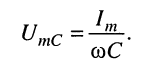
Из (8.12) для ёмкости получаем: комплексное сопротивление (ёмкостное сопротивление)
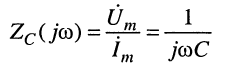
и комплексную проводимость (ёмкостную проводимость)
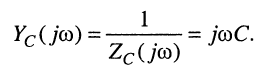
Выводы:
комплексные сопротивление (8.14) и проводимость (8.15) ёмкости имеют только реактивные составляющие:
поэтому элемент ёмкости также называют реактивным.
гармоническое напряжение на ёмкости отстаёт оттока на 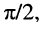
что следует из (8.11), т.е. ток и напряжение находятся в квадратуре (рис. 8.1, в);
значение средней мощности в элементе ёмкости так же, как и в индуктивности, равно нулю:
это объясняется тем, что в элементе ёмкости энергия не рассеивается; в режиме гармонических колебаний происходит обмен энергией между ёмкостью и подключённой к ней внешней цепью.
Комплексные сопротивления и проводимости двухполюсников
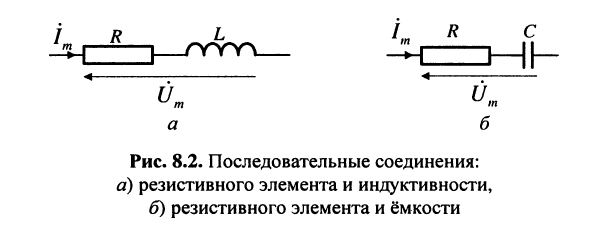
Проиллюстрируем вычисления комплексных сопротивлений и проводимостей на простейших примерах последовательного соединения резистивного элемента с индуктивным (рис. 8.2, а) и ёмкостным (рис. 8.2, б).
Последовательное соединение резистивного и индуктивного элементов
Алгебраическая форма записи комплексного сопротивления рассматриваемого двухполюсника (рис. 8.2, а)
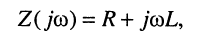
где активная составляющая 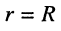
Полное сопротивление двухполюсника равно
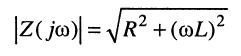
и аргумент
поэтому показательная форма записи комплексного сопротивления имеет вид
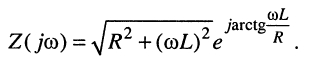
Комплексная проводимость по определению для данного двухполюсника такова:
Найдём активную и реактивную части комплексной проводимости, для чего умножим числитель и знаменатель полученного выражения на комплексное число, сопряжённое знаменателю, а затем выделим вещественную 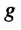
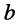
откуда
Отсюда модуль и аргумент комплексной проводимости соответственно равны:
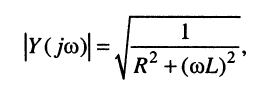
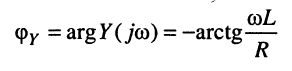
и, наконец, для показательной формы комплексной проводимости получаем:
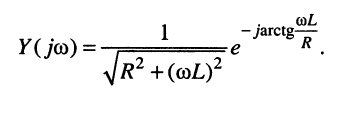
Последовательное соединение резистивного и ёмкостного элементов
Алгебраическая форма записи комплексного сопротивления рассматриваемого двухполюсника (рис. 8.2, б)
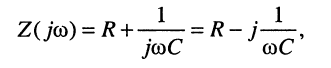
откуда
Полное сопротивление двухполюсника равно:
аргумент
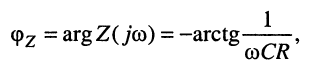
показательная форма имеет вид:
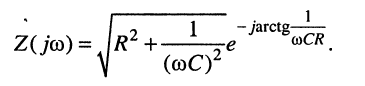
Комплексная проводимость по определению для данного двухполюсника такова:
B полученном выражении в силу равенства 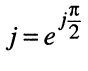
поэтому
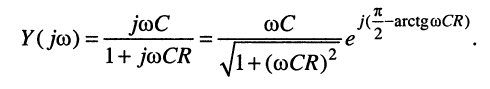
Из (8.26) получаем полную проводимость и аргумент двухполюсника соответственно:
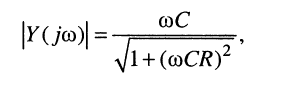
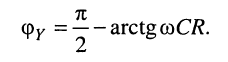
Наконец, найдём активную 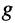
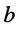
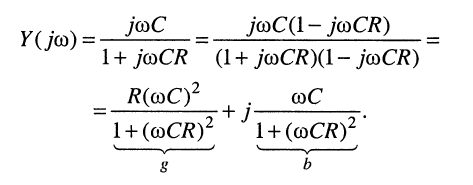
Выводы:
Реактивные составляющие сопротивления и проводимости пассивных двухполюсников могут иметь как положительные, так и отрицательные значения;
- если
, то говорят, что сопротивление двухполюсника имеет индуктивный характер (на входе двухполюсника колебания напряжения опережают по фазе колебания тока); при этом на частоте
сопротивление двухполюсника является чисто активным и равным R, поскольку сопротивление элемента индуктивности при постоянном токе равно нулю, т. е. индуктивность представляет собой короткое замыкание, а при
сопротивление двухполюсника стремится к поскольку сопротивление элемента индуктивности стремится к бесконечности, т. е. индуктивность представляет собой разрыв цепи;
- если же
, то говорят, что сопротивление двухполюсника имеет ёмкостной характер (на входе двухполюсника колебания напряжения отстают по фазе от колебаний тока); при этом на частоте
сопротивление двухполюсника стремится к
поскольку сопротивление ёмкости стремится к бесконечности, т. е. ёмкость представляет собой разрыв цепи; а при
сопротивление двухполюсника становится равным R, поскольку сопротивление ёмкости стремится к нулю, т. е. ёмкость представляет собой короткое замыкание.
Анализ установившихся гармонических колебаний в простейших цепях
Определения режимов состояния электрической цепи:
Колебания в цепях, имеющих реактивные элементы, качественно отличаются от колебаний, происходящих в резистивных цепях. Причиной качественных отличий является способность реактивных элементов выступать как в роли потребителя энергии, чему соответствуют положительные значения мгновенной мощности на зажимах элемента, так и в роли источника, когда элемент отдаёт накопленную энергию в цепь, чему соответствуют отрицательные значения мгновенной мощности на зажимах элемента. Процессы накопления и возврата энергии реактивными элементами не могут прекратиться и начаться сразу же после окончания внешних воздействий на цепь. Колебания в цепи продолжаются за счёт накопленной в реактивных элементах энергии, т. е. цепь обладает электромагнитной инерцией. Характер колебаний зависит от вида воздействия, схемы цепи, наличия начального запаса энергии в реактивных элементах к моменту приложения воздействия и т. д.
Колебания в цепях разделяют на установившиеся (стационарные) и неустановившиеся (нестационарные).
Колебания считаются установившимися, если все напряжения и токи в цепи изменяются как периодические функции времени с периодом Т, т. е. когда
Частным случаем периодических колебаний являются гармонические напряжения и токи.
Режим гармонических колебаний относится к числу установившихся режимов колебаний.
Режимом постоянного тока называется такое состояние цепи, в котором значения всех напряжений и токов не изменяются во времени:
Режимом покоя, или нулевыми начальными условиями называется такое состояние цепи, в котором значения всех напряжений и токов равны нулю.
Режимом переходных колебаний, или переходным процессом называется такое состояние цепи, в котором происходит переход из одного установившегося режима в другой установившийся режим. Режим переходных колебаний принадлежит к неустановившимся режимам.
Переходным временем называется время перехода из одного установившегося режима в другой установившийся режим.
Здесь и далее, если это не будет оговорено особо, рассматриваются цепи, находящиеся в режиме гармонических колебаний.
Анализ линейной цепи в режиме гармонических колебаний методом комплексных амплитуд состоит в следующем:
1. Гармонические токи и напряжения заменяются их комплексными изображениями: комплексными амплитудами 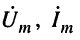
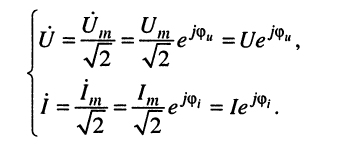
2. Составляются уравнения (системы уравнений) для комплексных изображений токов и напряжений согласно законам Ома и Кирхгофа.
3. Решаются уравнения (системы уравнений) относительно комплексных изображений требуемых токов и напряжений.
4. Осуществляется переход от комплексных изображений токов и напряжений к их оригиналам.
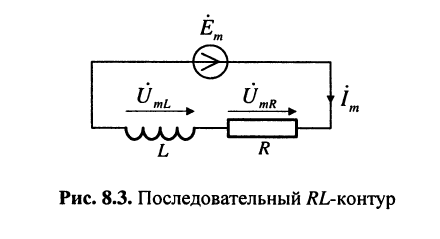
Анализ гармонических колебаний в последовательном RL-контуре
Задача 8.1.
Найти напряжения и токи в последовательном 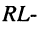
Решение. Как было показано ранее, такой контур обладает комплексным сопротивлением
Комплексная амплитуда тока в контуре согласно закону Ома равна:
где 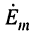
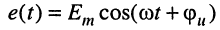
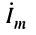
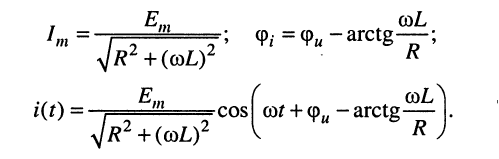
Определим комплексные амплитуды напряжений на элементах контура:
Отсюда для оригиналов напряжений имеем:
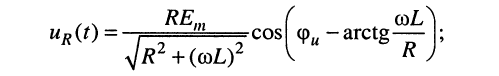
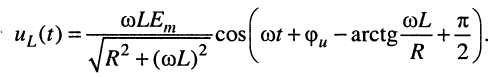
Выводы:
амплитуда тока в контуре зависит не только от значений индуктивности и сопротивления, но и от частоты 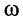
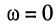
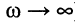
колебания напряжения на входе контура опережают по фазе колебания тока в контуре на угол 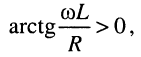
колебания напряжения на резистивном элементе происходят в фазе с колебаниями тока в контуре и отстают по фазе на угол 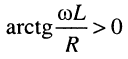
колебания напряжения на индуктивности опережают по фазе колебания напряжения источника на угол
и колебания тока в контуре на угол
Анализ гармонических колебаний в RLC-контуре
Задача 8.2.
Найти напряжения и токи в RLC-контуре, изображённом на рис. 8.4, а.
Решение.
1. Определим эквивалентную комплексную проводимость контура (рис. 8.4,6)
2. Вычислим комплексную амплитуду напряжения на зажимах двухполюсника
где 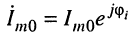
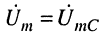
3. Найдём комплексные амплитуды токов в ветвях контура
4. Последние формулы позволяют записать выражения для комплексных амплитуд напряжений на элементах индуктивности и сопротивления:
Амплитуды и начальные фазы колебаний можно найти, представив комплексные амплитуды колебаний в показательной форме, что предлагается выполнить читателю.
Анализ сложных линейных электрических цепей в режиме установившихся гармонических колебаний
Ранее было показано (см. разд. 7.3), что комплексные амплитуды колебаний можно найти из решения систем уравнений Кирхгофа, узловых или контурных уравнений. Поэтому при составлении систем уравнений для комплексных амплитуд необходимо пользоваться правилами, установленными для резистивных цепей. Отличие будет состоять лишь в формальной замене обозначений сопротивлений и проводимостей на обозначения комплексных сопротивлений и проводимостей, а токи и напряжения заменить их комплексными амплитудами. Для удобства обозначений при составлении систем уравнений принято вместо комплексных амплитуд 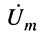
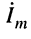
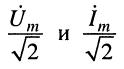
При этих обозначениях имеем канонические формы записи системы уравнений для комплексных узловых напряжений согласно (5.2)
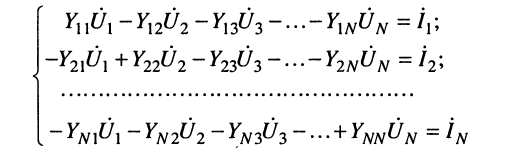
и системы контурных уравнении для комплексных контурных токов согласно (5.9)
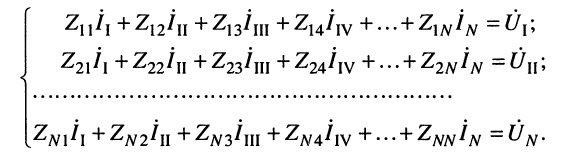
Перед решением задачи анализа гармонических колебаний символическим методом целесообразно сначала найти комплексные проводимости или сопротивления двухполюсников, составляющих ветви цепи, и только после этого составлять систему уравнений. При этом граф цепи упрощается и уменьшается число независимых уравнений.
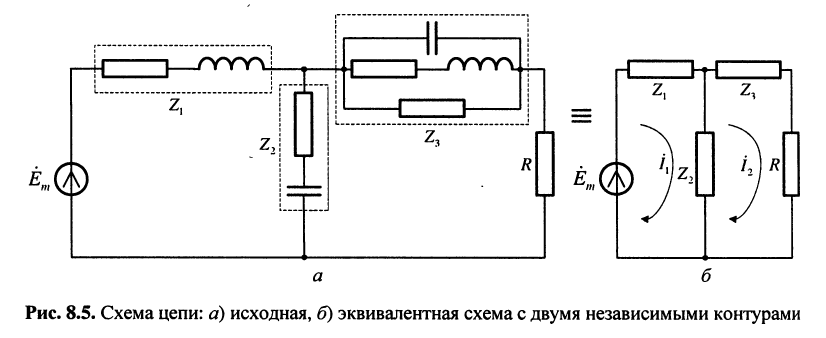
Пример 8.1.
Рассмотрим схему цепи, изображённую на рис. 8.5, а. В схеме выделены три двухполюсника с сопротивлениями 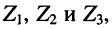
Для схемы (рис. 8.5, б) нетрудно составить систему контурных уравнений:
Из этой системы легко получить последовательно:
значения комплексных контурных токов,
значения комплексных напряжений на комплексных сопротивлениях 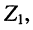
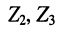
величины напряжений 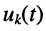
Особенности составления уравнений цепей с индуктивными связями
До сих пор рассматривались цепи, не содержащие индуктивно связанных элементов. Однако в реальных цепях широко используются трансформаторы, предназначенные для преобразования значений переменных напряжений и токов.
Основные соотношения
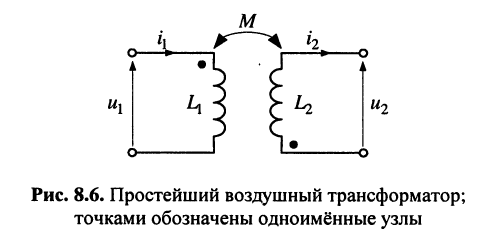
Простейший воздушный трансформатор без потерь (рис. 8.6) состоит из двух индуктивно связанных элементов индуктивности 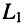
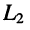
Напряжения и токи на внешних зажимах этих индуктивностей связаны соотношениями:
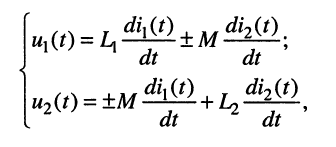
где М — взаимная индуктивность между элементами 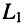
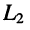
Коэффициент к называется коэффициентом связи; он характеризует степень магнитной связи между элементами 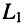
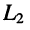
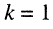
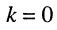
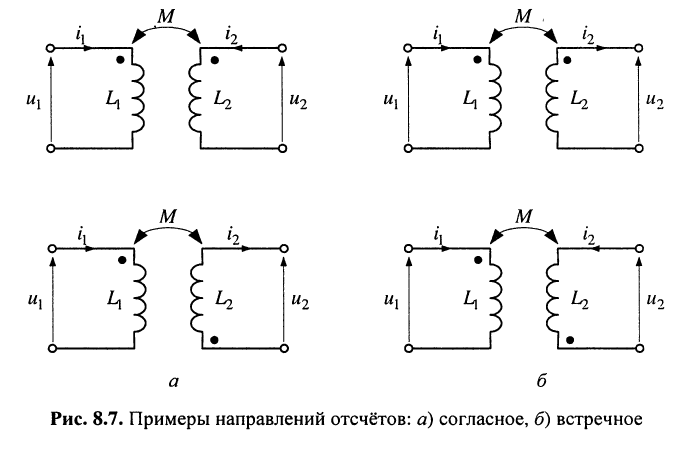
Знаки в равенствах (8.36) зависят от направлений магнитных потоков в индуктивностях, а сами магнитные потоки зависят от направлений токов, проходящих через индуктивности. На схемах зажимы индуктивностей, через которые положительные частицы проходят в одном и том же направлении (к индуктивности или от неё), помечаются точками. Такие зажимы (узлы) называются одноимёнными. Одинаково ориентированные относительно одноимённых узлов токи создают складывающиеся потокосцепления. Поскольку в задачах анализа направления токов в индуктивностях выбираются независимо и произвольно, различают согласное и встречное направления отсчётов токов и напряжений. В уравнениях (8.36) согласному направлению соответствует знак “+”, а встречному — знак “-“. Варианты согласного и встречного выбора направлений отсчётов токов представлены на рис. 8.7.
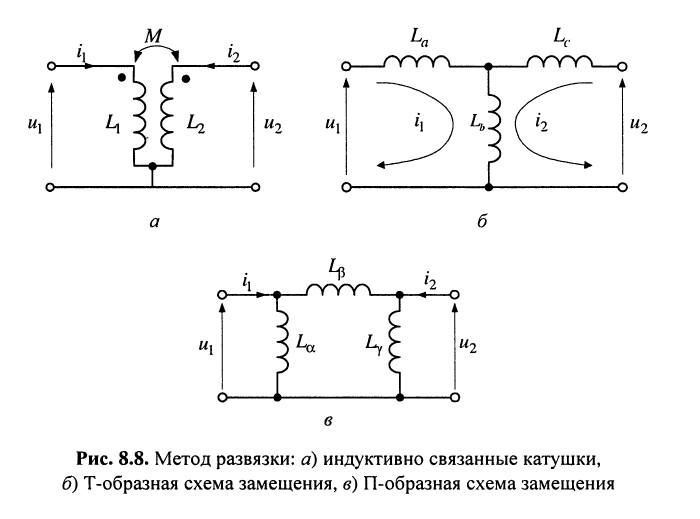
Метод развязки индуктивных связей
Для составления уравнений цепи, содержащей индуктивные связи, используют такие схемы их замещения, в которых индуктивные связи отсутствуют. Метод, приводящий к таким схемам замещения, называют методом развязки индуктивных связей.
Рассмотрим наиболее важный для практики случай, когда взаимодействующие катушки имеют один общий узел (рис. 8.8, а). Любая схема замещения, исходя из (8.36), составляется только из элементов индуктивности, число которых должно равняться как минимум трём, поскольку уравнения содержат три коэффициента:
Воспользуемся схемой замещения рис. 8.8, б, для которой запишем систему контурных уравнений:
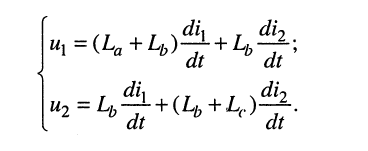
Полученная система не будет отличаться от системы (8.36) при условии:
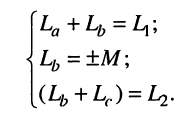
Таким образом, схема рис. 8.8, б является схемой замещения двух связанных магнитным потоком индуктивностей, если значения элементов этой схемы равны:
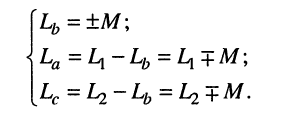
В формулах (8.39) следует выбирать нижние знаки лишь в том случае, когда только один из двух соединённых в узел зажимов цепи рис. 8.8, а помечен точкой. В других случаях необходимо выбирать нижние знаки. Полученная схема называется Т-образной схемой замещения.
Важно:
при жёсткой связи, когда 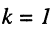
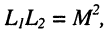
откуда после приведения подобных членов получаем, что значения индуктивностей Т-образной схемы замещения удовлетворяют соотношению
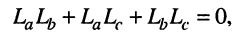
которое может выполняться, если одна из индуктивностей схемы замещения является отрицательной. Если связь не является жёсткой, т. е. 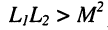
что также не исключает возможности появления отрицательной индуктивности. На пассивных элементах отрицательная индуктивность физически не осуществима, однако её наличие в схеме замещения не противоречит задаче анализа колебаний в цепи и способствует решению этой задачи.
Применяется также и другая схема замещения (рис. 8.8, в), называемая П-образной. Соотношения между элементами исходной схемы (рис. 8.8, a) и схемы замещения
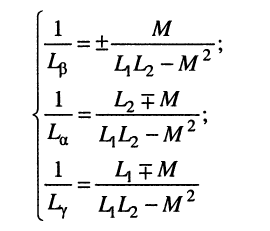
можно найти, если для рис. 8.8, в составить систему из двух узловых уравнений. Знаки в этих формулах выбираются по тому же правилу, что и в (8.39). В рассмотренной схеме замещения также возможно появление одной отрицательной индуктивности.
Символический метод расчета электрических цепей переменного тока
Действия над комплексными числами:
Символический метод нашел широкое применение для расчета сложных цепей переменного тока.
Символический метод расчета основан на использовании комплексных чисел.
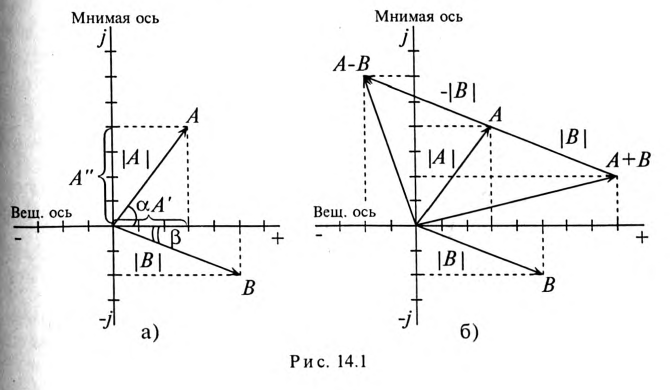
Комплексное число А состоит из вещественной 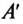
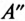
Комплексное число на комплексной плоскости можно представить вектором. Проекция вектора на вещественную ось (ось абсцисс) соответствует вещественной части комплексного числа 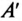
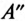
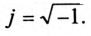
Комплексным числам 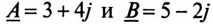
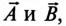
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Из построения (рис. 14.1а) видно, что модули комплексных чисел определяются выражением
Следовательно,
Углы 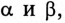
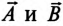
Аргументы комплексного числа (рис. 14.1а) определяются выражением
То есть
Как видно, аргумент комплексного числа 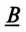
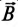
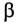
Существует три формы записи комплексного числа:
1) алгебраическая:
2)тригонометрическая:
так как
3) показательная:
где 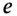
Для перевода из показательной формы записи комплексного числа в алгебраическую пользуются тригонометрической формой записи комплексного числа (14.4).
Для перевода из алгебраической формы записи комплексного числа в показательную определяют модуль по (14.1) и аргумент по (14.2) комплексного числа.
Для перевода комплексного числа из одной формы в другую можно использовать логарифмическую линейку или микрокалькулятор.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производится только в алгебраической форме
На рис. 14.16 видно, что сложение и вычитание комплексных чисел соответствует сложению и вычитанию векторов, изображающих эти числа.
Умножение и деление комплексных чисел можно производить 5 алгебраической форме:
Для того чтобы избавиться от комплексов в знаменателе, числитель и знаменатель умножают на комплекс, сопряженный с комплексом знаменателя. У сопряженного комплекса знак перед мнимой единицей 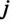
Произведение двух сопряженных комплексов — вещественное число, равное сумме квадратов вещественной и мнимой частей этих комплексов.
Однако умножение и деление комплексных чисел удобно производить в показательной форме.
При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются алгебраически:
При делении комплексных чисел в показательной форме модули этих чисел делятся, а аргументы вычитаются с учетом знаков:
Таким образом, сложение и вычитание комплексных чисел можно производить только в алгебраической форме, а умножение и деление удобней и проще производить в показательной форме.
Ток, напряжение и сопротивление в комплексном виде
Если ток и напряжение изменяются по синусоидальному закону 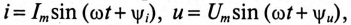
где 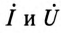
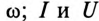
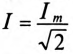
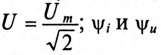
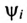
Для неразветвленной цепи с 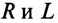
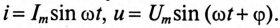
Комплекс полного сопротивления цепи 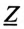
Комплексные величины, не зависящие от времени, обозначаются прописными буквами с черточкой внизу.
Модулем комплекса полного сопротивления является кажущееся сопротивление цепи 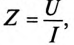
Алгебраическая форма записи комплекса полного сопротивления
Вещественная часть комплекса полного сопротивления есть активное сопротивление R, а коэффициент при мнимой единице j -реактивное сопротивление X. Знак перед поворотным множителем (мнимой единицей) указывает на характер цепи. Знак «плюс» соответствует цепи индуктивного характера, а знак «минус» – цепи емкостного характера.
Выражения комплексов сопротивлений различных цепей приедены в Приложении 7.
Обратная величина комплекса сопротивления — комплекс проводимости
Любую цепь переменного тока можно рассчитывать по заколам постоянного тока, если все величины представить в комплексной форме. В этом и заключается достоинство символического года расчета.
Мощность в комплексном виде
Для неразветвленной цепи с 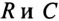
Комплексы напряжения и тока соответственно равны
Комплекс полной мощности цепи 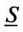
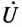
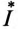
Таким образом, модулем комплекса полной мощности 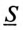
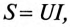
Если комплекс полной мощности 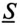
То есть вещественная часть комплекса полной мощности — активная мощность Р, а коэффициент при мнимой единице — реактивная мощность Q.
Знак перед поворотным множителем j указывает на характер цепи. В рассматриваемой цепи реактивная мощность емкостного характера
Комплексы величин токов, напряжений, сопротивлений, мощностей и других параметров цепи синусоидального тока необходимо выражать в двух видах записи комплексного числа: показательной и алгебраической. В этом случае сразу определяются действующие значения тока, напряжения, кажущееся сопротивление, его активные и реактивные части 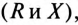
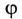
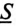
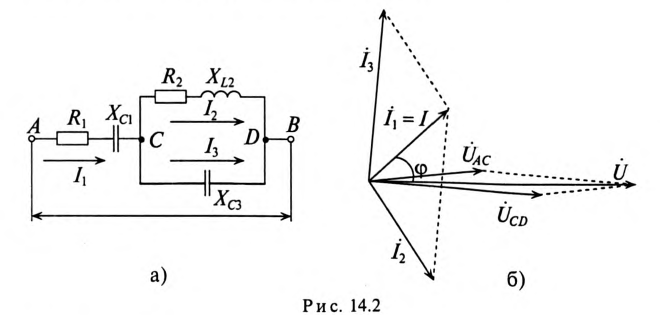
Пример 14.1
Для цепи, изображенной на рис. 14.2а, дано:
Определить токи 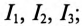
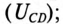
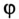
Построить векторную диаграмму цепи.
Решение
Комплексы сопротивлений участков (по номерам токов) и полного сопротивления цепи будут равны
Комплекс сопротивления участка CD цепи:
Тогда полное сопротивление цепи равно
Вектор заданной величины (тока или напряжения) можно направить в любом направлении. Однако удобнее совмещать его с вещественной или мнимой осью.
В рассмотренном примере заданное напряжение направляется по вещественной оси. Таким образом, комплекс общего напряжения будет равен
Комплекс тока цепи 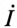
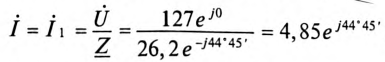
Комплекс напряжения на участке АС:
Комплекс напряжений на участке CD:
Комплексы токов
Комплекс полной мощности цепи:
Из расчета цепи (рис. 14.2а) символическим методом следует:
Характер цепи емкостной, так как угол 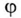
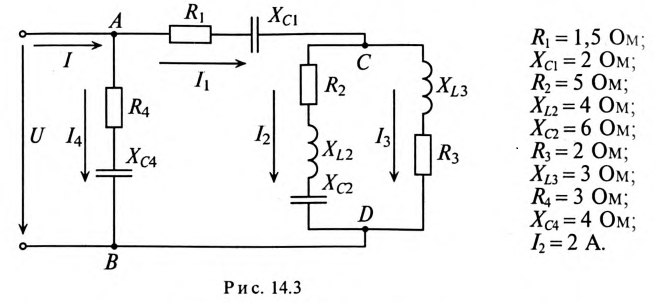
Пример 14.2
Для цепи, изображенной на рис. 14.3, дано:
Определить токи 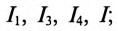
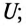
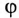
Решение
Комплексы сопротивлений участков (по номерам токов):
Вектор заданного тока 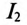
Комплекс напряжения на участке СD:
Значение токов будут равны соответственно
Комплекс напряжения на участке АС:
Комплекс напряжения на участке АВ, т. е. напряжение сети, равен
Комплекс тока
Комплекс тока цепи:
Комплекс полной мощности цепи:
Результаты расчета:
Характер цепи емкостной.
Пример 14.3
По условиям примера 14.2 определить полное сопротивление цепи (рис. 14.3).
Решение
Результаты расчета: полное сопротивление цепи (рис. 14.3) 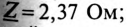
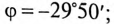
Погрешность 10′ при расчете угла 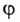
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Цепи с взаимной индукцией
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
- Цепи переменного тока























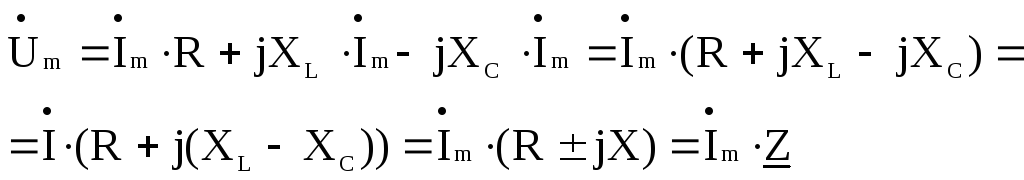























































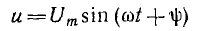
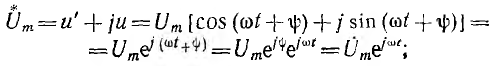
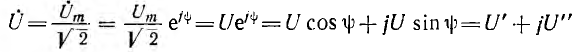
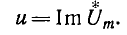
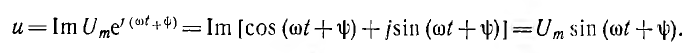
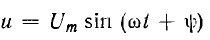
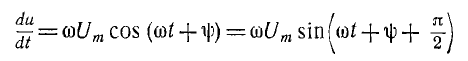
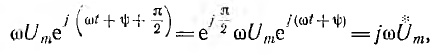
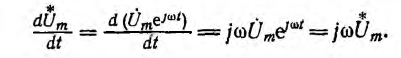
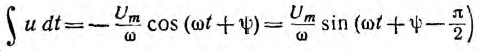
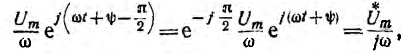
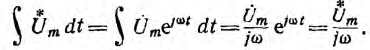
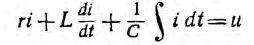
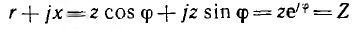
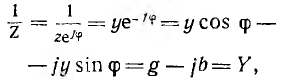
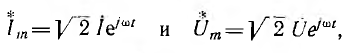
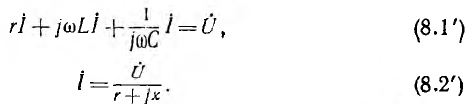
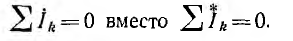
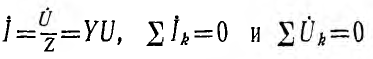
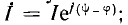
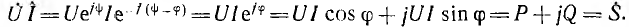
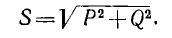
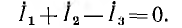
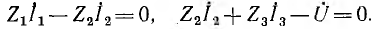
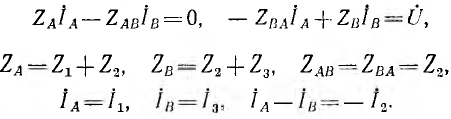
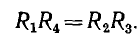
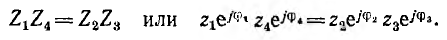
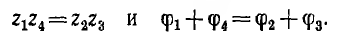
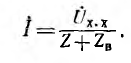
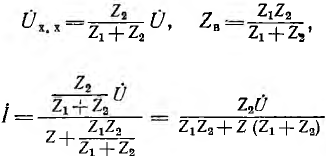
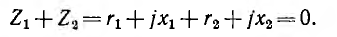
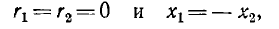
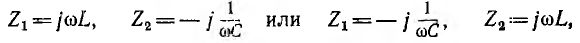
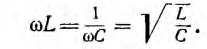
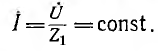
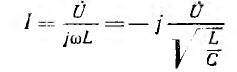
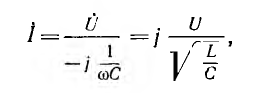
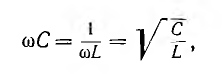
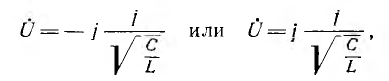
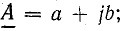
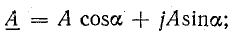
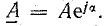
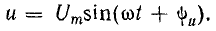

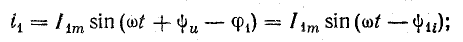
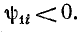
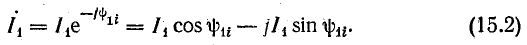
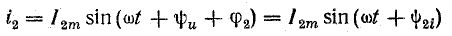
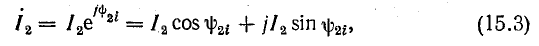
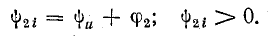
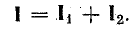
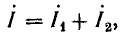
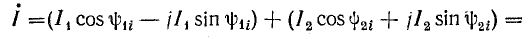
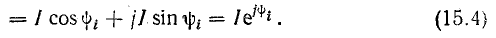
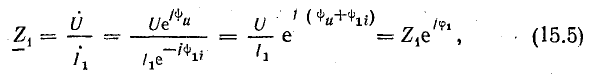
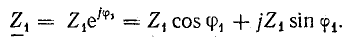

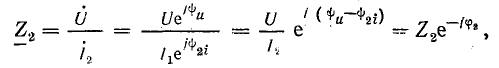
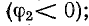
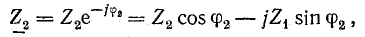

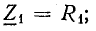
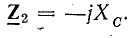
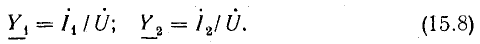

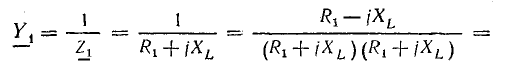
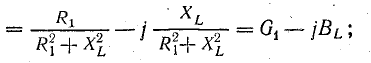
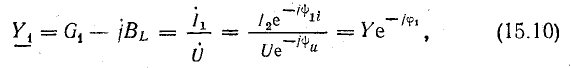
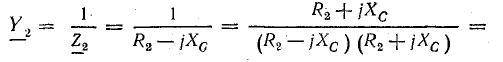
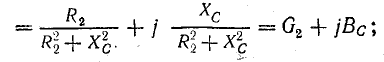
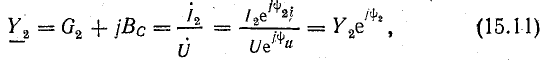
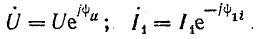
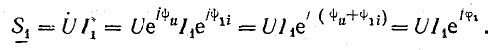
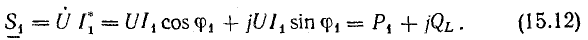
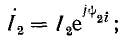
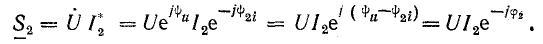
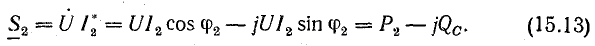
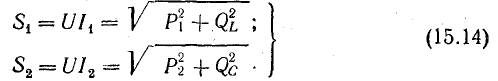

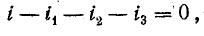
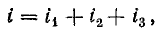
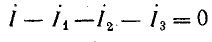
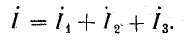

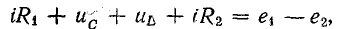
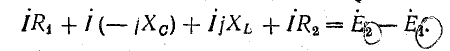
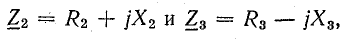
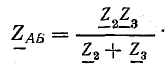
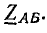
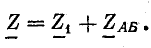
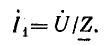
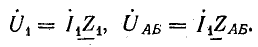
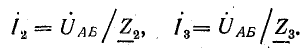



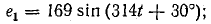
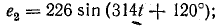
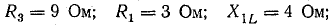
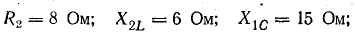
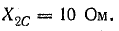
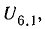
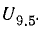
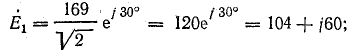
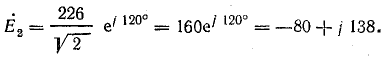
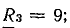
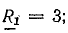
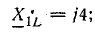
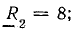
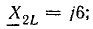
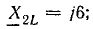
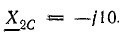
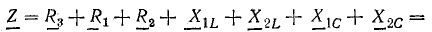
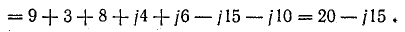
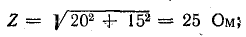
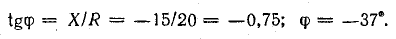
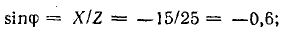
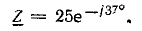
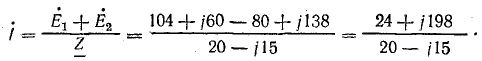
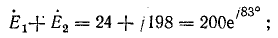
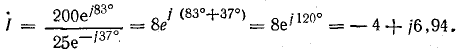
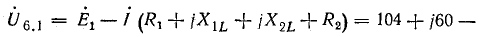
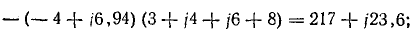
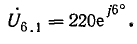
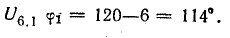
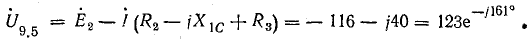
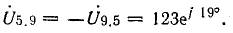
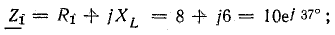
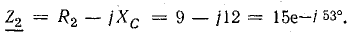
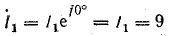

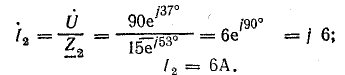
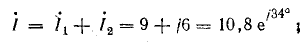
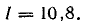
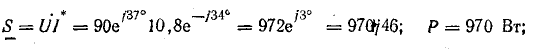
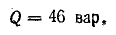
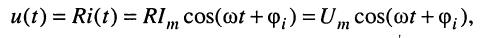
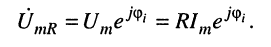
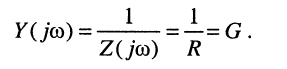
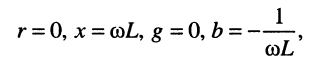
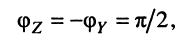
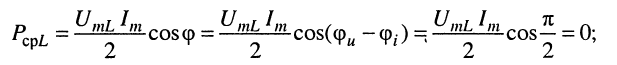

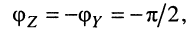
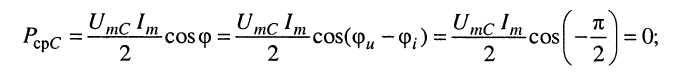
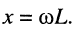
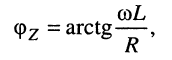
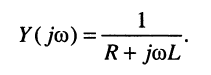
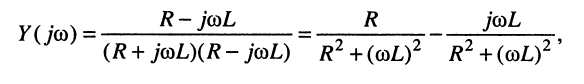
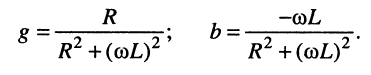
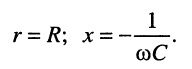
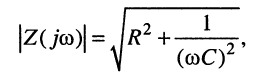
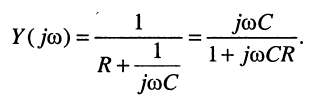
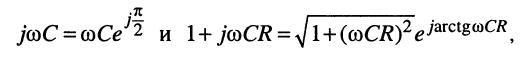
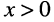 , то говорят, что сопротивление двухполюсника имеет индуктивный характер (на входе двухполюсника колебания напряжения опережают по фазе колебания тока); при этом на частоте
, то говорят, что сопротивление двухполюсника имеет индуктивный характер (на входе двухполюсника колебания напряжения опережают по фазе колебания тока); при этом на частоте 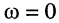 сопротивление двухполюсника является чисто активным и равным R, поскольку сопротивление элемента индуктивности при постоянном токе равно нулю, т. е. индуктивность представляет собой короткое замыкание, а при
сопротивление двухполюсника является чисто активным и равным R, поскольку сопротивление элемента индуктивности при постоянном токе равно нулю, т. е. индуктивность представляет собой короткое замыкание, а при 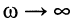 сопротивление двухполюсника стремится к поскольку сопротивление элемента индуктивности стремится к бесконечности, т. е. индуктивность представляет собой разрыв цепи;
сопротивление двухполюсника стремится к поскольку сопротивление элемента индуктивности стремится к бесконечности, т. е. индуктивность представляет собой разрыв цепи;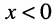 , то говорят, что сопротивление двухполюсника имеет ёмкостной характер (на входе двухполюсника колебания напряжения отстают по фазе от колебаний тока); при этом на частоте
, то говорят, что сопротивление двухполюсника имеет ёмкостной характер (на входе двухполюсника колебания напряжения отстают по фазе от колебаний тока); при этом на частоте 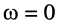 сопротивление двухполюсника стремится к
сопротивление двухполюсника стремится к 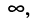 поскольку сопротивление ёмкости стремится к бесконечности, т. е. ёмкость представляет собой разрыв цепи; а при
поскольку сопротивление ёмкости стремится к бесконечности, т. е. ёмкость представляет собой разрыв цепи; а при  сопротивление двухполюсника становится равным R, поскольку сопротивление ёмкости стремится к нулю, т. е. ёмкость представляет собой короткое замыкание.
сопротивление двухполюсника становится равным R, поскольку сопротивление ёмкости стремится к нулю, т. е. ёмкость представляет собой короткое замыкание.