С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.
Cоставляем матрицу смежности A(D) размерности ![]() (N− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины Vi и входящая в Vj, то элемент матрицы смежности, стоящий на пересечении I-той строки и J-того столбца равен 1, иначе – 0.).
(N− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины Vi и входящая в Vj, то элемент матрицы смежности, стоящий на пересечении I-той строки и J-того столбца равен 1, иначе – 0.).
Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.
Алгоритм выделения компонент сильной связности
1. Присваиваем P=1 (P − количество компонент связности), ![]() .
.
2. Включаем в множество вершин Vp Компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то P– количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем P=P+1 и переходим к п. 2.
Пример
Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин N=5.

Рис. 6.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
 .
.
Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:
 ,
,  ,
,
 ,
,
Следовательно,

 .
.
Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:
 .
.
Присваиваем P=1 ![]() и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины
и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины ![]() .
.
Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине V1, чтобы получить матрицу S2(D):
 .
.
Присваиваем P=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть ![]() . Составляем матрицу смежности для компоненты сильной связности
. Составляем матрицу смежности для компоненты сильной связности ![]() исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
 .
.
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:
![]()
И присваиваем P=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины ![]() .
.
Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
| < Предыдущая | Следующая > |
|---|
Поиск компонент сильной связности: алгоритм Косарайю
Время на прочтение
2 мин
Количество просмотров 33K
На хабре нет ни одной статьи о поиске компонент сильной связности. Однако это интересная задача, имеющая приложения в самых разных сферах: системах рекомендаций, математической логике и, неожиданно, экологии. Ниже формулировка задачи и решение — алгоритм Косарайю.
К делу:

Заметим: отношение сильной связности — это отношение эквивалентности.
Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности.

Алгоритм Косарайю
- Инвертированием ориентированного графа назовем процедуру, в ходе которой поменяем направление каждого ребра на противоположное.
Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования.
Пусть дан ориентированный граф G = (V, E). Через G’ = (V, E’) обозначим интертирование G.
Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0…|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1.

Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G’. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности.

Время работы
Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices.
Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices.
Дополнительно
Корректность алгоритма и псевдокод можно посмотреть тут: www.jeffreykarres.com/blog/kosaraju
В начале статьи я упоминал приложения.
- На SO писали про использование этого алгоритма для формальной верификации:
stackoverflow.com/questions/11212676/what-are-strongly-connected-components-used-for - А про экологию можно почитать в статье:
www.nceas.ucsb.edu/~allesina/PDF/Allesina2005.pdf
Ориентированный граф (орграф) называется сильно связным (англ. strongly connected), если любые две его вершины s и t сильно связны, то есть если существует ориентированный путь из 



Компонентами сильной связности орграфа называются его максимальные по включению сильно связные подграфы. Областью сильной связности называется множество вершин компонентов сильной связности.
Определения[править | править код]
Орграф, не принадлежащий к классу сильно связных графов, содержит некоторый набор сильно связных компонент, и некоторый набор ориентированных рёбер, идущих от одной компоненты к другой.
Любая вершина орграфа сильно связна сама с собой.
Алгоритмы[править | править код]
Простейший алгоритм решения задачи о поиске сильно связных компонент в орграфе работает следующим образом:
- При помощи транзитивного замыкания проверяем, достижима ли
из
и
из
для всех пар
и
- Затем определяем такой неориентированный граф, в котором для каждой такой пары содержится ребро.
- Поиск компонент связности такого неориентированного графа даёт компоненты сильной связности орграфа.
Очевидно основное время работы данного алгоритма занимает транзитивное замыкание.
Также существует три алгоритма, решающих данную задачу за линейное время, то есть в V раз быстрее, чем приведённый выше алгоритм. Это алгоритмы Косарайю, поиска компонент сильной связности с двумя стеками и Тарьяна.
Пример[править | править код]
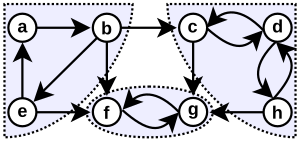
Ориентированный граф с показанными компонентами сильной связности
На рисунке изображён орграф, для которого показаны все три компоненты сильной связности (закрашенные области, обведённые пунктиром).
См. также[править | править код]
- Компонента связности графа
Литература[править | править код]
- Роберт Седжвик. Алгоритмы на графах = Graph algorithms. — 3-е изд. — Россия, Санкт-Петербург: «ДиаСофтЮП», 2002. — С. 496. — ISBN 5-93772-054-7.
Алгоритм выделения компонент сильной связности
1.
Присваиваем p=1
(p
− количество
компонент связности),
![]() .
.
2. Включаем в
множество вершин Vp
компоненты
сильной связности Dp
вершины, соответствующие единицам
первой строки матрицы Sp.
В качестве матрицы A(Dp)
возьмем подматрицу матрицы A(D),
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
Vp.
3. Вычеркиваем из
Sp
строки и столбцы, соответствующие
вершинам из Vp.
Если не остается ни одной строки (и
столбца), то p–
количество компонент сильной связности.
В противном случае обозначим оставшуюся
после вычеркивания срок и столбцов
матрицу как Sp+1,
присваиваем p=p+1
и переходим к п. 2.
Пример
Выделим
компоненты связности ориентированного
графа, изображенного на рис. 1. В данной
задаче количество вершин n=5.

Рис. 1.
Значит, для данного
ориентированного графа матрица смежности
будет иметь размерность 5×5 и будет
выглядеть следующим образом
 .
.
Найдем матрицу
достижимости для данного ориентированного
графа по формуле 1) из утверждения 3:
 ,
, ,
,
 ,
,
Следовательно,

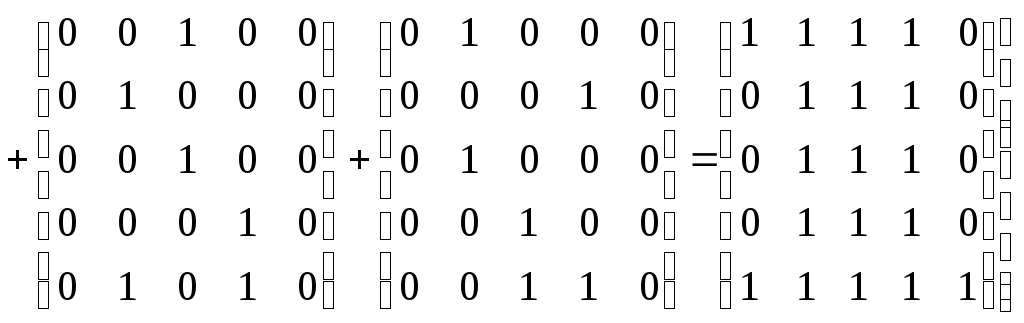 .
.
Таким образом,
матрица сильной связности, полученная
по формуле 2) утверждения 3, будет
следующей:
 .
.
Присваиваем
p=1
![]() и составляем множество вершин первой
и составляем множество вершин первой
компоненты сильной связностиD1:
это те вершины, которым соответствуют
единицы в первой строке матрицы S(D).
Таким образом, первая компонента сильной
связности состоит из одной вершины
![]() .
.
Вычеркиваем из
матрицы S1(D)
строку и столбец, соответствующие
вершине v1,
чтобы получить матрицу S2(D):
 .
.
Присваиваем p=2.
Множество вершин второй компоненты
связности составят те вершины, которым
соответствуют единицы в первой строке
матрицы S2(D),
то есть
![]() .
.
Составляем матрицу смежности для
компоненты сильной связности![]() исходного графаD
исходного графаD
− в ее
качестве возьмем подматрицу матрицы
A(D),
состоящую из элементов матрицы A,
находящихся на пересечении строк и
столбцов, соответствующих вершинам из
V2:
 .
.
Вычеркиваем из
матрицы S2(D)
строки и столбцы, соответствующие
вершинам из V2
,чтобы получить матрицу S3(D),
которая состоит из одного элемента:
![]()
и присваиваем p=3.
Таким образом, третья компонента сильной
связности исходного графа, как и первая,
состоит из одной вершины
![]() .
.
Таким образом,
выделены 3 компоненты сильной связности
ориентированного графа D:
|
D1:
|
D2:
|
D3:
|
Задание 2.
Расстояния в ориентированном графе
С помощью алгоритма
фронта волны найти расстояния в
ориентированном графе D:
диаметр, радиус и центры.
Пусть
![]() ориентированный граф сn³2
ориентированный граф сn³2
вершинами и v,w
(v¹w)
– заданные вершины из V.
Алгоритм поиска минимального пути из вв ориентированном графе
(алгоритм
фронта волны).
-
Помечаем вершину
 индексом 0, затем помечаем вершиныÎ
индексом 0, затем помечаем вершиныÎ
образу вершины
 индексом 1. Обозначаем ихFW1
индексом 1. Обозначаем ихFW1
(v).
Полагаем k=1. -
Если
 илиk=n-1,
илиk=n-1,
и одновременно то вершина
то вершина не достижима из
не достижима из .
.
Работа алгоритма заканчивается.
В
противном случае продолжаем:
-
Если
 ,
,
то переходим к шагу 4.
В
противном случае мы нашли минимальный
путь из
![]() в
в![]() и его длина равнаk.
и его длина равнаk.
Последовательность вершин

есть
этот минимальный путь. Работа завершается.
-
Помечаем
индексом k+1
все непомеченные вершины, которые
принадлежат образу множества вершин
c
индексом k.
Множество вершин с индексом k+1
обозначаем
 .
.
Присваиваемk:=k+1
и переходим к 2).
Замечания
Чтобы найти
расстояния в ориентированном графе,
необходимо составить матрицу минимальных
расстояний R(D)между
его вершинами. Это квадратная матрица
размерности
![]() ,
,
элементы главной диагонали которой
равны нулю (![]() ,i=1,..,n).
,i=1,..,n).
Сначала составляем
матрицу смежности. Затем переносим
единицы из матрицы смежности в матрицу
минимальных расстояний (![]() ,
,
если![]() ).
).
Далее построчно заполняем матрицу
следующим образом.
Рассматриваем
первую строку, в которой есть единицы.
Пусть это строка − i-тая
и на пересечении с j-тым
столбцом стоит единица (то есть
![]() ).
).
Это значит, что из вершины![]() можно попасть в вершину
можно попасть в вершину![]() за один шаг. Рассматриваемj-тую
за один шаг. Рассматриваемj-тую
сроку (строку стоит вводить в рассмотрение,
если она содержит хотя бы одну единицу).
Пусть элемент
![]() .
.
Тогда из вершины![]() в вершину
в вершину![]() можно попасть за два шага. Таким образом,
можно попасть за два шага. Таким образом,
можно записать![]() .
.
Следует заметить, что если в рассматриваемых
строках две или более единиц, то следует
прорабатывать все возможные варианты
попадания из одной вершины в другую,
записывая в матрицу длину наикратчайшего
из них.
Примечание: В
контрольной работе самый длинный путь
найти при помощи алгоритма фронта волны.
Пример
Найдем
расстояния в ориентированном графе D,
изображенном на рис. 2. В данной задаче
количество вершин n=7,
следовательно, матрицы смежности и
минимальных расстояний между вершинами
ориентированного графа D
будут иметь
размерность 7×7.

Рис.72.
Матрица смежности:
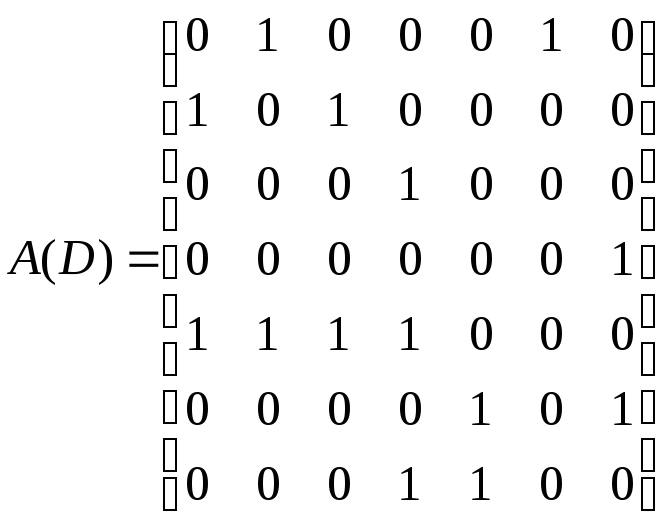 .
.
Начинаем
заполнять матрицу R(D)
минимальных расстояний: сначала ставим
нули по главной диагонали
и rij=aij,
если aij=1,
(т.е. переносим единицы из матрицы
смежности). Рассматриваем первую строку.
Здесь есть две единицы, то есть из первой
вершины за один шаг можно попасть во
вторую и шестую. Из второй вершины можно
попасть за один шаг в третью (путь в
первую вершину нас не интересует),
следовательно, можно записать
![]() .
.
Из шестой вершины можем добраться за
один шаг в пятую и седьмую, а значит,![]() ,
,![]() .
.
Теперь ищем маршруты, исходящие из
первой вершины, состоящие из 3 шагов: за
2 шага идем в третью вершину, оттуда за
один шаг попадаем в четвертую, поэтому![]() .
.
В итоге получаем следующую матрицу:

Таким образом,
диаметром исследуемого ориентированного
графа будет
![]() .
.
Для каждой вершины
заданного ориентированного графа найдем
максимальное удаление (эксцентриситет)
в графе G
от вершины нее по формуле, которая была
приведена выше
![]() :r(vi)
:r(vi)
− максимальное из расстояний, стоящих
в i-той
строке. Таким образом,
r(v1)=3,
r(v2)=3,
r(v3)=5,
r(v4)=4,
r(v5)=2,
r(v6)=2,
r(v7)=3.
Значит, радиусом
графа G
будет
![]()
Соответственно,
центрами графа
G
будут вершины
v5
и v6
, так как величины их эксцентриситетов
совпадают с величиной радиуса![]() .
.
Опишем теперь
нахождение минимального пути из вершины
v3
в вершину v6
по алгоритму фронта волны. Обозначим
вершину v3
как V0,
а вершину v6
–
как W
(см. рис. 3). Множество вершин, принадлежащих
образу V0,
состоит из одного элемента –
это вершина v4,
которую, согласно алгоритму, обозначаем
как V1:
FW1(v3)={v4}.
Поскольку искомая вершина не принадлежит
фронту волны первого уровня
![]() ,
,
продолжаем работу алгоритма. Строим
фронт волны второго уровня-
это множество вершин, принадлежащих
образу вершины
V1:
FW2(v3)={v7},
обозначаем v7≡V2.
В образ вершины V2
входят две вершины –
v5
и v4,
но, так как v4
уже была помечена как V0,
то фронт волны третьего уровня состоит
из одного элемента: FW3(v3)={v5},
v5≡V3.
Из непомеченных вершин в образ вершины
V3
входят v1
и v2,
соответственно, FW4(v3)={v1,
v2},
v1≡V4,
v2≡V4.
Теперь помечены все вершины, кроме v6,
которая входит в образ вершины
![]() ,
,
то естьFW5(v3)={v6≡W},
работа алгоритма закончена. Минимальный
путь (5 шагов) из вершины v3
в вершину v6
выглядит так: v3
v4
v7
v5
v1
v6.

Рис.3.
Соседние файлы в папке Diskretnaya_matematika
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1 Алгоритм
- 2 Доказательство корректности алгоритма
- 3 Время работы алгоритма
- 4 Псевдокод
- 5 Источники информации
Алгоритм
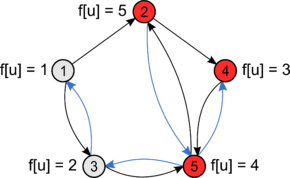
Вершины 2, 4, 5 сильносвязаны.
Синим цветом обозначен обод DFS по инвертированным ребрам
Компоненты сильной связности в графе можно найти с помощью поиска в глубину в 3 этапа:
- Построить граф с обратными (инвертированными) рёбрами
- Выполнить в поиск в глубину и найти — время окончания обработки вершины
- Выполнить поиск в глубину в , перебирая вершины во внешнем цикле в порядке убывания
Полученные на 3-ем этапе деревья поиска в глубину будут являться компонентами сильной связности графа .
Так как компоненты сильной связности и графа совпадают, то первый поиск в глубину для нахождения можно выполнить на графе , а второй — на .
Доказательство корректности алгоритма
| Теорема: |
|
Вершины и взаимно достижимы после выполнения алгоритма они принадлежат одному дереву обхода в глубину. |
| Доказательство: |
|
Если вершины и были взаимно достижимы в графе , то на третьем этапе будет найден путь из одной вершины в другую, это означает, что по окончанию алгоритма обе вершины лежат в одном поддереве.
Значит, из случая 2.1 и не существования случая 2.2 получаем, что вершины и взаимно достижимы в обоих графах. |
Время работы алгоритма
- Для того, чтобы инвертировать все ребра в графе, представленном в виде списка потребуется действий. Для матричного представления графа не нужно выполнять никакие действия для его инвертирования.
- Количество ребер в инвертированном равно количеству ребер в изначальном графе, поэтому поиск в глубину будет работать за
- Поиск в глубину в исходном графе выполняется за .
В итоге получаем, что время работы алгоритма .
Псевдокод
Пусть — исходный граф, —инвертированный граф. В массиве будем хранить номера вершин в порядке окончания обработки поиском в глубину в графе . В результате получаем массив , который каждой вершине сопоставляет номер её компоненты.
function dfs1(v):
color[v] = 1
for (v, u) in E
if not visited[u]
dfs1(G[v][u])
Добавляем вершину v в конец списка ord
function dfs2(v):
component[v] = col
for (v, u) in E
if (вершина u еще не находится ни в какой компоненте)
dfs2(H[v][u])
function main():
считываем исходные данные, формируем массивы G и H
for u in V
if not visited[u]
dfs1(u)
col = 1
for (по всем вершинам u списка ord[] в обратном порядке)
if (вершина u не находится ни в какой компоненте)
dfs2(u)
col++
Источники информации
- Р.Седжвик. “Фундаментальные алгоритмы на С++. Алгоритмы на графах” – СПб, ДиаСофтЮП, 2002
- MAXimal :: algo :: Поиск компонент сильной связности, построение конденсации графа
- Визуализация поиска компонент сильной связности




