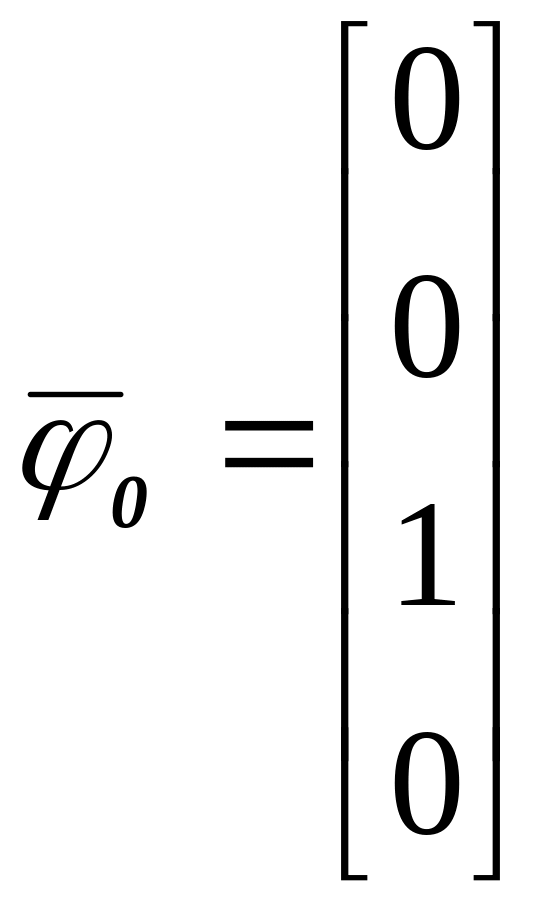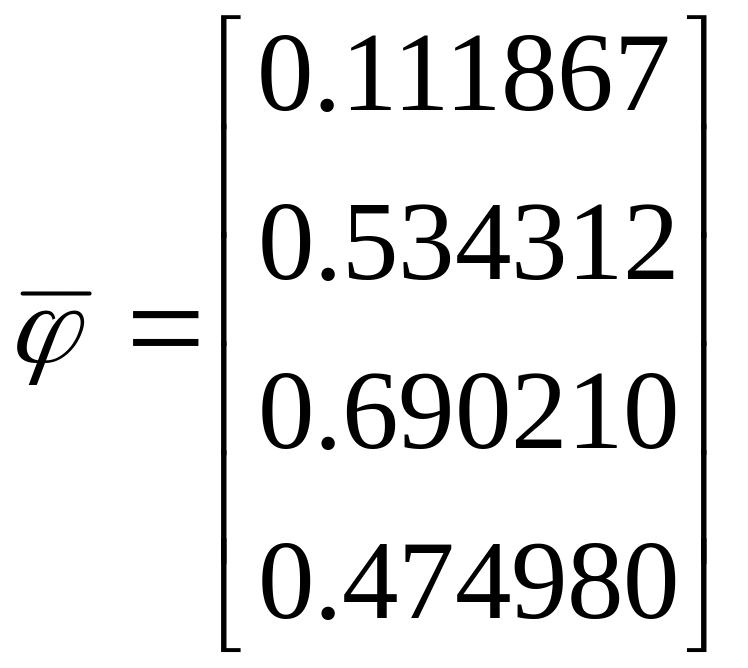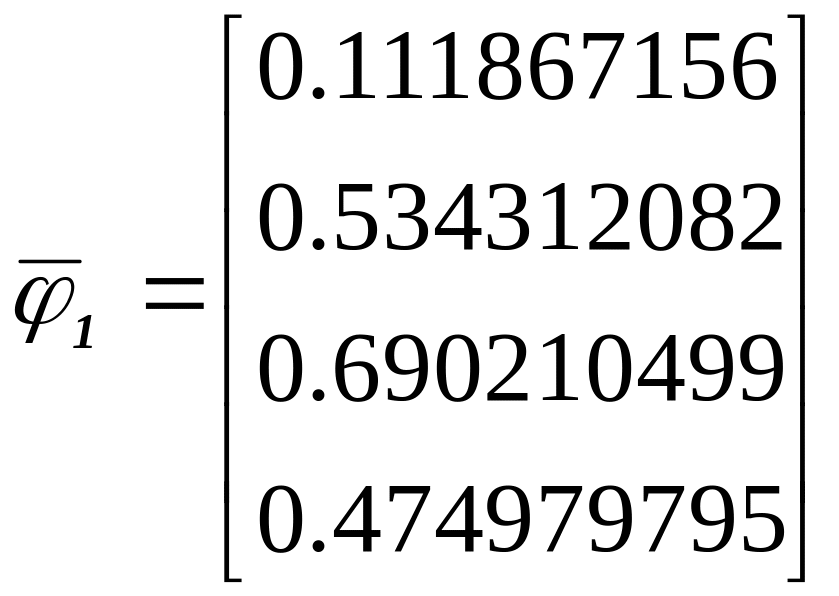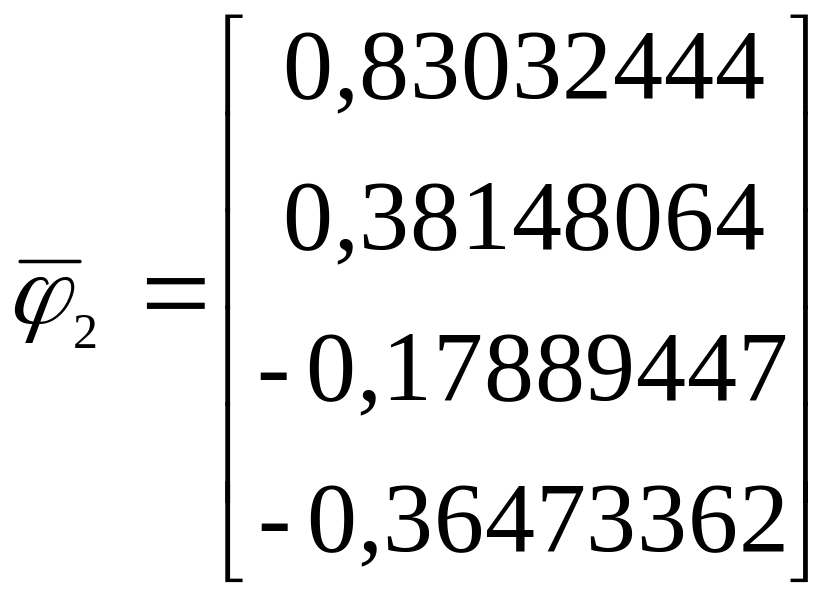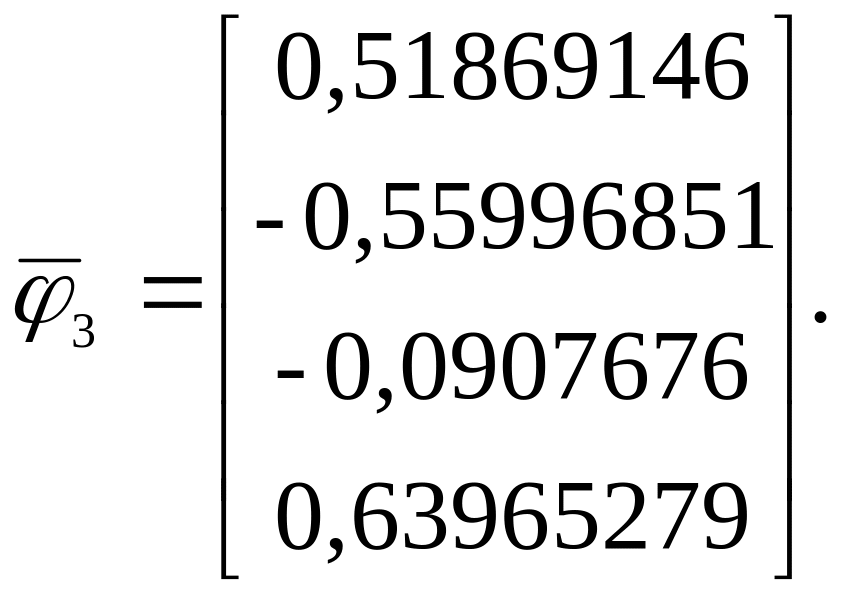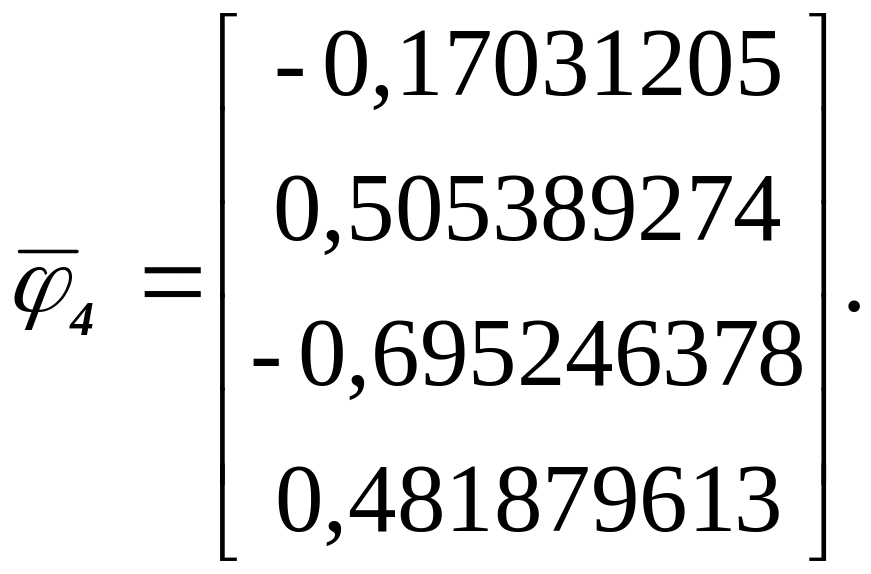Как найти компоненты собственного вектора

Найдем такие вектора (называются собственными векторами) v
и такие числа – значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.

Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.

Где учитесь?

Для правильного составления решения, укажите:

Собственные векторы матрицы

Онлайн калькулятор нахождение собственных чисел и собственных векторов – Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

Собственные числа, собственные векторы матриц и квадратичные формы

Проблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах математики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции).

Пусть задана квадратная матрица А размера (n X п), элементами которой являются действительные числа (R) и вектор неизвестных X размера (n X 1):

Предположим, что X — это некоторое неизвестное действительное число.

Если X и ненулевой вектор X удовлетворяют уравнению

то X называется собственным числом или собственным значением матрицы А, а X — собственным вектором этой же матрицы, соответствующим X.

Преобразуем уравнение (2.15) к следующему виду:

где Е — единичная матрица.

называется характеристической матрицей.

Так как по условию вектор неизвестных X не равен нулю, то среди его координат х , х₂, . х_п должна быть хотя бы одна ненулевая. А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли).

Число X = X_fc, где к = 1, п будет собственным числом только в том случае, если матрица (Х_кЕ -А) — вырожденная.

Уравнение (2.17) называется характеристическим уравнением матрицы А и представляет собой алгебраическое уравнение степени п относительно X:

Уравнение (2.18) имеет п корней X_v Х₂, Х_п. Множество всех корней уравнения (2.18) называется спектром матрицы А.

Заметим, что уравнение det (А – ХЕ) = 0 имеет те же корни, что и уравнение (2.17), т. е.

Каждому собственному значению спектра матрицы А ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя. Если Х_к есть кратный корень характеристического уравнения, то для произвольной квадратной матрицы число соответствующих собственных векторов может быть не равно кратности корня. С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменяется и вдоль которого пространство испытывает растяжение или сжатие в X раз.

Полином Х п + р^” -1 + . + р_п = 0 называют характеристическим полиномом. Коэффициенты р_к (k = 1, п) можно вычислить по следующим рекуррентным формулам [57]:

Здесь SpA = S а_кк — след матрицы (сумма элементов, стоя-

щих на главной диагонали матрицы А). Заметим, что р = (-1)” X X det А. При отыскании собственных чисел даже для матриц невысокого порядка неизбежно большое количество вычислений. Для общего случая нельзя предложить оптимальный способ нахождения собственных чисел и собственных векторов матрицы.

Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диагональная, либо верхняя или нижняя треугольная). В этом случае собственные числа ₂. _п совпадают с элементами главной диагонали исходной матрицы а_п, а₂₂. а_пп.

Пусть задана верхняя треугольная матрица А размера (n X п):

Отсюда видно, что собственные числа равны:

С появлением ЭВМ получили распространение итерационные методы нахождения собственных чисел, которые не используют вычисление характеристического полинома. К этим способам относятся: степенной метод, метод обратных итераций, QR-алгоритм, метод вращений Якоби, QL-алгоритм и др. Причем применение конкретного итерационного метода зависит от вида исходной матрицы А [4].

Теперь рассмотрим конкретные примеры.

Пример 2.8. Дана матрица А размера (3 X 3)

Найти собственные числа и собственные векторы матрицы А.

Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали

Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем уравнение (2.16).

Для Х₁ = -4 получаем

Далее раскроем матричное уравнение (2.20)

В результате получим

Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид:

т. е. получены искомые собственные вектора для Для Х₂ = Х₃ = 1 получаем

ил*

В результате получаем

т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для ₂.

Эти решения запишем в виде

Пример 2.9. Дана матрица А размера (2 X 2). Найти собственные числа и собственные матрицы А

Запишем характеристическое уравнение (2.17) для данного случая

Теперь найдем собственные векторы исходной матрицы А, соответствующие .₁ = 1 и Х₂ = -4.

В подробной записи получим

Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собственными векторами X_v которые мы и находим

Из первого уравнения системы получаем х₂ = 2x_v Из второго уравнения системы получаем х₂ = 2x_v т. е. она имеет бесконечное множество решений. И искомый собственный вектор Xj будет иметь вид

Аналогично, для Х₂ = -4 находим

В заключение приведем два полезных правила [38]:

1) сумма собственных чисел матрицы А равна следу этой матрицы, т. е.

2) произведение собственных чисел матрицы А равно определителю этой матрицы

Кратко рассмотрим квадратичные формы.

Квадратичной формой называется однородный многочлен второй степени от нескольких пременных. Обозначим их x_v х₂, . х .

Квадратичную форму в общем виде можно записать так:

В качестве примера рассмотрим квадратичную форму трех переменных:

Введем обозначения:

Тогда квадратичная форма примет вид

Дополнительно вводим симметричную матрицу В, вектор X.

В этом случае квадратичная форма примет вид

Последняя формула представляет собой матрично-векторный вид квадратичной формы.

А в общем случае получим:

где Ь..— коэффициенты при х 2 для всех i = 1, 2, n, a b’j = Ц_< равны полусуммам коэффициентов при элементах, содержащих произведения х. х. и х. х_< при всех г, j = 1, 2,п, г ^ j.

Матрица В является матрицей квадратичной формы.

В качестве примера запишем в матрично-векторном виде квадратичную форму

В данном случае получаем:

Матрица данной квадратичной формы принимает вид А ее матрично-векторная запись такова:

[spoiler title=”источники:”]

http://allcalc.ru/node/648

http://studref.com/549305/matematika_himiya_fizik/sobstvennye_chisla_sobstvennye_vektory_matrits_kvadratichnye_formy

[/spoiler]

Источник

Собственные векторы и собственные значения матрицы

Пусть — числовая квадратная матрица n-го порядка. Матрица A-lambda E называется характеристической для , а ее определитель $Delta_{A}(lambda)=det(A-lambda E)$ характеристическим многочленом матрицы

$A-lambda E=begin{pmatrix}a_{11}-lambda&cdots&a_{1n}\ vdots&ddots& vdots\ a_{n1}&cdots&a_{nn}-lambdaend{pmatrix}!,quad Delta_{A}(lambda)=det(A-lambda E)= begin{vmatrix} a_{11}-lambda&cdots&a_{1n}\ vdots&ddots&vdots\ a_{n1}&cdots&a_{nn}-lambdaend{vmatrix}!.$

(7.12)

Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.

Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец $x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}$ , удовлетворяющий условию

Acdot x=lambdacdot x,

(7.13)

называется собственным вектором матрицы . Число lambda в равенстве (7.13) называется собственным значением матрицы . Говорят, что собственный вектор соответствует {принадлежит) собственному значению lambda .

Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде (A-lambda E)x=o , где — единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему линейных алгебраических уравнений с неизвестными x_1,x_2,ldots,x_n:

$begin{cases}(a_{11}-lambda)x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+(a_{22}-lambda)x_2+ldots+a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{n1}x_1+a_{2n}x_2+ldots+(a_{nn}-lambda)x_n=0. end{cases}$

(7.14)

Поскольку нас интересуют только нетривиальные решения (xne o) однородной системы, то определитель матрицы системы должен быть равен нулю:

$det(A-lambda E)=begin{vmatrix}a_{11}-lambda&a_{12}&cdots&a_{1n}\ a_{21}&a_{22}-lambda&cdots&a_{2n}\ vdots&vdots&ddots&vdots\ a_{n1}&a_{n2}& cdots&a_{nn}-lambda end{vmatrix}=0.$

(7.15)

В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена $Delta_{A}(lambda)=det(A-lambda E)$ матрицы . Уравнение $Delta_{A}(lambda)=0$ называется характеристическим уравнением матрицы . Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде

$Delta_{A}(lambda)= det(A-lambda E)= a_{n}(lambda-lambda_1)^{n_1}cdot (lambda-lambda_2)^{n_2}cdotldotscdot(lambda-lambda_k)^{n_k},$

где lambda_1,lambda_2,ldots,lambda_k — корни многочлена кратности n_1,n_2,ldots,n_k соответственно, причем n_1+n_2+ldots+n_k=n . Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.

Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.

Действительно, если число lambda — собственное значение матрицы , которому соответствует собственный вектор xne o , то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число lambda удовлетворяет характеристическому уравнению (7.15). Наоборот, если lambda — корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е. operatorname{rg}(A-lambda E)<n .В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец xne o , удовлетворяющий условию (7.14). Значит, lambda — собственное значение матрицы .

Свойства собственных векторов

Пусть — квадратная матрица n-го порядка.

1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.

В самом деле, пусть s_1 и s_2 — собственные векторы, соответствующие собственным значениям lambda_1 и lambda_2 , причем lambda_1ne lambda_2 . Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:

alpha_1cdot s_1+alpha_2cdot s_2=o.

(7.16)

Надо показать, что это равенство возможно только в тривиальном случае, когда alpha_1=alpha_2=0 . Действительно, умножая обе части на матрицу и подставляя As_1=lambda_1s_1 и As_2=lambda_2s_2 имеем

A(alpha_1s_1+alpha_2s_2)=oquad Leftrightarrowquad alpha_1As_1+ alpha_2As_2= oquad Leftrightarrowquad alpha_1 lambda_1s_1+alpha_2 lambda_2s_2=o.

Прибавляя к последнему равенству равенство (7.16), умноженное на (-lambda_2) , получаем

alpha_1cdotlambda_1cdot s_1-alpha_2cdotlambda_2cdot s_2=oquad Leftrightarrowquad alpha_1cdot(lambda_1-lambda_2)cdot s_1=o.

Так как s_1ne o и lambda_1ne lambda_2 , делаем вывод, что alpha_1=0 . Тогда из (7.16) следует, что и alpha_2=0 (поскольку s_2ne o ). Таким образом, собственные векторы s_1 и s_2 линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.

2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.

Действительно, если собственному значению lambda соответствуют собственные векторы s_1,ldots,s_k , то из равенств S_i=lambda s_i, i=1,ldots,k , следует, что вектор s=alpha_1s_1+ldots+alpha_ks_k также собственный, поскольку:

As=A(alpha_1s_1+ldots+alpha_ks_k)= alpha_1lambda s_1+ldots+alpha_klambda s_k=lambda(alpha_1s_1+ldots+alpha_ks_k)=lambda s.

3. Пусть $(A-lambda E)^{+}$ — присоединенная матрица для характеристической матрицы . Если lambda_0 — собственное значение матрицы , то любой ненулевой столбец матрицы $(A-lambda E)^{+}$ является собственным вектором, соответствующим собственному значению .

В самом деле, применяя формулу (7.7) имеем $(A-lambda E)(A-lambda E)^{+}=Delta_k(lambda)cdot E$ . Подставляя корень lambda_0 , получаем $(A-lambda_0E)(A-lambda_0E)^{+}=O$ . Если — ненулевой столбец матрицы $(A-lambda_0E)^{+}$ , то (A-lambda_0E)s=oLeftrightarrow As=lambda_0s . Значит, — собственный вектор матрицы .

Замечания 7.5

1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.

2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений lambda_1,lambda_2, ldots,lambda_k записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем

(A-lambda_1E)cdot x=o,quad (A-lambda_2E)cdot x=o,quad ldots,quad (A-lambda_kE)cdot x=o.

Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.

3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.

4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).

5. Для простого корня lambda=lambda_0 характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы (A-lambda_0E) по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы , является собственным вектором.

Нахождение собственных векторов и собственных значений матрицы

Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.

1. Составить характеристический многочлен матрицы Delta_A(lambda)=det(A-lambda E) .

2. Найти все различные корни lambda_1,lambda_2,ldots,lambda_k характеристического уравнения Delta_A(lambda)=0 (кратности n_1,n_2,ldots,n_k (n_1+n_2+ldots+n_k=n) корней определять не нужно).

3. Для корня lambda-lambda_1 найти фундаментальную систему $varphi_1,varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений

(A-lambda_1E)cdot x=o , где $r=operatorname{rg}(A-lambda_1E)$

Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).

4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению lambda_1:

$s_1=C_1varphi_1,quad s_2=C_2varphi_2,quad ldots,quad s_{n-r}=C_{n-r}varphi_{n-r},$

(7.17)

где $C_1,C_2,ldots,C_{n-r}$ — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению lambda_1 , образуют ненулевые столбцы вида $s=C_1varphi_1+C_2varphi_2+ldots+C_{n-r}varphi_{n-r}$ . Здесь и далее собственные векторы матрицы будем обозначать буквой .

Повторить пункты 3,4 для остальных собственных значений lambda_1,lambda_2,ldots,lambda_k .

Пример 7.8. Найти собственные значения и собственные векторы матриц:

$A=begin{pmatrix}1&-2\3&8end{pmatrix}!,quad B=begin{pmatrix}1&-4\ 1&1 end{pmatrix}!,quad C=begin{pmatrix}1&1&1\1&1&1\1&1&1end{pmatrix}!.$

Решение. Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{A}(lambda)=begin{vmatrix}1-lambda&-2\3&8-lambdaend{vmatrix}= (1-lambda)(8-lambda)+6=lambda^2-9 lambda+8+6= lambda^2-9 lambda+14.$

2. Решаем характеристическое уравнение: $lambda^2-9 lambda+14=0~Rightarrow~! left[!begin{gathered}lambda_1=2,\ lambda_2=7.end{gathered}right.$ .

3(1). Для корня lambda_1=2 составляем однородную систему уравнений (A-lambda_1E)x=o:

$begin{pmatrix}1-2&-2\ 3&8-2 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-1&-2\ 3&6 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-1&-2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!&vline!!&0\ 3&6!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}-2\1end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1=2colon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы $begin{pmatrix}-1&-2\3&6end{pmatrix}$ , то есть $begin{pmatrix}2\-1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=7 составляем однородную систему уравнений (A-lambda_2E)x=o:

$begin{pmatrix}1-7&-2\ 3&8-7 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-6&-2\ 3&1 end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-6&-2!!&vline!!&0\ 3&1!!&vline!!&0end{pmatrix}sim begin{pmatrix}3&1!!&vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ -6&-2!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&1/3!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}!.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: $x_1=-frac{1}{3}x_2$ . Полагая x_2=1 , получаем решение $varphi_2=begin{pmatrix}-1/3\1end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=7colon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-6&-2\3&1end{pmatrix}$ , т.е. $begin{pmatrix}1\-3 end{pmatrix}$ . Поделив его на (- 3), получим varphi_2 .

Матрица . 1. Составляем характеристический многочлен матрицы

$Delta_{B}(lambda)= begin{vmatrix}1-lambda&-4\1&1-lambdaend{vmatrix}= (1-lambda)^2+4=lambda^2-2 lambda+1+4= lambda^2-2 lambda+5.$

2. Решаем характеристическое уравнение: $lambda^2-2 lambda+5=0~Rightarrow~! left[! begin{gathered}lambda_1=1+2i,\ lambda_2=1-2i.end{gathered}right.$ .

3(1). Для корня lambda_1=1+2i составляем однородную систему уравнений (B-lambda_1E)x=o

$begin{pmatrix}1-(1+2i)&-4\ 1&8-1-(1+2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}-2i&-4\ 1&-2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}-2i&-4!!&vline!!&0\ 1&-2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&-2i!!&vline!!&0\ -2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&-2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=2i,x_2 . Полагая x_2=1 , получаем решение $varphi_1= begin{pmatrix}2i\1 end{pmatrix}$ .

4(1). Записываем собственные векторы, соответствующие собственному значению lambda_1= 1+2icolon~ s_1=C_1cdotvarphi_1 , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2i&-4\1&-2iend{pmatrix}$ , то есть $begin{pmatrix}-2i\ -1 end{pmatrix}$ . Умножив этот столбец на (-1), получим varphi_1 .

3(2). Для корня lambda_2=1-2i составляем однородную систему уравнений (B-lambda_2E)x=o:

$begin{pmatrix}1-(1-2i)&-4\ 1&8-1-(1-2i) end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0end{pmatrix}quad Leftrightarrowquad begin{pmatrix}2i&-4\ 1&2i end{pmatrix}!cdot! begin{pmatrix}x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду

$begin{pmatrix}2i&-4!!&vline!!&0\ 1&2i!!&vline!!&0end{pmatrix}sim begin{pmatrix} 1&2i!!&vline!!&0\ 2i&-4!!&vline!!&0end{pmatrix}sim begin{pmatrix}1&2i!!& vline!!&0\ 0&0!!&vline!!&0end{pmatrix}.$

Ранг матрицы системы равен 1 (r=1) , число неизвестных n=2 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисную переменную x_1 через свободную: x_1=-2i,x_2 . Полагая x_2=1 , получаем решение $varphi_2= begin{pmatrix}-2i\1 end{pmatrix}$ .

4(2). Записываем собственные векторы, соответствующие собственному значению lambda_2=1-2icolon~ s_2=C_2cdotvarphi_2 , где C_2 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}2i&-4\1&2iend{pmatrix}$ , т.е. $begin{pmatrix}2i\-1 end{pmatrix}$ . Умножив его на (-1), получим varphi_2 .

Матрица 1. Составляем характеристический многочлен матрицы

$Delta_{C}(lambda)= det(C-lambda E)= begin{vmatrix}1-lambda&1&1\1&1-lambda&1\ 1&1&1-lambda end{vmatrix}= (1-lambda)^3+2-3(1-lambda)= -lambda^3+3 lambda^2.$

2. Решаем характеристическое уравнение: $-lambda^3+3 lambda^2=0~Rightarrow~! left[! begin{gathered}lambda_1=3,\ lambda_2=0end{gathered}right.$ .

3(1). Для корня lambda_1=3 составляем однородную систему уравнений (C-lambda_1E)x=o:

$begin{pmatrix}1-3&1&1\ 1&1-3&1\ 1&1&1-3end{pmatrix}!cdot! begin{pmatrix} x_1\x_2\x_3end{pmatrix}=begin{pmatrix}0\0\0end{pmatrix}quad Leftrightarrowquad begin{cases}-2x_1+x_2+x_3=0,\ x_1-2x_2+x_3=0,\ x_1+x_2-2x_3=0.end{cases}$

Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):

$begin{gathered}begin{pmatrix}C-lambda_1Emid oend{pmatrix}= begin{pmatrix} -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0\ 1&1&-2!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ -2&1&1!!&vline!!&0\ 1&-2&1!!&vline!!&0 end{pmatrix}sim\[2pt] simbegin{pmatrix} 1&1&-2!!&vline!!&0\ 0&3&-3!!&vline!!&0\ 0&-3&3!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&1&-2!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}sim begin{pmatrix} 1&0&-1!!&vline!!&0\ 0&1&-1!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.end{gathered}$

Ранг матрицы системы равен 2 (r=2) , число неизвестных n=3 , следовательно, фундаментальная система решений состоит из n-r=1 решения. Выражаем базисные переменные x_1,x_2 через свободную $x_3colon begin{cases}x_1=x_3,\x_2=x_3,end{cases}$ и, полагая x_3=1 , получаем решение $varphi=begin{pmatrix}1\1\1end{pmatrix}$ .

4(1). Все собственные векторы, соответствующие собственному значению lambda_1=3 , вычисляются по формуле s=C_1cdotvarphi , где C_1 — отличная от нуля произвольная постоянная.

Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы $begin{pmatrix}-2&1&1\1&-2&1\1&1&-2end{pmatrix}$ , то есть $begin{pmatrix}3\3\3end{pmatrix}$ , так как

$A_{11}=(-1)^{1+1}begin{vmatrix} -2&1\1&-2 end{vmatrix} =3;quad A_{12}=(-1)^{1+2} begin{vmatrix} 1&1\1&-2 end{vmatrix}= 3;quad A_{13}=(-1)^{1+3}begin{vmatrix}1&-2\ 1&1 end{vmatrix}=3.$

Разделив его на 3, получим varphi .

3(2). Для собственного значения lambda_2=0 имеем однородную систему Cx=o . Решаем ее методом Гаусса:

$begin{pmatrix}Cmid oend{pmatrix}= begin{pmatrix}1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0\ 1&1&1!!&vline!!&0 end{pmatrix}sim begin{pmatrix}1&1&1!!& vline!!&0\ 0&0&0!!&vline!!&0\ 0&0&0!!&vline!!&0 end{pmatrix}!.$

Ранг матрицы системы равен единице (r=1) , следовательно, фундаментальная система решений состоит из двух решений (n-r=2) . Базисную переменную x_1 , выражаем через свободные: x_1=-x_2-x_3 . Задавая стандартные наборы свободных переменных x_2=1,~x_3=0 и x_2=0,~ x_3=1 , получаем два решения

$varphi_1=begin{pmatrix}-1\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-1\0\1 end{pmatrix}!.$

4(2). Записываем множество собственных векторов, соответствующих собственному значению lambda_2=0colon~ s=C_1varphi_1+C_2varphi_2 , где C_1,C_2 — произвольные постоянные, не равные нулю одновременно. В частности, при C_1=0, C_2=-1 получаем $s_1=begin{pmatrix}1&0&-1end{pmatrix}^T$ ; при C_1=0,~C_2=-1colon $s_2=begin{pmatrix}1&-1&0end{pmatrix}^T$ . Присоединяя к этим собственным векторам собственный вектор $s_3=begin{pmatrix}1&1&1 end{pmatrix}^T$ , соответствующий собственному значению lambda_1=3 (см. пункт 4(1) при C_1=1 ), находим три линейно независимых собственных вектора матрицы

$s_1=begin{pmatrix}1\0\-1end{pmatrix}!,qquad s_2=begin{pmatrix}1\-1\0 end{pmatrix}!,qquad s_3=begin{pmatrix}1\1\1end{pmatrix}!.$

Заметим, что для корня lambda_2=0 собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы равно нулю.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

(1.1)

Если
для квадратной матрицы A
можно найти вектор

и число

,
отвечающие выражению (1.1), то этот
вектор и это число называются собственным
значением и собственным вектором матрицы
A.

Решение
(1.1) на первый взгляд несложно. В частности,
из (1.1) следует система линейных
уравнений, коэффициенты которых
выражаются через элементы матрицы
A
и
собственные числа

(1.2)

Система
однородных линейных уравнений (1.2) имеет
ненулевое решение

в том случае, если определитель матрицы
коэффициентов равен нулю:

.
(1.3)

Для
матрицы A
– порядка n
уравнение (1.3) есть алгебраическое
уравнение степени n,
решив которое можно найти n
собственных чисел

,
i=1,2,…..n,
после их подстановки в (1.3) и решения n
систем однородных линейных уравнений
n
– го порядка можно получить n
– собственных векторов.

Пример
№6:

Дано:

Найти:
собственные числа

собственные векторы

Решение:
составим характеристическое уравнение
(1.3):

Корни
этого уравнения есть собственные числа
матрицы А:

,

.
Находим собственные векторы, подставив
значение

в
(1.2):

откуда

,
из условия нормирования

находим

,

.
Аналогично находим компоненты второго
собственного вектора, после подстановки
в (1.2)

откуда

,
из условия нормирования

находим

,

.

Таким
образом, найдены матрицы собственных
значений

,
и собственных векторов

.

Из
изложенного выше следует, что описанный
метод хорош только для матриц невысокого
порядка и приводит к существенным
вычислительным трудностям при больших
n.

Для
матриц высокого порядка очень эффективен
способ итераций, который состоит в
следующем: задаются произвольным
вектором

,
затем используют (1.1), проводя вычисления
по схеме:

………

(1.4)

до
тех пор, пока в пределах требуемой
точности

,

не совпадут с

,

.

В
(1.4) i
это не номер собственного значения, а
номер приближения для одного и того же
собственного числа. Процесс (1.4) довольно
быстро сходится к большему по величине
собственному числу и к соответствующему
ему собственному вектору. Следовательно,
методом итераций можно найти только
старшее собственное число.

Пример
№7:

Дано:

Найти
старшее собственное число соответствующий
ему собственный вектор.

Решение:
зададим нормальный вектор:

после чего действуем по (1.4).

После
первой итерации находим

92,504053965=

После
второй итерации:

…………………………………………………………………………………………

После
четвертой итерации:

,

.

1.3. Полная проблема собственных значений. Метод итераций.

Простота
и легкость программирования метода
итераций для определения старшего
собственного числа объясняет стремление
применить этот метод к определению
остальных собственных чисел, т.е.
применить метод итераций к решению
полной проблемы собственных значений.

Равенство
(1.1) записано для одного собственного
числа. Матричный аналог этого равенства
выглядит следующим образом:

,
(1.5)

где

–
диагональная матрица n
– го порядка на главной диагонали
которой расположены собственные
числа.

матрица, составленная из собственных
векторов, записанных по столбцам.

Отметим
очень важное свойство собственных
векторов – свойство ортогональности:

при

.
В матричной форме это условие записывается
так:

где

– диагональная матрица. Обычно нормируют
собственные вектора:

,
тогда условие ортогональности примет
вид:

,
(1.6)

где
Е
–
единичная матрица.

Из
(1.6) следует, что для нормированных
собственных векторов

(1.7)

а
также

(1.8)

В
результате очередной итерации по
формулам (1.4) получаем

(1.9)

где

– нормированный , а

–
ненормированный вектор. Находим
нормирующий множитель

(1.10)

и
затем нормированный вектор

(1.11)

Отсюда
имеем

(1.12)

Сравнивая
с (1.4), замечаем, что нормирующий множитель
после очередной итерации

_i
=

.

(1.13)

В
(1.9) –(1.13) i
–
номер итерации, а не номер собственного
числа.

С
учетом (1.7) выражение (1.5) можно записать
в виде:

(1.14)

Переходя
к векторной форме записи, получим:

После
перемножения матриц в правой части,
имеем:

(1.15)

Обозначим

.
(1.16)

Тогда

,
(1.17)

…………………………………………

Применим
к (1.17) метод итераций и найдем старшие
собственные числа и собственные векторы
матриц A_i
.
Здесь i
– номер собственной формы. Предполагаем,
что правые части (1.15), (1.17) записаны в
порядке убывания собственных чисел.
Тогда из A_i
методом
итераций находится

Таким
образом, имеем следующую схему решения
полной проблемы собственных значений
матрицы A:

а)
методом итераций из A
находим

,
по формулам (1.9) – (1.13)

б)
по (1.16) определяем A₁,

в)
методом итераций из A₁
находим

и

,

г)
по (1.16) определяем A₂,

и
т.д. повторяем процесс, пока не найдем
все n
собственных чисел.

Пример
№8.
Найти все собственные векторы и
собственные числа матрицы

Применяем,
описанный выше метод итераций к матрице
А.
Вычисления
велись на ПК в программе Excel.

Находим

139.658735,

.
По формуле (1.16) вычисляем

Применив
метод итераций к А₁,
находим

=
18,03255539,
.

По
формуле (1.16) вычисляем

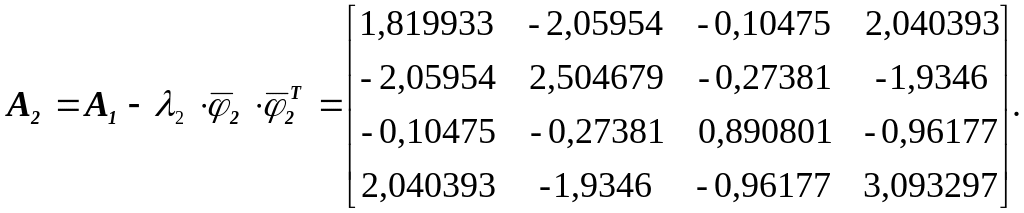
Применив
метод итераций к А₂,
находим

=
6,577921363,

.

По
формуле (1.16) вычисляем

Применив
метод итераций к А₃,
находим

=
1,730788224,

.

Применив
еще раз формулу (1.16), находим

Элементы
матрицы А₄
,
которые должны бать равны нулю, позволяют
оценить точность расчетов. Как видно,
погрешность имеет порядок 10^-12,
что очень хорошо, если учесть значения
элементов матрицы А₃
,
имеющие порядок 10^-0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Игра в собственные

Время на прочтение
13 мин

Количество просмотров 5.6K

Реализация собственного значения

Имеем набор данных в виде совокупности квадратных матриц, которые используются – вместе с известным выходом – в качестве тренировочного набора для нейронной сети. Можно ли обучить нейронную сеть, используя только собственные значения матриц? Во избежание проблем с комплексными значениями, упор делаем на симметричные матрицы. Для иллюстрации используем набор данных MNIST. Понятно, что невозможно восстановить матрицу по ее собственными значениям – для этого понадобится еще кое-что, о чем мы поговорим далее. Поэтому трудно ожидать некоего прорыва на данном пути, хотя известно, что можно говорить о чем угодно, строить грандиозные планы, пока не пришло время платить. О деньгах мы здесь не говорим, просто задаем глупый вопрос, на который постараемся получить осмысленный ответ, тем более что в процессе познания расширим свои научные горизонты. Например, сначала мы познакомимся с тем, как находить собственные векторы и собственные значения (eigenvalues and eigenvectors) для заданной квадратной матрицы, затем плавно выкатим на эрмитовы и унитарные матрицы. Все иллюстративные примеры сопровождаются простыми кодами. Далее возьмем MNIST , преобразуем в набор собственных значений симметричных матриц и используем молоток от Keras. Как говорят в Японии: “Торчащий гвоздь забивают”. Закроем глаза и начнем бить, а на результат можно и не смотреть: получится как всегда. Сразу скажу, что изложение будет проведено как можно ближе к тому, как я это дело понимаю для себя, не обращаясь к строгому обоснованию, которое обычно не используется в повседневной жизни. Иными словами, что понятно одному глупцу, понятно и другому. Все мы невежественны, но, к счастью, не в одинаковой степени. С другой стороны, предполагаю, что многие, хоть и в гимназиях не обучались, но имеют представление – по своему опыту обучения, – что значит впихнуть невпихуемое.

Собственно, собственные

Итак, пусть у нас задана произвольная квадратная матрица с компонентами $A_{i,j}$ . Мы ставим запятую между индексами, имея в виду оформление массивов в большинстве языков программирования; обычно так не делается, но мы делаем так, как нам хочется, да и выглядит все более разреженным и удобочитаемым. Мы можем умножить матрицу на произвольный вектор v_i , руководствуясь правилом умножения матриц (строка на столбец), $A_{i,j}v_j$ . По повторяющимся индексам производится суммирование; все получится, если размерность первой (нумерация с нуля) оси матрицы совпадает с размерностью вектора. Если будет желание, когда я что-то упускаю из виду, можно заглянуть в мои заметки . Вдруг приключилось так, что $A_{i,j}v_j=lambda v_iquadRightarrowquad Acdot v=lambda v$ , тогда говорят: lambda – собственное значение, – собственный вектор. Опять же, возвращаясь к глубокомысленной дискуссии о запятых в индексах, здесь мы используем точку, когда переходим от компонент к матрицам, имея в виду замечательную функцию dot() в превосходном NumPy. Теперь проведем ряд очевидных манипуляций

$A_{i,j}v_j=lambda v_iRightarrow A_{i,j}v_j=lambda delta_{i,j} v_jRightarrow (A_{i,j}-lambda delta_{i,j}) v_j=0Rightarrow (A-lambda I)cdot v=0tag{1},$

где $delta_{i,j}$ – символ Кронекера, – единичная матрица, 0 – нулевой вектор. Условие нетривиальности решения, vneq 0 , для собственного вектора приводит к характеристическому уравнению . Если размер матрицы равен n, получим алгебраическое уравнение n-й степени, которое имеет n корней (действительных или комплексных) – собственных значений (eigenvalues) . Каждому собственному значению соответствует собственный вектор (eigenvectors) $v_0, v_i, ...v_{n-1}$ (например, ). Совокупность собственных векторов образует матрицу с компонентами $v_{i,j}$ , где нулевая ось – компоненты вектора, а первая – нумерация собственных векторов. Теперь уравнение на собственные значения выглядит следующим образом: $A_{i,j}v_{j,k}=lambda_k v_{i, k}$ . Раз есть вектор, есть его длина, которая равна сумме квадратов компонент (квадрат длины). Например, для квадрата длины третьего вектора (нумерация с нуля) имеем

$v_{i,2}v_{i,2}=(V.T)_{2,i}v_{i,2}quadRightarrowquad (V.T cdot V)_{2,2},tag{2}$

где, вспоминая правила умножения матриц ( $C_{i,k}=A_{i, j}B_{j, k}$ , см. заметки ), мы воспользовались тождеством $v_{i,2}=(V.T)_{2,i}$ , в котором V.T – транспонированная матрица (используем обозначения NumPy). Здесь нет проблем, но это до тех пор, пока мы работаем с действительными векторами. В комплексной области квадрат длины вектора равен скалярному произведению вектора на комплексно сопряженный. В этом случае потребуется следующая модификация соотношения (2):

$v_{i,2}^*v_{i,2}=((V.T)^*_{2,i}v_{i,2}quadRightarrowquad (V.H cdot V)_{2,2},tag{3}$

где звездочка обозначает обычное комплексное сопряжение. Следует заметить, что – эрмитово-сопряжённая матрица. Длина вектора – число, отсюда открывается возможность выделить собственное значение путем умножения на собственный вектор. В результате для выделенного собственного значения получим

$A_{i,j}v_{j,2}=lambda_2 v_{i, 2}quadRightarrowquad v_{i,2}^*A_{i,j}v_{j,2}=lambda_2 v_{i,2}^*v_{i,2}quadRightarrowquad lambda_2 =frac{v_{i,2}^*A_{i,j}v_{j,2}}{v_{i,2}^*v_{i,2}}.tag{4}$

Все это выглядит не очень хорошо, поскольку произведение разных собственных векторов, например $v_{i,2}^*v_{i,3}$ , может быть не равно нулю. Это настораживает, поскольку мы привыкли иметь дело с единичными векторами, каждый из которых ортогонален другому. Вспомните хотя бы единичные векторы по трем осям в обычном пространстве. Но проблемы отложим на потом, а пока создадим видимость работы – побалуемся с кодами.

import numpy as np
from numpy import matrix
from numpy.linalg import eig 
# из субмодуля (submodule linalg) линейной алгебры берем метод
#для вычисления собственных значений и векторов 

# Возьмем матрицу, которую можно проверить вручную
A = matrix([[3, -0.65], [5, 1]])

# calculate eigendecomposition
values, V = eig(A)
print(values) # [2.+1.5j 2.-1.5j]
print(V) # [[0.18814417+0.28221626j 0.18814417-0.28221626j]
         #  [0.94072087+0.j         0.94072087-0.j        ]]

Действительно, характеристическое уравнение имеет решения $lambda_{+,-}=2pm 1.5j$ , где – мнимая единица. Столбцы матрицы – собственные векторы v_0 и v_1 .

# Первый собственный вектор - все элементы нулевого столбца и т.д.
v0=V[:,0]
v1=V[:,1]
v0.shape, v1.shape # ((2, 1), (2, 1))
# К счастью, они единичные
np.dot(v0.H,v0) # matrix([[1.+0.j]])
np.dot(v1.H,v1)[0,0] # (0.9999999999999999+0j). Ну, почти единица
# Но эти векторы не ортогональны
np.dot(v0.H,v1) # matrix([[0.84070796-0.10619469j]])

Эрмитовы матрицы

Мы научились находить eigendecomposition для произвольной квадратной матрицы. Пока не будем говорить о вырожденных матрицах , которых, по возможности, будем в дальнейшем избегать. Итак, в чем состоит загвоздка. С собственными значениями – все в порядке, а вот собственные векторы изрядно подгуляли. Дело в том, что они не ортогональны друг другу. Посмотрим, какие условия на матрицу нам потребуется наложить, чтобы добиться ортогональности, заодно откроем для себя ряд новых возможностей в деле познания собственных способностей.

Пусть из всего набора мы произвольно выделили два участника $A_{i,j}v_{j,k}=lambda_k v_{i, k}$ и $A_{i,j}v_{j,l}=lambda_l v_{i, l}$ , где, напомним, второй индекс нумерует собственные вектора. Берем первое соотношение и умножаем его на $v_{i,l}^*$ , а второе – на $v_{i,k}^*$ , в результате имеем

$v_{i,l}^*A_{i,j}v_{j,k}=lambda_k v_{i,l}^*v_{i, k}quadquad v_{i,k}^*A_{i,j}v_{j,l}=lambda_l v_{i,k}^*v_{i, l}.tag{5}$

Далее выполним комплексное сопряжение второго уравнения в (5)

$v_{i,k}A_{i,j}^*v_{j,l}^*=lambda_l^* v_{i,k}v_{i, l}^*quadRightarrowquad v_{j,l}^*A_{i,j}^*v_{i,k}=lambda_l^* v_{i,l}^*v_{i, k}.$

Поскольку индексы в последнем уравнении “немые” (по ним производится суммирование) , их можно назвать как угодно. Таким образом, после замены получим

$v_{i,l}^*A_{j,i}^*v_{j,k}=lambda_l^* v_{i,l}^*v_{i, k}quadRightarrowquad v_{i,l}^*(A.H)_{i,j}v_{j,k}=lambda_l^* v_{i,l}^*v_{i, k},tag{6}$

где A.H – эрмитово-сопряжённая матрица, элементы которой определяются как $(A.H)_{i,j}=A_{j,i}^*$ . Теперь из первого уравнения (5) вычитаем (6). В результате получим следующее замечательное выражение:

$v_{i,l}^*[A-A.H]_{i,j}v_{j,k}=(lambda_k-lambda_l^*) v_{i,l}^*v_{i, k}.tag{7}$

Пока мы не накладывали никаких ограничений на матрицу. Первое, что приходит на ум: положим A=A.H , определяя тем самым эрмитову матрицу Следует отметить: все что мы наблюдаем в окружающем нас мире связано, так или иначе, с собственными значениями эрмитовых матриц. Шарль Эрмит – вот кто Создатель Вселенных (см. превосходную биографию, Ожигова Е.П. Шарль Эрмит. – Л.:Наука, 1982.). Да, было время, когда математики занимались реальным миром, не то, что нынешнее племя.

Шарль Эрмит, 1822-1901

Итак, для эрмитовых матриц получаем выражение $(lambda_k-lambda_l^*) v_{i,l}^*v_{i, k}=0$ , которое связано с двумя важнейшими событиями для каждого, кто изучал квантовую механику. Во-первых, собственные значения эрмитовых матриц являются действительными величинами , поскольку при l=k из условия $v_{i,k}^*v_{i, k}>0$ имеем . Во- вторых, если lneq k и , получаем свойство ортогональности собственных векторов $v_{i,l}^*v_{i, k}=0$ . Для эрмитовых матриц собственные значения – действительные величины, а собственные векторы – ортогональны друг другу, вернее, ортонормированы, поскольку удобно включать условие нормировки. Таким образом, мы стремились к аналогии с обычным пространством, с единичными векторами по ортогональным осям, мы это и получили.

Теперь соорудим эрмитову матрицу. Для этого сгенерируем пару случайных матриц и , затем сложим их, умножив одну из матриц на мнимую единицу , A=X+jY . Затем возьмем полученную матрицу и сложим ее с эрмитово-сопряженной. Действительно, , так что – эрмитова матрица.

Пришло время окунуться в мутные воды искусственного интеллекта. Внести, так сказать, свой слабый голос в общий хор.

X=np.random.randint(0, 256, (28,28))# Вспоминаем молодость с MNIST
Y=np.random.randint(0, 256, (28,28))
A=matrix(X+1j*Y)
B=A+A.H
# выводим собственные значения и собственные вектора (в виде матрицы)
values, V = eig(B)
values=np.real(values)# только действительная часть
values

Собственные значения (values) получились с едва заметной мнимой частью, которую мы отрезаем по идеологическим соображениям. Для этого мы оставили только действительную часть. Напомним, что

$v_{i,l}^*v_{i, k}=(V.H)_{l,i}v_{i, k}=delta_{l,k}quadRightarrowquad V.Hcdot V=E,tag{8}$

где – единичная матрица (по диагонали единицы ). Проверим в коде

np.dot(V.H, V) # почти единичная матрица с формой (28,28)

Опять же получим почти единичную матрицу, но ничего округлять не будем. Теперь пришло время для громкого заявления : матрица, для которой выполняется (8) – унитарная матрица . Таким образом, эрмитово-сопряжённая унитарная матрица совпадает с обратной. К слову, эволюция во времени нашего мира осуществляется с помощью унитарных преобразований, хотя этот факт теряется во множестве событий. Не удивительно, что унитарную эволюцию попытались использовать (см. статью) и в машинном обучении, но для рекуррентной нейронной сети. Для многих концепция унитарности заставляет ощутить священный трепет познания. Но это одна среда обитания. В политическом же питательном бульоне тоже есть концепция унитарности, о которой можно думать все что угодно, и которая не связана ни с каким познанием.

Симметричный MNIST

Итак, в предыдущем разделе мы говорили о произвольных о эрмитовых матрицах. Если же мы имеем дело с действительными матрицами, комплексное сопряжение выпадает, поэтому эрмитовы – это просто симметричные матрицы, A=A.T .

В этом разделе мы возьмем набор данных MNIST и попробуем поработать с каждым элементом как с матрицей. Каждое рукописное изображение цифр (от 0 до 9) – матрица с формой (28,28), каждый элемент которой – число от 0 до 255 (8-битная шкала серого). Загрузим и посмотрим (рекомендую начать новый блокнот).

import keras
from keras.datasets import mnist
keras.__version__ # '2.4.3'
(x,y),(tx,ty)=mnist.load_data()

База данных MNIST состоит тренировочного (x,y) и тестового (tx,ty) наборов, где – набор рукописных изображений цифр(матриц), которые подаем на вход, а – набор правильных ответов (числа от 0 до 9); тестовый набор выделен для удобства. Теперь посмотрим, сколько их там, и что они из себя представляют. Для этого подключим “рисовалку”.

import matplotlib.pyplot as plt
# Сколько их?
x.shape[0], tx.shape[0] # (60000, 10000)
# Возьмем произвольный элемент
y[12345] # 3
# Посмотрим на каракули
plt.imshow(x[12345], cmap=plt.get_cmap('gray'))
plt.show()

Все выглядит замечательно, так что можно продолжать работать с нашим изображением. Тем не менее, проблемы вылазят тогда, когда мы посмотрим на матрицу, скрывающуюся под этим изображением.

x[12345]

Сразу можно отметить (посмотрите сами), что слишком много нулей. Это вырожденная матрица, определитель ее равен нулю.

import numpy as np
from numpy.linalg import eig 
np.linalg.det(x[12345])# 0.0 - детерминант

Если попробуем вычислить собственные значения, никакого сбоя не случится, просто некоторые из них будут равны нулю.

values, V = eig(x[12345])
values # array([   0.          +0.j        ,    0.          +0.j        ,
                1474.46266075  +0.j        ,  838.19932232  +0.j        ,
               -400.18280429+384.94168117j, -400.18280429-384.94168117j,
                297.89145581  +0.j        ,   90.51616055+144.4741198j ,
                 90.51616055-144.4741198j ,  -57.05178416 +68.44040035j,
                -57.05178416 -68.44040035j,    3.05833828 +80.86506799j,
                  3.05833828 -80.86506799j,  -32.62937655 +32.08539788j,
                -32.62937655 -32.08539788j,    4.36245913 +51.20712637j,
                  4.36245913 -51.20712637j,  -16.0035565   +0.j        ,
                  6.13140522  +0.j        ,   59.17272648  +0.j        ,
                  0.          +0.j        ,    0.          +0.j        ,
                  0.          +0.j        ,    0.          +0.j        ,
                  0.          +0.j        ,    0.          +0.j        ,
                  0.          +0.j        ,    0.          +0.j        ])

Как видно, собственные значения находятся в комплексной области. Монтировать комплексную нейронную сеть можно, но осторожно. Основы и ссылки можно подчерпнуть из диссертации. Это отличная тема для исследований и экспериментов; советую использовать только аналитические функции, несмотря на ограничения, связанные с принципом максимума модуля (это для тех, кто в теме).

Итак, хочется поскорее избавиться от комплексных чисел. Мы знаем, что эрмитовы матрицы обладают действительными собственными значениями. Поскольку матрица изображения полностью состоит из действительных чисел, то эрмитова матрица – просто симметричная матрица. Иными словами, нам потребуется соорудить симметричную матрицу, но перед этим избавиться от множества нулей. Для этого “закрасим” пикселями, выбирая их значения случайным образом.

from numpy import matrix
a=matrix(x[12345]+np.random.randint(0, 5, (28,28)))
np.linalg.det(a) # У меня -3.7667039553765456e+43, 
                 # у вас, конечно, получится другое значение

Пятерочки для закраски вполне достаточно, поскольку вероятность совпадения элементов в строке или столбце просто мизерная. Детерминант, конечно, громадный, но Python все стерпит, а пока закроем на это глаза. Если посмотрим на картинку, то поверьте, там все нормально: наша тройка практически не изменилась.

Итак, перейдем к симметричной матрице и посмотрим, что там нарисовано.

a=a+a.H # для действительных матриц a.H=a.T
plt.imshow(a, cmap=plt.get_cmap('gray'))
plt.show()

Кто скажет, что это не тройка, пусть первый бросит в меня камень! Теперь это число подготовлено для манипуляций в нейронной сети. Матрица симметричная, невырожденная, имеет замечательный набор собственных значений.

values, V = eig(a)
values # array([ 4.06238155e+03,  1.87437218e+03, -1.59889723e+03, -8.51935039e+02,
                5.58412899e+02, -3.53262264e+02, -2.36036195e+02,  2.29960516e+02,
                2.08312088e+02, -1.49974962e+02,  1.40811760e+02, -9.71188401e+01,
                8.27836555e+01, -6.51480016e+01, -4.65323368e+01,  3.90299000e+01,
                3.06552503e+01,  2.06100661e+01,  1.73972579e+01, -1.16491885e+01,
               -8.13295407e+00,  1.24942529e+01, -4.67339958e+00,  9.33795587e+00,
                6.67620627e+00,  2.96767577e+00,  1.13851798e+00,  1.86752842e-02])

Если с собственными значениями все в порядке, то собственные векторы малость подгуляли: мало того, что они комплексные (как обычно и бывает), так восстановление первоначальной матрицы по собственным векторам и собственным значениям может привести к комплексной матрице. Python не знает, что это не правильно, поэтому и вытянет наружу комплексные остатки. Само собой, можно от них избавиться с помощью метода np.real(), оставляя только действительную часть. Но пока попробуем в лоб, проверим прозорливость создателей NumPy на примере восстановления матрицы по собственным значениям и собственным векторам. Чтобы подготовить почву, необходимо вернуться к уравнениям (8), которые справедливы и для нашей матрицы , в которой столбцы – собственные векторы матрицы (см. выше). Таким образом, $а_{i,j}v_{j,k}=lambda_k v_{i, k}$ . Следует напомнить, что, несмотря на повторяющийся индекс , в правой части нет суммирования (берем фиксированное ). Далее имеем

$а_{i,j}v_{j,k}=v_{i, l}delta_{l,k}lambda_k quadRightarrowquad acdot V=Vcdot e(lambda),$

где – диагональная матрица собственных значений (по диагонали – собственные значения). Умножая последнее уравнение с правой стороны на V.H , получим

в котором использовали (8) . Теперь проверим в коде

e=np.diag(values) # сооружаем диагональную матрицу из собственных значений
b=np.dot(V,np.dot(e,V.H)) # восстанавливаем исходную матрицу по собственным
                          # значениям и векторам; ради приличия ввели новое 
                          # имя матрицы   
plt.imshow(b, cmap=plt.get_cmap('gray'))
plt.show()

Нет слов, все работает! Итак, наши подозрения были беспочвенны, но проверять все равно надо. Теперь мы знаем, что по собственным значениям и векторам можно четко восстановить исходную матрицу. Итак, если используем обратимые операции, царапая формулы на листке бумаге, лучше проверить, как с этим обстоит дело в коде.

Эксперимент

Итак, теперь мы умеем манипулировать симметричными матрицами, используя в качестве полигона базу данных MNIST. Теперь мы попытаемся представить набор данных как симметричные матрицы, затем вычислить собственные значения, на основе которых построить нейронную сеть по примеру обращения с обычным набором. Сразу скажу, что надежд на удачный исход мало. Действительно, как мы выяснили ранее, для того чтобы восстановить матрицу собственных значений недостаточно, для этого необходим набор собственных векторов, объединенных в матрицу , которая сама по себе имеет размер исходной матрицы. Так что, с первого взгляда, мы ничего не выигрываем. Тем не менее, есть надежда, что распределение и свойства собственных значений обладают необходимыми свойствами, чтобы их классифицировать по классам. Иными словами, собственные значения несут информацию о классах рукописных цифр. Распределением собственных значений мы займемся в следующей публикации, а сейчас будем использовать наивный подход, а именно : 1) представим набор MNIST в виде симметричных матриц (28*28); 2) для каждого экземпляра вычислим собственные значения (28 штук); 3) используем Keras. Первые шаги мы уже сделали в предыдущем разделе, а над последним особо заморачиваться не будем, поскольку мы просто ставим эксперименты.

Начинаем новый блокнот:

import numpy as np
from numpy.linalg import eig
import keras
from keras.datasets import mnist

(x,y),(tx,ty)=mnist.load_data()

Теперь напишем функцию, которая будет “закрашивать” матрицы из набора данных. Отмечу, что использую доморощенные функции, которые предпочитаю писать самостоятельно, чем искать на мутных форумах.

def paintSym(z):
    n=z.shape[0]    
    x=np.empty([n,28,28])
    for i in range(n):
        x[i]= z[i]+np.random.randint(0, 5, (28,28))
    return x

Используем эту функцию, затем масштабируем (это не обязательно).

x=paintSym(x)
x=x.astype('float32') / 260

На следующем шаге нам понадобится функция, которая делает симметричные матрицы и возвращает только собственные значения.

def eigSym(z):
    n=z.shape[0]    
    x=np.empty([n,28])
    for i in range(n):
        val, vec = eig((z[i]+z[i].T)/2)
        x[i]= val
    return x

Включаем и смотрим.

x=eigSym(x)
x[12345] # на всякий случай
# array([ 7.82546663e+00,  3.60277987e+00, -3.06879640e+00, -1.62636960e+00,
        1.07726467e+00, -6.77050233e-01, -4.54729229e-01,  4.45481062e-01,
        4.00029063e-01, -2.85397410e-01,  2.71449655e-01, -1.94830164e-01,
        1.41906023e-01, -1.15398742e-01, -8.69008303e-02,  7.79602975e-02,
        5.81430644e-02, -3.25826630e-02,  3.82260419e-02,  3.11152730e-02,
        1.78121049e-02, -1.12444209e-02, -6.83658011e-03,  8.95012729e-03,
        8.10696371e-03,  3.64418700e-03, -2.08872650e-03,  4.40481490e-05])
x.shape # (60000, 28)

Как видно, вполне приемлемые значения, с которыми можно и поработать. Для этого возьмем продвинутый молоток от Keras.

from keras import models
from keras import layers

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28,)))
network.add(layers.Dense(10, activation='softmax'))

network.compile(optimizer='rmsprop',
                loss='categorical_crossentropy',
                metrics=['accuracy'])

from keras.utils import to_categorical
y = to_categorical(y)

network.fit(x, y, epochs=100, batch_size=128)

За основу мы берем код из Глубокое обучение на Python. Если осмысленно побалуетесь с цифрами, что-то получите. Точность, которая едва-едва заваливает за 0,5 (за 100 эпох!!!), подкачала по сравнению с оригиналом (accuracy: 0.9897 за Epoch 5), когда используется полная матрица изображения, но хотя бы мы не множили сущности. Для обсуждения не требуется глубокомысленных обобщений, просто, как я наивно думал, если зайца долго бить по голове, он научится спички зажигать. Но оказалось, что этот принцип в глубоком обучении не всегда срабатывает. Возиться дальше – интересно, но бессмысленно. Самое главное, по пути к этому мутному результату можно много чему научиться.

Пару слов напоследок

Итак, пришло время подводить итоги. Понятно, что говорить пока не о чем. Мы попытались на собственных значениях матриц построить работающую схему. Не получилось. Но известно, что отрицательный результат – куда более значимое событие, чем положительный, поскольку при этом у нас открываются новые перспективы. Если бы у нас все получилось, настало бы время для рутинной работы, а так – продолжим идти дальше. Правда и ложь – два взгляда на одну и ту же реальность. Но мы, по крайней мере, не лгали. Просто посмотрели с другого ракурса, заодно открыли для себя новые возможности. К примеру, почему бы не найти преобразование, позволяющее связать все изображения одного класса без использования внешнего наблюдателя для подтверждения события? Иными словами, из одной цифры получить почти полную совокупность из данного набора данных; из “тройки” почти все “тройки”, и т.д.. Сразу приходит на ум конформное отображение двумерных поверхностей: локальные вращения и растяжения с сохранением углов между кривыми, а значит с сохранением формы бесконечно малых фигур. Заодно мы могли бы проследить за трансформацией собственных значений, дабы по их расположению выйти на классификацию по классам. И не обязательно использовать действительные собственные значения. Конечно, переход в комплексную область потребует дополнительных усилий, но там уже существует путь в один путь, многое успешно отработано.

Что касается реальных, на настоящий момент, дел, то это классификация собственных значений по примеру распределения уровней сложных систем. Опять же MNIST животворящий. Но это тема следующей публикации.

Источник

ОСНОВНАЯ МАТЕМАТИКА ДЛЯ НАУКИ ДАННЫХ

Основы математики для науки о данных: собственные векторы и их применение в PCA

Понять собственные векторы и собственные значения и их отношение к анализу главных компонентов (PCA)

Разложение матрицы, также называемое факторизацией матрицы, – это процесс разделения матрицы на несколько частей. В контексте науки о данных вы можете, например, использовать его для выбора частей данных, направленных на уменьшение размерности без потери большого количества информации (как, например, в Анализе главных компонентов, как вы увидите позже в этом посте). Некоторые операции также легче вычислить с матрицами, полученными в результате разложения.

В этой статье вы узнаете о собственном разложении матрицы. Один из способов понять это – рассматривать это как особую смену базы (подробнее об изменении базы в моем последнем посте). Сначала вы узнаете о собственных векторах и собственных значениях, а затем увидите, как их можно применить к анализу главных компонентов (PCA). Основная идея состоит в том, чтобы рассматривать собственное разложение матрицы A как изменение базиса, в котором новые базисные векторы являются собственными векторами.

Собственные векторы и собственные значения

Как вы можете видеть в главе 7 Основы математики для науки о данных, вы можете рассматривать матрицы как линейные преобразования. Это означает, что если вы возьмете любой вектор u и примените к нему матрицу A, вы получите преобразованный вектор v.

Возьмем пример:

а также

Если вы примените A к вектору u (с произведением матрица-вектор), вы получите новый вектор :

Нарисуем исходный и преобразованный векторы:

Обратите внимание, что, как и следовало ожидать, преобразованный вектор v не движется в том же направлении, что и исходный вектор u . Это изменение направления характеризует большинство векторов, которые можно преобразовать с помощью A.

Однако возьмем следующий вектор:

На рисунке 2 видно, что вектор x имеет особую связь с матрицей A: он масштабируется (с отрицательным значением), но исходный вектор x и преобразованный вектор y находятся на одном и том же линия.

Вектор x является собственным вектором для A. Он масштабируется только значением, которое называется собственным значением матрицы A. Собственный вектор матрицы A – это вектор, который сжимается или удлиняется при преобразовании матрицей. Собственное значение – это коэффициент масштабирования, на который вектор сжимается или удлиняется.

Математически вектор x является собственным вектором A, если:

где λ (произносится как «лямбда») – собственное значение, соответствующее собственному вектору x.

Собственные векторы

Собственные векторы матрицы – это ненулевые векторы, которые масштабируются только тогда, когда к ним применяется матрица. Если коэффициент масштабирования положительный, направления исходного и преобразованного векторов совпадают, если он отрицательный, их направления меняются местами.

Количество собственных векторов

Матрица n на n имеет не более n линейно независимых собственных векторов. Однако каждый собственный вектор, умноженный на ненулевой скаляр, также является собственным вектором. Если у вас есть:

Потом:

с c любым ненулевым значением.

Это исключает нулевой вектор как собственный вектор, так как у вас будет

В этом случае каждый скаляр был бы собственным значением и, следовательно, не был бы определен.

Практический проект: анализ основных компонентов

Анализ главных компонентов или PCA – это алгоритм, который можно использовать для уменьшения размерности набора данных. Это полезно, например, для сокращения времени вычислений, сжатия данных или предотвращения того, что называется проклятием размерности. Это также полезно для целей визуализации: данные большого размера трудно визуализировать, и может быть полезно уменьшить количество измерений для построения ваших данных.

В этом практическом проекте вы будете использовать различные концепции, которые вы можете изучить в книге Essential Math for Data Science, как изменение основы (разделы 7.5 и 9.2, некоторые примеры здесь), собственное разложение (глава 9). , или ковариационные матрицы (раздел 2.1.3), чтобы понять, как работает PCA.

В первой части вы узнаете о взаимосвязи между прогнозами, объяснении дисперсии и минимизации ошибок, сначала с помощью теории, а затем путем кодирования PCA в наборе данных о пиве (потребление пива как функция температуры). Во второй части вы будете использовать Sklearn, чтобы использовать PCA для аудиоданных для визуализации аудиосэмплов в соответствии с их категорией, а затем для сжатия этих аудиосэмплов.

Под капотом

Теоретический контекст

Цель PCA – спроецировать данные в пространство более низкой размерности, сохраняя при этом как можно больше информации, содержащейся в данных. Эту проблему можно рассматривать как проблему перпендикулярных наименьших квадратов, также называемую ортогональной регрессией.

Вы увидите, что ошибка ортогональных проекций сводится к минимуму, когда линия проекции соответствует направлению, в котором дисперсия данных максимальна.

Дисперсия и прогнозы

Во-первых, важно понять, что, когда характеристики вашего набора данных не полностью некоррелированы, некоторые направления связаны с большей дисперсией, чем другие.

Проецирование данных в пространство меньшей размерности означает, что вы можете потерять некоторую информацию. На рисунке 3, если вы проецируете двумерные данные на линию, дисперсия проецируемых данных говорит вам, сколько информации вы теряете. Например, если дисперсия прогнозируемых данных близка к нулю, это означает, что точки данных будут проецироваться на очень близкие позиции: вы теряете много информации.

По этой причине цель PCA – изменить основу матрицы данных таким образом, чтобы направление с максимальной дисперсией (u на рисунке 3) стало первым главный компонент. Второй компонент – это направление с максимальной дисперсией, ортогональное первому, и так далее.

Когда вы нашли компоненты PCA, вы измените основу ваших данных так, чтобы компоненты стали новыми базисными векторами. Этот преобразованный набор данных содержит новые функции, которые являются компонентами и представляют собой линейные комбинации исходных функций. Уменьшение размерности выполняется путем выбора только некоторых компонентов.

В качестве иллюстрации на рисунке 4 показаны данные после изменения основы: максимальная дисперсия теперь связана с осью x. Например, вы можете оставить только это первое измерение.

Другими словами, выражая PCA в терминах изменения базиса, его цель состоит в том, чтобы найти новый базис (который представляет собой линейную комбинацию начального базиса), в котором дисперсия данных максимизируется по первым измерениям.

Минимизация ошибки

Поиск направлений, максимизирующих дисперсию, аналогичен минимизации ошибки между данными и их проекцией.

Вы можете видеть на рисунке 5, что более низкие ошибки показаны на рисунке слева. Поскольку проекции ортогональны, отклонение, связанное с направлением линии, на которую вы проецируете, не влияет на ошибку.

Поиск лучших направлений

После изменения основы набора данных вы должны иметь ковариацию между объектами, близкую к нулю (как, например, на рисунке 4). Другими словами, вы хотите, чтобы преобразованный набор данных имел диагональную матрицу ковариации: ковариация между каждой парой главных компонентов равна нулю.

Вы можете увидеть в главе 9 Основы математики для науки о данных, что вы можете использовать собственное разложение для диагонализации матрицы (сделать матрицу диагональной). Таким образом, вы можете вычислить собственные векторы ковариационной матрицы набора данных. Они дадут вам направления нового базиса, в котором ковариационная матрица диагональна.

Подводя итог, основные компоненты вычисляются как собственные векторы ковариационной матрицы набора данных. Кроме того, собственные значения дают вам объясненную дисперсию соответствующего собственного вектора. Таким образом, сортируя собственные векторы в порядке убывания в соответствии с их собственными значениями, вы можете отсортировать главные компоненты по порядку важности и в конечном итоге удалить те, которые связаны с небольшой дисперсией.

Расчет PCA

Набор данных

Давайте проиллюстрируем, как PCA работает с набором данных о пиве, показывающим потребление пива и температуру в Сан-Паулу, Бразилия, за 2015 год.

Загрузим данные и построим график зависимости потребления от температуры:

Теперь давайте создадим матрицу данных X с двумя переменными: температурой и потреблением.

(365, 2)

Матрица X имеет 365 строк и два столбца (две переменные).

Собственное разложение ковариационной матрицы.

Как вы видели, первым шагом является вычисление ковариационной матрицы набора данных:

array([[18.63964745, 12.20609082], [12.20609082, 19.35245652]])

Помните, что вы можете прочитать это следующим образом: значения по диагонали – это соответственно дисперсия первой и второй переменных. Ковариация между двумя переменными составляет около 12,2.

Теперь вы вычислите собственные векторы и собственные значения этой ковариационной матрицы:

(array([ 6.78475896, 31.20734501]), array([[-0.71735154, -0.69671139], [ 0.69671139, -0.71735154]]))

Вы можете сохранить собственные векторы как два вектора u и v.

Давайте построим собственные векторы с данными (обратите внимание, что вы должны использовать центрированные данные, потому что это данные, используемые для вычисления ковариационной матрицы).

Вы можете масштабировать собственные векторы по их соответствующим собственным значениям, что и является объясненной дисперсией. Для визуализации воспользуемся вектором длины трех стандартных отклонений (равном трехкратному квадратному корню из объясненной дисперсии):

Вы можете видеть на рисунке 7, что собственные векторы ковариационной матрицы дают вам важные направления данных. Вектор v красного цвета связан с наибольшим собственным значением и, таким образом, соответствует направлению с наибольшей дисперсией. Серый вектор u ортогонален v и является вторым главным компонентом.

Затем вам просто нужно изменить основу данных, используя собственные векторы в качестве новых базисных векторов. Но сначала вы можете отсортировать собственные векторы по собственным значениям в порядке убывания:

array([[-0.69671139, -0.71735154], [-0.71735154, 0.69671139]])

Теперь, когда ваши собственные векторы отсортированы, давайте изменим основу данных:

Вы можете построить преобразованные данные, чтобы убедиться, что основные компоненты теперь не коррелированы:

На рисунке 8 показаны образцы данных в новом базисе. Вы можете видеть, что первое измерение (ось x) соответствует направлению с наибольшим отклонением.

Вы можете сохранить только первый компонент данных в этой новой основе, не теряя слишком много информации.

Ковариационная матрица или разложение по сингулярным числам?

Одно из предостережений при использовании ковариационной матрицы для вычисления PCA состоит в том, что его может быть трудно вычислить, когда есть много функций (как со звуковыми данными, как во второй части этого практического занятия). По этой причине обычно предпочтительно использовать разложение по сингулярным значениям (SVD) для расчета PCA.

Этот пост представляет собой образец моей книги Essential Math for Data Science!

Скачать книгу можно здесь: https://bit.ly/2WVf4CR!

Источник