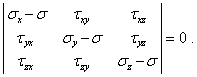Как найти компоненты тензора напряжения - Сайт, где вы сможете решить свои вопросы

Полный тензор механического напряжения элементарного объёма тела.

Те́нзор напряже́ний (иногда тензор напряжений Коши, тензор натяжений) — тензор второго ранга, описывающий механические напряжения в произвольной точке нагруженного тела, возникающих в этой точке при его (тела) малых деформациях. В случае объёмного тела, тензор часто записывается в виде матрицы 3×3:

${displaystyle {boldsymbol {sigma }}=left[{begin{matrix}mathbf {T} ^{(mathbf {e} _{1})}\mathbf {T} ^{(mathbf {e} _{2})}\mathbf {T} ^{(mathbf {e} _{3})}\end{matrix}}right]=left[{begin{matrix}sigma _{11}&sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}&sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}\end{matrix}}right]equiv left[{begin{matrix}sigma _{xx}&sigma _{xy}&sigma _{xz}\sigma _{yx}&sigma _{yy}&sigma _{yz}\sigma _{zx}&sigma _{zy}&sigma _{zz}\end{matrix}}right]equiv left[{begin{matrix}sigma _{x}&tau _{xy}&tau _{xz}\tau _{yx}&sigma _{y}&tau _{yz}\tau _{zx}&tau _{zy}&sigma _{z}\end{matrix}}right]}$

а в случае двумерного тела (см. пример ниже) матрицей 2×2:

${displaystyle {boldsymbol {sigma }}=left[{begin{matrix}mathbf {T} ^{(mathbf {e} _{1})}\mathbf {T} ^{(mathbf {e} _{2})}\end{matrix}}right]=left[{begin{matrix}sigma _{11}&sigma _{12}\sigma _{21}&sigma _{22}\end{matrix}}right]equiv left[{begin{matrix}sigma _{xx}&sigma _{xy}\sigma _{yx}&sigma _{yy}\end{matrix}}right]equiv left[{begin{matrix}sigma _{x}&tau _{xy}\tau _{yx}&sigma _{y}\end{matrix}}right]}$

где ${displaystyle mathbf {T} ^{(e_{n})}}$ — вектор механического напряжения, действующий на поверхность ${displaystyle e_{n}}$ .

В случае матричной записи (в декартовой системе координат) величины $sigma_{ij}$ (компоненты тензора напряжений), описывают напряжения испытываемые телом в какой-то заданной точке. В данной точке проводятся умозрительные плоскости с нормалями ${displaystyle color {Red}e_{1}}$ , ${displaystyle color {Red}e_{2}}$ , … Нормальные компоненты сил, действующих на данные плоскости, записываются на главной диагонали $sigma_{11}$ , $sigma_{22}$ , …, а в остальных позициях стоят касательные компоненты ${displaystyle tau _{yx}}$ , $tau_{xy}$ , … векторов напряжений на этих плоскостях.

В случае больших деформаций (конечные деформации), приходится использовать такие подходы как тензор напряжений Пиолы — Кирхгофа, тензор Биота или тензор напряжения Кирхгофа.

Физический смысл тензора напряжений на примере в двумерном случае[править | править код]

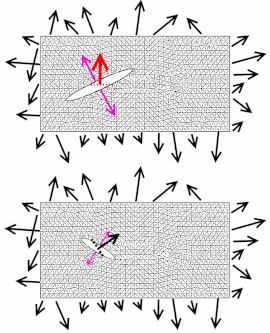
Рис. Б. Различный отклик ткани на разнонаправленные разрезы , совершённые в одной и той же точке.

Простейшей иллюстрацией, позволяющей понять физический смысл тензора напряжений, будет, вероятно, не рассмотрение случая напряжения в некотором объёмном теле, а, наоборот, рассмотрение напряжения в плоском двумерном теле. Для этого рассмотрим напряжение отрезка ткани под внешней нагрузкой (см. рис. А).

На рисунке изображен прямоугольный кусок ткани под внешней нагрузкой, которая изображена чёрными стрелками по периметру прямоугольника. В данном случае нагрузкой может служить растяжение её руками в разные стороны, или натягивание ткани на какую-то сложную форму.

Интуитивно понятно, что из-за формы, ориентации молекул, атомных слоёв и разного плетения волокон (на рис.А расположение волокон схематично изображено мелкой серой сеткой) в разных точках ткани напряжение будет разным: где-то будут области, которые подвергаются вертикальному растяжению, а в других областях волокна будут испытывать напряжение сдвига.

Каждой точке на поверхности отрезка ткани соответствует своё уникальное значение напряжения. Это значит, что каждой точке $(x_{0},y_{0})$ ткани соответствует свой математический объект — — тензор второго ранга.

Чтобы понять, как тензор показывает состояние напряжения в какой-нибудь точке ткани, можно сделать маленький разрез в данной точке и понаблюдать, в каком направлении будут расходиться данные разрезы. Так, на рис. А мы сделали два разреза в разных точках ткани: направление одного разреза показано красной пунктирной линией, направление другого — синей пунктирной линией. Чтобы математически описать направление данных разрезов, используется вектор нормали (вектор, перпендикулярный плоскости разреза). Так, у разреза вектор нормали красный и направлен перпендикулярно плоскости разреза, у разреза ситуация похожая. Направление роста разрыва в ткани обозначено фиолетовыми векторами .

Для предсказания того, куда будет развиваться разрез, как раз и используется тензор напряжений. Математически данное предсказание выглядело бы так:

Определить «тензорную функцию» ${displaystyle f(x,y)=mathbf {T_{x,y}} ,}$ аргументами которой являются координаты точек внутри тела, а значением является тензор, описывающий состояние напряжения в заданной точке тела.
Выбрать точку в теле, например, ${displaystyle (x_{0},y_{0}),}$ и из получить тензор, который описывает состояние напряжения в точке ${displaystyle mathbf {T_{x_{0},y_{0}}} .}$
Определить направление плоскости , в которой будет проводиться разрез тела.
Умножить направление разреза в точке $(x_{0},y_{0})$ на тензор напряжения в данной точке ${displaystyle mathbf {T_{x_{0},y_{0}}} }$ , что в математической записи выглядит как ${displaystyle {mathbf {T_{x_{0},y_{0}}} color {red}{vec {c}}}=color {RedViolet}{vec {t}}.}$
Вектор и покажет, куда будет распространяться разрез в точке $(x_{0},y_{0})$ .

Разрезы и — это вектора, а напряжение в точке — это тензор.

Следует понимать, что разнонаправленные разрезы, совершённые в одной и той же точке тела, повлекут за собой различный отклик ткани. Данное явление показано на рис. Б, где разрастание разрыва ткани происходит по разным направлениям и с разной интенсивностью , в ответ на различные направления первоначальных разрезов и , совершённых в одной и той же точке.

Как раз для описания такого сложного поведения и используются тензоры, которые в данном случае служат векторными функциями ${displaystyle f_{x_{0},y_{0}}({vec {c}})=mathbf {T_{x_{0},y_{0}}} {vec {c}}={vec {t}}}$ , определёнными в каждой точке $(x_{0},y_{0})$ куска ткани, которые ставят все возможные направления разрезов в соответствие со всеми возможными направлениями дальнейшего разрыва ткани.

Вывод компонентов тензора[править | править код]

Компоненты тензора напряжений $sigma_{ij}$ в декартовой системе координат Ox_i (то есть Oxyz ) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади $dS_{i}$ . На каждой грани $dS_{i}$ параллелепипеда действуют поверхностные силы $dF_{i}$ . Если обозначить проекции этих сил на оси $Ox_{j}$ как $dF_{ij}$ , то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:

$sigma_{ij} = frac{ d F_{ij}}{dS_{i}}$

По индексу здесь суммирования нет. Компоненты $sigma_{11}$ , $sigma_{22}$ , $sigma_{33}$ , обозначаемые также как $sigma_{xx}$ , $sigma_{yy}$ , $sigma_{zz}$ — это нормальные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на нормаль к площади рассматриваемой грани $dS_{i}$ :

$sigma_{11} = frac{ d F_{11}}{dS_{1}}$

и т. д.

Компоненты $sigma_{12}$ , $sigma_{23}$ , $sigma_{31}$ , обозначаемые также как $tau_{xy}$ , $tau_{yz}$ , $tau_{zx}$ — это касательные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на касательные направления к площади рассматриваемой грани $dS_{i}$ :

$sigma_{12} = frac{ d F_{12}}{dS_{1}}$

и т. д.

При отсутствии собственного момента импульса сплошной среды, а также объёмных и поверхностных пар тензор напряжений симметричен (так называемый закон парности касательных напряжений), что является следствием уравнения баланса момента импульса. В частности, тензор напряжений симметричен в классической теории упругости и в гидродинамике идеальной и линейно-вязкой жидкостей.

Тензор напряжений в релятивистской физике[править | править код]

С точки зрения теории относительности, компоненты тензора напряжений являются девятью пространственными компонентами тензора энергии-импульса.

Тензор напряжений в классической электродинамике[править | править код]

В классической электродинамике тензор напряжений электромагнитного поля (максвелловский тензор напряжений^[1], тензор натяжений Максвелла^[2]) в Международной системе единиц (СИ) имеет вид:

$T_{ij} = E_i D_j + B_i H_j - frac{1}{2}delta_{ij}(mathbf E cdot mathbf D + mathbf B cdot mathbf H) = E_i D_j + B_i H_j - delta_{ij}W,$

где — плотность энергии электромагнитного поля.

См. также[править | править код]

Тензор энергии-импульса
Теория упругости
Тензор деформации
Тензор упругости
Закон Гука

Примечания[править | править код]

↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 115. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
↑ Степановский Ю. П. Максвелла тензор натяжений // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 32—33. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

Литература[править | править код]

Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970. 492 c.
Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Наука, 1975. 592 с.
Димитриенко Ю. И. Нелинейная механика сплошной среды. М.: Физматлит, 2010.

Источник

Вектор
напряжений
p_n
является физическим объектом, имеющим
длину, направление и точку приложения.
В этом смысле он обладает векторными
свойствами. Однако этому объекту присущи
некоторые свойства, не характерные для
векторов. В частности, величина и
направление вектора напряжений зависят
от ориентации вектора n
нормали бесконечно малого элемента
поверхности dF.
Совокупность всех возможных пар векторов
п,
р_n
в точке определяет напряженное
состояние
в данной точке. Однако для полного
описания напряженного состояния в точке
нет необходимости задавать бесконечное
множество направлений вектора
n,
достаточно определить векторы напряжений
на трех взаимно перпендикулярных
элементарных площадках. Напряжения на
произвольно ориентированных площадках
могут быть выражены через эти три вектора
напряжений. Так, что ось Z
–
продольная ось бруса, а X
и
Y
– координаты любой точки его поперечного
сечения.

Проведем
через точку М
три взаимно перпендикулярных плоскости
с векторами нормалей, направления
которых совпадают с направлениями
координатных осей. Элементарные площадки
образуем дополнительными сечениями,
параллельными исходным плоскостям и
отстоящими от них на бесконечно малые
расстояния dx,
dy,
dz.
В результате в окрестности точки М
получим бесконечно малый параллелепипед,
поверхность которого образована
элементарными площадками dF_х=dydz,
dF_н==dxdz,
dF_я=dxdy.

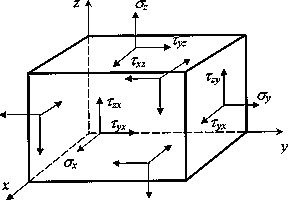
Разложим
каждый вектор напряжений на составляющие
вдоль координатных осей (рис. 4.1). На
каждой площадке действует одно нормальное
напряжение
,

,

,
где индекс обозначает направление
вектора нормали к площадке и два
касательных
напряжения
с
двумя индексами, из которых первый
указывает направление действия компоненты
напряжения, второй—направление вектора
нормали к площадке.

Рис.4.1.
Компоненты тензора напряженного
состояния

Совокупность
девяти компонент напряжений (по три на
каждой из трех взаимно перпендикулярных
площадок) представляет собой объект,
называемый тензором
напряжений
в точке. Тензор можно представить в виде
матрицы:

Для
компонент тензора напряжений общепринятым
является следующее правило знаков:
компонента считается положительной,
если на площадке с положительной внешней
нормалью (т. е. направленной вдоль одной
из координатных осей) эта компонента
направлена в сторону положительного
направления соответствующей оси. На
рис. 4.1 все компоненты тензора напряжений
изображены положительными. На площадках
с отрицательной внешней нормалью (грани
параллелепипеда, не видимые на рис. 4.1)
положительная компонента направлена
в противоположном направлении. Напряжения
на трех взаимно ортогональных площадках
с отрицательными направлениями нормалей
также характеризуют напряженное
состояние в точке. Эти напряжения,
являющиеся компонентами тензора
напряжений, определяются аналогично
напряжениям на площадках с положительной
нормалью.

Тензор
напряжений обладает свойством симметрии.
Для доказательства этого свойства
рассмотрим элементарный параллелепипед
с действующими на его площадках
компонентами тензора напряжений. Так
как тело находится в равновесии,
следовательно, находится в равновесии
любая его часть, в том числе и элементарный
объем. Запишем одно из шести уравнений
равновесия этого объема, а именно —
сумму моментов всех сил относительно
оси Ох.
Все силы, кроме двух, либо не создают
момента относительно ocи Ох,
либо взаимно уничтожаются. Отличные от
нуля моменты создают компоненты
(верхняя
грань) и(правая
грань):

Откуда
следует:

Аналогично,
приравнивая нулю сумму моментов всех
сил относительно осей Оу
и Ог,
получим еще два соотношения

Эти
условия симметрии тензора напряжений
называются также условиями парности
касательных напряжений:
касательные напряжения, действующие
по двум взаимно перпендикулярным
площадкам в направлениях, ортогональных
ребру, образованному пересечением этих
площадок, равны по величине. С учетом
этих свойств из девяти компонент тензора
напряжений независимыми оказываются
шесть компонент.

Покажем
теперь, что компоненты тензора напряжений
определенные для трех взаимно
перпендикулярных площадок, полностью
характеризуют напряженное состояние
в точке, т. е. позволяют вычислить
компоненты вектора напряжений на
площадках, произвольно ориентированных
относительно выбранной системы координат.
Для этого рассмотрим элементарный
объем, образованный сечением
параллелепипеда, изображенного на рис.
4.2 плоскостью, пересекающей координатные
оси и имеющей единичный вектор нормали

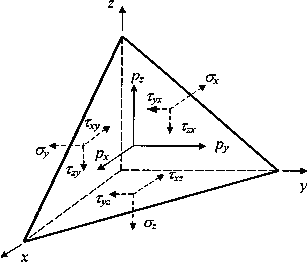
Рис.4.2.
Элементарный четырехгранник с компонентами
напряженного состояния.

п
с компонентами n_x,
n_y,
n_z.
На гранях полученного таким образом
бесконечно малого тетраэдра действуют
напряжения, показанные на рис. 4.2. При
этом вектор напряжений p_n
на наклонной площадке разложен па
составляющие р_x,
р_y,
р_z
вдоль координатных осей. Площади граней,
ортогональных координатным осям и
вектору нормали, обозначим соответственно
dF_x,
dF_y,
dF_z,
dF.
Эти площади связаны между собой
соотношениями

dF_x=dFn_x,
dF_y=dFn_y,
dF_z=dFn_z

вытекающими
из того, что грани, ортогональные
координатным осям, есть проекции
наклонной площадки на соответствующую
координатную плоскость.

Проектируя
силы, действующие на гранях элементарного
тетраэдра, на координатные оси, получим
уравнения равновесия для рассматриваемого
объема. Например, проекции всех
поверхностных сил на ось Ох
дают

С
учетом соотношений после сокращения
на dF
получим уравнение, связывающее проекцию
р_x
вектора напряжений с соответствующими
компонентами тензора напряжений.
Объединяя это уравнение с двумя
аналогичными уравнениями, полученными
проектированием сил на оси Оy
и Оz,
приходим к следующим соотношениям

носящим
название формул
Коши.
Эти формулы определяют вектор напряжений
на произвольно выбранной площадке с
вектором п
через компоненты тензора напряжений.

Формулы
Коши позволяют вычислить через компоненты
тензора напряжений

полное
напряжение

нормальное
напряжение

и
касательное напряжение

Среди
всех возможных направлений вектора
нормали n
существуют такие направления, для
которых вектор напряжений p_n
параллелен вектору п.
На соответствующих площадках действуют
только нормальные напряжения, а
касательные напряжения отсутствуют.
Такие
площадки
называются главными,
а нормальные напряжения на этих площадках
называются главными
напряжениями.
Пусть площадка с единичным вектором
нормали является главной. Условия
коллинеарности векторов p_n
и n
есть условия пропорциональности их
компонент:

С
учетом формул Коши получим систему
линейных однородных уравнений относительно
неизвестных компонент n_x,
n_y,
n_z
вектора нормали к главной площадке

Эта
система уравнений имеет ненулевое
решение, если определитель, составленный
из коэффициентов уравнений, обращается
в нуль:

Раскрывая
определитель, приходим к кубическому
уравнению относительно главного
напряжения

Здесь
введены обозначения

Выше
написанное уравнение называется
характеристическим
уравнением
для тензора напряжений. Коэффициенты
этого уравнения называются инвариантами
тензора напряжений. Решение
кубического уравнения имеет три
вещественных корня
которые
обычно упорядочиваются.

Каждому
значению
(j=1,
2, 3) соответствует вектор n
^j,
характеризующий
положение j-й
главной площадки, с компонентами n
^j₁,
n ^j₂,
n ^j₃.
Для нахождения этих компонент достаточно
в уравнения подставить найденное
значение
и
решить любые два из этих уравнений
совместно с условием нормировки

Главные
напряжения обладают важным свойством:
по сравнению со всеми другими площадками
нормальные напряжения на главных
площадках принимают экстремальные
значения. Для доказательства этого
свойства достаточно исследовать на
экстремум нормальное напряжение как
функцию n_x,
n_y,
n_z
при дополнительном ограничении. Можно
показать, что три главные площадки,
соответствующие главным напряжениям
,
взаимно перпендикулярны или, что то же
самое, векторыn^j
и n^k,
соответствующие различным значениям
j
и k
—;
ортогональны. Условие ортогональности
имеет вид

Кубическое
уравнение можно переписать в виде

Получим
следующие выражения для инвариантов
через главные напряжения:

Термин
«инвариантность» обозначает независимость
объекта от выбора системы координат.

Введем
среднее напряжение по формуле

Тензор
напряжений можно представить в виде
суммы двух тензоров
,
где

Первый
тензор называется шаровым,
он характеризует изменение объема тела
без изменения его формы. Второй тензор,
называемый девиатором,
характеризует изменение формы.
Особенностью девиатора напряжений
является равенство нулю его первого
инварианта:

Найдем
положение площадок, на которых касательные
напряжения принимают экстремальные
значения. Для этого нужно отыскать
экстремумы касательного напряжения.
Экстремальные
касательные напряжения
действуют на площадках, параллельных
одной из главных осей и образующих с
двумя другими осями угол
.
По величине эти напряжения равны

При
этом на площадках с экстремальными
касательными напряжениями присутствуют
нормальные напряжения, которые равны

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим приведенный в лекции 5 элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а именно — сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты (верхняя грань) и (права грань):

После сокращения на элемент объема dV=dxdydz получим

Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Ог, получим еще два соотношения

Эти условия симметрии и тензора напряжений называются также условиями парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.

Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 1, плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали

Рис.1. Элементарный четырехгранник с компонентами напряженного состояния.

п с компонентами n_x, n_y, n_z. На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 1. При этом вектор напряжений p_n на наклонной площадке разложен па составляющие р_x, р_y, р_z вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dF_x, dF_y, dF_z, dF. Эти площади связаны между собой соотношениями

dF_x=dFn_x, dF_y=dFn_y, dF_z=dFn_z

(1)

вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.

Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают

С учетом соотношений (1) после сокращения на dF получим уравнение, связывающее проекцию р_x вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz, приходим к следующим соотношениям

(2)

носящим название формул Коши. Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором п через компоненты тензора напряжений.

Формулы (2) позволяют вычислить через компоненты тензора напряжений

полное напряжение

(3)

нормальное напряжение

(4)

и касательное напряжение

(5)

Среди всех возможных направлений вектора нормали n существуют такие направления, для которых вектор напряжений p_n параллелен вектору п. На соответствующих площадках действуют только нормальные напряжения, а касательные напряжения отсутствуют. Такие площадки называются главными, а нормальные напряжения на этих площадках называются главными напряжениями. Пусть площадка с единичным вектором нормали является главной. Условия коллинеарности векторов p_n и n есть условия пропорциональности их компонент:

С учетом формул Коши получим систему линейных однородных уравнений относительно неизвестных компонент n_x, n_y, n_z вектора нормали к главной площадке

Эта система уравнений имеет ненулевое решение, если определитель, составленный из коэффициентов уравнений, обращается в нуль:

(6)

Раскрывая определитель, приходим к кубическому уравнению относительно главного напряжения

(7)

Здесь введены обозначения

Уравнение (7) называется характеристическим уравнением для тензора напряжений. Коэффициенты (9) этого уравнения называются инвариантами тензора напряжений. Решение кубического уравнения (8) имеет три вещественных корня которые обычно упорядочиваются .

Каждому значению (j=1, 2, 3) соответствует вектор n ^j, характеризующий положение j-й главной площадки, с компонентами n ^j₁, n ^j₂, n ^j₃. Для нахождения этих компонент достаточно в уравнения подставить найденное значение и решить любые два из этих уравнений совместно с условием нормировки

Главные напряжения обладают важным свойством: по сравнению со всеми другими площадками нормальные напряжения на главных площадках принимают экстремальные значения. Для доказательства этого свойства достаточно исследовать на экстремум нормальное напряжение как функцию n_x, n_y, n_z при дополнительном ограничении. Можно показать, что три главные площадки, соответствующие главным напряжениям , взаимно перпендикулярны или, что то же самое, векторы n^j и n^k, соответствующие различным значениям j и k —; ортогональны. Условие ортогональности имеет вид

(10)

Кубическое уравнение (8) можно переписать в виде

(11)

Приводя это уравнение к виду (8), получим следующие выражения для инвариантов (9) через главные напряжения:

(12)

Термин «инвариантность» обозначает независимость некоторой величины от выбора системы координат.

Введем среднее напряжение по формуле

(13)

Тензор напряжений можно представить в виде суммы двух тензоров , где

(14)

Первый тензор называется шаровым, он характеризует изменение объема тела без изменения его формы. Второй тензор, называемый девиатором, характеризует изменение формы. Особенностью девиатора напряжений является равенство нулю его первого инварианта:

(15)

Найдем положение площадок, на которых касательные напряжения принимают экстремальные значения. Для этого нужно отыскать экстремумы касательного напряжения. Экстремальные касательные напряжения действуют на площадках, параллельных одной из главных осей и образующих с двумя другими осями угол . По величине эти напряжения равны

(16)

При этом на площадках с экспериментальными касательными напряжениями присутствуют нормальные напряжения, которые равны

Фигура, которую образуют площадки с экстремальными касательными напряжениями, изображена на рис. 2. Она принадлежит к классу параллелоэдров и представляет собой 12-гранник с гранями в виде ромбов, отношение диагоналей которых равно .

Рис.2. Параллепоэдр распределения экстремальных касательных напряжений

Таким образом, общая теория напряженного состояния позволяет охватывать, в целом, весь комплекс видов сопротивлений, как простого, так и сложного характера.

Дальше…

Источник

Физический смысл тензора напряжений на примере в двумерном случае[править | править код]

Вывод компонентов тензора[править | править код]

Тензор напряжений в релятивистской физике[править | править код]

Тензор напряжений в классической электродинамике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти работу в радужном хмао

Как найти замок с приведением

Как найти множество значений функции пример

Добавить комментарий Отменить ответ