Бинарные отношения.
Пусть А и В – два произвольных
множества.
Определение 3. Бинарным
отношением
![]()
из множества А в
множество В называется
всякое подмножество прямого произведения
А на В; если А=В, то говорят
о бинарном отношении на множестве
А. Обозначение:
![]()
Пример 2.
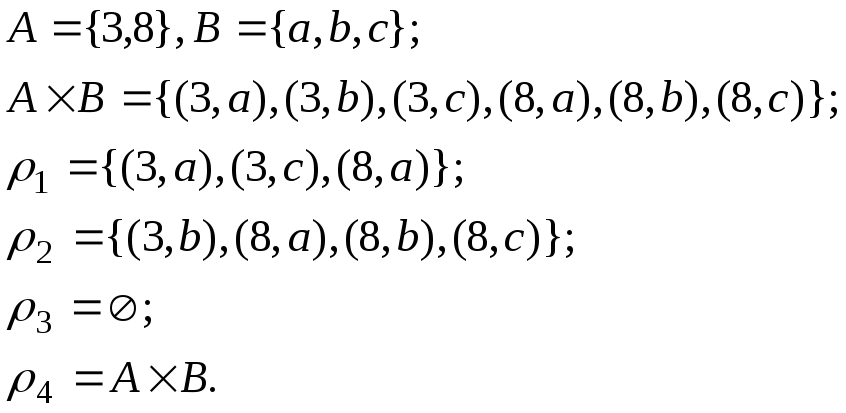
Используют две формы записи принадлежности
некоторой упорядоченной пары заданному
бинарному отношению:
Инфиксная:
![]()
Префиксная:
![]()
По аналогии с бинарным отношением вводят
понятие n – арного
отношения
произвольного подмножества упорядоченных
n – ок, выбранных из
прямого произведения данных n
множеств.
Пример 3.
M – множество;
2M – булеан
множества M;
бинарное отношение включения на
![]()
определяется так:
![]()
Определение 4. Множество
точек плоскости, координаты которых
(x,y),
образуют упорядоченные пары некоторого
бинарного отношения
![]()
называется графиком данного
бинарного отношения.
Пример 4.
1).
![]()
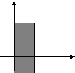
2
0
График
![]()
2).
![]()

График
![]()
Бинарные отношения – это множества, их
можно объединять, пересекать, дополнять
и т. д.
Пример 5.
1).
![]()
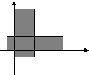
2
0
1
График
![]()
2).
![]()

0
1
2
График
![]()
Пусть
![]()
Определение 5. Областью
определения бинарного отношения
(обозначение:![]() ),
),
называется подмножество множества А
такое, что
![]()
Пусть
![]()
Определение 6. Областью
значения бинарного отношения
(обозначение:
![]() ),
),
называется подмножество множества В
такое, что
![]()
Пусть
![]()
Определение 7. Отношением,
обратным к отношению
![]() ,
,
называют подмножество прямого произведения
![]() ,
,
такое, что
![]() .
.
Пример 6.
![]()
![]()
Определение 8. Дополнением
отношения
![]()
называют бинарное отношение, определяемое
как множество всех упорядоченных пар,
не входящих в
![]() :
:
![]()
Пример 7.
![]()
![]()
Определение 9. Тождественным
отношением I
называют подмножество А2
такое, что
![]()
Пример 8.
![]()
Определение 10. Универсальным
отношением U
называют само прямое произведение
множеств
![]()
Композиция отношений.
Пусть
![]()
Определение 11. Композицией
отношений
![]()
называют бинарное отношение из множества
А во множество В, определяемое
так:
![]()
Пример 9.
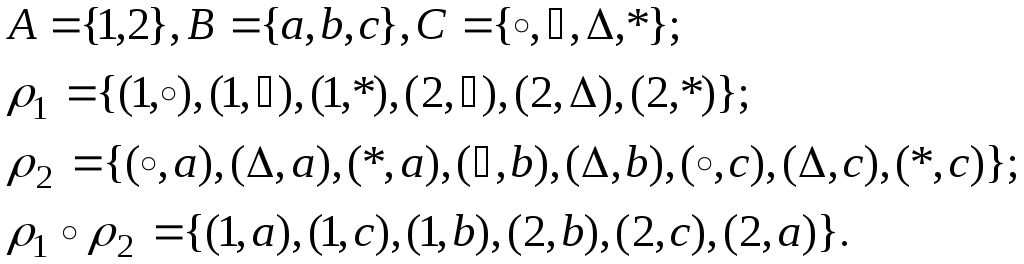
Пусть
![]()
– это отношение, заданное на множестве
А, тогда бинарное отношение
![]()
называется
-
.рефлексивным, если
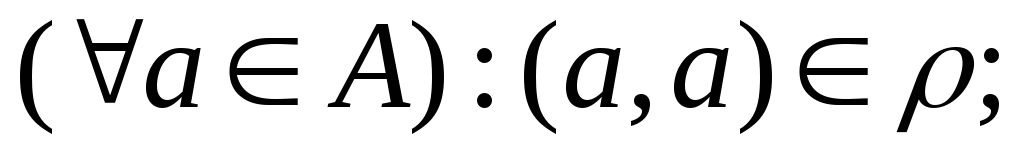
-
.антирефлексивным, если
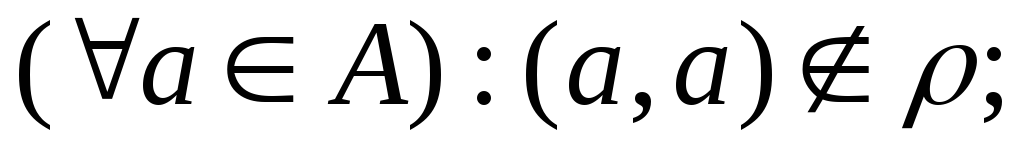
-
.симметричным, если
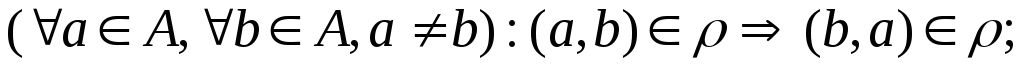
-
.антисимметричным, если
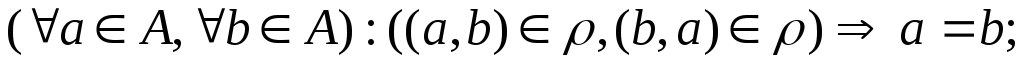
-
.транзитивным, если
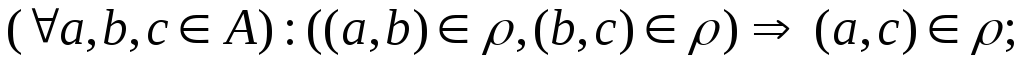
-
.полным если
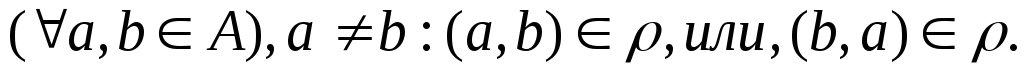
Пример 10.
Является ли
![]()
рефлексивным, антирефлексивным,
симметричным, антисимметричным, полным?
![]()
1).
![]()
нерефлексивно;
например,
![]()
2).
![]()
неантирефлексивно;
![]() ,
,
так как уравнение
![]()
имеет решения:
![]()
3).
![]()
несимметрично;
например,

4).
![]()
не антисимметрично.
Пусть
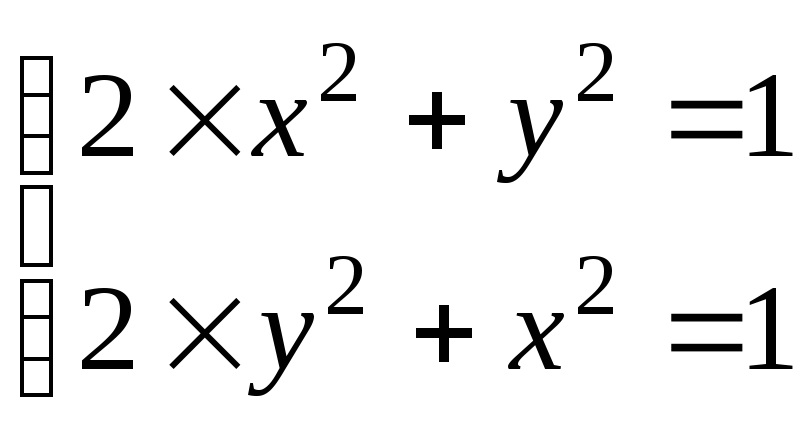
![]()
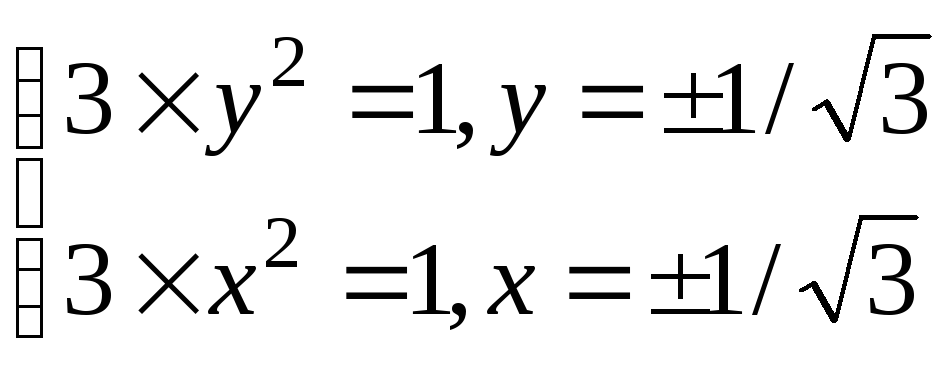 .
.
Тогда
![]()
5).
![]()
не транзитивно:
например
![]()
но
![]()
6).
![]()
не полное, что очевидно.
Пример 11.
![]()
1).
![]()
рефлексивно.
2). Пусть
![]()
тогда
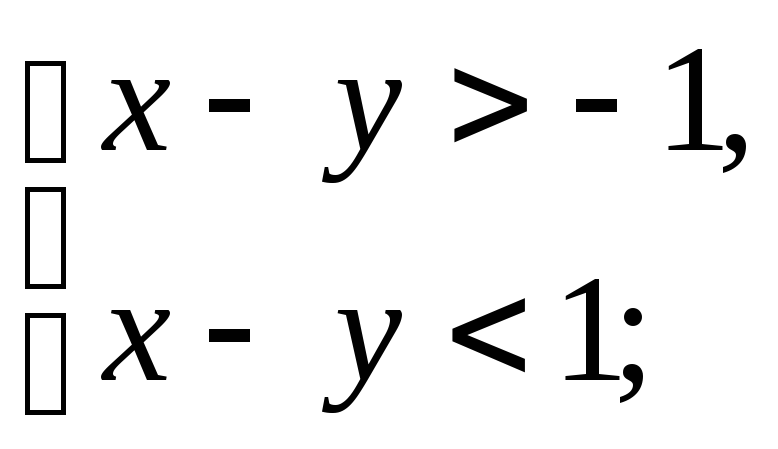
![]()
т.к. х, у – целые числа ![]()
антисимметрично.
-
Пусть
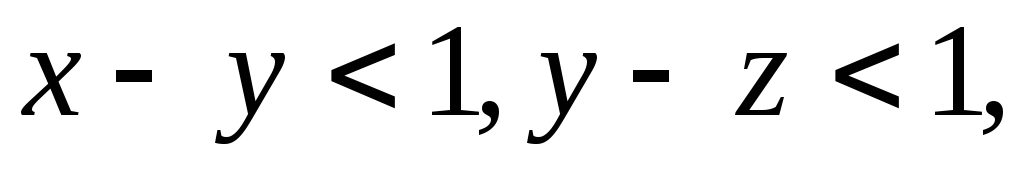
тогда
![]()
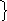
![]()
Значит
![]()
транзитивно.
-
Если
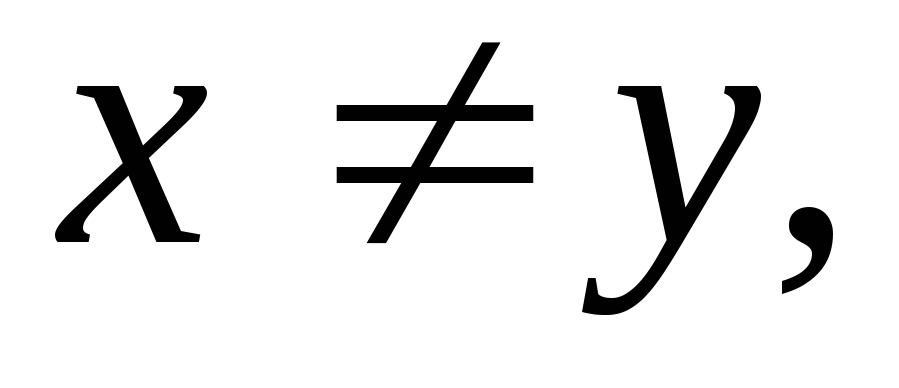
то или
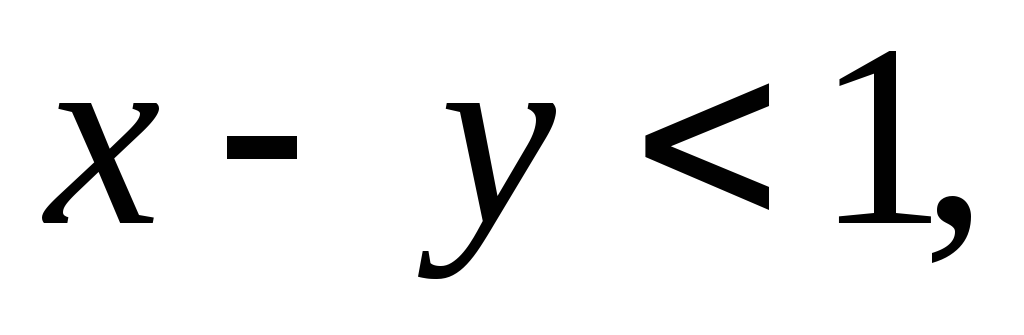
или
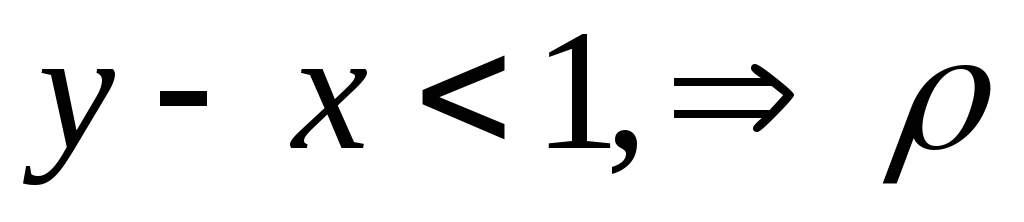
полное отношение.
Теорема о свойствах бинарного отношения.
Пусть
![]()
отношение на
множестве А(![]() ),
),
тогда справедливы следующие утверждения:
-
 -
-
рефлексивно

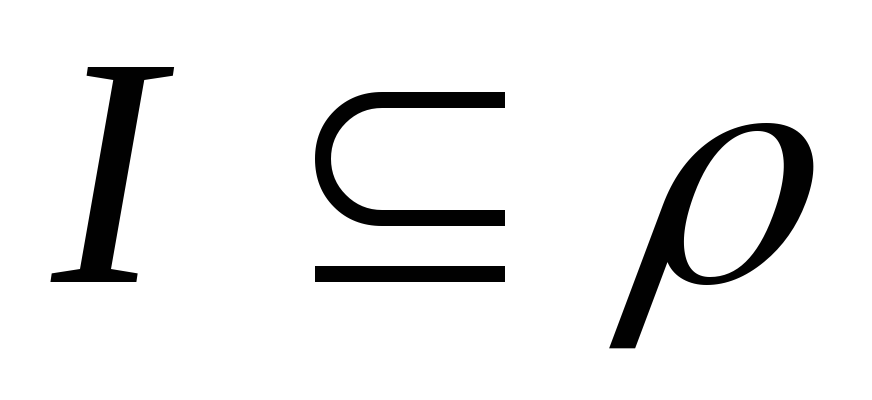 ;
; -

симметрично
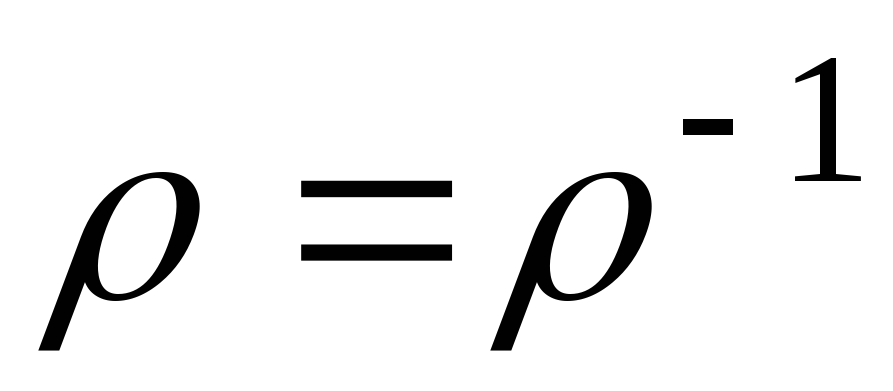 ;
; -

транзитивно
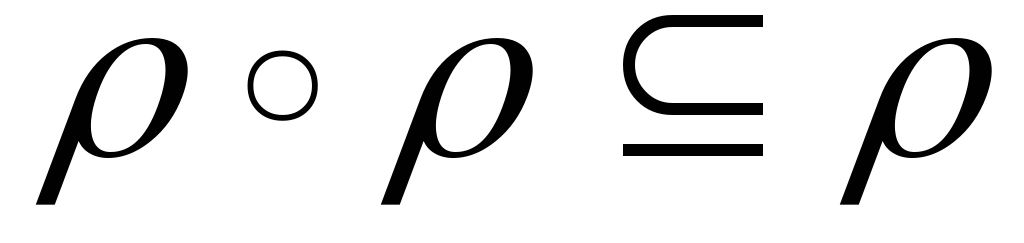 ;
; -

антирефлексивно
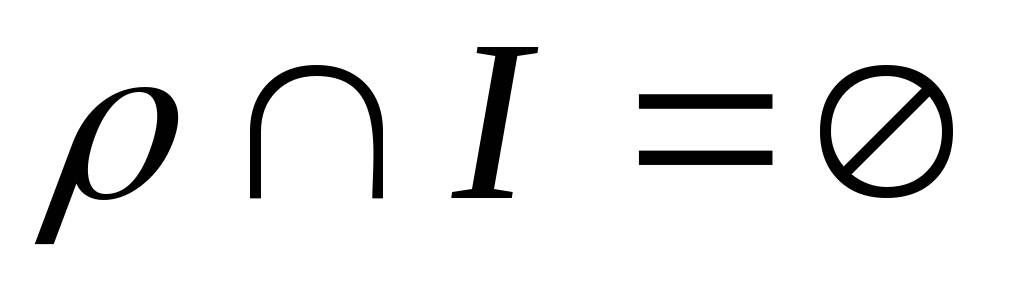 ;
; -

антисимметрично
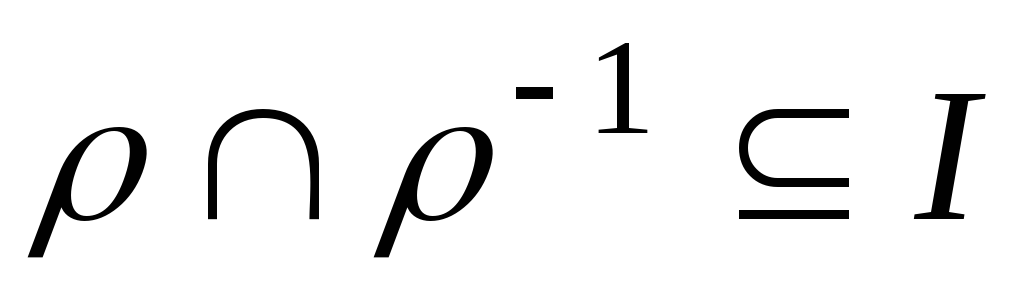 ;
; -

полно
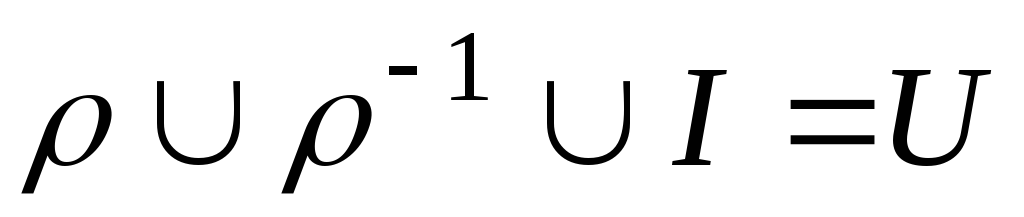 .
.
Доказательство.
1.
![]()
Пусть
![]()
рефлексивно,
![]() ;
;
1.
![]()
Пусть
![]() ,
,
тогда
![]()
– рефлексивно.
2.
![]()
Пусть
![]()
симметрично,
![]() .
.
Пусть
![]() .
.
Пусть
![]() .
.
Значит,
![]() .
.
2.
![]()
Пусть
![]() .
.
Тогда
![]()
– симметрично.
3.
![]()
Пусть
![]()
транзитивно,
![]()
и
![]()
Пусть
![]() 🙁
🙁![]() )
)![]()
и (![]() ;
;
3.
![]()
Пусть
![]() .
.
Пусть (![]() )
)![]() и
и
(![]()
![]() –
–
транзитивно.
4.
![]()
Пусть
![]()
антирефлексивно,
(![]() ):
):![]() ;
;
4.
![]()
Пусть
![]() :
:
![]()
![]()
антирефлексивно.
5.
![]()
Пусть
![]()
антисимметрично
(![]() ):(
):(![]() )
)![]()
и
![]() .
.
Если
![]()
и (![]() )
)![]() ,
,
то (![]() )
)![]() и
и
![]() ,
,
пересечение множеств
![]()
и
![]()
по парам, состоящих из разных элементов,
пусто
![]()
эти множества в качестве общих могут
иметь только элементы вида
![]() ,
,
что и означает:
![]() ;
;
5.
![]()
Пусть
![]()
это означает, что в пересечение
![]()
могут входить только пары вида
![]()
![]()
если
![]()
и
![]() ,
,
то
![]() .
.
6.
![]()
Пусть
![]() -полно,
-полно,
(![]() ,
,
![]() ):
):
(![]() )
)
или
![]()
Но
![]()
![]()
![]() ,
,![]() обе
обе
пары
![]()
и
![]()
принадлежат объединению:
![]()
![]()
![]() ;
;
-
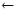
Пусть
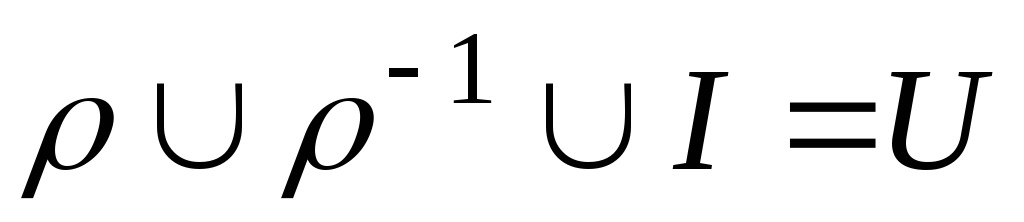 .
.
Если
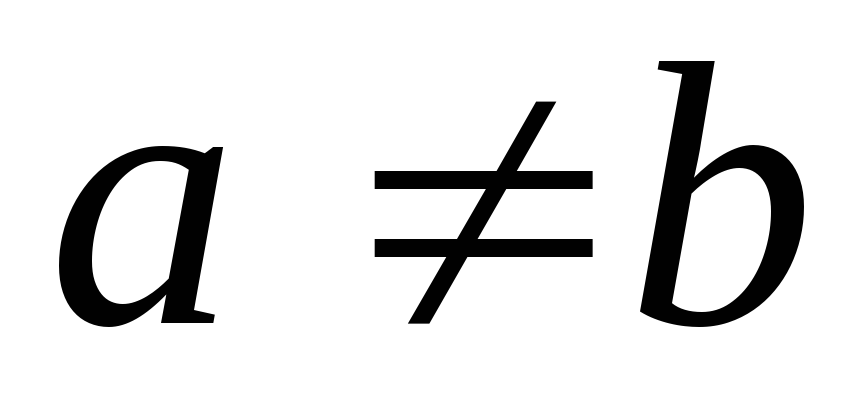 ,
,
то
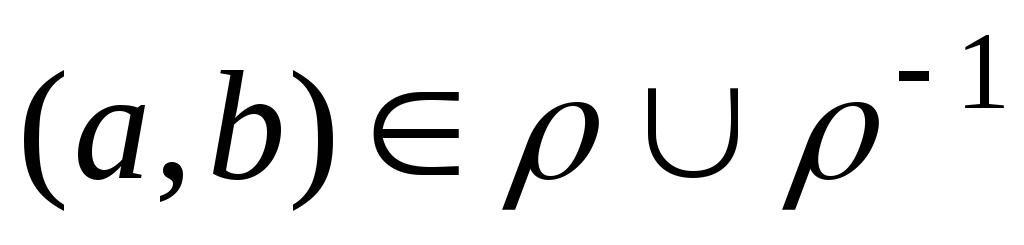 .
.
Либо
![]() .
.
Либо
![]()
![]()
– полно.
ЛЕКЦИЯ 7.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Операции над соответствиями на множествах
Поскольку соответствия можно считать множествами, то все операции над множествами (пересечение, объединение, разность, дополнение и т.д.) можно применить и к соответствиям. Заметим, что, говоря о дополнении соответствия из в
, мы имеем в виду дополнение до универсального соответствия из
в
, т.е. до декартова произведения
. Естественно, что и равенство соответствий можно трактовать как равенство множеств.
В то же время на соответствия можно распространить операции, определяемые для отображений. Мы рассмотрим здесь две такие операции.
Композиция соответствии. Следуя аналогии с композицией отображнений, композицией (произведением) соответствий и
называют соответствие
(1.3)
Поясним построение композиции двух соответствий. Обратимся сначала к отображениям (как частным случаям соответствий). Пусть заданы отображения (возможно, частичные): из
в
и
из
в
. Композиция
определяется как отображение из
в
, задаваемое формулой
. Тем самым задается график отображения
, т.е. множество упорядоченных пар
, таких, что
. При этом упорядоченная пара
будет принадлежать графику отображения
, если и только если найдется элемент
, такой, что
и
. Таким образом, график композиции отображений
и
есть
(1.4)
Необходимо заметить, что запись означает
, т.е. отображения в композиции пишутся в порядке, обратном тому, в каком они применяются. Мы же будем везде использовать запись
, полагая, что
и порядок записи отображений в композиции совпадает с порядком их применения. Это обусловлено тем, что композиция отображений определяется нами как частный случай композиции соответствий, при записи которой естественным оказывается именно такой порядок.
Легко видеть, что (1.4) есть частный случай (1.3). Отметим, что при построении композиции отображений обычно предполагают, что пересечение области значений отображения и области определения отображения
не пусто
, поскольку в противном случае композиция была бы пуста. Для отображений, не являющихся частичными,
, так как
. Поэтому в данном случае пересечение
всегда не пусто.
Полезно отметить также, что если и
— биекции, то и композиция их тоже будет биекцией.
Вернемся к рассмотрению композиции соответствий . Полагая, что область определения
соответствия
не пуста, возьмем произвольный элемент
. Пусть сечение
соответствия
не пусто и найдется такой элемент
, что сечение
также не пусто. Тогда непустое множество
будет подмножеством сечения соответствия
в точке
. Сечением соответствия
в точке
будет непустое в силу сделанных предположений множество всех таких упорядоченных пар
, что
, а
для некоторого
. Говоря неформально, нужно перебрать все элементы
из сечения
. Таким образом, различие в построении композиции соответствий и композиции отображений заключается в том, что “промежуточный” элемент z в общем случае не единственный и каждому такому элементу также ставится в соответствие не единственный элемент
.
Пример 1.8. Соответствие возьмем из примера 1.3. Соответствие
зададим как соответствие из множества программ
в множество заказчиков программного обеспечения
. Пусть
Рассмотрим процесс построения композиции соответствий и
. Начнем с элемента
. Имеем
Отсюда получаем сечение композиции по элементу
Рассуждая аналогично, получим и
.
Построение графа композиции проиллюстрировано на рис. 1.3.
Отметим, что область определения композиции соответствий содержится в области определения первого соответствия, а область значений композиции соответствий — в области значений второго соответствия. Из приведенных рассуждений следует, что для того, чтобы композиция соответствий была отлична от пустого соответствия, необходимо и достаточно, чтобы пересечение области значений первого соответствия и области определения второго соответствия было не пусто.
К определению композиции соответствий можно подойти с более общих позиций. Пусть и
. При этом на множества
и
априори не накладывается никаких органичений. Композиция
соответствий
и
в этом случае также определяется соотношением (1.3). Чтобы такая композиция была отлична от пустого соответствия, необходимо и достаточно выполнение условия
. В частности,
всякий раз, когда
.
Пример 1.9. Рассмотрим соответствие из множества
в множество
и соответствие
из множества
в множество
. В данном случае
, но
, поскольку
Заметим, что композиция соответствий и
не коммутативна, т.е. в общем случае
, поскольку
, а
.
Композиция бинарного отношения на множестве
Бинарное отношение на множестве является частным случаем соответствия. Для двух бинарных отношении и
, заданных на множестве
, их композиция
(1.3) как соответствий является бинарным отношением на том же множестве
. В этом случае говорят о композиции бинарных отношений на множестве
.
Композицию бинарного отношения
на некотором множестве с самим собой называют квадратом бинарного отношения
и обозначают
.
Рассмотрим пример построения композиции бинарных отношений на множестве и покажем, что в общем случае для двух бинарных отношений и
также имеет место неравенство
, хотя обе композиции, в отличие от аналогичных композиций двух произвольных соответствий, заданы на одном и том же множестве.
Пример 1.10. а. Зададим на множестве бинарные отношения
и найдем композицию
, если
.
Имеем и
. Следовательно,
. Далее
и
. Так как
, то в итоге получим
. Построение композиции проиллюстрировано на рис. 1.4,а.
Найдем композицию . Поскольку
, а
, то
. Аналогично
, а
, поэтому
. Далее
, поэтому
, а
и
. Построение композиции проиллюстрировано на рис. 1.4,б.
Легко видеть, что .
б. Пусть отношение на множестве действительных чисел определено как функция
. Найдем квадрат этого отношения (линейной функции от одного переменного).
Согласно (1.4), это будет функция , такая, что
, то есть
. Это тоже линейная функция, но с другими коэффициентами.
Свойства композиции соответствий
Приведем некоторые свойства композиции соответствий:
1) ;
2) для любого соответствия имеет место
;
3) ;
4) для любого бинарного отношения на множестве имеет место равенство
.
Эти свойства нетрудно доказать методом двух включений. Рассмотрим в качестве примера доказательство свойства 3. Пусть некоторая упорядоченная пара принадлежит композиции
. Тогда, согласно (1.3), найдется такой элемент
, что
и
. Последнее означает, что
или
. Таким образом, для элемента
имеем
и
или
и
. Первая альтернатива имеет место при
, а вторая — при
, что означает
. Тем самым включение
доказано.
Доказательство включения запишем коротко, используя логическую символику:
В данном случае доказательства двух включений не совсем симметричны: элементы и
во второй части доказательства не обязаны совпадать.
Замечание 1.4. В тождестве, выражающем свойство 3, нельзя вместо объединения поставить пересечение, так как в этом случае тождество нарушатся. Можно доказать, что сохранится лишь включение
а обратное включение в общем случае не имеет места.
Анализ свойств 2 и 4 показывает, что роль пустого соответствия аналогична роли нуля при умножении чисел, а диагональ множества играет роль, аналогичную роли единицы, на множестве всех бинарных отношений на
.
Обратное соответствие и его свойства
Соответствие, обратное к соответствию , есть соответствие из
в
, обозначаемое
и равное, по определению,
.
Для соответствия из примера 1.3
Обратное соответствие обладает следующими легко проверяемыми свойствами:
1) ;
2) .
Для бинарного отношения на множестве
обратное соответствие есть бинарное отношение на том же множестве. В этом случае говорят о бинарном отношении
на множестве
, обратном к
.
Заметим, что соответствия и
в общем случае не совпадают. Даже для бинарного отношения
на множестве
, а также
и
.
Например, для бинарного отношения на множестве
графы самого отношения, обратного отношения
, композиций
и
представлены на рис. 1.5.
Если — отображение, то оно является соответствием. Обратное к
соответствие из
в
в общем случае не является отображением. Действительно, соответствие
, обратное к
, состоит из всех упорядоченных пар вида
. Поскольку в общем случае могут найтись такие два различных элемента
и
, что
, то соответствие
в общем случае не будет функционально по второй компоненте и поэтому не будет отображением. Если отображение
инъективно, то обратное соответствие есть частичное отображение из
в
. Если отображение
биективно, то обратное соответствие является отображением из
в
, причем имеют место равенства
Отображение в этом случае называют отображением, обратным к
.
Ограничение соответствия
Пусть — соответствие из
в
и
. Ограничением соответствия
на подмножества
и
(или
-ограничением соответствия
) называется соответствие из
в
, обозначаемое
, такое, что
Таким образом, -ограничение соответствия
есть “то же самое” соответствие
, но из последнего берутся только упорядоченные пары, первая компонента которых принадлежит подмножеству
, а вторая — подмножеству
. Можно записать
Так, “малый” арксинус, т.е. функция , есть ограничение “большого” арксинуса
, который является соответствием на подмножества
и
.
Рассмотрим некоторые важные частные случаи ограничений соответствий (в частности, бинарных отношений и отображений).
Всякое -ограничение соответствия
будем называть сужением соответствия
на подмножество
(коротко — C-сужением соответствия
), а всякое
-ограничение соответствия
— строгим сужением соответствия
на подмножество
(строгим C-сужением соответствия р). C-сужения соответствия
будем обозначать
, а строгое сужение —
соответственно.
Полезно заметить, что для любого отображения строгое сужение
есть сюръекция
на
. Если, сверх этого,
является инъекцией, то
есть биекция
на
. Допуская некоторую вольность речи, можно сказать, что любое отображение сюръективно отображает свою область определения на свою область значений, в частности, любая инъекция устанавливает взаимно однозначное соответствие между областью определения и областью значений. Так, функция
сюръективно отображает множество
всех действительных чисел на отрезок
, а любая показательная функция биективно отображает
на подмножество всех положительных действительных чисел.
Для бинарного отношения и любого подмножества
(M,M)-ограничение бинарного отношения называют ограничением бинарного отношения
на подмножество
и обозначают
. Можно записать
.
Рассмотрим, например, отношение естественного порядка на множестве действительных чисел. Тогда отношение
есть ограничение этого порядка на подмножество целых чисел. Но ни в коем случае нельзя путать это отношение с
-сужением отношения
! Это последнее состоит из всех таких упорядоченных пар
, что
и
, т.е. вторая компонента пары может быть произвольным действительным числом, не меньшим заданного целого
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
| Определение: |
| Композицией (произведением, суперпозицией) бинарных отношений (англ. composition of binary relations) и называется такое отношение , что: . |
Примером такого отношения может служить отношение на некотором множестве населенных пунктов — отношение “можно доехать на поезде”, а — отношение “можно доехать на автобусе”. Тогда отношение — отношение “можно добраться из пункта А в пункт Б, сначала проехав на поезде, а потом на автобусе (только по одному разу)”.
Степень отношений
| Определение: |
Степень отношения (англ. power of relation) , определяется следующим образом:
|
В связи с этим понятием, также вводятся обозначения:
— Транзитивное замыкание (англ. transitive closure) отношения ;
— Транзитивно-рефлексивное замыкание отношения
Обратное отношение
| Определение: |
| Отношение называют обратным (англ. inverse relation) для отношения , если: |
| Определение: |
| Ядром отношения (англ. kernel of relation) называется отношение |
Свойства
Композиция отношений обладает следующими свойствами:
- Ядро отношения симметрично:
- Композиция отношений ассоциативна:
- Обратное отношение для отношения, являющемуся обратным к есть само
- Обратное отношение к композиции отношений и есть композиция отношений, обратных к и
- Обратное отношение к объединению отношений и есть объединение отношений, обратных к и
- Обратное отношение к пересечению отношений и есть пересечение отношений, обратных к и
См. также
- Бинарное отношение
- Транзитивное замыкание
Источники информации
- Новиков Ф. А. — Дискретная математика для программистов: Учебник для вузов. 3-е изд. — СПБ.: Питер, 2009 — 52 с.
- Wikipedia — Composition of relations
- UNC Charlotte — Lectures in Discrete Mathematics: Composition of Relations and Directed Graphs.
Определение. Композицией (суперпозицией) двух отношений ρ и σ называется отношение
σ∘ρ = {<x, z> |существует такое y, что <x, y> | ρ и < y, z> |σ}.
Пример 1.
ρ = {<x, y> |y = sinx}.
σ = {<x, y> |y = √x}.
σ∘ρ = {<x, z> |существует такое y, что <x, y> | ρ и < y, z> |σ} = {<x, z> |существует такое y, что y = sinx и z = √y} = {<x, z> | z = √sinx}.
Определение композиции двух отношений соответствует определению сложной функции:
y = f(x), z = g(y) ⟹ z = g(f(x)).
Пример 2.
ρ = {<1, 1>, <1, 2>, <1, 3>, <3, 1>}.
σ = {<1, 2>, <1, 3>, <2, 2>, <3, 2>, <3, 3>}.
Процесс нахождения σ∘ρ в соответствии с определением композиции удобно изобразить таблицей, в которой реализуется перебор всех возможных значений x, y, z. для каждой пары <x, y> | ρ нужно рассмотреть все возможные пары < y, z> |σ (табл. 1).
Таблица 1
|
<x, y> | ρ |
< y, z> |σ |
<x, z> |σ∘ρ |
|
<1, 1> <1, 1> <1, 2> <1, 3> <1, 3> <3, 1> <3, 1> |
<1, 2> <1, 3> <2, 2> <3, 2> <3, 3> <1, 2> <1, 3> |
<1, 2> <1, 3> <1, 2> <1, 2> <1, 3> <3, 2> <3, 3> |
Заметим, что первая, третья и четвертая, а также вторая и пятая строки последнего столбца таблицы содержат одинаковые пары. Поэтому получим:
σ∘ρ = {<1, 2>, <1, 3>, <3, 2>, <3, 3>}.
Пусть R1 и R2 – отношения на N:
R1 = {(a, b): b = 2a + 1; a, b  N}
N}
R2 = {(a, b): b = 4a+2; a, b  N}
N}
Определить составные отношения R1°R2, R1°R1 = R1(2), R2°R2=R2(2).
Решение:
Конкретизируем R1,R2
Так как они определены на множестве натуральных чисел, то
<1,3> R1,<2,5>
R1,<2,5> R1,<3,7>
R1,<3,7> R1,<4,9>
R1,<4,9> R1,<5,11>
R1,<5,11> R1,<6,13>
R1,<6,13> R1,…
R1,…
<1,6> R2,<2,10>
R2,<2,10> R2,<3,14>
R2,<3,14> R2,<4,18>
R2,<4,18> R2,<5,22>
R2,<5,22> R2,
R2,
<6,26> R2,<7,30>
R2,<7,30> R2…
R2…
Найдем R1°R2
R1°R2={<x,y > |  z (<x,z>
z (<x,z> R1,<z,y>
R1,<z,y> R2,) }
R2,) }
В нашем случае, например существует
такой z=3, что <1,3> R1 , <3,14>
R1 , <3,14> R2,отсюда имеем пару <1,14>
R2,отсюда имеем пару <1,14> R1°R2
R1°R2
такой z=5, что <2,5> R1 , <5,22>
R1 , <5,22> R2,отсюда имеем пару <2,22>
R2,отсюда имеем пару <2,22> R1°R2, и т.д
R1°R2, и т.д
R1°R2={<а,b > : b=4*(2а+1)+2; a, b  N }
N }
Найдем R1°R1
R1°R1={<x,y > |  z (<x,z>
z (<x,z> R1,<z,y>
R1,<z,y> R1,) }
R1,) }
например существует
такой z=3, что <1,3> R1 , <3,7>
R1 , <3,7> R1,отсюда имеем пару <1,7>
R1,отсюда имеем пару <1,7> R1°R1
R1°R1
такой z=5, что <2,5> R1 , <5,11>
R1 , <5,11> R1,отсюда имеем пару <2,11>
R1,отсюда имеем пару <2,11> R1°R1, и т.д
R1°R1, и т.д
в общем виде, можно записать, что:
R1°R1={<а,b > : b=2*(2а+1)+1; a, b  N }
N }
Найдем R2°R2
R2°R2={<x,y > |  z (<x,z>
z (<x,z> R2,<z,y>
R2,<z,y> R2,) }
R2,) }
например существует
такой z=6, что <1,6> R2 , <6,26>
R2 , <6,26> R2,отсюда имеем пару <1,26>
R2,отсюда имеем пару <1,26> R2°R2
R2°R2
такой z=10, что <2,10> R2 , <10,42>
R2 , <10,42> R2,отсюда имеем пару <2,42>
R2,отсюда имеем пару <2,42> R2°R2 и т.д
R2°R2 и т.д
в общем виде, можно записать, что:
R2°R2={<а,b > : b=4*(4а+2)+2; a, b  N }
N }
5,698 total views, 2 views today
