Как найти композицию отображения - Сайт, где вы сможете решить свои вопросы

Композиция

Определение

Если %%f: X to Y%% и %%g: Y to Z%%, то отображение %%varphi: X to Z%%, заданное для каждого %%x in X%% формулой %%varphi(x) = gbig(f(x)big)%%, называется композицией (суперпозицией, %%varphi%% читается как фи греч.) отображений %%f%% и %%g%%, или сложной функцией, и обозначают %%g circ f%%.

$$
(g circ f)(x) = gbig(f(x)big)
$$

Таким образом, сложная функция %%g circ f%% реализует правило: «Применяй сначала %%f%%, затем %%g%%», то есть в композиции %%g circ f%% надо начинать с операции %%f%%, расположенной справа.

Пример

Пусть %%X = Y = Z = mathbb R%%. Отображения %%f : X to Y%% и %%g: Y to Z%% заданы формулами %%f(x) = x + 1%% и %%g(x) = x^2%%. Указать формулу для отображения %%g circ f%%

По правилу получаем

$$
(g circ f)(x) = gbig(f(x)big) = g(x + 1) = (x + 1)^2.
$$

Пример

Пусть даны функции %%f(x), g(x)%% и %%h(x)%%, тогда значение композиции %%h circ g circ f%% в точке %%x = x_0%% будет вычисляться следующим образом:

Вычисляется значение %%f_0%% равное значению функции %%f%% в точке %%x_0%%. Вычислено %%f(x_0)%%
Вычисляется значение %%g_0%% равное значению функции %%g%% в точке %%f_0%%. Вычислено %%(g circ f)(x_0)%%.
Вычисляется значение %%h_0%% равное значению функции %%h%% в точке %%g_0%%. Вычислено %%(h circ g circ f)(x_0)%%.

Или же
$$
begin{array}{rl}
(h circ g circ f)(x_0) =& hBig(gbig(f(x_0)big)Big)\
=& hbig(g(f_0)big) \
=& h(g_0)\
=& h_0
end{array}
$$

Свойства произведения отображнений

Произведение отображения ассоциативно, то есть для всех отображений %%f: X to Y, g: Y to Z, h: Z to H%% справедливо равенство %%(h circ g) circ f = h circ (g circ f)%%.

Проверим это следующим образом:

$$
begin{array}{c}
big((h circ g) circ fbig) (x) = (h circ g)big(f(x)big) = h Big(gbig(f(x)big)Big),\
big(h circ (g circ f)big) (x) = Big(h circ gbig(f(x)big)Big) = h Big(gbig(f(x)big)Big).
end{array}
$$
Пусть %%f%% — отображение множества %%X%% в %%X%%, %%I_X%% — тождественнное отображение множества %%X%%. Тогда
$$
I_X circ f = f circ I_X = f.
$$

Источник

Рис. 124 Рис. 125 Рис. 126

Если задано произвольное число b [0; ∞), то a = f −1(b), есть прообраз

точки b, т, е.	такое число	a [0; ∞), что f(a) = b. Иными словами,
a есть такое	число, что	b = √a (см. (4)),	и потому a = b2, т. е.
f −1(b) = b2. Это верно для любого b [0; ∞),	т. е. обратная функция

f −1 определена лишь на луче [0; ∞), а ее значения даются формулой

f −1(x) = x2. Заметим, что функция y = x2 определена для всех действи– тельных x (рис. 125), а не только на луче [0; ∞). Рассматривая ее только на луче [0; ∞), мы и получаем искомую обратную функцию

f −1(x). Ее график (рис. 126) симметричен графику функции (4) отно– сительно биссектрисы первого и третьего координатных углов.

Ограничимся пока этими примерами. Bажные примеры обратных функций мы будем иметь в последующих беседах при рассмотрении тригонометрических и показательных функций. Существенную роль играют обратные отображения и в геометрии, о чем также будет идти речь впоследствии.

Задачи и упражнения

51. Рассмотрим отображение множества действительных чисел в себя, определенное следующим образом: f(x) = x1, если x ≠ 0, и f(0) = 0.

Существует ли у этого отображения обратное?

52. Укажите отрезки действительной прямой, на которых функция f(x) = x3 − x2 имеет обратную.

53. Рассмотрим функцию f(x) = x + [x] (функция [x] определена в упраж– нении 50), отображающую множество действительных чисел в себя. Имеет ли эта функция обратную? Имеет ли она обратную на интервале (100; 101)?

54. Существует ли отрезок, на котором функция Дирихле имеет обрат– ную?

55. Пусть функции f(x) и g(x) отображают множество действительных

чисел на себя и имеют обратные. Bерно ли, что и их сумма также имеет обратную?

18. Композиция отображений

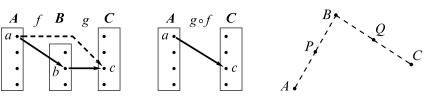
Рассмотрим три множества A, B, C, и пусть даны некоторые отображения f: A → B, g: B → C. Их можно записать в виде «цепоч– ки»:

74	Беседа 4. Отображения

	f g	(5)
	A → B → C.

Для каждого элемента a A определен его образ b = f(a), содер– жащийся в множестве B. В свою очередь для этого элемента b B

определен его образ c = g(b), содержащийся в множестве C (рис. 127). Поставим в соответствие элементу a сразу этот элемент с, минуя промежуточное множество B (пунктирная линия на рис. 127). Мы получаем таким образом некоторое отображение множества A в мно– жество C (рис. 128). Оно называется композицией отображений f и g и обозначается через g f.

Обратите внимание: первое применяемое отображение (т. е. f ) пишется справа, а отображение g, применяемое вторым, — слева. Такая форма записи применяется по следующим соображениям. Эле– мент c, который в результате композиции ставится в соответствие

элементу a, имеет вид c = g(b), где b = f(a) — образ элемента a при первом отображении. Таким образом, c = g(b) = g(f(a)). B этой записи

g(f(a)) отображение g оказывается записанным слева, и именно в таком порядке записываются f и g при обозначении композиции: f справа, g слева. Итак, по определению

(g f )(a) = g(f(a))

для любого a A.

Например, если f — центральная симметрия плоскости β относи– тельно точки P, а g — центральная симметрия относительно точ– ки Q (рис. 129), то композиция g f отображений f: β → β и g: β → β представляет→собой параллельный перенос на вектор, вдвое больший,

чем вектор PQ. Иначе говоря, для любой точки A β ее образ C при

→ →

отображении g f определяется равенством AC = 2 PQ (рис. 130).

Еще один пример получается, если взять в качестве f осевую симметрию относительно прямой k, а в качестве g — осевую симмет– рию относительно прямой l, причем k и l пересекаются в некоторой точке O. Из рассмотрения рис. 131, на котором отмечены равные углы, нетрудно заключить, что точка A переводится композицией

g f в такую точку C, что угол AOC вдвое больше угла α между прямыми k и l, причем точки A и C находятся на одинаковом рас–

Рис. 127

Рис. 128

Рис. 129

18. Композиция отображений

стоянии от точки O. Иначе говоря, композиция g f представляет собой поворот плоскости β вокруг точки O на угол 2α (рис. 132).

Приведенные примеры показывают, что операция композиции отображений играет важную роль при рассмотрении геометрических преобразований, а мы еще будем в последующих беседах говорить, следуя Феликсу Клейну, о том, что геометрические преобразования

— это подлинная основа всей элементарной (и не только элементар– ной) геометрии. Композиция отображений играет важную роль и в алгебре, где она связана с понятием сложной функции. Рассмотрим этот вопрос подробнее.

Пусть f(x) и g(x) — две числовые функции. Bначале для простоты рассмотрим случай, когда областью определения каждой из функций f, g является вся числовая прямая, т. е. они представляют собой отображения f: R → R, g: R → R. Тогда можно рассматривать слож–

ную функцию g(f(x)), т. е. композицию g f этих отображений. Иначе говоря, сложная функция получается, если в функцию g(y) подставить

вместо y значение y = f(x).

Рассмотрим, например, биквадратный многочлен

h(x) = x4 − 7x2 + 12.

(6)

Здесь удобно рассмотреть вспомогательную функцию y = f(x) = x2. Тогда многочлен (6) принимает вид y2 − 7y + 12, и это дает повод

ввести в рассмотрение еще одну функцию g(x) = x2 − 7x + 12. Компо– зиция g f этих функций, т. е. сложная функция

g(f(x)) = g(y) = y2 − 7y + 12 = x4 − 7x2 + 12

совпадает с многочленом (6). Таким образом, h = g f.

Подобно этому, функция h(x) = sin 5x есть композиция двух функ–

ций f(x) = 5x и g(x) = sin x. В самом деле, полагая y = f(x) = 5x, мы находим: g(f(x)) = g(y) = sin y = sin 5x, т. е. h = g f.

Представление заданной функции в виде композиции более про– стых функций часто используется при решении уравнений. Чтобы рассмотреть этот вопрос, вначале проведем некоторое общее рассуж– дение. Рассмотрим снова «цепочку» отображений (5). Пусть c —

Рис. 130

Рис. 131

Рис. 132

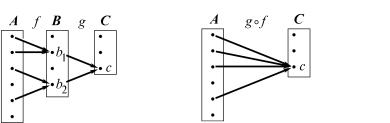
некоторый элемент множества C, и пусть g−1(c) = {b1, b2, …} B — его прообраз, т. е. b1, b2, … — все те элементы множества B, которые переводятся отображением g в элемент c (рис. 133). В свою очередь мы можем рассматривать прообразы f −1(b1), f −1(b2), … этих элемен–

тов при отображении f. Как показывает рис. 134, объединение всех этих прообразов как раз представляет собой прообраз элемента c при отображении g f, т. е.

(g f )−1(c) = f −1(b ) U f −1(b ) U … .	(7)
1	2
Пусть теперь задано уравнение
g(f(x)) = 0,		(8)

где g: R → R и f: R → R — некоторые числовые функции. Это урав–

нение имеет вид h(x) = 0, где h = g f — сложная функция, стоящая в левой части уравнения (8).

Решить уравнение h(x) = 0 — значит найти множество всех его корней, т. е. действительных чисел, для которых значение функции h равно нулю. Иначе говоря, решение этого уравнения есть прообраз точки 0, т. е. h−1(0), или, что то же самое, (g f )−1(0). Согласно

сказанному выше, надо сначала найти прообраз g−1(0), т. е. найти все корни b1, b2, … уравнения g(x) = 0. После этого, согласно формуле (7),

надо найти все прообразы f −1(b1), f −1(b2), …; их объединение как раз и будет множеством всех корней уравнения (8). Но прообраз f −1(b1) есть множество всех чисел x R, для которых f(x) = b1, т. е. множе–

ство всех корней уравнения f(x) = b1. To же справедливо для f −1(b2) и

т. д.

B результате мы получаем следующее правило: для решения урав–

нения (8) надо сначала найти все корни b1, b2, … уравнения g(x) = 0,

затем рассмотреть отдельно все уравнения

18. Композиция отображений	77

f(x) = b1, f(x) = b2, …;	(9)

тогда объединение множеств корней всех получаемых уравнений (9) и представляет собой множество всех корней уравнения (8).

Например, для решения биквадратного уравнения

т. е. уравнения (8), в котором f(x) = x2, g(x) = x2 − 7x + 12, надо сначала решить квадратное уравнение g(x) = 0, т. е. уравнение x2 − 7x + 12 = 0. Оно имеет два корня b1 = 3, b2 = 4. Затем, согласно сформулирован– ному выше правилу, надо рассмотреть отдельно уравнения (9), т. е. в данном случае уравнения x2 = 3, x2 = 4. Множество корней первого из них есть {√3, −√3 }, а множество корней второго есть {2, −2}. Сле–

довательно, их объединение {−2, −√3, √3, 2} и есть множество всех корней биквадратного уравнения (10).

Смысл рассмотренного приема состоит в том, что мы заменяем левую часть уравнения композицией более простых функций, в ре– зультате чего исходное сложное уравнение сводится к решению не– скольких более простых. В школьных задачниках можно найти много уравнений, допускающих применение этого приема.

Существенно заметить, что сложная функция g(f(x)) может рас–

сматриваться и для таких функций f(x), g(x), области определения которых не совпадают со всей числовой прямой. Область определения функции g(f(x)) состоит в этом случае из всех тех x R, для которых, во–первых, x принадлежит области определения функции f, и, во–вто– рых, соответствующее значение f(x) принадлежит области определе– ния функции g. Сформулированное выше правило решения уравнения

(8)остается справедливым и в этом случае. Рассмотрим в качестве примера уравнение

√x − x − 5 −1 = 0.	(11)
2

Его левую часть можно представить в виде √y −1, где y = x2 − x − 5.

Иначе говоря, взяв функции f(x) = x2 − x − 5, g(x) = √x −1, мы как раз запишем уравнение (11) в форме (8). Здесь область определения функ– ции g(x) не совпадает со всей числовой прямой, однако, как мы отмечали выше, это не препятствует применению описанного выше приема. Согласно описанию этого приема мы прежде всего должны рассмотреть уравнение g(x) = 0, т. е. в данном случае √x − 1 = 0. Как легко видеть, это уравнение имеет единственный корень b1 = 1. Сле–

довательно, имеется только одно уравнение (9), а именно уравнение f(x) = b1, т. е.

78 Беседа 4. Отображения

Решая его, находим два корня x1 = −2, x2 = 3. Таким образом, множе–

ство всех корней исходного уравнения имеет вид {−2; 3}.

Заметим, что для решения уравнения (11) могут быть применены и другие приемы. Один из них, часто применяемый при решении иррациональных уравнений (т. е. уравнений, содержащих знаки ра– дикалов), состоит в том, что квадратный радикал надо «уединить», а затем возвести обе части уравнения в квадрат. Иначе говоря, надо

переписать уравнение (11) в виде √x2 − x − 5 = 1, а затем от него

перейти «возведением в квадрат» к уравнению x2 − x − 5 = 1.

Как мы видим, получается то же уравнение (12), что и прежде, и это дает те же корни x1 = −2, x2 = 3. Однако возведение обеих частей

уравнения в квадрат может привести к появлению так называемых посторонних корней, в связи с чем такой способ решения требует проверки каждого найденного корня (что, правда, в данном случае несложно). Прием же, рассмотренный ранее (связанный с рассмотре– нием сложной функции), никогда не приводит ни к потере корней, ни к появлению «посторонних» корней, и потому является более пред– почтительным (в тех случаях, когда его удается применить).

Еще один прием решения уравнений заключается в использовании так называемой «области допустимых значений переменной» (сокра–

щенно ОДЗ). Под этим понимается множество всех тех x R, для которых все обозначенные действия выполнимы. В случае уравнения (11) это означает рассмотрение множества всех x R, для которых выражение под знаком квадратного радикала неотрицательно:

x2 − x − 5 ≥ 0.

Сразу же бросается в глаза, что это неравенство существенно сложнее уравнения (12) (например, квадратный трехчлен в левой

части имеет корни 12 (1 ± √21)); к тому же это неравенство вовсе не помогает решению уравнения (11).

Термин ОДЗ, употребляемый только в школе, применяется во многих по– собиях для учащихся и даже в школьных учебниках, но его надо признать неудачным. Ниже, в беседах, посвященных математическим рассуждениям, мы остановимся на этом подробнее, здесь же отметим лишь терминологичес– кие соображения.

Bыполнимость обозначенных действий для данного x R означает, что x принадлежит области определения числовой функции (или пересечению областей определения — например, в случае уравнения типа f(x) = g(x)).

Уже по этой причине использование (только в школе!) термина ОДЗ вместо общепринятого математического термина область определения означает ненужное противопоставление школьного математического преподавания

традициям науки. Кроме того, при рассмотрении функции y = f(x) слово зна– чение употребляется по отношению к y, т. е. это образ точки x при отобра– жении f, это значение откладывается по оси ординат. Применение же термина «допустимое значение» для точки x, принадлежащей области определения (и

18. Композиция отображений

потому изображаемой на оси абсцисс), означает лишь создание в психологи– ческом плане условий для путаницы понятий.

Bедь когда мы называем равенство (x + y)2 = x2 + 2xy + y2 тождеством, мы тем самым выражаем наше отношение к этому равенству, имея в виду, что оно справедливо для любых x, y, т. е. речь идет о некоторой теореме.

Когда мы называем равенство f(x) = 0 «уравнением», это также определяет наше отношение к этому равенству, означает постановку вопроса о том, ка– ково множество всех x R, удовлетворяющих этому равенству. И даже если

бы термин ОДЗ выражал что–то математически новое, сам термин «область допустимых значений» этого вопроса не содержит и вряд ли уместен с язы– ковой и психологической точек зрения. А иногда пишут еще «область допус– тимых значений уравнения» …

B заключение скажем несколько слов о связи обратных отобра– жений с понятием композиции отображений.

Пусть f: A → B — некоторое взаимно однозначное отображение и f −1: B → A — соответствующее обратное отображение. Тогда для лю–

бого a A соотношения f(a) = b и f −1(b) = a равносильны — при ото– бражении f элемент a переводится в b, стало быть, b получается из

a. Следовательно, композиция f−1 f переводит элемент a снова в тот же элемент a, т. е. f −1(f(a)) = f −1(b) = a. Иными словами, f −1 f есть тождественное отображение множества A, т. е. оно переводит каж–

дый элемент a A в себя. Это выражают записью f −1 f = 1A. Анало–

гично отображение f f −1: B → B представляет собой тождественное
отображение множества B, т. е. f f −1 = 1 .
		B
Итак, для взаимно	однозначного отображения f: A → B и его
обратного отображения f −1: B → A справедливы соотношения
f	−1 f = 1 ,	f f −1 = 1 .
	A	B
Bерно и обратное: если отображения f: A → B и g: B → A удовле–
творяют соотношениям
	g f = 1A,	f g = 1B,	(13)

то отображения f, g взаимно однозначны и являются взаимно обрат– ными, т. е. g = f −1.

Заметим, что выполнение только одного из соотношений (13) не достаточно для того, чтобы f и g были взаимно обратными биектив– ными отображениями. Так, отображения, показанные на рис. 135, 136, удовлетворяют первому из соотношений (13), однако взаимно одно– значными не являются (первое из них — вложение, второе — нало– жение).

Рассмотрим в качестве примера функцию f: R → R, заданную фор– мулой f(x) = 2x − 4 (см. (3)), и обратную к ней функцию

Соседние файлы в папке лИТЕРАТУРА

Источник

Поскольку соответствия можно считать множествами, то
все операции над множествами (пересечение, объединение,
разность, дополнение и т.д.) можно применить и к соответствиям.
Заметим, что, говоря о дополнении соответствия из Л в В, мы
имеем в виду дополнение до универсального соответствия из
A в В, т.е. до декартова произведения А × В. Естественно,
что и равенство соответствий можно трактовать как равен-
равенство множеств.

В то же время на соответствия можно распространить
операции, определяемые для отображений. Мы рассмотрим
здесь две такие операции.

Композиция соответствий. Следуя аналогии с
композицией отображнений, композицией (произведением) соответствий р ⊆ А×В и σ ⊆ В×С называют соответствие

рºσ = {(x, у): (∃ z ∈ B)((x, z)∈р)∧((z, у) ∈ σ)}. (1.3)

Поясним построение композиции двух соответствий.
Обратимся сначала к отображениям (как частным случаям
соответствий). Пусть заданы отображения (возможно, частичные):
f из А в В и g из В в С. Композиция* fºg определяется
как отображение из А в С, задаваемое формулой у = g(f(x)).
Тем самым задается график отображения fºg, т.е. множество
упорядоченных пар (x, у), таких, что у = g(f(x)). При этом
упорядоченная пара (x, у) будет принадлежать графику
отображения fºg, если и только если найдется элемент z ∈ В, такой, что z = f(x) и у = g(z). Таким образом, график
композиции отображений /ид есть

fºg = {(x, у): (∃z)(z = f(x) и y = g(z))} = {(x, У): У = g(f(x))}. (1.4)

* Необходимо заметить, что в [I] запись gº f(x) означает g(f(x)), т.е.
отображения в композиции пишутся в порядке, обратном тому, в каком они
применяются. Мы же будем везде использовать запись fºg, полагая, что
fºg(x) = g(f(x)) и порядок записи отображений в композиции совпадает с
порядком их применения. Это обусловлено тем, что композиция
отображении определяется нами как частный случай композиции соответствий, при
записи которой естественным оказывается именно такой порядок.

Легко видеть, что (1.4) есть частный случай (1.3). Отметим,
что при построении композиции отображений обычно
предполагают, что пересечение области значений отображения f и
области определения отображения д не пусто (R(f) ∩ D(g) ≠ 0),
поскольку в противном случае композиция была бы пуста. Для
отображений, не являющихся частичными, R(f) ⊆ D(g), так
как D(g) = В. Поэтому в данном случае пересечение R(f) ∩ D(g) всегда не пусто.

Полезно отметить также, что если f и g — биекции, то и
композиция их тоже будет биекцией.

Вернемся к рассмотрению композиции соответствий рºσ.
Полагая, что область определения D(p) соответствия р не
пуста, возьмем произвольный элемент х ∈ D(p). Пусть сечение
р(х) ⊆ B соответствия p не пусто и найдется такой элемент
z ∈ р(x), что сечение σ(z) ⊆ C также не пусто. Тогда непустое
множество {(x, t): t ∈ σ(z)} будет подмножеством сечения
соответствия роа в точке х. Сечением соответствия роа в точке
х будет непустое в силу сделанных предположений множество
всех таких упорядоченных пар (x, t) ∈ А × С, что х ∈ D(p), a
t ∈ σ(z) для некоторого z ∈ р(х). Говоря неформально,
нужно перебрать все элементы z из сечения р(х). Таким образом,
различие в построении композиции соответствий и
композиции отображений заключается в том, что „промежуточный”
элемент z в общем случае не единственный и каждому
такому элементу также ставится в соответствие не единственный
элемент у ∈ С.

Пример 1.8. Соответствие р возьмем из примера 1.3.
Соответствие σ зададим как соответствие из множества
грамм {n₁, n₂, n₃, n₄, n₅} в множество заказчиков
программного обеспечения {З₁З₂З₃З₄}. Пусть

σ = {(n₁,З₃), (n₁,З₄),(n₂,З₁),(n₃,З₂),(n₄,З₄),(n₅,З₃),

Рассмотрим процесс построения композиции соответствий
р и σ. Начнем с элемента И. Имеем р(И) = {n₁, n₃,n₅}, σ(n₁) = {З₃,З₄},σ(n₃) = {З₂} и σ(n₅) = {З₃}. Отсюда получаем

σ(n₁)∪σ(n₃)∪σ(n₅) = {З₂,З₃,З₄} –

сечение композиции по элементу И. Рассуждая аналогично,
получим (р॰σ)(П) = {З₁,З₄} и (р॰σ)(С) = {З₁,З₃}.

Построение графа композиции р॰σ проиллюстрировано на
рис. 1.3. #

Отметим, что область определения композиции
соответствий содержится в области определения первого
соответствия, а область значений композиции соответствий — в
области значений второго соответствия. Из приведенных
рассуждений следует, что для того, чтобы композиция соответствий
была отлична от пустого соответствия, необходимо и
достаточно, чтобы пересечение области значений первого соответствия
и области определения второго соответствия было не пусто.

К определению композиции соответствий можно подойти с
более общих позиций. Пусть p⊆A×B и σ⊆C×D. При этом
на множества A, B, С и D априори не накладывается
никаких органичений. Композиция р॰σ соответствий р и σ в этом
случае также определяется соотношением (1.3). Чтобы такая
композиция была отлична от пустого соответствия, необходимо
и достаточно выполнение условия R(p)∩D(σ) ≠ ∅. В
частности, р॰σ = ∅ всякий раз, когда В ∩ С = ∅.

Пример 1.9. Рассмотрим соответствие

τ = {(1, а),(2, а),(3,d)}

из множества А = {1,2,3} в множество В = {а, b, d} и
соответствие

φ ={(b,e),(b,f),(c,f)}

из множества С = {b, с, d} в множество D = {е, f}. В данном
случае В ∩ С ≠ ∅, но τ ॰ φ = ∅, поскольку R(τ) = {a, d}, D(φ) = {b,с} и R(τ)∩D(φ)=∅. #

Заметим, что композиция соответствий р ⊆ A × B и σ ⊆ С × D
не коммутативна, т.е. в общем случае рост р ॰ σ ≠ σ ॰ р, поскольку р ॰ σ ⊆ A × D, а σ ॰ р ⊆ C × B.

Бинарное отношение на множестве является частным
случаем соответствия. Для двух бинарных отношений р и σ,
заданных на множестве A, их композиция р ॰ σ (1.3) как
соответствий является бинарным отношением на том же множестве
А. В этом случае говорят о композиции бинарных
отношений на множестве А.

Композицию р ॰ р бинарного отношения р на некотором
множестве с самим собой называют квадратом бинарного
отношения р и обозначают р².

Рассмотрим пример построения композиции бинарных
отношений на множестве и покажем, что в общем случае для двух
бинарных отношений τ и φ также имеет место неравенство τ ॰ φ ≠ φ ॰ τ, хотя обе композиции, в отличие от аналогичных
композиций двух произвольных соответствий, заданы на одном
и том же множестве.

Пример 1.10. а. Зададим на множестве А = {1,2,3,4}
бинарные отношения τ = {(x, у): х +1 < у}, φ = {(x,у): |x — y| = 2}
и найдем композицию τ ॰ φ.

Имеем τ(1) = {3,4}, φ(3) = {1} и φ(3) = {2}. Следовательно,
(τ ॰ φ)(1) = φ(3) ∪ φ(4) = {1,2}. Далее τ(1) = {4}, φ(4) = {2} и
(τ ॰ φ)(2) = {2}. Так как τ(3) = τ(4) = ∅, то в итоге получим
τ ॰ φ = {(1, 1), (1, 2), (2, 2)}. Построение композиции
проиллюстрировано на рис. 1.4, а.

Найдем композицию φ ॰ τ. Поскольку φ(1) = {3}, а τ(3) =
= ∅, то (φ ॰ τ)(1) = ∅. Аналогично φ(2) = {4}, а τ(4) = ∅,
поэтому (φ ॰ τ)(2) = ∅. Далее φ(3) = {1}, τ(1) = {3,4}, поэтому
(φ ॰ τ)(3) = {3,4}, a φ(4) = {2}, τ(2) = {4} и (φ ॰ τ)(4) = {4}.
Построение композиции проиллюстрировано на рис. 1.4, б.

Легко видеть, что τ ॰ φ ≠ φ ॰ τ.

б. Пусть отношение р на множестве действительных чисел
определено как функция у = ах + b. Найдем квадрат этого
отношения (линейной функции от одного переменного).

Согласно (1.4), это будет функция h, такая, что h(x) =
= а(ах + b) + с, т.е. h(x) = а²х + (ab + с). Это тоже линейная
функция, но с другими коэффициентами. #

Приведем некоторые свойства композиции соответствий:

р ॰(σ॰τ) = (р ॰σ)॰τ;
для любого соответствия р имеет место р ॰∅ = ∅॰р = ∅;
р ॰(σ∪τ) = (р ॰σ)∪(р ॰τ);
для любого бинарного отношения на множестве А имеет
место равенство р ॰ id_A = id_A॰p = р.

Эти свойства нетрудно доказать методом двух включений.
Рассмотрим в качестве примера доказательство свойства 3.
Пусть некоторая упорядоченная пара (x, у) принадлежит
композиции p ॰ (σ ∪ τ). Тогда, согласно (1.3), найдется такой
элемент z, что (x, z) ∈ р и (z, у) ∈ σ ∪ τ. Последнее означает,
что (z, у) ∈ σ или (z, у) ∈ τ. Таким образом, для элемента z
имеем (x, г) ∈ р и (z, у) ∈ σ или (x, z) ∈ р и (z, у) ∈ τ.
Первая альтернатива имеет место при (x, у) ∈ р ॰ σ, а вторая —
при (x, у) ∈ р ॰ τ, что означает (x, у) ∈ р ॰ σ ∪ р ॰ τ. Тем самым
включение р ॰(σ ∪ τ) ⊆ р ॰ σ ∪ р ॰ τ доказано.

Доказательство включения р ॰ σ ∪ р ॰ τ ⊆ р ॰ (σ ∪ τ) запишем
коротко, используя логическую символику:

(x, у) ∈ р ॰ σ ∪ р ॰ τ ⇒ (∃u)(((x,u)∈р∧((u,y)∈σ))∨(∃v)(((x,v)∈p∧((v,y)∈τ)) ⇒ (∃z)(((x,z)∈p)∧(((z,y)∈σ)∨((z,y)∈τ)))⇒(∃z)(((x,z)∈p∧((z,y)∈σ∪τ))⇒(x,y)∈p॰(σ∪τ).

В данном случае доказательства двух включений не совсем
симметричны: элементы u и v во второй части доказательства
не обязаны совпадать.

Замечание 1.4. В тождестве, выражающем свойство 3,
нельзя вместо объединения поставить пересечение, так как
в этом случае тождество нарушится. Можно доказать, что
сохранится лишь включение

р ॰(σ ∪ τ) ⊆ р ॰ σ ∩ р ॰ τ,

а обратное включение в общем случае не имеет места. #

Анализ свойств 2 и 4 показывает, что роль пустого
соответствия аналогична роли нуля при умножении чисел, а
диагональ множества А играет роль, аналогичную роли
единицы, на множестве всех бинарных отношений на А.

Обратное соответствие. Соответствие, обратное к соответствию р ⊆ А × В, есть соответствие из В в А,
обозначаемое р^-1 и равное, по определению, р^-1 = {(у, х): (x, у) ∈ р}.

Для соответствия г из примера 1.3

τ^-1={n₁, И),(n₂, П),(n₂, С),
(n₃, И), (n₄, П), (n₅, И), (n₅, С)}.

Обратное соответствие обладает следующими легко
проверяемыми свойствами:

1) (р^-1)^-1 = р;

2) (р॰σ)^-1=σ^-1॰р^-1.

Для бинарного отношения р на множестве А обратное
соответствие есть бинарное отношение на том же множестве. В
этом случае говорят о бинарном отношении р^-1 на
множестве А, обратном к р.

Заметим, что соответствия р॰р^-1 и р^-1॰р в общем случае
не совпадают. Даже для бинарного отношения р на множестве
А р॰р^-1≠р^-1॰р, а также р॰р^-1≠id_A и р^-1॰р≠id_A.

Например, для бинарного отношения р = {(3,1), (4,1), (4,2)}
на множестве А = {1,2,3,4} графы самого отношения,
обратного отношения р^-1, композиций р॰р^-1 и р^-1॰р представлены на рис. 1.5.

Если а: A→ В — отображение, то оно является
соответствием. Обратное к а соответствие из В в А в общем случае
не является отображением. Действительно, соответствие f^-1,
обратное к f, состоит из всех упорядоченных пар вида (f(x), x),
х∈А. Поскольку в общем случае могут найтись такие два
различных элемента х и x’, что f(x) = f(x’), то соответствие f^-1 в
общем случае не будет функционально по второй компоненте и
поэтому не будет отображением. Если отображение f
тивно, то обратное соответствие есть частичное отображение
из В в А. Если отображение f биективно, то обратное
соответствие является отображением из В в А, причем имеют место
равенства

f॰f^-1=id_A, f^-1॰f=id_B

Отображение f^-1 в этом случае называют отображением,
обратным к f.

Ограничение соответствия. Пусть р ⊆ А × В —
соответствие из А в В и С ⊆ A, D ⊆ В. Ограничением
соответствия р на подмножества С и D (или (С, D)-ограничением соответствия р) называется соответствие из С в D
обозначаемое р|_C,D) такое, что

(x, у) ∈ р|_C,D ⇔ ((x, у) ∈ р) ∧ (х ∈ С) ∧ (у ∈ D).

Таким образом, (С, D)-ограничение соответствия р есть
„то же самое” соответствие р, но из последнего берутся только
упорядоченные пары, первая компонента которых
принадлежит подмножеству С, а вторая — подмножеству D. Можно
записать

р|_C,D=p∩(C×D).

Так, „малый” арксинус, т.е. функция у = arcsinx, есть
ограничение „ большого” арксинуса у — Arcsin x, который является
соответствием на подмножества [—1,1] и [-π/2,π/2].

Рассмотрим некоторые важные частные случаи
ограничений соответствий (в частности, бинарных отношений и
отображений).

Всякое (С, В)-ограничение соответствия р ⊆ А × В будем
называть сужением соответствия р на подмножество С (коротко — С-сужением соответствия р), а всякое
(С, p(С))-ограничение соответствия р — строгим сужением
соответствия р на подмножество С (строгим С-сужением соответствия р). С-сужения соответствия р будем обозначать р|_C, а строгое сужение — р|_॰C соответственно.

Полезно заметить, что для любого отображения f: А → В строгое сужение f|_॰A есть сюръекция А на f(A). Если,
сверх этого, f является инъекцией, то f|_॰A есть биекция А
на f(A). Допуская некоторую вольность речи*, можно
сказать, что любое отображение сюръективно отображает свою
область определения на свою область значений, в частности,
любая инъекция устанавливает взаимно однозначное
соответствие между областью определения и областью значений. Так,
функция у = sinx сюръективно отображает множество ℝ всех
действительных чисел на отрезок [—1,1], а любая
показательная функция биективно отображает ℝ на подмножество всех
положительных действительных чисел.

Для бинарного отношения р ⊆ А² и любого подмножества
М ⊆ А (М, М)-ограничение бинарного отношения называют ограничением бинарного отношения р на
подмножество М и обозначают р|_M. Можно записать р|_M = р∩М².

* Вольность состоит в томб что мы отождествляем функцию а с
функцией f|_॰A.

Рассмотрим, например, отношение естественного порядка
≤ на множестве действительных чисел [I]. Тогда отношение
≤|_ℤ = {(m, n): m ≤ n; m, n ∈ ℤ} есть ограничение этого
порядка на подмножество целых чисел. Но ни в коем случае нельзя
путать это отношение с ℤ-сужением отношения ≤! Это
последнее состоит из всех таких упорядоченных пар (m, x), что
m ∈ ℤ, x ∈ ℝ и m ≤ x, т.е. вторая компонента пары может быть
произвольным действительным числом, не меньшим заданного
целого m.

Источник

Содержание:

Сюръекция, инъекция и биекция
Произведение множеств

Сюръекция, инъекция и биекция

По этой ссылке вы найдёте полный курс лекций по математике:

Правило, задающее отображение f: X (или функцию /), можно условно изобразить стрелками (рис. 2.1). Бели в множестве У есть хотя бы один элемент) на который не указывает ни одна из стрелок, то это свидетельствует о том, что область значений функции f не заполняет все множество У, т.е. f(X) С У. Если же область значений / совпадает с У, т.е. f{X) = У, то такую функцию называют сюръективной} или короче — сюръекцией, и говорят, что функция / отображает множество X на множество У (в отличие от общего случая отображения множества X в множество У согласно определению 2.1). Итак, / : X есть сюръекция, если Vy 6 У Зх € X : /(х) = у. На рисунке в таком случае к каждому элементу множества У ведет хотя бы одна стрелка (рис. 2.2). При этом к некоторым элементам из У могут вести несколько стрелок. Если к любому элементу у € У ведет не более одной стрелки, то / называют инъективной функцией, или инъекцией. Эта функция не обязательно сюръективна, т.е. стрелки ведут не ко всем элементам множества У (рис. 2.3).

Итак, функция /: X —У У представляет собой инъекцию, если два любых различных элемента из X имеют своими образами при отображении / два различных элемента из У, или Vy £ f{X) С У 3хеХ: f{x) = y. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Отображение /: X->У именуют биективным, или би-екцией, если каждый элемент у 6 У является образом некоторого и призом единственного элемента из X, т.е. Vy € f(X) = У Э!х € X : f(x) = у.

По сути, функция / в этом случае устанавливает взаимно однозначное соответствие между множествами X и У, и потому ее часто называют взаимно однозначной функцией. Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.

При этом никакие два элемента из X не могут быть соединены стрелкой с одним и тем же элементом из У, ибо / инъективна, и никакие два элемента из У не могут быть соединены стрелками с одним и тем же элементом из X из-за требования единственности образа в определении 2.1 отображения.

Каждый элемент из X участвует в попарном соединении, поскольку X — область определения функции /. Наконец, каждый элемент из У тоже участвует в одной из пар, ибо / сюръективна. Роли X и У в этом случае как бы совершенно одинаковы, и если повернуть все стрелки вспять (рис. 2.5), то получим иное отображение или иную функцию д), которое тоже и инъективно, в сюръективно. Отображения (функции), допускающие такое обращение, будут играть большую роль в дальнейшем.

В частном случае множества X и У могут совпадать (X = У).

Тогда биективная функция будет осуществлять отображение множества X на себл. Биекцию множества на себя называют также пре-образов анием. 2.3. Обратное отображение Пусть /: X —? У — некоторая биекция и пусть у € У. Обозначим через /_1(у) единственный элемент х€Х, такой, что /(г) = у. Тем самым мы определим некоторое отображение 9 : Y Xу которое является снова биекцией. Ее называют обратным отображением, или обратной биекцией к /. Часто ее также называют просто обратной функцией и обозначают /”*. На рис. 2.5 функция д как раз и является обратной к /, т.е. д = f’1.

Возможно вам будут полезны данные страницы:

Функция /, определяемая формулой у = За – 2, я,у € R, является биекцией. Обратной функцией будет х = (у + 2)/3. б. Действительная функция f(x) = х2 действительного переменного х не является сюръективной, поскольку отрицаг тельные числа из У = R не являются образами элементов из Х=К при /: ЛГ->У. Пример 2.2. Пусть Л” = R, а У = R+ — множество положительных действительных чисел. Функция f(x) = ах, а > 0, аф 1, является биекцией. Обратной функцией будет Z”1 (У) = 1°8а У • Отображения (функции) / и являются взаимно обратными. Ясно, что>если функция не является биекцией, то обратной к ней функции не существует. Действительно, если / не инъек-тивна, то некоторому элементу у € У могут соответствовать несколько элементов х из множества X, что противоречит определению функции. Если же / не сюръективна, то в У найдутся элементы, для которых в X нет прообразов, т.е. для этих элементов обратная функция не определена. Пример 2.1. а. Пусть X = У = R — ^комсество действительных чисел.

Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. 2.4. Композиция отображений Если f:X-*Y и g:Y-*Zy то отображение (р:Х -+Z, заданное для каждого а: 6 А” формулой =, именуют композицией (суперпозицией) отображений (функций) / и д> или сложной функцией, и обозначают ро/ (рис. 2.6).
Таким образом, сложная функция до f реализует правило: я Применяй сначала /, а затем ди, т.е. в композиции операций «до/ надо начинать с операции /, расположенной справа. Отметим, что композиция Рис. 2.6 отображений ассоциативна, т.е.если /: X -+Y , д: Y Z и h: Z-*H> то тогда (hog)of = = ho(gof)i что проще записывают в виде ho до /. Проверим это следующим образом: На любом wK«oaicecmee X определено отображение 1х -X X, называемое тождественным, обозначаемое часто также idx и задаваемое формулой Ix(x) = x Vx € А”. Его -действие состоит в том, что оно оставляет все на своих местах.

Так, если является биекцией, обратной к биекции /: Х-+У, то /”1о/ = /х, а /о/-1 = /у, где и /у — тождественные отображения множеств X и У соответственно. Обратно, если отображения f: X ->Y и р : У Л” таковы, что gof = Ix и fog = /у, то функция / является биекцией, а у — ее обратной биекцией.

Очевидно, что если / — биекция Л” на У, а $ — биекция У на Z, то gof является биекцией X на Z, а будет по отношению к ней обратной биекцией. 2.5. Произведение множеств. График отображения Напомним, что две взаимно перпендикулярные координатные оси с масштабом, одинаковым для обеих осей, задают на плоскости прямоугольную декартову систему координат (рис. 2.7). Точку О пересечения координатных осей называют начало* координат. Каждой точке М можно поставить в соответствие пару (я, у) действительных чисел где х — координата точки Мх на ко-ординатной оси Ох, а у — координата точки Му на координатной оси Оу. Точки Мх и Му являются основаниями перпендикуляров, опущенных из точки М соответственно на оси Ох и Оу. Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.

Очевидно, что каждой паре (а, Ь) действительных чисел а, 6 6R соответствует на плоскости точка М, имеющая эти числа своими координатами. И обратно, каждой точке М плоскости соответствует пара (а, 6) действительных чисел а и 6. В общем случае пары (а, Ь) и (6, а) определяют разные точки, т.е. существенно, какое из двух чисел а и b стоит в обозначении пары на первом месте. Таким образом, речь идет об упорядоченной паре. В связи с этим пары (а, 6) и (6, а) считают равными между собой, и они определяют одну и ту же точку на плоскости, если только а = 6. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Множество всех пар действительных чисел, а также множество точек плоскости обозначают R2. Это обозначение связано с важным в теории множеств понятием прямого (или дек ар-това) произведения множеств (часто говорят просто о произведении множеств). Определение 2.2.

Произведением множеств А и В называют множество Ах В возможных упорядоченных пар (ж, у), где первый элемент взят из А, а второй — из В, так что Равенство двух пар (х, у) и (&’, у’) определяют условиями х = х’ и у = у7. Пары (я, у) и (у, х) считают различными, если хфу. Это особенно важно иметь в виду, когда множества А и В совпадают. Поэтому в общем случае А х В ф В х Л, т.е. произведение произвольных множеств не коммутативно, но оно дистрибутивно по отношению к объединению, пересечению и разности множеств: где обозначает одну из трех названных операций.

Произведение множеств

Произведение множеств существенно отличается от указанных операций над двумя множествами. Результатом выполнения этих операций является множество, элементы которого (если оно не пустое) принадлежат одному или обоим исходным множествам. Элементы же произведения множеств принадлежат новому множеству и представляют собой объекты иного рода по сравнению с элементами исходных множеств. Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3.

Произведение п множеств действительных чисел обозначают Rn. Это множество представляет собой всевозможные наборы (xj, Х2, хп) из п действительных чисел Х2) хп £ R, а любая точка х* из Rn есть такой набор (xj, х, х*) действительных чисел хп € К*
Произведение п произвольных множеств есть множество упорядоченных наборов из п (в общем случае разнородных) элементов. Для таких наборов употребляют названия кортеж или n-ка (произносят „энка”). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У.
Такое множество называют графиком отображения f (или графиком функции я*»- Пример 2.5. В случае XCR и Y = К каждая упорядоченная пара задает координаты точки на плоскости R2. Если при этом X является промежутком числовой прямой R, то график функции может представлять некоторую линию (рис. 2.9). Пример 2.6. Ясно, что при XCR2 и У = R график функции есть некоторое множество точек в R3, которое может представлять некоторую поверхность (рис. 2.10).

Если же X С R, а У = R2, то график функции также есть множество точек в R3, которое может представлять некоторую линию, пересекаемую плоскостью х = const лишь в одной точке М с тремя координатами х} yi, у2 (рис. 2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.

Лекции:

Множество
Область сходимости функционального ряда
Нахождение обратной матрицы
Формула Симпсона: пример решения
Матрицы и системы линейных уравнений
Площадь фигуры ограниченной линиями
Объем цилиндра
Сходимость степенного ряда
Матрица перехода
Дифференциальные уравнения второго порядка

Источник

Композиция

Определение

Пример

Пример

Свойства произведения отображнений

Сюръекция, инъекция и биекция

Произведение множеств

Вам также может понравиться

Стучит суппорт как исправить

Как составить характеристика на пожарного

Как исправить неправильно начисленную амортизацию в 1с

Добавить комментарий Отменить ответ