Как найти концентрацию атомов акцепторной примеси

Концентрация – акцепторная примесь

Cтраница 2

При обычных температурных условиях почти все примесные атомы ионизируются, поэтому pp yVa, где Na – концентрация акцепторной примеси, рр – концентрация дырок в полупроводнике р-типа. В этом случае основными носителями являются дырки, а неосновными – электроны проводимости. Соответственно Пр п, так как концентрация электронов при введении примеси уменьшается вследствие увеличения вероятности рекомбинации электронов с возросшим числом дырок.
 [16]

При обычных температурных условиях почти все примесные атомы ионизируются, поэтому рр ж Na, где Na – концентрация акцепторной примеси, рр – концентрация дырок в полупроводнике р-типа. В этом случае основными носителями являются дырки, а неосновными – электроны проводимости.
 [17]

Из ф-л (9.4) и (9.5) следует, что увеличение концентрации до-норных примесей смещает уровень Ферми вверх относительно середины запрещенной зоны, а увеличение концентрации акцепторных примесей – вниз относительно середины запрещенной зоны. При концентрации примесей порядка 1019 см-3 уровень Ферми электронного полупроводника располагается внутри зоны проводимости, а уровень Ферми дырочного полупроводника – внутри валентной зоны. Наличие столь высокой концентрации примесей существенно уменьшает удельное сопротивление полупроводника, так что по своим электрическим свойствам он мало чем отличается от проводника. В связи с этим полупроводники, характеризующиеся высокой концентрацией примесей, называют вырожденными полупроводниками.
 [18]

Чему равна концентрация дырок и электронов проводимости в примесном германии, содержащем 1 атом донорных примесей на 109 основных атомов и такую же концентрацию акцепторных примесей.
 [19]

Таким образом, чтобы, например, от материала типа п перейти к материалу типа р, необходимо так проводить циклы диффузии, чтобы концентрация акцепторных примесей в интересующей нас области превышала бы концентрацию ранее введенных донорных атомов. Изменение типа проводимости называют компенсацией. Понятно, что изменять тип проводимости можно ограниченное число раз, которое в пределе определяется твердофазной растворимостью атомов примеси. Практика позволила установить, что, не вызывая серьезных последствий, компенсацию можно проводить последовательно не более трех-четырех раз.
 [20]

Если необходимо получить высокую эффективность эмиттера, то толщина базы W должна быть сделана незначительной, концентрация донорной примеси в базе должна быть низкой, а концентрация акцепторной примеси в эмиттере – высокой.
 [21]

Чему равна концентрация дырок и электронов проводимости при этой температуре в примесном германии, содержащем 1 атом донорных примесей на Ю9 основных атомов и такую же концентрацию акцепторных примесей.
 [22]

Здесь VD – точка пересечения с осью напряжений экстраполированной зависимости С-2 от V, VD – точка на оси напряжений, соответствующая диффузионному потенциалу, е – диэлектрическая проницаемость полупроводника, NA – концентрация акцепторной примеси.
 [23]

Коэффициент усиления планарного транзистора в инверсном активном режиме чрезвычайно мал в основном по двум причинам: во-первых, / dK2 / dni, поскольку ( Лк – Аэ) Аа, и, во-вторых, / йк / dKi, поскольку NA NDK, где TV A – концентрация акцепторной примеси в базе, a NDK – концентрация донорной примеси в коллекторе.
 [24]

Если же источник тока Еу подключен плюсом к эмиттеру ( рис. 7 – 20, б), переход 1 для тока / у ( тока управления) будет открыт. Концентрация акцепторной примеси ( р) в слое эмиттера создается значительно более высокой, чем концентрация донорной примеси в слое базы. Сопротивление перехода 1 уменьшается пропорционально количеству подсосанных электронов.
 [26]

Концентрация донорной или акцепторной примеси характеризуется числом атомов примеси в единице объема полупроводника. Концентрация донорной примеси обозначается ND, а концентрация акцепторной примеси NA Чтобы примесь существенно повлияла на характер проводимости полупроводника, концентрация примеси ND или N А должна быть на порядок или несколько порядков больше собственной концентрации свободных носителей пг.
 [28]

Особенностью ее является ступенчатая форма / – я-перехода, имеющего круговую центральную часть J и кольцевую периферическую часть Jz. В периферической части J2 переход выполняется с мснь-шим градиентом концентраций акцепторных примесей ( алюминий) и с косым срезом по его наружной поверхности.
 [30]

Страницы:  

   1

   2

   3

Барьерная ёмкость зависит от величины приложенного
напряжения

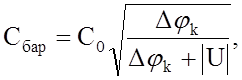
где С₀ – барьерная ёмкость диода при
нулевом напряжении. В свою очередь

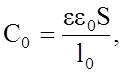 где

e₀ –
относительная диэлектрическая проницаемость вакуума;

e – диэлектрическая проницаемость материала полупроводника;

S –
площадь перехода;

l –
длина перехода.

16.     В сплавном германиевом р-n переходе с N_д = 10³N_а, причем на каждые 10⁸ атомов Ge
приходится один атом акцепторной примеси. Определить контактную разность
потенциалов (высоту потенциального барьера) при температуре 300К. Концентрация
собственных носителей для германия n_i = 2,5*10¹⁹  м^-3.

Решение:

Плотность атомов в Ge N = 4,4*10²⁰ м^-3, тогда концентрация
акцепторных примесей

 

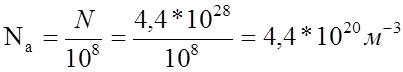
и
соответственно концентрация донорных примесей

Контактная
разность потенциалов определяется по формуле

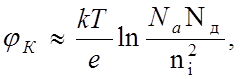                                      (1)

где n_i =
2,5*10¹⁹ м^-3 – собственная концентрация носителей в Ge.

Из
формулы (1)

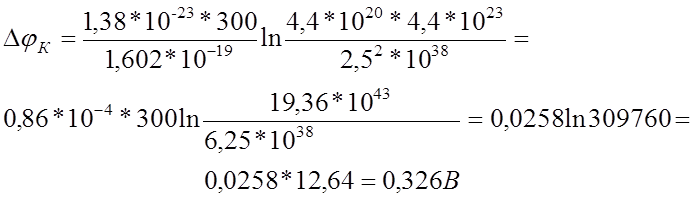
17. 
То же самое проделаем для
кремниевого р-n перехода. Концентрация собственных носителей для Si n_i = 10¹⁶ м^-3.

Для кремния концентрация атомов  N =
5*10²⁸ м^-3, тогда концентрация акцепторных примесей

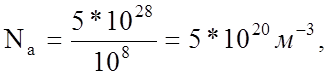
а донорных

Контактная разность потенциалов (n_i = 10¹⁶
м^-3)

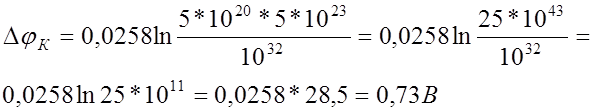
18.     Удельное сопротивление р – области Ge р-n
перехода r_p
= 0,02 Ом*м, а n- области  r_n  = 0,01 Ом*м. Какова контактная разность потенциалов
прт Т = 300К? Подвижность электронов и дырок в Ge
соответственно m_n
= 0,39 м²/В*с, m_р = 0,19 м²/В*с.

Решение:

Удельное сопротивление р – области

 

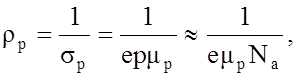
где N_a – концентрация акцепторов,

m_р –
подвижность дырок;

е – заряд электрона.

Отсюда

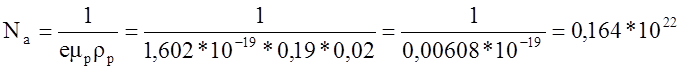 м^-3.

Аналогично найдём концентрацию доноров

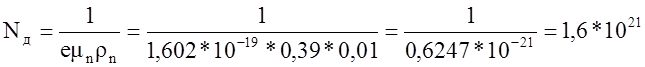 м^-3.

Контактная разность потенциалов

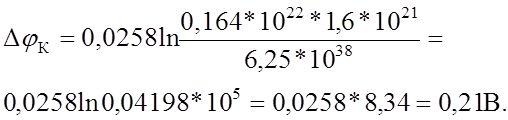
19.     Проделаем то же самое для Si диода.
Подвижности электронов и дырок для Si: m_n = 0,14 м²/В*с;
m_р = 0,05 м²/В*с.

Концентрация акцепторов

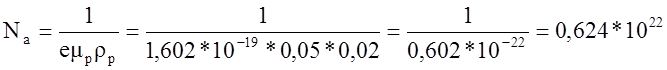 м^-3

и доноров

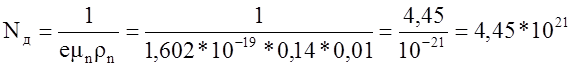 м^-3.

Контактная разность потенциалов

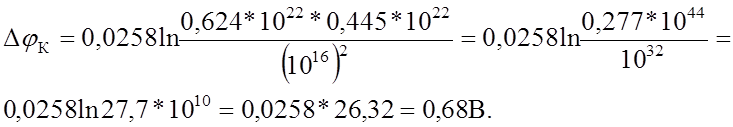
Таким образом, при равных условиях высота
потенциального барьера в Si диоде оказалась практически в 3 раза выше, чем в Ge.

20.     В    германиевом    р-n    переходе   
удельная    проводимость    р- области

s_р = 10⁴ См/м, а n- области s_n = 10²
См/м. Подвижности электронов m_n и дырок m_р соответственно равны 0,39 и 0,19 м²/В*с..
Концентрация собственных носителей в Ge при 300К n_i = 2,5*10¹⁹  м^-3.

Вычислить контактную разность потенциалов (высоту
потенциального барьера) при 300К.

Решение:

Значение контактной разности потенциалов
определяется положением уровня Ферми в областях р и n:

и в первом приближении можно считать, что

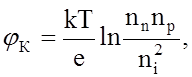                               (2)

где n_n и р_р
– концентрации основных носителей заряда в равновесном состоянии в области n и р. Учитывая, что в равновесном п/п при данной температуре

можно выражение (2) записать в виде:

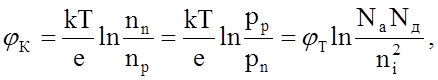          (3)

где 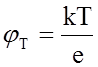 – температурный
потенциал.

Поскольку удельная проводимость р- области s_р = р_реm_р, отсюда

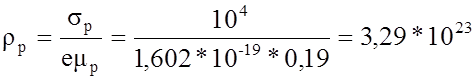 м^-3.

Аналогично для n- области s_n = р_nеm_n, откуда

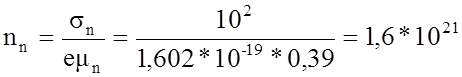 м^-3.

Воспользовавшись выражением (2), получим контактную
разность потенциалов

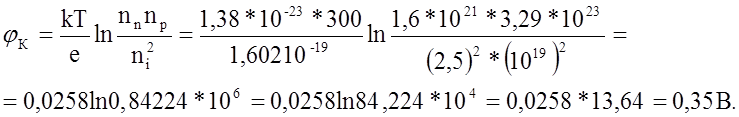
21.     Используя
данные и результаты предыдущей задачи, определить:

1). плотность обратного тока насыщения;

2).
отношение дырочной составляющей тока насыщения к электронной, если диффузионная
длина электронов и дырок одинакова L_p = L_n = 10^-3 м;

3).
напряжение, при котором плотность прямого тока j = 10⁵
А/м².

Решение:

1.  Плотность
обратного тока насыщения

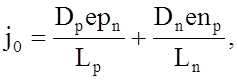                                  (4)

где D_p и D_n – соответственно коэффициенты диффузии дырок и
электронов, равные

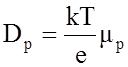   и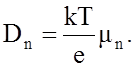  

Подставим эти значения в (4) и при равенстве L_p = L_n = L, получим

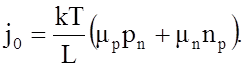                        (5)

Определим р_n и n_p, пользуясь соотношением   тогда

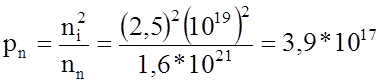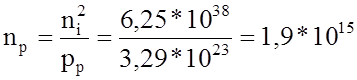 м^-3

 м^-3.

Плотность обратного тока насыщения

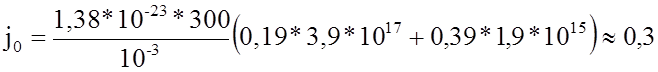 А/м².

2. Отношение дырочной составляющей обратного тока
насыщения к электронной

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Напомним, что
полупроводник называется собственным,
если в нем отсутствуют донорные и
акцепторные примеси. В этом случае
электроны появляются в зоне проводимости
только за счет теплового заброса из
валентной зоны, тогда n = p (рис. 1.5).

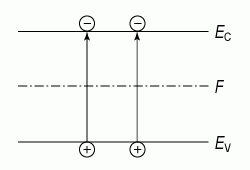
Рис. 1.5. Заброс
из валентной зоны

При
отсутствии внешних воздействий
(освещение, электрическое поле и т.д.)
будем обозначать концентрации свободных
электронов и дырок с индексом нуль, то
есть n₀
и p₀
соответственно. При n₀
= p₀
из (1.14) получаем:

(1.15)

Напомним,
что значком n_i
принято обозначать концентрацию
собственных носителей заряда в зоне
проводимости и в валентной зоне. Для
расчета N_C
и N_V
используется формула (1.11). Как следует
из соотношения (1.15), концентрация
собственных носителей определяется в
основном температурой и шириной
запрещенной зоны полупроводника. На
рисунке 1.6 представлена зависимость
концентрации собственных носителей от
температуры для наиболее распространенных
полупроводников – кремния, германия,
арсенида и фосфида галлия. Видно, что
при изменении ширины запрещенной зоны
в диапазоне от 0,6 эВ для германия до 2,8
эВ для фосфида галлия собственная
концентрация n_i
при комнатной температуре изменяется
от значения 10¹³
см^-3
до 10¹
см^-3.

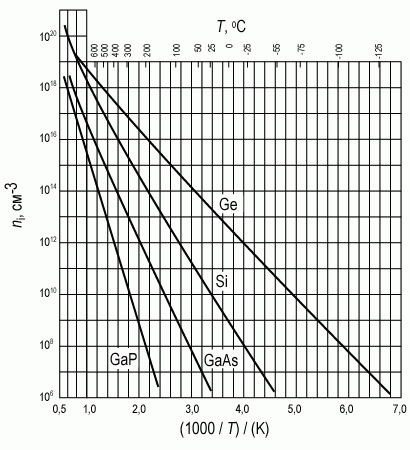
Рис. 1.6. Зависимость
концентрации собственных носителей от
температуры для наиболее распространенных
полупроводников – кремния, германия,
арсенида и фосфида галлия [2, 5]

1.5. Концентрация электронов и дырок в примесном полупроводнике

Уравнение (1.14)
справедливо только для равновесных
носителей заряда, то есть в отсутствие
внешних воздействий. В наших обозначениях

(1.16)

Пусть
полупроводник легирован донорами с
концентрацией N_D.
При комнатной температуре в большинстве
полупроводников все доноры ионизованы,
так как энергии активации доноров
составляют всего несколько сотых
электронвольта. Тогда для донорного
полупроводника (рис. 1.7)

(1.17)

Концентрацию дырок
в донорном полупроводнике найдем из
(1.16):

(1.18)

На
рисунке 1.7 приведена зонная диаграмма
полупроводника n-типа, показывающая
положение энергетических уровней
донорной примеси E_D
и схематическое соотношение концентраций
основных n₀
и неосновных p₀
носителей.

Рис. 1.7. Зонная
диаграмма полупроводника n-типа

Соответственно
если полупроводник легирован акцепторами
с концентрацией N_A,
то концентрации основных p₀
и неосновных n₀
носителей будут

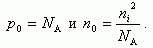(1.19)

На
рисунке 1.8 приведена зонная диаграмма
полупроводника p-типа, показывающая
положение энергетических уровней
акцепторной примеси E_A
и схематическое соотношение концентраций
основных p₀
и неосновных n₀
носителей.

Рис. 1.8. Зонная
диаграмма полупроводника p-типа

1.6. Определение положения уровня Ферми

В предыдущих
рассуждениях мы считали, что уровень
Ферми задан. Посмотрим теперь, как можно
найти положение уровня Ферми.

Для
собственного полупроводника уравнение
электронейтральности приобретает вид
p – n = 0 или p = n. Если ширина запрещенной
зоны полупроводника достаточно велика
(E_g
много больше kT) и если эффективные массы
электронов m_n
и дырок m_p
одного порядка, то уровень Ферми будет
достаточно удален от краев зон (E_C
– F > 2kT и F – E_V
> 2kT) и полупроводник будет невырожденным.

Подставляя
(1.10) и (1.13) в уравнение p + p_D
– n – n_A
= 0, имеем:

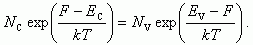(1.20)

Отсюда вычисляем
F. Уравнение (1.20) – это уравнение первого
порядка относительно exp(F/kT).

Это дает

(1.21)

где
через E_i
= (1/2)*(E_V
+ E_C)
обозначена энергия середины запрещенной
зоны. При выводе правого выражения для
F величина (N_C/N_V)
была заменена на (m_n/m_p)
с помощью уравнения (1.11).

Для
случая m_n^*
= m_p^*
энергия Ферми в собственном полупроводнике
находится посреди запрещенной зоны F =
(E_C
+ E_V)/2.

Положение уровня
Ферми зависит от того, какие другие
величины заданы. Если известны концентрации
носителей заряда в зонах n и p, то значение
F можно определить из формул (1.10) и (1.13).
Так, для невырожденного полупроводника
n-типа имеем:

(1.22)

Аналогично для
невырожденного полупроводника p-типа

(1.23)

Из
выражений (1.22 и 1.23) видно, что чем больше
концентрация основных носителей, тем
ближе уровень Ферми к краю соответствующей
зоны. Для донорного полупроводника n₀
= N_D
(1.17), тогда

(1.24)

Для
акцепторного полупроводника p₀
= N_A
(1.19), тогда

(1.25)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  15.02.201618.13 Mб26Схемотехника и средства проектирования цифровых устройств.pdf

• #
• #
• #
• #
• #
• #