| Концентрация | |
|---|---|
 |
|
| Размерность | L−3 |
| Единицы измерения | |
| СИ | м−3 |
| СГС | см−3 |
Концентра́ция части́ц — физическая величина, равная отношению числа частиц N к объёму V, в котором они находятся:
Размерность в СИ [n] = 1/м3, в системе СГС — [n] = 1/см3.
Если концентрация является функцией координаты 
Таким образом,
Однако такое представление является в некоторой степени условным, поскольку концентрация (как, например, и температура) относится к макропараметрам и при переходе к бесконечно малому объёму, по большому счёту, теряет смысл. Бесконечно малый объём в данном случае должен определяться как объём, число частиц в котором велико, однако изменение макропараметров в пределах объёма мало́.
Концентрация имеет следующую связь с плотностью и насыщенностью:
Формулы, в которых присутствует концентрация[править | править код]
[1] — давление идеального газа (см. уравнение Клапейрона).
— средняя длина свободного пробега молекулы газа (здесь D — эффективный диаметр молекулы).
— число ударов молекул газа о единицу поверхности стенки за единицу времени (здесь
— средняя скорость молекул).
— плотность тока (здесь q — заряд носителя,
— средняя скорость носителей заряда в данной точке).
См. также[править | править код]
- Концентрация смеси
Примечания[править | править код]
- ↑ Клапейрона уравнение // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 371. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
Формулы молекулярной физики
Формула концентрации молекул
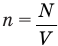
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
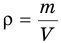
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
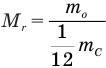
Здесь 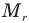 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 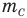 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
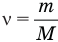
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
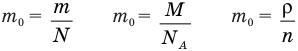
Здесь 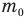 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 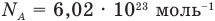 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
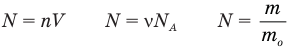
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 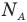 — число Авогадро
— число Авогадро 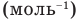 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
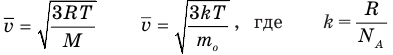
Здесь 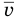 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 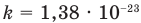 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 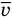 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
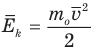
Здесь 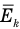 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 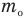 — масса одной молекулы (кг),
— масса одной молекулы (кг), 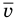 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
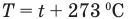
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
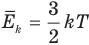
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
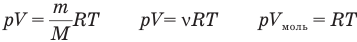
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 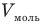 — объем моля
— объем моля 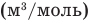 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 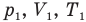 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 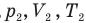 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 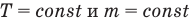
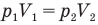
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 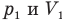 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 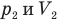 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 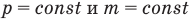
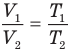
Здесь р — давление газа (Па), m — масса газа (кг), 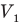 и
и 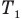 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 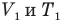 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 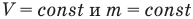
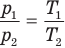
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 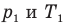 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 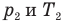 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
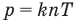
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
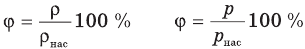
Здесь 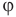 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 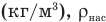 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 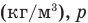 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 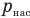 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
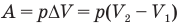
Здесь А — работа (Дж), р — давление газа (Па), 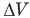 — изменение объема газа
— изменение объема газа 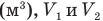 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
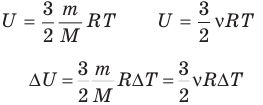
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 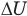 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 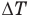 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
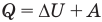
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 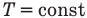
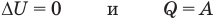
к изохорному: при V = const
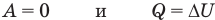
к изобарному: при р = const
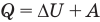
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 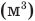 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
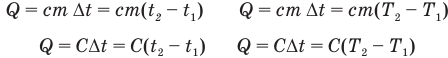
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 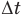 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 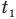 и
и 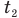 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 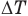 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 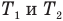 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 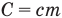 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
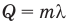
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 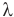 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
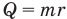
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
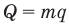
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
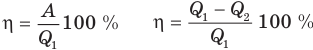
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 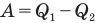 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 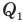 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 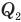 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
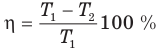
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 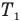 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 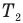 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

• Основное уравнение
кинетической теории газов
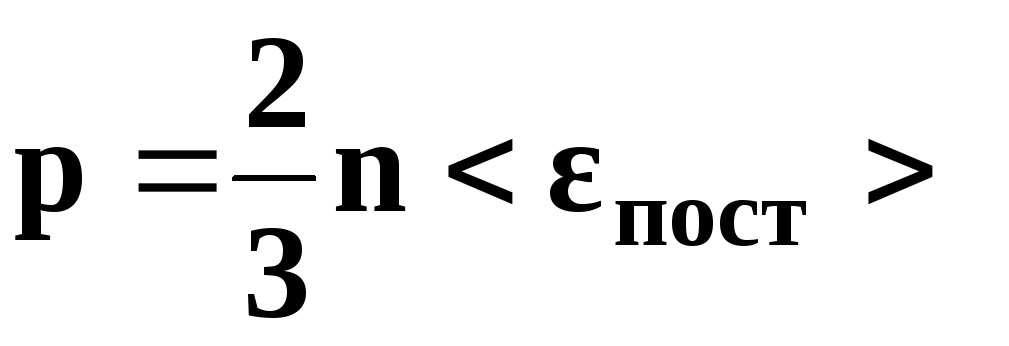 ,
,
где
р – давление
газа, n
– концентрация
молекул (число молекул в единице объема),
![]() –
–
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по
большому
ансамблю частиц, m0
– масса
молекулы,
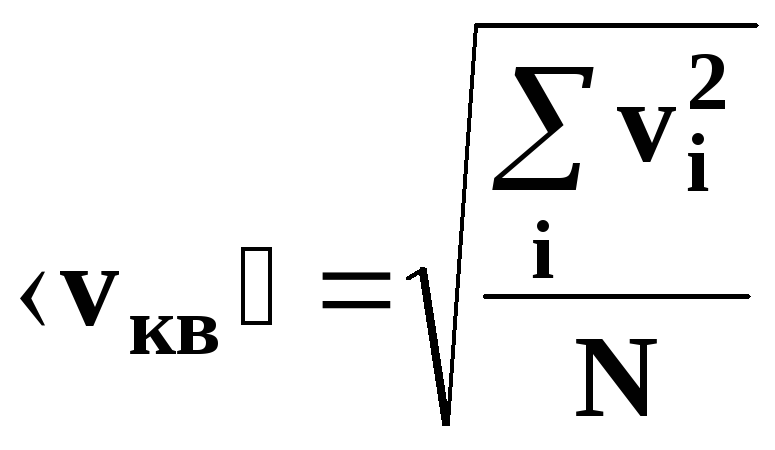 –
–
средняя квадратичная скорость движения
молекул.
• Средняя
кинетическая энергия поступательного
движения одной молекулы
![]()
![]() ,
,
где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.
•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):
![]() ,
,
где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.
• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.
• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
![]() .
.
• Средняя
кинетическая энергия вращательного
движения одной молекулы:
![]()
![]()
•
Средняя суммарная
кинетическая энергия одной молекулы:
![]() ,
,
где
i
– число степеней свободы молекулы
(i=iпост+
iвр).
• Средняя
квадратичная скорость молекулы:
![]()
• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:
![]() ,
,
где m0
– масса одной молекулы, М
– молярная масса вещества, причем
![]()
![]() ,
,
NA=
6,023·1023
1/моль –
число Авогадро.
• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:![]()
![]() или
или
![]() ,
,
где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.
•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:
![]()
![]() ,
,
где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
– концентрация
частиц в точках поля с Wп
= 0.
Примеры
решения задач
Задача
1. Найти
среднюю кинетическую энергию
![]() вращательного движения одной молекулы
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
![]() вращательного движения всех молекул
вращательного движения всех молекул
кислорода массойm
= 4 г.
Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
![]() ,
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.
Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:
![]()
Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим
![]()
Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:
![]()
Число
всех молекул газа можно вычислить по
формуле:
![]() ,
,
где NA
– число
Авогадро,
![]() –
–
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:
![]()
Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
![]() =
=
4,83·10-21
Дж:
![]()
![]()
![]() Выведем
Выведем
размерность полученной величины:
![]()
Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.
Решение.
Воспользуемся формулой распределения
Больцмана:
![]() ,
,
где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.
Подставив
это выражение в формулу распределения
Больцмана, получим:
![]()
Логарифмируем
обе части уравнения по основанию е,
тогда:![]()
![]() ,
,
откуда

Подставив
числовые значения в полученную формулу,
найдем
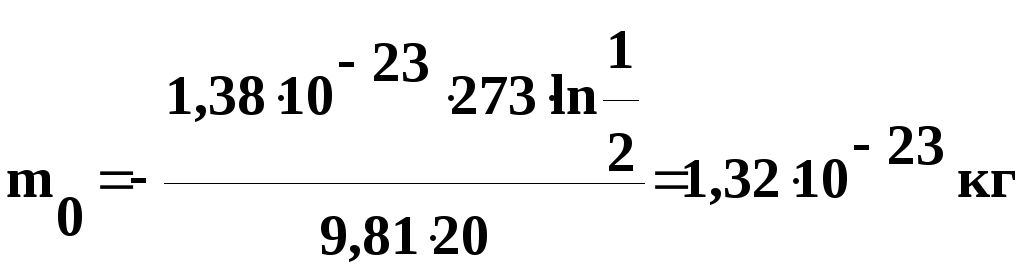
Выведем
размерность полученной величины:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти концентрацию молекул
Концентрация частиц – это величина, показывающая, сколько частиц вещества находится в каком-либо объеме. Она вычисляется по формуле: c = N/V, ее размерность 1/м^3. Часто возникает необходимость определить концентрацию молекул, причем исследуемое вещество может быть в любом агрегатном состоянии: твердом, жидком или газообразном.

Инструкция
Представьте, что любознательный царь Гиерон дал своему придворному математику еще одну корону, приказав: «Вот она-то точно из чистого золота. Определи, Архимед, какова концентрация молекул в ней». Гениального ученого такая задача поставила бы в тупик. Ну, а вы решите ее очень быстро. Предположим, корона весила бы ровно 1,93 килограмма, занимая при этом объем в 100 см^3.
Прежде всего найдите, сколько молей золота содержится в таком количестве вещества. С помощью таблицы Менделеева вы узнаете молекулярную массу золота: 197 а.е.м. (атомных единиц массы). А масса одного моля любого вещества (в граммах) численно равна его молекулярной массе. Следовательно, один моль золота весит 197 грамм. Разделив фактическую массу короны на молярную массу золота, вы получите: 1930/197 = 9,79. Или, округленно, 9,8 молей золота.
Умножьте количество молей на универсальное число Авогадро, показывающее, сколько элементарных частиц содержится в моле любого вещества. 9,8*6,022*10^23 = 5,9*10^24. Вот сколько молекул золота приблизительно содержится в короне.
Ну, а теперь найти концентрацию молекул проще простого. 100 кубических сантиметров – это 0,0001 м^3. Разделим: 5,9*10^24/0,0001 = 5,9*10^28. Концентрация молекул золота равна 5,9*10^28/м3.
Теперь предположим, что вам задана такая задача: при давлении Р, средняя квадратичная скорость молекул углекислого газа равна V. Требуется определить концентрацию его молекул. И здесь нет ничего сложного. Существует так называемое основное уравнение кинетической теории идеального газа: Р = V^2m0C/3, где C – концентрация молекул газа, а m0 – масса одной его молекулы. Следовательно, искомая концентрация С находится так: С = 3P/m0V^2.
Единственная неизвестная величина – m0. Ее можно узнать в справочнике по химии или физике. Можно также вычислить по формуле: m0 = M/Na, где М – молярная масса углекислого газа (44 грамм/моль), а Na – число Авогадро (6,022х1023). Подставив все величины в формулу, вычислите искомую концентрацию С.
Видоизмените условие задачи. Предположим, вам известны только температура Т и давление Р углекислого газа. Как по этим данным найти концентрацию его молекул? Давление и температура газа связаны формулой: P = CkT, где С – концентрация молекул газа, а К – постоянная Больцмана, равная 1,38*10^-23. То есть С = P/kT. Подставив в формулу известные величины, вы вычислите концентрацию С.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.




