
4.11. ФОТОННЫЙ ГАЗ
|
На поверхности Солнца T = 5000 К , |
kT = 0, 43 эВ, для оптических фо- |
||||
|
тонов с энергией ω = (1,6…3,3) эВ |
заполненность состояний мала |
||||
|
n(ω) = (25 −0,5) 10−3 и |
выходит |
на |
единицу |
при температуре |
|
|
T =1,44 ω/ k = (2,68…5,52) 104 К. |
Для сравнения у лазера заселен- |
||||
|
ность моды излучения |
n(ω) >>1 |
и из |
(4.101) |
находим e ω/kT ~1, |
kT >> ω, поэтому лазерное излучение имеет высокую эффективную температуру kT ~ ω n и способно резать металл.
|
Концентрация фотонов в интервале частот (ω,ω+ dω) |
|
|
dn(ω) = n(ω) g(ω) dω. |
(4.102) |
Используя число волн в единице объема (4.98) и число фотонов в волне (4.101), из (4.102) находим концентрацию фотонов в интервале частот (ω,ω+ dω)
|
dn(ω) = |
1 |
ω2 |
dω. |
||||||||||||||||||||
|
π2C3 e ω/kT |
−1 |
||||||||||||||||||||||
Концентрация фотонов со всеми частотами |
|||||||||||||||||||||||
|
1 |
∞ |
ω2d |
ω |
||||||||||||||||||||
|
n = ∫dn(ω) = |
∫ |
. |
|||||||||||||||||||||
|
π |
2 |
C |
3 |
ω/kT |
−1 |
||||||||||||||||||
|
0 e |
|||||||||||||||||||||||
Вычисляем интеграл по формуле |
|||||||||||||||||||||||
|
∞ |
tndt |
1 |
|||||||||||||||||||||
|
∫ |
= |
Γ(n +1) ζ(n +1) . |
|||||||||||||||||||||
|
e |
at |
−1 |
a |
n+1 |
|||||||||||||||||||
|
0 |
|||||||||||||||||||||||
Получаем |
|||||||||||||||||||||||
|
n = |
2 kT |
3 |
|||||||||||||||||||||
|
ζ(3) , |
|||||||||||||||||||||||
|
π2 |
|||||||||||||||||||||||
|
C |
где дзета-функция Римана ζ(3) = 1,202, тогда
n= 0,244 kT 3 20,3 (см К)−3 T 3,
C
313

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
|
k 3 |
3 |
−3 |
3 |
||||||||
|
N = nV = 0,244 |
T |
V = 20,05 (см К) |
T |
V. |
(4.106) |
||||||
|
C |
Число фотонов пропорционально объему полости и третьей степе-
ни температуры стенок. При нормальной температуре T = 300 К находим n 0,54 109 см−3 . Эти фотоны поддерживают тепловое рав-
новесие тел, находящихся в полости. В (4.106) величина kTC ≡ Lк –
размер области, занятой фотоном, или длина когерентности, т. е. расстояние, на протяжении которого согласована фаза электромагнитной
волны теплового излучения. При T = 300 К получаем Lк = 7,7 мкм.
|
Величина |
C 3 |
≡V |
– объем когерентности, в пределах которого |
|
|
к |
||||
|
kT |
взаимно согласованы фазы волн. Из (4.106) следует, что число фотонов в объеме когерентности порядка единицы, поэтому между фотонами теплового излучения нет фазовой согласованности.
Реликтовое излучение (от лат. reliquiae – «остатки») испущено при образовании Вселенной в результате «большого взрыва», произо-
шедшего 13,8 109 лет тому назад. По мере расширения шара огня тем-
пература и энергия фотонов уменьшались, через ~350 103 лет температура стала порядка 3000 К. При такой температуре энергия кулоновского притяжения протона и электрона превысила энергию теплового фотона и образовались атомы водорода. Фотоны перестали интенсивно взаимодействовать с материей, Вселенная стала прозрачной. Число фотонов перестало существенно изменяться и сохранилось до нашего времени. Из (4.106) при N = const находим связь характерного расстояния между галактиками с температурой реликтового излучения:
T 3R3 = const , T ~ 1/ R .
Следовательно, температура излучения понижается обратно пропорционально растущему расстоянию R между космическими телами. В настоящее время спектральные измерения газа реликтовых фотонов
дают температуру T = 2,726 К и химический потенциал µ <10−4 kT . Максимум излучения приходится на длину волны ~1,3 мм. Из (4.106)
314

4.11. ФОТОННЫЙ ГАЗ
находим текущую концентрацию n = 406 см−3 и с учетом (П.11.1) поток фотонов Сn/ 4 = 3 1012 частиц /см2 c. Для сравнения поток
нейтрино от Солнца у Земли 6,6 1010 частиц /см2 c. Поток реликто-
вых фотонов не зависит от времени года и от направления наблюдения. Максимальное различие по направлениям регистрируемых температур ~0,006 К вызвано эффектом Доплера и связано с движением Земли
вместе с галактикой Млечный Путь со скоростью ~370 км/с относи-
тельно собственной системы отсчета большого взрыва.
Реликтовое излучение предсказал Г.А. Гамов (1904–1968) на основе модели «горячей Вселенной», предложенной им в 1946 г. В 1956 г. он оценил температуру излучения в 6 К. Излучение, не зависящее от времени, с одинаковой интенсивностью по всем направлениям с температурой T 2,7 К обнаружил в 1955 г. аспирант Т.А. Тер-Шмаонов,
работающий под руководством С.Э. Хайкина и Н.Л. Кайдановского. Использовалась радиоаппаратура на волне 3,2 см с рекордной чувствительностью, предназначенная для радиотелескопа РАТАН-600. Статья опубликована в журнале «Приборы и техника эксперимента», № 1, 1957 г. Обнаруженное излучение Тер-Шмаонов объяснил радиоизлучением атмосферы. Независимо зарегистрировали излучение на волне 7,35 см А. Пензиас и Р. Вильсон в 1965 г. Им дали Нобелевскую премию в 1978 г.
Термин «реликтовое излучение» ввел астрофизик И.С. Шкловский, поскольку это излучение отражает состояние Вселенной на ранних этапах эволюции. Спектральный, угловой и поляризационный анализ реликтового излучения позволил получить закон изменения скорости разбегания галактик с течением времени и доказать, что средняя плотность всех видов материи близка к критической
ρc ~ 10−29 г/см3 , геометрия Вселенной евклидова, пространство плоское.
Спектральная плотность излучения. Одному состоянию, т. е.
волне с частотой ω, соответствует при температуре T число фотонов (4.101). Учитывая энергию фотона (4.97), получаем среднюю тепловую энергию волны с частотой ω
|
(ω) = ω n(ω) = |
ω |
. |
(4.107) |
||
|
E |
|||||
|
1 |
e ω/kT −1 |
||||
315

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
Кроме тепловой энергии (4.107) колебательное состояние включает квантовую энергию нулевых колебаний ω/ 2, существенную при низкой температуре, что использовано в примере 11.5. При высокой температуре kT >> ω экспоненту в (4.107) разлагаем в ряд, ограничива-
емся первыми двумя слагаемыми e ω/kT 1+ ω/ kT и находим E1 kT . Отсутствие зависимости от частоты при высокой температуре
соответствует теореме классической физики о распределении энергии по степеням свободы, где согласно (П.4.2) средняя энергия линейного гармонического осциллятора равна kT . Эта теорема не выполняется при низкой температуре в квантовой области.
В единице объема фотонного газа в интервале частот (ω,ω+ dω) находится число состояний g(ω) dω, каждое с энергией (4.107), тогда плотность тепловой энергии
du(ω) = E1(ω) g(ω) dω = ω dn(ω) ,
где использовано (4.102). Учитывая число фотонов (4.103), для энергии единицы объема фотонного газа в интервале частот (ω,ω+ dω) полу-
чаем формулу Планка
|
du(ω) = |
ω3 |
dω ≡ ρ |
(ω) dω. |
(4.108) |
||
|
π2C3 |
e ω/kT −1 |
T |
||||
Спектральная плотность равна энергии единицы объема полости в единичном интервале частоты ω = 2πν
|
ρ |
(ω) ≡ du(ω) |
, |
ρ |
(ν) ≡ du(ν) |
, |
2π ρ |
(ω) = ρ |
(ν) . |
|
T |
dω |
T |
dν |
T |
T |
|||
Из (4.108) находим
|
ρ |
(ω) = |
ω3 |
, |
(4.109) |
||
|
T |
π2C3 e ω/kT −1 |
|||||
|
ρ (ν) = |
8πh |
ν3 |
. |
(4.110) |
|
T |
C3 |
ehν/kT −1 |
||
316
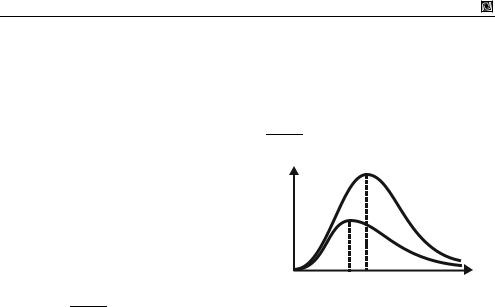
4.11. ФОТОННЫЙ ГАЗ
Функция ρT (ω) показана на рис. 4.22. При низкой частоте ω << kT
учитываем e ω/kT 1+ ω/ kT и из (4.109) получаем формулу Рэлея–
Джинса
ρT (ω << kT / ) = π21C3 kT ω2 .
При высокой частоте ω >> kT пренебрегаем единицей в знаменателе (4.109) и получаем фор-
мулу Вина
ρT (ω >> kT / ) =
= π2C3 ω3 e− ω/kT .
ω
0 ωm(T1)
Рис. 4.22. Спектральная плотность излучения
Положение экстремума ωm (T ) спектральной плотности находим из условия
Для переменной x = ω/ kT из (4.109) получаем
|
d |
x3 |
= 0 . |
|||
|
dx ex −1 |
|||||
|
x |
|||||
|
m |
Приходим к уравнению
(3 − xm ) exm = 3 .
Решение xm 2,822 дает закон смещения Вина
ωm = 2,822 kT ,
|
νm = 2,822 |
k |
T = 5,88 |
10 |
Гц |
T, |
(4.111) |
|
|
h |
10 |
К |
|||||
установленный В. Вином в 1893 г. При изменении температуры положение максимума спектральной плотности излучения сдвигается.
317

Г л а в а 4. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВ ФЕРМИОНОВ И БОЗОНОВ
|
Например, при T = 5000 К |
максимум находится в желто-зеленом |
||||
|
участке спектра. Подставляя (4.111) в (4.109) и (4.110), получаем |
|||||
|
ρ (ω |
m |
) = |
5,69 |
(kT )3 , |
|
|
T |
h2C3 |
||||
|
ρ |
(ν |
m |
) = 35,7 |
(kT )3 . |
(4.112) |
|
T |
h2C3 |
||||
С ростом температуры максимум спектральной плотности излучения увеличивается пропорционально кубу температуры.
Плотность энергии излучения со всеми частотами находим из
(4.108)
|
∞ |
∞ |
ω3dω |
|||||||
|
u = ∫du(ω) = ∫ρT (ω) dω = |
∫ |
. |
|||||||
|
2 |
C |
3 |
e |
ω/kT |
−1 |
||||
|
0 |
π |
0 |
Используя (4.104), вычисляем интеграл
|
Γ(4) |
ζ(4) |
kT 4 |
π4 kT 4 |
||||
|
= |
15 |
. |
|||||
Для энергии единицы объема полости с температурой Т находим закон
Стефана–Больцмана
|
′ |
4 |
′ |
π2 k4 |
−16 Дж |
|||||||
|
u = σ |
T |
, |
σ = |
= 7,56 10 |
. |
(4.113) |
|||||
|
15 |
( C)3 |
м3 К4 |
Результат получил экспериментально Й. Стефан в 1879 г. и теоретически Л. Больцман в 1884 г. Из (4.113) следует, что площадь под кривой спектральной плотности энергии ρT (ω) на рис. 4.22 пропорциональна
четвертой степени температуры.
Внутренняя энергия, или энергия излучения в полости объемом V, следует из (4.113)
|
′ |
T |
4 |
V . |
(4.114) |
|
U (T,V ) = uV = σ |
Средняя энергия фотона ε . Используем среднюю энергию единицы объема (4.113) и концентрацию фотонов (4.106), получаем
318

4.11. ФОТОННЫЙ ГАЗ
|
ε = |
u |
= |
π2 |
kT 2,7kT . |
(4.115) |
|||
|
n |
15 |
0,244 |
||||||
Для частицы классического трехмерного газа ε =1,5kT .
Свободная энергия. Используем внутреннюю энергию (4.114) и уравнение Гиббса–Гельмгольца (2.97), находим
|
′ |
T |
2 |
1 |
′ 4 |
1 |
||||||
|
∫T |
dT =− |
U . |
(4.116) |
||||||||
|
F = −Tσ V |
3 |
σ T V = − |
3 |
||||||||
|
0 |
|||||||||||
|
Энтропия. Используя (2.45) S = −∂F / ∂T и (4.116), получаем |
|||||||||||
|
4 |
′ |
3 |
4 U |
||||||||
|
S = 3 |
σ T V |
= |
3 T |
3,6kN . |
(4.117) |
В последнем равенстве учтено (4.106) и (4.113). Энтропия, приходящаяся на один фотон:
|
S1 = S / N 3,6k , |
(4.118) |
|||
|
не зависит от температуры. |
||||
|
Давление. Используем (2.44) P = −∂F / ∂V и (4.116), |
получаем |
|||
|
давление фотонного газа на абсолютно поглощающую стенку |
||||
|
1 |
′ 4 |
1 U |
||
|
P = 3 |
σ T |
= 3 V |
0,9nkT , |
(4.119) |
|
где использованы U = ε nV и (4.115) |
ε 2,7kT . В результате давле- |
ние равно одной трети от внутренней энергии единицы объема по-
лости. Для классического газа давление на абсолютно поглощающую стенку P = 0,5nkT , на упруго отражающую – P = nkT .
Термодинамический потенциал Гиббса находим из (2.174)
|
Φ = F + PV . Подставляем |
(4.116) |
F = −U / 3 и (4.119), получаем |
|
|
Φ = 0 . Из (2.176) Φ = Nµ следует, что химический потенциал фотона |
|||
|
равен нулю. Это согласуется с (4.99). |
|||
|
Адиабатический |
процесс, |
определяемый |
уравнением |
S = const , происходит с изменением объема полости, температуры и давления. Из (4.117) S 3,6kN получаем N = const . При адиабатиче-
ском процессе сохраняется число фотонов.
319
Соседние файлы в папке Лекции Квант.мех. СГФ
- #
- #
- #
- #
- #
- #
Монохроматический пучок света с длиной волны метров падает на пластину и оказывает давление
70% света отражается, остальное пластинка пропускает. Найти концентрацию фотонов в пучке света. Считать, что фотоны в пучке расположены равномерно.
Спрятать решение
Решение.
На пластину могут оказывать давление те фотоны, которые отражаются, т. е. При отражении фотоны меняют направление своего движения на противоположное, поэтому изменение импульса одного фотона равно
Импульс фотона
Второй закон Ньютона в импульсной форме
Поэтому давление, которое оказывают отраженные от пластины фотоны равно
За промежуток времени
объем пучка света равен
Объединяя все формулы, получаем
Так как по определению концентрация фотонов находим ее значение:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: выражение для энергии фотона, постулаты Бора, условия максимальности и минимальности частот); II) описаны все вводимые в решение буквенные обозначения физических величин (за исключением, возможно, обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи); III) проведены необходимые математические преобразования (допускается вербальное указание на их проведение) и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины. |
3 |
| Правильно записаны необходимые положения теории и физические законы, закономерности, проведены необходимые преобразования и представлен правильный ответ с указанием единиц измерения искомой величины. Но имеется один из следующих недостатков.
Записи, соответствующие одному или обоим пунктам: II и III — представлены не в полном объёме или отсутствуют. ИЛИ При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т. п.). ИЛИ При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. |
2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа.
ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения задачи (или утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
В этой статье будем определять концентрацию фотонов в световом луче, и количество фотонов, падающих за определенное время на поверхность известной площади.
Задача 1.
Рубиновый лазер дает импульс монохроматического излучения с длиной волны А. Определить концентрацию фотонов в пучке, если мощность излучения лазера
МВт, а площадь сечения луча
м
.
Концентрация – это количество фотонов в объеме. Объем найдем как . Количество фотонов определим как
Определим теперь концентрацию:
Ответ: 1/м
.
Задача 2. Сколько квантов излучения падает за время с на поверхность площадью
см
, если ее облучают потоком гамма-лучей с длиной волны
см, мощность которого на площадь
см
составляет
Вт?
Число фотонов можно найти как:
Число фотонов, падающих на единицу поверхности:
Мощность на площадь можно выразить как , тогда
Ответ:
Задача 3.
Сколько гамма-квантов падает ежесекундно на поверхность, которую облучают гамма-лучами мощностью Вт и длиной волны
м?
Число фотонов, падающих на единицу поверхности:
Число фотонов можно найти как:
А за время :
Ответ: 1/см
с
Задача 4.
Точечный источник света мощностью испускает свет с длиной волны
. Сколько фотонов
падает за время
на маленькую площадку площадью
, расположенную перпендикулярно к падающим лучам, на расстоянии
от источника?
Число фотонов, падающих на единицу поверхности:
Но источник излучает во все стороны, то есть лучи образуют сферу, а площадь площадки относится к площади сферы как , тогда количество квантов, попавших «в нужное место» равно
Ответ:
Задача 5.
Мощность точечного источника монохроматического излучения с длиной волны мкм
Вт. Определить число фотонов, падающих за 1 с на
см
площади, расположенной перпендикулярно лучам на расстоянии
м.
По аналогии с предыдущей задачей
Ответ: .
Чтобы вычислить эту энергию, приходитсяввести еще одну характеристику — концентрацию фотонов nф(число фотонов, приходящихся на единицу объема V = 1м3 электромагнитного поля). Тогда энергия фотонов в объеме ( cdtΣ)Eф = nф ⋅ =ω⋅ ( cdtΣ) ,(1.10)а плотность энергииϖ = nф =ω ,(1.11)и интенсивность волны (средняя плотность потока энергии)Eф= nф=ω⋅ c .I=(1.12)ΣdtСравнивая (1.8) и (1.11), видим, что плотность энергии с однойстороны (волновой), пропорциональна квадрату амплитуды, а сдругой стороны (корпускулярной) – концентрации фотонов:1ϖ = εε0E02 = nф=ω .(1.13)2При неизменной частоте источника и увеличении его мощности, например, в два раза, амплитуды напряженностей электрического и магнитного полей возрастают в 2 раз (волновое описание), и в два раза возрастает средняя концентрация фотонов (корпускулярное описание).Аналогично (1.10)–(1.12) находим импульс фотонов, заключенных в объеме ( cdtΣ) :Гл.
1. Корпускулярные свойства электромагнитных волн. Фотоны17=ω⋅ (cdt Σ) ,(1.14)cгде =ω / c = =k = pф — импульс одного фотона (см. (1.2) и (1.4));и среднюю плотность потока импульса:pΣфI= nф =ω = ϖ = .(1.15)dt ΣcВ табл. 1.1 приведены соотношения характеристик, используемые для описания света в корпускулярной и волновой моделях.pΣф = nф ⋅Таблица 1.1Основные характеристики света, их соотношения в рамках волновой и корпускулярной моделейСветКорпускулярная теорияВолновая теорияE = E0 cos ( ωt − kx )Eф = =ωB = B0 cos ( ωt − kx )E = cB , [ E / E , B / B ] = k / kpф = =kЗакон дисперсииEф = cpω = ckСредняя плотность энергииεεϖ = 0 E022ϖ = nф=ωИнтенсивность (средняя плотность потока энергии) I = c ϖI =cεε0 2E02I = cnф=ωСредняя плотность потока импульсаI /ccnф=kЗадача 1.1.
Длины волн видимой части спектра расположены впределах от λ = 0, 4 до λ = 0,75 мкм. В каких пределах заключеныэнергии квантов видимого света? Какой скоростью ve должен обладать электрон, чтобы его кинетическая энергия была равна энергии фотона видимого света?ВВЕДЕНИЕ В КВАНТОВУЮ ФИЗИКУ В ВОПРОСАХ И ЗАДАЧАХ18Решение. Энергию фотона выразим через длину волны:Eф = =c ( 2 π λ ) (см.
(1.6)). При заданном в задаче интервале изме-нения длин волн энергия фотонов лежит в пределах2π ⋅ 10−34 ⋅ 3 ⋅ 1080,75 ⋅ 10−6=2,5 ⋅ 10−19 Дж < Eф <2π ⋅ 10−34 ⋅ 3 ⋅ 1080,4 ⋅ 10−6= 4,7 ⋅ 10−19 Дж.(1.16)Для столь малых значений энергии принято использовать единицу энергии электрон-вольт:1эВ = 1,6 ⋅ 10−19 Дж .Тогда для энергии фотонов1,6 эВ < Eф < 2,9 эВ (рис. 1.1).видимого(1.17)светаимеемПри равенстве кинетической энергии электрона энергии фотона, его скорость равна ve = 2 Eф / m , где m = 9,11 ⋅ 10−31 кг – массасвободного электрона.
Интервалу энергий (1.16) соответствует интервал скоростей для электрона (см. рис. 1.1)0,73 ⋅ 106 м/с < ve < 1,0 ⋅ 106 м/с .Верхняя предельная скорость электрона в 300 раз меньше скорости фотонов.Ответ. 1,6 эВ < Eф < 3,2 эВ , 0,73 ⋅ 106 м/с < ve < 1,0 ⋅ 106 м/с .Рис. 1.1. Диапазон длин волн λ и энергии Еф фотонов соответствующий видимойобласти спектра.
Скорости v электронов, обладающих энергией, равной энергиифотонов.Задача 1.2. Интенсивность светового потока от Солнца наЗемле в полдень составляет около I = 1,3 кВт/м2. Считая свет моно-Гл. 1. Корпускулярные свойства электромагнитных волн. Фотоны19хроматическим с длиной волны λ = 0,6 мкм, определить концентрацию фотонов у поверхности Земли.Решение. Из формулы для интенсивности (1.12) с учетом (1.5)находимnф =IIλ1,3 ⋅ 103 ⋅ 0,6 ⋅ 10−6==≈ 1,3 ⋅ 1013 м −3 = 1,3 ⋅ 107 см −3 =c =ω 2π=c 2 2 π ⋅ 10−34 ⋅ (3 ⋅ 108 )2= 13 млн фотонов в см3.Ответ: nф =Iλhc2= 1,3 ⋅ 1013 м −3 .Задача 1.3.
Какой скоростью ve должен обладать электрон,чтобы иметь такой же импульс, как и фотон с λ = 0,1 нм?Решение. Импульс фотона равен pф = h / λ , релятивистскийимпульс электрона – pe =mve1 − ve2 / c 2. Из записанных соотноше-ний, с учетом условия задачи pф = pe получаемve ==pфm 2 + ( pф / c )2=c1 + ( λmc / h )2=3 ⋅ 108(1 + 0,1 ⋅ 10−9 ⋅ 0,9 ⋅ 10−30 ⋅ 3 ⋅ 108 (6,6 ⋅ 10−34 )Ответ.
ve =c1 + ( λmc / h )2)2≈ 7 ⋅ 106 м/с ≈c.40≈ 7 ⋅ 106 м / с .§1.2. Работа выхода. Внешний фотоэффект и его законыРассмотрим кристаллический металл. В узлах кристаллическойрешетки находятся атомы металла. Каждый атом отдает свои валентные электроны «в общее пользование», превращаясь в положительно заряженный ион. Валентные электроны могут перемещаются по всему объему металла. Таким образом, каждый валентный электрон электрически взаимодействует сразу со всеми иона-20ВВЕДЕНИЕ В КВАНТОВУЮ ФИЗИКУ В ВОПРОСАХ И ЗАДАЧАХми кристаллической решетки металла (их концентрация очень велика: порядка 1023см–3). Однако, чем дальше электрон от какоголибо иона, тем слабее к нему притяжение.Благодаря силам притяжения электрона ко всем ионам решетки, электрон остается в объеме металла, как в потенциальном ящике.
Следует отметить, что силы отталкивания отдельного электронаот всех других свободных электронов металла ослабляют результирующую силу притяжения, уменьшают глубину потенциальнойямы. Глубина потенциальной ямы U0 различна для разных металлов и определяет ту минимальную энергию, которую необходимосообщить электрону, чтобы он покинул металл и стал «понастоящему» свободным. Эта энергия называется работой выходаΔAвых .Как можно сообщить электрону энергию, равную работе выхода?Это можно сделать, например, нагревая металл. При определенных температурах наблюдается эмиссия электронов. Это явление называется термоэлектронной эмиссией, а вышедшие электроны — термоэлектронами.Другой способ высвобождения электронов из металла — внешний фотоэффект.Фотоэффект — испускание электронов твердыми телами (илижидкостями) при поглощении фотонов.
При этом энергия фотоновпередается электронам вещества (фотокатода), так что электроныприобретают возможность покинуть фотокатод (внешний фотоэффект).Пусть на поверхность металла падает свет. Рассмотрим следующую модель внешнего фотоэффекта. Каждый падающий наметалл фотон поглощается одним электроном, находящийся вблизиповерхности. Если энергия фотона удовлетворяет соотношению=ω ≥ ΔAвых , то электрон вырывается из металла. Излишек энергиифотона переходит в кинетическую энергию электрона, максимальное значение которой Eмакс линейно возрастает с частотой падающего света:=ω − ΔAвых = Eмакс .(1.18)Полученное соотношение называется уравнением Эйнштейна.Выбитые фотонами электроны (фотоэлектроны) образуютвблизи поверхности металла электронное облако. Электроны в об-Гл.
1. Корпускулярные свойства электромагнитных волн. Фотоны21лаке в общем случае имеют скорости, направленные в разные стороны. Для регистрации фотоэлектронов необходимо создать поблизости на другом металлическом электроде (аноде) положительныйпотенциал относительно фотокатода. Тогда выбитые электроныприобретают дополнительную скорость движения в направлении каноду (рис. 1.2), т.е. течет электрический ток — фототок, которыйможно зафиксировать амперметром (гальванометром Г).Рис. 1.2. В сосуде воздух откачандо состояния вакуума. Два электрода А (анод) и K (катод) подключены к источнику питания ИП. Дляизмерения силы тока используетсягальванометр Г, а напряжения –вольтметр В.
Через окно O пучоксвета падает на поверхность катодаK под углом θ к нормали.Из уравнения Эйнштейна следует, что работа выхода определяет минимально возможную частоту света =ωmin = ΔAвых , прикоторой фотоэффект наблюдается (I закон фотоэффекта).Поскольку работа выхода – характеристика вещества катода,то из (1.18) следует также, что максимальная кинетическая энергияфотоэлектронов у поверхности катода линейно зависит от частотыпадающего света и не зависит от интенсивности падающего света(III закон фотоэффекта).Даже при отсутствии разности потенциалов между катодом ианодом, некоторое количество электронов, чьи скорости направлены к аноду, попадают на анод, создавая ток J(0). С ростом по модулю отрицательного напряжения V < 0 (при отталкивающем потенциале) сила тока уменьшается, достигая нуля при напряженииV = V0 < 0 , называемом запирающим напряжением. При V > 0сила фототока растет: J > J (0), и стремится к насыщениюJ → J нас .
Насыщение достигается тогда, когда все выбиваемыефотоэлектроны попадают на анод (рис. 1.3).Вычислим силу тока насыщения и определим, от каких параметров зависит его величина. Число dN e выбитых электронов завремя dt равно числу dN ф падающих фотонов за то же время. Ес-22ВВЕДЕНИЕ В КВАНТОВУЮ ФИЗИКУ В ВОПРОСАХ И ЗАДАЧАХли поток фотонов направлен под углом θ к нормали поверхностиметалла, то dN ф = nф ⋅ ( Σcdt cos θ ) иdN e = nфc(Σ cos θ)dt ,(1.19)где Σ — площадь освещаемой поверхности, (Σcdt cos θ) — объемсветового пучка, фотоны которого достигают катода за время dt.В режиме насыщения все dN e достигают анода.
Причем, учитываянепрерывность электрического тока, dN e электронов поступают наанод каждые dt секунд. Таким образом, сила фототока насыщенияравнаdq e ⋅ dN eJ ф нас === enфcΣ cos θ(1.20)dtdtили, учитывая (1.12),eJ ф нас =(1.21)( I ⋅ Σ cos θ ) .=ωВыражение в скобках ( I ⋅ Σ cos θ ) — поток световой энергии,падающий на поверхность с площадью Σ под углом θ к нормалиповерхности.Рис.
1.3. Зависимость силы фототока J отразности потенциалов V между анодом икатодом фотоэлемента при интенсивностях падающего света I1 и I 2 ( I 2 > I1 ).Таким образом, сила фототока насыщения J ф нас пропорциональна интенсивности I падающего света и не зависит от материала катода (II закон фотоэффекта).С увеличением интенсивности света фототок насыщения увеличивается и достигаться он будет при бо′льших значениях напряжения.Итак, сформулируем все три закона фотоэффекта:Гл.
1. Корпускулярные свойства электромагнитных волн. Фотоны231. Существует красная граница фотоэффекта – граничнаячастота ωmin , ниже которой для данного материала фотоэффектотсутствует: =ωmin = ΔAвых .2. С увеличением напряжения на фотоэлементе сила фототокаJ достигает насыщения. Значение силы тока насыщения J ф нас прификсированной частоте падающего света прямо пропорциональноего интенсивности I : J ф нас = ( e =ω)( I ⋅ Σ cos θ ) .3. Максимальная кинетическая энергия фотоэлектронов у поверхности катода линейно зависит от частоты падающего света ине зависит от интенсивности падающего света: Emax = =ω − ΔAвых .Важной особенностью фотоэффекта является его практическаябезынерционность – время запаздывания фототока не превышает10 – 9 с.Задача 1.4. В вакуумном фотоэлементе сила фототока при насыщении достигает значения J нас = 2 ⋅ 10−10 А .
Фотоны
-
Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
-
Энергия фотона
-
Импульс фотона
-
Давление света
-
Двойственная природа света
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
В результате исследования явлений, связанных с взаимодействием света и вещества (тепловое излучение и фотоэффект), физики пришли к выводу, что свет состоит из отдельных порций энергии — фотонов. Излучение света, его распространение и поглощение происходит строго этими порциями.
Фотоны обладают энергией и импульсом и могут обмениваться ими с частицами вещества (скажем, с электронами или атомами). При этом мы говорим о столкновении фотона и частицы. При упругом столкновении фотон меняет направление движения — свет рассеивается. При неупругом столкновении фотон поглощается отдельной частицей или совокупностью частиц вещества — так происходит поглощение света.
Словом, фотон ведёт себя как частица и поэтому — наряду с электроном, протоном, нейтроном и некоторыми другими частицами — причислен к разряду элементарных частиц.
к оглавлению ▴
Энергия фотона
Выражение для энергии фотона с частотой мы уже знаем:
(1)
Часто бывает удобно работать не с обычной частотой , а с циклической частотой
.
Тогда вводят другую постоянную Планка «аш с чертой»:
Дж · с.
Выражение (1) для энергии фотона примет вид:
Фотон движется в вакууме со скоростью света и потому является релятивистской частицей: описывая фотон, мы должны привлекать формулы теории относительности. А там имеется такая формула для энергии тела массы
, движущегося со скоростью
:
(2)
Если предположить, что , то формула (2) приводит к бессмысленному заключению: энергия фотона должна быть бесконечной. Чтобы избежать этого противоречия, остаётся признать, что масса фотона равна нулю. Формула (2) позволяет сделать и более общий вывод: только безмассовая частица может двигаться со скоростью света.
к оглавлению ▴
Импульс фотона
Обладая энергией, фотон должен обладать и импульсом. Действительно, важнейшая формула теории относительности даёт связь энергии и импульса частицы:
(3)
Для фотона, имеющего нулевую массу, эта формула сводится к простому соотношению:
Отсюда для импульса фотона получаем:
(4)
Направление импульса фотона совпадает с направлением светового луча.
Учитывая, что отношение есть длина волны
, формулу (4) можно переписать так:
(5)
В видимом диапазоне наименьшими значениями энергии и импульса обладают фотоны красного света — у них самая маленькая частота (и самая большая длина волны). При движении в сторону фиолетового участка спектра энергия и импульс фотона линейно возрастают с частотой.
к оглавлению ▴
Давление света
Свет оказывает давление на освещаемую поверхность. Такой вывод был сделан Максвеллом из теоретических соображений и получил экспериментальное подтверждение в знаменитых опытах П.Н. Лебедева. Если понимать
свет как поток фотонов, обладающих импульсом , то можно легко объяснить давление света и вывести формулу Максвелла.
Предположим, что на некоторое тело падает свет частоты . Лучи направлены перпендикулярно поверхности тела; площадь освещаемой поверхности равна
(рис. 1).
Рич. 1. Давление света
Пусть — концентрация фотонов падающего света, то есть число фотонов в единице объёма.
За время на нашу поверхность попадают фотоны, находящиеся внутри цилиндра высотой
.
Их число равно:
При падении света на поверхность тела часть световой энергии отражается, а часть — поглощается. Пусть — коэффициент отражения света; величина
показывает, какая часть световой энергии отражается от поверхности. Соответственно, величина
— это доля падающей энергии, поглощаемая телом.
Как мы теперь знаем, энергия света пропорциональна числу фотонов. Поэтому можно написать, какое количество фотонов (из общего числа ) отразится от поверхности, а какое — поглотится ею:
Импульс каждого падающего фотона равен . Поглощённый фотон испытывает неупругое столкновение с телом и передаёт ему импульс
. Отражённый фотон после упругого столкновения меняет направление своего импульса на противоположное, и поэтому импульс, переданный телу отражённым фотоном, равен
.
Таким образом, от каждого фотона, входящего в световой поток, тело получает некоторый импульс. Вот простая и очевидная причина того, что свет оказывает давление на освещаемую поверхность.
Суммарный импульс, полученный телом от падающих фотонов, равен:
На нашу поверхность действует сила
, равная импульсу, полученному телом в единицу времени:
Давление света есть отношение этой силы к площади освещаемой поверхности:
(6)
Выражение имеет простой физический смысл: будучи произведением энергии фотона на число фотонов в единице объёма, оно равно энергии света в единице объёма, то есть объёмной плотности энергии
. Тогда соотношение (6) приобретает вид:
Это и есть формула для давления света, теоретически выведенная Максвеллом (в рамках классической электродинамики) и экспериментально проверенная в опытах Лебедева.
к оглавлению ▴
Двойственная природа света
В результате рассмотрения всей совокупности оптических явлений возникает естественный вопрос: что же такое свет? Непрерывно распределённая в пространстве электромагнитная волна или поток отдельных частиц — фотонов? Теория и эксперименты приводят к заключению, что оба ответа должны быть утвердительными.
1. Явления интерференции и дифракции света, характерные для любых волновых процессов, не оставляют сомнений в том, что свет есть форма волнового движения материи.
Таким образом, мы должны признать: да, свет имеет волновую природу, свет — это электромагнитная волна.
2. Однако явления взаимодействия света и вещества (например, фотоэффект) указывают на то, что свет ведёт себя как поток отдельных частиц. Эти частицы — фотоны — ведут, так сказать, самостоятельный образ жизни, обладают энергией и импульсом, участвуют во взаимодействиях с атомами и электронами. Излучение света — это рождение фотонов.
Распространение света — это движение фотонов в пространстве. Отражение и поглощение света — это соответственно упругие и неупругие столковения фотонов с частицами вещества.
Все попытки истолковать указанные явления излучения и поглощения света в рамках волновых представлений классической физики окончились неудачей. Оставалось лишь согласиться с тем, что свет имеет корпускулярную природу (от латинского слова corpusculum — маленькое тельце, частица), свет — это совокупность фотонов, мчащихся в пространстве.
Таким образом, свет имеет двойственную, корпускулярно-волновую природу — он может проявлять себя то так, то эдак. В одних явлениях (интерференция, дифракция) на передний план выходит волновая природа, и свет ведёт себя в точности как волна. Но в других явлениях (фотоэффект) доминирует корпускулярная природа, и свет ведёт себя подобно потоку частиц.
Странно всё это, не правда ли? Но что поделать — так устроена природа. Мы, люди, живём среди макроскопических тел, и наше воображение оказалось не способным полноценно представить себе явления микромира.
Природа, однако, неизмеримо шире и богаче того, что может вместить в себя человеческое воображение. Признав это и руководствуясь не столько собственным воображением, сколько наблюдениями, результатами экспериментов и весьма изощрённой математикой, люди начали успешно создавать квантовую теорию микроскопических явлений и процессов.
О некоторых парадоксальных на первый взгляд — но тем не менее подтверждённых экспериментально! — выводах квантовой теории мы поговорим в следующем листке.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Фотоны» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023

