Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
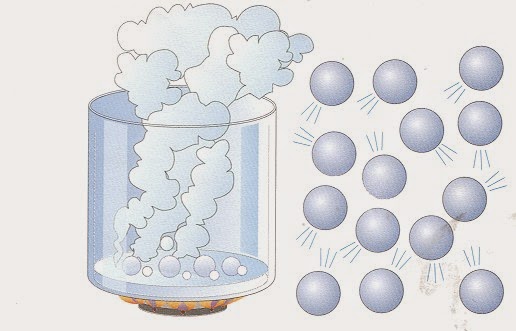
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.
Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
P*V = n*R*T.
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R – это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление
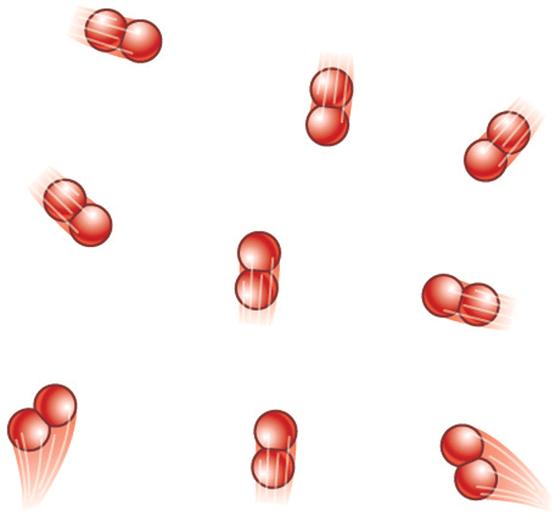
Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
cN = N/V.
Где N – общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
n = N/NA;
kB = R/NA.
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
P*V = n*R*T =>
P*V = N/NA*R*T = N*kB*T =>
cN = N/V = P/(kB*T).
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
cn = n/V = P/(R *T).
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 oC (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
cn(O2) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м3.
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*1021 молекул.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Химия. 11 класс |
| Книга: | § 6.1. Молярная концентрация газа |
| Напечатано:: | Гость |
| Дата: | Суббота, 20 Май 2023, 18:13 |
Газообразные вещества, в отличие от твёрдых и жидких, занимают весь предоставленный им объём. Поэтому в одном и том же сосуде может находиться разное количество газа. От этого количества будет зависеть давление в системе.
Определение количества газа и его доли в газовой смеси важно для разных практических целей. Например, следует выяснить, опасен ли для жизни уровень содержания метана или угарного газа в воздухе, пригоден ли для дыхания воздух в помещении с большим количеством углекислого газа или воздух на высоте 10 км, взрывоопасна ли данная смесь воздуха с водородом, в каком соотношении пары бензина должны смешиваться с воздухом в двигателе внутреннего сгорания.
Для решения подобных задач в качестве количественной характеристики используют молярную концентрацию газообразного вещества, которая показывает количество данного газообразного вещества в единице объёма.
Молярная концентрация газообразного вещества — величина, равная отношению его количества к объёму, который этот газ занимает:
Молярная концентрация газов измеряется в моль/дм3.
Например, молярная концентрация СО2 при нормальных условиях составляет:
Из приведённой выше формулы следует, что количество газообразного вещества в сосуде есть произведение молярной концентрации газа на объём сосуда, так как газ заполняет весь объём:
Понятие молярной концентрации газообразного вещества сходно с понятием молярной концентрации растворённого вещества, с которым вы ознакомились в курсе химии 8-го класса:
Причиной сходства является то, что растворённое вещество равномерно распределяется во всём объёме раствора, как и газообразное — во всём объёме сосуда.
Пример 1. Определите молярную концентрацию углекислого газа массой 3 г, находящегося в сосуде объёмом 4 дм3.
Дано:
m(CO2) = 3 г
V(сосуда) = 4 дм3
с(СО2) — ?
Решение
Ответ: с(СО2) = 0,017 моль/дм3.
Молярная концентрация газообразного вещества — величина, равная отношению его количества к объёму, который этот газ занимает:
Вопросы, задания, задачи
1. Установите соответствие между величинами.
|
1. Объём газа. 2. Молярная концентрация газа. 3. Количество вещества. 4. Молярная концентрация вещества в растворе |
А. с(NО2) = 0,15 моль/дм3. Б. с(NaOH) = 0,15 моль/дм3. В. V(H2S) = 4 дм3. Г. n(СО2) = 2 моль |
2. Определите молярную концентрацию аммиака количеством 0,7 моль в сосуде объёмом 14 дм3.
3. Определите массу сернистого газа в сосуде объёмом 400 см3, если молярная концентрация SO2 равна 0,5 моль/дм3.
4. Определите и сравните молярные концентрации трёх газов — водорода, азота и кислорода, если известно, что они находятся в сосудах объёмом по 5 дм3, а масса каждого из газов равна 7 г.
5. Сосуд объёмом 50 дм3 содержит гелий массой 10 г. В этот сосуд добавили гелий массой 8 г. Во сколько раз изменилась молярная концентрация газа? Как на исходную концентрацию гелия повлияет добавление аргона массой 8 г?
6. При газификации угля образовалась смесь газов, в которой на 1 дм3 СО приходится 4 дм3 Н2, 1 дм3 СН4, 3 дм3 СО2. Рассчитайте молярную концентрацию каждого газа в смеси.
7. Озон относится к веществам класса высокой опасности. Его предельно допустимая концентрация (ПДК) в воздухе рабочей зоны равна 0,1 мг/м3. При этом порог человеческого обоняния приблизительно равен 0,01 мг/м3. Рассчитайте молярную концентрацию озона в воздухе при его содержании 0,01 мг/м3.
8. Рассчитайте молярную концентрацию кислорода в воздухе (объёмная доля кислорода равна 21 %).
9. При действии соляной кислоты на твёрдое вещество выделился газ, относительная плотность которого по воздуху составляет 1,172. Какое из веществ использовал экспериментатор: СаС2, СаСО3, CaS, СаСl2?
10. Определите объём углекислого газа, выделившегося при действии соляной кислоты объёмом 0,5 дм3 на мрамор (карбонат кальция). Молярная концентрация кислоты составляет 2,7 моль/дм3.
Самоконтроль
1. Молярную концентрацию можно рассчитать по формулам:
а) ;
б) ;
в) ;
г) .
2. Молярная концентрация газообразного вещества имеет размерность:
- а) дм3/моль;
- б) моль/дм3;
- в) г/дм3;
- г) моль–1.
3. При н. у. объём 22,4 дм3 имеют вещества количеством 1 моль, формулы которых:
- а) СаС2;
- б) С2Н6;
- в) СО2;
- г) О3.
4. Молярная концентрация азота массой 5,6 г, находящегося в сосуде объёмом 20 дм3, равна (моль/дм3):
- а) 0,001;
- б) 0,01;
- в) 0,02;
- г) 0,1.
5. При нормальных условиях в сосуде объёмом 5 дм3 содержится газ массой 5,6 г. Его молярная концентрация составляет 0,04 моль/дм3. Этим газом может быть:
- а) С2Н4;
- б) С2Н6;
- в) N2;
- г) CО.
В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.
Идеальный газ
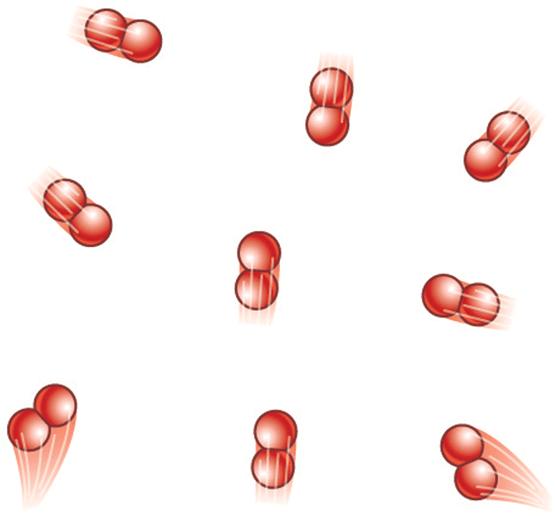
Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.
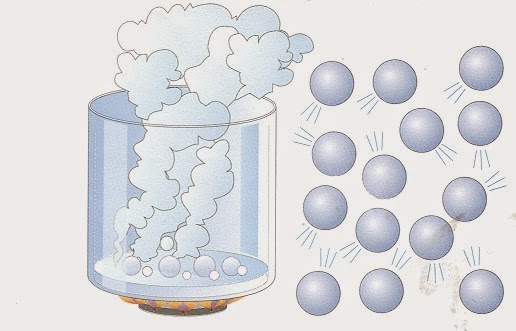
Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.
Универсальное уравнение
Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
P * V = n * R * T.
Где R – постоянная, равная 8,314 Дж/(моль*К), n – количество вещества.
Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).
Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций
Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.
В случае газов, как правило, пользуются тремя следующими концентрациями:
- Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
- Массовая. Показывает отношение массы компонента к объему газа.
- Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.
Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.
Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.
Формула концентрации молекул газа
В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:
cn(i) = ni / V.
Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:
P * V = n * R * T =>
cn = n / V = P / (R * T).
Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
cn = n / V = N / (NA * V) = cN / NA =>
cN = cn * NA = NA * P / (R * T) = P / (kB * T).
Здесь NA и kB – число Авогадро и постоянная Больцмана. Соответственно, N – число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10-23), то cN принимает огромные значения, что неудобно для ее практического использования.
Пример задачи
В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.
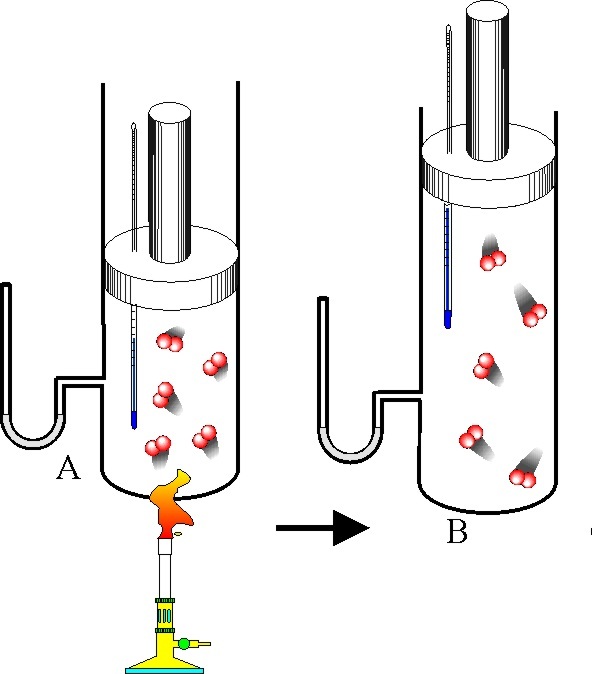
Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м3.
Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м3.
Изменение концентрации составило:
Δcn = cn2 – cn1 = 45,7 – 60,9 = -15,2 моль/м3.
Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.
Формулы молекулярной физики
Формула концентрации молекул
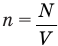
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
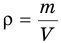
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
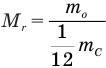
Здесь 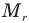 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 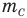 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
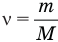
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
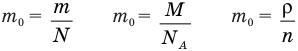
Здесь 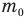 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 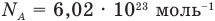 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
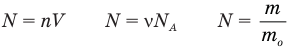
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 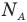 — число Авогадро
— число Авогадро 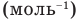 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
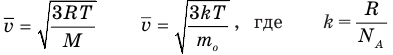
Здесь 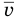 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 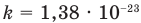 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 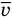 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
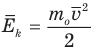
Здесь 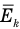 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 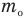 — масса одной молекулы (кг),
— масса одной молекулы (кг), 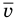 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
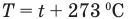
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
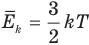
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
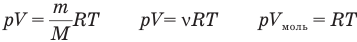
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 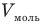 — объем моля
— объем моля 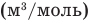 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 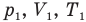 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 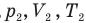 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 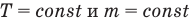
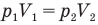
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 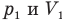 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 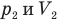 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 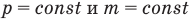
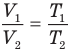
Здесь р — давление газа (Па), m — масса газа (кг), 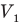 и
и 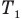 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 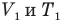 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 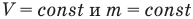
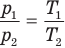
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 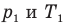 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 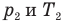 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
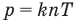
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
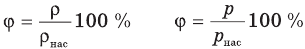
Здесь 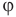 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 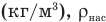 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 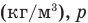 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 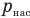 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
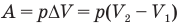
Здесь А — работа (Дж), р — давление газа (Па), 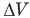 — изменение объема газа
— изменение объема газа 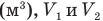 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
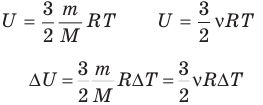
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 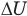 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 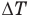 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
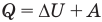
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 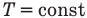
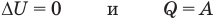
к изохорному: при V = const
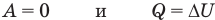
к изобарному: при р = const
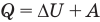
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 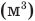 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
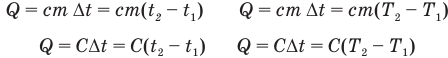
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 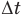 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 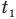 и
и 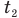 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 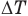 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 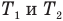 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 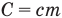 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
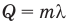
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 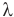 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
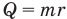
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
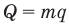
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
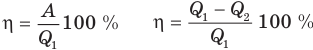
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 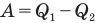 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 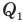 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 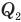 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
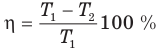
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 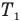 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 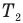 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Содержание
- Идеальный газ. Формула концентрации молекул газа. Пример задачи
- Идеальный газ
- Универсальное уравнение
- Понятие о концентрации молекул: виды концентраций
- Формула концентрации молекул газа
- Пример задачи
- § 20. Атомы и молекулы, их характеристики (окончание)
- Концентрация молекул
- Концентрация молекул идеального газа. Формулы и пример задачи
- О каком газе пойдет речь?
- Универсальный закон Клапейрона-Менделеева
- Концентрация молекул и ее вычисление
- Пример задачи
Идеальный газ. Формула концентрации молекул газа. Пример задачи
В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.
Идеальный газ

Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.
Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.

Универсальное уравнение
Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
Где R — постоянная, равная 8,314 Дж/(моль*К), n — количество вещества.
Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).
Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций
Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.
В случае газов, как правило, пользуются тремя следующими концентрациями:
- Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
- Массовая. Показывает отношение массы компонента к объему газа.
- Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.
Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.
Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.
Формула концентрации молекул газа
В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:
Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:
Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
Здесь NA и kB — число Авогадро и постоянная Больцмана. Соответственно, N — число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10 -23 ), то cN принимает огромные значения, что неудобно для ее практического использования.
Пример задачи
В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.

Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м 3 .
Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м 3 .
Изменение концентрации составило:
Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.
Источник
§ 20. Атомы и молекулы, их характеристики (окончание)
Концентрация молекул
7. Постоянная Авогадро. Поскольку молекулы имеют малые размеры, их число в любом макроскопическом теле очень велико.
Число молекул в единице объёма называют концентрацией. Концентрация n вычисляется по формуле
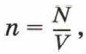
где N — число молекул в теле, V — его объём.
Концентрацию молекул в теле также можно определить, зная плотность вещества ρ и массу молекулы этого вещества m0. Поскольку 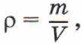 где m — масса тела, и m = m0N, то
где m — масса тела, и m = m0N, то
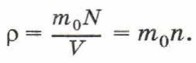
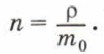
Если плотность воды ρ = 1000 кг/м 3 , а масса молекулы воды m0 = 3 • 10 -26 кг, то концентрация молекул воды равна:
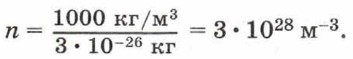
Плотность газов существенно меньше, чем плотность жидкостей, поэтому и концентрация молекул газов меньше, чем концентрация молекул жидкости. Так, если плотность водорода 9 • 10 -2 кг/м 3 , масса молекулы водорода 3,3 • 10 -27 кг, то концентрация молекул водорода равна 2,68 • 10 25 м -3 . Концентрация молекул любого газа при нормальных условиях (нормальном атмосферном давлении и температуре 0 °С) одинакова и равна приведённому для водорода значению. Это число называют постоянной Лошмидта: L = 2,68 • 10 25 м -3 .
Чтобы представить себе, насколько велико это число, предположим, что в воздушном шаре сделали настолько тонкий прокол, что за каждую секунду через него проходит 10 молекул. В этом случае, для того чтобы вышли все молекулы, потребуется 30 миллиардов лет.
Из определения моля следует, что 1 моль любого вещества содержит одинаковое число молекул (атомов). Это число называют постоянной Авогадро.
Постоянная Авогадро NА — число молекул или атомов в количестве вещества 1 моль.
Постоянную Авогадро можно рассчитать, зная, что углероду количеством вещества 1 моль соответствует масса 0,012 кг, а масса одной молекулы углерода m 0С = 1,995 • 10 -26 кг. Тогда в одном моле углерода содержится число молекул:
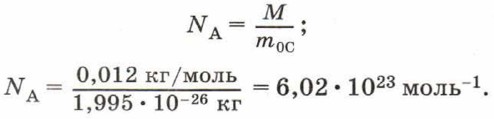
Поскольку в одном моле любого вещества содержится одинаковое число молекул, то при одинаковых условиях 1 моль любого газа занимает одинаковый объём.
Объём, занимаемый при нормальном атмосферном давлении любым газом количеством вещества 1 моль, равен 0,0224 м 3 .
1. Сформулируйте первое положение молекулярно-кинетической теории строения вещества.
2. Поясните выражение: «Молекула — мельчайшая частица вещества, сохраняющая его химические свойства».
3. Опишите опыт, позволяющий оценить размеры молекулы. Предложите способ измерения объёма капли масла.
4. Что называют относительной молекулярной массой; количеством вещества; молярной массой; концентрацией молекул; постоянной Авогадро?
6. Каков порядок значений размеров, массы молекул, их концентрации, числа молекул в одном моле вещества?
1Д. Подготовьте краткое сообщение об исследованиях М. В. Ломоносова, результаты которых внесли вклад в развитие учения о строении вещества. Воспользуйтесь для этого интернет-ресурсами и другими источниками информации. Докажите, что результаты исследований М. В. Ломоносова имели принципиальное значение для развития взглядов на строение вещества.
2. Сравните количество вещества, содержащееся в телах равной массы из алюминия и железа.
3. Найдите число атомов в алюминиевой ложке массой 30 г.
4. Деталь площадью 30 см 2 покрыли слоем серебра толщиной 2 мкм. Сколько атомов серебра содержится в покрытии?
5. Сравните массы и объёмы двух тел, сделанных из свинца и меди, если в них содержатся равные количества вещества.
6. Вычислите постоянную Авогадро, если известно, что масса молекулы кислорода 5,312 • 10 -26 кг.
Почему мы уверены в существовании молекул и атомов, ведь мы их не видим?
Источник
Концентрация молекул идеального газа. Формулы и пример задачи

Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.

Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R — это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление

Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
Где N — общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 o C (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*10 21 молекул.
Источник
