концентрация воздуха. Как определить концентрацию воздуха при нормальных условиях?
Юлия Холина
Знаток
(390),
закрыт
5 месяцев назад
Трудное детство
Оракул
(70151)
11 лет назад
концентрация воздуха – это что? может быть концентрация молекул воздуха? тогда n=N/V, где N число молекул в объеме V. но N=m/M*Na, а V=m/M*RT/P, тогда n=NaP/RT, где Na=6,02*10^23 1/моль число Авагадро, P0=101325Па нормальное атмосферное давление, R=8,31 Дж/мольК, T0=273К.
Физика Какова концентрация молекул в воздухе при нормальных условиях?
Канал видеоролика: Решение задач Математика и Физика

Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Физике (листай):
С этим видео ученики смотрят следующие ролики:

Физика Найдите среднюю квадратичную скорость молекул кислорода при нормальных условиях
Решение задач Математика и Физика

Физика Абсолютная температура идеального газа уменьшилась в 3 раза, а концентрация молекул
Решение задач Математика и Физика

Физика Какова средняя квадратичная скорость молекул азота при температуре 27 С
Решение задач Математика и Физика

Физика Какова средняя кинетическая энергия поступательного движения молекул газа, если при
Решение задач Математика и Физика
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
24.09.2019
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.
Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
P*V = n*R*T.
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R – это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление
Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
cN = N/V.
Где N – общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
n = N/NA;
kB = R/NA.
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
P*V = n*R*T =>
P*V = N/NA*R*T = N*kB*T =>
cN = N/V = P/(kB*T).
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
cn = n/V = P/(R *T).
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 oC (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
cn(O2) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м3.
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*1021 молекул.
Формулы молекулярной физики
Формула концентрации молекул
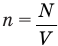
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
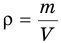
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
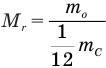
Здесь 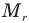 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 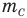 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
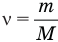
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
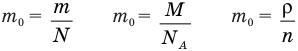
Здесь 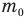 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 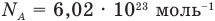 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
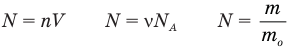
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 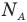 — число Авогадро
— число Авогадро 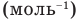 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
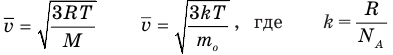
Здесь 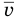 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 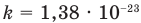 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 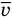 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
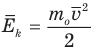
Здесь 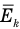 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 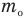 — масса одной молекулы (кг),
— масса одной молекулы (кг), 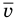 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
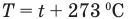
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
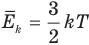
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
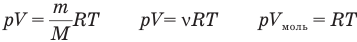
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 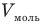 — объем моля
— объем моля  .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 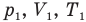 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 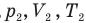 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 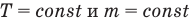
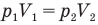
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 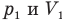 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 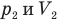 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 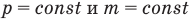
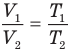
Здесь р — давление газа (Па), m — масса газа (кг), 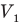 и
и 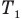 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 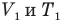 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 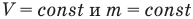
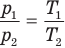
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 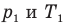 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 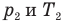 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
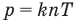
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
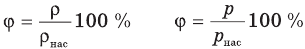
Здесь 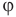 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 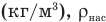 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 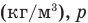 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 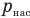 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
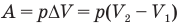
Здесь А — работа (Дж), р — давление газа (Па), 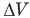 — изменение объема газа
— изменение объема газа 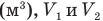 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
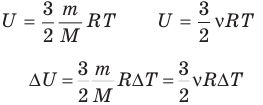
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 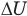 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 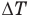 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
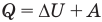
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 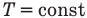
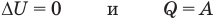
к изохорному: при V = const
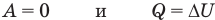
к изобарному: при р = const
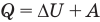
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем  , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
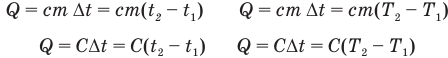
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 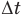 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 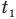 и
и 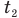 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 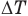 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 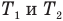 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 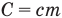 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
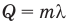
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 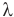 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
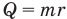
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
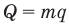
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
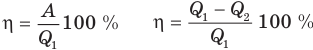
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 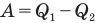 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 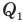 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 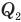 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
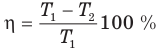
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 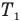 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 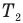 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

При
рассмотрении закона распределения
Максвелла предполагалось, что молекулы
равномерно распределяются по всему
объему сосуда, что справедливо, если
объем сосуда небольшой.
Для
больших объемов равномерность
распределения молекул по объему
нарушается из-за действия силы тяжести,
вследствие чего плотность, а
следовательно, и число молекул в единице
объема будут неодинаковым.
Рассмотрим
молекулы газа, находящегося в поле
тяготения Земли.
Выясним
зависимость давления атмосферы от
высоты над поверхностью Земли.
Допустим, на поверхности Земли (h
= 0) давление атмосферы P0.
На высоте h
оно равно P.
При увеличении высоты на dh
давление уменьшится на dP:
dP
= – ρgdh
(9.49)
[ρ
— плотность воздуха на данной высоте,
ρ
= mn0,
где m
— масса молекулы, n0
— концентрация молекул].
Используя
соотношение P
= n0kТ,
получаем
тогда
![]()
(9.50)
Полагая,
что на некоторой высоте h
Т = соnst,
g
= соnst,
разделяя переменные, интегрируем
выражение (9.50):
![]() ,
,
![]()
Получаем
![]()
(9.51)
—
барометрическая
формула.
Барометрическая
формула показывает зависимость давления
газа от высоты над поверхностью Земли.
Если
учесть, что концентрация молекул воздуха
в атмосфере определяет давление, то
формулу (9.51) можно записать в виде
![]() (9.52)
(9.52)
Из
формулы (9.52) следует, что с понижением
температуры число частиц на высоте,
отличной от нуля, убывает и при Т = 0К
обращается в нуль, т. е. при 0К все молекулы
расположились бы на земной поверхности.
Так
как потенциальная энергия молекул на
различной высоте различна и на высоте
h
определяется по формуле где ЕП
= mgh,
то [см.
![]()
(9.53)
— закон
Больцмана,
показывающий распределение участвующих
в тепловом движении молекул в
потенциальном поле сил, в частности в
поле силы тяжести.
Методика решения задач
В задачах
данного типа используют свойства
распределения Максвелла и Больцмана.
Пример
3.3. Определите
среднюю арифметическую скорость <υ˃
молекул идеального газа, плотность
которого при давлении 35 кПа составляет
0,3 кг/м3.
Дано:
Р=35кПа=35∙103
Па; ρ=0,3
кг/м3.
Найти:
<υ˃.
Решение:
Согласно
основному уравнению молекулярно-кинетической
теории идеальных газов,
![]() ,
,
(1)
где
n
– концентрация молекул; m0–
масса одной молекулы; <υкв˃.-
средняя квадратичная скорость молекул.
Учитывая,
что
![]() ,
,
а![]() ,
,
получаем
![]()
Так
как плотность газа
![]() ,
,
где
m
– масса газа; V
– его объём; N
– число молекул газа, уравнение (1) можно
записать в виде
![]()
или
![]() .
.
Подставляя это выражение в формулу (2),
находим искомую среднюю арифметическую
скорость:
![]()
Ответ:
<υ˃=545
м/с.
Пример
3.5. Найти относительное
число газа, скорость которого отличается
не более чем на δη = 1% значения средней
квадратичной скорости.
Дано:
δη = 1%.
Найти:
![]()
Решение В распределении
Максвелла
![]()
подставим
значение
![]() ;
;
δυ = υквδη.
Относительное
число молекул будет
![]()
Ответ:
![]()
Пример
3.6. При какой температуре
газа число молекул со скоростями в
заданном интервале υ, υ + dυ будет
максимальной? Масса каждой молекулы m.
Решение
Для
нахождения искомой температуры необходимо
исследовать функцию распределения
Максвелла на экстремум
![]() .
.
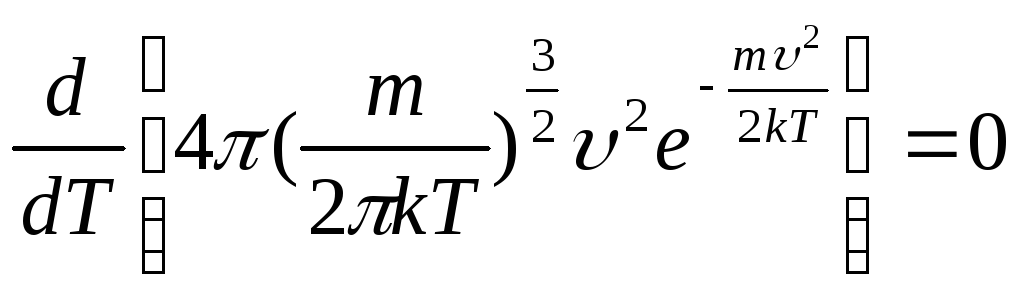
![]() .
.
Пример
3.7. Вычислить наиболее
вероятную, среднюю и среднюю квадратичную
скорости молекул идеального газа, у
которого при нормальном атмосферном
давлении плотность ρ = 1кг/м3.
Решение
Умножив числитель и знаменатель
в подкоренных выражениях (3.4) на число
Авогадро Nа,
получим следующие формулы для скоростей:
![]()
![]()
![]() .
.
Запишем уравнение Менделеева-Клапейрона,
введя в него плотность
ΡRT = MP
Определим отсюда величину
![]() и, подставив её в выражения, определяющие
и, подставив её в выражения, определяющие
скорость молекул, получим:
![]()
![]()
![]()
Пример
3.4. Идеальный газ с
молярной массой M находится в однородном
поле тяжести, ускорение свободного
падения в котором g. Найти давление газа
как функцию высоты h, если при h = 0 давление
Р = Р0,
а температура меняется с высотой как T
= T0(1
– α·h), где α – положительная постоянная.
Решение
При
увеличении высоты на бесконечно малую
величину давление получает приращение
dP = – ρgdh, где ρ – плотность газа. Знак
минус появился, так как с увеличением
высоты давление уменьшилось.
Поскольку рассматривается идеальный
газ, плотность ρ может быть найдена из
уравнения Mенделеева-Клапейрона:
![]()
Подставим значение плотности
ρ и температуры Т, получим разделяя
переменные:
![]()
Интегрируя это выражение, находим
зависимость давления газа от высоты h:
![]()
Так
как при h = 0 Р = Р0
получаем значение постоянной интегрирования
С = Р0.
Окончательно функция Р( h ) имеет вид
![]()
Необходимо отметить, что, так
как давление является величиной
положительной, полученная формула
справедлива для высот
![]() .
.
Пример.
Французский
физик Ж.Перрен, наблюдал под микроскопом
изменение концентрации взвешенных в
воде (ρ=1г/см3)
шариков гуммигута (ρ 1=1,25г/см3)
с изменением высоты, экспериментально
определил постоянную Авогадро. Определите
это значение, если температура взвеси
Т=298К, радиус шариков =0,21 мкм, а при
расстоянии между двумя слоями Δh=30мкм
число шариков гуммигута в одном слое в
два раза больше, чем в другом.
Дано:
ρ=1г/см3=1000кг/м3;
ρ=1,25 г/см3=1250кг/м3;
Т=280 К; r=0,21мкм=0,21∙10-6
м; Δh=30мкм=3∙10-5
м;
![]() .
.
Найти:
NA.
Решение.
Барометрическую
формулу
![]() ,
,
Используя
уравнение состояния P=nkT,
можно преобразовать для высот h1
и h2
к виду
![]() и
и
![]() ,
,
где
n0,
n1
и n2–
соответственно концентрация молекул
на высоте h0,
h1
и h2;
М – молярная масса; g-
ускорение свободного падения; R-
молярная газовая постоянная.
Тогда
 .
.
(1)
Прологарифмировав
выражение (1), получим
![]() (2)
(2)
Масса
частицы
![]() ;
;
m=ρV=ρ![]() πr3.
πr3.
Подставив эти формулы в (2) и учитывая
поправку на закон Архимеда, получим

Откуда
искомое выражение для постоянной
Авогадро

Ответ:
NA=6,02∙1023моль-1.
Пример.
Какова
температура Т азота, если средняя длина
свободного пробега <ℓ˃ молекул азота
при давлении Р=8кПа составляет 1мкм.
Эффективный диаметр молекул азота
d=0,38нм.
.
Дано:
<ℓ˃
=1мкм=1∙10-6
м;
Р=8кПа=8∙103
Па;
d=0,38нм=0,38∙10-9м;
Найти:
Т.
Решение.
Согласно
уравнению состояния идеального газа
P=nkT,
где
n
– концентрация молекул; k
– постоянная Больцмана.
Средняя
длина свободного пробега молекул газа
![]() ,
,
откуда
![]() .
.
Подставив эту формулу в выражение (1),
найдём искомую температуру азота
![]()
Ответ:
Т=372 К.
Пример.
При
температуре Т=280 К и некотором давлении
средняя длина <ℓ1˃
свободного
пробега молекул равна 0,1 мкм. Определите
среднее число <z2˃
столкновений
молекул в 1с, если давление в сосуде
уменьшить до 0,02 первоначального давления.
Температуру считать постоянной, а
эффективный диаметр молекулы кислорода
принять равным 0,36нм .
Дано:
Т=280 К; <ℓ1˃
=0,1мкм=0,1∙10-6
м;
М=32∙10-3
кг/моль;
![]() ;
;
d=0,36нм=0,36∙10-9м;
Найти:
<z2˃.
Решение.
Среднее число <z2˃
столкновений молекулы в 1с при конечном
давлении определяется отношением
средней скорости <υ˃.
молекулы к средней длине её свободного
пробега <ℓ2˃.
при том же давлении:
![]() ,
,
(1)
где
средняя скорость молекул определяется
по формуле
![]() (2)
(2)
где
R
– молярная газовая постоянная; М –
молярная масса вещества.
Из
формул
![]() иP=nkT
иP=nkT
следует, что средняя длина свободного
пробега молекул обратно пропорциональна
давлению:
![]() ,
,
откуда
![]() .
.
Подставив это выражение в формулу (1) и
учитывая (2), получаем искомое среднее
число столкновений молекул в 1с:

Ответ:
<z2˃
= 8,61∙107с-1.
Пример.
Можно
ли считать вакуум 100мкПа высоким, если
он создан в колбе радиусом r=15
см, содержащей азот при 0ºС. Эффективный
диаметр молекулы азота d=0,38нм.
.
Дано:
P=100мкПа=10-4Па;
r
=15см=0,15
м;
T=273
К;
d=0,38нм=0,38∙10-9м.
Найти:
![]()
Решение.
Вакуум
можно считать высоким, если средняя
длина свободного пробега молекул газа
гораздо больше линейных размеров сосуда,
т.е. должно выполняться условие
![]() ˃˃2r
˃˃2r
Средняя
длина свободного пробега молекул газа
![]()
(учли
P=nkT).
Вычисляя,
получаем
![]() =58,8
=58,8
м, т.е 58,8 м ˃˃0,3 м.
Ответ:
да, вакуум высокий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
