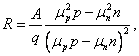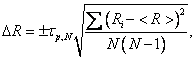Как найти концентрацию носителей тока

Лабораторная
работа № 405.

ОПРЕДЕЛЕНИЕ
КОНЦЕНТРАЦИИ НОСИТЕЛЕЙ ТОКА В ПОЛУПРОВОДНИКЕ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА

Цель работы:   1)
определение  постоянной Холла;

2)
определение концентрации носителей заряда.

Приборы и принадлежности:  установка для изучения эффекта Холла,
образец  (датчик Холла), источник
питания образца, цифровые вольтметры.

1.     
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Более века
тому назад (1879г.) американский физик Холл, поместив тонкую золотую
пластинку в магнитное поле, обнаружил, что при протекании по ней
электрического тока в направлении, поперечном вектору магнитной индукции и вектору
плотности тока, появляется электрическое поле. Этот эффект впоследствии был
назван эффектом Холла, а поперечное электрическое поле – полем Холла.

Эффект Холла
непосредственно связан с подвижностью и концентрацией носителей заряда, а
знак ЭДС Холла зависит от знака заряда. Поэтому эффект Холла широко применяется
при исследовании электрических свойств различных материалов и для контроля
качества полупроводниковых материалов, идущих на изготовление приборов.

Изучение
температурной зависимости эффекта Холла дает важную информацию о механизмах
рассеяния[1]
носителей заряда, о ширине запрещенной зоны материала и энергии ионизации различных
примесей.

Весьма
широкое применение эффект Холла находит в современной технике, являясь
основой для создания приборов различного назначения: магнитометров,
преобразователей постоянного тока в переменный и переменного в постоянный,
усилителей постоянного и переменного тока, микрофонов, приборов автоматики и
контроля, элементов вычислительной техники и многого другого.

Эффект Холла
является прямой демонстрацией действия силы Лоренца на движущиеся
электрические заряды.

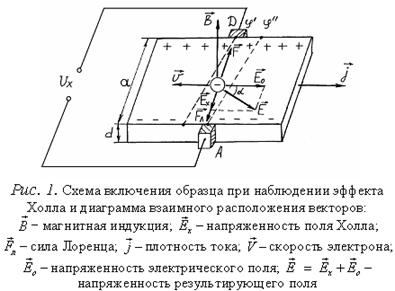
Рассмотрим
проводник (или полупроводник) в виде параллелепипеда шириной а и толщиной d, через
который протекает электрический ток плотностью, как показано на рис.1.
Предположим также, что в проводнике имеются носители заряда одного знака:
либо электроны, либо дырки. Проведем рассмотрение электронного проводника.
Выберем на гранях, параллельных току, точки А и D, лежащие на одной эквипотенциальной
поверхности[2]
. Напряжение между этими точками U_x=
0.

Поместим
проводник в магнитное поле, вектор индукции  которого
перпендикулярен направлению тока и боковым граням. Под действием силы Лоренца

электроны отклоняются к
передней (по рисунку) грани образца, заряжая ее отрицательно. На
противоположной грани образца накапливаются нескомпенсированные положительные
заряды. Это приводит к появлению электрического поля  

Смещение и разделение зарядов
будет продолжаться до тех пор, пока сила Лоренца не уравновесится силой  действующей на
электроны со стороны поля Холла

Сила,
действующая на электрон в условиях динамического равновесия, равна

или

Отсюда поле
Холла

Результирующее электрическое поле

повернется при этом на угол
Холла a,
определяемый выражением

относительно вектора  Соответственно
эквипотенциальные поверхности  и  тоже изменят свое
положение, и точки А и D в результате окажутся на разных эквипотенциальных поверхностях
и между ними появится напряжение (ЭДС Холла):

Так как

и                      то
есть         

то можно записать, что

и ЭДС Холла

где учтено, что

Величина  называется
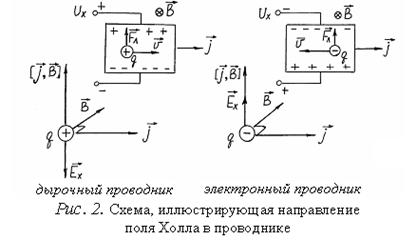
постоянной Холла. Знак постоянной Холла зависит от знака заряда и определяет
направление поля Холла (рис.2). У
электронных полупроводников (полупроводников n–типа) R имеет отрицательный знак, у дырочных (полупроводников р-типа) – положительный.

Таким образом,
определяя постоянную Холла и ее знак, можно определить концентрацию и знак
носителей тока в полупроводнике.

Рассмотренная
модель эффекта Холла применима для проводников (металлов) и вырожденных
полупроводников[3],
т.е. к проводникам, в которых имеются носители одного знака, обладающие
одинаковой скоростью  В невырожденных
полупроводниках скорость носителей подчиняется распределению Максвелла. Учет
этого обстоятельства приводит к формуле

где А – постоянная, зависящая от механизма рассеяния носителей.

В
полупроводниках со смешанной проводимостью перенос тока осуществляется
одновременно электронами и дырками. Так как они обладают противоположными по
знаку зарядами и под действием внешнего поля перемещаются в противоположные
стороны, то сила Лоренца  отклоняет их в одну
и ту же сторону. Поэтому при прочих равных условиях ЭДС Холла и постоянная
Холла у таких проводников меньше, чем у проводников с одним типом  носителей. Расчет показывает, что для таких
проводников

где n и р –
концентрации электронов и дырок, m_n и m_р
– их подвижности.

В
зависимости от того, какое из слагаемых числителя больше, знак Холла может
быть положительным или отрицательным. Для собственных полупроводников, у
которых концентрации электронов и дырок одинаковы, знак постоянной Холла
определяется знаком носителей, имеющих более высокую подвижность. Обычно
такими носителями являются электроны. Поэтому в примесном дырочном
полупроводнике (полупроводнике р-типа)
при повышении температуры и переходе к собственной проводимости постоянная
Холла проходит через нуль и меняет знак.

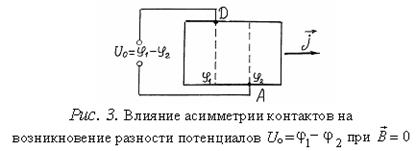
При
измерении постоянной Холла и напряжения Холла следует иметь ввиду, что между
холловскими электродами А и D имеется некоторая разность потенциалов U_о и в отсутствии магнитного поля  Эта разность потенциалов
обусловлена асимметрией контактов (на практике очень трудно расположить их на
одной эквипотенциальной поверхности, см.
рис.3), и термоэдс, связанной с неизотермичностью образца. Для исключения
влияния начальной разности потенциалов U_о на результаты
измерения можно воспользоваться следующим методическим приемом.

При
изменении направления магнитного поля на обратное знак ЭДС Холла U_х изменится, в то время как знак U_о остается прежним. При этом в зависимости от
соотношения величин U_х и U_о возможны два подхода к определению U_х .
Чаще встречается случай, когда  Тогда для различных
направлений  (условно
обозначенных ниже знаками + и – ) измеряемое напряжение U меняет
свой знак, и можно записать:

                  

                

Вычитая из
первого уравнения второе, получим

                                                                              (1)

Если U_х < U_о , тогда при различных направлениях  знак измеряемого
напряжения не изменяется и можно записать

                  

                  

Вычитая из
первого уравнения второе, получим

                                                                              (2)

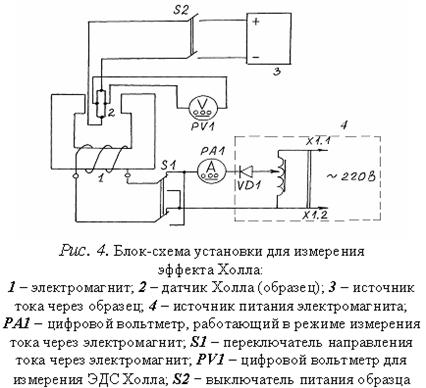
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ

Установка
состоит из трех основных частей: 1) – электромагнит со схемой питания; 2) –
схема питания датчика Холла; 3) – измерительная часть для определения знака и
величины ЭДС Холла.

3. ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА

РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1.     
Включить источник питания электромагнита 4.

2.  Включить  источник  тока 3 через образец.  Ток, протекающий через образец   I = 35 мА.

3. 
Провести измерения холловской разности потенциалов, меняя величину
тока I_э, текущего через электромагнит с шагом
примерно 0,02 А в интервале от 0,02
до 0,12 А. Величина тока
электромагнита регулируется лабораторным автотрансформатором, включенным в
цепь питания электромагнита и измеряется цифровым вольтметром РА1,
работающим в режиме измерения силы тока.

Измерения
холловской разности потенциалов при каждом установленном значении тока I, выполнять при двух направлениях тока (одному направлению
соответствует значение напряжения , другому – ). Направление тока изменяется переключателем S1, установленным
на лицевой панели прибора. Результаты измерений  и  занести в таблицу.

Таблица
результатов

№ п/п	IЭ А	мВ	мВ	мВ	В Тл	R м3/Кл	<R> м3/Кл	n, м–3	%	%
1 2 3 4 5 6

4. 
По формуле (1) или (2) рассчитать ЭДС Холла U_х  для каждого значения тока электромагнита I_э. Если при смене направления тока  I_э  знак противоположен знаку , то следует пользоваться формулой (1), в противном случае
– формулой (2).

5. 
По графику зависимости индукции магнитного поля от тока в обмотке
электромагнита, имеющегося на рабочем столе, или по формуле

где а и b – коэффициенты, определить
величину индукции магнитного поля В.

6. 
Определить значение постоянной Холла по формуле

где  d = 5,0×10^–5
м, I = 35,0×10^–3
A.

7.  Определить среднее значение постоянной
Холла.

8. Рассчитать концентрацию носителей
тока на основании соотношения

   где   е
= 1,6×10^–19
Кл.

9.     
Определить погрешность постоянной Холла методом
Стьюдента:

где  N – число измерений.

4. ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

1.     
Назвать основные части установки и объяснить их назначение.

2.  Объяснить, с какой целью в процессе
измерений изменяется направление тока, текущего через электромагнит.

3.  Пояснить, как в работе определяется
величина индукции магнитного поля?

4.  Привести порядок выполнения работы.

5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.     
Дать определение эффекта Холла.

2.     
Пояснить механизм возникновения ЭДС Холла в металлах.

3.     
Вывести формулу для определения поля Холла и ЭДС
Холла в металлах.

4.     
Указать, от каких причин зависит постоянная Холла в металлах.

5. Объяснить,
чем отличаются механизмы возникновения ЭДС Холла в металлах и полупроводниках?

6.  От каких величин зависит постоянная Холла в
полупроводниках?

Рекомендуемая
литература

1. Трофимова
Т.И. Курс физики. –
М.: Высш. шк, 2002. – 542 с.

2. Савельев
И.В. Курс общей физики. Кн.5. Квантовая оптика. Атомная физика. Физика
твердого тела. Физика атомного ядра и элементарных частиц. –
М.: АСТ, 2001. –
368с.

3. Детлаф
А.А., Яворский Б.М. Курс физики. – М.: Высш. шк., 2002. – 718 с.

Концентрация носителей тока и их подвижность

При Т=0^о
К в полупроводнике нет свободных
носителей заряда, все энергетические
уровни валентной зоны заняты электронами,
а энергетические уровни в зоне проводимости
свободны.

Будем рассматривать
процессы, в которых электроны располагаются
на нижних уровнях зоны проводимости,
на верхних уровнях валентной зоны и на
локальных уровнях примеси в запрещенной
зоне кристалла.

Вероятность
заполнения электроном энергетического
уровня определяется функцией Ферми

.
(1)

Вероятность того,
что энергетический уровень занят дыркой

.
(2)

Концентрация
свободных электронов в зоне проводимости

.

Концентрация дырок
в валентной зоне

.

Здесь

–
плотность разрешенных состояний в зоне;

–
число состояний в интервале энергии от

до

.

Начало отсчета –
потолок валентной зоны.

Поскольку

вероятности заполнения уровней зоны
проводимости

и заполнения валентных уровней << 1,
то в формулах (1) и (2) можно пренебречь 1
по сравнению с экспонентой. Тогда

,

.

Эти выражения
представляют собой функцию распределения
Больцмана и выражают распределение
частиц по энергиям.

При небольших
концентрациях свободных электронов и
дырок, с которыми мы имеем дело, в
полупроводнике эти частицы образуют
невырожденный электронный и дырочный
газ.

При повышении
температуры концентрация примесных
носителей тока быстро достигает
насыщения. Это означает, что практически
освобождаются все донорные или заполняются
электронами все акцепторные уровни. С
ростом температуры сказывается
собственная проводимость полупроводника,
обусловленная переходом электронов из
валентной зоны в зону проводимости.
Таким образом, при высоких температурах
проводимость полупроводника будет
складываться из примесной и собственной
проводимостей.

При низких
температурах преобладает примесная, а
при высоких – собственная проводимость.

Эффект Холла

Изучение свойств
полупроводников заключается в определении
знака и концентрации носителей заряда.
Наиболее распространенным методом
измерения концентрации и знака носителей
заряда в проводнике является метод
измерения напряжения Холла.

В

1880г. американский физик Э.Холл обнаружил
следующее явление: если
металлическую пластинку, вдоль которой
течет постоянный электрический ток,
поместить в перпендикулярное к ней
магнитное поле, то между параллельными
току и полю гранями возникнет разность
потенциалов.

Величина ее
определяется выражением:

,


(1)

где i
– сила тока;

– ширина пластины;

R
– постоянная Холла (величина ее для
различных металлов разная).

Эффект Холла
можно объяснить следующим образом:

Ток в пластине
обусловлен упорядоченным движением
электрических зарядов е.
обозначив через

–
число зарядов в единице объема, а через

– среднюю скорость их упорядоченного
движения, силу тока можно выразить как

.

Откуда

,

(2)

где

– площадь поперечного сечения пластины.

Если заряды е
положительны,
то направления

и

совпадают. Если – отрицательны, то – не
совпадают.

На заряд, движущийся
в магнитном поле с индукцией В действует
сила Лоренца, в нашем случае равная

.
Так как

перпендикулярна

и

,
то заряды будут описывать криволинейные
траектории (см. рис.) и создавать на одной
пластине избыток, а на другой – недостаток
зарядов. На сторонах пластины возникает
разность потенциалов. В результате
этого возникнет поперечное электрическое
поле, направленное сверху вниз, если
заряды положительны и снизу вверх –
если они отрицательны.

Так как, в случае
изображенном на рисунке, заряд е
отрицателен, то, сила, действующая на
заряд со стороны электрического поля
еЕ будет
направлена противоположно Е,
то есть в нашем случае вниз.

В случае положительного
заряда эта сила так же направлена
противоположно силе Лоренца.

В установившемся
состоянии должно соблюдаться равенство

или

.
Откуда

.

Подставив вместо

ее значение из формулы (2), получим

.

Если пластина
достаточно длинная и широкая, то
электрическое поле в ней можно считать
однородным. Тогда

.

Сравнивая эту
формулу с формулой (1). Получим

.

Как видно из этой
формулы, знак константы Холла совпадает
со знаком носителей тока е.
поэтому на
основании измерения константы Холла
для полупроводников можно судить о
характере проводимости (при электронной
проводимости R<0,
при дырочной R>0).

По измерению
постоянной Холла можно найти концентрацию
носителей тока (их число в единице
объема).

Определив из
опытных данных константу Холла, можно
вычислить концентрацию носителей заряда
в проводнике. Если для образца известно
значение R
и удельной электропроводности

,
то для носителей одного знака их
подвижность равна

.

Эффект Холла широко
используется в измерительной технике.
Миниатюрные датчики Холла, сделанные
из небольшой полупроводниковой пластинки
с двумя электродами для подводки тока
и с двумя другими- для измерения поперечной
разности потенциалов, применяются для
измерения таких величин, как сила тока
через датчик, индукция и напряженность
внешнего магнитного поля, ориентировка
датчика относительно этого поля и т.д.

Кроме этого, эффект
Холла используется во многих электро-
и радиотехнических установках для
модуляции электрических колебаний,
преобразования токов, записи звуков,
усиления постоянного и переменного
токов и т.д.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лабораторная работа №1

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ И ПОДВИЖНОСТИ НОСИТЕЛЕЙ ТОКА У
ПОЛУПРОВОДНИКОВ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА

ЦЕЛЬ РАБОТЫ

Эффект Холла относится к группе гальваномагнитных явлений
и заключается в том, что под действием магнитного поля, перпен-дикулярного к
электрическому току, электроны в материале откло-няются перпендикулярно как
направлению электрического тока, так и магнитного поля. С помощью эффекта Холла
стало возмож-ным понять суть процессов проводимости в полупроводниках и
провести грань между полупроводниками и другими типами плохо проводящих
материалов. Это обусловлено тем, что измерение ЭДС (разности потенциалов)
Холла, возникающей в материале перпен-дикулярно направлению электрического тока
и внешнего магнит-ного поля, дает возможность непосредственно определить концен-трацию
и знак носителей заряда. Последнее позволяет определить принадлежность
материала к тому или иному типу полупровод-ников (p или n–типа). Измерения эффекта Холла дают возможность отделить
случай ионной проводимости от случая электронной про-водимости. Наличие эффекта
Холла в проводниках и полупрово-дниках свидетельствует об электронном характере
проводимости. С помощью эффекта Холла возможно получить данные и о под-вижности
носителей заряда (так называемая «холловская» подвиж-ность). Таким образом,
эффект Холла – один из наиболее эффек-тивных методов исследования
электрических свойств полупровод-никовых материалов.

Целью работы является
изучение зависимости ЭДС Холла в по–лупроводниковом образце
от величины магнитного поля и опреде–ление концентрации
носителей заряда и некоторых других пара–метров.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

Наблюдение эффекта Холла сводится к измерению поперечной ЭДС, возникающей между узкими сторонами пластинки под
дейст-вием магнитного поля. По сути это внешнее напряжение, необ-ходимое для
того, чтобы электрический ток был направлен точно по оси, например, вдоль длины
образца. Пусть образец имеет форму прямоугольной пластинки длиной , шириной , толщиной
 (рис. 1).

Если вдоль длины образца (ось )
пропустить электрический ток , вдоль оси  приложить магнитное поле , то в направ-лении, перпендикулярном  и  (ось ), возникает электрическое поле,
называемое полем Холла с напряженностью .

На практике, как правило, поле Холла характеризуют
разностью потенциалов, которую измеряют между симметричными точками С и D
на боковых поверхностях образца.

Эта разность потенциалов называется холловской разностью
по-тенциалов  или ЭДС Холла. В классической теории
проводи-мости эффект Холла объясняется тем, что в магнитном поле на движущиеся
электрические заряды действует сила Лоренца, вели-чина и направление которой
определяется векторным уравнением:

,                                        (1)

где  – индукция магнитного
поля,

 – дрейфовая скорость движения
зарядов,

 – заряд носителей тока с учетом знака, «» –
для ды-рочной проводимости, «» – для электронной
проводимости.

Таким образом, дрейф электронов будет иметь составляющую
не только по оси , но и по оси . При этом дрейф электронов вдоль оси  будет продолжаться до тех пор, пока
возникающее электри-ческое поле  не уравновесит силу
Лоренца.

Электрическое поле Холла

                                          (2)

связано с холловской разностью потенциалов  следующим образом:

                             (3)

Сила тока, протекающего через единицу поверхности
образца, т.е. плотность тока, равна:

,                                         
 (4)

где  – число носителей тока в единице
объема образца (кон-центрация носителей тока), то сила тока

,                                      (5)

что позволяет записать:

                                         (6)

и

                                     
 (7)

Таким образом, ЭДС Холла пропорциональна силе тока через
образец  и обратно пропорциональна толщине образца
.

Экспериментальное определение ЭДС Холла проводят на образ-це
с заданной толщиной  при фиксированном токе через
образец. Формула (7) может быть записана в виде:

,                                       
(8)

где
коэффициент пропорциональности

                                              
(9)

является характеристикой изучаемого вещества и называется
коэффициентом Холла или постоянной Холла. Из уравнения (9) видно, что
коэффициент Холла обратно пропорционален концен-трации носителей заряда и его
знак совпадает со знаком носителя заряда. Измеряя в ходе эксперимента разность
потенциалов , индукцию магнитного поля , ток  и толщину
образца , можно, исходя из формулы (8), вычислить
постоянную Холла:

                                      
(10)

Рассмотрим далее, как меняется знак  в зависимости от зна-ка носителей заряда.
На рис.2 проводящая пластина изображена в плоскости листа, магнитное поле  направлено к нам, перпенди-кулярно
листу, ток  течет по стрелке.

     
а)                                                       
б)

Если носители тока – электроны, то направление их
дрейфовой скорости будет противоположно направлению тока. При таком
нап-равлении скорости в указанном магнитном поле на электрон будет действовать
сила Лоренца, направленная вниз. Верхняя грань про-водящей пластины должна
заряжаться положительно, а нижняя – отрицательно.

На рис.2б видно, что в случае положительных носителей заряда (при том же
направлении тока) меняется направление дрейфовой скорости зарядов, а
направление силы Лоренца остается той же, т.е. в этом случае вниз будут
отклоняться положительные заряды. Именно это и позволяет экспериментально
определить знак носи-телей заряда в проводящей пластине. Направление поля Холла
за-висит от знака носителей заряда. В нашем случае в полупро-водниковой
пластине -типа поле Холла направлено вверх, а в
случае полупроводника -типа – вниз. Таким образом, по
знаку холловской разницы потенциалов определяется знак постоянной Холла и,
соответственно, знак носителей заряда.

Теперь, исходя из формулы (9), можно вычислить
концентрацию носителей заряда в полупроводнике

,                                           
(11)

где  Кл – заряд электрона.

Рассмотренный эффект Холла, причиной которого является
действие силы Лоренца на движущиеся в магнитном поле заряды, называется
классическим эффектом Холла.

Мы будем изучать эффект Холла в полупроводниках, поскольку в них эффект
Холла имеет в основном классическую природу, и, следовательно, для его описания
справедливо выражение (9). Вы-ражение (9) для классической постоянной Холла
получено в пред-положении, что все носители тока имеют одинаковую дрейфовую
скорость движения , которая не изменяется при
движении носи-телей заряда в веществе. В действительности, необходимо учиты-вать
механизм рассеяния носителей заряда в твердом теле, что не-избежно приведет к
уточнению значения постоянной Холла. В об-щем случае  определяется
следующим выражением:

 ,                                      
(12)

где  –Холл-фактор.

С помощью Холл-фактора учитываются разные механизмы рас-сеяния
носителей заряда. При рассеянии на тепловых колебаниях решетки расчет дает
значение . Это случай собственных полупроводников и
полупроводников, имеющих носители заряда одного знака. В случае вырожденных
полупроводников и металлов , а при
преимущественном рассеянии на ионах примеси ,.
Таким образом, в чистых полупроводниках с собст-венной проводимостью
преобладает рассеяние на колебаниях ре-шетки (например, в германии и кремнии
при высоких и комнатных температурах), а для постоянной Холла получается
выражение

                                      
(13)

Следует обратить внимание на то, что концентрация
носителей заряда (как положительных –, так и отрицательных –
) сильно зависит в полупроводниках от
температуры. Следовательно, и пос-тоянная Холла также зависит от температуры. В
области собствен-ной проводимости  уменьшается по модулю
с ростом темпера-туры.

При экспериментальном определении  следует
обратить внимание на то, что наряду с эффектом Холла наблюдаются также
некоторые другие эффекты: гальваномагнитный, термомагнитный эффекты и др. Для
исключения влияния побочных эффектов ис-пользуют свойство четности этих
эффектов, т.е. их независимость от направления магнитного поля. Между тем
эффект Холла, явля-ясь нечетным эффектом, меняет свой знак при изменении направ-ления
магнитного поля.

Для того чтобы исключить побочные эффекты и определить ис-тинное
значение , (для определения концентрации носителей
заряда), напряжение между холловскими контактами измеряют при двух направлениях
магнитного поля. Действительно, пусть при вы-бранном направлении поля напряжение
между холловскими кон-тактами ; при изменении
направления поля на про-тивоположное напряжение .
Отсюда:

                                  (14)

Таким образом, , обусловленное побочными
четными эф-фектами, исключено.

Если наряду с постоянной Холла определить удельное сопро-тивление
полупроводника, то можно вычислить еще такую важную характеристику, как
подвижность носителей заряда.

Подвижностью носителей заряда  называется
дрейфовая ско-рость носителей заряда, которую они приобретают в электрическом
поле с напряженностью 1 В/м.

Очевидно, что если носители заряда движутся в поле с
напря-женностью , то их дрейфовая скорость:

.                                        
(15)

Если концентрация носителей заряда – , заряд – ,
то плот-ность электрического тока через образец равна

.                                  
(16)

По закону Ома

,                                           
(17)

где  – удельная
электропроводность вещества (проводимость), которая согласно (16) и (17)
выражается через подвижность форму-лой:

,                                         
(18)

тогда удельное электрическое сопротивление:

 ,                                      
(19)

откуда:

                                         (20)

С учетом выражения (13) для постоянной Холла (), подвиж-ность носителей заряда
выражается следующим образом:

                                        
(21)

Подвижность, которая определяется с помощью эффекта Холла,
называется «холловской» подвижностью носителей заряда, в отли-чие от дрейфовой
подвижности. В области собственной проводи-мости ()
обычно подвижность электронов () больше подвиж-ности
дырок (), поэтому в собственных полупроводниках .

Если же ,
то  и .
Это означает, что отклоняе-мые в одну и ту же сторону электроны и дырки не
создают поля Холла (их заряды компенсируют друг друга, и поле не возникает). В
случае, когда  и , знак  определяется знаком но-сителей заряда,
которые имеют большую подвижность.

Для определения удельного электрического сопротивления изу-чаемого
полупроводника измеряют электрическое сопротивление между двумя контактами (А и
В на рис.1), расположенными на длинной поверхности образца на расстоянии . С этой целью про-пускают электрический
ток  вдоль длины образца и измеряют па-дение
напряжения  между указанными контактами. Тогда удель-ное
сопротивление вычисляется по формуле:

 ,

где  – поперечное сечение
образца.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Включить установку. Дать прогреться приборам 10 минут.

2. С помощью регулятора «Установка тока датчика Холла»
уста-новить ток датчика 0,5–1,5 мА (по указанию преподавателя).

3. Произвести установку нуля микровольтметра. Для этого:

– установить переключатель S1 в положение «2», при этом
цепь питания соленоида разрывается, то есть ток соленоида равен нулю (убедиться
в этом по показанию прибора).

– с помощью регулятора микровольтметра «Установка нуля»
уста-новить нуль микровольтметра, измеряющего ЭДС Холла (при этом возможен
дрейф младшего разряда прибора).

4. Перевести переключатель S1 в положение «1», установить ток соленоида
2,0–2,5 мА.

5. Измерить ЭДС Холла с помощью микровольтметра. Результат измерения  записать в таблицу 1.

6. Перевести переключатель S1 в положение «3», при этом ток потечет в
противоположном направлении. Вновь произвести изме-рение ЭДС Холла. Результат
измерения  записать в таблицу 1.

Таблица 1

№	1	2	3	4	5	6	7	8
I соленоида, мA
, мкВ
, мкВ
, мкВ

Примечание:  – значения ЭДС Холла для противоположно
направленных токов соленоида.

Величина  вычисляется по формуле (14).

7. Увеличить ток через соленоид на 1,5–2,0 мА и произвести из-мерение
ЭДС Холла по пунктам 5,6. Всего произвести 8–10 изме-рений ЭДС Холла,
увеличивая при каждом новом измерении ток через соленоид на 1,5–2,0 мА.
Последнее измерение произвести при токе соленоида 10–15 мА.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Построить график зависимости ЭДС Холла от тока соленоида и провести
по экспериментальным точкам прямую линию, выража-ющую зависимость:

,                                       (22)

учитывая, что точка (0,0) является результатом измерений, пря-мая должна
проходить через начало координат.

2. Вычислить из графика постоянную :

,                                         
(23)

где  – тангенс угла наклона прямой на графике.

3. Вычислить постоянную Холла по формуле:

 ,                                      
(24)

где  – толщина германиевой пластинки в датчике;

 Гн/м – магнитная постоянная;

 – число витков на единицу длины соленоида;

 – ток датчика Холла.

Для Л.Р.№ 421, 422:     вит/м;      мм.

Для Л.Р.№ 423:             вит/м;      мм.

4. По формулам (11) и (13) вычислить концентрацию
носителей за-ряда в полупроводнике германия.

5. Вычислить по формуле (13) концентрацию носителей
заряда и по формуле (21) подвижность носителей заряда для кремния – типа (примесь – фосфор) с удельным
сопротивлением   и
известным значением постоянной Холла   и для образца кремния  – типа (примесь – бор) с удельным
сопротив-лением  и .

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чём состоит эффект Холла?

2. Какова природа носителей тока
в полупроводниках?

3. Как создаются полупроводники –типа и –типа?

4. Что такое дрейфовая скорость
носителей тока?

5. Как определяется физическая
величина, называемая «подвиж-ность носителей тока»?

6. Что такое собственная
проводимость и примесная проводи-мость полупроводников?

7. Коэффициент Холла у
полупроводников на несколько поряд-ков больше, чем у металлов. Чем это
объясняется?

8. При измерении эффекта Холла в
некотором полупроводнике оказалось, что полярность холловской разности
потенциалов про-тивоположна той, которая наблюдалась у медной пластинки. Как
это можно объяснить?

9. Можно ли по измеренной
постоянной Холла (не имея другой информации о данном образце) определить концентрацию
носи-телей тока в примесном полупроводнике?

10. В чём состоит главная причина
того, что электрическая про-водимость металлов на несколько порядков больше,
чем у полупро-водников?

11. В некотором образце измерили
холловскую разность потен-циалов U_холл при токе через
образец, равном I. Как изменится U_холл,
если образец по ширине d
(см. рис.1) уменьшить вдвое, а плот-ность тока в образце оставить прежней?

12. Как изменится холловская
разность потенциалов U_холл, если толщину образца уменьшить
вдвое, а плотность тока оставить прежней?

13. Как изменится холловская
разность потенциалов U_холл, если все геометрические размеры
образца (длина, ширина, толщина) уменьшить вдвое, а ток через образец оставить
прежним?

14. Наблюдается ли эффект Холла в
собственных полупроводни-ках?

15. Зависит ли эффект Холла от
температуры?

16. В аналоговых ЭВМ эффект Холла
используется для умно-жения двух сигналов. На вход устройства подаются два тока
I₁ и I₂, а на выходе получается сигнал,
пропорциональный произведению токов: (I₁·I₂).
Как это можно сделать, используя эффект Холла?

17. Чувствительность датчиков Холла »0,1 В/Тл. Можно ли с
помощью датчика Холла измерить индукцию магнитного поля Зем-ли?

18. Почему для измерения эффекта
Холла используется изме-рение ЭДС Холла, а не тока?

19. При установке датчика Холла
внутрь соленоида датчик слу-чайно сместился и плоскость пластинки оказалась
наклонённой к оси соленоида на угол 70°.Как это скажется на измерении
ЭДС Холла?

20. При установке датчика Холла
внутрь соленоида датчик слу-чайно сместился и оказался точно на краю соленоида.
Как это ска-жется на измерении ЭДС Холла?

21. При увеличении тока через
датчик пропорционально току увеличивается ЭДС Холла. Сохраняется ли эта
зависимость при большом токе?

22. Чем ограничивается увеличение
тока через датчик Холла?

23. Как исказятся результаты
измерений, если ток в датчике Холла превысит максимальное значение, указанное в
паспорте на датчик?

24. Как должна быть установлена
поверхность пластины дат-чика Холла относительно оси соленоида?

25. Напряжение Холла при одном и
том же значении тока соле-ноида измеряется дважды: при одном направлении тока и
при из-менении тока на противоположное. Зачем это нужно?

26. Датчик Холла не выдаёт ЭДС,
но все электрические кон-такты в порядке. В чём может быть причина
неисправности и как её устранить?

27. Что можно сделать для
увеличения чувствительности при-обретённого (т.е. уже изготовленного) датчика
Холла?

28. В паспорте на один из типов
датчиков Холла (ДХГ–2) указан интервал температур, в котором может работать
датчик. Минимальная температура для этого датчика – минус 60°. Чем объясняется такое
ограничение температуры?

29. Будет ли наблюдаться эффект
Холла у датчика ДХГ-2 (см. предыдущий вопрос) при температуре ниже –60°.

30. При подключении датчика Холла
были перепутаны кон-такты: к контактам для пропускания тока подключили
измеритель ЭДС Холла, а контактом, предназначенным для измерения ЭДС,
подключили источник тока. Будет ли наблюдаться эффект Холла в этом случае?